MRC/Tutorials/Frame transformations: Difference between revisions
No edit summary Tag: 2017 source edit |
No edit summary Tag: 2017 source edit |
||
| Line 1: | Line 1: | ||
We have the position of objects in a world model and we have the position of our robot in the world model, but what is the position of the object with respect to our robot. | We have the position of objects in a world model and we have the position of our robot in the world model, but what is the position of the object with respect to our robot. | ||
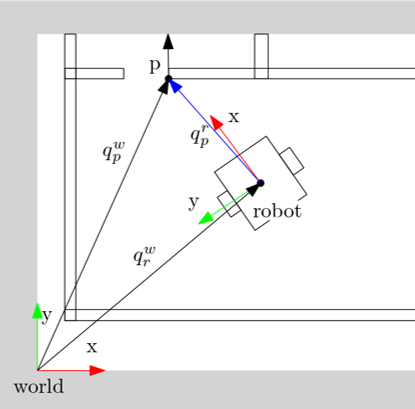
We can make explicit in which frames positions are expressed with a superscript. This helps keep track of things and prevents errors due to mixing of frames. For example a pose | We can make explicit in which frames positions are expressed with a superscript. This helps keep track of things and prevents errors due to mixing of frames. For example a pose <math>p</math> expressed in world frame <math>w</math> can be denoted as | ||
:<math> q^w_p = \begin{bmatrix} | :<math> q^w_p = \begin{bmatrix} | ||
| Line 9: | Line 9: | ||
\end{bmatrix} </math> | \end{bmatrix} </math> | ||
where we use | where we use <math>q</math> to denote a 2D pose. <math>\theta_{p/w}</math> denotes the angle between frames <math>p</math> and <math>w</math>. Angles are not dependent on the frame in which they are expressed, hence they don't have a superscript. However it is still important to note which two objects are being compared. | ||
[[File:frame_conventions.png]] | [[File:frame_conventions.png]] | ||
We can transform a pose p in robot frame r to a pose in | We can transform a pose <math>p</math> in robot frame <math>r</math> to a pose in world frame <math>w</math> using transformation | ||
:<math> \begin{bmatrix} | :<math> \begin{bmatrix} | ||
| Line 31: | Line 31: | ||
:<math> \theta_{p/w} = \theta_{p/r} + \theta_{r/w} </math> | :<math> \theta_{p/w} = \theta_{p/r} + \theta_{r/w} </math> | ||
Or the inverse. We can transfrom a pose given in | Or the inverse. We can transfrom a pose given in world frame into a pose given in robot frame using transformation | ||
:<math> \begin{bmatrix} | :<math> \begin{bmatrix} | ||
Revision as of 15:49, 25 March 2025
We have the position of objects in a world model and we have the position of our robot in the world model, but what is the position of the object with respect to our robot.
We can make explicit in which frames positions are expressed with a superscript. This helps keep track of things and prevents errors due to mixing of frames. For example a pose [math]\displaystyle{ p }[/math] expressed in world frame [math]\displaystyle{ w }[/math] can be denoted as
- [math]\displaystyle{ q^w_p = \begin{bmatrix} x^w_p \\ y^w_p \\ \theta_{p/w} \end{bmatrix} }[/math]
where we use [math]\displaystyle{ q }[/math] to denote a 2D pose. [math]\displaystyle{ \theta_{p/w} }[/math] denotes the angle between frames [math]\displaystyle{ p }[/math] and [math]\displaystyle{ w }[/math]. Angles are not dependent on the frame in which they are expressed, hence they don't have a superscript. However it is still important to note which two objects are being compared.
We can transform a pose [math]\displaystyle{ p }[/math] in robot frame [math]\displaystyle{ r }[/math] to a pose in world frame [math]\displaystyle{ w }[/math] using transformation
- [math]\displaystyle{ \begin{bmatrix} x^w_p \\ y^w_p \end{bmatrix} = \begin{bmatrix} cos(\theta_{r/w}) & -sin(\theta_{r/w}) \\ sin(\theta_{r/w}) & cos(\theta_{r/w}) \end{bmatrix} \begin{bmatrix} x^r_p \\ y^r_p \end{bmatrix} + \begin{bmatrix} x^w_r \\ y^w_r \end{bmatrix} }[/math]
- [math]\displaystyle{ \theta_{p/w} = \theta_{p/r} + \theta_{r/w} }[/math]
Or the inverse. We can transfrom a pose given in world frame into a pose given in robot frame using transformation
- [math]\displaystyle{ \begin{bmatrix} x^r_p \\ y^r_p \end{bmatrix} = \begin{bmatrix} cos(\theta_{r/w}) & sin(\theta_{r/w}) \\ -sin(\theta_{r/w}) & cos(\theta_{r/w}) \end{bmatrix} \begin{bmatrix} x^w_p - x^w_r\\ y^w_p - y^w_r \end{bmatrix} }[/math]
- [math]\displaystyle{ \theta_{p/r} = \theta_{p/w} - \theta_{r/w} }[/math]