MRC/Tutorials/Frame transformations

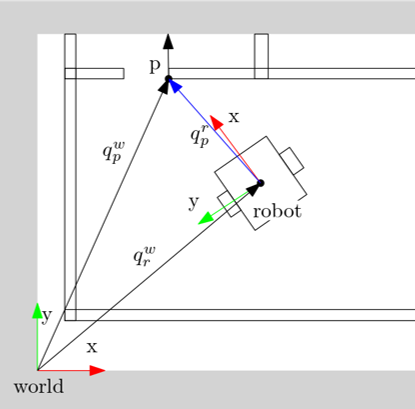
We have the position of objects in a world model and we have the position of our robot in the world model, but what is the position of the object with respect to our robot.

We can make explicit in which frames positions are expressed with a superscript. This helps keep track of things and prevents errors due to mixing of frames. For example a pose [math]\displaystyle{ p }[/math] expressed in world frame [math]\displaystyle{ w }[/math] can be denoted as

[math]\displaystyle{ q^w_p = \begin{bmatrix} x^w_p \\ y^w_p \\ \theta_{p/w} \end{bmatrix} }[/math]

where we use [math]\displaystyle{ q }[/math] to denote a 2D pose. [math]\displaystyle{ \theta_{p/w} }[/math] denotes the angle between frames [math]\displaystyle{ p }[/math] and [math]\displaystyle{ w }[/math]. Angles are not dependent on the frame in which they are expressed, hence they don't have a superscript. However it is still important to note which two objects are being compared.

In mobile robot control two frames will come up often, robot frame and map frame (or world frame). We will often need to convert from one frame to the other.

We can transform a pose [math]\displaystyle{ p }[/math] in robot frame [math]\displaystyle{ r }[/math] to a pose in world frame [math]\displaystyle{ w }[/math] using transformation

[math]\displaystyle{ \begin{bmatrix} x^w_p \\ y^w_p \end{bmatrix} = \begin{bmatrix} cos(\theta_{r/w}) & -sin(\theta_{r/w}) \\ sin(\theta_{r/w}) & cos(\theta_{r/w}) \end{bmatrix} \begin{bmatrix} x^r_p \\ y^r_p \end{bmatrix} + \begin{bmatrix} x^w_r \\ y^w_r \end{bmatrix} }[/math]

[math]\displaystyle{ \theta_{p/w} = \theta_{p/r} + \theta_{r/w} }[/math]

Or the inverse. We can transfrom a pose given in world frame into a pose given in robot frame using transformation

[math]\displaystyle{ \begin{bmatrix} x^r_p \\ y^r_p \end{bmatrix} = \begin{bmatrix} cos(\theta_{r/w}) & sin(\theta_{r/w}) \\ -sin(\theta_{r/w}) & cos(\theta_{r/w}) \end{bmatrix} \begin{bmatrix} x^w_p - x^w_r\\ y^w_p - y^w_r \end{bmatrix} }[/math]

[math]\displaystyle{ \theta_{p/r} = \theta_{p/w} - \theta_{r/w} }[/math]