MRC/Tutorials/Frame transformations: Difference between revisions
Jump to navigation
Jump to search
add frame transformation info |
add image Tag: 2017 source edit |
||
| Line 8: | Line 8: | ||
\theta_{p/w} | \theta_{p/w} | ||
\end{bmatrix} </math> | \end{bmatrix} </math> | ||
[[File:Frame_conventions.png]] | |||
We can transform a pose p in robot frame r to a pose in map frame m using transformation | We can transform a pose p in robot frame r to a pose in map frame m using transformation | ||
Revision as of 14:00, 25 March 2025
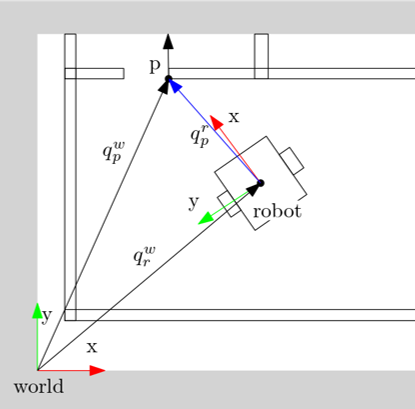
We have the position of objects in a world model and we have the position of our robot in the world model, but what is the position of the object with respect to our robot.
We can make explicit in which frames positions are expressed. This helps keep track of things and prevents errors due to mixing of frames.
- [math]\displaystyle{ q^2_p = \begin{bmatrix} x^w_p \\ y^w_p \\ \theta_{p/w} \end{bmatrix} }[/math]
We can transform a pose p in robot frame r to a pose in map frame m using transformation
- [math]\displaystyle{ \begin{bmatrix} x^w_p \\ y^w_p \end{bmatrix} = \begin{bmatrix} cos(\theta_{r/w}) & -sin(\theta_{r/w}) \\ sin(\theta_{r/w}) & cos(\theta_{r/w}) \end{bmatrix} \begin{bmatrix} x^r_p \\ y^r_p \end{bmatrix} + \begin{bmatrix} x^w_r \\ y^w_r \end{bmatrix} }[/math]
- [math]\displaystyle{ \theta_{p/w} = \theta_{p/r} + \theta_{r/w} }[/math]
Or the inverse. We can transfrom a pose given in map frame into a pose given in robot frame using transformation
- [math]\displaystyle{ \begin{bmatrix} x^r_p \\ y^r_p \end{bmatrix} = \begin{bmatrix} cos(\theta_{r/w}) & sin(\theta_{r/w}) \\ -sin(\theta_{r/w}) & cos(\theta_{r/w}) \end{bmatrix} \begin{bmatrix} x^w_p - x^w_r\\ y^w_p - y^w_r \end{bmatrix} }[/math]
- [math]\displaystyle{ \theta_{p/r} = \theta_{p/w} - \theta_{r/w} }[/math]