Ezra Abbo	1009342
K.A. van Akkerveken	1007960
L.J.H.W. Bastiaansen	1010973
Ibrahim Kurt	1017232
J.G.E.C Martens	1011778

Eindhoven,

'

Symbol	Variable	Unit	Abbreviation unit
$[math]\displaystyle{ h }[/math]$	Height of the robot	meter	$[math]\displaystyle{ m }[/math]$
$[math]\displaystyle{ r_{track} }[/math]$	Distance from center robot to tank tracks	meter	$[math]\displaystyle{ m }[/math]$
$[math]\displaystyle{ s }[/math]$	Distance	meter	$[math]\displaystyle{ m }[/math]$
$[math]\displaystyle{ t }[/math]$	Time	second	$[math]\displaystyle{ s }[/math]$
$[math]\displaystyle{ v }[/math]$	Velocity of the robot	meter per second	$[math]\displaystyle{ m/s }[/math]$
$[math]\displaystyle{ w }[/math]$	Width of the robot	meter	$[math]\displaystyle{ m }[/math]$
$[math]\displaystyle{ \alpha }[/math]$	Angle to which the robot is heading	degrees	$[math]\displaystyle{ \degree }[/math]$
$[math]\displaystyle{ \omega }[/math]$	Angular velocity	degrees per second	$[math]\displaystyle{ \degree / s }[/math]$

Introduction

Every year there are major innovations in the field of technology. Self-driving cars, reusable rockets and even face-recognition abilities of current smart-phones are some examples. Not all innovations, however, get the same amount of attention and some are thus less widely known. This report focuses on the improvement of a small and less impactfull technological piece of equipment, namely the window-cleaning robot. Window-cleaning robots are currently build for two main application domains, domestic use and professional use on big skyscrapers or flats. The advancements in the capabilities of these window-cleaning robots are still in the early stages. Nevertheless, there is already a range of window-cleaning robots available on the market, differing in size and performance. However, the existing window-cleaning robots for domestic use have all a major shortcoming in common: their movement is based on a simple, inefficient motion planning. This is mainly due to the thought of minimal gain and the aim for simplicity. Therefore, an optimized motion planning algorithm is developed in this project. This optimized algorithm will be applicable to the smaller sized window cleaning robots that are used for domestic applications. The design question is:

How should the main, currently used motion-planning algorithm for small sized window-cleaning robots for domestic use be improved such that it is more efficient in terms of cleaning speed, energy consumption and water consumption?

The answer to this question will be relevant for the users, window cleaning companies, since they can buy a set of window cleaning robots operating on this algorithm to improve their services and increase their revenue as an enterprise. Besides that, the developed algorithm will help the customers through better scheduling and faster clean ups and help society through advancement of planning-algorithms which may spark further improvements on the algorithms of motion planning robots.

The main scenario for which the motion planning is designed is a small window cleaning company that has multiple cleaning robots in its possession, with one employee who can move the cleaning robots from one window to another, allowing him to clean multiple windows simultaneously, thereby reducing the time it takes to clean all the windows in the building and reducing labor cost.

This report consists of six chapters, starting with a literature study on the capabilities of current window-cleaning robots and their motion planning algorithms. Followed by a systematic design process, including approach, user requirements, design choices, concepts, assumptions, robot specifications and a simulation model. In this model the performance of two innovative algorithms will be tested and compared to the current approach listed in the literature study. The results from the model will subsequently be thoroughly evaluated. At the end, a well-funded conclusion will be given.

State of the Art

Heren, check alsjeblieft de grammatica van dit stuk. Verder mis ik een duidelijke uitleg over het standaard algoritme en waarom het slecht is. In order to notably contribute to any technological development it is necessary to know the current state of the technology of that piece of technology. This section summarizes therefore a literature study performed on scientific articles regarding the subject of motion planning algorithms of window-cleaning robots, specifications of existing window-cleaning robots, potential user needs for window-cleaning robots and expectations of window-cleaning robots. First it is explained what the existing window-cleaning robots are capable of. Subsequently, it is explained why their motion planning algorithms are not optimal. When the reader is interested in more detailed information obtained during the literature studies, it is recommended to take a closer look at the summaries of all the articles which can be found ENKEL OP DE WIKI TE ZETTEN EN DAN NAAR DE WIKI TE VERWIJZEN, ANDERS WORDT HET VERSLAG WEL ERG LANG.

Window-cleaning Robots

Exacte dimensies zijn niet relevant, graag meer gedetailleerde info over hoe zo’n robotje precies werkt en gebruik witregels. Kijk naar alle artikelen aub, ik mis o.a. bijvoorbeeld info over hoe skyskraper robots zich bewegen over een gevel waar we best wel wat artikelen over hebben gelezen. Het lijkt alsof er alleen naar de eigen artikelen is gekeken. As mentioned in the introduction, window cleaning robots are currently on the market in the form of a domestic or professional robots. The most obvious difference between the two type robots is the size. Window cleaning robots which are build for domestic use are much smaller than professionally used skyscraper robots. WINDORO is the best known example of a domestic window cleaning robot, with dimensions of 200 x 200 x 50 mm. With these dimensions it is small enough to fit on almost every window in an ordinary house. An example of a professional robot is IPC Eagle’s HighRise505 which is 2908 x 930 x 2115 mm. A consequence of the size difference can also be seen in the performances of both types. The HighRise is able to clean surface area at a higher rate than the WINDORO. The main difference in behavior of domestic and professional robots is that domestic robots are only supposed to clean one window at a time and require to be manually transfered to a different window while most industrial robots are capable of cleaning an entire facade without human interaction.
There are other different features between window cleaning robots in general that can be considered, the water supply can be implemented through a depot or hose, movement is possible through tracks, external ropes or rails, energy through an battery or socket cable, cleaning through high pressure water beams, brushing or movement of a wipe. Some robot are equipped with sensors to measure dirt levels on the surfaces those robots pass and other sensors to better understand the environment the robot is working in.
These are some of the possible characteristics of current window cleaning robots regarding mechanical features. Besides all these differences in geometry the robots also differ in software. The way the robot moves over the window is called the motion planning of the robot. Motion planning is dependent on the mechanical possibilities of the robot in its environment, as well as the complexity of the algorithms it uses.

For this project the focus is on domestic window cleaning robots, more specifically the motion planning of these domestic robots. The set specification regarding the hardware will be explained in the upcoming chapters. Because the focus is put on the improvement of the motion algorithms, the current technological state of the abilities on the terrain of motion planing are analyzed in Section 2.2.

Motion planning algorithms

soms is de beschrijving van de algoritmes best wazig of juist erg uitgebreid. Verder zou ik iets meer ingaan op de robots voor domestic use aangezien dat voor ons het belangrijkst is. The literature study shows that there is already a wide variety of motion planning approaches possible, which differ between the types of window cleaning robots. As mentioned before, these approaches are fairly simple and inefficient. The most common approaches to the movement of the robots will be discussed in this section.
For professionally used cleaners the movements are mostly straightforward. They move in parallel lanes over the buildings façade from the top to the bottom of the building, as seen with the SkyScraper-I model citeSkyScraper-I
More advanced methods are also developed in the form of multi-robot systems or sensory adjusted movement. These multi-robot systems can be divided into so-called ’parent-robots’ and ’child-robots’. One parent-robot can transport n-number of child-robots to the designated site. Each robot can move only vertically or horizontally. The task of cleaning is performed by the child-robots that have modular facade maintenance tools. A variation of this also exist with a different system, which consist of horizontal and vertical moving robots. The horizontal robot carries out window cleaning work while moving along a horizontal (transom) rail. The vertical robot transports the horizontal robot to another level along a vertical rail. After cleaning a floor, the horizontal robot docks into the vertical robot where it is securely held in place with rail breaks. Then the vertical robot is transported up or down by a wire winch, making it able for the horizontal robot to clean another floor.
For the sensory robots, a number of built-in guide-type robots must move along predefined rails. They can measure the contamination level of the building’s surface using detection sensors and can adjust their movement speeds accordingly. Thus, moving slower at places with high contamination level creating more focused cleaning of the façade.
The domestically used robots move in simple ways as well. Most window cleaners start at the top of the window, moving down in horizontal lanes, also adjusting for the dripping of water down the window.
More advanced robots try to estimate the dimensions of the window by making ’smart movements’, followed by repeated movements to clean the windows surface. This can be done using vertical positions estimation units, which are similar to the system used in old computer mouses. Using a ball to track its movement relative to its starting point. On top of that, a control loop is used to keep track of the vertical displacement.This method prevents cleaning areas twice or cleaning them not at all. Further systems include remote control and different variations of the discussed motions.
A range of multiple coverage algorithms existing are shown in Figure [fig:tabel] in Appendix [sec:SumLitStudy].

Design Process

Approach

Prior to the development of the model, a literature study on currently available window cleaning robots was performed (see Chapter 2). This literature study motivated the idea to design an efficient motion planning algorithm for window cleaning robots.

The design process of the motion planning algorithm is divided into the following phases:

Analysis of the user, user requirements, preferences and constraints (section 3.2)
Conceptualization (section 3.4)
Choosing the solutions with the most potential
Modeling the motion planning algorithms by means of NetLogo (Chapter 4)
Refine the motion planning algorithms
Evaluation of the obtained results (Chapter 5)

Upon finishing each step the solutions or results are fed back and reflected with regard to the requirements, preferences and constraints defined in Section 3.2. This makes sure that the user stays central during the whole design process and undesirable results are excluded.

User requirements, preferences and constraints

As mentioned in Chapter 1, window cleaning companies are considered during this project. This makes the window washing companies the primary users in the design process. They can use window cleaning robots to improve their services. The considered scenario is that these companies are hired by private individuals (secondary users) to clean the windows of their houses or buildings. It is assumed that window cleaning companies own multiple of these robots that can be deployed on different windows and can so clean the windows simultaneously. The faster, cheaper and more efficient these robots can accomplish this, the more profit the company can make since the windows of more houses can be cleaned in the same time span. A major factor in accomplishing this purpose would be a motion planning algorithm that determines how to clean the windows of a house in a highly efficient way.

In order to develop such a motion planning algorithm, requirements, preferences and constraints should be made explicit. If one considers the view of the primary and secondary users, the window washing companies and private individuals respectively, the following requirements, preferences and constraints could be distinguished.

Requirements

The robot should at least inspect and clean every window once, regardless of the dirtiness of the window. In other words, even windows that are not dirty should be cleaned. This is a very reasonable requirement, because people who hire a window washing company expect that they will clean every window.
The window cleaning robot is not allowed to leave stripes due to the dripping of water or incomplete horizontal movements.
For window washing companies, speed in terms of surface area cleaned per unit of time is of major importance. The higher the rate at which the windows can be cleaned, the more profit can be made. The goal is to reach a speed of 125 $[math]\displaystyle{ m^2 / hr }[/math]$ , which is the highest of three popular commercially available window cleaning robots that are considered (see Appendix 2). This seems to be an acceptable requirement for the model.
The water consumption is another important aspect, since this has an influence on the speed of the cleaning process and also has a minor impact on the total cost of the cleaning job. All current window cleaning robots of the considered size of roughly 25 x 25 $[math]\displaystyle{ cm }[/math]$ do not have a water supply or tank, but use detergent instead. The innovative part of the model is therefore that a water supply in the form of a tank is included. This is similar to real window washers, because they also do not solely use detergent. The requirement for the water consumption is based on a bigger window cleaning robot (GEKKO Facade Robot ) which has a water consumption of approximately 1 $[math]\displaystyle{ L/min }[/math]$ . Because this bigger robot has a size of around 4 times the size of the considered cleaning robots, a requirement of maximum 0.25 $[math]\displaystyle{ L/min }[/math]$ seems suitable.
Due to the presence of the water tank, it is important that its volume is large enough to clean a window without requiring the employee to do a refill.
Energy consumption is the last relevant aspect, since this has an impact on the total cost of the cleaning job. The requirement for the energy consumption is also determined by averaging over the considered window cleaning robots: maximum 73.5 $[math]\displaystyle{ W }[/math]$ (see Appendix 2).
The battery capacity of the window-cleaning robot should be large enough to clean an entire window without requiring the employee to replace it during the cleaning job.

Preferences

The window should be made as clean as possible in a reasonable time span.
Speed in terms of surface area cleaned per unit should be as high as possible.
Water consumption should be as low as possible. This is important because of two reasons. First because it is not desired that the robot runs out of water. The second reason is that is has a influence on the total cost, but this is of course less important since the price of water is relatively low, and using soapy water is already better for the environment than using conventional detergents.
Energy consumption should be as low as possible.

Constraints

The robot should be able to clean rectangle windows with a dimensions between 0.5 x 0.5 $[math]\displaystyle{ m }[/math]$ and 4.0 x 4.0 $[math]\displaystyle{ m }[/math]$ . In this range most common windows will be covered.

Design choices

Before starting the modeling, an important choice needed to be made in order to construct a model of the motion planning. This considers the choice of the program that is used for modeling this algorithm. The program that was eventually chosen is NetLogo. There are several reasons for this particular choice of program. An important reason is that Netlogo makes it easy to create graphical output alongside the numerical simulation of the motion planning algorithm. This enables the visualization of the window cleaning robot using the programmed motion planning algorithm to clean a window. The visualization reduces the risk of incorrect programming of the movement patterns. Additionally, in NetLogo there is a predefined relation between agents, the so-called turtles, and the square sections of the underground over which they move, the so-called patches. This relation is of course particularly useful for modeling the cleaning of the window (the patches) by the robot (the agent) and the checking of the cleanliness of a section of the window by the robot. NetLogo also has the ability to create sliders for some of the parameters of the model. This makes it easy to test the motion planning algorithm in different environments (e.g. different dirt distributions or different window sizes). Furthermore, NetLogo is relatively easy to program and its program language is already known by the members of the group from a previous course.

Another choice was made about prototyping. At first there was the intention to create a real physical prototype by making use of a LEGO Mindstorms robot. Unfortunately, this was not viable. Making a robot from LEGO that moves in a programmable pattern on a flat surface is possible, but the problem lies with the color sensor that would be used to detect dirty places. Most current window cleaning robots have multiple dirt sensors in a line that detect whether dirt passes under that line. The LEGO Mindstorms robot would only have one color sensor, which means that it would constantly have to move the sensor perpendicular to the direction the vehicle is moving in order to check for dirt. This would result in a robot that moves at such a slow pace that practical experiments would be infeasible. Because of this, it was decided to stick to just the development of the model.

The concepts

Many discussions about what the most efficient motion planning algorithm would be, leaded to the selection of two algorithms which were eventually modeled in NetLogo together with the reference algorithm that is used by most of the state of the art window cleaning robots for domestic use (as discussed in Section 2.2). In this section, a rough explanation of the eventually chosen algorithms is given. This is done by introducing a step by step plan for the movement of window-cleaning robot. Besides that, it is indicated where the main gains of the algorithms lie with respect to the reference method.

Algorithm 1

The behavior that the window cleaning robot would have when using algorithm 1 can be divided in the following rough steps:

The window cleaning robot is placed at a random position on the window, facing in a random direction.
Due to gravity sensors, the robot knows where to find the upper side of the window, so it moves upwards till its force sensors detect that the upper edge is touched.
The robot turns and moves to the upper left corner until it detects the left edge of the window with its force sensors. During this movement the robot is already cleaning. When it reaches the upper left corner, it turns to face to the right.
The robot moves over a horizontal path and inspects and cleans this path. When the dirt detection sensors notice that a dirty spot remains, a reciprocating motion is initiated. This reciprocating motion is continued until the dirty spot is entirely clean or does not become any cleaner (more detailed explanation in Section 3.5.5).
The window cleaning robot moves on to the next dirty spot and the behavior above is repeated.
When the upper right corner of the window is detected with the force sensors (Section 3.5.2), the robot turns and wipes the first row another time to make sure no stripes will remain on the window surface. In this back-going stroke, the cleaning mechanism is not used since the stroke is already clean and does only require the motion of the squeegee.
When the first row is entirely clean, the robot makes a certain movement to go to the second row (more about that in Section 3.5.4).
The window cleaning robot turns and starts with the next horizontal path. The steps 4-7 are executed again. Note that the turning movement in the second horizontal path will take less time because the upper edge of the window is not an obstacle anymore.
This process is repeated until the window is cleaned entirely.

The main gain of this algorithm with respect to the standard method lies in the reciprocating movement. Due to this reciprocating motion, the robot does not have to travel large unnecessary distances any more to clean a spot of dirt that has remained. This reduces of course the time the window cleaning robot needs to fully clean a specific stroke of window. Another possible gain is found in the energy consumption. In the standard motion planning algorithm, the robot is continuously cleaning and thus continuously operating at maximum power. In the here considered algorithm however, the robot does not necessarily have to clean at already cleaned places so less energy is consumed since the friction of the cleaning pad is no longer conquering the vacuum which should be preserved. It is now obvious that the same goes for water consumption, because the reference algorithm consumes water continuously.

Algorithm 2

The behavior that the window cleaning robot should perform when using algorithm 2 can be divided in the following rough steps:

The robot is placed at a random position on the window.
The robot moves to the upper edge of the window.
The robot cleans the upper row of the window like in the default algorithm, and moves to the second row.
The robot cleans this row once, but keeps track of where any dirty spots are left.
It will turn at the end of the row, go back over all the dirty spots in the middle of the row, turn again and repeat this motion until all the dirty spots in the middle of the row are gone.
The robot cleans the entire row once again in order to get rid of any stripes, and continues to the next row.
The 3 steps above will be repeated until the robot reaches the bottom row, which will be cleaned like the top row.

The main advantage of this algorithm above the default algorithm is that, like algorithm 1 (section [subsec:algorithm1]), the robot can skip most of the already clean spots on the window when cleaning harder to clean dirty spots. However, unlike algorithm 1 the reciprocating motion goes over as many dirty spots as possible at once. This may be advantageous when there are large, harder to clean dirty spots in the middle of the window, since the robot does not have to continuously move backwards in order to check with its dirt sensors whether or not the dirty spot is cleaned. The dirt sensors will automatically move over the just cleaned spots since the robot turns at the end of the still to be cleaned part of the row. This means that this motion planning algorithm will be a more efficient cleaning tactic for the above mentioned dirt distribution.

Assumptions and simplifications

In order to make a model of the motion planning algorithms, a number of assumptions and simplifications needed to be made. One should keep in mind that making too much assumptions could result in an inaccurate model which is of little use for the user and for checking of the developed motion planning algorithms perform better. Therefore it is important to be careful when making simplifications or assumptions. This section explicitly describes the simplifications and assumptions that are made in the model.

The Window

In the model created with NetLogo, the window is modeled as a grid of patches. This means that the shape of window is assumed to be rectangular, which is appropriate for the domain of the considered window cleaning robots. In the model, a single patch represents an area of 50 x 50 $[math]\displaystyle{ mm }[/math]$ in reality. The height and width of the window is however restricted to a multiple of 250 $[math]\displaystyle{ mm }[/math]$ (the same dimension as the robot). This is done because modeling a multiple of 50 $[math]\displaystyle{ mm }[/math]$ is quite complex and would take too long to program. For the height of the window, this has to do with the fact that the robot then has to consider incomplete rows. Since both the standard motion planning algorithm and the developed algorithms have these simplifications and would both have the same problems in real life, they and their results can still reasonably be compared.

It is assumed that each of the above mentioned patches of the window will get a certain dirtiness value in the model. Patches with a higher dirtiness value will ask for more wiping motions of the window cleaning robot. To model realistic dirt, clusters of persistent dirt (thus with a higher value of dirtiness) are created, together with a more or less even distribution of dirt with a lower value of dirtiness on the rest of the window surface. In reality, the former type of dirt is comparable with for example bird droppings, while the latter can represent dust particles on the window. Besides that, all patches get a number that denotes how hard it is to clean each of them. This number will be taken into account when the dirt reduction that the robot causes when it moves over the patch is calculated. This hard to clean number is chosen from an exponential distribution for each patch. For a small number of patches, this will have the result that the dirtiness value is much harder to reduce than for the others. They thus require a huge amount of wiping motions before they are entirely clean. These little spots are comparable with a situation in reality were a dirty spot on the window could not be cleaned at all or is very hard to clean, for example stickers or scratches on the window. How the algorithms cope with these hard to clean spots will be discussed in section 3.5.5. More precise information about how the dirt distribution was eventually exactly modeled can be found in section 4.

Window Cleaning Robot

The robot is assumed to have a square shape and covers an area of 5 x 5 patches, which thus equals an area of 250 x 250 $[math]\displaystyle{ mm }[/math]$ . These dimensions are very similar to the current commercially available window cleaning systems such as the Hobot, Windoro and Winbot (see Appendix 2). Because this project considers the motion planning algorithms and not the particular geometry of the robot, the geometry of the robot needed to be set as fixed. Which means that the variables relating to this geometry are removed from the problem. The bottom side of the robot is divided in 5 x 5 squares, see Figure [fig:simplification robot].

[H]

The outermost left and right columns of the 5 x 5 grid consist of optical sensors to detect dirt and cleaning surface, also called a cleaning pad, respectively. A couple of important remarks regarding the latter should be made. First, there is assumed that the robot cleans the window without moving parts (e.g. rotating disks). Only the movement of the robot makes sure that the window surface is cleaned. Second, the cleaning pad is adjustable in height. This enables the robot to lift its cleaning pad while turning which will prevent the robot from drawing extra stripes on the window surface. Also, when the robot is moving over surface that is already clean, the cleaning pad is lifted in order to achieve less power consuming movement. This has to do with the fact that the normal force of the cleaning pad on the window does not counteract the vacuum any more. Besides optical sensors and cleaning surface, two crawler tracks are added in between these two outer columns which enable the window cleaning robot to move and turn over the window. The remaining white square in the middle of the simplified robot is the suction area, which makes sure that the robot will stick to the window.

The simplified window cleaning robot has, besides the dirt sensors, also a few other sensors, namely gravity and force sensors. Both sensors are not explicitly modeled, but do make up an important part of the model. For example, the existence of gravity sensors enables the robot to know what the upper and lower side of the window is. Force sensors, on the other hand, are mounted on each side of the robot. These sensors enable the robot to detect whether it hits one of the edges of the window.

At last, an important remark should be made about the abstraction of the rubber ring that is enclosing the robot, commonly referred to as the squeegee. In window cleaning robots, the squeegee has actually two functions. First, it is of course needed to wipe away the water that is supplied. Second, it is necessary for creating a vacuum to make sure that the robot sticks to the window. Because the squeegee is part of the outer edge of the window cleaning robot, and the outer edge is only a minor part of the robot, it is decided to abstract over the rubber ring that is functioning as squeegee.

This simplified layout of the window cleaning robot is derived from current window cleaning robots and therefore represents the reality sufficiently.

Water consumption, energy consumption and velocity

The window cleaning robot is supplied with water by means of a water tank, and the capacity of the water tank is supposed to be sufficient to be able to clean a window without interruptions.

There are a few decisions and assumptions that had to be made in order to model the water consumption. The water consumption of the robot for a time step is taken to be $[math]\displaystyle{ \frac{1}{8640} }[/math]$ $[math]\displaystyle{ L / s }[/math]$ . This specific value for the water consumption is determined by looking at the amount of water a window washer uses per hour, together with the cleaning speed in terms of area per hour. According to an experienced window washer, the average cleaning speed is is 50 $[math]\displaystyle{ m^2/hr }[/math]$ . In Moon’s analysis , it is given that five window cleaners cleaned a surface of 626.4 $[math]\displaystyle{ m^2 }[/math]$ in 2 hours including preparation time and intermission time. This would mean that a single window cleaner would clean approximately 60 $[math]\displaystyle{ m^2/hr }[/math]$ . Given this number, the water consumption becomes $[math]\displaystyle{ \frac{5}{12} }[/math]$ $[math]\displaystyle{ L/hr }[/math]$ and thus $[math]\displaystyle{ \frac{1}{8640} }[/math]$ $[math]\displaystyle{ L/s }[/math]$ . Note that these numbers are of course fairly dependent on the size, height and difficulty level of the window, but for modeling purpose the average seems to be a plausible choice.

The energy consumption is modeled in a similar way. The energy consumption of the robot for a time step is taken to be 73.5 $[math]\displaystyle{ W }[/math]$ when it is cleaning (and thus consuming maximum energy). This number is determined by averaging over the power consumption of the three considered window cleaning robots as shown in Appendix 2. However, when the window cleaning robot moves over a window surface that has already been cleaned, it consumes less energy since it does not have to clean it. As mentioned before, this has to do with the fact that the friction force of the cleaning pad is not counteracting the vacuum any more. The energy consumption during this motion is therefore estimated to be 50 $[math]\displaystyle{ W }[/math]$ .

The velocity of the robot is estimated to be 0.1 $[math]\displaystyle{ m/s }[/math]$ , which is determined by looking at a comparable window cleaning robot (WINDORO ). Accelerations of the window cleaning robot are not taken into account.

Turns & Rotations

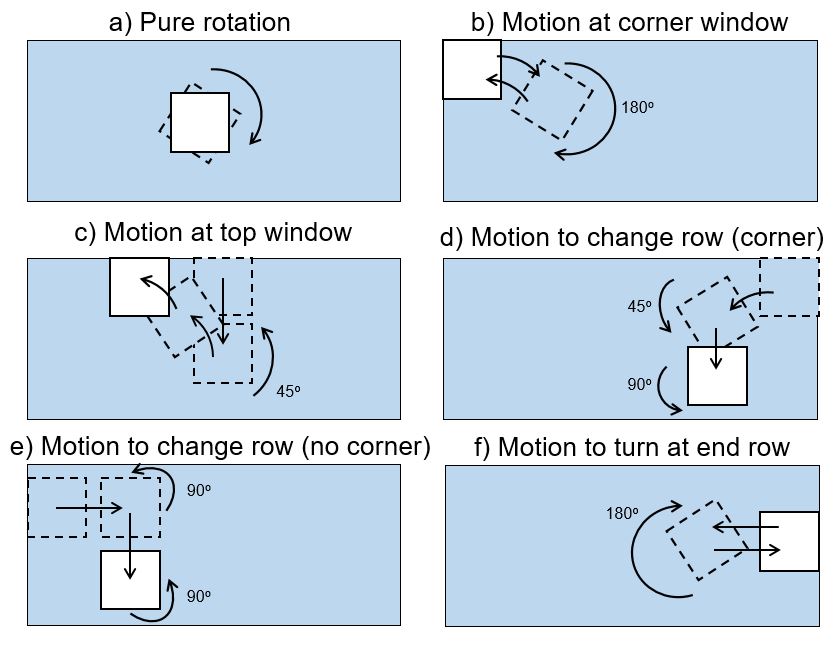
In NetLogo it is very hard or rather impossible to visualize the proper rotations of the window cleaning robot during its motion and subsequently end up at exactly the right position. Therefore it was decided to not visualize the rotations, but instead the turning movements are modeled by letting the robot ’teleport’ from the place before to the place after the turn. The time it takes to make a certain turn is then simply added to the time instance before the rotation. In this way it is still possible to model the turns and rotations of the window cleaning robot in a realistic way. The question becomes then what will be the time that each specific turn takes? To give realistic values for this, the characteristic rotations and turns of the window cleaning robot are studied.

In total there are six different turns or rotations which the window cleaning robot should be able to make. They are schematically shown in Figure [fig:turning motions].

[H]

The first turn the robot should be able to perform is a pure rotation (Figure [fig:turning motions].a). This motion is very often needed during the robot’s cleaning job. To assign a time to the rotation, two parameters should be known: the angle to which the robot is currently heading, the angle to which the robot should head and the rotational speed of the robot when it is rotating. In reality the robot knows how it is oriented by means of gravity sensors and thus knows the angle to which it is currently heading (Section 3.5.2). Therefore it seems appropriate to use the angle at which the robot is heading in NetLogo as the current angle. The time it takes to perform a pure rotation can then be calculated by means of the following equation: $[math]\displaystyle{ t_{rotation} = \frac{\Delta \alpha}{\omega} \label{eq:rotation time} }[/math]$ where $[math]\displaystyle{ t_{rotation} }[/math]$ is the time it takes to perform a pure rotation ( $[math]\displaystyle{ s }[/math]$ ), $[math]\displaystyle{ \omega }[/math]$ is the angular velocity of the robot ( $[math]\displaystyle{ \degree / s }[/math]$ ) and $[math]\displaystyle{ \Delta \alpha }[/math]$ is the angle over which the robot should be rotated to face the upper edge of the window ( $[math]\displaystyle{ \degree }[/math]$ ) (the angle to which the robot should head). The angular velocity of the robot is determined by using its speed and its dimensions: $[math]\displaystyle{ \omega = \frac{v}{r_{track}} \cdot \frac{360}{2\pi} }[/math]$ where $[math]\displaystyle{ v }[/math]$ is the speed of the window cleaning robot ( $[math]\displaystyle{ m/s }[/math]$ ) and $[math]\displaystyle{ r_{track} }[/math]$ is the distance from the center of the robot to one of the crawler tracks. The value $[math]\displaystyle{ v }[/math]$ equals 0.1 $[math]\displaystyle{ m/s }[/math]$ which is determined by looking at a comparable window cleaning robot (WINDORO ) while $[math]\displaystyle{ r_{track} }[/math]$ is estimated to be 0.09 $[math]\displaystyle{ m }[/math]$ .

Another important motion of the window cleaning robot should be performed when it is for example in the upper left corner with its cleaning section headed to the window edge. The robot has to perform the motion that can be seen in Figure [fig:turning motions].b. First, it has to drive backwards to a position where it is able to turn. Since the robot has dimensions of 25 x 25 $[math]\displaystyle{ cm }[/math]$ the distance from the upper edge that is needed to do a rotation can be simply calculated with use of the Pythagorean theorem: $[math]\displaystyle{ s_{turn} = \sqrt[]{(0.5w)^2 + (0.5h)^2} \label{eq: s_turn} - \frac{h}{2} }[/math]$ where $[math]\displaystyle{ s_{turn} }[/math]$ is the distance from an arbitrary edge of the window that is needed to do a rotation ( $[math]\displaystyle{ m }[/math]$ ), $[math]\displaystyle{ w }[/math]$ is the width of the window cleaning robot ( $[math]\displaystyle{ m }[/math]$ ) and $[math]\displaystyle{ h }[/math]$ is the height of the window cleaning robot ( $[math]\displaystyle{ m }[/math]$ ). Because the robot moves over an arc, calculating the distance that it travels is very hard analytically. Therefore a MATLAB script has been written to calculate the length of the arch over which the robot is moving numerically (see Appendix 3). One important decision that has been made in the script is the distance between the edge of the robot and the edge of the window in the starting position. There needs to be a little distance between them in order to allow the robot to turn to move away from the edge. The further the robot moves away from edge, the more it can turn and the faster it can get away from that edge. This means that the distance between the edge of the window and the robot has a huge influence on the time it takes to move away from that edge, as well as the distance traveled in the direction parallel to that edge. In the script, the distance between the robot and edge of the window is assumed to be 5mm. Running the script with this value yields a traveled distance $[math]\displaystyle{ s_{arc,corner} }[/math]$ of 0.33 $[math]\displaystyle{ m }[/math]$ . Assumed in this calculation is that after making the bend, the robot has an angle of 45 $[math]\displaystyle{ \degree }[/math]$ with the vertical. Subsequently, the window cleaning robot has to do a pure rotation over 180 $[math]\displaystyle{ \degree }[/math]$ to make sure its cleaning pad will face the right side of the window after the entire movement. To calculate the time that this rotation takes, Equation [eq:rotation time] can be used again. Eventually the robot moves again back to the left upper corner of the window over the same arch ( $[math]\displaystyle{ s_{arc,corner} }[/math]$ ) as mentioned before. Hence the following expression for the time of the entire movement is obtained: $[math]\displaystyle{ t_{turn,corner} = \frac{s_{arc,corner}}{v} + \frac{180}{\omega} + \frac{s_{arc,corner}}{v} \label{eq:t turn corner} }[/math]$ where $[math]\displaystyle{ t_{turn,corner} }[/math]$ is the time it takes to perform the motion depicted in figure [fig:turning motions].b ( $[math]\displaystyle{ s }[/math]$ ) and $[math]\displaystyle{ s_{arc,corner} }[/math]$ the length of the arc over which the window cleaning robot has to move in this motion ( $[math]\displaystyle{ m }[/math]$ ).

A third motion that the robot should perform is the turn at the top of the window, see Figure [fig:turning motions].c. This motion is needed to orient the robot parallel to the upper edge of the window. Because of this turn the robot is able to move eventually to the upper left corner. To achieve an expression for the time it takes to perform this motion, the movement is split up into three consecutive phases. The first phase consists of the robot simply driving backwards till it has enough space to do a rotation. This distance can again be calculated with equation [eq: s_turn]. The second phase of this motion consist of a pure rotation over 45 $[math]\displaystyle{ \degree }[/math]$ . The time this rotation takes can again be calculated with equation [eq:rotation time]. In the third and last phase of this particular movement the window cleaning robot should make a turn till it aligns with the upper edge of the window. The length of the arc of this motion is the same as $[math]\displaystyle{ s_{arc,corner} }[/math]$ which is already determined by using the MATLAB script. Hence the following expression is obtained for the time of the entire movement at the top of the window: $[math]\displaystyle{ t_{turn,top} = \frac{s_{turn}}{v} + \frac{45}{\omega} + \frac{s_{arc,corner}}{v} }[/math]$ where $[math]\displaystyle{ t_{turn,top} }[/math]$ is the time that the movement at the top takes ( $[math]\displaystyle{ s }[/math]$ ).

Another characteristic movement of the robot is changing from row to row. Since this movement is dependent on the location of the robot it is split up into two cases. The first movement case is when the robot is located in a corner (see Figure [fig:turning motions].d). The second movement case is when the robot is located anywhere between two corners (see Figure [fig:turning motions].e). In other words it touches only one side edge of the window. The former case will be discussed first. Note that in both cases it is assumed that robot faces the edge of the window that is the furthest away with its cleaning pad.

When the robot is located in a corner, it first has to move out of the corner to create space to perform a turn. It has to travel again the distance $[math]\displaystyle{ s_{turn,corner} }[/math]$ that is calculated with the MATLAB script as mentioned before. After this bend, the robot makes an angle with vertical of 45 $[math]\displaystyle{ \degree }[/math]$ . To move down the robot heading should be perpendicular to the upper edge of the window, so it rotates another 45 $[math]\displaystyle{ \degree }[/math]$ . Now it is able to move vertically down to the next row that should be cleaned. The vertical distance $[math]\displaystyle{ s_{change row} }[/math]$ of this is also determined by means of the developed MATLAB script and equals 0.2 $[math]\displaystyle{ m }[/math]$ (Appendix 3). The next part of the motion is again a pure rotation, but now over 90 $[math]\displaystyle{ \degree }[/math]$ . After this, the robot’s heading is again parallel to the upper edge but in a different row. Hence the expression for the time that is needed to change row when the robot is located in a corner is as follows: $[math]\displaystyle{ t_{change row,corner} = \frac{s_{arc,corner}}{v} + \frac{45}{\omega} + \frac{s_{change row}}{v} + \frac{90}{\omega} }[/math]$ where $[math]\displaystyle{ t_{change row,corner} }[/math]$ is the time needed to change row when the robot is located in a corner ( $[math]\displaystyle{ s }[/math]$ ) and $[math]\displaystyle{ s_{changerow} }[/math]$ is the vertical displacement the robot should perform to get to the next row ( $[math]\displaystyle{ m }[/math]$ ).

The second case happens when the robot only touches one of the side edges of the window. The motion that it should perform in that instance is quite simple. First the robot has to move the distance $[math]\displaystyle{ s_{turn} }[/math]$ away from the edge to create space to rotate. Next it rotates over 90 $[math]\displaystyle{ \degree }[/math]$ and moves 0.25 $[math]\displaystyle{ m }[/math]$ down to go to the row below. After that, it should rotate again 90 $[math]\displaystyle{ \degree }[/math]$ to face the other side edge of the window. The time that this procedure takes is then as follows: $[math]\displaystyle{ t_{change row,normal} = \frac{s_{turn}}{v} + \frac{90}{\omega} + \frac{0.25}{v} + \frac{90}{\omega} }[/math]$ where $[math]\displaystyle{ t_{change row,normal} }[/math]$ is the time to change row when the robot is not located in a corner at the beginning of the motion ( $[math]\displaystyle{ s }[/math]$ ).

The last characteristic motion of the window-cleaning robot is its turning motion at the end of each row (see Figure [fig:turning motions]f). This motion is of course necessary in all algorithms since remaining stripes should be wiped away, or because the row is simply not clean yet. It consists out of three phases. First, moving away a distance $[math]\displaystyle{ s_{turn} }[/math]$ from the edge of the window to enable the robot to rotate. Second, a pure rotation over 180 $[math]\displaystyle{ \degree }[/math]$ and third, a movement back to the edge of the window (again over distance $[math]\displaystyle{ s_{turn} }[/math]$ ), but now facing the other side of the window. Hence the equation for the time of this motion becomes: $[math]\displaystyle{ t_{turn,row} = \frac{s_{turn}}{v} + \frac{180}{\omega} + \frac{s_{turn}}{v} }[/math]$ where $[math]\displaystyle{ t_{turn,row} }[/math]$ is the time it takes to turn the robot to the other side of the window when it is at the end of a certain row ( $[math]\displaystyle{ s }[/math]$ ).

As mentioned before, the equations above are implemented in NetLogo to model the times of the rotations. The rotations itself are not explicitly made visible, but the robot is ’teleported’ from its location before to the location after the turn.

Cleaning

For the cleaning action, it is assumed that when a patch is located under one of the cleaning squares of the robot and when this patch has a dirtiness that is greater than 0, the dirtiness value of the patch is reduced with a random number between 30 and 60 per time step. When the reduction in dirtiness is greater than the actual dirtiness of a patch, the dirtiness of the patch is set to zero. The numbers for the dirt reduction are freely chosen since no scientific articles could be found on that topic. A reduction between 30 and 60 seemed plausible, but one cannot be sure that this is representative of reality. It does not matter that much that these numbers are not based on scientific research and thus are maybe not entirely realistic. This is because both the developed motion planning algorithms as well as the reference motion planning algorithm use these numbers, so for the comparison between them it is unlikely to have a major impact.

For the dirt detect action, it is assumed that when a patch is located under one of the dirt detect sensor squares of the robot, the dirtiness of this patch is assessed with a accuracy of 100%. In reality this might not be the case, but again, for the comparison purposes it is not relevant since it effects all algorithms identically.

Another important part of cleaning the window is avoiding stripes. To include this in the model, it has to be clearly defined when the robot leaves stripes on the window surface. Therefore it is assumed that the robot will leave stripes on the surface when the window is cleaned in any way except in horizontal rows from top to bottom. This has to do with the dripping of water. Besides that, stripes will also appear when horizontal paths are not completely finished. In other words, when the robot has for example cleaned a very persistent dirty spot by means of reciprocating movements and goes directly to the next row, stripes will appear. Hence it is of high importance to avoid these situations because it yields undesirable results (see Section 3.2).

A last remark should be made regarding the hard to clean spots, as mentioned earlier in Section 3.5.1. Hard to clean patches were patches that required a huge amount of wiping movements. Making infinitely many wiping motions over these spots is definitely not efficient, so a method should be developed to skip these spots when they do not get any cleaner after a certain amount of wiping motions. The method that is used is quite simple. The window cleaning robot keeps track of the changes in dirtiness value of all patches. When it notices that after a certain amount of wiping motions, the dirtiness value of a patch does not decrease significantly any more, it is skipped and the robot moves on to the next part of its motion planning. In reality this means that it could be that the window cleaning robot leaves some very persistent spots that should be cleaned manually, but this is indeed better than a very long feedback loop which will have a very large impact on the performance of the motion planning algorithm. In addition the robot could signal that such a hard to clean spot is detected, in order to manually remedy the problem whilst the robot continues with its cleaning.

The Model

In this section it is explained how the NetLogo model is constructed and how it works. Besides that, it is also indicated what the limitations of the model are. The NetLogo model can downloaded on the Wiki page of group 3.

User interface & General considerations

The first step in modeling the motion planning algorithm with NetLogo consisted of creating the window with an adjustable dirt distribution that represents reality. The entire user interface including the window and robot is shown in Figure [fig:model]. As mentioned before, a single patch from the window represents an area of 50 x 50 $[math]\displaystyle{ mm }[/math]$ . As can be seen in Figure [fig:model], the dimensions of the window can be adjusted by means of sliders. The width-window slider can be incremented with 250 $[math]\displaystyle{ mm }[/math]$ which corresponds to 5 patches, while the height-window slider has an incrementation of 250 $[math]\displaystyle{ mm }[/math]$ which corresponds to 5 patches. The reasons for these choices was already explained in Section 3.5.1. When the sliders are moved, and the button Setup Window is pressed, the model will adjust the amount of patches to the dimensions that are chosen. From a certain window size, the patch size is adjusted slightly to make sure that the whole window fits on the screen of the user of the model.

[H] fig:

The above mentioned dirt distribution is again modeled with the ideas as stated in Section 3.5.1. At the start of each run of the model, each of the patches will receive a value of dirtiness between 0 and 100 denoted with the variable dirt-level. The dirtiness value of patches is indicated by the color of the patches. The darker the color of the patch, the higher the dirtiness value of the patch. When a patch is completely clean, its color changes to blue. The earlier mentioned more or less even distribution of dirt will result in a random dirtiness value for all patches that lies between 10 and 30. Subsequently, a number of patch clusters, which can be specified with the nr-of-dirt-cluster slider, is selected from which the previously received dirtiness value is overwritten with a random number between 40 and 100. Additionally, there is a dirt-intensity slider included in the model. The value of this slider in % is divided by 100 and all the dirtiness values of the patches are multiplied with this number. So, when a patch would receive a dirtiness value of for instance 30 and the slider is at 50 %, the dirtiness value that the patch eventually receives is equal to 15. As has been stated earlier, all patches are assigned a number that denotes how hard it is to clean each of them. This number is obtained for each patch by taking a sample from an exponential distribution with mean 1 and multiplying this value by 100. Next, if the number is bigger than 1, it is set to 1. The resulting number is eventually stored in the variable hard_to_clean for each patch. When the robot moves over patches, its dirt-reduction will be multiplied with this number. Most of these patches will have a value for this number that is equal to 1, which has no effect on the dirt-reduction. A small number of patches will get a smaller number and are thus harder to clean. They thus require a lot more wiping motions to fully clean them. The just explained hard to clean possibility for patches can be turned on or off by means of a switch in the user interface denoted by hard_to_clean_active. Switching this off, results in a state that all patches have a hard-to-clean value of 1, which means that this variable has no effect anymore on the dirt-reduction of each patch. The dirt distribution is generated with the button Add Dirt. Re-clicking the button results in a newly generated dirt distribution.

As has been mentioned previously in section 3.5.5, the modeled window cleaning robot keeps track of the changes in dirtiness value of all patches. In the model this is done by storing not only the current dirtiness value of a patch in the variable dirt-level, but also storing the previous dirtiness value of a patch in the variable previous_dirt-level. The robot then compares the previous dirtiness value with the current dirtiness value when it moves over a particular patch with its cleaning section. When the reduction is smaller than a predefined standard, the patch is not considered by the robot anymore. This predefined standard is set with the min_dirtdecrease slider. The value of the slider is the minimum difference of the previous dirtiness value and the current dirtiness value for which the robot will still consider the patch as a patch that needs to be cleaned. The value of this slider is both used for the standard and the newly developed motion planning algorithms.

Apart from the already mentioned elements of the user interface, there are still a couple of buttons, monitors and one chooser that need to be explained. First, the Place Robot button places, as the name would suggest, the robot on the window. It however always places the robot in the middle of the window and not at a random position as has been stated earlier. This is done for a specific reason. When the robot starts cleaning the window, which is initiated with the Clean Window button, the robot first starts to move to the upper left corner for every programmed motion planning algorithm. The time that it takes to reach this top left corner is also added to the total cleaning time. To be able to compare the cleaning times of the considered motion planing algorithms with each other in an objective way, it is thus necessary that this time to reach the top left corner is always the same for all algorithms for a fixed window configuration. This is the reason for always placing the robot in the same position. Additionally, this is also the reason for not taking the time into account that the robot needs to turn at its initial place in the middle of the window to face the upper edge of the window. The robot is namely always placed with a random heading direction. To eliminate this source of randomness from the time that is necessary to move to the upper left corner, the initial rotation time is thus not considered.

Another choice in the model that was made in order to be able to make an objective comparison between the modeled algorithms was the choice for the implementation of the Import Window button. With this button, it is possible to import a previously used dirt distribution again. This option is necessary to test the considered motion planning algorithms on exactly the same conditions. It is a very welcome addition to the model, since there is a big factor of randomization included in the dirt distribution which can be eliminated in this way when that is deemed necessary. This button is also used to obtain the results presented in the Section 5.2. To select a specific motion planning algorithm for testing, the chooser select_motion_planning is used. The option standard denotes the reference algorithm, zigzag denotes algorithm 1 as described in Section [subsec:algorithm1] and turndirt denotes algorithm 2 as described in Section [subsec:algorithm2]. The monitor time keeps track of the time that it takes the robot to clean the window. The monitors energy consumption and water consumption keep track of the energy consumption respectively the water consumption of the robot during the cleaning of the window.

Implementation of the motion planning algorithms

The standard motion planning algorithm that is explained in section ADD REFERENCE is implemented without major changes. When the robot starts in the upper left corner, it moves to the upper right corner while it is continuously cleaning. It then turns in the upper right corner and thus also checks the last bit of the row with its dirt detect sensors. The robot then assesses the cleanliness of the entire row. If the row is perceived as clean, the robot moves to the next row and repeats the process. If not, it moves to the upper left corner while continuously cleaning, turns again and checks again and so fort. It should be noted that when the robot perceives a row as clean, it is not necessarily entirely clean. This is because patches that have a difference of previous dirtiness value and current dirtiness value that is smaller than the set minimum difference are not considered anymore by the robot. The only real difference that the implementation has when compared to the explanation is that the robot is not actually continuously checking with its dirt detect sensors, but checks once every time all the patches in the row have been in contact with a dirt detect sensor of the robot. This is done for practical purposes in Netlogo and results in exactly the same behavior as described in the earlier explanation.

To implement algorithm 1, which is also denoted as zigzag, some small modifications had to be made. When the robot starts at the upper left corner and starts cleaning and moving to the right, it continuously checks the patches below the dirt detect sensor. When the dirt detect sensor detects at least one dirty patch, the robot is "teleported" back five patches (this is called the backwards movement) and moves again over these dirty patches with its cleaning section. This is done to model the reciprocating motion. It should be noted that the time and the consumed energy for the backwards movement are still respectively added to the time and energy consumption variables. The major problem of the backwards movement is that it is not possible to execute this movement when the robot is (partly) located in the first five columns of patches of the row. This is of course also the case when the robot is heading in the other direction, thus the backwards motion is not applicable in the first and last five columns of patches of the row. When a persistent spot of dirt is located in one of these columns, the robot uses the standard cleaning method with the exception that it is not continuously cleaning but only cleans when its cleaning section comes into contact with a considered dirty patch. To prevent stripes, the robot cleans the row one more time when it has used the reciprocating motion in its last movement over the row and has determined that the row is clean. The cleanliness of the entire row is again determined after reaching an end of the row and turning and checking the cleanliness of the considered patches.

For the implementation of algorithm 2, which is also denoted by turndirt, some small modifications had to be made again. The first and last row are cleaned with the standard method. The reason for this is that when the robot has to turn in these rows, it has to first move away form the window edge, then turn and then move back. For the top row this would mean that the robot comes into contact with the part of the window that is still dirty which would potentially mean that dirt from this part is again introduced to the top row. For the bottom row it would mean that the robot moves from the dirty bottom row into the clean row above that and that the turning motion would potentially leave stripes there. Because of these reasons, these rows are thus cleaned with the standard method. For the other rows, the motion pattern is as follows: The robot starts at one window edge and moves to the other while continuously cleaning like the standard algorithm. When it has reached the other edge it turns and checks the cleanliness of the row. When the row is considered clean the robot moves to the next one. When the row is not yet considered clean, the robot determines the outermost dirty patches in the row and repeats the previously mentioned movement between these patches with the exception that the robot only cleans when its cleaning section comes into contact with a dirty patch. When the robot reaches one of the outermost dirty patches, it turns and checks the cleanliness of the patches again. When the row is still not considered clean, the robot again determines the outermost dirty patches and repeats the motion. This goes one until the entire row is clean with one exception. If the two outermost dirty patches are placed closer together than the dimensions of the robot, or just one dirty patch remains, the robot moves somewhat further than an outermost dirty patch to make sure that the cleaning section can reach the dirty patches after turning. This ensures that the robot does not end up in an endless loop of turning without being able to clean the patches for which it turns. When the row is considered clean and turned in the middle of the row, the robot moves to one of the outer edges of the window and moves over entire row one more time to remove any stripes. Thereafter, it moves to the next row. One special case still needs to be considered. This is the case that there is one persistent dirty patch that is still considered and is located in the first or last five patch columns of the row. In this case the robot is not able to move a little further since the dirty spot is located so close to the window edge. In this case, the robot cleans the entire row like the standard algorithm with the exception that the robot only cleans when its cleaning section comes into contact with a dirty patch.

Evaluation Results

In this section it is explained how the results of the NetLogo model are treated. Furthermore, the performance of the developed algorithms are compared with the reference algorithm (denoted as standard in the previous section). At last, the results are fed back to the user needs, requirements and preferences.

Treatment of the results

To make a sensible comparison between the three algorithms, it is of high importance that they are tested on the same conditions. The conditions here are the settings of the sliders and buttons in NetLogo. A choice has to be made for the following buttons and sliders:

width-window (slider)
height-window (slider)
dirt-intensity (slider)
nr-of-dirt-clusters (slider)
min_dirtdecrease (slider)
hard_to_clean_active (switch)

Regarding the width and the height of the window, it is decided to evaluate the algorithms on the following window sizes: 1 x 1, 1 x 3, 3 x 1, 4 x 2, 2 x 4 and 4 x 4 $[math]\displaystyle{ m }[/math]$ . These particular numbers are chosen since they represent square and narrow as well as wide rectangular windows. Due to this, it is possible to conclude that a certain algorithm is better for a certain window size. Every window size is tested five times, each test containing an alternative dirt distribution. Note that each test the dirt distribution was the same for each motion-planning algorithm. This was done by importing the settings with the Import Window button. The results for time, energy and water consumptions are averaged over the five tests to get more accurate results.

The dirt distribution together with the hard to clean patches in particular, determine a significant part of the overall time it takes for the robot to clean the window. Therefore, to compare the motion-planning algorithms, it is important to make a well-funded choice for the values of dirt-intensity, nr-of-dirt-clusters, min_dirtdecrease and hard_to_clean_active. For each test case it is decided to keep the values for these sliders and buttons the same. Overall, most of the values are set to the maximum values, since ’hard’ cleaning conditions will result in larger differences in performance and reveal the specific beneficial characteristics of the algorithms more clearly.

The slider dirt-intensity is set to 100%. This value will not have a major effect on the performance of the different algorithms. The slider nr-of-dirt-clusters is set to 10. This slider will have a little more impact, since the dirt values of clusters are significantly higher and may require the algorithms (the reference algorithm in particular) to do extra wiping motions. Subsequently, the slider min_dirtdecrease is set to 1. There are two reasons for this particular choice. When the slider is moved to its minimum, all the algorithms will clean the window till almost every single patch is clean, resulting in less differences in performance indicators. When the slider is moved to its maximum, apart from the hard to clean patches also a lot of other dirty patches remain, which also results in less difference in performance of the three algorithms. Hence the value of 1 is chosen since it gives a significant difference in performance for each algorithm. At last, the switch hard_to_clean_active is turned on, since these hard to clean patches are crucial for the algorithms and will have the largest effect on the performance of the three algorithms. Furthermore, this creates a test environment that is more realistic.

Since the model calculates the time, energy used and water used during the cleaning job, a MATLAB script is made to convert this data to performance indicators such as cleaning speed ( $[math]\displaystyle{ m^2/hr }[/math]$ ), water consumption ( $[math]\displaystyle{ L/hr }[/math]$ ) and mean energy consumption ( $[math]\displaystyle{ W }[/math]$ ). The code of this MATLAB script is shown in Appendix 4.

Comparison motion planning algorithms

In Table [tab:results], the average results of the model as well as the calculated performance indicators are shown for the three different motion-planning algorithms at each test case.

-2in-2in

|C2cm|C1.9cm|c|C2.3cm|C2cm|C2cm|C2cm|C1.5cm| Window & Algorithm & Time ( $[math]\displaystyle{ s }[/math]$ ) & Energy consumed ( $[math]\displaystyle{ J }[/math]$ ) & Water used ( $[math]\displaystyle{ L }[/math]$ ) & Cleaning speed ( $[math]\displaystyle{ m^{2}/hr }[/math]$ ) & Water consumption ( $[math]\displaystyle{ L/min }[/math]$ ) & Mean power ( $[math]\displaystyle{ W }[/math]$ )
1 x 1 $[math]\displaystyle{ m }[/math]$ & standard & 441.73 & 27214.54 & 0.023669 & 8.150 & 0.003215 & 61.609
1 x 1 $[math]\displaystyle{ m }[/math]$ & zigzag & 319.59 & 17553.14 & 0.006134 & 11.26 & 0.001152 & 54.923
1 x 1 $[math]\displaystyle{ m }[/math]$ & turndirt & 417.25 & 22448.60 & 0.006227 & 8.628 & 0.000895 & 53.801
1 x 3 $[math]\displaystyle{ m }[/math]$ (N) & standard & 647.13 & 41015.63 & 0.032716 & 16.69 & 0.003033 & 63.381
1 x 3 $[math]\displaystyle{ m }[/math]$ (N) & zigzag & 606.24 & 34327.51 & 0.012948 & 17.81 & 0.001281 & 56.624
1 x 3 $[math]\displaystyle{ m }[/math]$ (N) & turndirt & 611.01 & 34556.95 & 0.015683 & 17.68 & 0.00154 & 56.557
3 x 1 $[math]\displaystyle{ m }[/math]$ (W) & standard & 730.69 & 50526.06 & 0.063715 & 14.78 & 0.005232 & 69.148
3 x 1 $[math]\displaystyle{ m }[/math]$ (W) & zigzag & 601.64 & 34424.34 & 0.016181 & 17.95 & 0.001614 & 57.217
3 x 1 $[math]\displaystyle{ m }[/math]$ (W) & turndirt & 767.74 & 42750.40 & 0.016285 & 14.07 & 0.001273 & 55.683
2 x 4 $[math]\displaystyle{ m }[/math]$ (N) & standard & 1553.27 & 105411.0 & 0.129572 & 18.54 & 0.005005 & 67.864
2 x 4 $[math]\displaystyle{ m }[/math]$ (N) & zigzag & 1370.22 & 78187.20 & 0.040567 & 21.02 & 0.001776 & 57.062
2 x 4 $[math]\displaystyle{ m }[/math]$ (N) & turndirt & 1554.91 & 87445.45 & 0.040683 & 18.52 & 0.001570 & 56.238
4 x 2 $[math]\displaystyle{ m }[/math]$ (W) & standard & 1867.42 & 131646.7 & 0.180468 & 15.42 & 0.005798 & 70.497
4 x 2 $[math]\displaystyle{ m }[/math]$ (W) & zigzag & 1254.22 & 72603.44 & 0.040474 & 22.96 & 0.001936 & 57.887
4 x 2 $[math]\displaystyle{ m }[/math]$ (W) & turndirt & 1839.45 & 101881.6 & 0.040556 & 15.66 & 0.001323 & 55.387
4 x 4 $[math]\displaystyle{ m }[/math]$ & standard & 3224.87 & 227514.2 & 0.315683 & 17.86 & 0.005873 & 70.550
4 x 4 $[math]\displaystyle{ m }[/math]$ & zigzag & 2109.73 & 123720.7 & 0.079109 & 27.30 & 0.00225 & 58.643
4 x 4 $[math]\displaystyle{ m }[/math]$ & turndirt & 2920.60 & 164271.2 & 0.079132 & 19.72 & 0.001626 & 56.246

There are a few remarks that can be made based on the results above. First, the zigzag algorithm has overall performed best on the field of time-efficiency, having spent the least time on most of the window surfaces. The standard algorithm on the other hand takes on average the longest time to clean the windows. Despite that the turndirt algorithm is overall faster than the reference algorithm, there are two situations in which the reference algorithm is faster. This is the case for a window size of 3 x 1 and 2 x 4 $[math]\displaystyle{ m }[/math]$ . Since performance of the turndirt algorithm is highly dependent on the dirt distribution (it is namely more efficient when persistent spots are in the center of each row), this could be an explanation for these remarkable results.

If the water consumption is considered, the zigzag and turndirt algorithms yield most of the cases similar values while the water consumption of the reference algorithm is much higher. When the window area is more and more increased, the difference between the two developed algorithms becomes more visible and one can conclude that the zigzag algorithm is slightly better in terms of water consumption. The large difference between the reference algorithm and developed algorithms can be explained by the fact that the standard algorithm continuously uses water, while the other two algorithms only use water when needed.

The zigzag algorithm is overall the second best in the field of energy-efficiency, just after the turndirt algorithm. The differences in mean power between these two are very small, while the difference between the two developed algorithms and the reference algorithm is much larger. Nevertheless it should be noted that despite the mean power of the turndirt algorithm is overall slightly lower than the zigzag algorithm, it consumed in each case more energy as can be seen in the fourth column in Table [tab:results]. Thus the mean power of the turndirt algorithm is lower since the algorithm is slower than the zigzag algorithm.

At last, attention is spent to the window sizes and their influence. As can be seen in Table [tab:results], the difference in cleaning speed between the zigzag algorithm and both other algorithms is more significant for wider and bigger windows. This can be explained by the diversity in strategy of the algorithms. Since the main gain of the developed algorithms lie in their ability to skip already cleaned surfaces, the difference in performance will become clearer when the rows are longer. Hence the developed motion planning algorithms will exhibit their benefits especially at larger and wider windows.

Feedback to user needs, requirements and preferences

The performance indicators in the last three columns of the results of Table [tab:results] are important values for the primary and secondary users, mentioned in Chapter

3

. The requirements of no water stripes and minimal coverage, are implemented in the algorithm script beforehand and are achieved this way. However, the performance requirements have still to be met. A cleaning speed of a speed of 125 $[math]\displaystyle{ m^{2}/hr }[/math]$ was desired. From the results however, it can be seen that this goal is far from reached. With a maximum of 27.30 $[math]\displaystyle{ m^{2}/hr }[/math]$ , the zigzag algorithm is the closest to the goal. This large difference in cleaning speed can be explained through the interpretation of the definition of cleaning speed. It is assumed that the manufacturers meaning of the term is the surface area covered by the robot, but not specifically fully cleaned. The current modeled algorithms cover specific areas multiple times in order to clean the window. This repeatedly traveled distance is not taken into account in the definition of the cleaning speed as derived from the results of the model. Besides that, a contradiction emerges when the cleaning speed and the reference algorithm are compared. The standard algorithm represents the state-of-the-art algorithm, however it does not hold up with the specifications of the state-of-the-art robots. Despite not corresponding with the state-of-the-art specifications, the zigzag algorithm is still faster than the reference algorithm, meaning that the time taken to clean a window is shortened which is beneficial for both window cleaning companies and for individual clients.

The requirement for the water consumption was equal to 0.25 $[math]\displaystyle{ L/min }[/math]$ . From the results it can be seen that both developed algorithms are far from reaching this value, which is a positive result. For the window cleaning companies, the choice to either save time or water is now based on the results of the test. However, it is assumed that the profit on time-savings is more relevant than the earnings on water-savings. If the individual client is the supplier of the water, which is likely, the chance that the window cleaning company could change its algorithm for a particular job based on feedback could increase.

The last important requirement for the algorithms is to stay below an energy consumption of 73.5 $[math]\displaystyle{ W }[/math]$ . From the results the only algorithm which comes closes to this value is the Standard algorithm with a value of 70.6 $[math]\displaystyle{ W }[/math]$ , which would mean that all the algorithms meet the requirement. The most energy-efficient algorithm is the turndirt algorithm, followed by the zigzag algorithm. The manufacturer would be able to use the same batteries as for the state-of-the-art window cleaning robots. The same goes for the water tank.

Altogether, the results indicate that the zigzag algorithm is the the fastest cleaning algorithm, the turndirt algorithm the most water- and energy efficient algorithm. Both algorithms beat the reference algorithm on all fields. This means that the manufacturer has a choice in whether to choose for either the most time-efficient or the most energy- and water-efficient algorithm.

Conclusion

In this project, a literature study on current window-cleaning robots and their motion-planning algorithms was performed. This literature study gave insight in the shortcomings of the motion-planning of current window-cleaning robots and therefore provided the motivation to design a better motion-planning algorithm. The design question was as follows:

How should the main, currently used motion-planning algorithm for small sized window-cleaning robots for domestic use be improved such that it is more efficient in terms of cleaning speed, energy consumption and water consumption?

After defining user needs, requirements, preferences and constraints, two innovative motion-planning algorithm concepts were designed. To compare these two algorithms with the currently used, less optimal, motion-planning algorithm, it was decided to develop a NetLogo model for each of the algorithms. In order to make a good comparison, specifications and quantifications of the window cleaning robot needed to be obtained. To obtain these quantifications, additional research was done and several assumptions and simplifications were made. All this together formed the basis of the developed NetLogo model. With the finished NetLogo model, both the reference algorithm and the developed algorithms were extensively tested at different conditions to obtain data for a proper comparison between these three algorithms. From the results it was concluded that as well algorithm 1 (zigzag) as algorithm 2 (turndirt) was better than the standard motion-planning algorithm in terms of cleaning speed, water consumption and energy consumption. The difference was particularly notable for wider and bigger windows. The question then became which algorithm of the two was the best. In terms of cleaning speed, it turned out that algorithm 1 was significantly better. In terms of water consumption and mean power however, it turned out that algorithm 2 was actually slightly better. This leaves the primary user, a certain window-cleaning company, with the choice between algorithm 1 and 2, based on their preferences. Nevertheless, if one should advice a certain algorithm, the best choice seems to be algorithm 1, since cleaning speed is of higher importance for both the primary as the secondary user than energy and water consumption.

All in all, it is now possible to answer the design question of this project. The motion-planning algorithm of current small sized window-cleaning robots for domestic use should be improved with short reciprocating movements that are used when the dirt sensors sense a persistent spot of dirt as stated in the explanation of algorithm 1. The usage of this motion-planning algorithm will improve cleaning speed, water consumption and energy consumption and is therefore a very useful alternative for the main, currently used, motion-planning algorithm for domestic use. As a result, the implementation of this algorithm, denoted as algorithm 1, will be very beneficial for as well primary as secondary users, since window-washers will now be able to reduce their cleaning times while still being able to deliver the same results with less water and energy consumption.

99 GEKKO Facade Robot. (Date unkown). Retrieved February 15, 2018, from https://serbot.ch/en/facade-cleaning/gekko-facade-robot Sung Min Moon, Chang Yeob Shin, Jaemyung Huh, Kyeong Won Oh and Daehie Hong. Window Cleaning System with Water Circulation for Building Façade Maintenance Robot and Its Efficiency Analysis. International Journal of Precision Engineering and Manufacturing-green Technology Vol. 2, No. 1, pp. 65-72, 2015. Peter. Schoonmaak startpagina. [Prijs per m2 ramen wassen en hoeveel m2 per uur]. https://schoonmaak.startpagina.nl/forum/topic/1470996/prijs-per-m2-ramen-wassen-en-hoeveel-m2-per-uur/ Author unknown. User Manual HOBOT 268-288. 2017. Author unknown. Ecovacs Winbot W950 Robot. https://nl.hardware.info/product/418859/ecovacs-winbot-w950-robot/specificaties Author unknown. Instruction manual Winbot 950. Publication date unknown. Author unknown. User manual WINDORO [Super smart cleaning for window!]. Publication date unknown. http://mywindoro.com/wp-content/uploads/2012/10/MyWindoro_WCRI001_UserManual.pdf Author unknown. WINBOT 950. [The New Era of Window-Cleaning]. 2017. https://www.ecovacs.com/global/winbot-window-cleaning-robot/WINBOT-950/specs/ Choi,Y. & Jung,K WINDORO: The World’s First Commercialized Window Cleaning Robot for Domestic Use..2011 November 26. http://ieeexplore.ieee.org/document/6145947/?reload=true Choi,Y-H. Lee,J-Y. Lee,J-D. & Lee,K-E. SMART WINDORO V1.0: Smart Window Cleaning Robot.. 2012 November 29. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6462948 Moon,S M. Shin,C Y. Huh,J. Won,K. & Hong,D. Window Cleaning System with Water Circulation for Building Façade Maintenance Robot and Its Efficiency Analysis. https://link.springer.com/content/pdf/10.1007%2Fs40684-015-0009-8.pdf Imoaka,N. Roh,S. Yusuke,N. & Hirose,S. SkyScraper-I: Tethered Whole Windows Cleaning Robot. 2010 October 22. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5649537

FORMAT BRONNEN AANPASSEN: VOOR WEBSITE: TITEL. (JAAR, MAAND DAG). Retrieved MAAND DAG, JAAR, from WEBSITE VOOR ARTIKEL: AUTEUR, VOORLETTERS (JAAR). TITEL. PAGINA’S.

Relevant specifications of 3 commercially available window cleaning robots

In Table [tab:specs window cleaning robots] relevant specifications of three popular commercially available window cleaning robots are shown.

| a | L2.5cm | L2.5cm | L2cm | a | Type & WINDORO , & Winbot 950 , , , & Hobot 268 , & Mean
Cleaning surface & 21.8 x 21.1 $[math]\displaystyle{ cm }[/math]$ & 27.2 x 27.2 $[math]\displaystyle{ cm }[/math]$ & 24 x 24 $[math]\displaystyle{ cm }[/math]$ & 24.33 x 24.1 $[math]\displaystyle{ cm }[/math]$
Weight & 2.9 $[math]\displaystyle{ kg }[/math]$ & 2.3 $[math]\displaystyle{ kg }[/math]$ & 1.2 $[math]\displaystyle{ kg }[/math]$ & 2.1 $[math]\displaystyle{ kg }[/math]$
Cleaning speed & 62 $[math]\displaystyle{ m^2/hr }[/math]$ & 125 $[math]\displaystyle{ m^2/hr }[/math]$ & 25 $[math]\displaystyle{ m^2/hr }[/math]$ & 71 $[math]\displaystyle{ m^2/hr }[/math]$
Energy consumption & - & 75 $[math]\displaystyle{ W }[/math]$ & 72 $[math]\displaystyle{ W }[/math]$ & 73.5 $[math]\displaystyle{ W }[/math]$

MATLAB code turning motion

In this section, the MATLAB code that is used for calculating the arc length $[math]\displaystyle{ s_{arc,corner} }[/math]$ as indicated in equation [eq:t turn corner] is presented.

D2= sqrt((0.25/2)^2*2); % distance from center to corner robot;                     
y1=0.130; % distance from center robot to edge window, 0.13 means   half a centimeter between edge window and edge robot
y = y1;
angle = 1/4*pi-acos(y/D2);  
v = 1; % speed of the robot, when 1 the distance traveled is equal to the time it takes
x = 0; % x position of the robot
dt = 0.000001; % time interval
t = 0;                      
track = 0; % distance traveled by the fastest moving track, limiting factor
d1 = 0.09; % distance from center robot to middle tank tracks

while y<D2
   dd = v*dt; % distance traveled forwards during interval
   dx = cos(angle)*dd; % distance traveled in x direction during interval
   track = track + dd; % distance traveled by track during interval
   t = t+dt;
   dy = sin(angle)*dd; % distance traveled in y direction during interval
   
   % the next part calculates how much the robot can turn due to the extra
   % room between the edge of the window and the robot
   angle2 = 1/4*pi-acos(y/D2);          
   dangle = angle2 - angle;
   angleSpeed = v/d1;
   track = track + dangle/angleSpeed;
   angle = angle2;
   x = x+dx;
   y = y+dy;
end

t = track/v; %the time it takes to make the turn
yMovement = y-y1; %how much the robot moves in y direction (away from the window)

MATLAB code performance indicators

In this section, the MATLAB code that is used for calculating the mean cleaning speed ( $[math]\displaystyle{ m^2/hr }[/math]$ ), mean water consumption ( $[math]\displaystyle{ L/min }[/math]$ ) and mean energy consumption ( $[math]\displaystyle{ W }[/math]$ ) is presented. Note that the first four matrices should be filled with data obtained from the NetLogo model.

%% Close all windows, clear work space and command window
close all; clear all; clc;

%% Obtained data from NetLogo model
waterconsumed = [3.55 1.00 6.77 2.37 9.07 2.43 17.28 5.83 17.72 5.83 65.69 12.01]; % Total water consumed to clean window [L]                 
time = [390.79 305.63 632.64 610.57 634.18 456.20 1223.56 1098.76 1071.47 1055.43 4079.96 2653.58]; % Total time that is taken to clean window [s] 
area = [1 1 3 3 3 3 8 8 8 8 16 16]; % Area of the considered window [m^2]
energy = [13669.0 15934 24391.5 31008.13 35380.3 24531.4 64085.5 60287.4 65434.8 59280.8 259224.3 145609.3]; % Total energy consumed during cleaning te window [J]

%% Calculation performance indicators
speed = (area./time)*3600; % Cleaning speed [m^2/hr]
speed' % Tranposed to display as column in command window             
waterconsumption = (waterconsumed./time)*60; % Mean fuel consumption [L/min]
waterconsumption' % Tranposed to display as column in command window
meanpower = (energy./time); % Mean energy consumption [W]
meanpower' % Tranposed to display as column in command window

Report

Contents

Introduction

State of the Art

Window-cleaning Robots

Motion planning algorithms

Design Process

Approach

User requirements, preferences and constraints

Requirements

Preferences

Constraints

Design choices

The concepts

Algorithm 1

Algorithm 2

Assumptions and simplifications

The Window

Window Cleaning Robot

Water consumption, energy consumption and velocity

Turns & Rotations

Cleaning

The Model

User interface & General considerations

Implementation of the motion planning algorithms

Evaluation Results

Treatment of the results

Comparison motion planning algorithms

Feedback to user needs, requirements and preferences

3

Conclusion

Relevant specifications of 3 commercially available window cleaning robots

MATLAB code turning motion

MATLAB code performance indicators

Navigation menu

Report

Introduction

State of the Art

Window-cleaning Robots

Motion planning algorithms

Design Process

Approach

User requirements, preferences and constraints

Requirements

Preferences

Constraints

Design choices

The concepts

Algorithm 1

Algorithm 2

Assumptions and simplifications

The Window

Window Cleaning Robot

Water consumption, energy consumption and velocity

Turns & Rotations

Cleaning

The Model

User interface & General considerations

Implementation of the motion planning algorithms

Evaluation Results

Treatment of the results

Comparison motion planning algorithms

Feedback to user needs, requirements and preferences

3

Conclusion

Relevant specifications of 3 commercially available window cleaning robots

MATLAB code turning motion

MATLAB code performance indicators

Navigation menu

Search