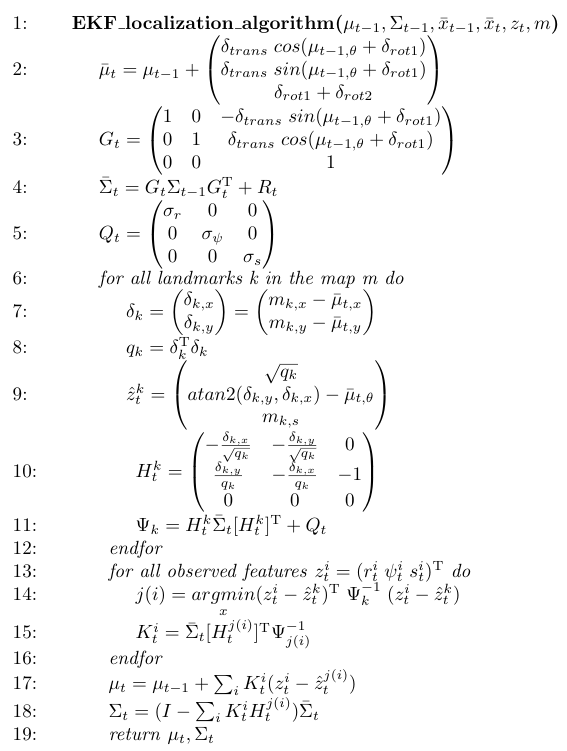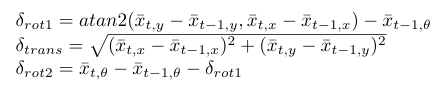Group information

Group Members

Name	Student Number
J.J.W. Bevers	0904589
J. Fölker	0952554
B.R. Herremans	0970880
L.D. Nijland	0958546
A.J.C. Tiemessen	1026782
A.H.J. Waldus	0946642

Meeting Summaries

A logbook with a summary of the contents of each meeting is documented and can be found here.

Course description

In this section, a short description of the context of the course is given.

Introduction

Figure 1: PICO.

As is proven during the current situation concerning the COVID-19 pandemic, our healthcare system is of high importance. However, there are shortcomings for which an efficient solution is required. At the time, hospitals are occupied by many patients. Therefore, doctors and nurses have limited time for human-to-human contact with patients. By automating simple tasks, doctors and nurses have more time for contact with patients. An option is to use an autonomous embedded robot to assist in everyday tasks such as getting medicine, moving blood bags or syringes and getting food and drinks. During this course, software for such an autonomous robot is developed. The goal is to complete two different challenges in a simulated environment: the Escape Room Challenge and the Hospital Challenge.

PICO

The mobile robot used is called PICO and is shown in Figure 1. PICO consists of multiple components. This year's edition of the course will be completely based on the PICO simulator (as developed by the project team) and will, thus, not contain the implementation of the software on the actual robot. Only the relevant components for simulations are, therefore, briefly explained. For actuation purposes, PICO has three Omni-wheels which make for a holonomic base. A Laser Range Finder (LRF) is used by PICO to scan its surroundings, providing PICO with distance data. Furthermore, the wheel encoders data is used to keep track of PICO's translations and rotation (odometry).

Figure 2: Example of the map used for the Escape Room Challenge (left) and the Hospital Challenge (right).

Description Escape Room Challenge

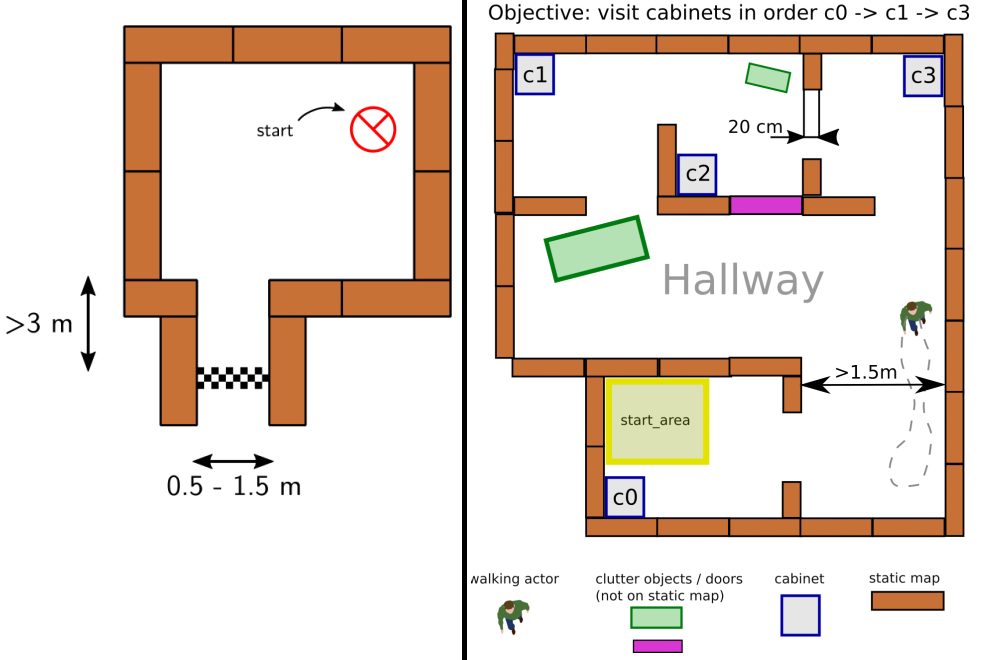
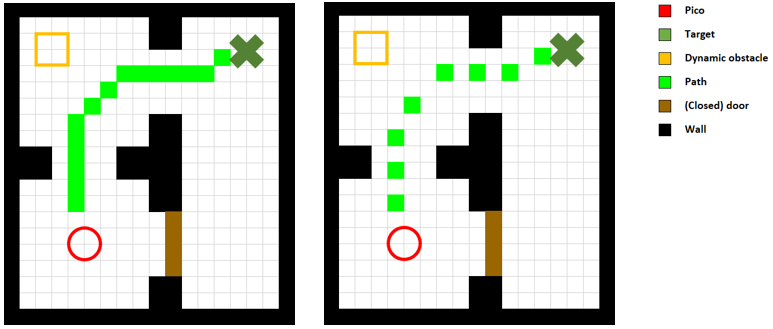
The goal of this challenge is to navigate PICO, through a corridor, out of a rectangular room of unknown dimensions without bumping into walls. An example of an environment map that might be encountered during this challenge is shown on the left side of Figure 2. PICO has an unknown initial position within this room. Thus, PICO first needs to detect and recognize the exit. When the exit is found, PICO has to leave the room as fast as possible by moving through the corridor. The challenge is finished when the rear wheels of PICO cross the finish line entirely. In the Section Escape Room Challenge, the approach is explained in more detail. Here, the algorithms used and its implementations are explained. Moreover, the results of the challenge are shown and discussed.

Description Hospital Challenge

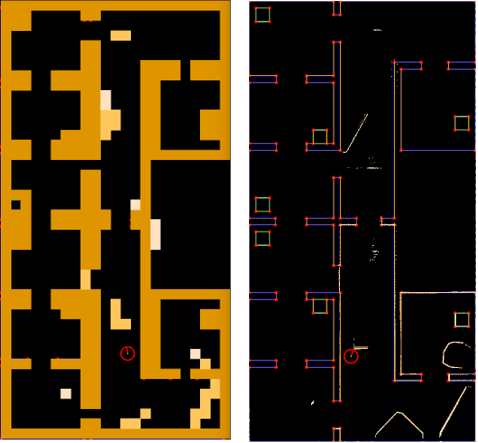
This challenge represents an example of the application of an autonomous robot in a more realistic environment. In this challenge, PICO has to operate in a hospital environment. The environment will consist of multiple rooms, a hallway and an unknown number of static- and dynamic objects. In the rooms, cabinets are present that contain medicine. In this challenge, PICO will first need to recognize its initial position in the known environment. Next, PICO has to plan a path to various cabinets in a predefined order, representing the collection and delivery of medicine. When executing this path, PICO needs to prevent collisions with walls and static- and dynamic objects. An example environment is shown on the right side of Figure 2. In Section Hospital Challenge, more information will be provided.

Design Document

In the design document, a generic approach for the Escape Room Competition and the Hospital Competition is introduced. Requirements are proposed, which are clarified by means of specifications. Based on these, a finite state machine is designed. In each state, groups of functions are proposed. This functionality is, in turn, structured in an information architecture which covers the components and the interfaces. Undoubtedly, throughout the remainder of the course, this document needs to be updated, but its current content functions more as a guideline. Since the Escape Room Challenge is the first challenge, functional specifics may be more focused towards this goal. Because software design is use-case dependent, for the Hospital Challenge the current approach will need to be adapted and improved. The design document deliverable can be found here.

Escape Room Challenge

In this section, the strategy for the Escape Room Challenge is discussed, as well as the algorithms that are used. The software for this challenge can be roughly divided into three main parts: the finite state machine, the potential field algorithm and the exit detection algorithm. These will be covered next. Moreover, for testing, an extra output window is created in which the behaviour of PICO with the created software is shown. This output window will also be used to demonstrate how the different algorithms work.

Finite state machine

Figure 3: Finite state machine for the Escape Room Challenge.

In the design document, the first version of the finite state machine that describes PICO's behaviour is presented. However, for the Escape Room Challenge, a new version has been made, since not all states that were originally present are required. The updated version of the finite state machine is shown in Figure 3. When comparing this to the version as presented in the design document, two states have been left out: planning and recovering. The planning state is left out since it is not required to plan a path, PICO simply needs to leave the room. Including this would unnecessarily complicate the software. The recovering state is left out since it is expected that PICO will not encounter difficult situations, such as moving too close to an unexpected object, in which recovery is needed. The remaining four states will be explained in more detail. Also, the transitions, as indicated by the Roman numerals, and the corresponding guards will be elaborated.

States:

INITIALIZING: PICO starts in this state. In this state PICO is not allowed to translate, only a rotation is permitted. In case the exit detection algorithm detects the opening of the corridor leading to the exit directly, a target is placed in front of the opening of the corridor within the room. Then, transition I is taken which leads to the state EXECUTING. In case the exit detection algorithm does not detect the exit yet, PICO performs a first scan of its surroundings and searches for the exit by rotating. Since PICO has a field of view of 4 rad, which corresponds to approximately 230 degrees, a maximum rotation of 130 degrees is allowed. If the exit is detected during this rotation, again a target will be placed in front of the opening of the corridor. In case the exit is still not detected, transition III occurs leading to state EXPLORING.
EXPLORING: PICO reaches this state if it is unable to detect the exit by rotating. A potential field algorithm is used to explore the environment. Untill the exit has been detected, PICO will drive in a straight line untill it reaches a wall. PICO will be pushed away by this wall because of the repulsive field that is located on the walls (which will be explained in more detail when discussing the potential field algorithm). PICO then rotates and starts a new, straight-line motion towards another wall. These motion steps are repeated untill the exit is detected. As soon as the exit is detected, a target is placed in front of the opening of the corridor and transition IV is taken which leads to the state EXECUTING.
EXECUTING: In this state, the potential field algorithm places an attractive field on the target placed in front of the corridor of the exit. The vector that follows from the combined attractive and repulsive field is translated into translational and rotational velocities, which are used as input for PICO's motion. Multiple targets can be identified in this state, i.e. the beginning of the exit corridor and the end of the exit corridor. When PICO has reached the final target and it no longer detects any walls, it has successfully left the room and transition II is taken that leads to the final state REACHED.
REACHED: After path execution has finished and PICO has reached the end of the exit corridor, PICO stops moving as it has reached its final target location.

Transitions

I: This transition occurs from the INITIALIZING state to the EXECUTING state if the exit is detected directly or after an initial scan by rotating only.
II: This transition occurs from the EXECUTING state to the REACHED state as soon as PICO successfully has left the room.
III: This transition occurs from the INITIALIZING state to the EXPLORING state if the exit is not detected after the initial scan by rotating.
IV: This transition occurs from the EXPLORING state to the EXECUTING state as soon as the exit is detected while exploring the room.

Artificial potential field algorithm

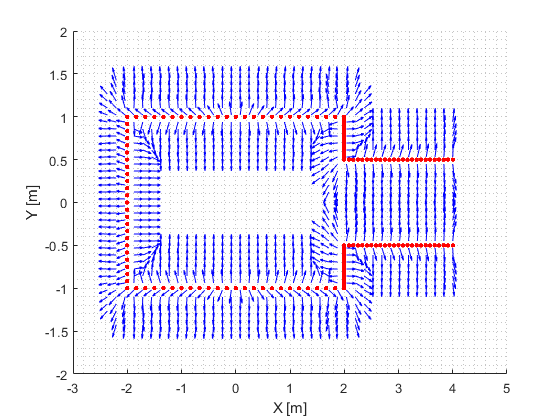
During the Escape Room Challenge, the direction and magnitude of the velocity of PICO are guarded by the potential field algorithm. The potential field within an environment consists of a rejective field and an attractive field. This field consists of gradients defined in 2D space, which at each position point away from surrounding obstacles. An example of a gradient field from the rejective field is shown in Figure 4. For the Escape Room Challenge, however, it is chosen not to use a world map in which the environment of PICO is constructed and saved in a 2D coordinate frame. This decision is made because the goal to which PICO needs to move to, can be defined with respect to PICO's local coordinate frame. Due to this definition, no mapping of the environment is required. A rejective field vector, which represents the gradient vector pointing away from visible objects, is computed continuously at PICO's current position. This vector is based on all current LRF data, such that the gradient with respect to PICO's local coordinate frame (x-axis in PICO's forward direction and y-axis to PICO's left) is computed. For the attractive field, the current goal relative to PICO's local coordinate frame is used. This goal is provided by the exit detection algorithm. The vector corresponding to the gradient of the attractive field is computed by means of a parabola in the xy-plane with respect to the local coordinate frame of PICO, which has its minimum at the goal relative to PICO's local coordinate frame. The attractive field vector equals the gradient of this parabola at PICO's position with respect to the local minimum. Both the rejective and the attractive field vectors are normalized to have a magnitude of 1. This avoids the effect that the rejective field is stronger when PICO observes more datapoints at a certain moment, which could give a distorted effect in the magnitude of the rejective field gradient vector. This effect is caused by the variability in the number of laserbeams that provide a sensible reading.

Figure 4: Example of rejective field gradients.

The normalized field vectors are then used to control the direction of the motion of PICO. In order for PICO to always be able to see the goal, and thus obtain an estimation of the goal relative to PICO's coordinate frame, the orientation of PICO is controlled such that it always aligns with the direction of the attractive field vector. This is done because the LRF data does not obtain distance measurements towards the rear. This control is a feedback loop, with the error equal to the angle of the attractive field vector with respect to PICO's x-axis, and as controller a simple gain.

The velocity in x and y with respect to PICO's local coordinate frame is controlled using both the normalized attractive and repulsive field vectors, such that the x and y components of this vector with respect to PICO's local coordinate frame correspond with the lateral and longitudinal velocity, respectively. In order to combine these vectors, the minimum distance to an object D_min is measured. This measurement is used to compute the contributing factors of the attractive and repulsive field as follows: When D_min is smaller than a tuneable tolerance D_min,t, these factors are multiplied with the corresponding field vectors and then the average is used. This way the rejective field is stronger when PICO is near a wall. A 1/x function allows to drive fairly close to a wall, but not collide with it. Furthermore when D_min is larger than the tolerance D_min,t, the forward vector component in x- and y-direction consists of the attractive field vector and repulsive field vector with factor 1. The repulsive field vector is only defined at a distance Q from obstacles. When obstacles are further away than this distance Q, LRF measurements of these obstacles do not contribute to the repulsive field.

Figure 5: Contribution factors of rejective and attractive field vectors.

This thus yields a new vector relative to PICO's local coordinate frame. This vector can still have a magnitude smaller or larger than 1. When the magnitude of this vector is larger than 1, it is limited to 1, such that the x and y components of this vector can be multiplied with PICO's maximum velocity. Therefore the maximum velocity is never exceeded, but it still enables PICO to drive slower when wanted, i.e. when moving through a narrow corridor in which the rejective field is very strong.

During testing, it was noticed that the exit detection algorithm sometimes rapidly switches between detected targets relative to PICO. When this rapid switching occurs, it is unwanted that PICO rapidly adjusts its direction. Therefore, when this rapid switching is detected, the vector corresponding to the gradient of the attractive field is filtered using a low-pass filter with a relatively low bandwidth. When no switching is detected, thus in the regular case (in which the target is not rapidly switching with respect to PICO's position), this vector is filtered using a low-pass filter with a relatively high bandwidth allowing for faster adjustment of this vector.

Of course, it is possible that at a certain time instance PICO receives a relative goal, while at the next time instance, the exit detection algorithm does not provide a goal. Therefore, each time the potential field algorithm obtains a goal, the orientation of PICO's local coordinate frame with respect to the world coordinate frame (PICO's local coordinate frame at initiation) is captured based on odometry. Furthermore, the distance to the goal relative to this local coordinate frame is logged. In the next iteration, when the potential field algorithm is called with a flag “0”, corresponding to the case that at this call no relative goal is provided, PICO uses the odometry data to move to the last known goal with respect to the last known coordinate frame. During this motion, PICO maintains the orientation of the last known attractive field vector when a goal was still provided. Of course, when the distance to its last known coordinate frame increases, the position error increases. Nonetheless, when the exit detection algorithm initially provides a goal which lies 1 meter in front of PICO, and then can no longer detect this relative goal, PICO will move forward and measure the traveled distance using the odometry until it has travelled the distance of 1 meter with respect to PICO's local coordinate frame when a goal was provided. When this distance has been traveled, PICO stops moving. This way some additional redundancy has been built in, such that PICO can still move when no goal can be provided at a certain time instance.

Exit detection algorithm

For the Escape Room Challenge, it is not required to compute PICO's global location and orientation, i.e. its global pose, within the room. In fact, this is not even possible, because the dimensions of the room are not known and the room may also not be perfectly rectangular. Even if it were, it is unlikely that it would be possible to uniquely compute the robot pose from the LRF data. Since the mere goal of this challenge is to drive out of the room via the corridor, the exit detection algorithm must detect where the exit is relative to PICO's current position, i.e. the target. This information then serves as an input to the potential field algorithm to compute the attractive field. Note that this algorithm, thus, serves as a means of meeting (border-)requirement 'Identify Exit'.

The following considerations are taken into account:

Looking forward, it is decided that it is preferred to already implement as much intelligence as possible which may later function as part of the localization component of the software for the final Hospital Challenge.
In order to feed the potential field algorithm effectively, i.e. in such a way that it is expected to yield a smooth motion, it is also preferred to first compute the center position of the start of the corridor. Only once PICO is positioned sufficiently in front of (or in) the corridor, the center position of the end of the corridor should be computed. If, for example, the target were always placed at the end of the corridor, guided by means of the potential field algorithm, PICO will first drive on a path deemed for collision with a wall. Only when sufficiently close to the wall, PICO would be guided along the wall, towards the corridor.
Moreover, a significantly accurate estimate of these positions is required.

For this reason, instead of simply detecting gaps in the LRF data, the exit detection algorithm must be able to:

i) divide the LRF data into segments belonging to seperate walls,

ii) fit lines on these walls (to minimize the influence of LRF data noise on PICO's perception),

iii) use these fits to compute corners and edges, and

iv) use theses corners and edges to compute the target position.

The exit detection algorithm, therefore, incorporates data pre-processing, data segmentation, line fitting, corners and edges computations, and target computations. These individual parts of the algorithm will be further elaborated below.

Data pre-processing

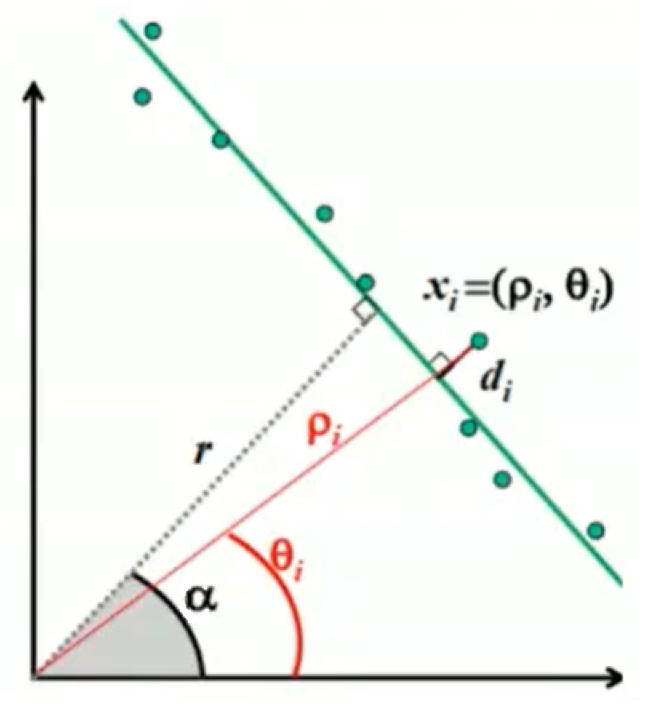
Firstly, the LRF data is pre-processed by simply filtering out data that lies outside of the LRF range, i.e. below its smallest and above its largest measurable distances, 0.01 and 10 m, respectively. It is then converted to Cartesian coordinates relative to PICO's local frame (see Figure 6):

where ρ_i is the measured distance and θ_i the corresponding angle. Note that the index i starts at 0 (and, thus, ends at 999).

Figure 6: PICO's local frame and conventions.

Data segmentation

The procedure that is applied to divide the LRF data into segements is inspired by the famous image processing technique, split and merge segmentation. It is based on the criterion that, if all data points in a considered range lie within a treshold distance to a straight line connecting the first and last data point of that range, a segment is found. This approach is especially suited in the context of the two challenges, because the walls of PICO's environment are (sufficiently) straight. Moreover, the static objects of the Hospital Challenge are (sufficiently) rectangular. The iterative procedure encompasses the following steps and computations:

1. Start with the first and last data points, corresponding to θ = -2 rad and θ = 2 rad, respectively (assuming these have not been filtered out during pre-processing). Set i_start and i_end, respectively, equal to the corresponding indices (0 and 999).

2. Compute the perpendicular distances, d_i, of all other data points to a straight line from data point i_start to i_end [1]:

Here, (x₁,y₁) and (x₂,y₂) are the Cartesian coordinates of data points i_start and i_end, respectively.

3a. Compute the maximum of all distances computed at step 2 and the corresponding index. If this distance is below a certain treshold (which accounts for measurement errors), go to step 4, otherwise, go to step 3b.

3b. Split the segment, i.e. set i_end equal to the index computed at step 3a, and go back to step 2.

4. A new segment is found. Save the indices of the first and last data point belonging to the segment, i.e. i_start and i_end. Set i_start = i_end + 1 and i_end = 999 (again, assuming this data point is not filtered out during pre-processing), and return to step 2.

5. Repeat this procedure until all data points are considered, i.e. until i_start is no longer smaller than the index corresponding to the last data point.

After the segmentation procedure has terminated, segments consisting of a number of data points that is below a certain treshold are discarded. This adds robustness, because occasionally segments only consist of 2 data points, for example, and thereby may form the two edges of an opening. Moreover, a sufficient number of data points is required to obtain a reliable fit.

Line fitting

Next, a line y = a x + b is fitted onto each segment by means of the linear least-squares method. It can be shown that the solution is

where N_seg is the number of data points in the considered segment and the sums run over index i, going from the indeces corresponding to the first data point of the segment to the last [2]. For each segment, the coefficients a and b are stored. The resulting fits are shown in Figures 7-9 as blue lines.

A serious drawback of this approach is that it is not possible to represent vertical lines, because coefficient a goes to infinity. This means that no reliable fit is found for walls that are more or less parallel to the y-axis of PICO’s local coordinate frame. Nonetheless, it is a very simple approach that will show to suffice for exit detection purposes.

Corners and edges computations

For subsequent segments, the Euclidian distance between their neighbouring endpoints, i.e. the last data point of segment j and the first of segment j + 1, is computed. If this distance is below a small treshold, a corner is assumed to be found. To compute its Cartesian coordinates, the intersection of the line fits of the two segments is computed. If the distance is not below the treshold, an edge is found which is a point at which either a jump in the LRF data is observed or at which there is a gap (a set of angles over which no distance within range is measured) in the LRF data. Within the context of the Escape Room challenge, the first occurs if, for instance, PICO ‘looks’ at the corridor at an angle; the latter occurs if, for instance, PICO ‘looks’ into the corridor. Edges, obviously, also occur at the first and last data point of the (pre-processed) LRF data.

For each segment, the coordinates of its first and last point are saved, whether it is a corner or an edge. The resulting corners and edges are shown in Figures 7-9 as red circles.

Target computation

A corridor (entrance) is possibly detected if edges occur between two subsequent segments (in order to exclude the edges at the very first and last data points). Two cases are distinguished for the situation where PICO can ‘see’ the corridor:

1. PICO scans both of the walls on either side of the corridor, i.e. PICO is located in the region directly in front of the corridor, and

2. PICO scans one of the walls of the corridor and the corner of the entrance on the other side of the corridor.

Determining which case is observed is based on the slopes (coefficient a) of the lines fitted through the subsequent segments. In case 1, the observed walls should be more or less parallel, so their slopes should be equal up to a certain treshold. In case 2, on the other hand, the walls should be more or less perpendicular, so a_j should equal -1 / a_k up to a certain treshold.

1. In case 1, the edge that is furthest away from PICO is used. A line is drawn through it, perpendicular to the line fit of the opposite corridor wall. If the length of this line equals the specified corridor width (0.5 meter) up to a certain treshold, the Cartesian coordinates of the midpoint of this line serves as target. This extra check serves as an additional layer of robustness.

2. In case 2, the edge closest to PICO is used. Similarly, a line is drawn through it, perpendicular to the line fit of the opposite corridor wall. Again, if the length of this line equals the specified corridor width (0.5 meter) up to a certain treshold, the Cartesian coordinates of the midpoint of this line serves as target.

The resulting target is shown in Figures 7-9 as a yellow circle. The method described here serves the purpose well, because a target is first placed at the entrance of the corridor. Only after PICO is already in front of the corridor, the target is placed further into the corridor and, eventually, at the actual end of the corridor.

Visualization and testing

In order to see how the developed algorithms operate, a visualization window is created using the openCV library. With this library, dot, line, arrow, circle and rectangle shapes are created to represent the laser range data, detected walls, velocity vectors, corners and PICO, respectively. These shapes are drawn in an output window iteratively representing PICO and its interpretation of its surroundings, as can be seen in the right frames of Figures 7-9. PICO is represented by a red, rectangular box in the center of the window. Red, open circles are used to show the corners and egdes as determined by the exit detection algorithm. Moreover, walls are represented by blue lines. The target to which PICO should move is shown as a yellow, open circle. Finally, a red arrow is used to show the rejective field, a green arrow represents the attractive field and an orange arrow is used to depict the resulting velocity of PICO in its direction of motion.

Using this visualization, the software can be tested and optimized based on the behaviour of PICO. To explain main parts of the testing phase, three cases are considered. Note that a large amount of cases have been tested in order to ensure robust behaviour of PICO during the Escape Room Challenge.

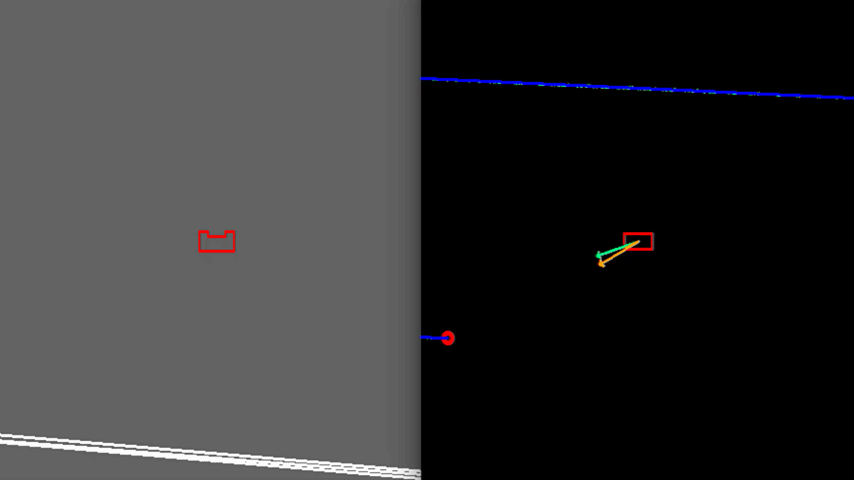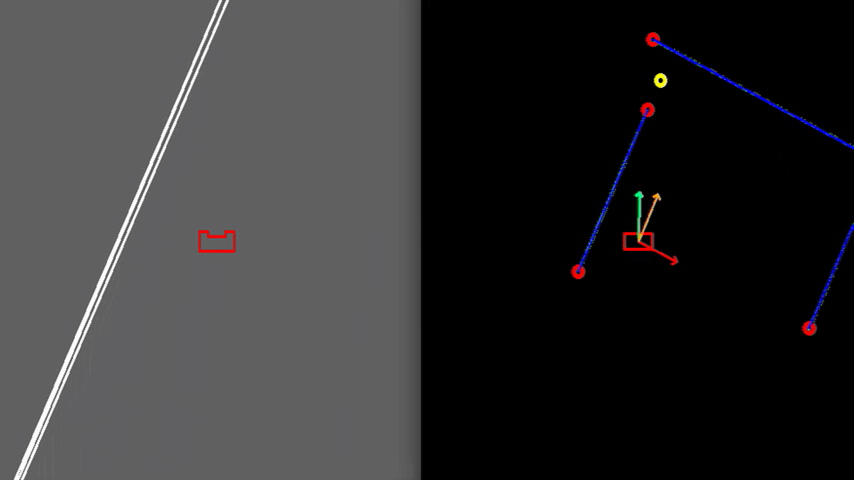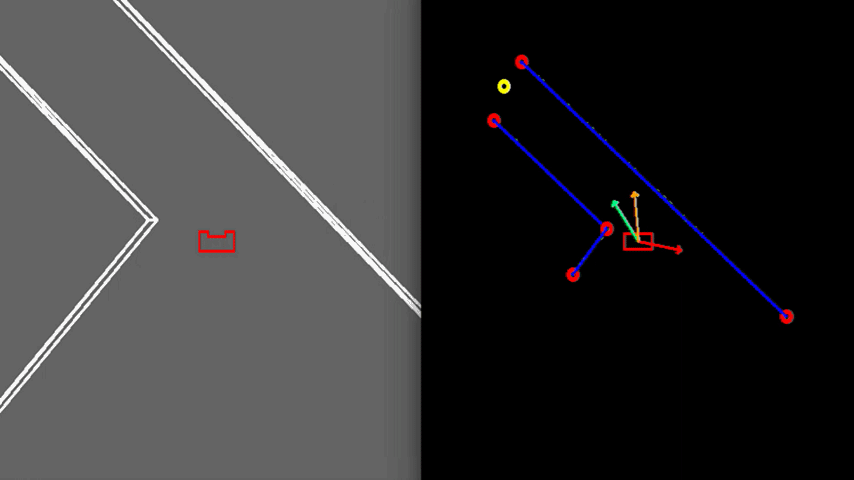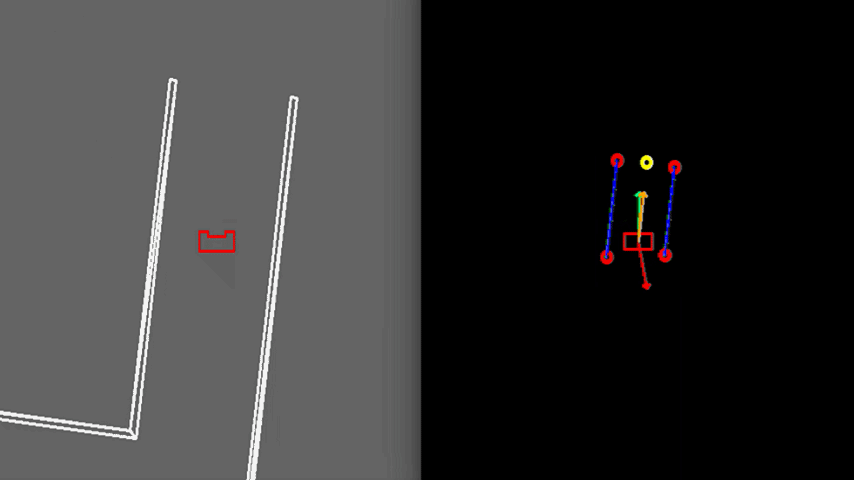
Test 1: Large room and exit in the extension of a wall

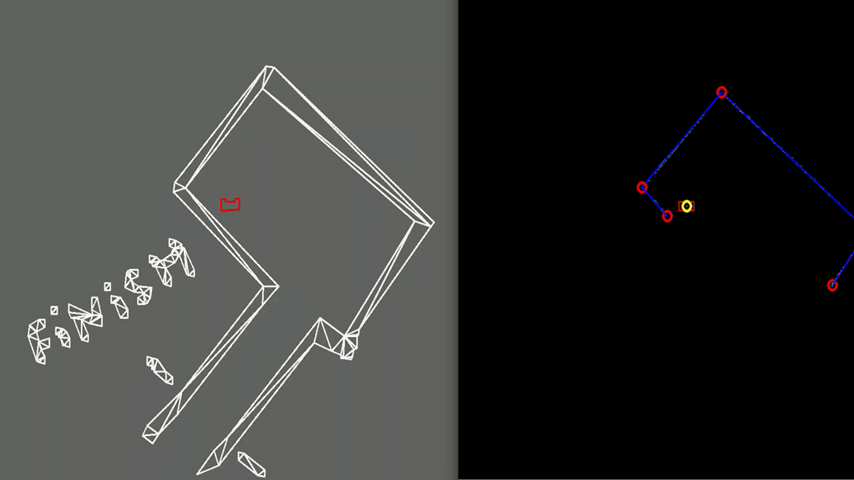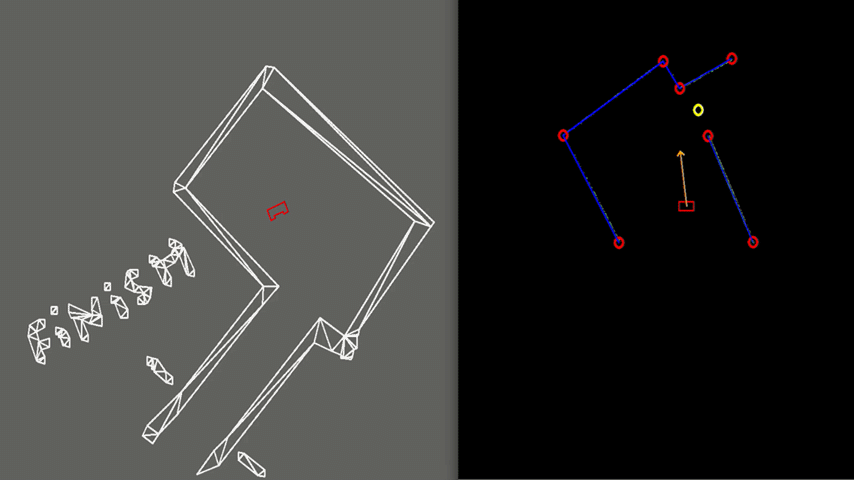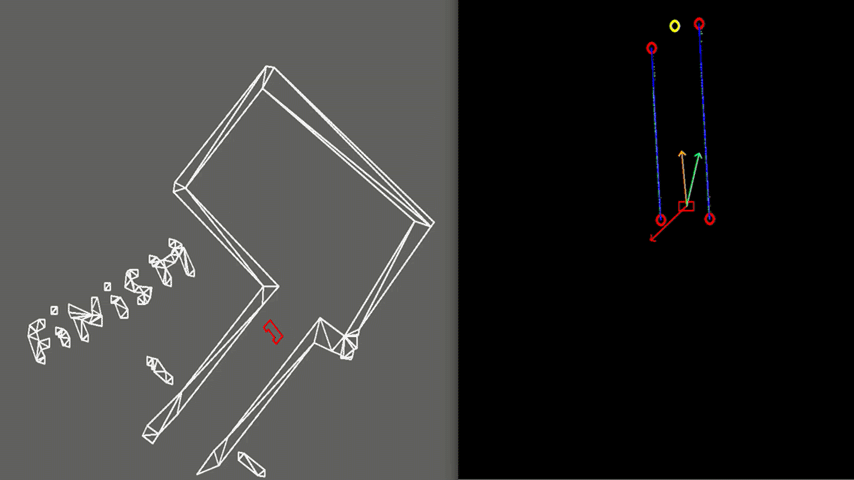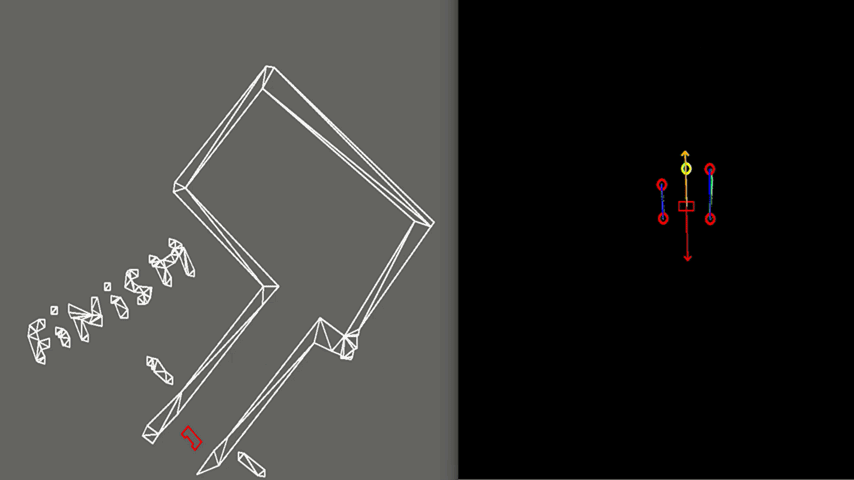
As shown in Figure 7, PICO is positioned in a large, wide room in which one of the corridor walls of the exit is in the extension of one of the walls of the room. In this case, PICO is not able to see the whole room at once because some walls are out of its range that it can observe. Therefore, detection of the exit can be a challenge and hence PICO is programmed to start moving away from the walls untill the exit is detected. This allows PICO to have a better view of the room, since it will start moving more towards the center of the room. If the exit is then detected, PICO starts to move towards it. In the example of Figure 7, this happens quite rapidly. In case the exit would have not been detected yet, PICO would start exploring the room by placing a temporary target in front of him, which is updated until the exit is detected. Detection of an exit of which one of the walls of the corridors is an extension of one of the walls of the room is an unique case which has been tested extensively. However, the exit detection algorithm has no problems to detect these special kind of exits.

Figure 7: Large room and one of the walls of the corridor is an extension of one of the walls of the room.

Test 2: Narrow exit

Another case, illustrated in Figure 8, can be challenging due to the narrow exit of around 0.5 meters. Here PICO’s positioning is made accurate enough to fit through without colliding. To gain more accuracy, PICO is driving slower which is caused by a larger amplitude of the rejective field in the narrow corridor, making the overall velocity vector smaller.

Figure 8: A room with a narrow exit.

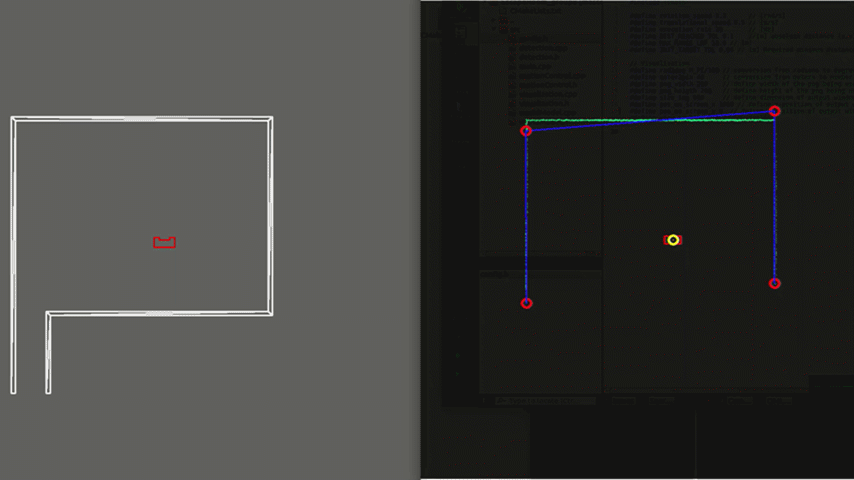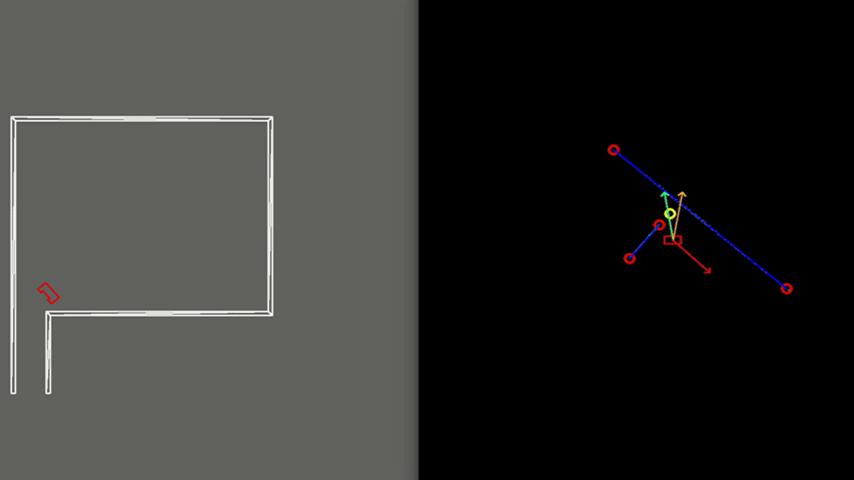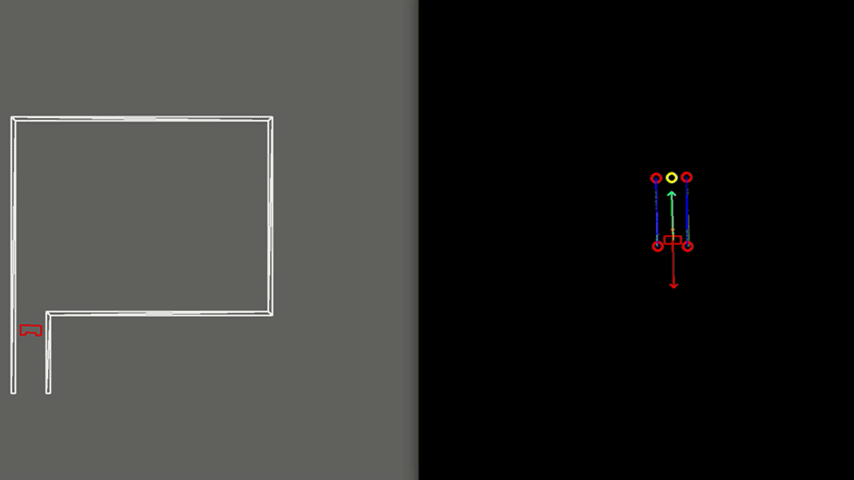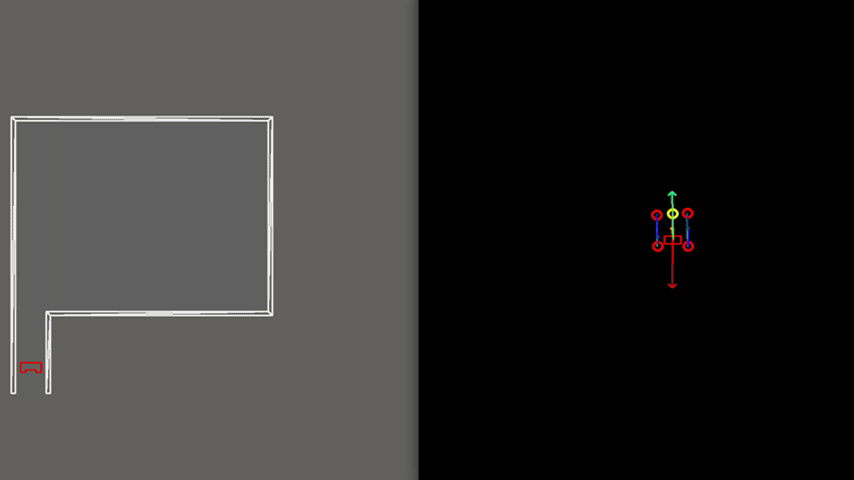
Test 3: Realistic environment

As visible in Figure 9, the walls of the room consist of separated blocks as is expected to be the case in the actual Escape Room Challenge. The exit detection algorithm is able to distinguish these gaps from the exit such that it does not mistake such a gap as the exit. This is achieved by using a minimal threshold which states that an exit must be at least a particular width, this thus provides robustness. As shown, PICO does not mistake these gaps for an exit and successfully leaves the room.

Figure 9: Room with realistic walls containing gaps.

Results Escape Room Challenge

Figure 10 shows the final result of the Escape Room Challenge. During this challenge, PICO managed to escape the room within 15 seconds, as the fastest of all groups. In the beginning, it is visible that PICO starts with rotating counterclockwise. This happens because PICO did not see the exit immediately and therefore starts scanning its surrounding. When the exit is found, a target is placed, indicated by the yellow circle. Next, PICO starts to move towards the exit according to the attractive field placed on the target, represented by the green arrow. It can be seen that the target does not stay located at the exit, but rotates with PICO. This is because the target is updated at a lower frequency and therefore PICO remembers a fixed target relative to himself for a short period of time. When driving, PICO is pushed away from the walls by the rejective field, represented by the red arrow. The resulting velocity of PICO is represented by the orange arrow. When entering the exit, the target is relocated at the end of the corridor.

Figure 10: Final result Escape Room Challenge.

Software architecture

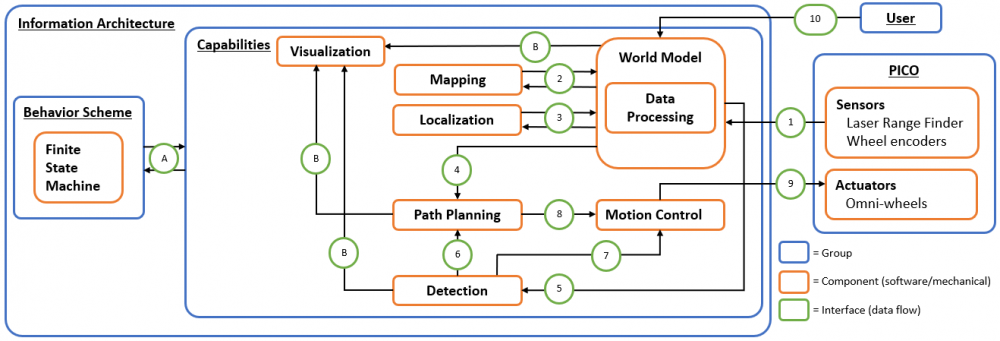
The information architecture, as proposed in the design document, is depicted in Figure 11. It shows a generic approach, so not all depicted components and interfaces may be necessary/used for a specific challenge. Moreover, it is somewhat open to interpretation what functionality is embedded in which component. A short explanation per challenge, therefore, follows below, but the architecture is further clarified first.

In the central section, this schematic overview visualizes what capabilities are intended to be embedded in the software. Between the software and mechanical components, information is shared via interfaces marked in green and labelled with an arbitrary number or letter. These interfaces dictate what information is set by which component, what information is shared and among which components. They are shortly explained below:

10: data received from the user, which may include a JSON file with a map and markers, depending on the challenge.
1: sensor data coming in from PICO (including the provided software layer), i.e. structs with distance data from the Laser Range Finder (LRF) and odometry data based on the Omni-wheel encoders.
2, 3, 5: (possibly) processed sensor data used to map PICO’s environment (mapping), to estimate PICO’s position and orientation (localization), and to detect static/dynamic obstacles (detection). This knowledge is stored in the world model, serving as a central database.
4: a combination of the current map, PICO’s pose and the current (user-provided) destination are sent, to plan an adequate path.
8: computed path, possibly in the form of reference data for the (x,y,θ)-coordinates.
9: velocity inputs computed by the motion control component, ensuring PICO follows the computed path. Simultaneously, the detection monitors any static/dynamics obstacles on the current path online.
6, 7: knowledge of detected static/dynamic obstacles, sent back to either the path planning component to adjust the path or directly to motion control to make a stop.
A: control inputs from the high-level finite state machine to manage what functionality is to be executed and when.
B: data that is chosen to be visualized to support the design process. With other words, the visualization serves as a form of feedback for the designer.

The (software) components are intended to be explicitly embedded in the code through the use of classes. This makes it possible to implement various functionalities that belong to one component as methods of that specific class. Moreover, the use of classes makes it possible to explicitly implement the interfaces described above. More specifically, certain information can be allocated to a certain class.

Figure 11: Software architecture.

Implementation of the software architecture: Escape Room Challenge

Considering the limited requirements of the Escape Room Challenge, the proposed software architecture is a bit 'overkill'. Most functionality, for this challenge, was implemented within the world model component. More specifically, the exit detection functionality and (repulsive/attractive) potential field computations are all embedded in this class. A simple motion control method to move PICO, i.e. to send velocity input references to its base, is then fed with the vector, computed by the potential field algorithm, and the maximum velocities. Furthermore, the detection component just contains a function to check if new sensor data was obtained. In conclusion, the mapping, localization and path planning components were not used for the Escape Room Challenge.

Implementation of the software architecture: Hospital Challenge

For the Hospital Challenge, on the other hand, the proposed software architecture is very well-suited, because this challenge represents a significantly more useful and, simultaneously, a more typical mobile robot application. The discussion in the next chapter will, therefore, be structured based on the exact software components as shown in Figure 11. The only remark is that the detection component, again, just contains a simple method to check whether new sensor data was received. This will be further explained below.

Moreover, it must be noted that in the software for this challenge, the interfaces 2-5 are not implemented as proposed. Instead, multiple interfaces directly between Mapping, Localization, Path Planning and Motion Control are created. This will be discussed in the recommendation section as well.

Hospital Challenge

In this section, the strategy for the Hospital Challenge is discussed, as well as the algorithms that are used. First, the finite state machine is discussed. Afterwards, the four main parts of the software are discussed, which are localization, mapping, path planning and motion control. Once again, visualization is used to test and improve the software. Finally, the results of the Hospital Challenge are shown and an additional, more challenging, case is presented.

Figure 12: Finite state machine for the Hospital Challenge.

Finite State Machine

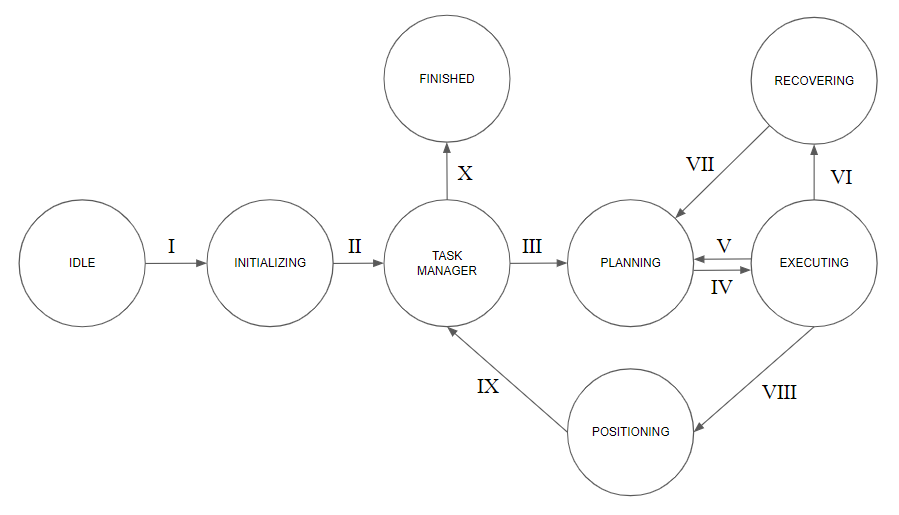
For the Hospital Challenge, a new finite state machine is composed as is shown in Figure 12. In comparison to the finite state machine of the Escape Room Challenge, more states are needed to properly represent the behaviour of PICO. This is expected, since the Hospital Challenge is far more complicated than the Escape Room challenge. This time, a task manager is needed which keeps track of which cabinets PICO already has visited, and which it still needs to visit. Moreover, it is required to make use of path planning, which was intentionally left out for the Escape Room Challenge. Similarly, a recovering state is incorporated as well since PICO now operates in a more complex environment, and therefore might find itself stuck in a difficult situation. Also, since it is required that PICO aligns properly with respect to a cabinet once it has arrived in its near proximity, a new state is introduced for this.

First, the different states depicted in circles are briefly explained, after which the transitions labelled with Roman numerals are discussed.

States:

IDLE: This is the starting state. Transition I is taken to state INITIALIZING as soon as the challenge commences.
INITIALIZING: PICO starts with the initialization procedure, in which it finds its exact position in the predefined starting area of the hospital environment. As soon as PICO has finished this procedure, transition II is taken to the state TASK MANAGER.
TASK MANAGER: PICO is given a task, which can either be to visit a specific cabinet or nothing in case all cabinets have been visited already. In case PICO needs to visit a new cabinet, transition III is taken to the state PLANNING. In case PICO has finished visiting the required cabinets, transition X to state FINISHED is taken. The sequence of cabinets that PICO needs to visit are provided beforehand by the user.
PLANNING: PICO will plan a path to a cabinet using the constantly updated map and location. Transition IV is taken to state EXECUTING as soon as path planning is finished.
EXECUTING: In this state, PICO is executing its path. In case PICO finds that it is unable to follow the path, e.g. when a door is closed, transition V is taken to the state PLANNING, in which a new path from the current position of PICO is produced. It might also occur that PICO runs into a different kind of problem where it is insufficient to simply plan a new path. This can be the case when PICO is stuck or when it almost bumped into a wall or an object. In this case, transition VI to the state RECOVERING is taken in which a solution for the current problem is found. Finally, if PICO has successfully reached its destination and now is located close to a cabinet, transition VIII is taken to the state POSITIONING, where it properly positions in front of the cabinet in order to retrieve the medicine.
POSITIONING: Now that PICO is near a cabinet, proper alignment is needed. As soon as it has properly aligned, transition IX is taken to the state TASK MANAGER, where it is given a new task.
RECOVERING: In this state, last-minute resources, such as resetting the map under specific conditions, are used in order to enable PICO to recover from the difficult situation it has found itself in. As soon as a solution is found, transition VII is taken to the PLANNING state, where a new path is planned taking the solution into account.
FINISHED: This state is reached once all the cabinets provided by the user have been visited, and hence the challenge is finished.

Transitions:

I : This transition occurs from the IDLE state to the INITIALIZING state as soon as the challenge commences.
II : This transition occurs from the INITIALIZING state to the TASK MANAGER state as soon as the initialization procedure has finished.
III : This transition occurs from the TASK MANAGER state to the PLANNING state in case PICO has been given a cabinet it needs to visit.
IV : This transition occurs from the PLANNING state to the EXECUTING state as soon as a path to a cabinet is planned.
V : This transition occurs from the EXECUTING state to the PLANNING state in case PICO notices that the current path is not viable anymore.
VI : This transition occurs from the EXECUTING state to the RECOVERY state in case PICO got stuck or almost bumped into an object while executing.
VII : This transition occurs from the RECOVERING state to the PLANNING state after a solution has been found for the current problematic situation.
VIII : This transition occurs from the EXECUTING state to the POSITIONING state as soon as PICO has reached its goal and is close to the cabinet.
IX : This transition occurs from the POSITIONING state to the TASK MANAGER state as soon as the built-in alignment procedure is successfully finished.
X : This transition occurs from the TASK MANAGER state to the FINISHED state in case that there are no cabinets that need to be visit by PICO.

The finite state machine, as it is described above, is a schematic representation that will be implemented in the switch-case loop of the main file. It then uses the states as cases, and the transition requirements to switch between them.

Localization

Clearly, autonomous behavior of PICO in the context of the Hospital Challenge requires the implementation of a localization algorithm. Recall that, in the Escape Room Challenge, only the relative position of PICO with respect to the exit was required to autonomously drive out of the room. In the Hospital Challenge, however, (an estimate of) PICO's global pose is needed, i.e. its pose with respect to some global coordinate frame, because it needs to know where it is with respect to the provided map of the hospital environment, in order to autonomously visit the next cabinet in a sensible way.

Since a certain starting area is specified on the provided map, the localization problem can be classified as a tracking problem. A certain initialization procedure is, however, required to infer an estimate of the initial pose using the knowledge of the starting area. To solve the tracking problem, typically, extended Kalman filters (EKFs) or particle filters (i.e. Monte Carlo localization) are used. The key difference is that EKFs represent the belief of the robot's pose, or the state, by a single multivariate Gaussian, whereas particle filters represent a multimodal belief by finitely many samples, i.e. weighted particles. As a consequence, EKF algorithms are computationally significantly more efficient. This forms the main motivation to use an EKF algorithm for the localization software component. Moreover, the EKF is relatively simple and tuning is quite intuitive.

An odometry-based motion model is used, because it is generally more accurate than velocity-based ones as it does not suffer from the mismatch between velocity references sent to the robot's base and the actual velocities (if drift and slippage are ignored for the sake of the argument). Other than that, odometry is directly available. Moreover, a feature-based measurement model is used. Such models are computationally cheap compared to beam-based models, because, by extracting features from the raw LRF data, the measurements are projected into a low-dimensional feature space. An additional benefit, as mentioned before, is that quite some software of the exit detection algorithm from the Escape Room Challenge can be reused for the feature extraction algorithm. Furthermore, a maximum likelihood estimator is used for the data association problem. With other words, for each observed feature, the landmark that corresponds best is used for updating the belief.

The feature extraction algorithm will be discussed first, followed by the EKF algorithm and its motion and measurement models, and, finally, the initialization procedure is covered. Both the feature extraction algorithm and the EKF localization algorithm are based on chapters 3, 5, 6 and 7 of [3].

Feature extraction

As mentioned before, a significant part of the exit detection algorithm of the Escape Room Challenge could be used for the feature extraction algorithm. In this section the main changes and improvements will, therefore, be discussed that are done with respect to the exit detection algorithm, in order to transform it into a feature extraction algorithm.

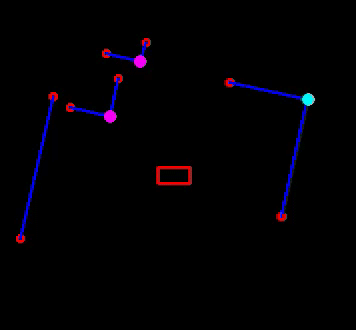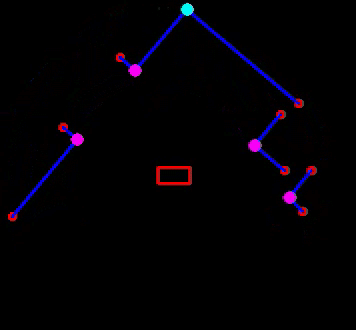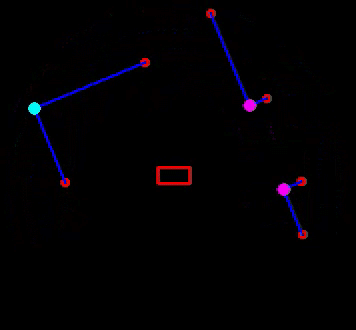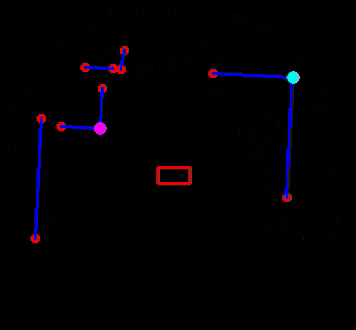
Considering typical Hospital Challenge maps, such as the example map in Figure 2, and the fact that the implemented EKF algorithm accepts point landmarks, it is most straightforward to use corners as landmarks, i.e. room corners, door posts and cabinet corners. A distinction will be made between convex and concave corners to ease the data association problem. As signatures, the integers 1 and 2, for convex and concave, respectively, are used. The feature extraction algorithm will, thus, based on LRF data, compute a number of features currently visible. This will be in the form of a vector z_t containing the range, bearing and signature of each observed feature. The range r_tⁱ is the Euclidean distance from PICO's local frame to feature i and the bearing ψ_tⁱ is the angle between the line connecting PICO's local frame to the feature (of length r_tⁱ) and the x-axis of PICO's local frame. Of course, the same convention is used as before, in Figure 6 (anti-clockwise rotations are positive).

Figure 13: Normal form of a line.

The same exact data pre-processing and data segmentation are used as in the Escape Room Challenge, the line fitting part is improved significantly, and the corners and edges computations and target computation parts are merged and converted into a feature computations part.

Line fitting

In the line fitting part, instead of fitting a linear relation y = a x + b by means of classic least squares regression, total least squares regression is applied to fit r and α, onto each data segment, which define a line in terms of its normal form (r,α), see Figure 13. Note that the definition of d_i in this figure is (slightly) different from the definition used for segmentation purposes. It can be derived that

and

where x and y are simply the means of x and y [4]. In practice, the four-quadrant arctangent atan2 is used to compute α. Moreover, a negative r is corrected and α is adjusted accordingly, i.e. π is added or abstracted such that the resulting angle is in the range [-π, π].

Figure 14: Results of the feature extraction algorithm.

Feature computation

The feature computation part of the feature extraction algorithm starts, identical to the Escape Room Challenge software, by checking whether the Euclidean distance between neighboring endpoints of consecutive data segments is below a certain threshold. If it is not, an edge is found and the ranges (ρ_i) are corrected using the line fit, i.e. the normal form parameters, of the corresponding segment. Note that this is done solely for visualization purposes: the corners and edges of every line segment are stored to visualize the line that is fitted. If the threshold is met, a corner is found. In that case, the Cartesian coordinates of the intersection of the two line fits (of the segments to the right and left of the corner) is computed. These are then converted to the range, r_tⁱ, and bearing, ψ_tⁱ, of the intersection point. A very simple test verifies whether the corner is convex or concave. Namely, if the computed bearing is bigger than α_j and smaller than α_j+1, the corner is convex and s_tⁱ = 1. If, instead, α_j+1 < ψ_tⁱ < α_j, the corner is concave and s_tⁱ = 2.

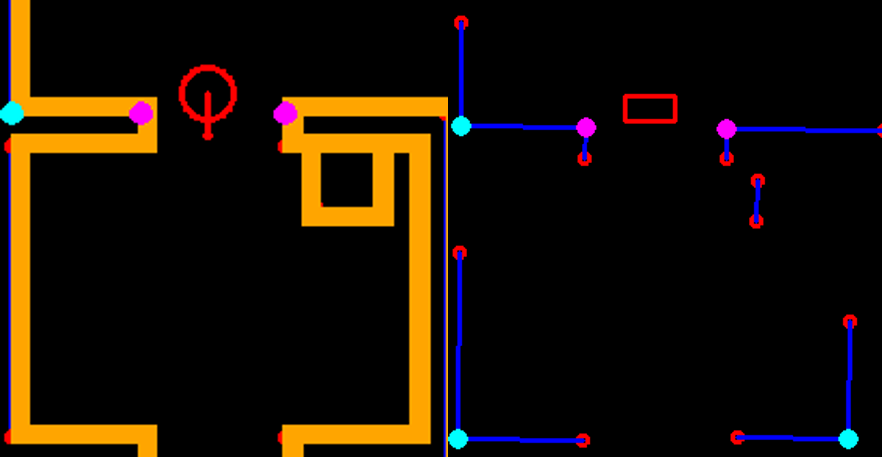
In Figure 14, the results of the feature extraction algorithm are shown. Edges are shown as an open red circle. Solid circles of different color are used for observed features: cyan is used for convex corners and magenta for concave ones. The line fits, for walls and sides of cabinets, are shown in blue and PICO itself is represented by the red rectangle. Note that a feature, i.e. a corner, is only identified if the multiple thresholds, as discussed above, are met. Although this means some visible corners are not identified as such, this adds significant robustness, because features are only used for localization if there is a sufficient amount of information available to accurately compute its position.

Extended Kalman filter

As mentioned, an EKF algorithm is used for localization. The implemented algorithm is given in pseudocode by

As inputs, the EKF algorithm requires the previous belief of PICO's pose given by the mean μ_t-1 and the covariance Σ_t-1 at time t-1 . Moreover, the odometry readings at times t-1 and t, x̅_t-1 and x̅_t, the observed features at time t, z_t, and the feature-based map m, containing the Cartesian coordinates and the signature of all landmarks, are needed. Note that, in the context of the Hospital Challenge, the feature-based map is obtained by adding signatures to the corners in the provided vector map. The EKF algorithm gives an estimate of PICO's pose at time t as output, again given by a mean and covariance μ_t and Σ_t, respectively. Also note that all vectors corresponding to a pose of PICO (μ_t-1, μ_t, x̅_t-1 and x̅_t) contain coordinates (x, y, θ)^T.

In the EKF algorithm, lines 2-4 represent the prediction step, which incorporates the odometry-based motion model, and lines 5-18 the correction step, which uses the feature-based measurement model. Both will be explained in more detail. Actual implementation of the EKF algorithm slightly deviates from the EKF algorithm presented above, but this will be explained later.

Prediction step

The prediction step of the EKF algorithm uses the odometry-based motion model. In this part, a prediction of PICO's pose at time t is determined based on the available odometry data at times t-1 and t. PICO's movement is divided into three separate motions: a rotation δ_rot1, a translation δ_trans and another rotation δ_rot2. The three motions are determined using the odometry readings at times t-1 and t, and are calculated by

In line 2, the mean of the prediction of PICO's pose at time t is determined by adding a vector g_t to the mean of PICO's pose estimate of time t-1. The vector g_t maps the three previously determined motions to the global frame. Note that the angle is again mapped to the range [-π, π]. Next, in line 3, the Jacobian G_t of vector g_t is determined, which is needed in line 4, where the covariance of the prediction of PICO's pose at time t is calculated. Note that a covariance matrix R_t is added, which models the odometry uncertainty and is taken constant over time, so R_t = R.

Correction step

Next, the prediction of PICO's pose is used in the correction step, which uses the feature-based measurement model. First, in line 5, a covariance matrix Q_t = Q is introduced, which models the measurement uncertainty and linearisation errors, and which is taken constant. Next, in lines 6-12, a loop over all landmarks is given. In line 7, a vector δ_k is introduced in which the differences in x and y of a specific landmark and the prediction of PICO's pose are stored. In line 8, the transpose of this vector is multiplied by the vector and stored in q_k, which represents the squared Euclidean distance between PICO and a particular landmark. Obviously, the features in vector z are given in the form (r, φ, s)^T. Therefore, in line 9, the distance between the prediction of PICO's pose and a particular landmark is used to produce a vector in the same form of that of the features. For the first entry, the root of q_k is taken, which corresponds to the range between the prediction of PICO's pose and the landmark. The second entry corresponds to the bearing which is the angle between the prediction of PICO's pose and the landmark, that is corrected for the orientation of PICO's pose prediction. The third and final entry simply copies the signature of the landmark, since this is not dependent of PICO's pose prediction. The bearing is again mapped to the range [-π, π]. Next, the Jacobian of this vector is determined in line 10. In line 11, The Jacobian is used in combination with the covariance of the prediction of PICO's pose in order to produce Ψ_k. Note that the covariance matrix Q of line 5 is added.

In line 13-16, a loop over all observed features at time t is shown. The purpose of this loop is to determine which landmarks correspond to the features that are observed, i.e. to solve the data association problem. As discussed before, a maximum likelihood estimator is applied, which simply means that the landmark that corresponds best to an observed feature is used. This is achieved by minimizing a quadratic Mahalanobis distance function in line 13. The indexes of the landmarks, which are matched to the observed features, are stored in a vector j. Next, the Kalman gain K_tⁱ is determined.

Finally, in lines 17 and 18, the estimate of PICO's pose, represented by mean μ_t, and covariance Σ_t are determined using the Kalman gain and the previous pose estimates. Here, one can see that if all angles would not be mapped to the range [-π, π], this would yield a false injection term for the correction step.

Implementation

Figure 15: Only features observed in the room where PICO is currently positioned in are used for localization.

The implementation of the EKF algorithm (see the code snippet as linked to in Section Code snippets) roughly follows the algorithm as presented above. However, there are some implementation details that will be elaborated further.

Initially, the covariance matrix, Σ₀, of PICO's pose estimate resulting from the initialization procedure is set to zero. In combination with educated guesses for the uncertainty matrices R and Q, this results in convergence of the estimate of PICO's pose to the true pose.

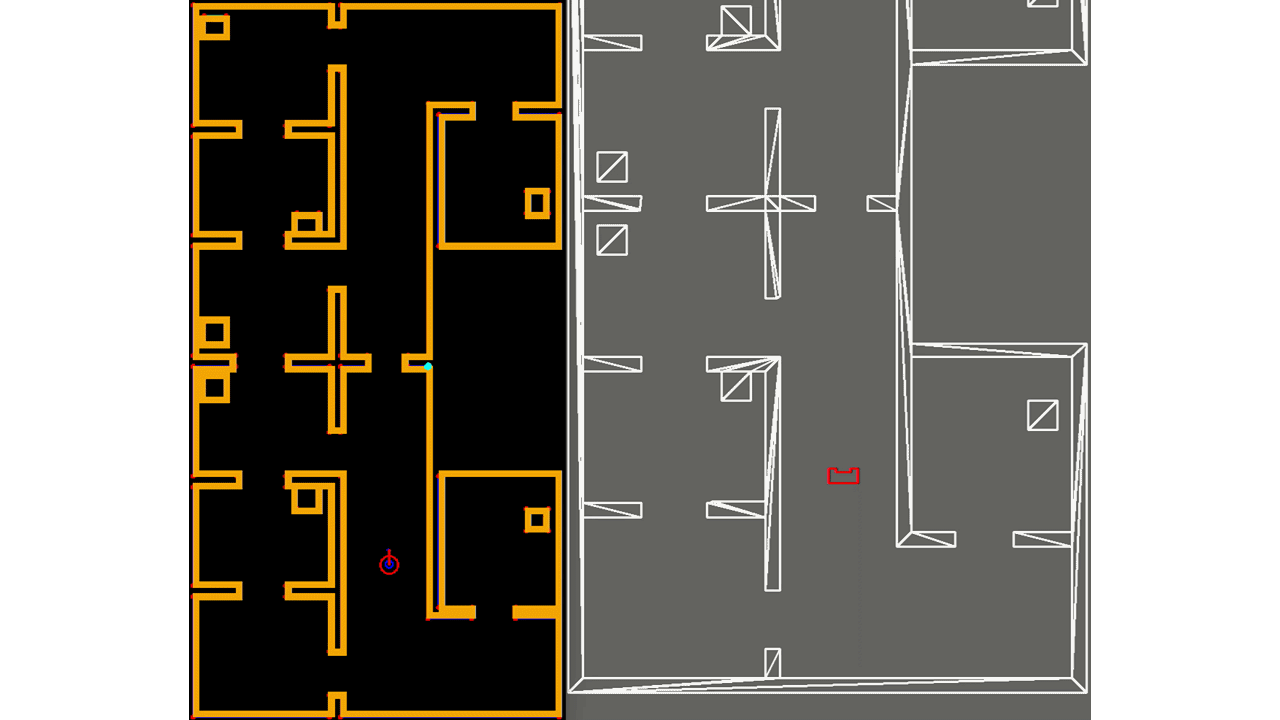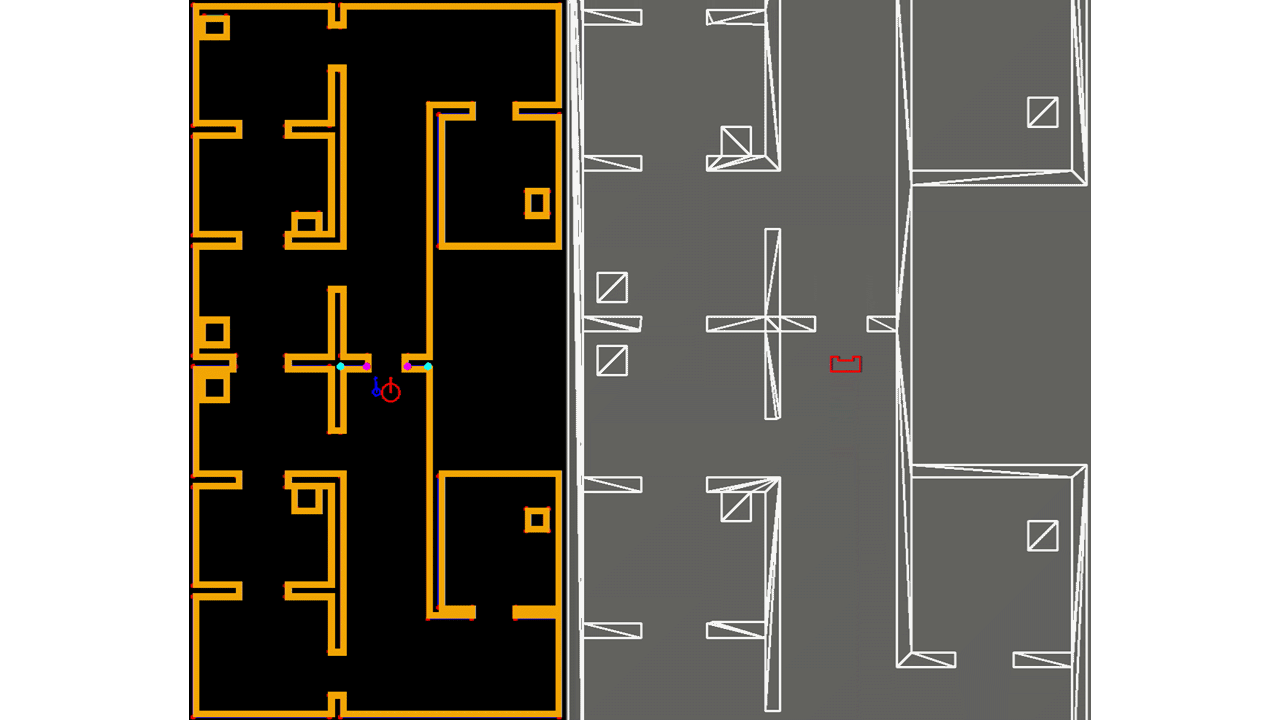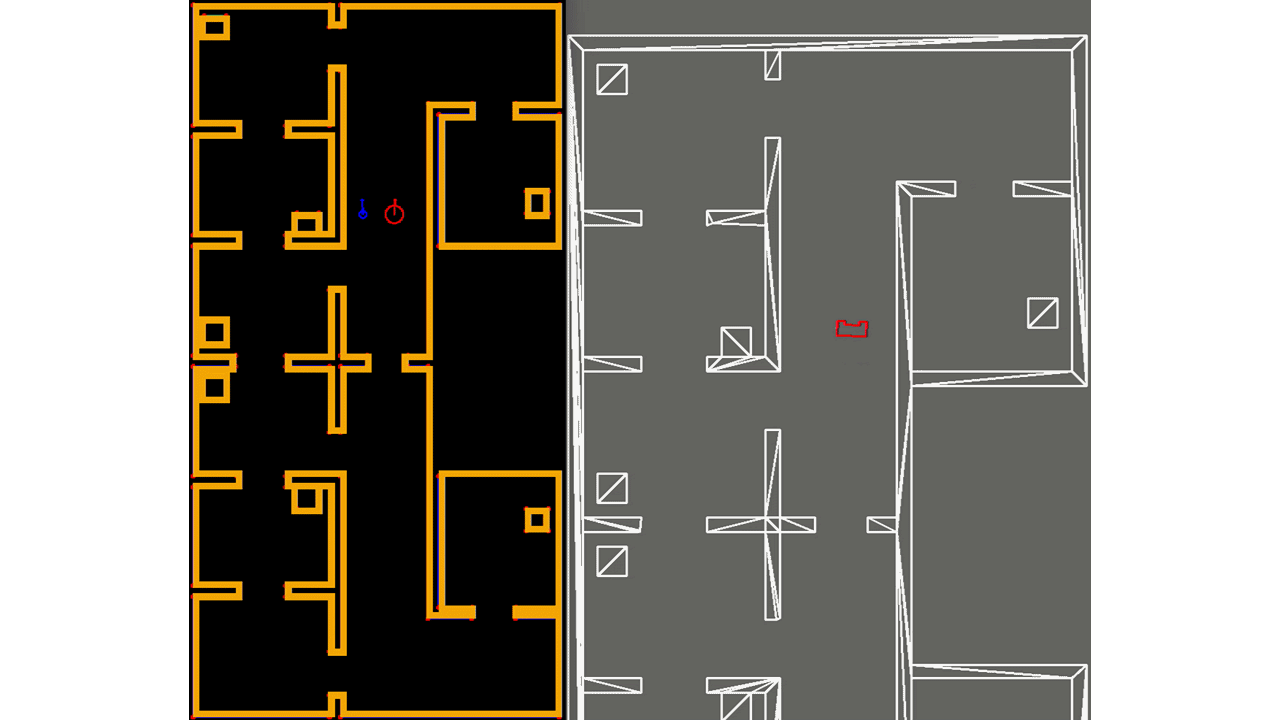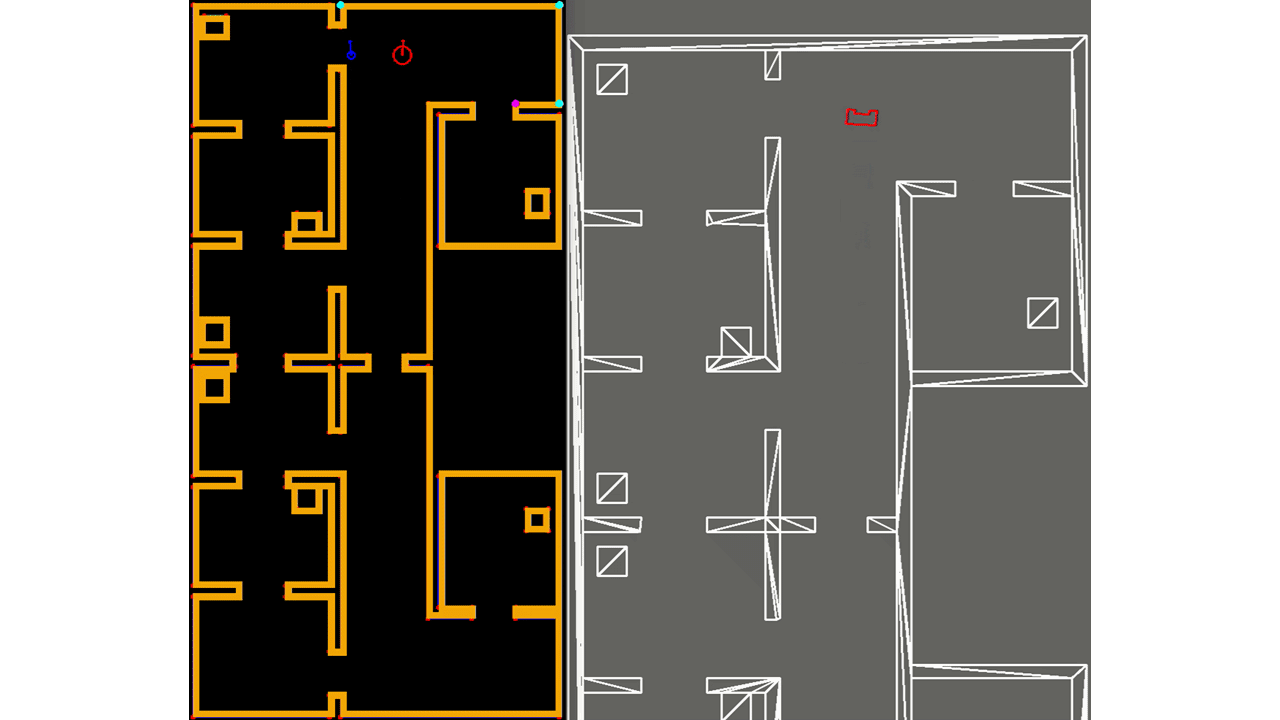
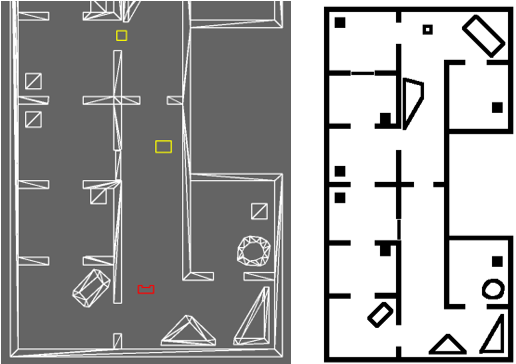
Next, in the loop of lines 6-12, not all landmarks are used, but only those of the room or part of the hallway that PICO is located in. The hospital environment is divided into nine different segments of which seven are rooms and two are a half of the hallway. The result can be seen in Figure 15, where in the left window the features are shown that are used for localization and in the right all features that are observed. As seen, the feature extraction algorithm already recognizes two features in the room that PICO is about to enter, however, they are not used yet. Two advantages of this change are that the computational complexity of the software is reduced and that it provides robustness, since it reduces the chance that wrong data associations are made, which can have serious consequences.

Figure 16: Situation where no features are observed.

Moreover, not all observed features (and the landmark matched to it) are used when computing PICO's next pose estimate, but only those of which the cost function value passes a certain minimum threshold. This adaption also reduces the chance that wrong data assoications are made (or that features that may be observed that do not correspond to any landmark, e.g. corners of a static/dynamic object), which also provides robustness. It might occur that none of the observed features pass this threshold test, or that no features are observed at all. The latter is shown in Figure 16, where PICO is driving through a hallway. In such situations, the prediction of PICO's pose as determined in lines 2-4 is used for the estimate of PICO's pose, as the reader may notice.

Finally, since transpose and inverse matrices are widely used throughout the algorithm as well as many matrix products, separate functions have been created which are used from within the EKF algorithm. This way, the algorithm remains organized.

The essence of localization is shown in Figure 17, where clearly the effect of drift is observed. In this figure, two frames are shown. The left frame corresponds to the produced software where the EKF algorithm is implemented for localization. The right frame shows the actual simulation. In the left frame, two versions of PICO's pose are compared by means of a red and blue open circle. In red, PICO's pose as result of localization using the EKF algorithm is shown. In blue, PICO's pose is shown according to the odometry readings. As seen, when comparing PICO's pose corresponding to the odometry readings to PICO's actual pose in the simulation frame, it is clearly observed that at the end of the upward movement, PICO's pose corresponding to the odometry readings has drifted away significantly. On the contrary, PICO's pose as result of the EKF algorithm corresponds perfectly with PICO's actual pose in the simulation frame. Note that the simulation shown in Figure 17 is shown at 2 times the normal speed.

Figure 17: The effect of drift during movement, shown at twice the original speed. In red, PICO's pose as result of the EKF algorithm and in blue, PICO's pose corresponding to the odometry readings.

Figure 18: Final map for the Hospital Challenge.

Initialization procedure

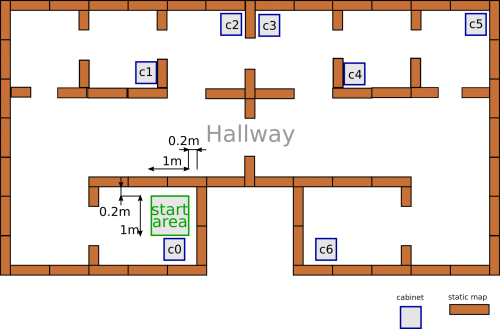
The initialization procedure, as discussed before, is used to compute an estimate of PICO's initial pose which will then be fed to the EKF algorithm. It consist of 2 procedures which are based on the specified starting area as shown in Figure 18. Both procedures use the two corners of the room to the right of the starting area. These will be called corner 1 (top-right corner) and corner 2 (bottom-right corner). The two procedures will be covered next. If the first procedure is unsuccessful, the software switches to the second.

1. In the first procedure, PICO rotates for a maximum of 150 degrees to ensure the whole room is scanned. The angle provided by odometry is used to check this which is sufficiently accurate for these purposes. If two convex corners are found, the distance between them is computed and compared to the length of the wall connecting corner 1 and 2. If the two lengths are equal up to a threshold ánd the two convex corners are part of the same segment, i.e. a wall without an opening is found, corners 1 and 2 are found. The initial estimate of PICO's pose is then easily computed by orientating with respect to either one of the corners and/or the wall.

2. If the first procedure failed, i.e. PICO rotated 150 degrees and was not able to identify corners 1 ánd 2, procedure 2 is applied. It is then assumed that corner 2 is not visible and, moreover, it is assumed corner 1 is always visible. PICO, therefore, starts rotating the other way around until a convex corner is observed. It is then checked whether the range, corresponding to this corner, is within bounds (up to a threshold) that one can compute based on the size of the starting area and its distance to the walls that connect at corner 1. If this is the case, corner 1 is found and PICO's initial pose is easily estimated by orientating with respect to this corner.

Note that, of course, the computed initial orientation of PICO (i.e. with respect to the global frame) is mapped to the range [-π, π].

Mapping

As described in Path Planning, a grid based A* algorithm is chosen. Therefore, a grid-based mapping software component is needed to generate a map. With this map, obstacles can be detected to which the planned path can be adjusted. This map is created based on the occupancy probability of each grid. First, the provided hospital map is imported to the mapping algorithm, giving a high occupancy probability to the grid points corresponding to known walls and cabinets. Then, the map is updated with the current measurement data, increasing the occupancy probability on the grid points which can be seen by PICO. The probability of the grid points between PICO and the measured data points is decreased since the measurement confirms that there is no object in that area. In this way, the map is updated each time new measurement data is received. By increasing and decreasing the occupancy probabilities, the mapping algorithm is able to correct for measurement errors. Note that in Section Code snippets, a link to a snippet of the code of mapping can be found.

Bresenham’s Line Algorithm

Figure 19: Bresenham's Line Algorithm.

To map an environment using a grid-based method, it is necessary to use matrices. These matrices for the occupancy grid-based method are filled with either a 0 or a 1. To eventually be able to determine which grid gets a 0 and which grid gets a 1, probabilities per grid need to be calculated. The first step in doing so is to know which grids need to be updated based on the LRF data PICO received. For that purpose, Bresenham’s line algorithm is used. This is an algorithm that selects which grids in the matrix together make a close approximation of a line. The line, in this case, is one of the laser beams emitted by PICO. By receiving PICO’s global pose and transforming the endpoints of the laser beams to global coordinates (so with respect to the bottom left corner of the map), the algorithm is able to determine what grids of the global mapping matrix need to be updated. It can be the case that the same grid is updated twice in one routine, but this would make sense since, especially close to PICO, multiple lines would pass through the same grid. The actual updates will be discussed later on. A schematic overview of the problem is shown in Figure 19 on the right, wherein the bottom left corner the global world frame is shown. The matrix grids are depicted as grey boxes (either filled or white). Also, PICO is shown on an arbitrary position, with its own frame and one laser beam emitted from it. The filled grids shows how the Bresenham’s algorithm interprets alaser beam, where still a distinction is made between an obstructed grid (as marked in orange) and a free grid.

Since there are a lot of laser beams per update received by the sensor, and constant updating of the surroundings is desirable, the entire algorithm should be able to quickly execute. Otherwise, other software components would be delayed by the mapping updates, which would counteract its whole purpose. By using this specific algorithm, only updates are applied to grids that are relevant and lie within PICO’s detection range. Together with the local updating, these computations are generally very efficient from a computational standpoint.

Bayesian Logit Updating

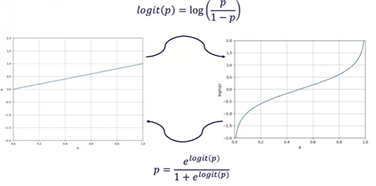
Figure 20: Logit conversion of a value between 0 and 1 to negative and positive infinity [5].

When determining an occupancy probability for a grid point between 0 and 1, the values become very close to these integers. When a grid point is certainly unoccupied, the probability is decreased every time this is confirmed, resulting in a probability close to 0. The same goes for certainly occupied grid points, which results in an probability close to 1 with very high significance. Multiplication of such numbers on a computer can lead to significant rounding errors and is very inefficient. To solve this, the probabilities are converted to log odd probabilities using the logit function. This logit function maps the probabilities to numbers ranging from minus infinity to infinity instead of 0 and 1, as is shown in Figure 20.

The current belief of the grid cell occupancy is determined by the Bayesian log odd update function:

Here, the first term is the logit of the inverse measurement model which indicates the update based on the measurement. This update is added to the second term, which is the previous probability at time t-1. The third term is the initial probability that a grid cell is occupied. In this case, this value is set to a 50% probability, so to zero in the logit form, since the provided map is implemented as a high initial probability. This way, a grid cell in the initially provided hospital map is occupied with a very high probability, instead of a certain determined probability, to be able to correct for localization errors.

After each Bayesian update, the probability value is converted to a value between 0 and 1. When this probability is higher than an adjustable threshold, the grid cell is displayed as occupied. Moreover, the weights of the increment and decrement of the probability updates are adjustable. These parameters are tuned in such a way that static objects are rapidly drawn on the map and errors in the measurements can be erased. Dynamic objects are drawn on the map, but removed after a short period of time since PICO observes that the object is no longer occupying those grid cells. In this way, a “shadow-like form” is drawn following the dynamic object which is used in path planning to avoid the obstacle.

Added functionality

In some circumstances, it may be the case that the grids in the map have been updated in such a way that they do not represent the real situation accurately anymore. This may be the case due to a moving object leaving a trace which cannot be corrected since PICO has no line of sight on these grids anymore. It may be a rare situation, but the mapping software component has some functionality built-in that can be used to reset the map to its initial state, only showing the known walls, corners and cabinets again. From there onwards, mapping continues to update the now reset map according to what PICO sees. This functionality is carefully used so that the map is not reset unnecessarily, losing vital information such as the location of closed doors and objects.

Functionality is also added through different shades of the grids based on their probability. This mainly functions as feedback to see what PICO thinks. If grids are coloured using the relatively lighter shade of orange, it indicates that PICO does not have enough information to almost certainly say that an object is at that position. The implementation of this can be seen in the simulations of the Hospital Challenge. Currently, PICO does not base its decisions on the three different shades since they all lie above the tuned probability threshold that distinguishes free and occupied grids. This can be a future improvement.

When PICO has seen the entire hospital, the generated map would give a result as shown in Figure 21. Figure 22 shows the different grid sizes that can be used. Typically, a rather large grid size is used in the challenge since high resolution mapping is not needed to plan and execute a path.

Figure 21: Example of the mapping of static objects.

Figure 22: Example of the possible grid sizes of the map, 0.3 meter (left) 0.06 meter (right)

Path planning

In the Escape Room Challenge, a feature detection algorithm was used to find the exit of the Escape Room. This data was then used as input for the attractive field of the potential field algorithm, resulting in PICO having a goal relative to its local coordinate frame (the exit corridor) to drive towards. This approach worked very well for the Escape Room Challenge, but since the Hospital Competition is much more complex, a dedicated path planner is required to guide PICO through the map and towards the cabinets.

Considered optimal path planning algorithms

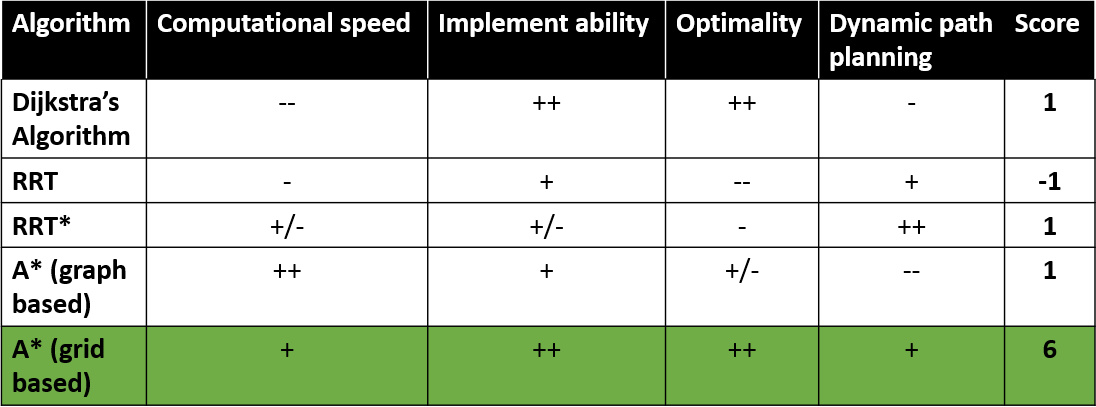
Several options for path planning algorithms have been considered for this cause. Dijkstra's Algorithm, Rapidly Exploring Random Tree (RRT), RRT* and graph- and grid-based A* algorithms have been examined and evaluated for several important properties. Based on the fast computation time with respect to other grid-based path planning algorithms, and relative ease of implementing, it is chosen to work with a grid-based A* algorithm. The main argument of choosing the A* algorithm is that a grid can easily be updated with obstacles dynamically, such that paths can be planned around detected obstacles. In comparison with, for example, weighted graph A* planning, it is required to choose nodes which can not be altered dynamically easily. An overview and rating of the algorithms that are examined can be seen in Table 1. A snippet of the code of path planning can be found in Section Code snippets.

Table 1: Considered path planning algorithms with scores for relevant properties.

A* Algorithm

The A* algorithm works as follows: In a global coordinate frame, a path needs to be planned from a continuous starting point in meters to a continuous target in meters. This global map is transformed into a grid, as explained in Section Mapping. In this grid of size N x M, a path has to be planned from a start point (i,j) index towards a goal point. From the start point, all adjacent grid points that are not obstacles are evaluated. For each adjacent grid node n the cost g(n) is calculated, which represents the Euclidean distance from the start node to node n, and the cost h(n), which represents the Euclidean distance from the target node to node n. The algorithm then goes to the node which has the lowest cost f(n) = g(n) + h(n), and evaluates all adjacent nodes in a similar fashion. All visited nodes are iteratively stored in a CLOSED list, such that nodes can only be visited once by the algorithm. Furthermore, all evaluated adjacent nodes are stored in the OPEN list, such that cost functions of adjacent nodes only have to be computed once. and then starts evaluating all adjacent nodes that have not been evaluated before. Prior to the iterative search of finding nodes with minimum cost functions until the target node is found, obstacles are placed in the CLOSED list, such that these can not be visited by the algorithm. Obstacles like walls have a very high value for g(n) and h(n), and are thereby automatically avoided by the lowest cost determination. In case no unevaluated adjacent nodes of the currently evaluated node are present, or if the available adjacent nodes are obstacles, the node with the minimum cost function f(n) from the OPEN list is taken. When a dead-end is reached by the algorithm, it automatically returns to the last grid point with the lowest combined cost that is not evaluated yet. This process is then repeated until a path of grid nodes is found from the start to the goal. Using this approach, it is of course also possible that no path can be found, for example when the starting point is enclosed by obstacles. In the latter case, the algorithm provides an exitflag which indicates that no path could be found.

Figure 23: Path planned with the normal map (left) and with the weighted map (right).

Weighted Map

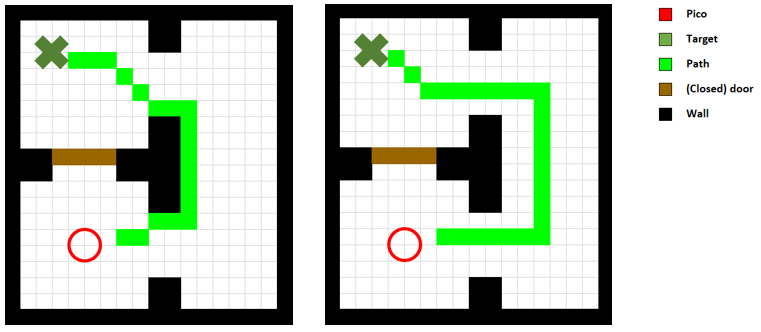
If the A* algorithm would be implemented like this, it is likely that a path would be planned directly next to walls and/or other obstacles, as it treats a minimal travelled distance as being optimal. In order to avoid paths to be planned close to corners, close to walls in a hallway or tightly past edges of door openings, a weighted map is made and added to the cost function, such that the evaluated cost function becomes f(n) = g(n) + h(n) + w(n). The weighted map is constructed on the last known grid map as explained in Mapping, before the A* algorithm is called. It is constructed by evaluating each node (i,j) in the map. First, adjacent nodes are evaluated and checked whether they contain an obstacle. If they do not contain an obstacle, the evaluation radius of node (i,j) is increased such that all next adjacent nodes are evaluated. This is repeated until an obstacle in the evaluated circumference is present, or the evaluation radius exceeds a threshold, which represents the maximum distance from an obstacle from which the weighted map affects the planned path. If one or more obstacles in the circumference are detected, the Euclidean distance with respect to node (i,j) is computed. Then node (i,j) is assigned the minimum of these Euclidean distances multiplied with a weight factor W, such that node (i,j) in the weighted map contains a weight based on the Euclidean distance to the nearest obstacle w(n). Thus, now, when a node is evaluated by the A* algorithm and the cost function f(n) is calculated, the corresponding cost w(n) is extracted from the weighted map. Figure 23 shows the difference between a path that is planned with and without the weighted map.

Figure 24: Path planned with the weighted map (left) and with the blocked map (right).

Blocking Map

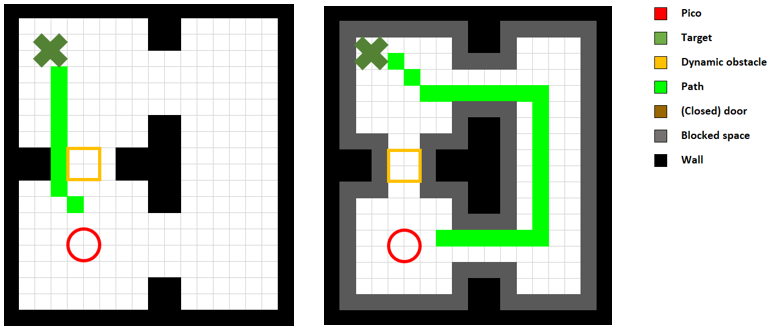
As the grid size of the map is parameterized, it can be chosen to have a smaller length than the maximum width of PICO. Therefore, for the A* algorithm, it would be possible for PICO to plan paths through openings which it does not physically fit throuh. An example of such a case is when a dynamic obstacle is standing in a door opening. It then partially blocks the door, but if the grid size is sufficiently small, grids in between the dynamic obstacle and the edge of the door are interpreted as free space by the mapping algorithm. Therefore, in this case, a path could be planned through this small opening through which PICO does not fit. The weighting algorithm takes care of this problem in regular cases, as this adds a sense of optimality of rather taking a detour than driving close through a wall, which is the case for such small openings. However, when this detour becomes very long, it is no longer optimal. Increasing the threshold of seeing lager detours still as being optimal with respect to planning through small gaps can be achieved by increasing the maximum weight of the weight map. Increasing this weight, however, negatively affects the planned paths in regular cases as the weighted map is constructed using the Euclidean distance of each node with respect to the closest wall. This would then thus result in the path planner planning through the minimum of the weighted map, which is not always desirable. Therefore, the solution to this problem is to also interpret nodes which are less or equal than 0.5 times the width of PICO away from obstacles, as being obstacles, and hence adding these nodes to the CLOSED list. Therefore, a path can never be planned through gaps or near walls through which PICO does not physically fit, or at which PICO cannot physically be present without having a collision. Figure 24 shows how this approach leads to the desired path.

Reducing computational time using compression

Figure 25: Fine (left) and coarse path (right) from a certain starting location to the target.

At this point, the computation time of the path is relatively long compared to the time it takes PICO to follow it. An easy way to increase the computational speed would be to simply increase the grid size, but this has the large disadvantage of losing detail. This detail is not required in a lot of cases, but in some cases, i.e. in tight spaces, this detail is required to be able to compute a detailed map around obstacles. Therefore, it would be desirable to be able to switch between coarse path planning with low computational times, and fine/detailed path planning in cases where coarse path planning does not suffice. Therefore, path planning with a variable grid size was implemented based on [6]. This way of planning allows for grid sizes of distant nodes to be larger and nodes closer to the current position to be smaller. This way, a fine path is planned and the computational time is reduced. The downside, however, is that each time the end of the fine path is reached, a new path must be computed. Therefore, the total time it takes to compute a fine path is spread out over the distance being travelled. After implementation and tuning, this did not result in satisfactory behaviour. The essence of using a coarse grid and a fine grid for path planning, however, was maintained. With respect to mapping capabilities, this can lead to walls or other objects being portrayed bigger than they actually are. Several improvements have been tried, where some were more successful than others. The most significant improvement is elaborated below.

In order to be able to dynamically switch between coarse and fine path planning using a provided grid map obtained from Mapping, it is necessary to be able to compress the map. The compression function uses the map and a compression factor N as an input. When using a compression factor of 2, (2x2) grids are compressed into a single grid, hence reducing the dimension of the map, but also removing detail. The map is compressed by looping over blocks consisting of size N x N, where N is the compression factor. If there is an obstacle in any of the elements of block N x N, the compressed element is assigned a 1 indicating an obstacle is present, and otherwise is assigned a 0 indicating it is free. As the map spans a 2D space, the number of potentially evaluated nodes by the path planning algorithm reduces quadratically as a function of the compression factor N.

The compressed map is then used as input for the path planning algorithm. After a path is computed, the path is decompressed such that the path is defined in the mapping grid. Figure 25 on the right shows the uncompressed (left, fine) path and the compressed (right, coarse) path for a given starting point and target. Of course, compressing the map has downsides. For example if the compression factor is too high, too much detail is lost and door openings are no longer detectable in the map. It can thus happen that due to compression, no path can be planned from the starting point to a certain target. In this case, the corresponding exitflag by the A* algorithm is activated, and the compression factor can be reduced.

Potential Improvement

One of the ways to detect if a path needs to be computed is if a previously unmapped obstacle is now in the way of the planned path. The way that this is detected is by simply checking if no obstacles are present on the nodes of the path in the grid map provided by Mapping. Of course, a coarse path is computed using compression and by decompressing the computed optimal path, it is possible that no obstacles are present in the provided map on the nodes of the path, but an obstacle is actually in between the nodes of the planned path. For example, a door could be initially assumed to be open, but as soon as PICO sees it, the obstacle is updated on the map. When this obstacle only consists of a single node and this node does not match a coarse path node, then the path being blocked is not detected. In order to enable this detection, the nodes in between the coarse path nodes must also be checked. Such an algorithm has not been implemented for this course, but is certainly a good improvement as then, similarly as is implemented for a fine path, PICO can replan the path as soon as it detects an obstacle being in the way of the path.

Motion control

The path planning algorithm now provides various options to compute an optimal path, due to the compression function. From this function, a path in (x,y) coordinates in meters is obtained. Simultaneously, from the localization algorithm, PICO’s (x,y) position within the global coordinate frame is obtained. In order to follow the path, PICO’s (x,y) position in the global frame and a goal on the path with respect to this global frame are used to compute a relative goal with respect to PICO’s local coordinate frame. This relative goal is then provided to the attractive field, as also used during the Escape Room Challenge. The resulting effect of this approach is a control loop which actuates PICO to a goal on the path with a simple gain. This gain can be increased by choosing a steeper attractive field towards the relative goal.

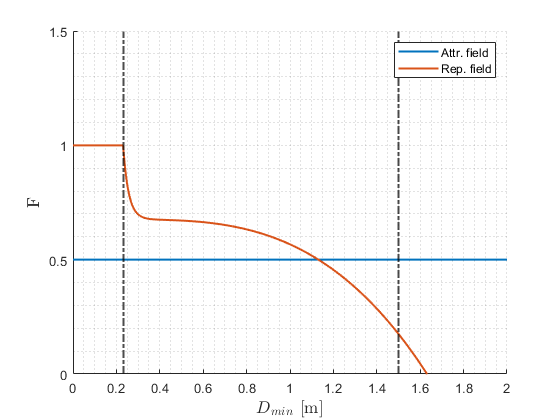
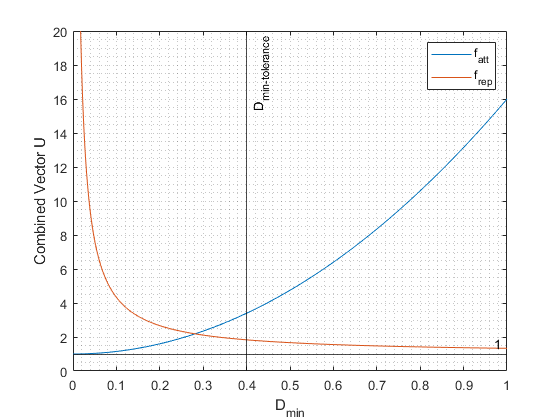
Figure 26: Combination of attractive and repulsive field vector as function of minimum distance to an obstacle.

In order to enable the possibility that a coarse path can be followed continuously, without hitting details of objects in the world which are not taken into account in coarse path planning due to compression, a rejective field is added. The rejective field takes into account all the LRF data within a radius of PICO, which is set to be 1.5 meters. Any laser-beam within this range contributes to a repulsive vector. Both the repulsive and attractive field vector are normalized, and combined into a single vector which is used to control the direction of motion. The orientation of PICO is similar as introduced during the Escape Room Challenge, aligned with the attractive field vector, such that PICO is always facing its target. The normalized vectors of the attractive and repulsive field are combined using the corresponding weight factors F as indicated in Figure 26, representing the attractive field in blue and the repulsive field in orange. The factor for the repulsive field is dependent on the minimum distance, D_min, of a visible object with respect to PICO. The effect of the repulsive field vector with respect to the attractive field vector is increased when PICO is closer to an obstacle. The dotted black line on the left is the threshold at which PICO executes an emergency stop.

Another tuneable parameter is the goal on the path which is provided. The distance of the target on the path with respect to PICO’s position can be tuned. For coarse path planning, this distance is relatively large, as this provides more flexibility for the potential field algorithm. For example, tight corners of the path can be cut off safely, due to the incorporation of the rejective field. This enables that a relatively coarse computed path still result in a smooth optimal trajectory of PICO’s motion. The distance of the target on the path can be interpreted as if PICO is being dragged along by an imaginary rope. The target on the path can be interpreted as being an imaginary rail, dragging PICO along the path using the rope. Increasing the length of this rope allows more flexibility in movement with respect to the computed path, but requires more effort by the rejective field algorithm to avoid obstacles. Decreasing the length of the rope enforces that the computed optimal path is followed more closely, and thus reduces the effort of the rejective field. By adjusting this length, it is possible to dynamically make an adjustment between the potential field algorithm and the rejective field algorithm, where the potential field algorithm is fast, but less robust, and the A* path planning algorithm is robust, but is slower to compute.

Coarse path planning is always the initial option of path planning and actuation of motion, but when PICO has detected an object within a near collision radius, it is likely to be in a tight space, where the coarse path planning in combination with the imaginary long rope is insufficient. In the latter case, the compression is reduced such that a fine path is computed. Simultaneously, the length of the rope is reduced such that the computed path is followed more closely and the effort of the rejective field is reduced. This way, it is possible to compute paths out of tight spaces where a potential field algorithm in combination with a coarse path does not suffice.

Furthermore, as PICO does not obtain LRF data from the rear, it is desired for PICO to avoid driving backwards as much as possible. This is because the rejective field from the potential field is constructed from all LRF beams, and thus does not take into account the obstacles from the rear. In order to ensure that PICO drives forward while it is following a path, a control policy is made in which PICO's translational speed is limited when the angle of PICO's x-axis with respect to the attractive field vector is large. When this angle reduces, a larger translational speed is allowed. This way it is ensured that, when PICO has to follow a path which starts behind him in a certain situation, PICO first turns. Only when he has turned sufficiently (angle reduces below 30 degrees), the translational velocity is increased.

Recovery state

For situations in which it is impossible for PICO to follow the fine path as well, another solution has been incorporated. The situations in which a fine path is calculated, but cannot be followed can occur when static obstacles block the path, when a dynamic obstacle has appeared on the path and is stationairy because PICO is too close to it, or when the goal is actually unreachable due to obstacles and/or closed doors. For the first two situations, a recovery state is introduced.

The recovery state is triggered whenever PICO has to make an emergency stop, meaning that an unexpected obstacle has appeared on the path and PICO cannot continue its current movement. In the recovery state, PICO's direct surrounding is mapped more accurately than in the planning state, increasing the likelihood of the path planning algorithm to find a path that leads PICO out of this situation. In the recovery state, the same approach of first looking for a coarse path and only then producing a fine path is used. For the situation that a dynamic obstacle blocks PICO and thus results in the dynamic obstacle being prohibited from moving, a counter is used such that the amount of path planning attempts remains limited. If a threshold value is reached, PICO will stop planning, and will instead follow its repulsive field gradient for 1.5 seconds to move away from the dynamic obstacle, therefore resolving the situation since the dynamic object is now allowed to move again.

Detection

In the original software architecture, a detection component was taken into account. The function of this component mainly evolved around the detection of objects and walls, influencing the motion control and path planning components via the earlier described interfaces. However, while developing the motion control and path planning components of the software, the detection functionality, as it was imagined beforehand, was already incorporated within these components themselves. So path planning took the responsibility to detect and plan around static/dynamics obstacles on the path, while motion control detects whether or not the current goal position is reached. Therefore the detection component has eventually been dropped in the final architecture.

Visualization

The visualization output window, is initialized by using the walls, corners and cabinets as given in the provided vector map of the hospital environment. The occupancy-based grid map is drawn in the same window. Here, objects are colored in different shades of orange, where objects with high occupancy probabilities, such as the walls, are given a darker tone than detected objects with lower occupancy probabilities. At the localized position and orientation, PICO is drawn as a red, open circle. The detected convex and concave corners, used for localization of PICO's pose, are indicated by cyan and magenta filled circles, respectively. On the map, the planned path that PICO is about to follow is drawn in green. When following this path, PICO uses an attractive and repulsive field which are visualized by arrows, similarly as explained for the Escape Room Challenge.

When PICO is aligned to a cabinet, a new window is drawn with PICO in the center, showing the environment from PICO’s point of view. Here the raw sensor data is visualized with on top of that the lines and corners detected. At every reached cabinet this window is saved as a snapshot. Example of snapshots are shown in Figure 28, where the snapshots of the Hospital Challenge are shown. In this figure, PICO is represented as a red, rectangular box, LRF data is plotted in green, the lines fitted on the LRF data in dark blue, corners are plotted by red, filled circles, and the detected features are shown in magneta and cyan for concave and convex corners, respectively.

Results Hospital Challenge

Figure 28: Snapshots made during the Hospital Challenge.

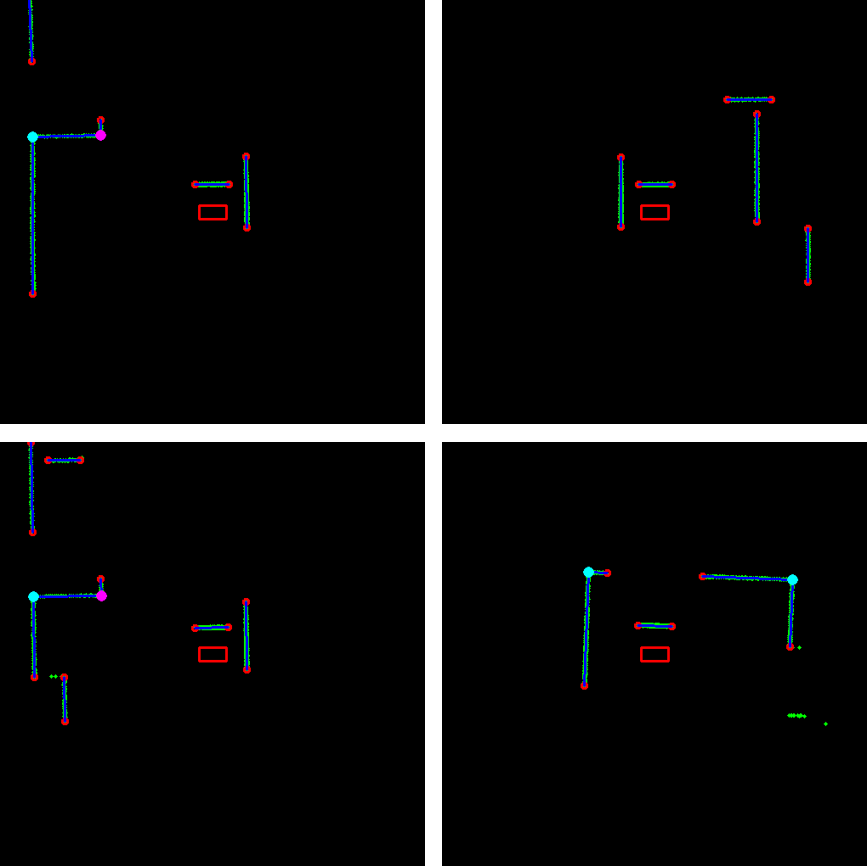
Figure 27 shows a rerun of the final result of the Hospital Challenge. In this challenge, PICO had to follow the cabinets according to the order 3, 6, 1, 0. PICO was able to finish the challenge in 2 minutes and 53 seconds, which was also the fastest time since none of the other groups managed to finish the challenge. In this rerun, PICO finishes the challenge in 2 minutes and 25 seconds. Note that the simulation is shown at 2.5 times the actual speed. The behaviour of PICO during the challenge will be analyzed next.

First, PICO determines its exact position within the starting area. PICO directly recognizes two convex corners in the initial room and thereby the initialization procedure is finished almost instantly. Next, a coarse path is planned to the third cabinet and PICO starts its movement. While moving along the planned path, PICO observes objects (such as the dynamic object located directly outside the initial room and the static object in the bottom-left room) and plots these in the left frame. According to its path, PICO wants to move through the room where cabinet 2 is located to the room above it, where cabinet 3 is found. However, approximately halfway PICO observes that the door to the room of cabinet 2 is closed, thus a new path is planned which uses the entrance of the room where cabinet 3 is located in. However, shortly after, PICO observes that this door is closed as well. Therefore, again a new path is planned, using the entrance to the top-left room. Along the way, PICO sometimes moves quite close to objects or a corner when entering a room. The latter is observed when PICO enters the top-left room. If a similar situation occurs, PICO stops and makes a transition to the recovery state, where a new path is planned. This path can then be followed until PICO reaches cabinet 3. Here, PICO positions directly in front of the cabinet as required.

From here onwards, the remainder of the challenge is completed easily. PICO is aware which doors are closed and plans the remainder of the paths accordingly. Some interesting aspects to observe are the way how dynamic objects are updated in the left frame and which features are used for localization. Moreover, between the top-right and bottom-right room, there is some free-space which is used to provide information on PICO's current state. Among others, this can for instance be that PICO is planning a path towards a certain cabinet, that it is executing a path or that it is in its recovery state. A part of the challenge is also to make snapshots when PICO has arrived at a cabinet. These can be seen in Figure 28. From top-left to bottom-right, these correspond to the order of the visited cabinets, thus 3, 6, 1, 0.

Figure 27: Simulation of the Hospital Challenge shown at 2.5 times the original speed.

Beforehand, the amount of static and dynamic objects that would be used was unknown. Therefore, numerous different situations were tested and the software was tuned accordingly. Eventually, unrealistic cases were tested as is shown in Figure 29 which were purely created to test PICO in very difficult situations and to make the software as robust as possible. Note that this simulation is shown in 3 times the actual speed, PICO is able to finish this map in 3 minutes and 6 seconds.

In this simulation, PICO has to visit the cabinets in the order 0, 2, 4, 6, 1. Cabinet 0 is easily reached, as PICO starts in the same room. When trying to move to cabinet 2, PICO runs into a dynamic object that moves along the opening of the initial room. After trying to plan two new, fine paths, the recovery state kicks in as no path can be found for PICO to exit the room. In the recovery state, PICO again tries to plan another fine path, but now with more detailed information about his direct enviroment. The dynamic obstacle is however still in the way, and since still no path can be found, PICO reverses while taking the static object in the initial room into account. This gives room for the dynamic object to continue its motion. By the time PICO has planned a new path, PICO is able to leave the room before the dynamic object blocks the opening again. From here onwards, PICO is able to reach cabinet 2 fairly easily. When moving from cabinet 2 to cabinet 4, PICO path is blocked by the dynamic object that is moving up and down between the rooms where cabinets 2 and 3 are located. Therefore, PICO plans a new path using the hallway. When PICO is moving from cabinet 4 to cabinet 6, it is observed that PICO has no trouble entering the room where cabinet 6 is located in, even though the entrance to this room is partially blocked by a static object leaving little room for PICO to fit through. Also, PICO encounters no problem from the dynamic object that is moving diagonally in this room. When moving to the final cabinet, which is cabinet 1, it is observed that PICO nicely avoids the dynamic object in the lower part of the hallway by moving around it. This simulation proves that PICO is able to operate safely, even in very complex environments.

Figure 29: Simulation of PICO operating in a complex environment shown at 3 times the original speed.

Recommendations and discussion

Even though both challenges were very successful as both challenges were finished in first place, there are still some points of improvement. Firstly, at the start of the project, a design document was created which incorporated a clear structure. However, the produced software deviates from this and thereby its structure became less obvious. Moreover, since the design document was only a first draft of what was expected to be needed before actually working on the software, it would have been nice to constantly update some of its contents, such as the table of PICO's functions. Especially since the design document was produced with focus on the Escape Room Challenge, it would have been better to make a second version for the Hospital Challenge. However, it must be said that one of the most important parts of the design document is recreated for the Hospital Challenge, which is the finite state machine as shown in Figure 12.

Code snippets

Extended Kalmann filter [1]

Mapping [2]

Path planning [3]

References

[1] https://en.wikipedia.org/wiki/Distance_from_a_point_to_a_line

[2] https://nl.mathworks.com/help/curvefit/least-squares-fitting.html

[3] Probabilistic ROBOTICS - Sebastian Thrun, Wolfram Burgard, Dieter Fox - 2006. Massachusetts Institute of Technology.

[4] A tutorial on the total least squares method for fitting a straight line and a plane - Leonardo Romero Muñoz, Moisés García Villanueva and Cuauhtémoc Gómez Suárez - December 2014, Faculty of Electrical Engineering, UMSNH, México - Journal of Science and Engineering, ITESCO, No. 1.

[5] Course: Motion Planning for Self Driving Cars at the University of Toronto https://www.coursera.org/lecture/motion-planning-self-driving-cars/lesson-2-populating-occupancy-grids-from-lidar-scan-data-part-1-p4Na5

[6] Variable Sized Grid Cells for Rapid Replanning in Dynamic Environments – Rachel Kirby, Reid Simmons, and Jodi Forlizzi – October 11-15-2009, St. Louis USA – IEEE/RSJ International Conference on Intelligent Robots and Systems.

Mobile Robot Control 2020 Group 8

Group information

Group Members

Meeting Summaries

Course description

Introduction

PICO

Description Escape Room Challenge

Description Hospital Challenge

Design Document

Escape Room Challenge

Finite state machine

Artificial potential field algorithm

Exit detection algorithm

Data pre-processing

Data segmentation

Line fitting

Corners and edges computations

Target computation

Visualization and testing

Test 1: Large room and exit in the extension of a wall

Test 2: Narrow exit

Test 3: Realistic environment

Results Escape Room Challenge

Software architecture

Implementation of the software architecture: Escape Room Challenge

Implementation of the software architecture: Hospital Challenge

Hospital Challenge

Finite State Machine

Localization

Feature extraction

Line fitting

Feature computation

Extended Kalman filter

Prediction step

Correction step

Implementation

Initialization procedure

Mapping

Bresenham’s Line Algorithm

Bayesian Logit Updating

Added functionality

Path planning

Considered optimal path planning algorithms

A* Algorithm

Weighted Map

Blocking Map

Reducing computational time using compression

Potential Improvement

Motion control

Recovery state

Detection

Visualization

Results Hospital Challenge

Recommendations and discussion

Code snippets

References

Navigation menu

Search