Group2 19-1 Week6

Back to the main page

Notulen tutor meeting

• Afweging om aan oppervlakte te blijven/ naar de bodem, duidelijker beschrijven. Zijn ‘luxe-positie’ dingen,
• Deel onder navigation verduidelijken,
• Parts list verder uitwerken, staat nog veel ‘stuff’ op
• Als we experimenten 2x (of meer) willen uitvoeren, moeten sommige instrumenten ook meerdere keren mee
• Welke experimenten willen we waar doen?
• (comsol evt. gebruiken voor temperatuur modellen)
• Kan de power source een beperking zijn voor de kwaliteit van de experimenten?
• Necessary bandwidth, eigenlijk een methode nodig om uit te rekenen. Wat nu gebruikt wordt is niet echt een valid argument. Daarnaast zijn bijv. cameras al beter geworden.
  • Uitrekenen hoeveel data je uit welk experiment krijgt, en dit met hoe lang de missie duurt.
• Willen we ons experiment nog uitvoeren? Dan langs Harry van de stikstof
• Movement under water kan wel uitgebreider. Wat is de aandrijver en wat zit er tussen de nucleaire bron en de propulsion?
  • Does it work at high pressure?
  • Uitzoeken hoe electromotor onder water zou kunnen werken
• Ballast water naar binnen stromen en eruit pompen kost ook veel energie, berekenen hoeveel de submarine in totaal gebruikt
• Extraterrestrial life - precautionary principle opzoeken
• Het onderzoek gaat steeds meer in op of de missie wel kan, hier op anticiperen
• Autonomie

Week 6 Logbook: Overall

Navigation under water

density of the water in Europa’s ocean

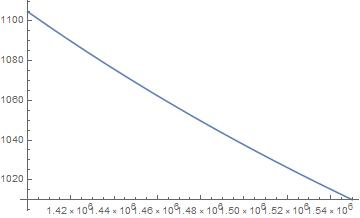
To allow navigation up and down, it is most convenient if the submarine will stay afloat at rest. For this, it should have a density equal to that of water. But water, although it has a low compressibility, is not entirely incompressible. As Fine and Millero showed, the specific volume of water decreases (and thus the density increases) as the external pressure increases. [1] Due to this fluctuation in density, the buoyant force on the submarine will increase as the submarine goes deeper down (where the pressure is higher). Hence, if the submarine floats at crust level, it will be pushed up. From the data of Fine and Millero, a pressure dependency of the density of water can be derived: =1004.79*e3.20629*10-5p With ρ the density in kg/m^3 and p the pressure in bar. (The observant reader may note that at p=0 Pa, the density of water is 1004.79 kg/m^3, rather than 1000. That is due to the fact that an increase in temperature accompanying the increase in depth was taken into account. The first data point is at 16 MPa, 0 degrees Celsius. Supposing you could then decrease the pressure on the water, the function assumes that you are also decreasing the temperature, which results in a density increase. However, as the pressure in Europa’s ocean won’t decrease below 16 MPa, the function works just fine in the relevant regime.) The figure below shows ρ(p(r)); the density of the water in Europa’s ocean between the seafloor and the sub-crust surface. Ideally, the submarine itself has a density a little over 1100 kg/m^3, making it sink. However, if the submarine carries a kind of balloon filled with a material X with the following properties: X has a lower density than water X has a higher compressibility than water. What ideally happens is that the submarine is attached to the balloon. Their total mass is m. The volume of the submarine is V0, the balloon’s is V(p), so that the density of the combination is =m/(V0+V(p)). V(p) is inversely proportional to the pressure, so as the pressure increases, V(p) decreases, so the density goes up. If this decrease in V(p) can be made to occur in such a way that the average density of the combination is at all times equal to the density of the water it is floating in. Let’s illustrate this with an example. Suppose the submarine has a mass of 750 kg, and a volume of .5 m^3. The balloon has a mass of 50 kg. The density of the combination is then: =800/(0.5+V(p))=1004.79*e3.20629*10-5p, Where the last equality follows from the density of water. Rewriting this equation results in a formula for V(p): V(p)=0.7962*e-3.20629*10-5p-0.5 Filling in a few particular values gives V(1)=.2962 m^3, V(160)=.2921 m^3, V(3000)=.22317 m^3. The density of X as function of pressure then becomes: (p)=50/(0.7962*e-3.20629*10-5p-0.5) An idea for materials with the required densities can be acquired here. The accurate value of the density of suitable materials can then be found in literature. (Such as oxygen: https://www-sciencedirect-com.dianus.libr.tue.nl/science/article/pii/0378437177900826)

How to let water in and out of the submarine

Sketch of the system

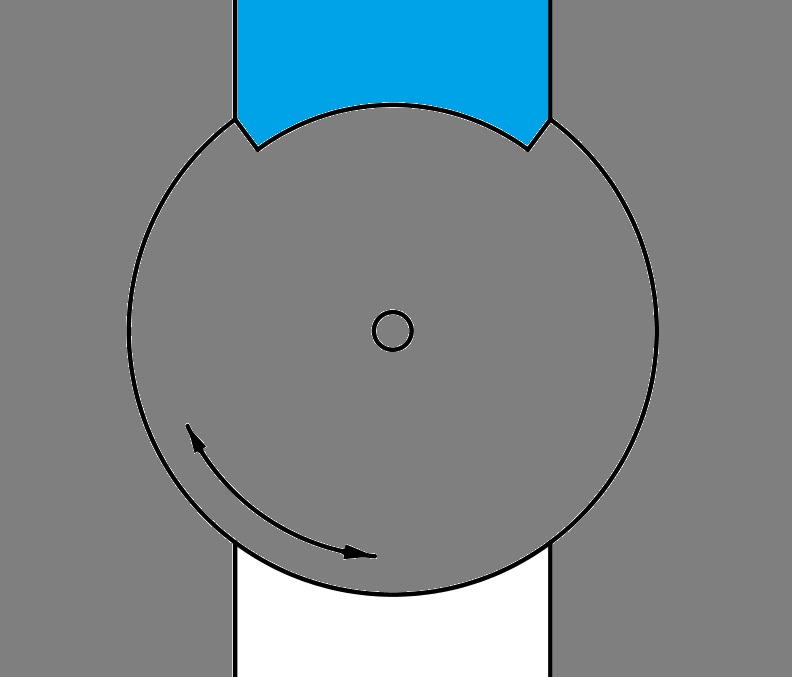
The main problem when letting water in and out is to overcome the .3 GPa of pressure without having to do too much work, as this work requires energy that is probably not available. To achieve this, we propose a rotating disk with a small slot for sampling water, as shown to the right. This disk will be encapsulated in the hull of the submarine, with sufficient strengthening around it to compensate for the puncturing of the hull. As the disk rotates, it will take with it a volume of water equal to the volume missing from the full disk. After half a rotation, it will deposit the water on the inside where it can flow to where it needs to be sampled via a simple tube. A disadvantage is that the submarine needs a particular orientation for the water to be able to fall in or out of the slot. However, being a submarine this should not be a problem. The volume of water sampled is equal to t*a*(R^2-(R-d)^2), where t is the disk thickness, a the angle that the slot spans in radians, R the outer radius of the disk and d the depth of the slot. For instance, at t=.3 cm, R=14 cm and d=2 cm, a needs only be 1.28 radians (73.4 degrees) for the slot to contain 10 mL. The biggest advantage of this system is that because the water is allowed to push on both sides of the slot in the disk, it attempts to push the disk both forward and backward with equal force, resulting in a net force due to water pressure of 0 N. By comparison, the total torque applied on either side of the slot at 150 km depth with the above parameters is 4680 Nm. By comparison, the SSC Tuatara ‘Hypercar’ caps out at a meagre 1735 Nm of torque, and it has a motor weighing nearly 200 kg. This goes to show the significant advantage of using the rotating slot. Of course it will still require some force, as the disk needs to rotate without gaps for the water to seep through. Hence both the disk and the casing around it need to be extremely smooth to decrease the coefficient of friction as much as possible. Hwang and Zum Gahr found the friction coefficient between 2 plates of polished steel to be about 0.116. With a slot depth of 6 cm and volume of 10 ml, this means that as the water pushes down on the disk through the opening - 7 cm wide - with a total force of .3*10^9*.003*.07=62962 N, the friction force to be overcome is 7304 N, resulting in a torque of 1023 Nm. This is still a lot, but the benefit is that the disk does not need to turn extremely fast, like would be desirable for the Tuatara. With gears or a worm drive, torques significantly below this 1023 Nm can be transformed into much higher torques. As an order-of-magnitude example, we will look at this motor. The parameters relevant to us are the:

• Box volume (the volume of the smallest rectangular box one can place it in): 4.5 L
• Mass: 4.5 kg
• Power: 120 W
• Torque: 1.3 Nm
• Maximum speed: 850 RPM
• Input voltage: 230 V AC

The required torque factor is 1023/1.3=787. This is a lot of tooth for one gear, and we intend to keep it compact. To that end, 2 the same worm drives might be used, each having a ratio of at least 28:1 (30 is a customary number of teeth, which is convenient as it thus goes about 15% over the required torque). These are available at industrial levels at diameters below 5 cm. If custom-made, they can probably be made to fit inside a volume of about 1 L. The total transmission then becomes 30*30=900. At this ratio, the disk would be made to turn at .944 RPM. That means that the disk will turn halfway in about 28 seconds. The total energy requirement for this turn will be 120*28=3400 Joules. A battery on board the submarine should be able to take in a sample and deposit it outside again at least three times in a row + some to spare to allow for repeated and thus more reliable sampling. Thus, the battery should be able to store at least 23800 (7 half turns) but ideally 34000 Joules of electric energy. 34000 Joules is not a lot. A typical AA rechargeable battery can easily store such energies. The problem is in the 230 V AC requirement, with which you’re automatically looking at heftier battery packs, such as this one. In a custom design this can probably be made a lot smaller, especially if it needs only 1 or 2 output ports. The volume of this pack is 5.6 L and it has a mass of 5.4 kg. We will divide this number by 3 for our battery.

Updated Parts list

Surface base:

• Fixation stuff
• Power source
• Communications
  • Emitter
  • Receiver
• Research equipment
  • Seismometer
  • Spectrometer
  • Camera

Digger:

• Digging stuff
• Power source
  • Shielding
  • Battery
• Accelerometer
• Fixation stuff
• Pressure-resistant hull
• Communications
  • Emitter
  • Receiver
  • Cable
  • The cable spool is with the digger to avoid having to drag all that length of cable all the way through the ice, and to make sure that it’s possible to unroll the cable.

Submarine:

	Volume	Weight
Barometer	d=4 cm, r=5 cm	~50 g
Propulsion	external	3 kg
*Up-down
*Sideways
Gyroscope	in computer	negligible
Accelerometer	in computer	negligible
Research equipment
*Gas emission	~30x30x30 cm	~2.5g
*Camera x2 (each)	6.2x4.5x2.8 cm	100 g
*Spectrometer	6x8x2 cm	100 g
Pressure-resistant hull	~15 cm external	dependent on dimensions
Power source (100 W?)	9 cm3	170 g
*Shielding	0.51 cm	200 g
*Rechargeable battery	1.9 L	1.8 kg
Communications	~10x5x5 cm	~200 g
*Emitter
*Receiver
Method to sample water
*Disk	1 L	15 kg
*Gears	4.5 L	4.5 kg
*Motor	1 L	1 kg
Lights	0.06 m3	1 kg
Computer	1 L	3 kg

Radiation resistance of experimental equipment

Cameras resistant to radioactive radiation are easily available, such as this one. However these are a lot larger than for instance the gopros mentioned before. Wang et al. showed that regular HD cameras show some deterioration after exposure to radiation. Camera sensitivity decreases up to 70% at dose rates of 1000 rad/h during 8 hours exposure. However, due to shielding we will be dealing with less than 1 mrad/h. That means that the total dose of 8000 rads will be reached after 8 million hours, i.e. 900 years. We will be exposing the camera to less than 1/50th of that radiation over the course of the mission. Furthermore, the fact that the radiation intensity is much lower may ensure that the camera is not damaged at all. That means that in regards to the camera, the radiation will not be a problem.

Spectrometric experiments usually require a correction, but this can be applied to the measurements after the fact and does not need any shielding.

Integrated circuits do require shielding from radiation, as high-energy gamma photons can excite electrons and cause signal spikes, as explained by Yu et al.. For that we propose additional shielding for the integrated circuits.

Hydrophobic coatings in viscous media (discussion point)

Something to take into consideration is the fact that at high pressures, the viscosity of water increases slightly. As the viscosity increases, shear stresses on external components of the submarine will increase as the submarine goes deeper down. This may decrease the time scale over which coatings on electrical equipment deteriorate and wear down. However, the magnitude of this effect can only determined sufficiently with modelling software unavailable to us. Hence this will just be left as something to consider for others to take into account when continuing with the design.

Mass, pressure shielding and flotation

The total mass of the internal components is 77.2 kg. The total volume of the internal components then stops at 97 L. In a spherical configuration this results in an inner hull radius of 28.5 cm.

To build a 15 cm steel hull (density 7840 kg/m^3) around that, requires 1942 kg of steel. Since the maximum capacity of the Falcon Heavy rocket is 3.5 metric tonnes, and this 2 ton ball still needs to be encapsulated in a torpedo, held up by a landing base, this is too heavy. Thus we shall look at lighter and stronger materials, to reduce both the volume and the mass required.

We could use diamond; easy for the cameras to see through. Diamond has a compressive strength of roughly 60 GPa. This is a factor of 10.4^2 more than steel. Taking this 10.4 as our thickness ratio, we get a diamond layer thickness of 1.436 cm. This would have a weight of only 54 kg. This is equivalent to 270,000 carat. At an uncut diamond price of $375 per carat, this results in a hull cost of about 100,000,000 USD. Furthermore, since diamond is very difficult to weld together, this would require a spherical diamond of the required volume; which then needs to be hollowed out. The costs of finding and cutting such a diamond are probably well beyond anything anyone would ever be willing to pay, if it is possible at all.

The solution is probably to use composite materials, specifically a Metal Matrix Composite: 6061 Al/SiC fibre UD. At a compressive strength of 3000 MPa (Nearly 5.5 times that of high-strength steel), much less material is required; we shall assume a factor 3 decrease in the thickness of the material with respect to steel. Furthermore, it has a density of 2700 kg/m^3, a 66% decrease from steel. A 5 cm layer around a 28.5 cm sphere has a volume of .0605 m^3, which with a density of 2700 kg/m^3 will have a mass of 163.4 kg. The total density of the submarine is then 240.6/.1575=1528 kg/m^3

The formula to carry this mass with a solid buoy is m=(m0-V0w)/(w/-1). Where m and are the mass and density of the buoy respectively. Looking at this list to get an idea of densities of several solids, we find that the main solids with densities lower than 1 can be subdivided into 2 categories: solids with air in them - like wools, snow or foams - and wood. The problem with the aerated solids is that they will either collapse under the pressure, or soak themselves with water. Both scenarios will cause the air to escape from, leaving a much denser material behind. This leaves the woods. Wood does also soak in water, but can be coated more easily. The lightest wood mentioned is balsa wood, at a density of 130 kg/m^3. Filling this in in the formula above gives 12.4 kg of balsa wood, which translates to a sphere with a diameter of 56.7 cm, or a cylinder with diameter and height 50.0 cm. However, the problem is that balsa wood already has trouble with pressures between 10 and 20 MPa (as shown here), well below the required 300 MPa. Woods in general tend not to work all too well, as outlined Bucur et al.. The problem is that although wood as a whole is rather strong, the cellular structure is not resistant to too high pressures, as the long cylindrical shells are at risk of lobar buckling. After extended periods of time under high pressures, this will compromise the structural integrity, causing the wood to fail entirely. Furthermore, the US forest service showed that very few woods (used commercially in the united states) have a compressive strength higher than 100 MPa, and the ones that do (Kaneelhart and Macawood) have a density of 94% that of water. That density would require 1302 kg of wood. Furthermore, this compressive strength only works along the grain. Perpendicular to the grain they too would already fail just below the Europan surface.

For flotation, one can also use a watertight balloon filled with a light liquid. One can for instance use pentane, which has a density of 626 kg/m^3. Pentane also has the added benefit of being a liquid at and just above room temperature. This will require 139 kg of pentane; i.e. a sphere with a radius of 37.6 cm. If we attach one to the top and one to the bottom of the submarine (to remove the orientations up and down from the submarine), each could have a radius of 29.8 cm, smaller than the submarine.

That leaves 2 more options for automatic flotation: A ‘steel balloon’ (not necessarily made out of steel), or a larger submarine. The benefit of increasing the submarine size, is that the hull has the most efficient distribution of volume; one sphere has less area per unit volume than 2 spheres. That means that less material will be required to make the hull. However, two spheres can be aligned inside the digger, to allow for a slimmer, longer digger, which would require less power to dig through the crust and less material to build.

If increasing the submarine size, we need to determine the radius of the vessel that will result in an average density equal to water. The density of the vessel will be: =(m0+4/3 *3000 ((R+.05)3-R3)/(4/3 R3), using the MMC mentioned above. R is the outer radius of the hull. Then we set =1000 kg/m3, solve for R and find: R=50.1 cm. The mass of the hull will then be 428.4 kg. In practice, we should account for the fact that a larger hull radius will require a thicker (and thus heavier) hull as well, which should thus be larger and therefore thicker, etc. For an MMC balloon, the above formula transforms into =(m0+4/3 *3000 (R3-(R-.05)3)/(V0+4/3 R3) V0 is equal to the .1575 cubic metres of the submarine. Solving for R gives: R=43.9 cm. The mass of the balloon is 405.5 kg.

In the first case, the total mass will be about 505 kg. The second case will yield a 645 kg balloon. This shows that a larger submarine will have a significant mass advantage over a ballooned submarine. Using the idealised case of diamond would yield a 34.9 kg balloon with a radius of 30.4 cm (costing 65 million USD) giving a total of 275 kg. A full diamond hull allowing flotation would give the total a mass of 265 kg, but the hull would cost over 300 million USD.

In conclusion, if the submarine should be made to float, this cannot be done with a solid buoy, as virtually all materials light enough are too weak or porous. The two hull solutions will both result in immense masses, unless a material like diamond could be used. The best solution is thus to use 2 balloons filled with pentane. They can be attached to the top and bottom of the submarine. This will ensure that it is balanced in its buoyancy, so that it can still turn in every direction, and keep it afloat with a reasonable mass.

Where to go?

The points of interest on Europa have been mentioned before. Although the submarine probably moves slow, it does move at a steady pace due to the RTG power source which can function largely independently of environmental factors such as the sun. As a result, assuming no obstacles get in the way, the submarine should be able to complete a journey around Europa’s core in a reasonable amount of time. Since we’d want to investigate both the Jovian and Anti-Jovian poles, the main consideration of interest is then where to dig into the crust, i.e. where to land.

In this case, there are a few considerations to be made.

• First off, due to Jupiter’s gravitational pull, gravity towards the Europan core is lower at the Jovian side than the anti-Jovian. Thus, on the anti-Jovian pole the digger would be pulled down into the ice with more force and could presumably dig faster.
• Secondly, again due to the inhomogeneous gravitational field on Europa, the hydrostatic pressure is higher at the anti-Jovian side than the Jovian side; up to 60 percent. It is possible that the submarine can only withstand the pressures at the Jovian side of the seafloor with certainty. If that is the case, exploring the seafloor on the anti-Jovian side may be dangerous. By starting at the Jovian side, the submarine starts in a relatively lower-pressure environment, allowing it to safely explore at least some portion of Europa before potentially failing.
• There may be deviations in Europa’s crust thickness. However, these deviations are no larger than 160 m [2]. These deviations are thus considered a negligible factor in this discussion.
• Furthermore, Europa’s ionosphere has stronger currents at the Jovian pole, being closer to Jupiter. Thus, to require less shielding of electrical equipment, it is safer to land at the Anti-Jovian pole.
• Lastly, if the surface base has to communicate with a satellite connected to earth, it is more convenient if the surface base is facing outward (w.r.t. its orbit) rather than inward.

From this analysis, the only disadvantage to landing on the anti-Jovian pole is that the pressures experienced start off higher. That means that if the submarine is not sufficiently equipped to handle these pressures, the mission will fail sooner. However, that simply means that more care has to be taken to shield the submarine from the pressures.

Necessary bandwidth

The amount of bandwidth that is necessary to ensure that all collected data reaches Earth is of course difficult to determine beforehand. We can, however, make an estimate of the bandwidth that will be necessary. It should be noted that the most significant hurdle that must be overcome when it comes to bandwidth, is to get collected data from the lander on Europa to NASA’s DSN on Earth. As for the acoustic communication between the submarine and the sub-surface station, some research has shown a bitrate of 5000 bps at a range of up until 6000 meters, and a bitrate of 200 bps at a range of up to 11000 meters. Other research has managed to obtain a bitrate of 16 kbps at depths of more than 6500 meters. Since it would not make sense to send more data to the surface lander than the lander can send to the Earth, the bitrate that should be necessary from the lander to Earth should be the same bitrate. If this mission is to be played really safe, then the actual bitrate should be a little bit higher, to ensure that the lander gets to send all the data to Earth that it receives from the submarine.

Movement in salt water

Since our submarine will be using propellers driven by electric motors for movement underwater, these motors will have to be protected well from the saline water. Not only does the salt water corrode any electric circuitry, it also conducts electricity well. This conductivity may very well to lead a short circuit, definitely damaging (part of) the submarine. The corrosion will also definitely not be beneficial to the mission, as it may also cause the submarine to malfunction. Therefore, the electric motors (or any circuitry, for that matter) should be well guarded from the salt water. As for the magnets inside the electric motors, there should not be any problem using them in the salt water of Europa.

As for the design of the propulsion system itself, it is comprised of four turbines with propellers, oriented downwards, similar to how many quadcopter drones are built. These turbines can all four be tilted 90 degrees clockwise and anticlockwise, on the axis that they are connected to the submarine body with. It goes without saying that these turbines can be activated independently at will. This way, side-to-side, up-and-down, and forward-and-back movement can all be achieved.

Sub-crust base

Once the digger has dug all the way through the ice, it anchors itself into the ice with a system that is described in this paper. Once it has fully anchored itself, it opens the compartment that the submarine is contained in. The part of the digger that remains anchored to the ice, becomes the sub-crust base. This base then communicates through acoustic waves with the submarine, while being tethered to the surface lander through an electrical cable.

Design of the surface lander

Once the lander has landed on the surface of Europa, it will remain stationary. This means that there is no use for any locomotion utilities on the lander. The envisioned design of the lander reminds one a little of the Apollo Lunar Module. However, since there does not have to be a enclosure to harbor any astronauts, this lander can be made smaller. Similar to the Apollo Lunar Module, this lander will have 4 feet to stand on, so that it remains stable (source, although an official source could not be found). In the center of this lander, the digger is located vertically. This way, the digger is oriented towards the ice, and the lander needs but to let go of the digger is ready to start digging. This digger is connected to the lander via an electrical cable, of which the spool that it unwinds from is located on the digger itself. So, the cable is unwound by the digger, from the digger, not from the lander.

Distance travelled by low frequency sounds (whale calls)

The ocean on Earth contains a layer of water referred to as the SOFAR layer. This is the layer of water where the speed of sound in the water is the lowest. This layer of water is also where sound travels the farthest in the ocean, tested up to about 5000 kilometers away. Since the SOFAR channel in water is dependent on multiple factors of the water, it is not unthinkable that the ocean on Europa will also have such a layer. If this layer can be found in the ocean of Europa, it will enable the submarine to communicate with the subsurface station for a very long distance, with minimal loss of the sound signal through the water. There exist also formulas to calculate the propagation of sound in salt water, but because the salt content of the water on Europa is yet unknown, these formulas are almost useless to us.

Underwater thrusters for maneuverability

In order for the AUV to maintain its maneuverability under water, regular thrusters with propellers are incapable of withstanding the extreme conditions that the submarine will very likely encounter at certain depths in the ocean of Europa. Instead, underwater thrusters are required, which have a different design from conventional thrusters. (cannot find a more specific difference than that underwater thrusters have the ability to work under heavy water pressure, sometimes up to full ocean depth, also cannot find a specific difference in design)

Submarine grease maintenance

Submarines have their grease applied quarterly when they are in port. This grease is applied to several locations on the outside of the hull of the submarine, specifically locations where there are moving parts on the outside. Since no person will be present on Europa to apply and refresh the grease on the submarine, it is a necessity to ensure that the submarine is greased well enough to endure a very long time in a very cold saltwater environment.

Location of performance of experiments

Since it is of high interest to maximize the chances of a successful mission on Europa, it is a good idea to keep designs as simple as possible. As such, we have decided to only give the surface lander a seismometer and a camera, and not a spectrometer and a gas emission tool. This means that, on the surface, on the ice, the lander will perform seismic measurements. These measurements may give us an indication of the structure of the ocean. It may also show us that the ocean on Europa is only one big ocean, or whether there are multiple, smaller oceans. Furthermore, the surface lander will also take close up (macro) photos of the surface, which may enable us to identify any traces that organic life may have left there.

The submarine, in turn, does not carry a seismometer, only a camera, a spectrometer, and a gas emission tool. Using the camera, the submarine will take photos at different depth in the ocean. Since on Earth, different depths in the ocean harbor different forms of life, the mission probably has the highest chance of success if the search for life is performed at different depths. The spectrometric experiments and the gas emission experiments are also performed at different depths, ranging from just below the ice to as deep as the submarine can go without being crushed.

Autonomy

In this section we will outline how much autonomy our robot must have. First of all we must calculate how long communication will cost between the robot and earth. The communication between earth and the surface-receiver on Europa’s surface can go via electromagnetic waves, which travel on the speed of light (299,8 *106 m/s). Since the distance between earth and Europa is 628,3*106 km, the signal will travel for 0,58 hour before it reaches Europa. The communication from the surface-receiver to the sub-crust base will go through an electrical cable, and since the estimated speed through an electric cable is 270*106 m/s, the time it costs to travel 10-20 kilometers through the ice negligible. For the communication from the sub-crust base to the submarine, acoustic waves will be used. The speed of sound waves is 1550 m/s, and the maximal distance the submarine will be apart from the sub-crust base is …, so ... With an one-way communication time of 0,58 hour, it will last at least 1,16 hour to receive a signal on earth and deliver a signal back to the robot on Europa. When the submarine encounters a big object, for instance a piece of ice, it should be able to go pass it without ‘asking’ the controllers on Europa what to do. This will save lots of time. Therefore, the submarine must contain sensors connecting to self-deciding devices for small problems like this. The bigger decisions, like if the robot is on the right site to land and dig, and whether the sub-crust base is in the right position in the ice, should be a human call. Where to execute the experiments should be on human order too, so the human controllers on earth can see if the submarine is in the right place and environment to execute these experiments. Another point where we have to determine the level of autonomy is with the navigation. Since the submarine has quite a track to run, it should have a certain level of autonomy. The path it needs to go should be programmed in the computer of the submarine.

From earth to Europa – General description about the journey and the risks

This research focusses on the landing on Europa, digging through the icy layer and sending a submarine into the sub-surface ocean. The trip from earth to Europa won’t be described in much detail, because previous spacecraft missions have shown the possibility to travel this far. There is one constraint to take in account; the maximum payload a rocket can send to Europa. The most powerful operational rocket is the Falcon Heavy rocket, which can take twice as much payload into space as other rockets. It is unknown how much payload the Falcon Heavy rocket can take to Europa, but it can take a maximum payload of 63800 kg into a low earth orbit, 16800 kg to Mars and 3500 kg to Pluto. (https://www.spacex.com/falcon-heavy) Since the maximum payload seems to decrease exponentially as the distance increases, the assumption is made that the maximum payload that can be delivered to Europa is also 3500 kg. The true value will probably be a bit higher, but 3500 kg is a safe estimation. With the help of the rocket, the spacecraft makes its way into space. With a varying travel speed it will cost the spacecraft about six years to reach Europa. During this travel time it has a very little, negligible chance of bumping into some meteorite or something else in space. (https://www.space.com/18901-nasa-mission-jupiter-moon-europa.html)

Introduction

Europa is a very interesting, mysterious moon of Jupiter, discovered by Galileo Galilei in the year 1610. The moon raised a lot of interest the past couple of decades, because there are some indications of liquid water on the moon. Since water is at top of the list of ingredients that make life possible, the speculations for extraterrestrial life on Europa began to rise. Water dissolves nutrients for organisms to eat, transports important chemicals within living cells and allow those cells to get rid of waste. (https://europa.nasa.gov/europa/life-ingredients/) But due to the circumstances at Europa, the water is believed to be hidden underneath a thick coat of ice. This coat of ice is estimated to be 10 kilometers at its thinnest points. (https://www-sciencedirect-com.dianus.libr.tue.nl/science/article/pii/S0378475407003242)

Presence of liquid water on the surface

But can’t there be water present in liquid form somewhere at the surface of Europa? Probably not. One of the reasons to assume this, is based on the phase diagram of water, shown to the right. As can be seen in the image, the lowest pressure at which water can still exist in liquid form is its triple point at 611.73 Pa (0.0061 atm), at the usual temperature of 273.15 K (0 oC). Below that pressure, water has no liquid form. Since the pressure at Europa’s surface is about 10^-10 atm, this means that liquid water can not stably exist on the surface of Europa. Some water may come to surface for a brief moment, but will almost instantaneously either freeze or boil, leaving no water remaining. It should be noted that indeed this diagram does not extend below 10^-5 atm, and that based on this image it is thus technically not possible to say that water does not have a liquid form at such ultra-low pressures. However, it is first of all unlikely that such an out-of-place phase change exists based on this and other phase diagrams. Secondly, this ‘liquid’ may not be liquid as we know it and still be unable to support life. Much like solid water has different crystalline structures at different temperatures and pressures, so can this liquid water have very different properties based on the environment it is in. Hence based purely on physical grounds it is unlikely that liquid water in a familiar form exists on the surface of Europa. (https://www-sciencedirect-com.dianus.libr.tue.nl/science/article/pii/S0079678615000035)

Presence of a sub-surface ocean

Why do researchers belief there is an sub-surface ocean? The first theories that the planet has a sub-surface ocean came after the fly-by mission of Voyager 1. This spacecraft was, in march 1979, the first that made images in significant detail of Europa’s surface, with a resolution of about 2 kilometers per pixel. These images revealed a surprisingly smooth surface, brighter than that of earth’s moon, crisscrossed with numerous bands and ridges. Researchers noted that some of the dark bands had opposite sides that matched extremely well, comparable to pieces of a jigsaw puzzle. These cracks had separated, and dark, icy material appeared to have flowed into the opened gaps, suggesting that the surface had been active at some time in the past. The images also showed only a handful of big craters, which are expected to build up over billions of years as the planetary surface is bombarded by meteorites, until the surface is covered in craters. Thus, a lack of much craters suggested that Europa’s surface was relatively young and implied that something erased the craters, such as icy, volcanic flows. Next to that, scientist found patterns of some of the longest linear features in the images that did not match the predicted patterns of the features, created by tides as Europa orbits Jupiter. They determined that the found patterns would fit very well if Europa’s surface could move independently and was not locked to the rest of the interior. These interesting findings led to the next mission to Europa, Galileo. This spacecraft was launched in 1989 and entered orbit around Jupiter in 1995. Galileo eventually made 12 close flybys of the icy moon, including images of Europa at a range of scales, revealing new details about the surface and providing context for how those details were related to the moon as a whole. One important measurement made by the Galileo mission showed how Jupiter’s magnetic field was disrupted in the space around Europa, implying that a special type of magnetic field is being created within Europa by a deep layer of some electrically conductive fluid beneath the surface. Scientists belief, based on Europa’s icy composition, that the most likely material to create this magnetic signature is a global ocean of salty water. Above described are four strong indications of a sub-surface ocean on Europa, which is why the common belief under scientists is that the ocean really exists. (https://europa.nasa.gov/about-europa/ocean/)

Indications for life

The three basic requirements for life to be present are liquid water, chemical building blocks and a source of energy. The first requirement is explained in previous paragraph. The second requirement, the chemical building blocks are also believed to be partly present. The ice and other materials on Europa’s surface are bombarded with radiation from Jupiter, that could alter them into some of the chemical building blocks of life, like oxygen (O2), hydrogen peroxide(H2O2), carbon dioxide (CO2) and sulfur dioxide (SO2). If these compounds reach the sub-surface ocean, they can be valuable nutrients to start and sustain life. Besides, the ocean water can react with the rocks and minerals of the subsurface ocean’s floor to liberate other nutrients to support life. The third requirement is a source of energy. Europa’s position in space is within the powerful gravitational field of Jupiter, causing the moon into an orbit with one hemisphere constantly facing Jupiter. This elliptical orbit takes Europa alternatively closer to and further away from Jupiter. This constant increase and decrease of gravitational force on Europa results in elongating and relaxing of the moon witch each trip around the planet. This internal movement, combined with gravitational forces caused by neighboring moons, produces internal friction and heat within Europa. This internal heat could be the energy source that keeps the subsurface ocean from freezing and sustains any life that exists there. Next to that, there could be hot water vents on the floor of the subsurface ocean that deliver energy and nutrients from the planet’s interior. On earth, organisms have been discovered in the subglacial lakes of Antarctica and in hot ion-rich waters of hydrothermal vents. Life in Europa’s sub-surface ocean could be supported in a similar way. (https://geology.com/stories/13/life-on-europa/) These indications for life in Europa’s ocean has led to a future mission of NASA to the moon. They planned to launch the Europa Clipper mission in 2025. The spacecraft will conduct an in-depth exploration of Europa, investigating whether the moon could harbor conditions suitable for life. (https://www.nasa.gov/feature/europa-clippers-mission-to-jupiter-s-icy-moon-confirmed) This mission is of course very interesting, but with the strong indications for life as described above, we want to take it one step further. In this project we are investigating whether it is possible to land on Europa, dig through the icy layer and send a submarine into the sub-surface ocean to search for life.

Communication

The communication chain will be divided in three parts; from Earth to surface receiver, from surface receiver to sub-surface receiver and from this sub-surface receiver to the submarine.

From Earth to surface receiver

On Earth, NASA uses a system called DSN to communicate with spacecraft (https://deepspace.jpl.nasa.gov/about/). DSN stands for Deep Space Network, and it allows NASA to communicate with spacecraft as far as Opportunity 1, which is, by now, outside of our solar system. This means that a satellite, as intermediate station, around Europa is not absolutely necessary, but it may provide a faster way to get our data to Earth. Since Europa is tidally locked to Jupiter (https://phys.org/news/2015-09-jupiter-moon-europa.html), and since its orbital period is about 3.5 earth days (https://solarsystem.nasa.gov/moons/jupiter-moons/europa/in-depth/#orbit_and_rotation_otp), a large part of the time, the lander will not be able to directly send data back to Earth. T This is due to either Jupiter being in the way, or Europa itself is in the way when the lander is at the back of Europa, relative to Earth. If, for this mission, there was another satellite orbiting Europa or Jupiter, the lander would be able to send its data to this satellite with a much higher data rate. During the Mars Curiosity mission, NASA has an orbiter around Mars, which intermittently communicates with the Rover. The communications between Curiosity and this orbiter are about 150 times as fast as the communications would be between Curiosity and Earth directly. Since this orbiter has more power that it can focus on communications, the data will reach Earth much faster through this orbiter, than it would directly (https://mars.nasa.gov/msl/mission/communications/#data). So in conclusion, a satellite would increase the speed of communication, but it is not required.

Necessary bandwidth

The amount of bandwidth that is necessary to ensure that all collected data reaches Earth is of course difficult to determine beforehand. We can, however, make an estimate of the bandwidth that will be necessary. It should be noted that the most significant hurdle that must be overcome when it comes to bandwidth, is to get collected data from the lander on Europa to NASA’s DSN on Earth. As for the acoustic communication between the submarine and the sub-surface station, some research has shown a bitrate of 5000 bps at a range of up until 6000 meters, and a bitrate of 200 bps at a range of up to 11000 meters. Other research has managed to obtain a bitrate of 16 kbps at depths of more than 6500 meters. Since it would not make sense to send more data to the surface lander than the lander can send to the Earth, the bitrate that should be necessary from the lander to Earth should be the same bitrate. If this mission is to be played really safe, then the actual bitrate should be a little bit higher, to ensure that the lander gets to send all the data to Earth that it received from the submarine.

From surface receiver to sub-surface receiver

In this section different options of communication through this difficult medium will be discussed; wireless communication through ice, fiber-optic cable and electrical cable.

Wireless communication through ice

Ice is quite a good isolation material when it comes to wireless signals. Radio signals are very quickly absorbed by ice (https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2005JB003903), and optical signals do not travel through ice very far either. Low frequency radio waves, however, are a medium that does travel through ice better (https://www.era-learn.eu/network-information/networks/eurostars/eurostars-cut-off-2/through-ice-location-and-communication-system). The question arises, however, whether these radio waves will survive through 10 km of ice, as that would be a very unusual situation here on Earth for researchers to test on. So we assume wireless communication through the ice crust on Europa is for all intents and purposes impossible.

Fiber-optic cable

This a method of transmitting information from one place to another by sending pulses of light through an optical fiber. An fiber-optic cable was used in the ARTEMIS mission, where the navigation and communication under and through the ice in Antarctica was examined. The function of this fiber was to monitor ARTEMIS under water and allow the scientists to display the real time outputs of the sensors on a screen. There were high noise levels on some sensors. The fiber was 15 km long, but ARTEMIS was at its maximum 10 km from the base. Due to the ocean currents the fiber damaged so it couldn’t be re-used. (https://caves.org/section/commelect/drupal/files/Presentations/NSS2016%20Under%20Ice%20Nav%20And%20Com.pdf https://onlinelibrary.wiley.com/doi/full/10.1002/rob.21740?sid=worldcat.org) The ice of Europa is also believed to be moving around due to tectonic activity, tides and gravitational forces. Since the cable needs to last at least the whole 5 years of the mission, a fragile cable that is damaged only by the currents of the Antarctic sub-surface ocean is not an option.

Electrical cable

density of the water in Europa’s ocean

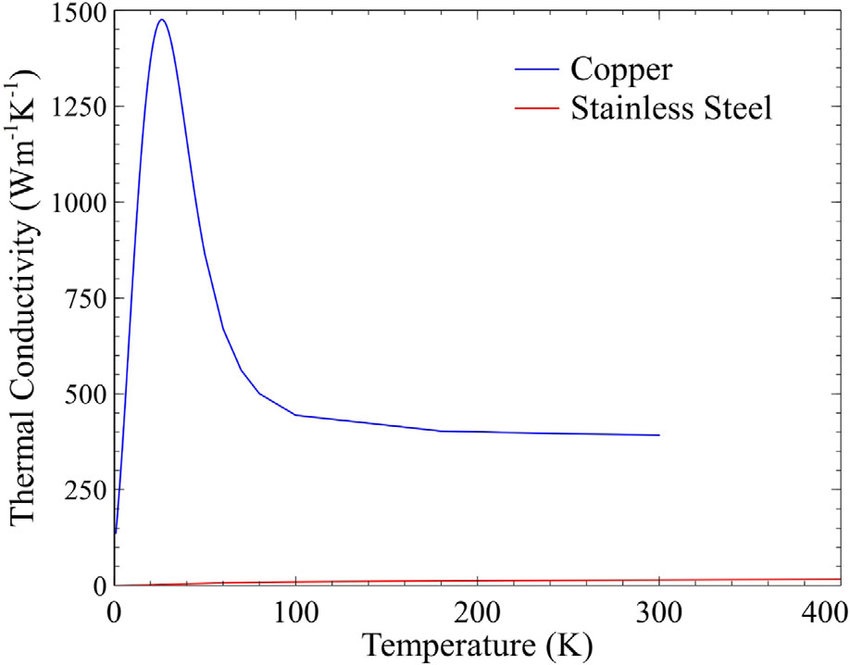
In current society, most electrical cables are made of copper or aluminum. These cables are used for their high conductivity and low resistance. Where aluminum is mostly used for heavy industrial wirings, copper is at the core of most everyday electrical cables. Copper’s conductivity decreases as temperature increases, but as the temperature goes down, the conductivity increases. This happens until about 30 Kelvin, at which point lower temperatures drastically decrease copper’s conductivity. Even though copper’s conductivity at around 30 Kelvin reaches a very high point, at no point is copper itself considered to be a superconductor. Conclusion why we want to use electrical cable?https://www.researchgate.net/figure/Variation-of-thermal-conductivities-of-copper-and-stainless-steel-with-temperature_fig4_319575524