Integration Project Systems and Control 2013 Group 4

Group Members

Name:	Student id:	Email:
Koen Gruntjens	0760934	k.g.j.gruntjens@student.tue.nl
Erik van Broekhoven	0637413	e.c.v.broekhoven@student.tue.nl
Wouter Geelen	0744855	w.geelen@student.tue.nl
Leroy Hazeleger	0651762	l.hazeleger@student.tue.nl

Planning

February 18 - February 24

• Qualitative analysis of robot
• Derivation of kinematics and dynamics (Leroy, Erik)
• Preparation of first experiment session (Wouter, Koen)
• Investigate different control-design
• Group meeting

February 25 - March 3

• FRF-measurement and analyse (Wouter,Leroy (Tuesday))
• Coupled/decoupled experiment (Wouter,Koen (Friday))
• Nonlinearity experiment (Wouter,Koen (Friday))
• Static friction experiment (Wouter,Koen (Friday))
• Group meeting (Friday)

March 4 - March 10

• Continue making FRF-measurements
• Design PID controllers for all joints
• Trajectory planning for all joints
• Group meeting

March 11 - March 17

• Verify trajectory planning (minimum time trajectory)
• Optimization of PID controller
• Group meeting

March 18 - March 24

• Design feedforward controller
• Implementing feedforward controller
• Discuss and design ILC
• Group meeting

Progress

Week 1

• The first step in this project was to identify the pizza-robot by creating a list of all the design requirements of the pizza-robot (to design experiments) such as:
  • The pizza is not allowed to fall during transport, therefore the maximum acceleration in directions is limited.
  • The robot is not allowed to touch the pizza holding brackets, therefore the trajectory must be designed in such a manner that the pizza-robot does not collide with the brackets.
  • 3 pizza's must be transported and the pizzas must be transported as fast as possible (approx. 10-15 [s]). To achieve this a good controller and trajectory for axis have to be designed.
  • The controller must be stable.
  • The output of the controller is limited for each axis i.e. we are dealing with saturation.
  • The accuracy of the pizza-robot end-effector when obtaining a pizza from the brackets should be approximate 5 [mm].
• Identifying limitations of the pizza-robot such as:
  • Degrees of freedom to specify the work space of the end-effector.
  • Possibly non-linear coulomb and viscous friction.
  • The maximum input signals [V] of the motors of the pizza-robot and consequently the maximum velocity/acceleration of each joint.
• To identify the pizza-robot in a more specific way:
  • The kinematics of the pizza-robot are derived which are helpful for the trajectory design and determining the dynamics of the pizza-robot using the DH convention.
  • A simple model of the pizza-robot is determined to possibly use model-based control design (dynamics of the pizza-robot in terms of the generalized coordinates is difficult, consider a simple model for each joint separately)
  • FRF-measurement experiments are prepared (designing a reference trajectory, a stabilizing controller)
• Different types of feedback-control are considered which are usable (and possible with the knowledge of the groupmembers)
  • Linear quadratic regulator
  • Adaptive control
  • Iterative learning control

Week 2

• As already mentioned in week 1, a simple model is proposed to (possibly) use for model-based control design instead of the dynamics of the pizza-robot in terms of its generalized coordinates since this is too complex and not usable as model-based control design. (for every joint a model, with disturbances from other joints)
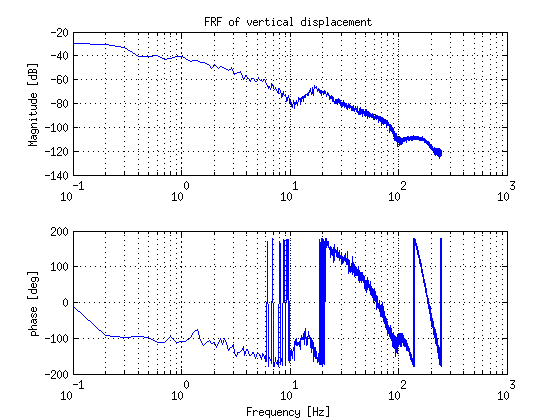
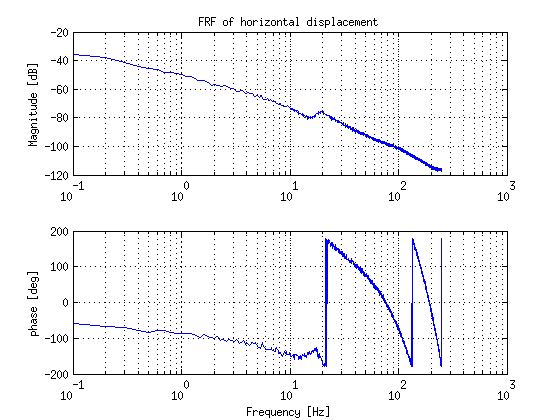
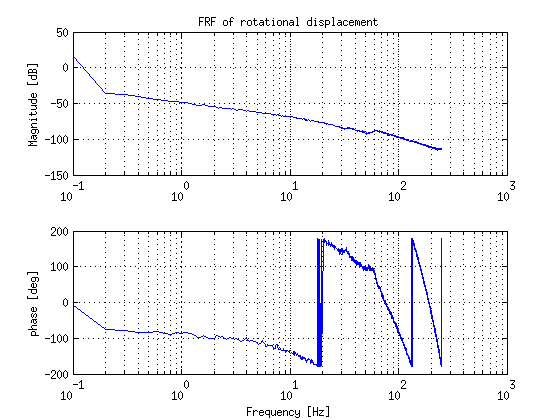
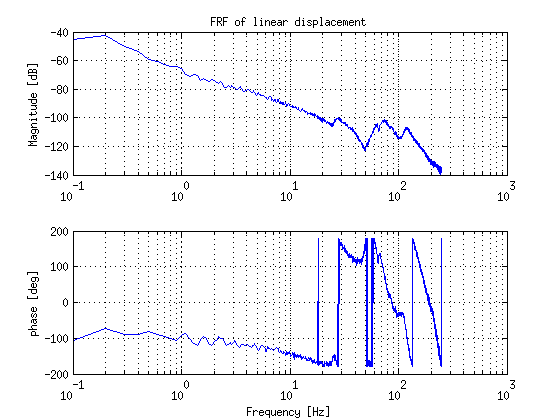
• FRF-measurements are performed of each joint with a stabilizing controller and a specific reference trajectory, however large friction is encountered which seems to be not constant along the trajectory of each joint. This influence the FRF-measurements at low frequency. (improve FRF-measurements)

Week 3

• It took a bit more time for doing the FRF-measurements. Finally we have all FRF's of the joints and all group members designed a stable controller for two joints e.g. such that every joint had at least two controllers made by 2 different members of the group.

Vertical displacement	Horizontal displacement
Rotational displacement	Linear displacement