Embedded Motion Control 2015 Group 3/Localisation

Localisation

This page is part of the EMC03 CST-wiki.

This page goes into details about localisation.

Requirements of Localisation

In order to be able to locate itself within its environment, the robot needs information. The is required to obtain global position data:

1. global x-position [m]
2. global y-position [m]
3. global a-angle [rad.]

The error in the position data must be quantified and must be minimized, in order not to make mistakes in the location in the long run. For example, if the robots x-and y-coordinates differ due to an error, the robot will think is it at a different location, whereas it actually is standing still in exactly the same location and position.

The sensor data required to obtain the above mentioned position data are the following:

1. odometry: global x [m] , global y [m] , global a [rad.]
2. LRF: all laser ranges [m]
3. velocity input to robot

Method of localisation

The robot will need global coordinates. There are two sensors which it can use to determine these coordinates. However both sensors have their own drawbacks.

• The odometry sensor provides global x-y coordinates and angle. There is not much variance in the data of the sensor, but there is a drift (bias) that will accumulate over time. The odometry data can be viewed as feedforward information for the system.
• The LRF sensor provides 1000 ranges [m] with distances to objects over a scope of 270 degreess around the robot. This sensor shows no bias, but has a variance however. Furthermore the LRF data does not provide the global coordinates that we want with its raw data. Therefore these ranges data have to be converted into additions to the global coordinates. The LRF data can be seen as the Feedback loop of the system.

When the robot starts its program initially, the global coordinates will be all zero. So the start position of the robot determines the direction of the x- and y-axes. The data from the odometry and the LRF will be updated at each time instant. The odometry just works very intuitively: it tells you how far you have moved based on wheel-rotation. In the case of LRF however, the following happens: It measures the distances to the objects in the environment at time t0. It measures again at t1. The difference in distance, converted to the wanted coordinates, should be equal to the odometry data. Of course this will not happen due to the errors in the sensors, but that is why a filter is used to filter the data in between each next update step.

A Kalman filter is used to filter the data obtained from odometry as well as from LRF, in order to maximize the accuracy.

Kalman filter

The kalman filter uses an update cycle with two steps. In the first step the new position is estimated based on the previous position and the input. An estimate of its error is then made which is used in the second step. In the second step data from measurements is used to correct the estimated position. Since the definition of the directions of the x and y axis is arbitrary, they are aligned to the corridor in which pico starts. The algorithm that is used is shown in the figure below:

Scheme Kalman

The various variables used in the figure above, are explained here:

[math]\displaystyle{ \hat{x}_k^- }[/math] is the predicted ahead state variable at discrete time instance [math]\displaystyle{ k }[/math]. This column vector consists of the global x-position, global y-position and the global angle. So logically, [math]\displaystyle{ \hat{x}_{k-1}^- }[/math] is the same vector at a previous time instance.

[math]\displaystyle{ A }[/math] is an n by l matrix that relates the state at the previous time step [math]\displaystyle{ k-1 }[/math] to the state at the current step [math]\displaystyle{ k }[/math], in the absence of either a driving function or process noise.

[math]\displaystyle{ B }[/math] is an n by n matrix that relates the optional control input u to the state variable.

[math]\displaystyle{ u_{k-1} }[/math] is the control input at the previous state of time. So this corresponds to a 3 by 1 column vector containing the velocities that were sent to the wheel base:

1. vx: translational velocity in x-direction [m/s]
2. vy: translational velocity in y-direction [m/s]
3. va: angular velocity around z axis [rad./s]

[math]\displaystyle{ P_k^- }[/math] is a n by n matrix containing the error covariance predicted ahead at time instance [math]\displaystyle{ k }[/math].

[math]\displaystyle{ Q }[/math] is a n by n matrix containing covariance of the process noise.

[math]\displaystyle{ K_k }[/math] is an n by n matrix that represents the Kalman gain.

[math]\displaystyle{ H }[/math] is an n by m matrix that relates the state to the measurement [math]\displaystyle{ z_k }[/math].

[math]\displaystyle{ R }[/math] is an n by n matrix that contains the measurement noise covariance.

[math]\displaystyle{ z_k }[/math] is the measured data in a column vector (to be compared to predictions).

During the second step of the kalman update both the LRF and odometry are used. For both sensors the difference between the current and last value is used to determine the position change since the last update. This value is then added to the previous positions from the kalman update. The odometry data can be used directly. For the LRF however, the x, y and a values first have to be calculated from the raw LRF data. This is done by measuring the distance to the end of the corridors. Since Pico can see 270 degrees around itself, it can always measure the distance to one end of the corridor it is in as wel as the distance to one of the side walls of the corridor.

LRF Kalman

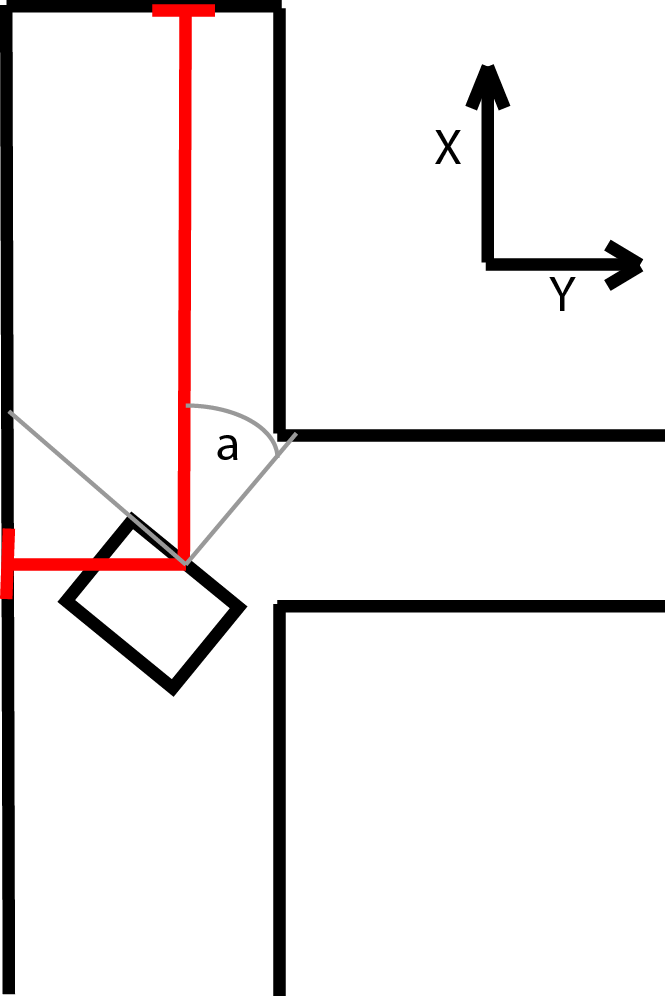
The estimated angle is used to calculate which sensor should point towards the end of the corridor. An interval around the corresponding LRF beam is searched for a local minimum, which should belong to the beam that hits the end perpendicularly. This beam points directly at the end of corridor and is then used to calculate the LRF value for the angle of pico. The difference is calculated between the previous and current distance to the end wall which is the position change for either x or y used in the kalman update. The other position change is calculated in similarly, but in stead of the end of the corridor the distance to the side wall is used. Since it is possible to lose sight of a wall, for instance when driving on an intersection, a safeguard is put in place. If the position change based on the lrf is to big, it is assumed that the LRF data is unreliable for that update cycle and only the odometry data is used. This is done by switching between two R matrices, one of which sets the contributions of the laserdata to zero. In the regular R matrix the contribution of the LRF data is weighed more heavily under the assumption that the LRF is more reliable overall.

Implementation of method

Here the implementation of the method will be briefly discussed.

Interface

Localisation is a separate cpp-file which can be seen as a block. It uses the Scan class data to read sensor data. Also it uses the Drive class to retreive information on the velocity. the variables that are used as arguments are copies and are not used by reference, as they are only needed to calculate the position of the robot. The variables that are only used within the localisation class are ofcourse set to private status.

Technicalities

Integration

.... ....