Embedded Motion Control 2013 Group 1

Group Info

Name:	Abbr:	Student id:	Email:
Groupmembers (email all)
Paul Raijmakers	PR	0792801	p.a.raijmakers@student.tue.nl
Pieter Aerts	PA	0821027	p.j.m.aerts@student.tue.nl
Wouter Geelen	WG	0744855	w.geelen@student.tue.nl
Frank Hochstenbach	FH	0792390	f.g.h.hochstenbach@student.tue.nl
Niels Koenraad	NK	0825990	n.j.g.koenraad@student.tue.nl
Tutor
Jos Elfring	n.a.	n.a.	j.elfring@tue.nl

Meetings

1. Meeting - 2013-09-04
2. Meeting - 2013-09-11
3. Meeting - 2013-09-18
4. Meeting - 2013-09-25

Planning

Week 1 (2013-09-02 - 2013-09-08)

• Installing Ubuntu 12.04
• Installing ROS Fuerte
• Following tutorials on C++ and ROS.
• Setup SVN

Week 2 (2013-09-09 - 2013-09-15)

• Discuss about splitting up the team by 2 groups (2,3) or 3 groups (2,2,1) to whom tasks can be appointed to.
• Create 2D map using the laser scanner.
• Start working on trying to detect walls with laser scanner.
• Start working on position control of Jazz (within walls i.e. riding straight ahead, turning i.e. 90 degrees).
• Start thinking about what kind of strategies we can use/implement to solve the maze (see usefull links).

Week 3 (2013-09-16 - 2013-09-22)

• Start work on trying to detect openings in walls.
• Start working on code for corridor competition.
• Continue thinking about maze solving strategy.

Week 4 (2013-09-23 - 2013-09-29)

• Decide which maze solving strategy we are going to use/implement.

Week 5 (2013-09-30 - 2013-10-06)

• To be determined.

Week 6 (2013-10-07 - 2013-10-13)

• To be determined.

Week 7 (2013-10-14 - 2013-10-20)

• To be determined.

Week 8 (2013-10-21 - 2013-10-27)

• To be determined.

Progress

Week 1

Week 2

Week 3

• Programmed reasoning for right wall follower.
• Finalized the design of the localization

Week 4

• Integrated all the nodes into a single launch file.
• Debugged all the nodes and made sure that the output was correct.
• Finalized the design of the situation

Week 5

• First integral testing are done.
• Made the situation node more robust for false-positives.

Week 6

• Tested with our software architecture with Pico, unfortunately the bag files we created were to big to be used (for some reason they could not be exported).
• Started with vision, we did choose to use template matching to detect the arrow.

Week 7

• testing on pico

Software architecture

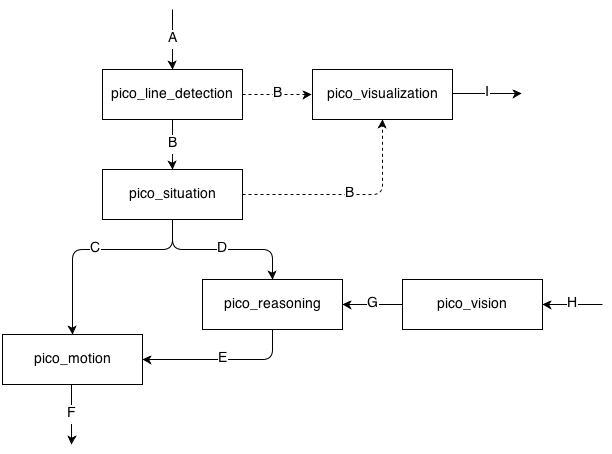
IO Data structures

#	Datatype	Published by	Topic	Freq [Hz]	Description
A	LaserScan.msg	Pico	/pico/laser	21	Laser scan data. For info click here.
B	Lines.msg	pico_line_detector	/pico/line_detector/lines	20	Each element of lines is a line which exists out of two points with a x- and y-coordinate in the cartesian coordinate system with Pico being the center e.g. (0,0). The x- and y-axis in centimeters and the x-axis is in front/back of Pico while the y-axis is left/right. Further the coordinate system moves/turns along with Pico.
C	Localization.msg	pico_situation	/pico/situation/localization	20	The four floats represent the angular mismatch and respectively the distance to the wall with respect to the front, left and right.
D	Situation.msg	pico_situation	/pico/situation/situation	20	Each boolean, which represents a situation e.g. opening on the left/right/front, is paired with a float which represents the distance to that opening.
E	Reasoning.msg	pico_reasoning	/pico/reasoning	20	The two floats represent the distance to the next decision point and the angle to turn
F	geometry_msgs/Twist	pico_motion	/pico/cmd_vel	20	first float is the average angle (in radians) between the 2 lines at the sides of pico. The second is the distance to the left hand detected line, the third is the distance to the right hand detected line
G
H
I	visualization_msgs/MarkerArray	pico_visualization	/pico/line_detection/visualization	5	The marker array contains a set of markers. A marker can be defined to be a certain type of shape either 2D or 3D. In this case the marker is defined as a 2D line.

Pico standard messages

To let the different nodes communicate with each other they send messages to each other. ROS defines already a number of different messages such as the standard and common messages. The first provides a interface for sending standard C++ datatypes such as a integer, float, double, et cetera, the latter defines a set of messages which are widely used by many other ROS packages such as the laser scan message. To let our nodes communicate with each other we defined a series of messages for ourself.

Line

The line message includes two points, p1 and p2, which are defined by the geometry messages package. A point can have x-, y- and z-coordinates we however only use the x- and y-coordinate.

   geometry_msgs/Point32 p1                                                        
   geometry_msgs/Point32 p2

Lines

The lines message is just a array of the Line.msg. Using this messages we can send a array of lines to another node.

   Line[] lines

Localization

The localization message includes 4 float32's. Angle holds the angular mismatch of the robot with respect to the wall. The distance_front holds the distance with respect to the front wall if any is detected, in case no front wall is detected a special value is assigned. Respectively distance_left and distance_right are used for the distance w.r.t. wall for the left and right side.

   float32 angle                                                                   
   float32 distance_front                                                          
   float32 distance_left                                                           
   float32 distance_right   

Reasoning

The reasoning message includes 2 float32's one to represent the distance to the next decision point, and one to describe the angle to turn.

   float32 distance
   float32 angle

Situation exit

The situation exit message uses a boolean and a float32 to specify if a exit is present and the distance from the robot to that exit.

   bool state                                                                      
   float32 distance

Situation

Since there are three types of exits the situation message has three variables of the type Situation_exit, described above, for either the front, left and right wall.

   Situation_exit front                                                            
   Situation_exit left                                                             
   Situation_exit right

Encoder

The message tells how much Pico has turned, it increases from 0 degrees to either 90 degrees or 180 degrees.

   float32 incAngle

Drive

The drive message sends commands to the drive node which actually sends the velocity commands to pico. The message contains two float32, one to specify the velocity forwards and one to represent the velocity by which Pico turns around his axis.

   float32 speed_angle
   float32 speed_linear

Line detection

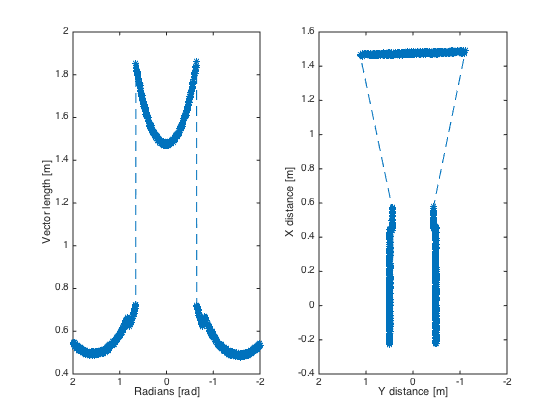
The pico_line_detection node is responsible for detecting lines with the laser scanner data from Pico. The node retrieves the laser data from the topic /pico/laser. The topic has a standard ROS sensor message datatype namely LaserScan. The datatype includes several variables of interest to us namely;

Definition of the x- and y-axis of Pico

1. float32 angle_min which is the start angle of the scan in radian
2. float32 angle_max the end angle of the scan in radian
3. float32 angle_increment the angular distance between measurements in radian
4. float32[] ranges a array with every element being a range, in meters, for a measurement

Using the above data we can apply the probabilistic Hough line transform to detect lines. The detected lines are then published to the topic /pico/line_detector/lines.

Each line is represented by 2 points in the Cartesian coordinate system which is in centimeters. In the coordinate system Pico is located in the center i.e. at (0,0) and the world (coordinate system) moves along with Pico. The x-axis is defined to be front to back while the y-axis is defined to right to left.

Hough transform

Line expressed Cartesian coordinate system with [math]\displaystyle{ (x,y)\,\! }[/math] and in Polar coordinate system with [math]\displaystyle{ (r, \theta)\,\! }[/math]

The Hough transform is a algorithm which is able to extract features from e.g. a image or a set of points. The classical Hough transform is able to detect lines in a image. The generalized Hough transform is able to detect arbitrary shapes e.g. circles, ellipsoids. In our situation we are using the probabilistic Hough line transform. This algorithm is able to detect lines the same as the classical Hough transform as well as begin and end point of a line.

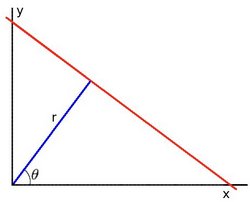
How it works. Lines can either be represented in the Cartesian coordinates or Polair coordinates. In the first they are represented in [math]\displaystyle{ y = ax + b\,\! }[/math], with [math]\displaystyle{ a\,\! }[/math] being the slope and [math]\displaystyle{ b\,\! }[/math] being the crossing in the y-axis of the line. Lines can however also be represented in Polair coordinates namely;

[math]\displaystyle{ y = \left(-{\cos\theta\over\sin\theta}\right)x + \left({r\over{\sin\theta}}\right) }[/math]

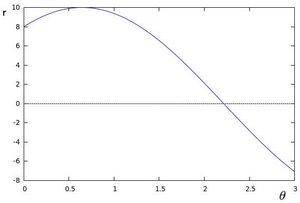
which can be rearranged to [math]\displaystyle{ r = x \cos \theta+y\sin \theta\,\! }[/math]. Now in general for each point [math]\displaystyle{ (x_i, y_i)\,\! }[/math], we can define a set of lines that goes through that point i.e. [math]\displaystyle{ r({\theta}) = x_i \cos \theta + y_i \sin \theta\,\! }[/math]. Hence the pair [math]\displaystyle{ (r,\theta)\,\! }[/math] represents each line that passes by [math]\displaystyle{ (x_i, y_i)\,\! }[/math]. The set of lines for a given point [math]\displaystyle{ (x_i, y_i)\,\! }[/math] can be plotted in the so called Hough space with [math]\displaystyle{ \theta\,\! }[/math] being the x-axis and [math]\displaystyle{ r\,\! }[/math] being the y-axis. For example the Hough space for the point [math]\displaystyle{ (x,y) \in \{(8,6)\} }[/math] looks as the image below on the left. The Hough space for the points [math]\displaystyle{ (x,y) \in \{(9,4),(12,3),(8,6)\} }[/math] looks as the image on the right.

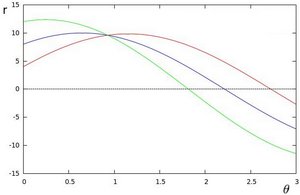The three plots intersect in one single point namely [math]\displaystyle{ (0.925,9.6)\,\! }[/math] these coordinates are the parameters [math]\displaystyle{ (\theta,r)\,\! }[/math] or the line in which [math]\displaystyle{ (x_{0}, y_{0})\,\! }[/math], [math]\displaystyle{ (x_{1}, y_{1})\,\! }[/math] and [math]\displaystyle{ (x_{2}, y_{2})\,\! }[/math] lay. Now we might conclude from this that at this point there is a line i.e. to find the lines one has to find the points in the Hough space with a number of intersections which is higher then a certain threshold. Finding these points in the Hough space can be computational heavy if not implemented correctly. However there exists very efficient divide and conquer algorithms for 2D peak finding e.g. see these course slides from MIT.

In pseudocode the HoughTransform looks as follows.

algorithm HoughTransform is
    input: 2D matrix M
    output: Set L lines with the pair (r,theta)

    define 2D matrix A being the accumelator (houghspace) with size/resolution of theta and r

    for each row in M do
        for each column in M do
            if M(row,column) above threshold
                for each theta in (0,180) do
                    r ← row * cos(theta) + column * sin(theta)
                    increase A(theta,r)

    look at boundary, the center row and the center column of A
    p ← the global maximum within

    if p is a peak do
        add pair (row,column) to L
    else
        find larger neighbour
        recurse in quadrant

    return L

Robustness

Sometimes however the algorithm jitters a little e.g. it detects a line and in the next sample with approximatly the same data it fails to detect a line. To make the algorithm more robust against this we implemented three methods from which we can choose. They were implemented at the same time since they were quiet easy to implement in the code and it gave us a option to compare them and decided which method we wanted to use in the end. We collect a multiple set of datapoints of data points after which we use either one of the three methods

1. Upsampling, use all of the collected datapoints for line detection.
2. Moving average filter, average the datapoints from the multiple sets, then use the average.
3. Median filter, for corresponding datapoints find the median.

These three very simple approaches reduce the jitter to approximately no jitter at all. It is hard to tell which method gives the best result. However it seemed that the third method is best, this can also be explained because the median filter makes sure that samples that are off are not taken into account while in the moving average filter they are taken into account, since of the averaging.

In action

Simulation

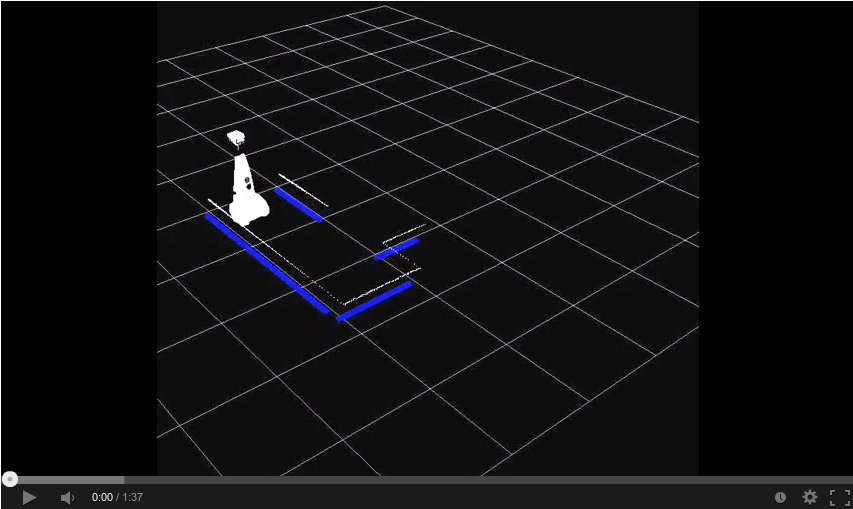
Practice

Situation

The situation node interprets the lines which are being published by the pico_line_detector. First it categorizes each detected line. Then it determines the situation regarding Pico's localization followed by the characterization of the hall way e.g. checking if Pico can turn left, right to a new corridor or can keep moving forward in the same corridor.

Categorization

As explained the situation node first categorizes all the lines which are published by the pico_line_detector. Each line has a type number which tells us something about the line. The type is a bitmask field. We use 6 bits to specify a line type:

Definition of the quadrants and the line types.

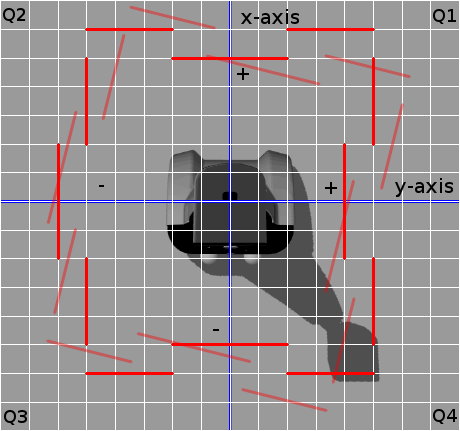
• Q1 - 1 - First quadrant
• Q2 - 2 - Second quadrant
• Q3 - 4 - Third quadrant
• Q4 - 8 - Fourth quadrant
• VE - 16 - Vertical line
• HO - 32 - Horizontal line

The first 4 bits tell us in which quadrant the line lays. The first bit is set if a point of a line belongs to quadrant 1. If the second point also belongs to that same quadrant then nothing changes e.g. the first bit is still set and the other three are still zero. If however the second point belongs to quadrant 2 for example then the second bit is set as such the first and second bit are set and we know that the line overlaps to quadrant 1 and 2.

The last two bits determine if a line is vertical or horizontal (One might wonder why we use two bits but this is to rule out some special cases which may occure e.g. a line which stretches from Q1 to Q3 or similar cases). A line is deemed horizontal if the slope of that line is less then 1, otherwise it is deemed to be a vertical line.

The characteristics Q1,...,HO of the line type have been defined as a enum such that we can easily work with it in our code. Using this technique we can easily determine the type of all the different lines with which we are represented with. Further what comes in handy is that we can store our categorized lines in a map with the line type being the key and the line itself the value. Also since we are not interested in the order of the map we even use a hash map. This enables us to access elements from the map in constant time while a normal map has a lookup time which is logarithmic to the size of the map. To select a certain line we only have to do hashmap.find(Q1 | Q2 | VE), herein | is a bitwise-or operation, to select the vertical line which overlaps from Q1 to Q2.

Now it maybe possible that we detect some multiple lines with the same type. When this is the case the line with the largest length over rules the others.

Localization

To make sure that the robot does not drive against a wall we need to localize Pico with respect to the walls and give a reference to the motion node regarding it.

As explained the lines from pico_line_detector are categorized. There are 9 line types which are eligible to use for localization of Pico. These are:

1. Right side
   1. Q1 | Q4 | VE
   2. Q1 | VE
   3. Q4 | VE
2. Left side
   1. Q2 | Q3 | VE
   2. Q2 | VE
   3. Q3 | VE
3. Front
   1. Q1 | Q2 | HO
   2. Q1 | HO
   3. Q2 | HO

Now we loop threw the entries of the right side e.g. first check if line type Q1 | Q4 | VE exists then Q1 | VE and then Q4 | VE. If either one of them exists we calculate the distance and the angular mismatch with respect to wall and break out of the loop. We then continue by checking the left side and following up the front side. Further since we only sent out one angle we determine the angle with find the angle with the highest priority e.g. first Q1 | Q4 | VE, then Q2 | Q3 | VE, then Q1 | Q2 | HO, then Q1 | VE, etcetera. In pseudo code it looks like this:

algorithm localization is
    input: map M with (key,value)-(line_type,line)
    output: A tuple msg with the elements (distance_right,distance_left,distance_front,angle)

    define 1D array l
    define 2D array t
    define 2D array lineTypes with the following elements { { Q1|Q4|VE, Q1|VE, Q4|VE },
                                                            { Q2|Q3|VE, Q2|VE, Q3|VE },
                                                            { Q1|Q2|HO, Q1|HO, Q2|HO } }
    
    for each row in lineTypes do
        for each column in lineTypes do
            if key lineType exists in M
                l(row) ← calculate distance w.r.t. to the wall
                t(row,column) ← calculate angular mismatch w.r.t. to the wall
                stop with looping around the columns and start with the next row.
    
    for each column in lineTypes do
         if t(1,column) is set
             msg.angle ← t(1,column)
             stop with looping
         else if t(2,column) is set
             msg.angle ← t(2,column)
             stop with looping
         else if t(3,column) is set
             msg.angle ← t(3,column)
             stop with looping
          
    msg.distance_right ← l(1)
    msg.distance_left  ← l(2)
    msg.distance_front ← l(3)
    
    return msg

Situation

The situation determines using the categorized lines in what kind of situation/state the robot is in. If it is approaching a junction and if yes what kind of junction and what is the distance to that junction. The situation nodes posts its result using the Situation message.

The situation can determine if there is a left, right of front junction by a number of manners. For the front case this is pretty easy. If we don't detect a horizontal line which spans over Q1 and Q2 and if the opening between two possible lines which we might find in Q1 and Q2 is width enough then we can move forward.

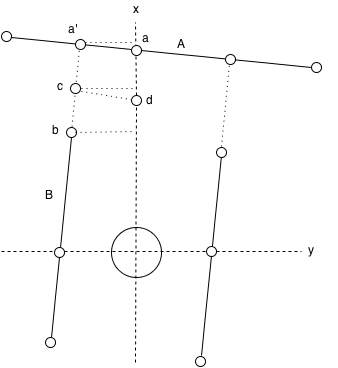
For the left and right case it is somewhat more difficult since there are multiple cases which may occure and may indicate that there is a opening to the left respectively the right. We will not discuss all possible situation. Assume that we have the following lines, see figure.

• A, a horizontal line which spans over Q1 and Q2.
• B, a horizontal line which spans over Q2 and Q3.

Now to calculate the width of the opening we need to find the point a' which is the intersection of the lines A and B. After finding this point the width of the opening can be easily calculated by substracting the x-coordinate of point b from the x-coordinate of point a'. When the width of the opening is larger then the threshold of a opening we continue by calculating the distance at which the robot should turn 90 degrees. This distance is calculated by first determining the x-intercept of the line A, following by substracting half of the width of the previously determined opening, i.e. the x-coordinate of point c, by which we obtain the x-coordinate of point d (which has 0 as the y-coordinate) and thus the distance to the opening of the left.

Reasoning

The reasoning module is responsible to solve the maze. For this task the module uses the wall follower algorithm also known as the left-hand or right hand-rule. The principle of wall follower algorithm is based on always following the right wall or always following the left wall. This means that the wall is always on your right hand for example (see picture maze). If the maze is not simply connected (i.e. if the start or endpoints are in the center of the structure or the roads cross over and under each other), than this method will not guarantee that the maze can be solved. For our case there is just one input and output on the outside of the maze, and there are also no loops in it. So the wall follower algorithm is in our case very useful.

The reasoning module gets information from the previous module about the next decision point. These decision points, are points where a decision should be made for example at crossroads, T-junctions or at the end of a road. At the decision points, the reasoning module determines the direction in which the robot will drive, by using the wall follower algorithm. For example when module gets information about the next decision point, which is a crossroad, then the reasoning module determines that the robot turn 90 degrees at this point so that the robot following the right wall. There also comes information from the vision module this module, search to arrows on the wall. This arrows refer to the output of the maze and help to solve the maze faster. When there is relevant data from the vision module, this data will overrule the wall follower algorithm.

Motion

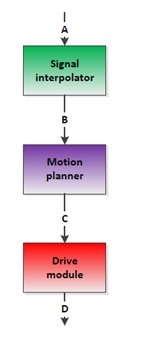
The motion node consists of three parts: signal interpolator, motion planner and the drive module. Al this parts determine dependent of the input signals (actual position and target position) the drive speed and rotation speed of the Pico robot.

Signal interpolator

The goal of the signal interpolator is twofold. First, it provides a steady fixed rate of information for the other modules in the local planner. Secondly, it provides relative information between actual data form localization and reasoning. It does so by combining data acquired from the localization and reasoning module with the odometry data from the encoders. Herein the data from localization is presumed to be ideal, meaning the data is always correct. However both types of data are given in different frames.

The localization and reasoning data is provided relative to the corridor section the robot is currently in. Localization gives the distances to both the left and right wall as well as the angle between the corridor and the robot orientation. Reasoning provides the distance to the decision point and the action to be taken there.It can be seen that when localization data is not provided, information is desired about these parameters based on the odometry data.

The odometry data cannot be represented in an external frame by definition. Therefore this data is the relative position of the robot with respect to the start point. This data is calculated by measuring the angle of the wheels over time. Consequently loss of traction is not detectable by this data. However is we presume infinite tractions or limited loss of traction we can use the odometry data to interpolate the localization and reasoning data.

To do so we need to transform the odometry data to the frame of the localization and reasoning data. The transformation has to be reset as the robot rounds a corner because this defines the frame of the localization and reasoning data. The transformation consists of two parts, the translational and the rotational component. The translational component is handled by setting an offset in the odometry data based on the localization data. However this offset alone would result in a flip of the x and y axis because the robot has a different orientation in the odometry frame but the same in the localization frame. To adjust the odometry frame has to be turned to match the difference in corridor orientations. This rotation is done using the first sample of localization data when the turn is complete, using the orientation fault to adjust for any errors made in the turn, thus aligning both frames.

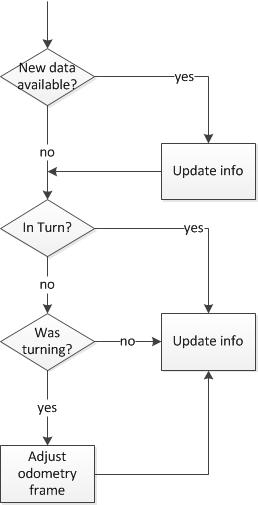
The flow of the module can be described by the following diagram:

Motion planner

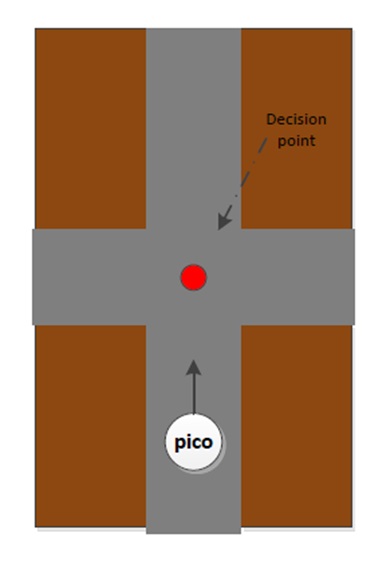
The motion planner has two main goals. The first one is to navigate the robot between the walls dependent of the input information from the signal interpolator. The second goal is to navigate the robot in the right direction on the decision points. These decision points, are points where a decision should be made, for example at a crossroad. These decision points, and the decision itself, will be determined by a previous module.

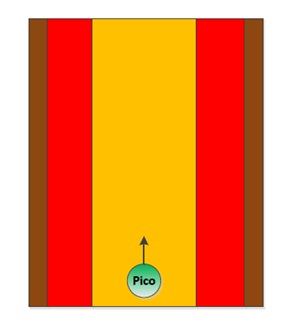
Firstly the navigation to stay between the walls, this navigation provides that the robot stays between the walls and doesn’t hit them. To fulfil this task a simple controller is used, which works on the following principle: When the Pico robot stays in the orange zone it always drives forward. During the ride it is possible that the robot will drive a little skewed, for example by friction on the wheels. In this situation the robot will adjust in the correct direction. When it is not possible to send the robot in the correct direction, the robot will drive into the red zone. In the red zone the robot stops driving straight forward and turn in the correct direction, away from the wall. When the orientation of the robot is correct, the robot will drive straight forward.

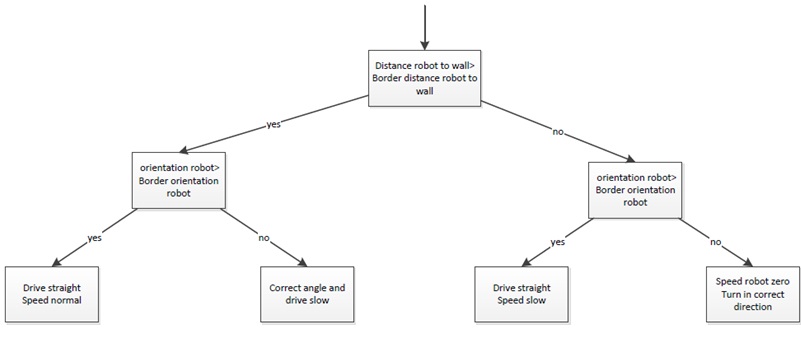Secondly the navigation for the decision points. When the robot is inside the border of the decision point the robot will stop driving (the information about the distance up to the decision point itself comes from the reasoning module). On this moment the navigation to stay between the walls is overruled by the navigation for the decision points. After the robot is stopped the robot will rotate in the correct direction, for example turn -90 degrees. When the rotation is done the navigation to stay between the walls takes over and the robot will drive forward until it is on the next decision point.

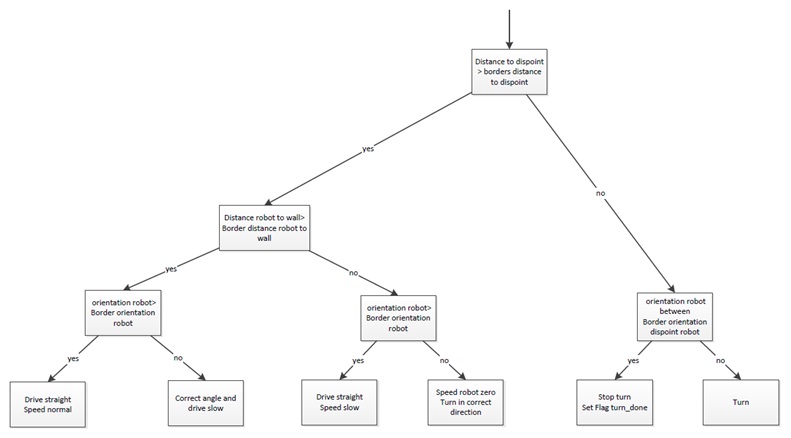Drive module

The drive module is meant to realize the desired velocity vector obtained from the motion planner. In the current configuration the desired velocity vector is directly applied to the low level controllers since these controllers causing maximum acceleration. Test on the actual machine must point out whether or not the loss of traction due to this acceleration causes significant faults in the position.

Tests

Simulation

The following video's show some simulation tests.

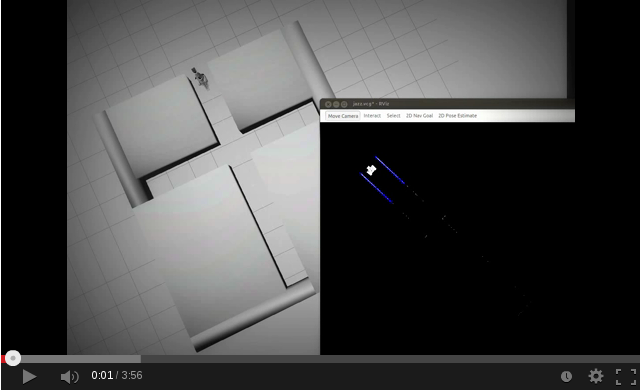
Line detection	Forwards	Left junction
Right junction	T junction	Junction

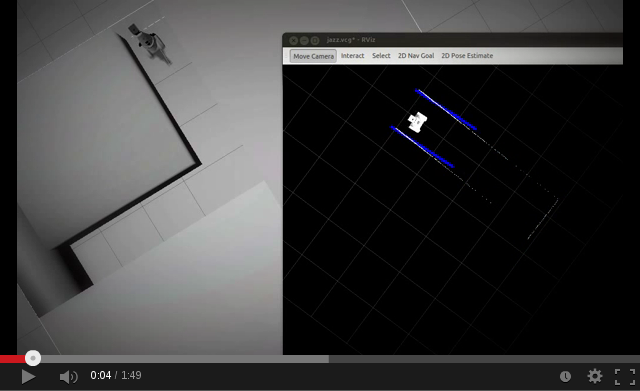Week 6: 2013-10-11

Test parameters:

Data logged:

           Standard pico topics: 
           /pico/camera
           /pico/laser
           /pico/odom
           /tf
           /pico/joint_states
           Our topics:
           /pico/situation/situation
           /pico/situation/localization
           /pico/line_detection/lines
           /pico/line_detection/lines_filtered
           /pico/signalInterpolator
           /pico/MotionPlanner

Tested with corridor width of 750mm and 1000mm

Test results:

Motion

• After turning start using localization data in order to keep driving straight
• Start using localization data (width corridor) to determine safety margin distance from wall
• Turning angle is to large, more than 90 degrees
• Margin turn before wall increased, robot kept hitting wall when turning 180 degrees

Localization

• Keep publishing data at all times

Usefull links / References

• Information about maze solving: http://en.wikipedia.org/wiki/Maze_solving_algorithm
• Nice java applet about Hough transform http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/HNF.html
• OpenCV Hough transform tutorial http://docs.opencv.org/doc/tutorials/imgproc/imgtrans/hough_lines/hough_lines.html