Embedded Motion Control 2013 Group 1

Group Info

Name:	Abbr:	Student id:	Email:
Groupmembers (email all)
Paul Raijmakers	PR	0792801	p.a.raijmakers@student.tue.nl
Pieter Aerts	PA	0821027	p.j.m.aerts@student.tue.nl
Wouter Geelen	WG	0744855	w.geelen@student.tue.nl
Frank Horstenbach	FH	0792390	f.g.h.hochstenbach@student.tue.nl
Niels Koenraad	NK	0825990	n.j.g.koenraad@student.tue.nl
Tutor
Jos Elfring	n.a.	n.a.	j.elfring@tue.nl

Meetings

1. Meeting - 2013-09-04
2. Meeting - 2013-09-11
3. Meeting - 2013-09-18
4. Meeting - 2013-09-25

(Global) Planning

Week 1 (2013-09-02 - 2013-09-08)

• Installing Ubuntu 12.04
• Installing ROS Fuerte
• Following tutorials on C++ and ROS.
• Setup SVN

Week 2 (2013-09-09 - 2013-09-15)

• Discuss about splitting up the team by 2 groups (2,3) or 3 groups (2,2,1) to whom tasks can be appointed to.
• Create 2D map using the laser scanner.
• Start working on trying to detect walls with laser scanner.
• Start working on position control of Jazz (within walls i.e. riding straight ahead, turning i.e. 90 degrees).
• Start thinking about what kind of strategies we can use/implement to solve the maze (see usefull links).

Week 3 (2013-09-16 - 2013-09-22)

• Start work on trying to detect openings in walls.
• Start working on code for corridor competition.
• Continue thinking about maze solving strategy.

Week 4 (2013-09-23 - 2013-09-29)

• Decide which maze solving strategy we are going to use/implement.

Week 5 (2013-09-30 - 2013-10-06)

• To be determined.

Week 6 (2013-10-07 - 2013-10-13)

• To be determined.

Week 7 (2013-10-14 - 2013-10-20)

• To be determined.

Week 8 (2013-10-21 - 2013-10-27)

• To be determined.

Progress

Week 2

State diagram made of nodes Localisation and Situation

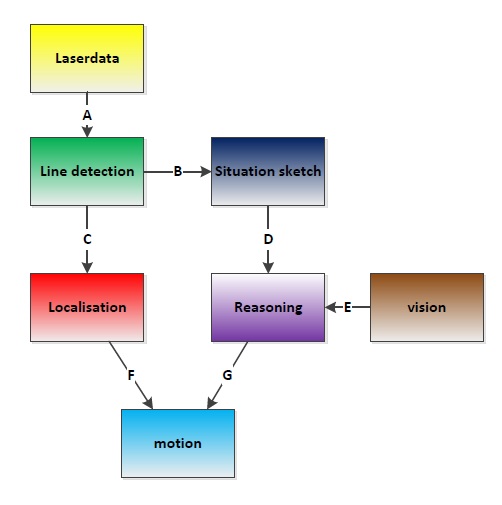
Software architecture

IO Data structures

#	Datatype	Published by	Topic	Description
A	LaserScan	Pico	/pico/laser	Laser scan data. For info click here
B	Int32MultiArray	pico_line_detector	/pico/line_detector/lines	Every 4 elements represent a line element i.e. [x,y,x',y',...] with a maximum of n lines. Hence the array will at most contain 20 elements. The coordinates represent a line in the cartesian coordinate system with Pico being the center e.g. (0,0). The x- and y-axis in centimeters and the x-axis is in front/back of Pico while the y-axis is left/right. Further the coordinate system turns along with Pico.
C	Int32MultiArray
D	Custom message (3x booleans, 1x Float32)
E
F	Custom message (3x Float32)
G	Custom message (2x Float32)

Line detection

The pico_line_detection node is responsible for detecting lines with the laser scanner data from Pico. The node retrieves the laser data from the topic /pico/laser. The topic has a standard ROS sensor message datatype namely LaserScan. The datatype includes several variables of interest to us namely;

Definition of the x- and y-axis of Pico

1. float32 angle_min which is the start angle of the scan in radian
2. float32 angle_max the end angle of the scan in radian
3. float32 angle_increment the angular distance between measurements in radian
4. float32[] ranges a array with every element being a range, in meters, for a measurement

Using the above data we can apply the probabilistic Hough line transform to detect lines. The detected lines are then published to the topic /pico/line_detector/lines.

Each line is represented by 2 points in the Cartesian coordinate system which is in centimeters. In the coordinate system Pico is located in the center i.e. at (0,0) and the world (coordinate system) moves along with Pico. The x-axis is defined to be front to back while the y-axis is defined to right to left.

Hough transform

Line expressed Cartesian coordinate system with [math]\displaystyle{ (x,y)\,\! }[/math] and in Polar coordinate system with [math]\displaystyle{ (r, \theta)\,\! }[/math]

The Hough transform is a algorithm which is able to extract features from e.g. a image or a set of points. The classical Hough transform is able to detect lines in a image. The generalized Hough transform is able to detect arbitrary shapes e.g. circles, ellipsoids. In our situation we are using the probabilistic Hough line transform. This algorithm is able to detect lines the same as the classical Hough transform as well as begin and end point of a line.

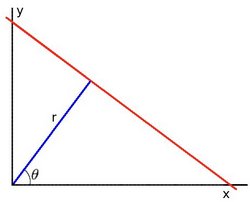
How it works. Lines can either be represented in the Cartesian coordinates or Polair coordinates. In the first they are represented in [math]\displaystyle{ y = ax + b\,\! }[/math], with [math]\displaystyle{ a\,\! }[/math] being the slope and [math]\displaystyle{ b\,\! }[/math] being the crossing in the y-axis of the line. Lines can however also be represented in Polair coordinates namely;

[math]\displaystyle{ y = \left(-{\cos\theta\over\sin\theta}\right)x + \left({r\over{\sin\theta}}\right) }[/math]

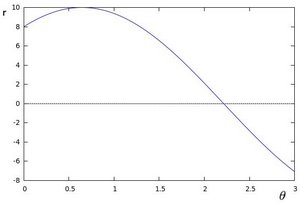
which can be rearranged to [math]\displaystyle{ r = x \cos \theta+y\sin \theta\,\! }[/math]. Now in general for each point [math]\displaystyle{ (x_i, y_i)\,\! }[/math], we can define a set of lines that goes through that point i.e. [math]\displaystyle{ r({\theta}) = x_i \cos \theta + y_i \sin \theta\,\! }[/math]. Hence the pair [math]\displaystyle{ (r,\theta)\,\! }[/math] represents each line that passes by [math]\displaystyle{ (x_i, y_i)\,\! }[/math]. The set of lines for a given point [math]\displaystyle{ (x_i, y_i)\,\! }[/math] can be plotted in the so called Hough space with [math]\displaystyle{ \theta\,\! }[/math] being the x-axis and [math]\displaystyle{ r\,\! }[/math] being the y-axis. For example the Hough space for the point [math]\displaystyle{ (x,y) \in \{(8,6)\} }[/math] looks as the image below on the left. The Hough space for the points [math]\displaystyle{ (x,y) \in \{(9,4),(12,3),(8,6)\} }[/math] looks as the image on the right.

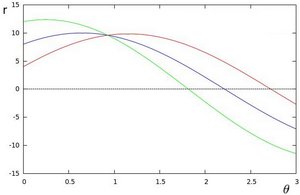The three plots intersect in one single point namely [math]\displaystyle{ (0.925,9.6)\,\! }[/math] these coordinates are the parameters [math]\displaystyle{ (\theta,r)\,\! }[/math] or the line in which [math]\displaystyle{ (x_{0}, y_{0})\,\! }[/math], [math]\displaystyle{ (x_{1}, y_{1})\,\! }[/math] and [math]\displaystyle{ (x_{2}, y_{2})\,\! }[/math] lay. Now we might conclude from this that at this point there is a line i.e. to find the lines one has to find the points in the Hough space with a number of intersections which is higher then a certain threshold.

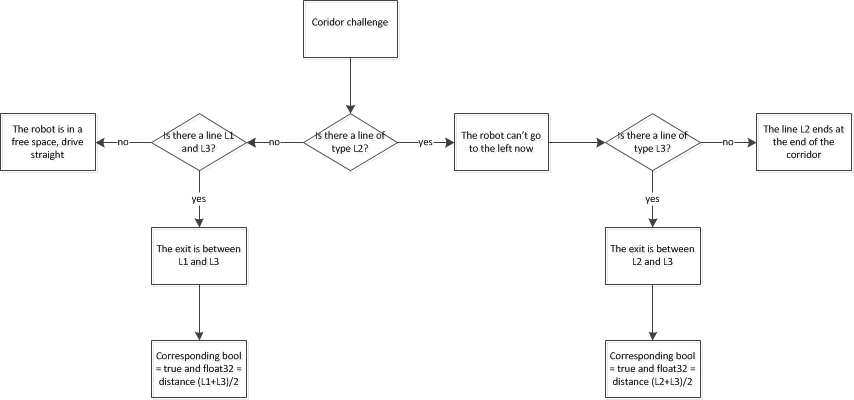
Situation sketch

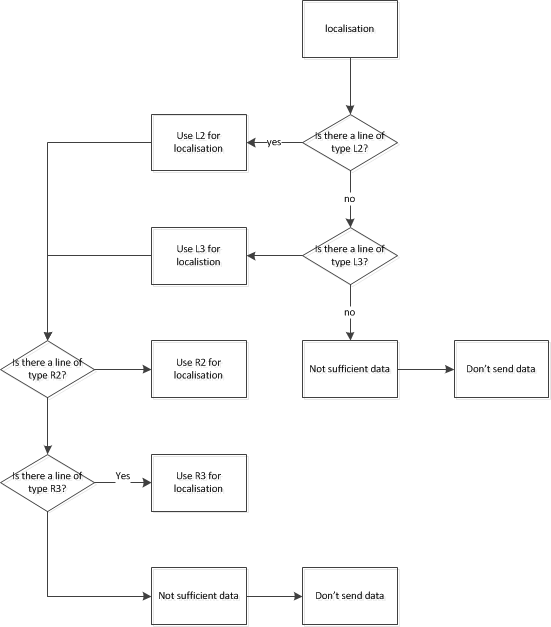
Localisation

Reasoning

Motion

Software development

localisation code (matlab generated)

clc %%x is driving direction!

Y1_1=-5; X1_1=-2;

Y1_2=-6; X1_2=6;

Y2_1=6; X2_1=-5;

Y2_2=5; X2_2=-6;

rc1=(X1_1-X1_2)/(Y1_1-Y1_2) %%of left-hand line
rc2=(X2_1-X2_2)/(Y2_1-Y2_2) %%of right-hand line

%%##determine relative driving angle
Theta=tan(rc1+rc2)/2

%%##determine distance to left wall
offset1=X1_1-Y1_1*rc1;
Y1=-offset1/rc1

%%##determine distance to right wall
offset2=X2_1-Y2_1*rc2;
Y2=-offset2/rc2

Theory

include hough transform here

Usefull links

• http://en.wikipedia.org/wiki/Maze_solving_algorithm