Mobile Robot Control 2023 The Iron Giant

Group members:

Name	student ID
Tobias Berg	1607359
Guido Wolfs	1439537
Tim de Keijzer	1422987
Marijn van Noije	1436546
Tim van Meijel	1415352
Xander de Rijk	1364618
Stern Eichperger	1281232

Midterm presentation

The midterm presentation of The Iron Giant: File:Midterm-presentation-The-Iron-Giant.pdf

The feedback and questions received regarding the midterm presentation of The Iron Giant are as follows:

Feedback point 1:

• The current state diagram does not include a recovery state to resolve a deadlock situation. If a passage suddenly becomes blocked and remains blocked, the robot could potentially end up in a deadlock. This could occur, for example, if a person obstructs a pathway between obstacles and does not move away.

Solution: To address this issue, an additional recovery loop should be added for handling suddenly blocked pathways. In this loop, the obstructing obstacle is added to the map, and a alternative new path is calculated using the A* algorithm.

Question 1:

• How does the robot transition into the pose recovery state? What parameter or condition is used?

Solution/answer: A condition based on the standard deviation of the particle spread should be implemented. If the deviation is too large, indicating a significant spread of particles and therefore an uncertain estimation, the robot has lost knowledge of its position in the world and needs to recover it.

Question 2:

• Why was the "happy flow" defined in this manner? Won't the robot always encounter disturbances and dynamic objects that cause it to loop through parts of both the happy and unhappy flows? In such cases, the loop may not necessarily be considered an unhappy flow.

Solution/answer: It is true that the definition of the happy flow was somewhat rigid. It is true that certain segments of the "unhappy flow" may occur within the expected states the robot will loop trough during the challenge. This does not pose a problem and does not represent an unhappy flow.

Figure 1. Updated state diagram after design presentation.

We updated the state diagram according to the feedback and questions as shown in Figure 1.

Final Challenge

Introduction

In this project, the goal is to successfully drive the Hero robot to a table in a restaurant, using a predefined map, with unknown static and dynamic obstacles. To apply the developed code to the Hero robot, the C++ programming language is used. The goal is to enable the Hero robot to navigate and locate itself within the environment. Localization and navigation are two aspects of autonomous robots that will be focussed on.

For a robot to drive autonomously, it is important the robot knows its current location and orientation. This requires localization of the robot. This localization method must be based on a predefined map, but should also compensate for partial imperfect situations (living in the real world). The key idea of localization is to have a map of the environment and sensor measurements, which is used in a so-called particle filter to get a better localization of the robot pose. This particle filtering method uses a probabilistic approximation of particles, each representing a possible hypothesis for the robot position.

Next, the robot must be able to navigate itself to the desired position by following a certain path. To plan the path of the Hero robot, the A* path planning algorithm is used to calculate the most optimal path for the robot to effectively reach its destination. This is the so-called global navigation the robot uses. In addition, the local navigation allows the robot to effectively navigate through the map and avoid obstacles in real time. To account for the objects in the final challenge, the so-called artificial potential field method is used.

To complete the final challenge, localization and navigation techniques must be combined. By developing the software for the final challenge, the robot will identify its location on the map, plan an optimal path and complete the task by moving precisely to the designated table. This wiki page thoroughly describes these algorithms and explains how they are implemented. In addition, it discusses how these algorithms interact and their performance and robustness is determined. An evaluation is given at the end, with a conclusion, discussion and future steps.

Strategy description

Hoe willen we het gaan bereiken Beschrijven dat we deuren willen toepassen, en in het hoofdstuk robustness omschrijven welke moeilijkheden we zijn tegenkomen

Figure 2. Final state diagram used in challenge

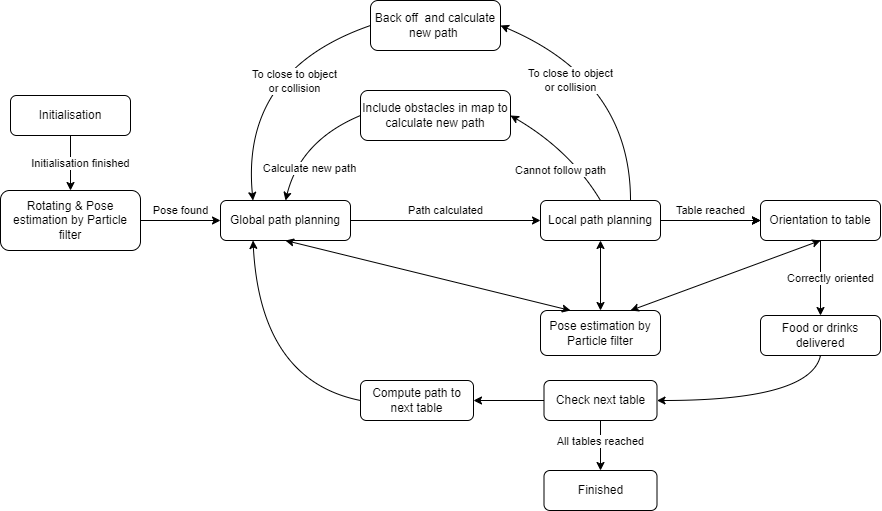
Algorithms used, software Architecture

A star

For the global path planner we use the A* algorithm with some adjustments. Initially, the particle filter determines the input in map frame in meters. This is converted to pixels for the input of the global planner. Goals are predefined in pixel positions and are also given as input for the planner. For robustness first the node list is calculated after which the closest node for those pairs of pixels is used as entrance and final node.

For calculating the node list, we read the image of the map with gray scaling. Since pixels can be either black (0), gray (128) and white (255), these values serve as threshold for squeezing values to binary values. Another input of the global planner is a list of which doors we want to use. Each door has a cluster of nodes, which are then used for updating the map after thresholding depending if they serve as wall or not. Similarly, with use of the particle filter and the laser data, the objects are converted from meters to pixels. A min and max function is applied to ensure all laser point locations are within the map and are then added to the obstacle map, separate from the map with walls and “closed” doors. For added robustness a margin of a 15 pixels is applied for which an open node needs to be away from walls and obstacles. Each node is defined on a grid from the map with a defined step size of pixels, in this case 10 pixels per step size.

With the remaining node list, a list of connections for each node is made in the directions, up, down, left, right and diagonal.  

Before running A* the position and distances from the goal are computed in map frame. An additional cost function is defined for every pixel near a wall or obstacle. If it is within a range of 20 the node has a high cost of 100, whereas within 30 in has a low cost of 2.

For A* we take with every step the node with the lowest cost-to-come. For this node, it will add all connected nodes and applies the lowest cost-to-go. The cost-to-go is determined by the step size from one node to the next (meaning going to a diagonal node has a higher cost) with addition of the added cost of being near a wall or obstacle for the node-to-go. After A* has reached the final node, it will create a path in map frame in meters. Since the distance between nodes is small, the new path is every third step of the full path. This is then send to the local path planner.

For visualization after each time it has found a path towards a goal it will make an image plotting both the walls, doors, path and obstacles in respective colors black, gray, red and blue. Each time the global path planner is run a new image is made, not overwriting the previous one.

Similar to the A* algorithm, the Dijkstra algorithm is used to determine which nodes are a door. By putting the algorithm in a for loop of the nodes that are a door, it is possible to cluster all node positions per existing door. The reason for doing this is because it makes it robust if we want to make a path through one door but not the other. The node list is determined similarly as previous by applying a threshold on the image and finding the nodes of the door. It is sufficient to only look in the directions up down, left and right for the node connections. This information is also used as input for the global path planner.

Particle filter

TA particle filter is a commonly used probabilistic filtering technique in robotics that estimates the pose of a robot based on sensor measurements while navigating in an environment. The presence of wheel slip and noisy data causes imperfections in the odometry data, therefore it is not possible to fully rely on the odometry data to get an accurate enough estimation of the robot’s pose. In order to get a better estimation of the pose of the robot while it is going to the tables in the restaurant, it is important to implement a localizing algorithm that estimates the pose of the robot on the map. Therefore, a particle filter algorithm is used in the final challenge.

The particle filter made in the previous assessments forms the bases of the algorithm that was eventually implemented. In this algorithm, each particle describes a hypothesis of the current pose of the robot. At first, the particles are distributed with a Gaussian distribution around the robot, resulting in a broad range of the potential pose of the robot, see Figure 4.  Based on the lidar and odometry data of the robot, the particles are resampled with weights based on the likelihood of their pose. This is done by a filter that approximates the probability distribution of the robot’s pose. A  “Recursive State Estimation Beam-based model” is implemented that computes the likelihood of each measurement given a prediction. This model accounts for measurement errors including, measurement noise, unexpected objects, errors due to failures to detect objects and random unrecognized noise. Finally, the particles will be resampled so that high likelihoods are represented heavily in the new particle set. A multinomial resampling method is used. This method selects particles based on their weights, with emphasis on particles that have a higher likelihood of representing the true pose. This results in a final estimation of the robot’s pose.

For the restaurant challenge, the particle filter is updated during each iteration in the main “while loop”. Updating the filter during each cycle ensures smaller differences in robot poses, which makes it easier for the particle filter to update and predict a more accurate pose when the robot is moving. To increase the computation speed, the number of particles was slightly reduced.

Conclusion

Wat hebben we bereikt

Discussion

Discusseer wat verbeterd kan worden

Future steps

Expliciet beschrijven wat de volgende stappen zijn