Embedded Motion Control 2015 Group 3/Localisation: Difference between revisions
No edit summary |
|||
| (54 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
= Localisation = | = Localisation = | ||
This page is part of the [ | This page is part of the [[Embedded_Motion_Control_2015_Group_3|EMC03 CST-wiki]]. | ||
This page goes into details about localisation. | This page goes into details about localisation. | ||
| Line 6: | Line 6: | ||
== Requirements of Localisation == | == Requirements of Localisation == | ||
In order to be able to locate itself within its environment, the robot needs information. The | In order to be able to locate itself within its environment, the robot needs information. The required data to obtain global position are: | ||
# global x-position [m] | # global x-position [m] | ||
# global y-position [m] | # global y-position [m] | ||
| Line 21: | Line 21: | ||
The robot will need global coordinates. There are two sensors which it can use to determine these coordinates. However both sensors have their own drawbacks. | The robot will need global coordinates. There are two sensors which it can use to determine these coordinates. However both sensors have their own drawbacks. | ||
*The odometry sensor provides global x-y coordinates and angle. There is not much variance in the data of the sensor, but there is a drift (bias) that will accumulate over time. The odometry data can be viewed as feedforward information for the system. | *The odometry sensor provides global x-y coordinates and angle. There is not much variance in the data of the sensor, but there is a drift (bias) that will accumulate over time. The odometry data can be viewed as feedforward information for the system. | ||
*The LRF sensor provides 1000 ranges [m] with distances to objects over a scope of 270 degreess around the robot. This sensor shows no bias, but has a variance however. Furthermore the LRF data does not provide the global coordinates that we want with its raw data. Therefore | *The LRF sensor provides 1000 ranges [m] with distances to objects over a scope of 270 degreess around the robot. This sensor shows no bias, but has a variance however. Furthermore the LRF data does not provide the global coordinates that we want with its raw data. Therefore this data has to be converted into position changes in terms of the global coordinates. The LRF data can be seen as the Feedback loop of the system. | ||
When the robot starts its program initially, the global coordinates will be all zero. So the start position of the robot determines the direction of the x- and y-axes. The data from the odometry and the LRF will be updated at each time instant. The odometry just works very intuitively: it tells you how far you have moved based on wheel-rotation. In the case of LRF however, the following happens: It measures the distances to the objects in the environment at time t0. It measures again at t1. The difference in distance, converted to the wanted coordinates, should be equal to the odometry data. Of course this will not happen due to the errors in the sensors, but that is why a filter is used to filter the data in between each next update step. | When the robot starts its program initially, the global coordinates will be all zero. So the start position of the robot determines the direction of the x- and y-axes. The data from the odometry and the LRF will be updated at each time instant. The odometry just works very intuitively: it tells you how far you have moved based on wheel-rotation. In the case of LRF however, the following happens: It measures the distances to the objects in the environment at time t0. It measures again at t1. The difference in distance, converted to the wanted coordinates, should be equal to the odometry data. Of course this will not happen due to the errors in the sensors, but that is why a filter is used to filter the data in between each next update step. | ||
| Line 36: | Line 36: | ||
<math>\hat{x}_k^- </math> is the predicted ahead state variable at discrete time instance <math>k</math>. This column vector consists of the global x-position, global y-position and the global angle. So logically, <math>\hat{x}_{k-1}^- </math> is the same vector at a previous time instance. | <math>\hat{x}_k^- </math> is the predicted ahead state variable at discrete time instance <math>k</math>. This column vector consists of the global x-position, global y-position and the global angle. So logically, <math>\hat{x}_{k-1}^- </math> is the same vector at a previous time instance. | ||
<math>A</math> is an n by | <math>A</math> is an n by n matrix that relates the state at the previous time step <math> k-1 </math> to the state at the current step <math> k </math>, in the absence of either a driving function or process noise. | ||
<math>B</math> is an n by n matrix that relates the optional control input u to the state variable. | <math>B</math> is an n by n matrix that relates the optional control input u to the state variable. | ||
| Line 72: | Line 72: | ||
== Implementation of method == | == Implementation of method == | ||
Here the implementation of the method will be briefly discussed. | |||
===Interface=== | |||
Localisation is a separate cpp-file which can be seen as a block. It uses the Scan class data to read sensor data. Also it uses the Drive class to retreive information on the velocity. the variables that are used as arguments are copies and are not used by reference, as they are only needed to calculate the position of the robot. The variables that are only used within the localisation class are ofcourse set to private status. After all necessary blocks are defined in the header file localisation.h , accompanied with the function prototypes, the file localisation.cpp can be properly used. The file consists of 6 functions in total: | |||
* Initializing initial position | |||
* Retreiving LRF-data and converting this into useful X,Y,A data, stored to be used in another function | |||
* Retreiving ODO-data and storing this to be used in another function | |||
* Composing the Z column-vector used in the Kalman algorithm | |||
* Composing the B matrix that is used in the Kalman algorithm | |||
* Function containing the actual Kalman algorithm, which uses the information retreived in the above function to give an accurate localisation | |||
The resulting X,Y,A coordinates are made available to the mapping block for further use. There this info can be used to pinpoint and save nodes, as well as recognizing whether the robot has visited these coordinates before and much more. See the mapping section for further details on this block. | |||
=== Function 1: initialize position: SetX0()=== | |||
In this function the position is determined by means of a for-loop that loops over all of the laser ranges. It determines the minimum range by means of an if-statement. If the minimum range is found, it is stored along with its beam number. This direction is set to correspond to the global Y-direction, and the global angle A is calculated as well, using the beam number. Now the global X-axis is set by using the global Angle. These values are all stored and X,Y,A are initialized. | |||
=== Function 2: LRF-retreival and conversion: LrfLocalisation()=== | |||
This function uses the range data to extrapolate the position of the robot. | |||
First the angular position A is evaluated. If this angle is larger than pi, or smaller than minus pi, it will be wrapped by subtracting or adding 2 pi respectively. | |||
This wrapped angle is used to determine the beam numbers of the current minimal ranges. This is simply done using the following relation: | |||
n_x = X[2]+robot.angle_max / robot.angle_increment; | |||
In this equation n_x corresponds to the beam number of the global X-axis and position. X[2] is the global angle A and the other parameters are self explanatory. The range belonging to this beam number is stored. The same procedure is used to determine the Y-data. | |||
In order to create robustness and in order to prevent problems in other function calls, there are some if-statements included to switch axes if necessary. If the beam number n_x is smaller than 4 or bigger than 994, it is one of the outer ranges. If one of these if-statements is true, the beam number n_x will be changed. We switch from the positive to negative axis or the other way around, by adding pi to the angle. This way, the axis can not get out of sight of the robot. Simple boolean expressions are used to notify the system whether the positive or negative axis is being tracked. This is important because it changes whether distances should be counted negative or positive. This system using axis-switches is incorporated, because there is no assumption made regarding initial position. It should be able to determine an axis to track, regardless of the initial angle of the robot in the maze. | |||
Next the values of the ranges are checked between n_x-5 and n_x+5 using a for-loop. If a minimum range is found it is stored. However, if the minimum value lies on the outer bounds of the loop, or if the difference is too small (noise) , then no minimum is found. This is done for both the x- and y-direction. | |||
Finally, using the laser distance in x- and y-direction, the difference is range is calculated with the previous function call. These differences represent the movements made between function calls, and therefore the difference in position. Every function call, the differences in each direction are added to the total of differences calculated in previous calls. These variables therefore represent the global X,Y and A position. | |||
deltaXLFR = min_x_value*pow(-1,neg_x_axis) - oldXLFR; // Calculate change in X by LRF | |||
deltaYLFR = min_y_value*pow(-1,neg_y_axis) - oldYLFR; // Calculate change in Y by LRF | |||
deltaALFR = CorrectedAngleA - oldALFR; // Calculate change in angle using LRF from previous program call | |||
oldXLFR = min_x_value*pow(-1,neg_x_axis); // Calculate the new oldXLFR | |||
oldYLFR = min_y_value*pow(-1,neg_y_axis); // Calculate the new oldYLFR | |||
oldALFR = CorrectedAngleA; // Calculate the new oldALFR | |||
=== Function 3: ODO-retreival: ODOLocalisation()=== | |||
This function creates an odometry object and reads the odometry data from the io-layer. It starts with an initial X=0,Y=0,A=A_init . It calculates the differences each time the function is called. So if the x position is 5 meter, and the next function call it reads 5.2 meter, then the difference equals the recent reading minus the old reading. The differences are stored, as well as the old position and the sum of the differences (actual position). This info is to be used by the other functions that need it in the file. | |||
void Localisation::ODOLocalisation(){ | |||
emc::OdometryData odom; // Creating odometry data object to retreive odo-info | |||
deltaXODO = odom.x - oldXODO; // Calculating change in x-position using odo | |||
deltaYODO = odom.y - oldYODO; // Calculating change in y-position using odo | |||
deltaAODO = odom.a - oldAODO; // Calculating change in a-position using odo | |||
oldXODO = odom.x; // Setting retreived odo global x-position info to oldXODO | |||
oldYODO = odom.y; // Setting retreived odo global x-position info to oldXODO | |||
oldAODO = odom.a; // Setting retreived odo global x-position info to oldXODO | |||
} | |||
=== Function 4: Making Z: MakeZ()=== | |||
Z is a 6-entry column vector. Every time it is called, it will update the entries as follows: | |||
The first three entries (corresponding to X_lrf,Y_lrf and A_lrf respectively) equal their global position plus the difference in position calculated in the LRF retreival function. | |||
The latter three entries correspond in the same manner to their odometry counterparts. | |||
These second X_odo,Y_odo and A_odo are updated in the same manner, but using the difference in odometry instead of LRF. | |||
The odometry differences are calculated in function 3. | |||
Now the Z-column vector is ready to be used by the Kalman filter. | |||
void Localisation::MakeZ(){ | |||
z[0] = X[0] + deltaXLFR; //Lrf set of x,y,a | |||
z[1] = X[1] + deltaYLFR; | |||
z[2] = X[2] + deltaALFR; | |||
z[3] = X[0] + deltaXODO; //Lrf set of x,y,a | |||
z[4] = X[1] + deltaYODO; | |||
z[5] = X[2] + deltaAODO; | |||
} | |||
=== Function 5: Making B: MakeB()=== | |||
This function simply constructs the 3x3 matrix B that is used in the Kalman algorithm. The first two rows concern the X-and Y-position. Therefore the first row consists of the cos([X[2]) and the sin(X[2]) and zero respectively. | |||
Ofcourse the mirror is true for the Y-position. So the second row consists of sin([X[2]) and the cos(X[2]) and zero respectively. | |||
The third row contains zero entries for the first two columns, and a value of 1 for the angular entry. | |||
void Localisation::MakeB(){ | |||
B.at<double>(0,0) = cos (X[2]); | |||
B.at<double>(0,1) = sin (X[2]); | |||
B.at<double>(1,0) = sin (X[2]); | |||
B.at<double>(1,1) = cos (X[2]); | |||
B.at<double>(2,2) = 1; | |||
B = B/30; | |||
} | |||
=== Function 6: Kalman filter: UpdateKalman()=== | |||
A short explanation on this function: | |||
First it is checked whether X0 is set. If this is true, Lrflocalisation (function 2) is called, as well as ODOlocalisation (function 3). | |||
No we have to sets of X,Y and A position, each with its on accuracy (odo drift, lrf variance). | |||
Function 4 and 5 are called next, in order to construct Z and B. | |||
If no minimum ranges were found, the R matrix is switched from R1 to R2 (only odometry data to be taken). If however, a minimum has been found, than R1 is used (both odometry and lrf info). | |||
Next the U vector is constructed, consisting of the velocity components in X,Y and A direction. | |||
The ahead projection of position is done using this data (X). If that has been done, the projected error covariance matrix P is calculated. The Kalman gain is calculated and finally the estimates are updated with the measurements, by which a filtered position is presented. | |||
If X0 was not set, the function SetX0() is called again, until X0 is set. | |||
The figure below shows the structure of the algorithm far more clearly. | |||
=== | void Localisation::UpdateKalman(ScanVariables robot){ | ||
if(X0set){ // If-statement :If X0set is true | |||
LrfLocalisation(robot); // If-statement :Calling Lrflocalisation function to get x , y, a from lrf | |||
ODOLocalisation(); // If-statement :Calling ODOlocalisation function to get x , y, a from lrf | |||
MakeZ(); // If-statement :Calling MakeZ() function to putx , y, a from lrf and odo in matrix | |||
MakeB(); // If-statement :Calling MakeB() function to putx , y, a from lrf and odo in matrix | |||
if (!min_y_found || !min_x_found){ | |||
R=R2; | |||
} | |||
else { | |||
R=R1; | |||
} | |||
U = Vec3d(drive.vx,drive.vy,drive.va); // If-statement :Creaing matrix U, containing vx ,vy,va | |||
X = Mat((A * Mat(X)) + B * Mat(U)); // If-statement :Project X[] state containing global position ahead using prediction | |||
P = A * P * A_transpose + Q; // If-statement :Project the error covariance matrix ahead | |||
if(X[2] > M_PI) | |||
{ | |||
X[2] = X[2] - 2*M_PI; | |||
} | |||
else if (X[2] < -M_PI) | |||
{ | |||
X[2] = X[2] + 2*M_PI; | |||
} | |||
Mat matrixToInverse = H * P * H_transpose + R; // If-statement :Preparing matrix to be inverted for usage of calculation Kalman gain | |||
inverseMatrix = matrixToInverse.inv(); // If-statement :Actually inverting this matrix | |||
Mat K = P * H_transpose * ( inverseMatrix); // If-statement :Calculating the Kalman gain | |||
X = Mat(Mat(X) + K * (Mat(z) - H * Mat(X))) ; // If-statement :Updating estimate with measurement Z | |||
P = (Mat::eye(3,3,CV_64F) - K * H) * P ; // If-statement :Updating the error covariance | |||
} | |||
else{ // Else-statement :So if X0set is false | |||
SetX0(robot); // Else-statement :Calling SetX0 function | |||
} | |||
} | |||
== | == Technicalities and solutions== | ||
=== | === Problems with Localisation block=== | ||
The ambitious idea to use no assumptions, and make the robot able to have proper localisation in any arbritrary environment proved to take more time to make effective than predicted. | |||
The problem that occurred is that the angle A would sometimes get weird values. And by means of this error, the whole program produces jibberish, as the angle is widely used throughout the functions. Various strategies were used to make the program work properly. However, every time it seemed to work in a certain maze, it would provide problems in a different maze. | |||
As the localisation is of vital importance for the mapping to work, we had to think of a back-up plan if this would not work out. In order to do this, we devised several simplified versions of localisations. These versions use more assumptions, as well as an accuracy that would be less than before. However, it seemed better to have somewhat less accuracy - but knowing that the procedure would work in any maze - , than a very accurate, but unstable procedure. | |||
=== | === Alternative 1: Simpler localisation, using axis-alignment and phase snaps === | ||
For this localisation method, both laser data and odometry data are used, without using a Karman filter. | |||
====Localisation method==== | |||
[[File:Dirty_loca.jpg|thumb|left|Schematic view of the localisation method]] As shown in the diagram, at the initial position 1, the robot will store the distance from it to the furthest wall in front of it, which is done by finding the element of the laser data with the largest range and the corresponding angle of this element. Then, at position 2, where robot starts to turn, it will run a startpoint() function, which is a function which will again calculate its distance to the wall. Comparing the distance change between position 1 and 2, the traveled distance A can be obtained, which is used to update the global coordinates. In addition to this, it also saves the odometry data at this point.<br> | |||
Then when it stops turning at position 3, the function endpoint() is called. Because it is not possible to use laser data to update global coordinates. Therefore, the change in odometry data between these two positions will be used for coordinate updating. After the turn has finished, at the end turning position 3, robot will again restore its distance to further wall, shown as distance B, which can be used to get next traveling distance. | |||
====Turn detection==== | |||
Now, the difficulty lies in recognising point 2 and 3, or in other words the time at which to call the startpoint() and endpoint() functions. For this, the change of the angular data in the odometry is used, since the angular value will change because of the applied angular velocity. However, only comparing two subsequent elements to eachother is not robust, as we know from experiments that the odometry data can sometimes have very high peaks. Therefore, the angular data is stored in an array, and each iteration the current odometry angle is added to a new array, which is then compared to the old array to obtain the angular change at each of the iterations saved in the array. By then setting conditions such as the threshold value from which we consider it to be turning, the amount of elements we require to be above this value, and the amount of elements in the array, the startpoint and endpoint of a turn can be detected. | |||
In another version of this code, an exponential weighted moving average was used, which requires only one variable instead of an array. The average can very easily be updated: | |||
= | <math>\dot{A}_{new}=\frac{(1-w)\dot{A}_{old}+w\dot{A}_{current}}{\Delta t}</math> with <math>w<1</math> a weighting variable. | ||
A high <math>w</math> discards old values faster, whereas a low <math>w</math> gives a smoother average. If the average exceeds a certain threshold, it is detected as a turn. | |||
====Tuning==== | |||
In order to get a very robust and simple code, certain assumptions were made. For instance, the turns which were detected by the odometry data were then translated to turns of a multitude of pi. Furthermore, the detected values of both the odometry and laser data were not used if they exceeded 100 [m]. <br> | |||
The code itself did appear to work quite well, the angle was correct around 19/20 times, and even then it seemed to correct itself after some time. The x and y values however still needed tuning. <br> | |||
=== | ====Final implementation==== | ||
.... | Three versions were implemented, in the spirit of 'divide and conquer'. Two versions did not completely integrate with the rest of the code in time. However, during the testing (in the maze challenge), some other flaws became apparent. First, the continuous requests for odometry data impeded other processes such as driving and reading the laserdata. Furthermore, the maze was so packed with corners that there was not much opportunity to drive straight and using the laserdata for the distance measurements, which means that the odometry was used so much that the position was no longer accurate. This also meant that some weird decisions were made, which interfered even further with the driving. | ||
Latest revision as of 14:07, 26 June 2015
Localisation
This page is part of the EMC03 CST-wiki.
This page goes into details about localisation.
Requirements of Localisation
In order to be able to locate itself within its environment, the robot needs information. The required data to obtain global position are:
- global x-position [m]
- global y-position [m]
- global a-angle [rad.]
The error in the position data must be quantified and must be minimized, in order not to make mistakes in the location in the long run. For example, if the robots x-and y-coordinates differ due to an error, the robot will think is it at a different location, whereas it actually is standing still in exactly the same location and position.
The sensor data required to obtain the above mentioned position data are the following:
- odometry: global x [m] , global y [m] , global a [rad.]
- LRF: all laser ranges [m]
- velocity input to robot
Method of localisation
The robot will need global coordinates. There are two sensors which it can use to determine these coordinates. However both sensors have their own drawbacks.
- The odometry sensor provides global x-y coordinates and angle. There is not much variance in the data of the sensor, but there is a drift (bias) that will accumulate over time. The odometry data can be viewed as feedforward information for the system.
- The LRF sensor provides 1000 ranges [m] with distances to objects over a scope of 270 degreess around the robot. This sensor shows no bias, but has a variance however. Furthermore the LRF data does not provide the global coordinates that we want with its raw data. Therefore this data has to be converted into position changes in terms of the global coordinates. The LRF data can be seen as the Feedback loop of the system.
When the robot starts its program initially, the global coordinates will be all zero. So the start position of the robot determines the direction of the x- and y-axes. The data from the odometry and the LRF will be updated at each time instant. The odometry just works very intuitively: it tells you how far you have moved based on wheel-rotation. In the case of LRF however, the following happens: It measures the distances to the objects in the environment at time t0. It measures again at t1. The difference in distance, converted to the wanted coordinates, should be equal to the odometry data. Of course this will not happen due to the errors in the sensors, but that is why a filter is used to filter the data in between each next update step.
A Kalman filter is used to filter the data obtained from odometry as well as from LRF, in order to maximize the accuracy.
Kalman filter
The kalman filter uses an update cycle with two steps. In the first step the new position is estimated based on the previous position and the input. An estimate of its error is then made which is used in the second step. In the second step data from measurements is used to correct the estimated position. Since the definition of the directions of the x and y axis is arbitrary, they are aligned to the corridor in which pico starts. The algorithm that is used is shown in the figure below:

The various variables used in the figure above, are explained here:
[math]\displaystyle{ \hat{x}_k^- }[/math] is the predicted ahead state variable at discrete time instance [math]\displaystyle{ k }[/math]. This column vector consists of the global x-position, global y-position and the global angle. So logically, [math]\displaystyle{ \hat{x}_{k-1}^- }[/math] is the same vector at a previous time instance.
[math]\displaystyle{ A }[/math] is an n by n matrix that relates the state at the previous time step [math]\displaystyle{ k-1 }[/math] to the state at the current step [math]\displaystyle{ k }[/math], in the absence of either a driving function or process noise.
[math]\displaystyle{ B }[/math] is an n by n matrix that relates the optional control input u to the state variable.
[math]\displaystyle{ u_{k-1} }[/math] is the control input at the previous state of time. So this corresponds to a 3 by 1 column vector containing the velocities that were sent to the wheel base:
- vx: translational velocity in x-direction [m/s]
- vy: translational velocity in y-direction [m/s]
- va: angular velocity around z axis [rad./s]
[math]\displaystyle{ P_k^- }[/math] is a n by n matrix containing the error covariance predicted ahead at time instance [math]\displaystyle{ k }[/math].
[math]\displaystyle{ Q }[/math] is a n by n matrix containing covariance of the process noise.
[math]\displaystyle{ K_k }[/math] is an n by n matrix that represents the Kalman gain.
[math]\displaystyle{ H }[/math] is an n by m matrix that relates the state to the measurement [math]\displaystyle{ z_k }[/math].
[math]\displaystyle{ R }[/math] is an n by n matrix that contains the measurement noise covariance.
[math]\displaystyle{ z_k }[/math] is the measured data in a column vector (to be compared to predictions).
During the second step of the kalman update both the LRF and odometry are used. For both sensors the difference between the current and last value is used to determine the position change since the last update. This value is then added to the previous positions from the kalman update. The odometry data can be used directly. For the LRF however, the x, y and a values first have to be calculated from the raw LRF data. This is done by measuring the distance to the end of the corridors. Since Pico can see 270 degrees around itself, it can always measure the distance to one end of the corridor it is in as wel as the distance to one of the side walls of the corridor.
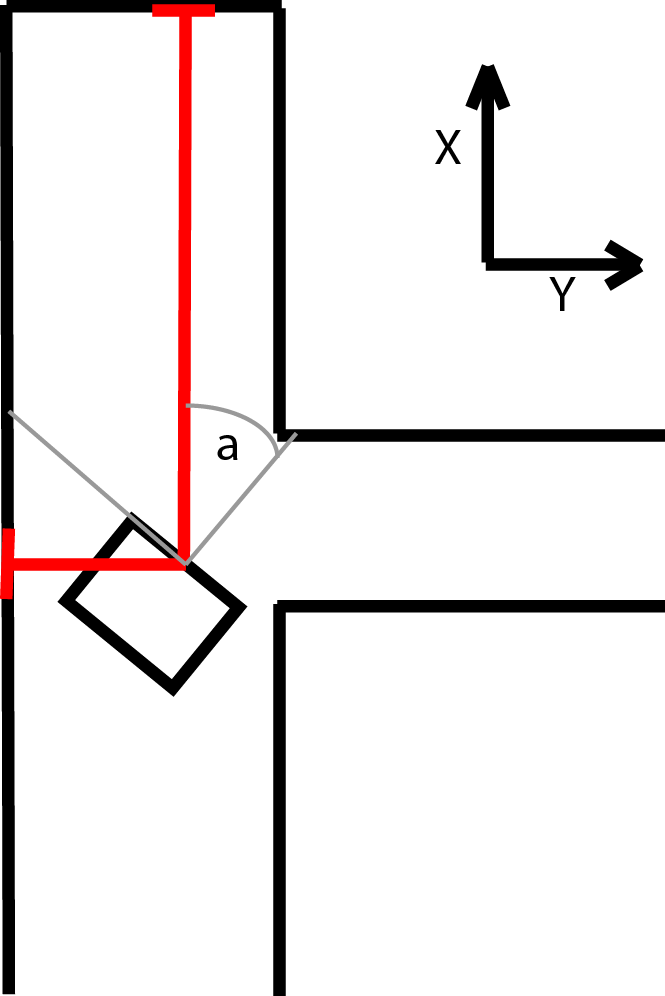
The estimated angle is used to calculate which sensor should point towards the end of the corridor. An interval around the corresponding LRF beam is searched for a local minimum, which should belong to the beam that hits the end perpendicularly. This beam points directly at the end of corridor and is then used to calculate the LRF value for the angle of pico. The difference is calculated between the previous and current distance to the end wall which is the position change for either x or y used in the kalman update. The other position change is calculated in similarly, but in stead of the end of the corridor the distance to the side wall is used. Since it is possible to lose sight of a wall, for instance when driving on an intersection, a safeguard is put in place. If the position change based on the lrf is to big, it is assumed that the LRF data is unreliable for that update cycle and only the odometry data is used. This is done by switching between two R matrices, one of which sets the contributions of the laserdata to zero. In the regular R matrix the contribution of the LRF data is weighed more heavily under the assumption that the LRF is more reliable overall.
Implementation of method
Here the implementation of the method will be briefly discussed.
Interface
Localisation is a separate cpp-file which can be seen as a block. It uses the Scan class data to read sensor data. Also it uses the Drive class to retreive information on the velocity. the variables that are used as arguments are copies and are not used by reference, as they are only needed to calculate the position of the robot. The variables that are only used within the localisation class are ofcourse set to private status. After all necessary blocks are defined in the header file localisation.h , accompanied with the function prototypes, the file localisation.cpp can be properly used. The file consists of 6 functions in total:
- Initializing initial position
- Retreiving LRF-data and converting this into useful X,Y,A data, stored to be used in another function
- Retreiving ODO-data and storing this to be used in another function
- Composing the Z column-vector used in the Kalman algorithm
- Composing the B matrix that is used in the Kalman algorithm
- Function containing the actual Kalman algorithm, which uses the information retreived in the above function to give an accurate localisation
The resulting X,Y,A coordinates are made available to the mapping block for further use. There this info can be used to pinpoint and save nodes, as well as recognizing whether the robot has visited these coordinates before and much more. See the mapping section for further details on this block.
Function 1: initialize position: SetX0()
In this function the position is determined by means of a for-loop that loops over all of the laser ranges. It determines the minimum range by means of an if-statement. If the minimum range is found, it is stored along with its beam number. This direction is set to correspond to the global Y-direction, and the global angle A is calculated as well, using the beam number. Now the global X-axis is set by using the global Angle. These values are all stored and X,Y,A are initialized.
Function 2: LRF-retreival and conversion: LrfLocalisation()
This function uses the range data to extrapolate the position of the robot. First the angular position A is evaluated. If this angle is larger than pi, or smaller than minus pi, it will be wrapped by subtracting or adding 2 pi respectively. This wrapped angle is used to determine the beam numbers of the current minimal ranges. This is simply done using the following relation:
n_x = X[2]+robot.angle_max / robot.angle_increment; In this equation n_x corresponds to the beam number of the global X-axis and position. X[2] is the global angle A and the other parameters are self explanatory. The range belonging to this beam number is stored. The same procedure is used to determine the Y-data.
In order to create robustness and in order to prevent problems in other function calls, there are some if-statements included to switch axes if necessary. If the beam number n_x is smaller than 4 or bigger than 994, it is one of the outer ranges. If one of these if-statements is true, the beam number n_x will be changed. We switch from the positive to negative axis or the other way around, by adding pi to the angle. This way, the axis can not get out of sight of the robot. Simple boolean expressions are used to notify the system whether the positive or negative axis is being tracked. This is important because it changes whether distances should be counted negative or positive. This system using axis-switches is incorporated, because there is no assumption made regarding initial position. It should be able to determine an axis to track, regardless of the initial angle of the robot in the maze.
Next the values of the ranges are checked between n_x-5 and n_x+5 using a for-loop. If a minimum range is found it is stored. However, if the minimum value lies on the outer bounds of the loop, or if the difference is too small (noise) , then no minimum is found. This is done for both the x- and y-direction.
Finally, using the laser distance in x- and y-direction, the difference is range is calculated with the previous function call. These differences represent the movements made between function calls, and therefore the difference in position. Every function call, the differences in each direction are added to the total of differences calculated in previous calls. These variables therefore represent the global X,Y and A position.
deltaXLFR = min_x_value*pow(-1,neg_x_axis) - oldXLFR; // Calculate change in X by LRF deltaYLFR = min_y_value*pow(-1,neg_y_axis) - oldYLFR; // Calculate change in Y by LRF deltaALFR = CorrectedAngleA - oldALFR; // Calculate change in angle using LRF from previous program call oldXLFR = min_x_value*pow(-1,neg_x_axis); // Calculate the new oldXLFR oldYLFR = min_y_value*pow(-1,neg_y_axis); // Calculate the new oldYLFR oldALFR = CorrectedAngleA; // Calculate the new oldALFR
Function 3: ODO-retreival: ODOLocalisation()
This function creates an odometry object and reads the odometry data from the io-layer. It starts with an initial X=0,Y=0,A=A_init . It calculates the differences each time the function is called. So if the x position is 5 meter, and the next function call it reads 5.2 meter, then the difference equals the recent reading minus the old reading. The differences are stored, as well as the old position and the sum of the differences (actual position). This info is to be used by the other functions that need it in the file.
void Localisation::ODOLocalisation(){
emc::OdometryData odom; // Creating odometry data object to retreive odo-info
deltaXODO = odom.x - oldXODO; // Calculating change in x-position using odo
deltaYODO = odom.y - oldYODO; // Calculating change in y-position using odo
deltaAODO = odom.a - oldAODO; // Calculating change in a-position using odo
oldXODO = odom.x; // Setting retreived odo global x-position info to oldXODO
oldYODO = odom.y; // Setting retreived odo global x-position info to oldXODO
oldAODO = odom.a; // Setting retreived odo global x-position info to oldXODO
}
Function 4: Making Z: MakeZ()
Z is a 6-entry column vector. Every time it is called, it will update the entries as follows: The first three entries (corresponding to X_lrf,Y_lrf and A_lrf respectively) equal their global position plus the difference in position calculated in the LRF retreival function. The latter three entries correspond in the same manner to their odometry counterparts. These second X_odo,Y_odo and A_odo are updated in the same manner, but using the difference in odometry instead of LRF. The odometry differences are calculated in function 3. Now the Z-column vector is ready to be used by the Kalman filter.
void Localisation::MakeZ(){
z[0] = X[0] + deltaXLFR; //Lrf set of x,y,a
z[1] = X[1] + deltaYLFR;
z[2] = X[2] + deltaALFR;
z[3] = X[0] + deltaXODO; //Lrf set of x,y,a
z[4] = X[1] + deltaYODO;
z[5] = X[2] + deltaAODO;
}
Function 5: Making B: MakeB()
This function simply constructs the 3x3 matrix B that is used in the Kalman algorithm. The first two rows concern the X-and Y-position. Therefore the first row consists of the cos([X[2]) and the sin(X[2]) and zero respectively. Ofcourse the mirror is true for the Y-position. So the second row consists of sin([X[2]) and the cos(X[2]) and zero respectively. The third row contains zero entries for the first two columns, and a value of 1 for the angular entry.
void Localisation::MakeB(){
B.at<double>(0,0) = cos (X[2]);
B.at<double>(0,1) = sin (X[2]);
B.at<double>(1,0) = sin (X[2]);
B.at<double>(1,1) = cos (X[2]);
B.at<double>(2,2) = 1;
B = B/30;
}
Function 6: Kalman filter: UpdateKalman()
A short explanation on this function: First it is checked whether X0 is set. If this is true, Lrflocalisation (function 2) is called, as well as ODOlocalisation (function 3). No we have to sets of X,Y and A position, each with its on accuracy (odo drift, lrf variance). Function 4 and 5 are called next, in order to construct Z and B. If no minimum ranges were found, the R matrix is switched from R1 to R2 (only odometry data to be taken). If however, a minimum has been found, than R1 is used (both odometry and lrf info). Next the U vector is constructed, consisting of the velocity components in X,Y and A direction. The ahead projection of position is done using this data (X). If that has been done, the projected error covariance matrix P is calculated. The Kalman gain is calculated and finally the estimates are updated with the measurements, by which a filtered position is presented.
If X0 was not set, the function SetX0() is called again, until X0 is set. The figure below shows the structure of the algorithm far more clearly.
void Localisation::UpdateKalman(ScanVariables robot){
if(X0set){ // If-statement :If X0set is true
LrfLocalisation(robot); // If-statement :Calling Lrflocalisation function to get x , y, a from lrf
ODOLocalisation(); // If-statement :Calling ODOlocalisation function to get x , y, a from lrf
MakeZ(); // If-statement :Calling MakeZ() function to putx , y, a from lrf and odo in matrix
MakeB(); // If-statement :Calling MakeB() function to putx , y, a from lrf and odo in matrix
if (!min_y_found || !min_x_found){
R=R2;
}
else {
R=R1;
}
U = Vec3d(drive.vx,drive.vy,drive.va); // If-statement :Creaing matrix U, containing vx ,vy,va
X = Mat((A * Mat(X)) + B * Mat(U)); // If-statement :Project X[] state containing global position ahead using prediction
P = A * P * A_transpose + Q; // If-statement :Project the error covariance matrix ahead
if(X[2] > M_PI)
{
X[2] = X[2] - 2*M_PI;
}
else if (X[2] < -M_PI)
{
X[2] = X[2] + 2*M_PI;
}
Mat matrixToInverse = H * P * H_transpose + R; // If-statement :Preparing matrix to be inverted for usage of calculation Kalman gain
inverseMatrix = matrixToInverse.inv(); // If-statement :Actually inverting this matrix
Mat K = P * H_transpose * ( inverseMatrix); // If-statement :Calculating the Kalman gain
X = Mat(Mat(X) + K * (Mat(z) - H * Mat(X))) ; // If-statement :Updating estimate with measurement Z
P = (Mat::eye(3,3,CV_64F) - K * H) * P ; // If-statement :Updating the error covariance
}
else{ // Else-statement :So if X0set is false
SetX0(robot); // Else-statement :Calling SetX0 function
}
}
Technicalities and solutions
Problems with Localisation block
The ambitious idea to use no assumptions, and make the robot able to have proper localisation in any arbritrary environment proved to take more time to make effective than predicted. The problem that occurred is that the angle A would sometimes get weird values. And by means of this error, the whole program produces jibberish, as the angle is widely used throughout the functions. Various strategies were used to make the program work properly. However, every time it seemed to work in a certain maze, it would provide problems in a different maze. As the localisation is of vital importance for the mapping to work, we had to think of a back-up plan if this would not work out. In order to do this, we devised several simplified versions of localisations. These versions use more assumptions, as well as an accuracy that would be less than before. However, it seemed better to have somewhat less accuracy - but knowing that the procedure would work in any maze - , than a very accurate, but unstable procedure.
Alternative 1: Simpler localisation, using axis-alignment and phase snaps
For this localisation method, both laser data and odometry data are used, without using a Karman filter.
Localisation method
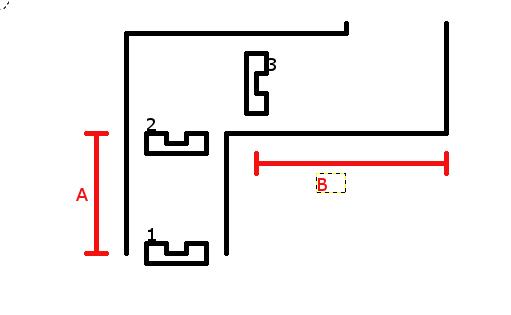
As shown in the diagram, at the initial position 1, the robot will store the distance from it to the furthest wall in front of it, which is done by finding the element of the laser data with the largest range and the corresponding angle of this element. Then, at position 2, where robot starts to turn, it will run a startpoint() function, which is a function which will again calculate its distance to the wall. Comparing the distance change between position 1 and 2, the traveled distance A can be obtained, which is used to update the global coordinates. In addition to this, it also saves the odometry data at this point.
Then when it stops turning at position 3, the function endpoint() is called. Because it is not possible to use laser data to update global coordinates. Therefore, the change in odometry data between these two positions will be used for coordinate updating. After the turn has finished, at the end turning position 3, robot will again restore its distance to further wall, shown as distance B, which can be used to get next traveling distance.
Turn detection
Now, the difficulty lies in recognising point 2 and 3, or in other words the time at which to call the startpoint() and endpoint() functions. For this, the change of the angular data in the odometry is used, since the angular value will change because of the applied angular velocity. However, only comparing two subsequent elements to eachother is not robust, as we know from experiments that the odometry data can sometimes have very high peaks. Therefore, the angular data is stored in an array, and each iteration the current odometry angle is added to a new array, which is then compared to the old array to obtain the angular change at each of the iterations saved in the array. By then setting conditions such as the threshold value from which we consider it to be turning, the amount of elements we require to be above this value, and the amount of elements in the array, the startpoint and endpoint of a turn can be detected.
In another version of this code, an exponential weighted moving average was used, which requires only one variable instead of an array. The average can very easily be updated:
[math]\displaystyle{ \dot{A}_{new}=\frac{(1-w)\dot{A}_{old}+w\dot{A}_{current}}{\Delta t} }[/math] with [math]\displaystyle{ w\lt 1 }[/math] a weighting variable.
A high [math]\displaystyle{ w }[/math] discards old values faster, whereas a low [math]\displaystyle{ w }[/math] gives a smoother average. If the average exceeds a certain threshold, it is detected as a turn.
Tuning
In order to get a very robust and simple code, certain assumptions were made. For instance, the turns which were detected by the odometry data were then translated to turns of a multitude of pi. Furthermore, the detected values of both the odometry and laser data were not used if they exceeded 100 [m].
The code itself did appear to work quite well, the angle was correct around 19/20 times, and even then it seemed to correct itself after some time. The x and y values however still needed tuning.
Final implementation
Three versions were implemented, in the spirit of 'divide and conquer'. Two versions did not completely integrate with the rest of the code in time. However, during the testing (in the maze challenge), some other flaws became apparent. First, the continuous requests for odometry data impeded other processes such as driving and reading the laserdata. Furthermore, the maze was so packed with corners that there was not much opportunity to drive straight and using the laserdata for the distance measurements, which means that the odometry was used so much that the position was no longer accurate. This also meant that some weird decisions were made, which interfered even further with the driving.