Control

De robotscheidsrechter krijgt zijn fysieke voorstelling in de vorm van een drone. Deze zal autonoom het spel in de gaten houden en beslissingen nemen gebaseerd op eigen waarnemingen en camera's.

Recente update

vlucht:


besturing met behulp van matlab:


Door middel van een MatLabscript hebben we de drone kunnen laten vliegen. Deze besturing geschied nog aan de hand van de pijltjestoetsen voor rotaties, stijgen en dalen, en WASD voor de horizontale translaties.

Met een camera onder de drone bevestigd is getest of deze autonoom kan vliegen met behulp van het geschreven matlab-script autonoomvliegen_1.gif

Positiebepaling

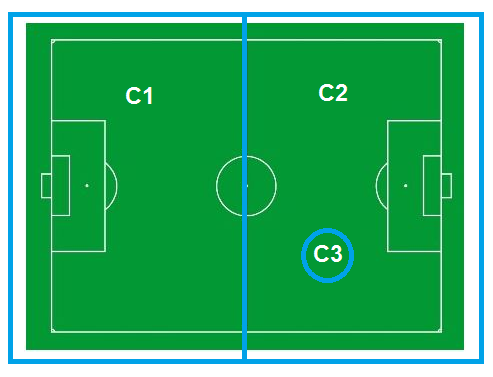
Om de essentie van het doel aan te grijpen en het realiseerbaar te houden is er gekozen voor de opstelling te zien in onderstaande figuur.

Camera 1, 'C1', en camera 2, 'C2', zullen respectievelijk het linker- en rechterdeel van het veld in de gaten houden.
Hierbij zullen ze vooral focussen op de zijlijnen en de bal.

• Als de bal de zijlijnen passeert, zullen ze dit aan de scheids doorgeven zodat deze daar adequaat naar kan handelen.
  
• Als de bal naar het andere cameraveld beweegt zullen de camera's een signaal uitwisselen
• De positie van de bal wordt aan de drone doorgegeven.
  
• Als de bal uit is wordt dit aan de drone doorgegeven.
  

Bovenstaand proces van interactie tussen de camera's en de drone wordt ook wel 'multi-camera netwerking' genoemd.

De doorgegeven positie wordt aan de hand van x,y coördinaten gedaan. De camera's zijn een gefixeerd punt in de ruimte. Dit stelt ons in staat een oorsprong te definiëren en de ruimte in coördinaten te beschrijven.
De hoek linksonder in het veld is het (0,0) punt. De drone ontvangt van de camera's de positie van de bal en kan zo aan de eis voldoen dat de drone boven de bal moet blijven vliegen. De camera van de drone kan, mits in het bereik, ook de positie van de bal spotten. De drone zal zichzelf oriënteren aan de hand van C1 en C2. De drone heeft een eigen X,Y-assenstelsel op zijn camera met (0,0) het middelpunt van het beeld. In een wedstrijd kan voor de drone twee situaties voorkomen. Een waarbij de drone de bal zelf kan 'zien' en een waarbij de bal buiten het beeld van de drone is.

Situatie 1

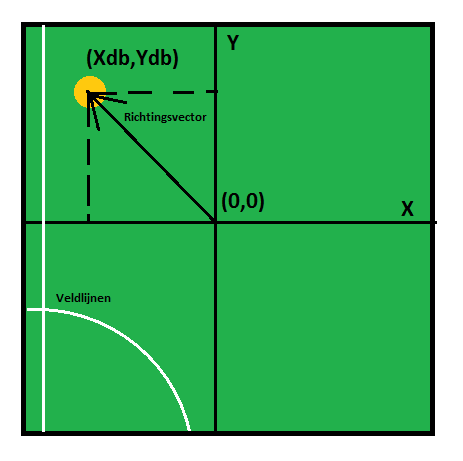
Dit is de situatie waarbij de camera van de drone zelf de bal kan waarnemen. Het camerabeeld van de drone heeft een assenstelsel [math]\displaystyle{ (x_{db},y_{db}) }[/math] met (0,0) in het midden van het beeld. Door middel van videotracking kan de bal worden waargenomen door de camera met een bepaalde positie. Deze positie heeft een [math]\displaystyle{ (x,y) }[/math] waarde ten opzichte van middelpunt. Door deze te vergelijken kan een richtingsvector worden opgesteld: [math]\displaystyle{ r_{d1}^T=[x,y] }[/math]. Door de drone nu een bepaalde snelheid v in deze richting te geven zal de drone de bal volgen.

Situatie 2

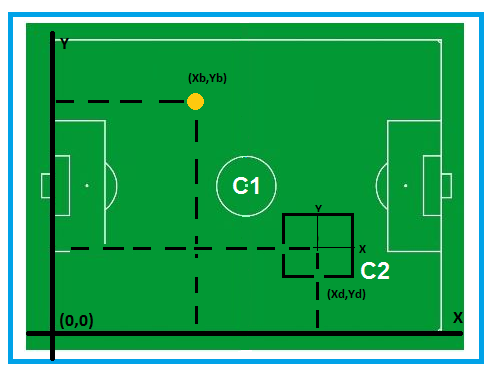
In deze situatie kan de drone zelf de bal niet 'zien'. Dit kan voorkomen als de bal sneller wegrolt dan de drone kan vliegen. Hier worden de drone en de bal door middel van de camera's boven het veld waargenomen met een positie voor de bal [math]\displaystyle{ (x_b,y_b) }[/math] en voor de drone [math]\displaystyle{ (x_d,y_d) }[/math]. Door het verschil van deze twee posities kan weer een richtingsvector worden opgesteld: [math]\displaystyle{ r_{d2}^T=[(x_d-x_b),(y_d-y_b)] }[/math]. De drone zal weer met een bepaalde snelheid in deze richting gaan vliegen.

Om een goed vliegende drone te hebben moeten de bovenstaande situaties 1 en 2 goed worden onderscheiden. Zo zijn er enkele voorwaarden waar het vliegen aan moet voldoen. Allereerst moet de drone een vaste hoogt proberen aan te houden. Deze is gesteld op 2 meter zodat de drone de spelers niet in de weg loopt en hoog genoeg is om niet geraakt te worden door hoog vliegende ballen. De volgende voorwaarde is dat als de drone de bal kan zien dat deze op eigen informatie handelt en de binnenkomende informatie van de vaste camera's negeert. Zodra de drone de bal niet meer waarneemt zal deze reageren op de informatie van de vaste camera's, totdat de drone zelf de bal weer kan zien en overschakelt op eigen informatie.

De camera van de drone kan echter meer toevoegen aan het systeem als deze de situatie van de een ander perspectief dan boven bekijkt, omdat de vaste camera's boven het veld hetzelfde kunnen zien. Daarom wordt er eerst geëxperimenteerd met een camera op de drone aan de voorkant. Op deze manier kan de drone overtredingen en dergelijke vanuit een ander perspectief zien en zo mogelijk een beter besluit nemen over een overtreding. Dit leidt tot een nieuwe situatie '3'. Deze situatie gaat nog steeds vóór situatie 2 waar de positie door de top-camera wordt bepaald. De drone zal eerst reageren op situatie 3 en dan op situatie 2. Situatie 1 wordt hier genegeerd, omdat deze vrij weinig toevoegt. Mocht het voor ons niet lukken om de camera aan de voorkant werkend te krijgen, zullen we terug gaan naar de camera op de drone die omlaag kijkt.

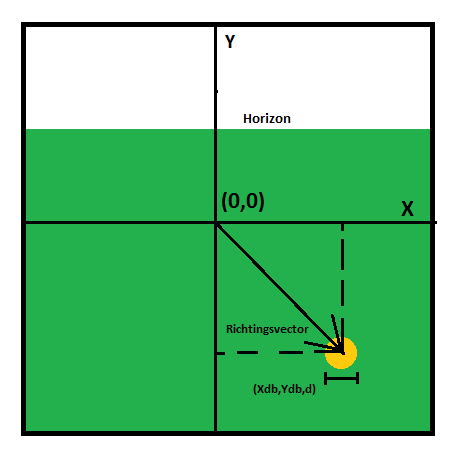
Situatie 3

Bij deze situatie zal de drone de bal zien in de richting van de horizon. Dit geeft een voordeel ten opzichte van de camera die naar beneden kijkt, omdat situaties van andere hoeken bekeken kan worden. De drone kan namelijk 360 graden om de bal heen draaien. Vanuit de camera komen weer verschillende variabelen voor. Nu namelijk [math]\displaystyle{ (x_{db},y_{db},d_{db}) }[/math]. De [math]\displaystyle{ x_{db} }[/math] en [math]\displaystyle{ y_{db} }[/math] staan voor de positie ten opzichte van het middelpunt van het camerabeeld. Hiermee kan dus de draairichting van de drone worden bepaald. De [math]\displaystyle{ d_{db} }[/math] is de diameter van de bal in het beeld. Deze wordt gedefinieerd als een aantal pixels in het scherm. Met deze informatie kan de afstand tot de bal worden berekent als de camera goed gekalibreerd is. Als de diameter kleiner wordt zou de drone dus naar voren moeten vliegen, omdat de bal wegrolt.

Matlab

In eerste instantie is geprobeerd om de drone te besturen met JavaScript en Node.js. Deze besturing lukte goed, maar het zou makkelijker zijn om de drone te kunnen besturen met matlab. Op 26/11/15 is het gelukt om de drone te besturen met behulp van een matlab script. Door het script uit te voeren start de connectie van de computer met de drone. Met behulp van toetsen op het toetsenbord kon de drone bestuurd worden. De verbinding van matlab met de drone maakt het proces gemakkelijker, omdat er geen link hoeft te worden gelegd tussen verschillende programma's. Dit is omdat het videotracking wordt gedaan met behulp van matlab. Omdat de besturing met matlab gedaan kan worden, wordt er een script geschreven zodat de robot autonoom zal gaan vliegen aan de hand van de balpositie.

survey

Om de drone naar de fans, de spelers en het publiek, is er een enquête opgesteld waarbij we graag willen weten hoe de Society graag wilt dat de drone communiceert.
Hierbij wordt de survey voorgelegd aan een zo breed mogelijk publiek.

Testlog drone

• 19/11/15 Drone opgehaald bij Lambèr Royakkers. Accu was leeg en daardoor geen tests kunnen doen. Accu wordt opgeladen voor de volgende keer.
• 23/11/15 We hebben de drone kunnen laten opstijgen en dalen.
• 26/11/15 De eerste volledige vlucht is uitgevoerd. Weliswaar zat hij nog aan manuele controle met MatLab.
• 3/12/15 Voor het eerst heeft de drone autonoom gevlogen, de rotatie d.m.v. baldetectie werkte redelijk.

---

Terug naar: PRE2015_2_Groep2