Report group 14
Return PRE2017 3 Groep14
Introduction
Slim In Rekenen
For the course Robots Everywhere from the Technical University of Eindhoven, a project about some form of robotics needed to be made. The only requirement given was that robotics has to be part of the project in some way and that a product needed to be delivered at the end. Because of the huge amount of freedom in this course, for this particular project it was decided to create a smart quizzing program for primary school classes. The program can be used in groups 3 and 4 from schools with a traditional educational tactics. Furthermore, all research is focused on these types of schools in the Netherlands.
This quiz will be able to test pupils on simple mathematical questions, using addition, subtraction, multiplication, and division, and all questions are multiple choice to make it esay for young children to input their answers. The purpose of the program is to easily identify students that need some extra attention of the teacher, in order for the teacher to properly divide their time effectively among the students. At the same time, another purpose of the program is the fact that it should be stimulating all students on their individual level. The way in which this is done is by finding the child’s knowledge boundary based on their answers to the previous questions and basing the difficulty of the upcoming question on this knowledge boundary. This way, the child will get questions that are still challenging enough to be interesting, but not so difficult that the pupil will give up. Due to the fact that the quizzing program will be started at the same time for the whole class, but all pupils will have their own individual personalized questions, it is a perfect combination of individualism while working as a class. This way, nobody feels left out and nobody gets bored.
The program also includes an overview screen that can be used by the teachers. Teachers can use the results in this overview to analyze which pupils have mastered the subjects sufficiently and are ahead of the program, but also which pupils lack behind. Because the pupils progress will be visible by the teachers during the test, and results can be viewed immediately after the test, the teacher knows sooner which children will need some extra attention to catch up. This extra attention can then be given where the teacher sees fit.
To test whether or not teachers think the program could make an actual difference in their teaching programs, a questionnaire was sent to elementary school teachers. The questionnaire focused on their opinions and whether they had tips to keep in mind while designing the program. An important question is whether or not they think the program will help them plan their time better, as this is one of our main goals, and if they would implement the program in their lesson.
The following report is an elaborate documentation of the program, the questionnaire, and its results. Both the survey and the final presentation can be found in the appendices.
Problem Description
The problem we based our project on is the fact that teachers sometimes have trouble recognizing which pupils need extra attention and teachers could use some assistance in dividing their time among the pupils. Another problem that we saw that the paper tests currently being used in the elementary school system cannot be personalized to the individual knowledge level of the children. Even the electronic tests being used in the current elementary school system use the same standardized tests for all children.
We wanted to tackle both these issues in this project. The purpose of our program therefore is to quickly recognize which children need extra help on a specific topic and to customize the test to each child, such that they can train specific topics on their own level in such a way that the teacher can still recognize which pupils need extra attention. Quickly recoginizing the children that need extra help will help the teacher to immediately step in. For example, at the start of the year teachers do not know the weaknesses of the children, but our program can find them immediately after one test. Furthermore, the personalised test ensures that the children will not lose interest, due to the questions being to easy, and ensures that they will not feel left out, due to always getting the questions wrong. These personalised questions are based on the pupils answers of previous questions. Our program determines the pupils knowledge level based on their answers of previous questions, and the difficulty of the upcoming questions of the test will be based on this acquired knowledge level.
Our program is now focussed on children in the third and fourth grade of the elementary school in the Netherlands using a tradional education system. The test consists of mathematical questions that are divided by subject, for example multiplication tables or adding numbers up to twenty. These choices were made to ensure an easy to use, but still firm basis for the program.
Objective
Develop a smart quiz program for a computer that can assess knowledge levels of the pupils, to give the teacher a better view on his pupils, and to ask questions to the pupils on their personal knowledge boundary, so they learn effectively.
Users
The users of the program will be the pupils of the third and fourth grade of the elementary school in the Netherlands using a tradional education system, the parents and teacher of these pupils. The users will have the following requirements:
- The pupils want:
- A program that stimulates their imagination.
- A test that remains interesting throughout the whole session.
- A test that does not make them feel dumb or left out.
- The parents want:
- A test that stimulates their children to learn and to perform the best they can.
- Their children to be happy.
- Check their children's progress.
- The privacy of their children to be guaranteed.
- The teacher wants:
- A test that motivates the pupils to learn and to perform the best they can.
- The system to match the curriculum, meaning the teacher has to be able to change the settings of each test.
- To check the progress of each pupil in an easy way.
- To divide his or her time in the best way over all the pupils.
While devleoping our program, we did not put our focus on privacy, because this is only a small part of our program. Also, we decided, at this stage of the project, to focus on pupils and teachers, not on the parents of the pupils. The program will therefore not contain an interface for the parents, due to fact that the goal only incorporates the pupils and the teachers. However, this could reasily be added at a later stage if desired. Almost all of the other the requirements will be implemented in our program, by basing our program on the traditional didactic system.
Desk Research
Before we could start developing our program, an intensive desk research needed to be done. Reasearch in the following areas needed to be done:
- the traditional didactic system
- the use of computer programs in the Dutch education, with special attention to:
- learning individually versus learning in class
- working on paper versus working working on an electronic device
- research that will determine the layout of the test, with special attention to:
- how to construct arethmetic questions
- mental arithmetic
- the use of symbols in arithmetic questions
- how to incorporate feedback on the pupils answers
These topics will now be discussed in detail below.
Didactic Systems
In the book, het didactische werkvormenboek [1], a few important aspects of teaching are found.
- The best way for pupils to take in information is when they read and/or see it.
- When asking questions, there need to be both open questions and closed questions.
- Make sure pupils work with the whole class, but also occasionally in smaller groups or on their own.
- Switching between teaching tactics stimulates learning. An example could be switching between a game and simple sums.
For our project we chose to focus on a traditional education system instead of a constructive education system. This means that we will keep in mind that
- The teacher largely decides on the curriculum and order in which subjects are taught.
- The focus lies on teaching the whole class at once.
- There is a curriculum in which some subjects are more central than others.
- Learning is an individual activity.
- Pupil’s progress is checked by means of tests.
The Use of Computer Programs in Dutch Education
From a government study [2], the following things became clear:
- Separating the class in smaller groups in year three has a positive effect on the pupils’ performances as it causes more interaction.
- More than 90 percent of the teachers in primary education use computers to teach. According to them, using ICT can contribute to a more efficient, effective and likeable education.
The next article[3] shows us that education often does not seem to fit the natural, experimental learning process that children have. In games it is possible to learn naturally, which is why using games can be relevant for primary education. There would have to be a good balance between playing and effectively learning, to make sure that the advantages of learning in a fun way are not lost. This means the following things need to be taken into account when asking questions:
- The information should not be presented in a way that is too abstract, make sure it speaks to the children’s imagination.
- There needs to be a lot of repetition.
- Important information should be taught in more than one way.
- Take some time, it should not be taught too fast.
- Use realistic characters.
- Use animation, childlike dialogues, interaction and direct feedback.
- Do not punish children for making mistakes.
The following factors influence the quality of a course:
- From the international and Dutch literature it follows that all researched interventions that focused on the methods used during instructions and lectures were effective. It is nearly impossible to identify the elements that make a certain intervention work effectively, as several effective interventions might have opposite starting points. Furthermore there are not a lot studies that directly compare different methods. The resulting idea is that `it works to manipulate the methods used'. This is in line with the report of the KNAW (2009) that the Dutch research available does not give a clear view on the relation between the didactics and the skills when it comes to teaching arithmetics.
- Using technology for teaching arithmetics has a positive influence on the prestations of children, just as using real three dimensional objects. This follows from both international and Dutch research, for example the use of the programs Snappet and Rekentuin. It is not clear how much the use of the programs increased the available time to teach arithmetics, and thus this will need some further investigation.
- The use test results to improve the learning process has a positive relation with the arithmetic prestations. This can either be feedback to the teacher, for example by means of a digital system to track students, or direct feedback to the students per question that is done.
- Dividing students in different groups which each have their own level has a positive influence on the prestations of the individual students. Note that further investigation is required with respect to the implementation of this division. In The Netherlands, it is common to divide students in three different groups.
Individual or in Class
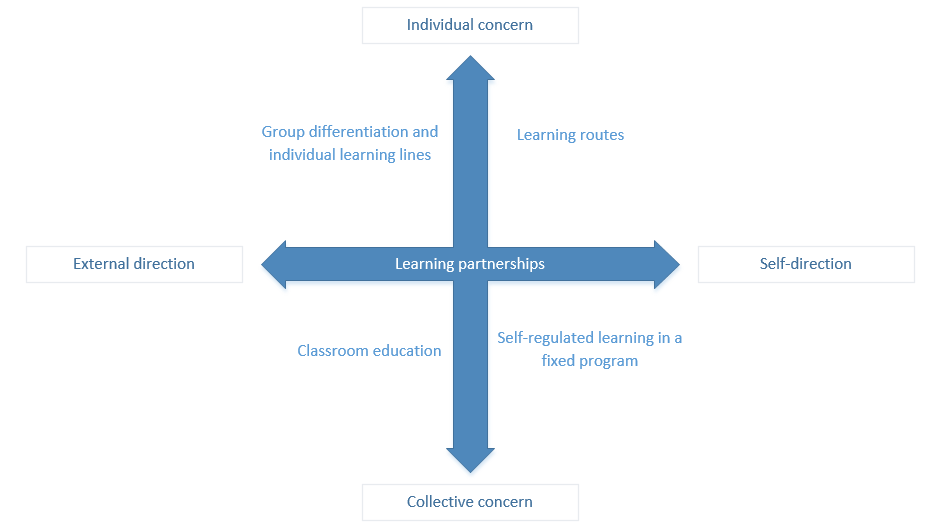
As we can see in the following article [4], the program is part of group differentiation with individual learling lines. This means that there is quite some form of external regie but with focus on the individuals. Consequently, the teacher has some set goals and subjects on which the pupils need to work, and they will work on these subjects when the teacher tells them to. However, as the program will ask questions on their personal knowledge levels, the individuals are also taken into account. This is a perfect combination of working with the class while working on one’s own. Note the figure below, showing the learning partnerships in a graph. If one were to place our program somewhere in this graph, it would be exactly in the middle, having the perfect balance between working with the class versus working individually.
Working on Paper vs Working on an Electronic Device
As indicated in the following atricle [5] using computers instead of paper to administrate achievement tests in elementary schools is supported. Using computers has multiple advantages such as being able to use an adaptive technology, which is the goal for the finished program. On the other hand, it is possible that children experience computer anxiety resulting in lower achievements, but for this project it is assumed that this will not be the case as most children these days work with computers from very early on.
Articles About the Layout of the Test
How to Construct Arithmetical Questions
When constructing arithmetic questions it is important to know how students put numbers and operations on numbers into context. In the article [6] it is explained what should be taken into consideration. One thing to keep in mind is mental arithmetic.
Mental arithmetic is insightfully doing calculations (arithmetic) with numbers, while the value of the numbers is kept in mind. While doing mental arithmetic one also makes use of ready knowledge, and properties of numbers, operations, and the underlying relations. There are three main methods for doing mental arithmetic:
- Step-by-step mental arithmetic: [math]\displaystyle{ 36 + 12 \rightarrow 36 + 10 \rightarrow 46 + 2 = 48 }[/math].
- Mental arithmetic by dividing the digits: [math]\displaystyle{ 36 + 12 \rightarrow 30 + 10 = 40 \rightarrow 6 + 2 = 8 \rightarrow 40 + 8 = 48 }[/math].
- Handy mental arithmetic, for example by compensation: [math]\displaystyle{ 73 + 29 \rightarrow 74 + 30 }[/math].
These findings were taken into account when developing the arithmetic questions in our program.
Use of Symbols in Mathematical Questions
In an article [7] about the mathematical development of children it is mentioned that in order to get a correct numerical magnitude representation, children need to practice with symbolic numbers, so digits, but also with non-symbolic formats, like the herd questions in our program. Therefore we have to keep this in mind when implementing this in the layout of the questions our program.
How to Incorporate Feedback
There are different feedback tactics being researched that the program's feedback system can be based on:
- In this article [8] it becomes clear that attributional feedback to children is useful as it is an effective way to promote rapid problem solving, self-efficacy, and achievement. This is probably because children have a sense of how well they are doing and attributional feedback helps to support these self-perceptions and validates their sense of efficacy. Because of this, the children will stay motivated to work on leading to a better performance in the end. The best way to do this is by giving them ability attributional feedback, so telling them they are either very smart, or not that good at math.
- Feedback in between. The major findings evidenced in this research[9] were the following:
- Feedback was generally effective for learning, but more so on the lower level (identical) questions than on the higher level (reworded) ones;
- Feedback information had greater impact in the absence of supporting text than with supporting text;
In this article they used several feedback methods such as knowledge of correct response (KCR), which identifies the correct response, and answer until correct (AUC). These two were shown to be the most effective.
When developing the feedback implementation of our program, based on the research mentioned above, the decision was made to use the KCR method with no supporting text, accompanied by attributional feedback, also with no supporting text. The decision to use no supporting text is based on the fact that the young pupils in our target user group are just learning how to read, which means using symbols or animations will be much more effective than supporting text.
Conclusion Desk Research
From these articles we can conclude that we want to focus on learning in a likeable way, using a computer program. We will do this by asking simple maths questions using fun pictures of animals. This way we hope to intrinsically motivate the children to learn with our program. The program will be used by the whole class at once, but the arithmetic questions will be personalized based on the pupils knowledge level. While developing our program, we will take the findings on our findings on mental arithmetic and our findings on the use of symbols in mathematical questions, into account. The implementation of our feedback method will be based on our findings on the different feedback strategies. Since our program is focused on schools that use a traditional didactical system, our findings on this didactical system will be taken into account.
Program
In this section, we describe the actual program that was developed. This program was based on the desk research. In the traditional didactic system, the pupils progress is checked by means of tests. Our research also shows that more than 90 percent of the teachers in primary education use computers to teach. The conclusion that computers can be used to teach in primary education is supported by our research on 'working on paper versus working on an electronic device'. This is why our program is a smart quizzing system for elementary schools. Based on our research on the traditional didactic system, we can assume the teacher largely decides on the curriculum and order in which subjects are taught. This means the settings of each test should be very customizable by the teacher. We will explain how we incorporated this in the subsection 'teacher initialization interface'. Also, the focus in the traditional didactic system lies on teaching hte whole class at once, while learning should be an individual activity. This is supported by our research on 'working individually versus in class'. This balance between group and individual learning is achieved by doing the test together with the whole class, while the actual questions being asked are personalized to the pupils knowledge level.
From our research on the use of computer programs in the Dutch education, especially article [3], it became clear that in order for the pupils to learn, there should be a lot of repitition, and topics should not be taught too fast. We incorporated these findings in our program as follows. The teacher uses the program to test and train the childrens knowledge level on a specific topic. This way, one test uses repetition to train the pupils knowledge on a specific topic. The fact that the topics should not be taught too fast is also incorporated a little in our program. In our program, the teacher has the ability to choose how much time the pupils have to answer one question. This option can be used by the teacher to make sure children have enough time to answer the question and enough time to learn. Article [3] also stresses that there should be direct feedback and that one should not punish children for making mistakes.The development of our feedback mechanism was based on our research in the different tactics of incorporating feedback. The way we implemented direct feedback in our program is further discussed in the subsection 'feedback' below.
Lastly, our research on how to implement the arithmetic questions in our program showed that it is important for pupils to train both with symbolic numbers, as well as in non-symbolic formats. The different question types we implemented in our program is based on this finding. This is discussed in further detail in the subsection 'questions'. Our findings on mental arithmetic and how to construct arithmetical questions were taken into account in the way we generate the arithmetic questions in our program. This is further discussed in subsection 'generating the next question'.
The overview of a typical test scenario is as follows. First, the teacher launches the teacher interface of the program and specifies the parameters of the current test, such as the types of operations used in the questions, the amount of time the students have to answer the questions, etc. Next, all pupils launch the pupil interface of the program and wait until a connection between the teacher- and pupil program is established. All pupils fill out their name, and are added to an overview presented in the teacher interface. The teacher clicks the 'next question' button and a question is presented on all pupil interfaces. All pupils answer this question by clicking on one of the answer buttons, and receive immediate feedback on their answer. The teacher then clicks the 'next question' button again, and the cycle is repeated, until all questions have been answered. Based on the previous answers on previous questions, the next question a pupil will receive will either be an easier or a more challenging question, that properly matches the pupils knowledge level. We will now get into the details of the program and the scenario outlined above.
Teacher Initialization Interface
According to this website [10] students from our target audience should be able to do the following things at the end of the school year:
- Group 3 can add and subtract from 0 to 20.
- Group 4 can multiply and add and subtract from 0 to 100.
For this reason exactly, we made sure the teacher can change the settings of the program to fit the needs of the current group. The settings of the current test are completely customizable to the current topic and current level of knowledge the teacher wants to test. We developed our program such that it can at least accomodate the testing needs of our target audients, i.e. addition, subtraction and multiplication can be tested from 0 to 100. However, while developing, we took care of the fact that the program can easily be extended to the testing needs of higher groups. We will expand on this later.
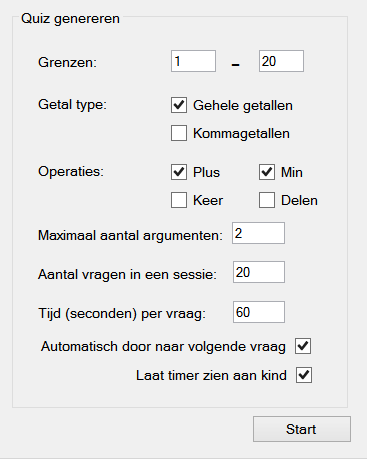
When the teacher first starts a new test, the teacher initialization interface is launched. A form will be shown on which they can adjust the settings for the upcoming test. This form is shown on the right, including all the settings customizable by the teacher and their standard setting. The standard settings shown on the right are set to accomodate our target audience of group 3, but can be easily customized to meet other testing needs. As can be concluded from our research, because we based our program on the traditional didactic system, it is assumed the teacher largely decides on the curriculum and order in which subjects are taught. This is why it is very important that the settings of each test in our program are very customizable, which is why the teacher initialization interface has a lot of different settings.
First, the teacher chooses the numerical bounds between which the questions of the current test have to lie. Initially, questions lie between the range [0,20]. The teacher chooses whether he wants to test integer or decimal numbers. The standard setting is integer numbers. The decimal option is currently disabled, because of the question types we have currently implemented, but we still included this option because our code is generic so that the test can easily be extended to include decimal numbers. Next, the teacher chooses the operations they wish to test: addition, subtraction, multiplication and/or division, by default set to addition and subtraction. The maximal amount of arguments per question, which is initially two, can also be customized. Even though our target audience will always use the standerd setting of two arguments per question, we still included this option for the possible extension to higher grades. By including this option now, extending the program for the use of higher grades will be a lot easier, because we already kept this in mind. The teacher chooses the amount of questions in the upcoming test. The standard setting here is twenty questions per test. The teacher also initializes the amount of time the pupils have to answer the question (in seconds), the default setting is 60 seconds per question. Lastly, the teacher chooses whether the program should automatically move to the next question if all children have answered or not, and whether a timer that displays the remaining time to answer the question should be enabled or disabled. When clicking the 'start' button, the program generates a test based on the settings provided by the teacher and starts searching for pupil programs that are trying to connect to the current test. We will expand on the connection process later.
Pupil Initialization Interface
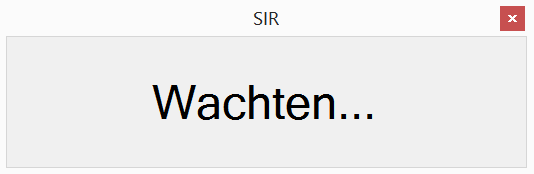
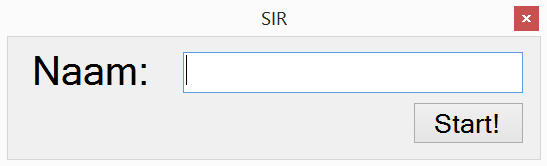
When the pupil interface is launched by the pupils, a waiting form will be displayed, as is shown on the right. At this point, the pupil program is trying to connect to a teacher program where a test was generated. We will expand on this connection process in the next subsection 'connection is established'. After the teacher has generated a quiz, i.e. after the teacher pressed the 'start' button on the initial teacher interface, this connection between the teacher and all pupil programs will be initiated. As soon as the connection has been established, a name form will be displayed to the pupils, as shown on the right.
The pupils all fill in their name and click the "Start!" button. By clicking start, their name will appear in the teacher overview, which is not visible for the children. We will expand on this overview later. An empty question form is now displayed to all children, until the teacher presses the 'next question' button on the teacher overview interface.
Connection is Establised
The connection process between the teacher and pupil program is made as intuitive as possible. After the teacher has filled in all the settings in the teacher initialization interface, the teacher program starts listening on a predefined port for any incoming connections. Once such a connection is received by the teacher program, i.e. a pupil program is trying to access the upcoming test, a 'handshake' message is returned to acknowledge the teacher program received the request.
Once the pupil program receives this feedback, the child is prompted to fill in their username (as discussed above). The teacher program keeps listening until the teacher receives a username.
At this point all the children wait for the initial question broadcast of the teacher. The teacher porgram generates the first question of the quiz and broadcasts this question to all pupils connected to the teacher program. As soon as the teacher program broadcasts an (empty) 'go' message to all pupils, the question is visualized on the screens of all pupils and the actual quiz has started.
Whenever a child sends an answer to the teacher program, the teacher program responds with the pupils next question, based on the pupils score (see section 'score'). However, this question is not yet actually visualized on the child's screen. It is not until the teacher hits the 'next question' button on his overview form (see section 'teacher overview during the quiz'), when the next question is visualized on the child's screen and the child can fill in the correct answer. If the teacher choose in the teacher initialization interface to automatically progress to the next question as soon as all children answered, then the next question is visualized on the child's screen as soon as all children answered the question, or as soon as a (predefined) timeout occurs.
Teacher Overview During the Quiz
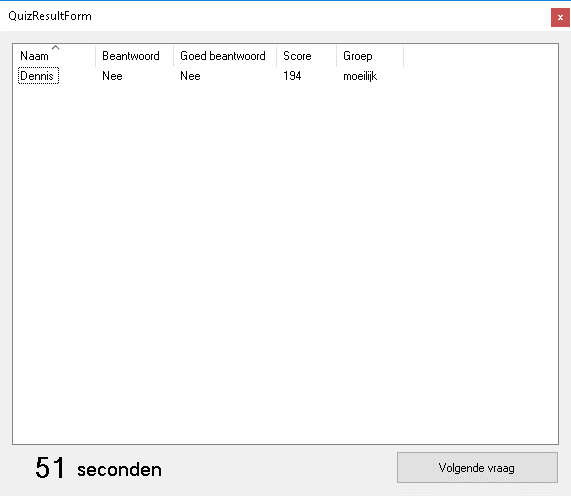
After the teacher pressed the 'start' button on the teacher setup screen, a teacher overview form is displayed to the teacher. Every time a pupil program establishes a connection with the current teacher program, the pupils name will appear in a new row on the teacher overview, as shown on the right. In this figure, one pupil called 'Dennis' is currently connected and able to take the test. The teacher overview has several other fields that give the information on how the pupils are doing:
- The first column tells the teacher whether the pupil has answered the current question.
- The second column tells the teacher if the pupil has answered the current question correctly or not.
- The third column shows the current score of the pupil.
- The last column shows the level of the pupil (see subsection 'score function').
This overview is an easy way for the teacher to see how all the pupils are doing, which pupils need extra attention and which pupils can move on to more challenging topics. We kept the code for this overview screen as generic as possible, so that adding additional columns to this overview at a later stage is easily done.
When the teacher presses the 'next question' button on this overview form, all pupils collectively move on to a new question, as explained in subsection 'connection is established'. Note that not all pupils will get the same next question. Every pupil receives a personalized question, based on their previous performance, i.e. their score (which will be discussed in detail below). The way in which questions are generated is also discussed below.
Questions
Currently, our tests can generate two different question types. Again, the code supporting these question types is generic, so adding additional question types at a later stage is easily done. As mentioned in our research on the 'use of Symbols in Mathematical Questions', we found that in order to get a correct numerical magnitude representation, children need to practice with symbolic numbers, so digits, but also with non-symbolic formats. Based on this finding, we developed two types of questions:
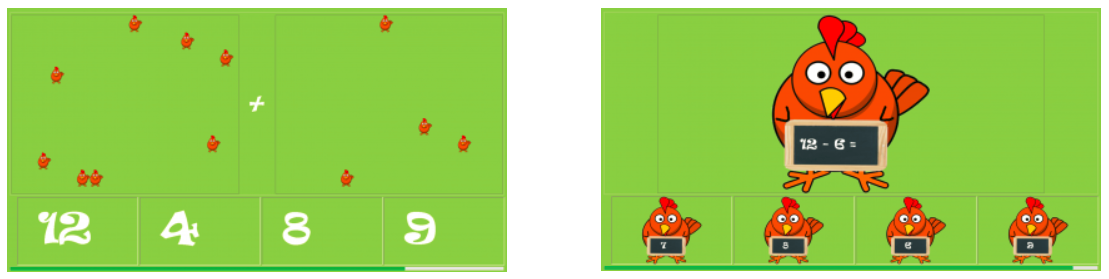
- Flock questions, where children can add or subtract flocks of pigs, cows, or chickens. These questions are a way for the pupils to practice with non-symbolic formats, by counting amounts of animals, and training with symbolic numbers, by transforming the amount they just counted into an actual numerical answer.
- Animals with small blackboards which have simple math questions on them. These questions are a way for the pupils to train their mathematical skills in a purely symbolic manner.
By combining these two different kinds of questions, the pupils both train and test test their numerical magnitude representation, as well as their understanding of basic symbols of mathematical representation. All questions are multiple choice to make it easy for the young children to answer the question.
We chose to use animal pictures to represent our questions, because our research showed that the visualizatoin should speak to the children’s imagination and the questions should be asked in a likeable way. As shown in the picture, both question types are depicted with the question-to-be-answered shown largely in the center of the screen. This question is either depicted by animals displayed in flocks (left) or by a symbolic equation written on a blackboard (right). Underneath are four multiple choice answers the pupils can choose from, one of which is the correct answer. At the bottom of the screen is a timer, that indicates the time the pupil has left to answer the question. This timer can be enabled or disabled by the teacher, based on the way they wish to test.
Feedback
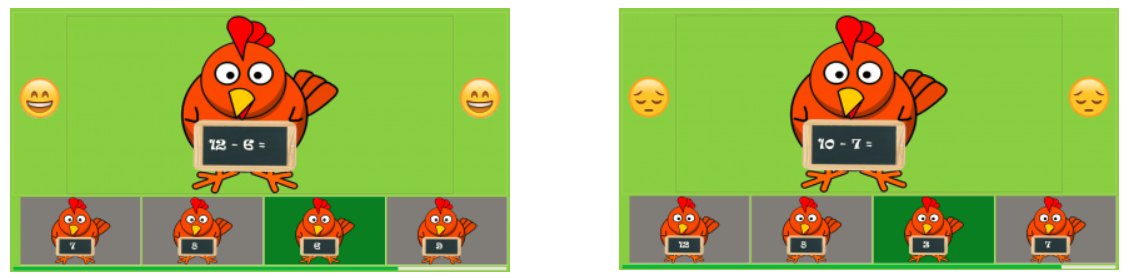
As soon as a pupil clicks on one of the answers of a question, the pupil will immediately receive feedback on their answer (rather than at the end of the test). This is supported by our research, that showed that it is best to incorporate direct feedback. As discussed in our desk research, it was chosen to use the KCR method with no supporting text, accompanied by attributional feedback, also with no supporting text. We chose not use any supporting text, because the young pupils have just started to learn how to read. Therefore we use smiley faces as our attributional feedback, to indicate to the children how they are doing. A happy face is displayed to indicate they answered the question correctly; a sad face means they answered the question wrong. If a pupil answers a question wrong, we wanted to highlight the correct answer, as supported by the KCR method, without focussing on the fact that they answered wrong, based on our findings in article [3], which states that children should not be punished for making mistakes. In order to achieve this, we visualized the feedback as follows. No matter the answer of the a pupil the correct answer is highlighted with a green background, and all other answers get a grey background. We chose not to highlight the incorrect answers of the pupils, so that we focus on what the answer should have been, and not on the fact that they answered wrong, as supported by our desk research. The two feedback possibilities are shown below.
Score
In the program, a score function is used to determine the current level of a pupil. As supported by our research findings on factors influence the quality of a course, it is common to divide students in three different groups. We therefore chose to work with three level categories: easy, average or hard. After each question that a pupil has answered, we use the score function to determine the knowledge level of the pupil, and so, to determine the question difficulty of the next question the pupil will receive. This means pupils can receive questions of different level categories during the test; the pupils can shift between different level categories, based on their score up-until-now. The final level category that the child ends up in after the test has completed determines whether the child needs extra help: children that ended in the easy level probably need some extra attention from the teacher, while children that end up in the hard level can probably move on to a more difficult topic. Note that this level category can also be viewed by the teacher during and after the test, in the last column of the teacher overview form.
The score function we used in our program is as follows:
[math]\displaystyle{ score = score+\frac{correct * current Time}{total Time} }[/math].
Here, 'correct' is a variable that is 100 if the pupil answered the previous question correctly, because this is the maximum amount of points a pupil can receive per question, and 0 otherwise. 'currentTime' is the time it took the pupil to answer the previous question. 'totalTime' is a variable that is set to the total time the pupils had to answer the question. To determine the level of the next question a pupil will receive, this score is then compared with two boundary variables. These two boundaries are:
[math]\displaystyle{ lowerBound= amountOfQuestions * 100 * \frac{1}{3} }[/math]
and
[math]\displaystyle{ upperBound= amountOfQuestions * 100 * \frac{2}{3} }[/math].
Here, 'amountOfQuestions' is the total amount of questions the pupils have already answered, and '100' is the maximum amount of points a pupil can receive per question. Therefore, amountOfQuestions * 100 is therefore the total amount of score a pupil could have earned up until now. If the pupil has a score lower than one third of this total score, i.e. his score is lower than the 'lowerBound' variable, the pupil is shifted to the easy level and his next question will be of the easy level category. If the pupil has a score higher than the upperBound variable, the pupil will be shifted to the high level and his next question will be of this level category. Otherwise, the pupil will be in the average level category, and his next question will be of average level.
Generating the Next Question
As explained above, when the teacher presses the 'next question' button on the teacher overview form, every pupil receives a question in their current level category (easy, average or hard) based on their score. The next question this pupil receives should thus be of the level category the pupil is in. We thus want to generate the next question of a child at the right level (easy, average or hard), while adhering to the settings set by the teacher in the initialization form.
Easy questions are generated the same as average questions, except the bound set by the teacher in the initialization form (by default set to the range [0,20]) is narrowed by 25 percent. For our target group, this means they will receive easier questions with lower numbers. The hard questions are also generated similarly to average questions, except the bound set by the teacher is expanded by 25 percent. For our target group, this means they will receive harder questions with higher numbers.
As for the generation of the questions themselves, we use a structure 'Category', which contains a lower and an upper bound, a number type, a list of operations, a number of arguments, a time limit and a max depth (of parentheses). Note that this 'category' thus holds all the settings set by the teacher in the teacher intitialization interface. The list of operations the teacher set is sorted according to the order of appliance (according to the Dutch rule of thumb 'Meneer Van Dalen Wacht Op Antwoord).
A question can be generated using an instance of the category of the current test. The question itself is generated using a recursive structure which is called 'ValuedOperation'. This recursive structure holds the category, a list of arguments, and a list of operations (with, of course, a size one less than the list of arguments). An argument is in turn either a number or again a ValuedOperation.
A ValuedOperation can be randomly generated using its catory, by creating random arguments within the category lower and upper bounds and using operations set available in the category. While generating questions, it takes into account the maximum number of arguments as well as the maximum depth.
Now, in order to generate a question, we loop over the list of arguments, and either set the argument to a random number within the boundaries of the test category, or a new valuedOperation with its own list of arguments and list of operations. These arguments in turn are again randomly generated within the test category, or are again valuedOperations, etc, until the maximum depth set in the category is reached. The operations are again randomly generated, while adhering to their order of appliance mentioned above.
The multiple choice answers are randomly generated within the bounds set by the category of the test.
Note that for the question types described in this project, the maximum depth is always equal to zero (i.e. no parentheses). We used this more complicated recursive structure in order to accomodate arithmetic questions using parentheses in the future. This recursive structure is also be used to easily calculate the actual answer of the arithmetic question; the answers of the valuedOperations at the maximum depth are first calculated, and are then used in the depth above, working the way up the recursive tree.
End of the Quiz
After the last question has been answered and feedback was received on this question, the pupil programs are automatically closed. The teacher now sees the teacher overview form, where every pupil is classified in a certain level category: easy, average or hard. Pupils in the easy level probably need extra attention from the teacher on the topic that was just tested, while pupils in the hard level can probably move on to more challenging topics. This final overview form can thus be used by the teacher to properly manage their time, and find out which children found it particularly challenging to answer the questions of this topic. The final score of the pupils can be used by the teacher to compare the knowledge levels of all the pupils relative to each other. If the teacher keeps track of the scores of students, they can also see the progress of the students by comparing this final score to a previous final score.
Results
Survey
We have distributed a short survey with Google Forms, see the appendices, in order to find out what actual elementary school teachers think about our program. A clear explanation of the program was given, including screenshots. The purpose of this survey was to find out the following things:
- Is there a demand for programs like ours?
- Would teachers actually implement our program into their lessons?
- Do teachers think it would be a fun new addition that will help the children?
- Do teachers think it would help them?
- Are there any other important features the program should have?
The survey has reached many people, however due to the planning we only had 15 reactions when it was time to analyze the data. Though this is not very much, 15 is enough to get some results. We asked all participants to consent to filling out the survey. The most important results can be seen below, with screenshots from the actual survey. The survey was Dutch as we focus on the Dutch education system, all questions will be translated here.
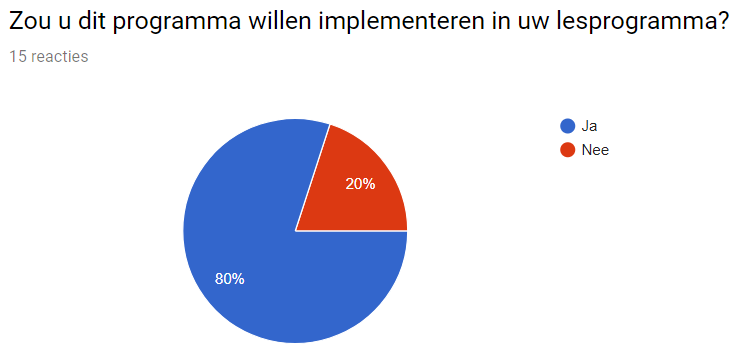
Would you implement this program in your lessons? And why?
As we can see, a decent 80% of the teachers indicated that they would in fact use this program in their lessons, mostly because it looks nice, it could help with quickly seeing the children’s levels, and that they expect children to be engaged as it is on a computer. The more negative reactions usually come down to that children do not need extra testing.
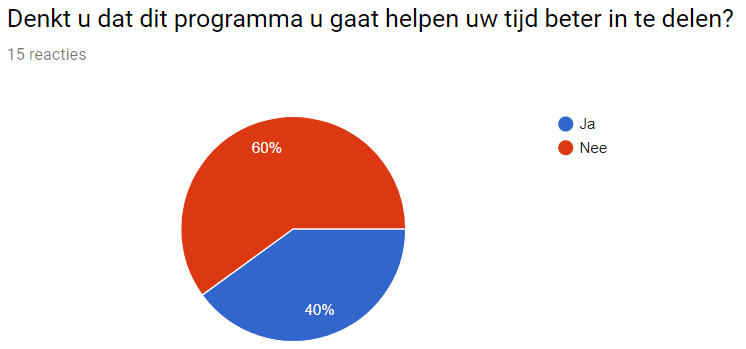
Do you think this program would help you to use your time more optimal?
60% of the teachers do unfortunately enough not think that the program will help them with dividing their time. But as most teachers are still positive about the program we do not think this is too bad. They could like it as it is fun and engaging for the children, even though they are already good at dividing their time. The results for this question could also be due to the fact that, in hindsight, the question is not formulated in the most clear way there is.
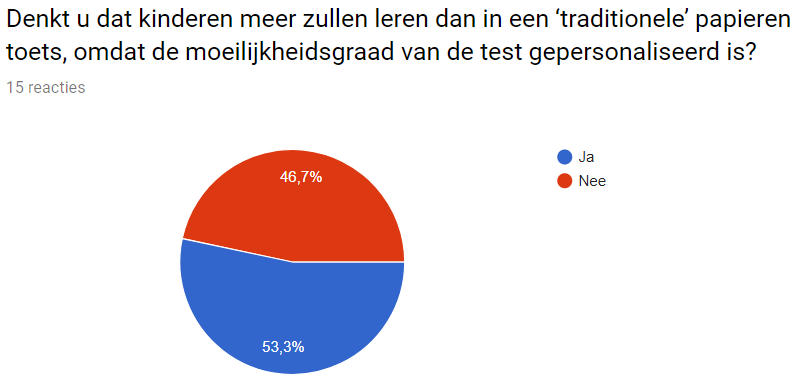
Do you think that the children will learn more with this program than with a ‘traditional’ test on paper, as the level of the test will adapt to the children individually?
This is practically a tie, the teachers are not convinced that this will effectively teach the children more than a paper test will. Obviously, this is not a very positive result but as still a bit more than half believes it is better than paper, we do not have to throw out our program immediately. Also when keeping in mind that there are relatively few reactions, this question could really go either way when asking more people.
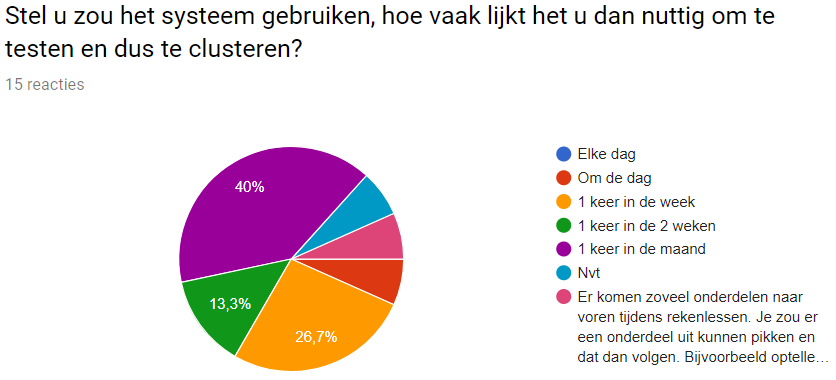
How often would you use the test, if you would implement the program?
It seems that most people think it is best to use it only once a month, this could probably be due to the fact that teachers do not want the children to use the computer to much or that they do not think clustering is necessary that often. Therefore we could keep this in mind when marketing our product.
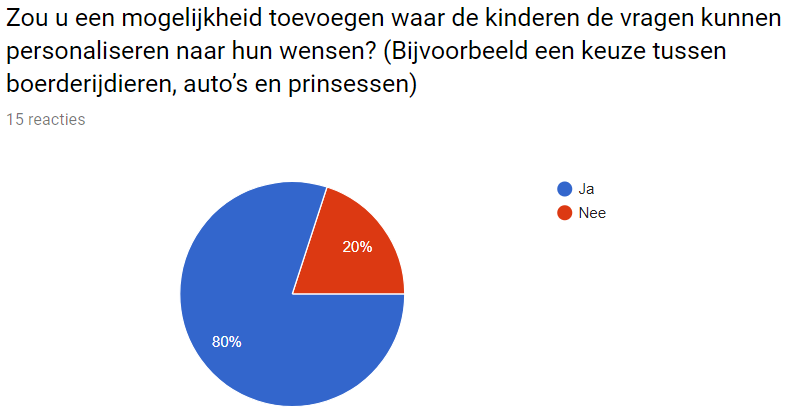
Would you add an extra feature so the children can personalise the test? (They could for example choose between animals, princess or cars)
80% of the teachers do think it is better, to add this feature. Meaning in the future this should be implemented and more research should be done to see what children want to change (a.k.a. personalise).
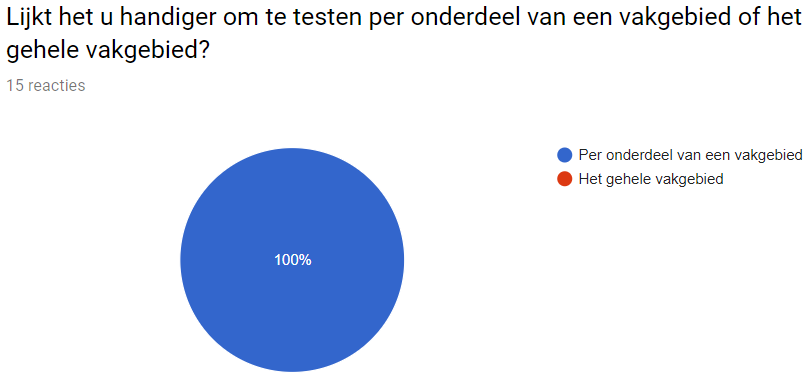
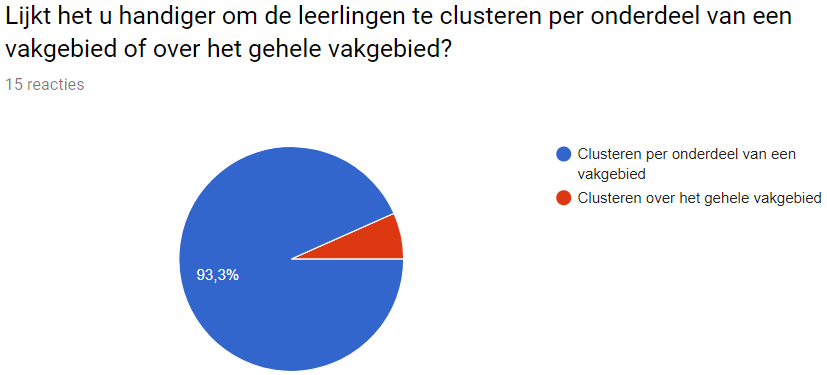
Do you think it is better to test and cluster on a whole subject or on a part of the subject?
Everyone agrees that the program has to test on parts of a subject instead of the whole subject. This confirmes our assumption that the teachers should be able to customize each test to their needs.
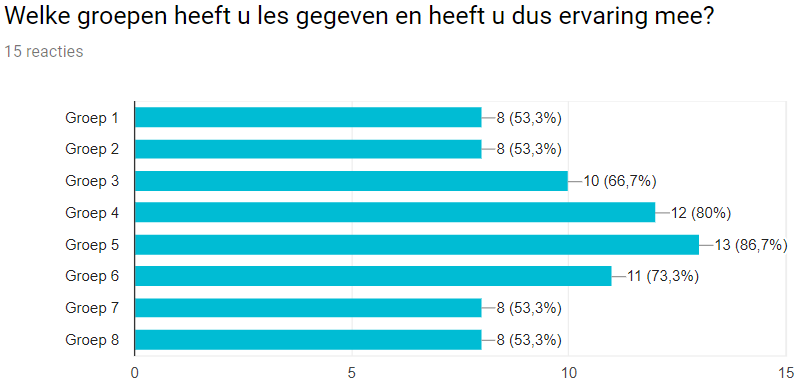
Demographics of the respondents
Almost all the respondents have experience in all the grades of a dutch elementary school and work at a traditional Catholic school. This has to be taken into account, when looking at the generallity of our program.
Do you have any other remarks?
In the remarks it becomes clear that most of the respondents are really excited to see this program develop and to eventually use it. However there was a respondent who was not as excited and thought it was not keeping in mind an other didactic system that let the pupils decide what to learn and when.
Conclusion
Overall we can conclude that the program is a success. It functions the way we intended it to function and most teachers have indicated that they would like to use the program in their lessons. Of course there can be many improvements, which we will talk some more about this in the discussion.
From our desk research we found that using computers is supported for our target audience and that it is best to give children knowledge of correct response after each question. Because we picked the traditional education system we ask a lot of basic arithmetic questions without text so the children can practice a lot.
Discusion
When looking back at this project, there are many things that could have been done differently, and even more efficiently.
Project
First of all, picking a correct topic was not easy at all, when discussing our ideas there were many instances where the conclusion was that our idea was not good enough. In hindsight, we should have picked an idea sooner in order to have enough time for the implementation and testing we wished to achieve.
For the survey it turned out we should have had some more time, right now we only had a small week to gather answers which resulted in only 15 reactions. 15 reactions is enough to base some conclusions on, but it would have been better if there had been more reactions and we are sure that this would have been the case if there had been more time. Another way to improve this would have been by going to elementary schools and asking them face to face whether teachers want to fill out the survey, as now the survey was distributed through email and Facebook, but as we had a very specific target audience (elementary school teachers with experience in grade 3 and/or 4) this could have been done better. Also how the survey was designed could have been improved. Based on the reactions we got the idea that not all questions were as clear to the participants as we had hoped. A big improvement would have been a short movie about the workings of our program, in addition to the explanation and screenshots we had now. The questions should have been formulated more clearly.
We were all pretty pleased with how the final presentation turned out, however the demo did not go as planned. This was due mostly to things out of our control, but it would have been better if we had just made a short movie about how our program worked than doing in in real life. We did not do this as we expected that if at all possible, a real life demo was necessary, but this turned out not to be the case.
Program
There are some topics that we used for our project that would be of interest in future research to improve our program:
- Implementation of more different types of questions, for example reading the clock. It would be interesting to see which kinds of questions are most efficient for the children to learn from. This implementation can be done in terms of plug-in forms in the program.
- Machine learning classification of pupils in the categories, there could also be more categories. At this point we only have three categories and we classify based on thresholds. Machine learning would probably work a lot better.
- How to validate the score function and possibly incorporating other variables such as answers that are ‘almost’ correct. A lot of improvement can probably be done here as right now the score only depends of whether or not the question is correct and the time the child took to answer.
- Generating multiple choice answers to a questions based on the question. Right now the answers are randomly generated, but a better option could be altering the correct answer in some way to get the other choices.
- Changing the question difficulty based on more question properties like operations or ‘tricky’ multiple choice questions as now the difficulty level is based solely on the boundaries of the question. It would be interesting to see the effects of these changes.
- Creating implementations of the quiz on more platforms such as a tablet or phone, instead of only on the computer. A survey could be of use to find out if this is something schools/teachers would like or need.
- Saving all performed tests in order to keep track of the overall progress of students, instead of just one test at a time.
- Based on our survey, it would also be a nice addition to make an option for the children to customize their interface. This would mean that they can choose between the farm animals we have now, and princesses or cars, for example.
- As most respondents from our survey work at a Catholic school, it would be interesting to see if other types of schools share the same opinions.
References
- ↑ P. Hoogeveen, J. Winkels, from: "Het didactische werkvormenboek", The Netherlands, March 2014
- ↑ Inspectie van het Onderwijs, "De staat van het onderwijs", Onderwijsverslag 2011/2012, The Netherlands, April 2013
- ↑ M. Hickendorf et al. "Rekenen op de basisschool", Universiteit Leiden, The Netherlands, October 2017
- ↑ A. van Loon et al., http://ixperium.nl/files/2014/08/dimensies-gepersonaliseerd-leren.pdf "Dimensies van gepersonaliseerd leren", The Netherlands, October 2016
- ↑ Steven L. Wise and Lee Ann Wise, https://ac.els-cdn.com/0747563287900069/1-s2.0-0747563287900069-main.pdf?_tid=09dccd7c-00f6-4fd7-9dbb-f4775a2aee61&acdnat=1521453097_4f6140382d37ec957a157e375f2e6a67, Computers in Human Behavior, Elsevier, 1987
- ↑ M. van Zanten et al., "Kennisbases", The Netherlands, 2009
- ↑ B. de Smedt et al., https://dspace.lboro.ac.uk/dspace-jspui/bitstream/2134/16152/1/DeSmedt,Noel,Gilmore%26Ansari(2013).pdf "How do symbolic and non-symbolic numerical magnitude processing relate to individual differences in children’s mathematical skills? A review of evidence from brain and behavior ", Belgium, 2013
- ↑ D. Schunk, "Ability Versus Effort Attributional Feedback: Differential Effects on Self-Efficacy and Achievement", Journal of Educational Psychology, 75, 848-856, 1983
- ↑ Roy B. Clariana, Steven M. RossGary R. Morrison "The effects of different feedback strategies using computer-administered multiple-choice questions as instruction" June 1991, Volume 39, Issue 2, pp 5–17
- ↑ Website "Wijzer over de basisschool"