Embedded Motion Control 2016 Group 4

Group Members

ID-Number	Name	E-mail
0811028	Tim Josten	t.j.josten@student.tue.nl
0790737	Tom Leenen	t.c.p.f.leenen@student.tue.nl
0832751	Martin Plantinga	m.plantinga@student.tue.nl
0816951	Joey Reinders	j.m.f.reinders@student.tue.nl

Email all groupmembers

Goal

The goal of this project is to make a robot (PICO or TACO) navigate autonomously and as seamlessly as possible through a maze and find the exit. The robot has a computer integrated in it that runs on Linux, with ROS (Robot Operating System) running on top. The software has to be written in the C++ programming language. To achieve the goal, a software architecture has to be designed that structurally makes room for the different requirements, functions, components, specifications and interfaces.

Requirements

To achieve the final goal several requirements are determined, which can be seen in the following list.

• Navigate autonomously to the exit of the maze as fast as possible
  • cruise as fast as possible while maintaining the different abilities

• Avoid obstacles
  • recognize the different obstacles (e.g. walls) and keep a "safe" distance from them

• Avoid getting trapped in a loop of the maze
  • recognize if the robot is navigating through the same path over and over and exit the loop

• Create a map of the maze

• Recognize door, open it and drive through it

• Navigate in open spaces
  • navigate if no obstacle is in sight

• Scalable system
  • the software should be able to work independently of the size and structure of the maze

Functions

The functions can be divided into two groups: the basic functions and the skill functions. The basic functions are basic actions that the robot will do. The skill functions are a set of actions to accomplish a certain goal.

The basic functions consist of:

• Actuation of the robot:
  • Provide signals to the actuators of the robot. Realize the desired motion by using a controller and meeting the requirements.
  • Input: location of robot, Output: motion of robot

• Detect:
  • Characterize different types of corridors based on telemetry provided by the Laser Range Finder (LRF).
  • Input: measured x, y and theta; Output: type of corridor

The skill functions consist of:

• Mapping:
  • Create and update a map of the explored maze. The robot will recall this map as its future moves will depend on this map.
  • Input: current x, y and theta of the robot; Output: new/updated maze map, new/adjusted objective of the robot.

• Feedback:
  • Check position of robot with position of the created map. Prevent the robot from collisions with the walls or other obstacles.
  • Input: current x, y, theta, LFR data and objective; Output: motion of the robot.

• Decision:
  • Check position of robot with position of the created map. Prevent the robot from collisions with the walls or other obstacles.
  • Input: current x, y, theta, LFR data and objective; Output: motion of the robot

• Monitor:
  • Control the exploration of the maze and prevent the robot from getting stuck in a loop.
  • Input: current x, y and theta of the robot; Output: previously unexplored area

• Door check:
  • Wait at the potential door location for a predetermined time period while scanning the distance to the potential door to check if it opens.
  • Input: current x, y and theta of the robot; Output: A door that either opens or stays closed, followed by pico's new objective based upon the result.

• Obstacle check:
  • Measure the preset minimum safe distance from the walls or measure not moving as expected according to the driving action.
  • Input: current and expected x, y and theta of the robot; Output: new motion of the robot based upon the result.

Components

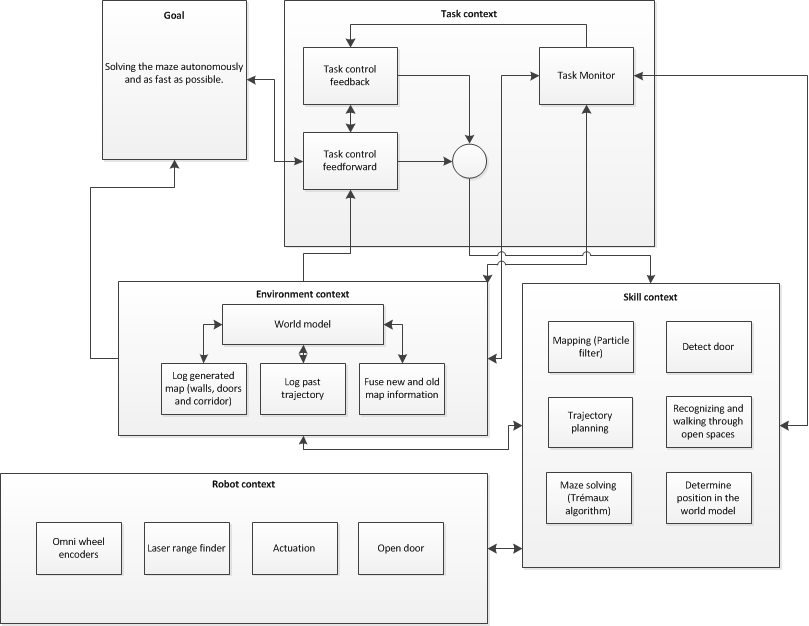
To fulfilll the previously mentioned functions and achieve the goal, the software should contain different components that interact with each other. This can be seen in Figure 1.

The C++ code should contain the components shown in Figure 1. There should be a task manager to switch between different tasks. An algorithm should be made that decides which task is performed or whether different tasks are performed simultaneously.

An algorithm should be implemented for controlling the robot and accurately position it, this algorithm uses the environment model, which is made using the laser range finder and omni-wheel encoders. This world model is logged and will be continuously updated during the maze solving of the robot.

The robot should have several skills and these should be programmed effectively with a fast algorithm. For the world model, the robot needs a mapping skill and it needs to determine its position in this world model. To solve the maze the robot needs a trajectory planning which uses an effcient maze solving algorithm (e.g. Trémaux).

Eventually when the robot has solved the maze, the algorithm has to be stopped.

Figure 1: Structure of the software implementation

Specifications

In the specifications the tasks that the robot has to conduct are quantified (i.e. given a value).

• The maximal translational velocity of PICO is 0.5 m/s
• The maximal rotational speed of PICO is 1.2 rad/s
• PICO has to solve the corridor challenge within 5 minutes
• PICO has to solve the maze challenge within 7 minutes
• PICO may not stop moving for more than 30 seconds (e.g. when opening the door)

Interfaces

To interpret the data that the robot collects, it is convenient to make a graphical user interface that visualizes this data. The omni-wheel encoder in combination with the laser range finder can be used to visualize the path of the robot and make the world model. The encoder data should be transformed to robot coordinates with a kinematic model of the robot.

The laser range finder also produces data, and to see if this data is interpreted in the right way a visualization should be made. It can be used to see if walls, doors and exits are detected in the right way. Possible algorithms for this are the Hough transform and particle filter.

Corridor Challenge

The goal of the corridor challenge was to let Pico take the first exit, either left or right, out of a corridor. It is decided to let Pico drive forward and use its potential force field to keep him in the middle of the corridor (The potential field is more comprehensively discussed under the section potential field). At the moment when Pico sees the exit, he should turn 90 degrees in the direction where the exit is and then continue with driving forward and use the potential force field. A animation is shown in the figure below.

Figure 2: Node detection

Although it would have been better and quicker to detect the exit before it is next to pico and then put a setpoint (point of attraction for the force field) at the exit. Because, this way Pico does not have to come to a complete stop and keeps driving. But because the potential field was well tuned it was possible to drive very fast which made us finish the corridor challenge the fastest. The video of our second run is shown below.

Maze Challenge

The next part of this wiki page contains the software architecture and methods which are used to finish the maze challenge, furthermore a conclusion is given and a reflection on the entire project.

Software architecture & approach

To make a good code first of all the software architecture is obtained. This is visually displayed in Figure 3. First of all data is obtained from Pico, this is done using the two sensors, the laser range finder and odometry. The laser range finder data is used to generate a potential field and to discover features (nodes) furthermore there is the odometry data, which is used to determine an initial guess for the position for the mapping block. Features (e.g. T-junction, dead end or corners) are detected using the node detection algorithm as described in the next part. Using these features and the odometry data a map is generated. The information in this map is used by the target to determine what step to take (i.e. open door, turn or drive). This target is combined with the potential field and is used to make Pico drive in the desired direction.

Figure 3: Software architecture

Node detection (Features)

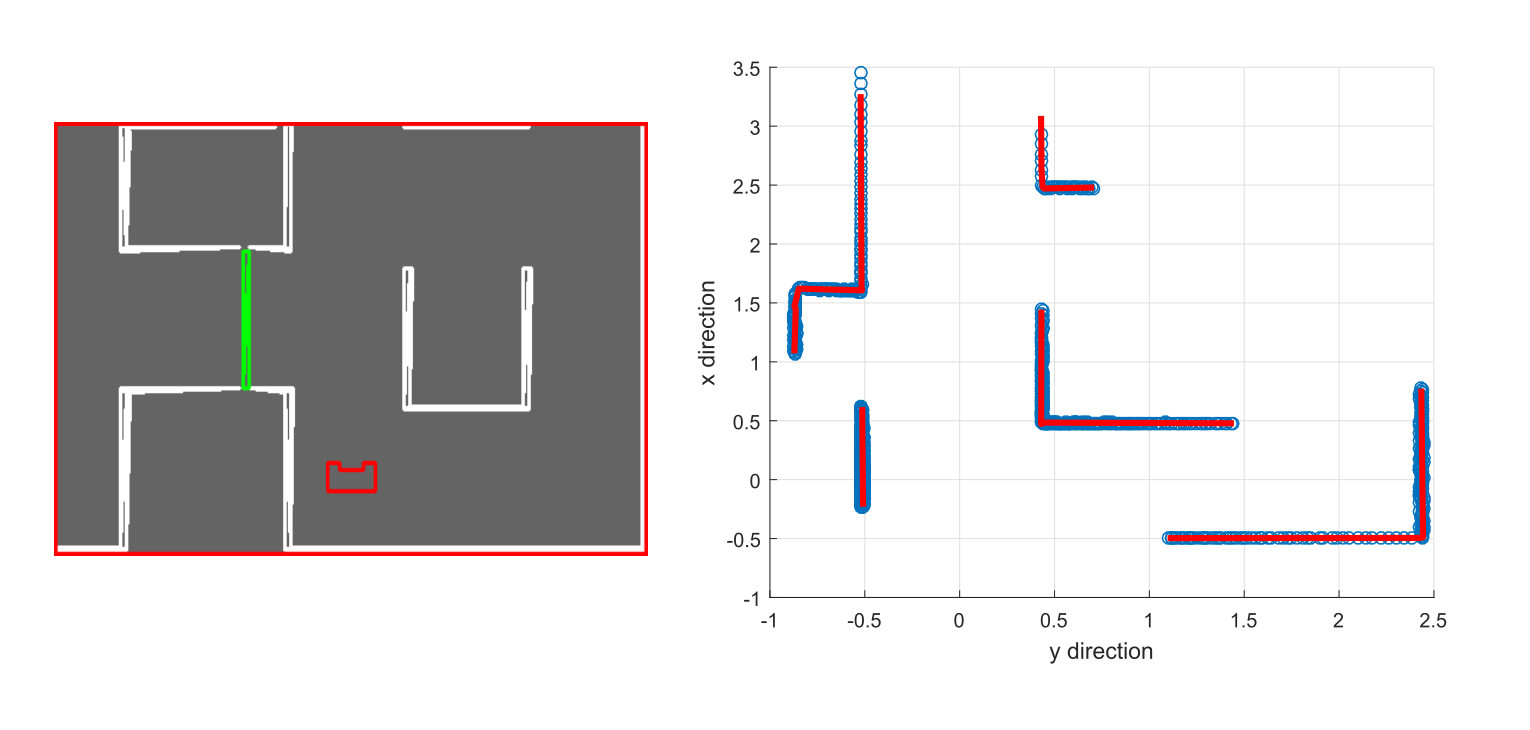
To drive through the maze correctly, locally nodes (e.g. T-junction or crossroads) have to be detected. To do this first of all a line extraction algorithm (Split and Merge) is used. Based on the extracted lines it is determined what nodes are "seen" by Pico. The line extraction algorithm works as follows (A visualization is shown in Figure 4):

1. Compute local x and y coordinates based on LRF
2. Compute sets of data based on distance between points
3. Fit straight lines through separate sets
4. Determine maximal error and split set again (if error is bigger then maximal value)
5. Repeat 3 and 4 until maximal error is small enough

Figure 4: Node detection

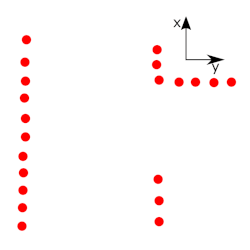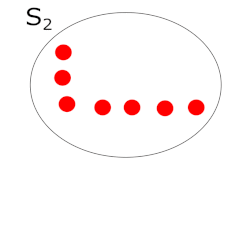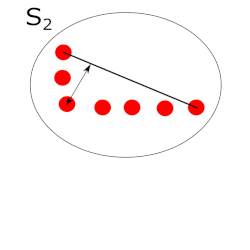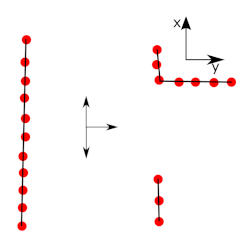
Using the lines as extracted with the algorithm described above a distinction is made in walls aligned with pico and walls which are orthogonal to pico. Based on the walls which are aligned with pico and the distance in x direction between those wall it is determined if it is possible to go right or left. An example of the fitted walls using the simulator is shown in Figure 5, with in the right part the LRF data and the fitted lines, and in the left part what the simulator shows. This clearly shows that all the walls of the simulation (up to the specified distance to see) are extracted nicely. Based on these lines the nodes (crossings) are positioned in local coordinates.

Figure 5: Example of the node detection in the simulator for the final maze.

SLAM (Simultaneous localization and mapping)

To estimate the location of Pico and to get a map of the maze, the SLAM algorithm is used. First some definitions are defined.

Definitions

1. Landmark: visible feature in the environment whose location is known with respect to some coordinate frame.
2. Dead reckoning: estimation of location based on estimated speed, direction and time of travel, wrt a previous estimate.
3. [math]\displaystyle{ x }[/math]: real robot pose
4. [math]\displaystyle{ \hat{x} }[/math]: estimated robot pose
5. Estimation: process of inferring the value of some quantity of interest, [math]\displaystyle{ q }[/math], by processing data that is some way dependent on [math]\displaystyle{ q }[/math].
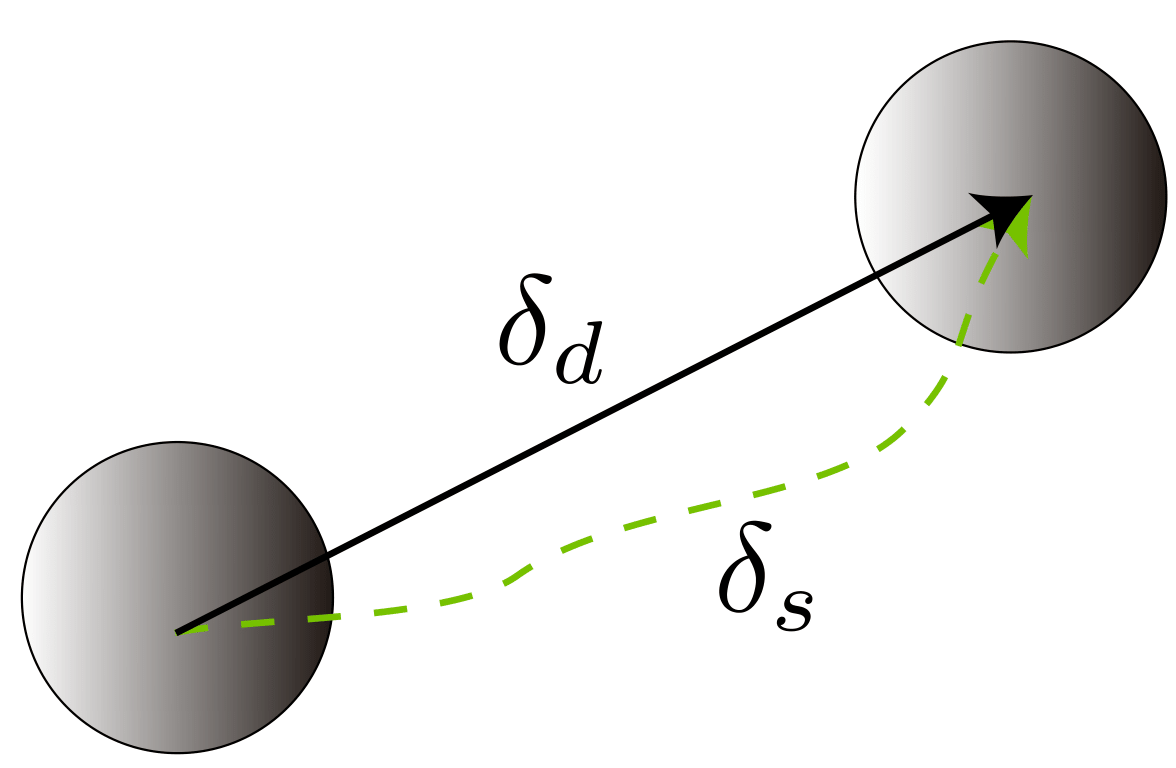
6. [math]\displaystyle{ \delta_{{\langle k \rangle}}= (\delta_d,\delta_\theta) }[/math]: distance travelled and change in heading over the preceding interval.
7. [math]\displaystyle{ k }[/math]: time step.

Position estimation and equations of motion

To estimate the position of Pico, odometry data is used. And since the frequency is high, the motions are relatively small and it is assumed that: [math]\displaystyle{ \delta_d= \delta_s }[/math] which can be seen in Figure 6.

Figure 6: Position estimation

• The discrete-time model is given as follows:
  

  [math]\displaystyle{ x_{{\langle k+1 \rangle}}= f(x_{{\langle k \rangle}}, \delta_{{\langle k \rangle}}, v_{ {\langle k \rangle}}) }[/math]

• The new configuration in terms of the previous configuration and odometry, together with the error in the odometry as continuous random variables, can be defined as:
  

  [math]\displaystyle{ \xi_{{\langle k+1 \rangle}}= \begin{bmatrix} x_{{\langle k \rangle}}+ (\delta_{d,{{\langle k \rangle}}}+v_d)\cos(\theta_{{\langle k \rangle}}+\delta_\theta + v_\theta)\\ y_{{\langle k \rangle}}+ (\delta_{d,{{\langle k \rangle}}}+v_d)\sin(\theta_{{\langle k \rangle}}+\delta_\theta + v_\theta)\\ \theta_{{\langle k \rangle}}+ \delta_\theta + v_\theta \end{bmatrix} }[/math]

  [math]\displaystyle{ \delta_d }[/math]:	movement in x direction
  [math]\displaystyle{ \delta_\theta }[/math]:	rotation
  [math]\displaystyle{ v_d, v_\theta }[/math]:	error in odometry

Laser Range Finder

The laser range finder can provide observations with regards to the robot as described by

[math]\displaystyle{ z = h(x_v, x_f, w), }[/math]

where [math]\displaystyle{ x_v }[/math] is the vehicle state, [math]\displaystyle{ x_f }[/math] is the location of the feature in the world frame and [math]\displaystyle{ w }[/math] is a random variable that models the sensor error.

The observation of the i-th feature [math]\displaystyle{ x_{f,i} }[/math] is expressed by

[math]\displaystyle{ z = \begin{bmatrix} r\\\beta \end{bmatrix} = \begin{bmatrix} \sqrt{(y_i - y_v)^2 + (x_i - x_v)^2}\\ \tan{^{-1} }\frac{y_i-y_v}{x_i - x_v} - \theta_v \end{bmatrix} + \begin{bmatrix} w_r\\w_\beta \end{bmatrix}, }[/math]

with [math]\displaystyle{ r }[/math] is the range, [math]\displaystyle{ \beta }[/math] is the bearing angle and the measurement noise is given by

[math]\displaystyle{ \begin{bmatrix} w_r\\ w_\beta \end{bmatrix} \sim N(0,W) }[/math]

[math]\displaystyle{ W = \begin{bmatrix} \sigma_r^2 &0\\0&\sigma_\beta^2 \end{bmatrix}. }[/math]

Estimated uncertainty [math]\displaystyle{ \sigma_r = 0.1 }[/math] m and [math]\displaystyle{ \sigma_\beta = 1^\circ }[/math].

The observation by the LRF is linearized:

[math]\displaystyle{ z_{{\langle k \rangle}}= \hat{h} + H_x(x_{{\langle k \rangle}}- \hat{x}_{{\langle k \rangle}}) + H_w w_{{\langle k \rangle}}, }[/math]

where the Jacobians are given by

[math]\displaystyle{ H_{x_i} = \left. \frac{\partial h}{\partial x_v}\right|_{w=0} = \begin{bmatrix} -\frac{x_i - x_{v,{{\langle k \rangle}}}}{r} &-\frac{y_i - y_{v,{{\langle k \rangle}}}}{r} &0\\ \frac{x_i - x_{v,{{\langle k \rangle}}}}{r^2} &-\frac{y_i - y_{v,{{\langle k \rangle}}}}{r^2} &-1 \end{bmatrix} }[/math]

[math]\displaystyle{ H_w = \left.\frac{\partial h}{\partial w}\right|_{w = 0} = \begin{bmatrix} 1 &0\\0&1 \end{bmatrix} }[/math]

Extended Kalman Filter

Given noisy odometry data, how can we estimate new pose given previous pose and noisy odometry? Kalman filter provides optimal estimate of the system state assuming zero mean Gaussian noise.

The used motion model is a non-linear model. Therefore the motion model is locally linearized wrt the current state estimate [math]\displaystyle{ \hat{x}_{{\langle k \rangle}} }[/math], resulting in

[math]\displaystyle{ \hat{x}_{{\langle k+1 \rangle}}= \hat{x}_{{\langle k \rangle}}+ F_x(x_{{\langle k \rangle}}- \hat{x}_{{\langle k \rangle}}) + F_v v_{{\langle k \rangle}}, }[/math]

where [math]\displaystyle{ F_x = \frac{\partial f}{\partial x} }[/math] and [math]\displaystyle{ F_v = \frac{\partial f}{\partial v} }[/math] are Jacobians. These are obtained by differentiating and evaluating for [math]\displaystyle{ v = 0 }[/math]:

[math]\displaystyle{ F_x = \left.\frac{\partial f}{\partial x}\right|_{v=0} = \begin{bmatrix} 1 & 0 &-\delta_{d,{{\langle k \rangle}}} - \sin(\theta_{{\langle k \rangle}}+ \delta_\theta)\\ 0&1&\delta_{d,{{\langle k \rangle}}}\cos(\theta_{{\langle k \rangle}}+ \delta_\theta)\\ 0&0&1 \end{bmatrix} }[/math]

[math]\displaystyle{ F_v = \left.\frac{\partial f}{\partial v}\right|_{v=0} = \begin{bmatrix} \cos(\theta_{{\langle k \rangle}}+\delta_\theta) &-\delta_{d,{{\langle k \rangle}}}\sin(\theta_{{\langle k \rangle}}+ \delta_\theta)\\ \sin(\theta_{{\langle k \rangle}}+\delta_\theta)&\delta_{d,{{\langle k \rangle}}}\cos(\theta_{{\langle k \rangle}}+ \delta_\theta)\\ 0&1 \end{bmatrix} }[/math]

Preliminaries

1. Define the initial state covariance [math]\displaystyle{ P_0 }[/math].
   The values of the elements of this matrix can be small given that a good initial state estimation is assumed.
2. Define the estimate of the odometry covariance ([math]\displaystyle{ V }[/math]) [math]\displaystyle{ , \hat{V} }[/math].
   Some experimentation is required to determine an appropriate value of [math]\displaystyle{ \hat{V} }[/math].
3. Determine the estimated LRF covariance [math]\displaystyle{ \hat{W} }[/math]

Steps

The steps are as follows:

1. EKF Prediction Equations

[math]\displaystyle{ \hat{x}_{\langle k+1 | k\rangle} = f(\hat{x}_{\langle k\rangle}, \delta_{\langle k \rangle}, 0) }[/math]

[math]\displaystyle{ \hat{P}_{{{\langle k+1 | k \rangle}}} = F_{x, \langle k \rangle}\hat{P}_{{\langle k | k \rangle}}F_{x, \langle k \rangle}{^\top}+ F_{v, \langle k \rangle }\hat{V} F_{v, \langle k \rangle}{^\top} }[/math]

1. EKF Sensor Update Equations [math]\displaystyle{ \hat{x}_{{\langle k+1 | k+1 \rangle}}= \hat{x}_{{\langle k+1 | k \rangle}}+ K_{{\langle k+1 \rangle}}\nu_{{\langle k+1 \rangle}} }[/math][math]\displaystyle{ \hat{P}_{{\langle k+1 | k+1 \rangle}}= \hat{P}_{{\langle k+1 | k \rangle}}F_{x,{{\langle k \rangle}}}{^\top}- K_{{\langle k+1 \rangle}}H_{x,{{\langle k+1 \rangle}}}\hat{P}_{{\langle k+1 | k \rangle}} }[/math][math]\displaystyle{ S_{{\langle k+1 \rangle}}= H_{x,{{\langle k+1 \rangle}}} \hat{P}_{{\langle k+1 | k \rangle}}H_{x,{{\langle k+1 \rangle}}}{^\top}+ H_{w,{{\langle k+1 \rangle}}}\hat{W}_{{\langle k+1 \rangle}}H_{w,{{\langle k+1 \rangle}}}{^\top} }[/math][math]\displaystyle{ K_{{\langle k+1 \rangle}}= \hat{P}_{{\langle k+1 | k \rangle}}H_{x,{{\langle k+1 \rangle}}}{^\top}S_{{\langle k+1 \rangle}}{^{-1} } }[/math]

Sensor Fusion

The EKF framework allows data from many and varied sensors to update the state. This is the reason the estimation problme is also referred to as sensor fusion. Compass heading angle, GPS position, gyroscope yaw rate and target bearing angle can be all used to update the state.

All that is needed is

1. observation function [math]\displaystyle{ h(.) }[/math]
2. Jacobians [math]\displaystyle{ H_x }[/math] and [math]\displaystyle{ H_w }[/math]
3. estimate of sensor output covariance [math]\displaystyle{ W }[/math]

The observation function [math]\displaystyle{ h(.) }[/math] can be both non-linear and non-invertible, the EKF does the rest.

Preliminaries

1. Define the initial state covariance [math]\displaystyle{ P_0 }[/math].
   The values of the elements of this matrix can be small given that a good initial state estimation is assumed.
2. Define the estimate of the odometry covariance ([math]\displaystyle{ V }[/math]) [math]\displaystyle{ , \hat{V} }[/math].
   Some experimentation is required to determine an appropriate value of [math]\displaystyle{ \hat{V} }[/math].
3. Determine the estimated LRF covariance [math]\displaystyle{ \hat{W} }[/math]

Steps

The steps are as follows:

1. EKF Prediction Equations

[math]\displaystyle{ \hat{x}_{\langle k+1 | k\rangle} = f(\hat{x}_{\langle k\rangle}, \delta_{\langle k \rangle}, 0) }[/math]

[math]\displaystyle{ \hat{P}_{{{\langle k+1 | k \rangle}}} = F_{x, \langle k \rangle}\hat{P}_{{\langle k | k \rangle}}F_{x, \langle k \rangle}{^\top}+ F_{v, \langle k \rangle }\hat{V} F_{v, \langle k \rangle}{^\top} }[/math]

1. EKF Sensor Update Equations [math]\displaystyle{ \hat{x}_{{\langle k+1 | k+1 \rangle}}= \hat{x}_{{\langle k+1 | k \rangle}}+ K_{{\langle k+1 \rangle}}\nu_{{\langle k+1 \rangle}} }[/math][math]\displaystyle{ \hat{P}_{{\langle k+1 | k+1 \rangle}}= \hat{P}_{{\langle k+1 | k \rangle}}F_{x,{{\langle k \rangle}}}{^\top}- K_{{\langle k+1 \rangle}}H_{x,{{\langle k+1 \rangle}}}\hat{P}_{{\langle k+1 | k \rangle}} }[/math][math]\displaystyle{ S_{{\langle k+1 \rangle}}= H_{x,{{\langle k+1 \rangle}}} \hat{P}_{{\langle k+1 | k \rangle}}H_{x,{{\langle k+1 \rangle}}}{^\top}+ H_{w,{{\langle k+1 \rangle}}}\hat{W}_{{\langle k+1 \rangle}}H_{w,{{\langle k+1 \rangle}}}{^\top} }[/math][math]\displaystyle{ K_{{\langle k+1 \rangle}}= \hat{P}_{{\langle k+1 | k \rangle}}H_{x,{{\langle k+1 \rangle}}}{^\top}S_{{\langle k+1 \rangle}}{^{-1} } }[/math]

Sensor Fusion

The EKF framework allows data from many and varied sensors to update the state. This is the reason the estimation problme is also referred to as sensor fusion. Compass heading angle, GPS position, gyroscope yaw rate and target bearing angle can be all used to update the state.

All that is needed is

1. observation function [math]\displaystyle{ h(.) }[/math]
2. Jacobians [math]\displaystyle{ H_x }[/math] and [math]\displaystyle{ H_w }[/math]
3. estimate of sensor output covariance [math]\displaystyle{ W }[/math]

The observation function [math]\displaystyle{ h(.) }[/math] can be both non-linear and non-invertible, the EKF does the rest.

Map Making

• State vector with estimated coordinates to [math]\displaystyle{ m }[/math] landmarks
  

  [math]\displaystyle{ \hat{x}=(x_1, y_1,\dots, x_m, y_m){^\top} }[/math]

• Prediction equations
  

  [math]\displaystyle{ \hat{x}_{{\langle k+1 | k \rangle}}= \hat{x}_{{\langle k | k \rangle}} }[/math]

  [math]\displaystyle{ \hat{P}_{{\langle k+1 | k \rangle}}= \hat{P}_{{\langle k | k \rangle}} }[/math]

• State vector evolution

  [math]\displaystyle{ g(x_v,z) = \begin{bmatrix} x_v + r_z\cos(\theta_v + \theta_z)\\ y_v + r_z\sin(\theta_v + \theta_z) \end{bmatrix} }[/math]

• Adding landmarks
  

  [math]\displaystyle{ x_{{\langle k | k \rangle}}^\star = y(x_{{\langle k | k \rangle}}, z_{{\langle k \rangle}}, x_{v,{{\langle k | k \rangle}}}) = \begin{bmatrix} x_{{\langle k | k \rangle}}\\ g(x_{v,{{\langle k | k \rangle}}}, z_{{\langle k \rangle}}) \end{bmatrix} }[/math]

Simultaneous Localization and Mapping

• State Vector
  

[math]\displaystyle{ \hat{x} = (x_v, y_v, \theta_v, x_1, y_1, ... , x_m, y_m) }[/math]

• Feature observation with regards to state vectors:
  

[math]\displaystyle{ H_x = \left(H_{x_v} \dots 0 \dots H_{x_i} \dots 0\right) }[/math]

Global and local path planning (Target and drive)

Maze solving

To solve the maze in an efficient way, Pico should know where to go based on information where it has been. A very efficient way of maze solving (when the maze is unknown and contains loops) is the Tremaux algorithm. The algorithm needs information from the map about which node it is approaching and in which direction it is approaching it. Based on this information it can determine which way to go. When a new node is reach it will take a random direction. When a node is already encountered before it will first take a direction it has not been yet. When every direction is already been taken at a junction it will turn around. Using this algorithm it will never get stuck in a loop and it should always find the exit, if there is no exit it will always return to its starting position.

For the maze challenge this algorithm was not implemented due to the fact that the mapping was not working good enough. When mapping does not work the above algorithm definitely won't work. For the maze challenge a random walk is implemented, which means that at every node it will make a random choice which direction it will continue. Because the maze is not really big (size of robocup field) it should be able to solve the maze using random walk.

Potential field

Pico is driving in the maze using a potential field, the potential field consists of virtual forces generated by the wall which are acting Pico. These forces are applied by every measurement point of the LRF data and are in the direction as the vector from the LRF point to Pico. The value of the force is based on the distance between Pico and the point, when the distance is becoming smaller the force should be bigger (to repel Pico from the wall), the value of the force is determined by the following equation

[math]\displaystyle{ F_i = \frac{1}{r_i^5} }[/math]

with [math]\displaystyle{ F_i }[/math] the force acting on Pico due to the point [math]\displaystyle{ i }[/math] and [math]\displaystyle{ r_i }[/math] the distance between Pico and the point [math]\displaystyle{ i }[/math]. Using the summation of all these forces gives a force in the x and y direction which are used to determine a x, y and rotational velocity. To get a nice balance between these speed gain have been tuned for these speed during tests for different widths of corridors.

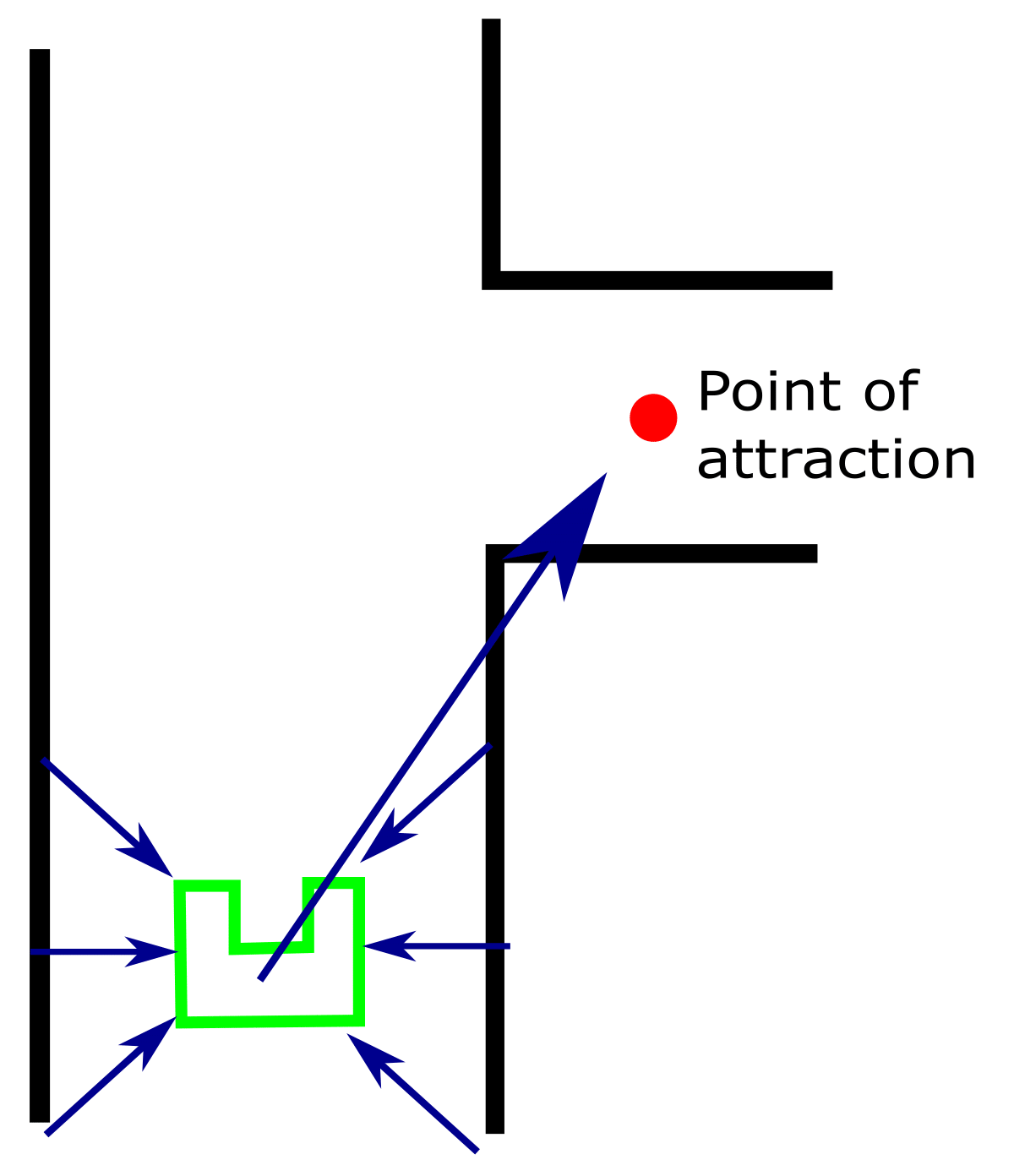
To take turns using the potential field a force of attraction is used as shown in Figure 7. This force is added to the repelling forces from the walls and thus pico will drive towards this point.

Furthermore the potential field is used as collision avoidance as well. Because when it is implemented in a good way it is impossible to drive into the wall when it is active.

Figure 7: Potential field as used to drive through the maze

Difficult Problems

Content

The final maze challenge

We won the maze challenge.

Figure 7: Design of the maze at the maze challenge

Documents

1. Initial design document (week 1): File:InitialDesignIdea - Group 4.pdf
2. Design presentation (week 4): File:Design Presentation.pdf
3. Final presentation (week 8): File:Final Presentation.pdf