Embedded Motion Control 2012 Group 5

Group Information

Name	Student number	Build
Fabien Bruning	0655273	Ubuntu 10.10 on Virtualbox in OSX 10.7
Yanick Douven	0650623	Ubuntu 10.04 dual boot with W7
Joost Groenen	0656319	Ubuntu 10.04 dual boot with W7
Luuk Mouton	0653102	Ubuntu 10.04 dual boot with W7 (Wubi)
Ramon Wijnands	0660711	Installed Ubuntu with wubi (included with the Ubuntu CD)

Planning and agreements

Planning by week

• Week 1 (April 23^th -April 29)
  • Install Ubuntu and get familiar with the operating system
• Week 2 (April 30^th - May 6^th)
  • Get the software environment up and running on the notebooks
    • ROS
    • Eclipse
    • Gazebo
  • Start with the tutorials about C++ and ROS
• Week 3 (May 7^th - May 13^th)
  • Finish the tutorials about C++ and ROS
  • Install smartsvn
  • Create a ROS package and submit it to the SVN
  • Read chapters of the book up to chapter 7
  • Make an overview of which elements of chapter 7 should be covered during the lecture
• Week 4 (May 15^th - May 20^th)
  • Make lecture slides and prepare the lecture
  • Finish the action handler
  • Finish the LRF-vision
  • Start with the strategy for the corridor competition
• Week 5 (May 21^th - May 27^th)
• Week 6 (May 28^th - June 3^rd)
• Week 7 (June 4^th - June 10^rd)
• Week 8 (June 11^th - June 17^rd)
• Week 9 (June 18^th - June 24^rd)

Agreements

• For checking out the svn and committing code, we will use Smartsvn
• Add your name to the comment when you check in
• Every Tuesday, we will work together on the project
• Every Monday, we will arrange a tutor meeting

Strategy and software description

Strategy

'Visual Status Report Because a picture is worth a thousand words.

ROS layout

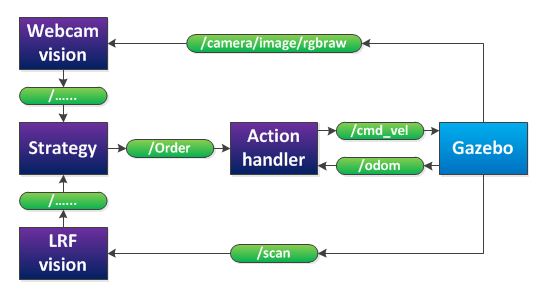
After a group discussing, we decided that our provisionally software layout will be as in the figure below.

The 'webcam vision' node processes the images, produced by the RGB-camera. It will publish if it detects an arrow and in what direction the arrow points. The 'LRF vision' node processes the data of the laser range finder. It will detect corners, crossroads and the distance to local obstacles. This will also be published to strategy. The 'strategy' node will decide, based on the webcam and LRF vision, what action should be executed (stop, drive forward, drive backward, turn left or turn right) and will publish this decision to the 'action handler' node. Finally, the 'action handler' node will send a message to the jazz-robot, based on the received task and on odometry data.

Action Handler

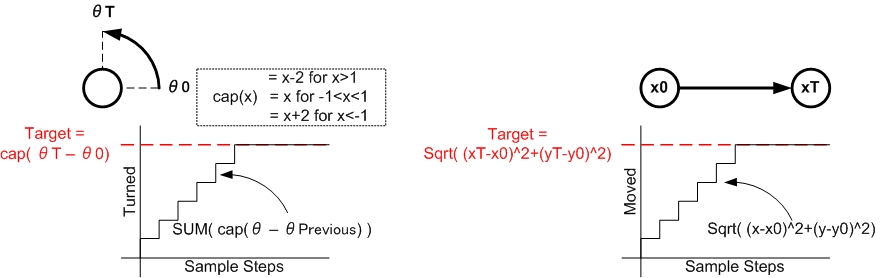
To ensure that the strategy node does not need to continuously 'spam' instructions to the actual robot, an intermediate node is installed to perform low-level actions. This node receives orders such as: "Go 1m forwards." (written as an order-amount pair) and translates them to a stream of instructions to the robot itself (over the /cmd_vel channel) which persists until the robot has travelled the desired amount. The two main difficulties with this method are the inaccuracy of the odometer data when moving and its limited range (between -1 and 1, fixed around the reference frame it pretends to know). To reduce the impact of these issues, the movement of the robot is measured relative to the point where it received the order instead of to its initial position. This procedure works as follows:

1. As soon as the order is received, the node stores the current position and heading, and the first movement order is sent out.
2. Every time the odometer data is updated, a callback is activated which determines the progress as shown in the figure below.
   1. For rotation, the change in angle is determined by finding the smallest distance between the current and previous angle. This change is added to the total change.
   2. For lateral movement, the absolute distance between the current and initial point is measured.
3. If the change in angle or lateral movement exceeds the original target value, the node goes back to its default state and the robot stops moving.

Also, LRF data can be mixed with odometer data via a ROS package (laser_scanner_matching) to improve accuracy. Since a well documented ROS package called the "Laser Scan Matcher" is available, we opted to use this instead of developing our own algorithm. The package is largely based on the work by Andrea Censi, described in his paper 'An ICP variant using a point-to-line metric" (2008). It basically works as follows:

1. At time [math]\displaystyle{ k }[/math], the laser scanner measures a set of points [math]\displaystyle{ p }[/math].
2. At time [math]\displaystyle{ k+1 }[/math], the laser scanner measures a set of points [math]\displaystyle{ p_{k+1} }[/math]. This set of points is presumed to be the same set of points translated and rotated by an operator [math]\displaystyle{ q }[/math].
3. A minimization of the error between [math]\displaystyle{ p_{k+1} }[/math] operated on by operator [math]\displaystyle{ q }[/math] is now performed, which yields [math]\displaystyle{ q_{k+1} }[/math]

Of course, the new set of points does not exactly match the original set of points exactly and the data is noisy. The paper deals with a multitude of tricks to make the algorithm perform up to spec.

LRF vision

The Laser Range Finder of the Jazz robot is simulated in the jazz_simulater with 180 angle increments from -130 to 130 degrees. The range is 0.08 to 10.0 meters, with a resolution of 1 cm and an update rate of 20 Hz. The topic is /scan and is of the type sensor_msgs::LaserScan. The data is clipped at 9.8 meters, and the first and last 7 points are discarded, since these data points lie on the jazz robot.

The LRF data can be processed in multiple ways. Since it not exactly clear what the GMapping algorithm (implemented in ROS) does, we decided to write our own mapping algorithm. But first the LRF needs to be interpreted. Therefore, a class is created that receives LRF data and fits lines through the data. The fitting of lines can be done in two ways; a hough transform and a fanciful algorithm.

Hough transform

A hough transform interprets the data points of the LRF in a different way; each point in x-y-space can be seen as a point through which a line can be drawn. This line will be of the form [math]\displaystyle{ y=ax+b }[/math], but can also be parametrized in polar coordinates. The parameter [math]\displaystyle{ r }[/math] represents the distance between the line and the origin, while [math]\displaystyle{ \theta }[/math] is the angle of the vector from the origin to this closest point. Using this parameterization, the equation of the line can be written as

[math]\displaystyle{ y = \left(-{\cos\theta\over\sin\theta}\right)x + \left({r\over{\sin\theta}}\right) }[/math]

So for an arbitrary point on the image plane with coordinates ([math]\displaystyle{ x_0 }[/math], [math]\displaystyle{ y_0 }[/math]), the lines that go through it are the pairs ([math]\displaystyle{ r }[/math],[math]\displaystyle{ \theta }[/math]) with

[math]\displaystyle{ r(\theta) =x_0\cdot\cos \theta+y_0\cdot\sin \theta }[/math]

Now a grid can be created for [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ r }[/math], in which all pairs ([math]\displaystyle{ r }[/math],[math]\displaystyle{ \theta }[/math]) are drawn. Now a 3D surface is created that shows peaks for the combinations of [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ r }[/math] that are good fits for lines in the LRF data.

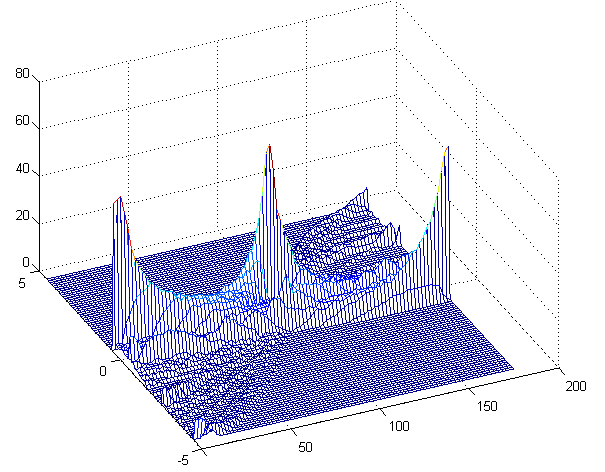
In the figure on the right this transform has been performed on the LRF data. Several peaks can be seen that represent walls. The difficulty with this transform is the selection of the right peaks. This can be solved by using some image processing and some general knowledge on the LRF data. This method will however not be used by our group but it is kept in mind in case the fanciful algorithm fails.

Another drawback of this method is that holes in the wall are difficult to detect, since the line is parametrized with [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ r }[/math] and has therefore no beginning or end. This problem can be fixed by mapping all data points to the closest line and snipping the line in smaller pieces. An advantage is that a Hough transform is very robust, and can handle noisy data.

Fanciful algorithm

We thought of an own algorithm for line detection as well. Since the data is presented to the /scan topic in array of points with increasing angle, the points can be checked individually if they contribute to a line. A pseudocode version of the algorithm looks as follows:

create a line between point 1 and point 2 of the LRF data (LINE class)
loop over all data points
   l = current line
   p = current point
   if perpendicular distance between l and p < [math]\displaystyle{ \sigma }[/math] AND angle between l and p < 33 degrees AND dist(endpoint of l, a) < 40 cm
     // point is good and can be added to the line
     then add point to line
     else false_points_counter++
  end

  if false_points_counter > 3
    then end the line
         decrease the data point index with 3
         create a new line with the first two points
         increase the line index with 1
  end
end loop

LRF processed data

The output of the line detection algorithm is published on /lines, and the map-node is subscribed to this topic.

Webcam vision

RGB image

Color segmented image

Line detection

Corner detection

Detected arrow

The images that are captured by Jazz's webcam, can be used to detect the arrows that will point him in the right direction. This section will describe the progress of the development of the Webcam vision node.

In the RGB colorspace, there are three channels (red, green and blue) that determine the color of a pixel. To detect red pixels, this does not give very large problems since it has it's own color channel in the RGB colorspace. However, it is easier to use the HSV colorspace (hue, saturation and value), where the color is only described by the hue, where the saturation and value determine how bright a pixel is. This makes it easier to describe which section of the colorspace is accepted as red. Therefore, the first step in the image processing is to convert the RGB image to the HSV colorspace. Using the openCV library makes this an easy task, using the cvCvtColor() function. For testing purposes, we used a webcam image that is loaded with cvLoadImage() (An example is given above in the first picture). This creates an image object in which the order of the channels is BGR instead of RGB. Therefore, the conversion is BGR to HSV instead of RGB to HSV.

IplImage *rgbImg, *hsvImg;
 
rgbImg = cvLoadImage("arrow2.jpg",CV_LOAD_IMAGE_COLOR);
hsvImg = cvCreateImage(cvGetSize(rgbImg), IPL_DEPTH_8U, 3 );
 
cvCvtColor(rgbImg, hsvImg, CV_BGR2HSV);

Since HSV data is available now, we can determine for each pixel it is red or not. This segmentation leads to a binary image that is displayed in color segmented image which is shown above. To reduce noise in the image and to sharpen the corners of the arrow, an erosion filter (cvErode()) is applied twice with a 3x3 pixels structuring element. Moreover, a canny algorithm (cvCanny()) is used to detect the bounding lines of the arrow. The result of this filtering is shown in the third figure: 'Line detection' .

The next step in the arrow detection process is to detect the seven corners that determine the shape of the arrow. This is done by calling another openCV function: cvGoodFeaturesToTrack()

// Create temporary images required by cvGoodFeaturesToTrack 
IplImage* imgTemp = cvCreateImage(cvGetSize(rgbImg), 32, 1); 
IplImage* imgEigen = cvCreateImage(cvGetSize(rgbImg), 32, 1);
 
// Create array to store corners 
int count = 15; 
CvPoint2D32f* corners = new CvPoint2D32f[count];
 
// Find corners 
cvGoodFeaturesToTrack(binImg, imgEigen, imgTemp, corners, &count, 0.1, 20);

This functions detects up to 15 corners in the image, depending on how accurate the image is. In the most optimal situation, only seven corners will be returned. Applying this algorithm leads to the fourth image shown above, where the detected corners are superimposed on the RGB-image.

With these corners available, the last step in the arrow detection algorithm can be executed. By looping over the corners, the highest and lowest corner can be found, with these two points, the perpendicular bisector of these points can be constructed. The blue line in the last picture represents this line. In the most ideal case, the tip of the arrow would be exactly located at this line. Therefore, the corners that located at minimal distance from this bisector, is expected to be the tip of the arrow. If this corners is located left with respect to the average of the points that construct the bisector, the arrow points to left. In the contrary case, the arrow points right.

The algorithm to detect arrows is still work in progress. The following issues still have to be dealt with:

• Robustness of color segmentation
• Robustness of corners detection
• Detection of smaller arrows
• Check if indeed an arrow is seen or only noise

Node-based Mapping

Storing the entire maze as a series of points (or even lines) consumes a lot of space; therefore it makes sense to store the known map of the world in a smaller format. One way to do this is by storing all of the junctions, corners, and endpoints as a set of nodes that keep track of the directions in which the robot can travel when it stands on one of them. Including the approximate distance to the next node for each direction is not required, but may help to prevent duplicate points after looping around or otherwise ending up at the same spot twice. Arrows or other ‘clues’ can easily be included by removing or adding paths as instructed.

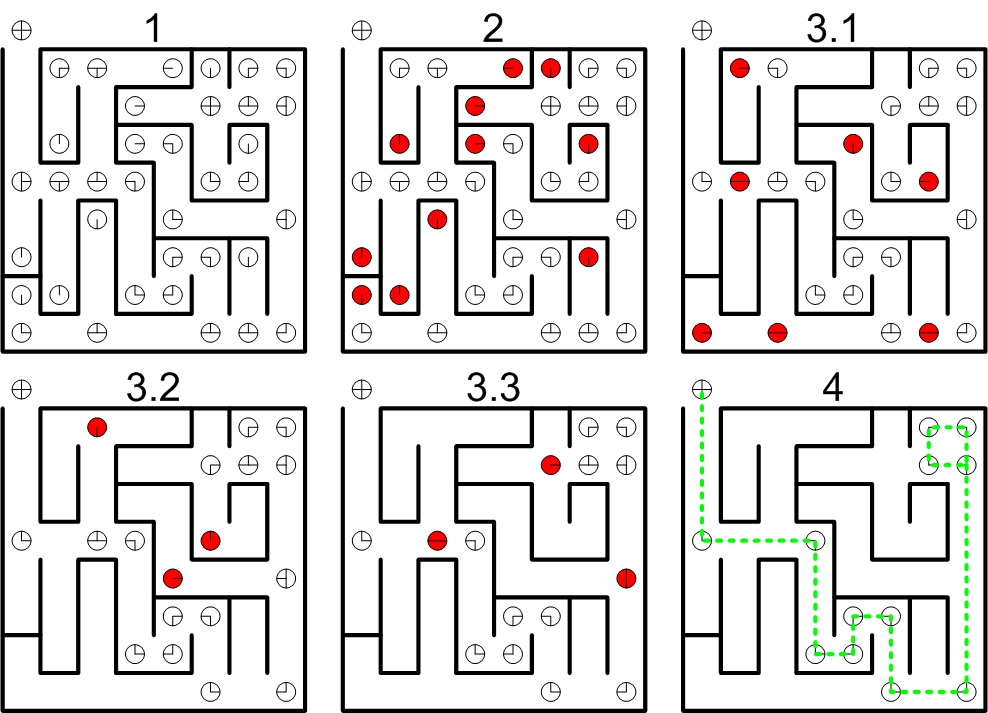
Node-based Known Maze Solving When the maze is known in nodular form, solving it becomes a trivial matter. The following procedure is demonstrated in the figure below.

1. The maze is stored as a set of corner points, each with one to four directions of possible travel. The robot starts in the upper-right corner and needs to reach the exit in the upper-left.
2. All nodes from which the robot can travel in only one direction are obviously dead ends.
3. The dead ends are removed (with the possible exception of the robot’s starting position), after which the remaining nodes are updated. Because of this, further nodes will now become dead ends or straight paths. These are removed in turn and the process repeats until no more nodes are removed.
4. The only remaining nodes are now the ones that lead from the robot’s initial position to the end of the maze.

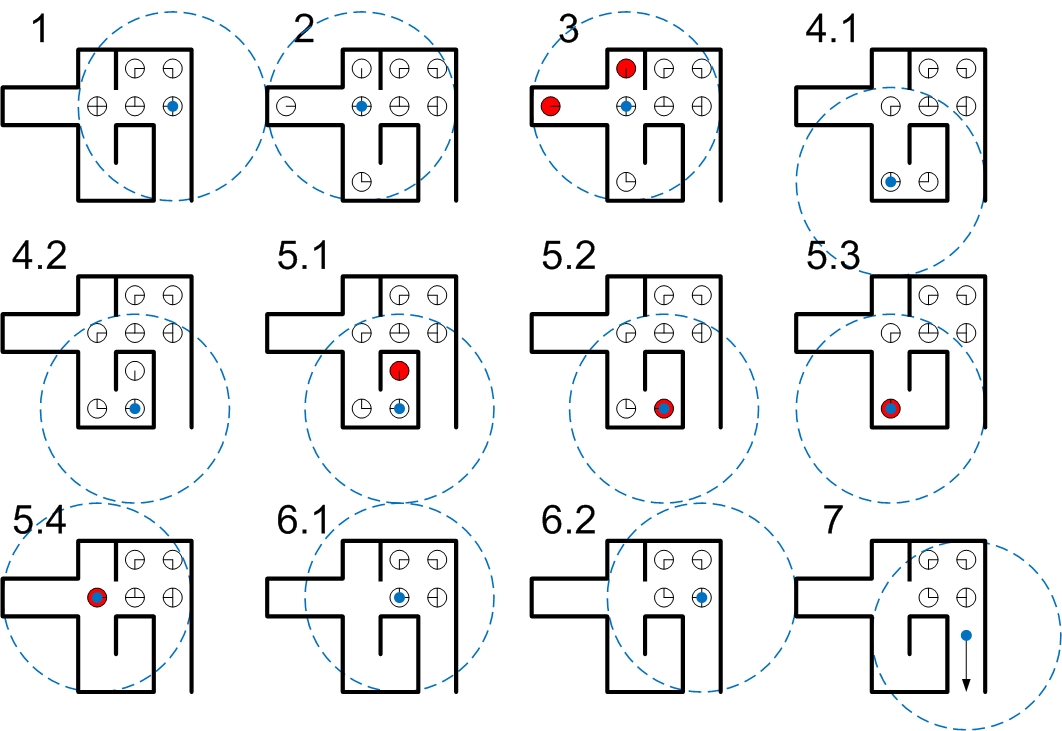
Node-based Unknown Maze Solving More interesting for the project is the scenario in which the maze is not yet known. This too can be solved using a node-based approach, as demonstrated here. In the image below, the blue dot represents the robot, and the surrounding circle the limit of its sensors.

1. The robot begins and creates nodes for the area it can detect.
2. It moves to the node which currently contains the most paths leading into the unknown (whilst avoiding immediate backtracking in case of ties) and updates its map.
3. Dead ends are detected and removed as in the scenario with a known maze.
4. The robot progresses deeper down its chosen path.
5. Eventually, a dead end is reached which is eliminated. This in turn causes the node the robot is currently on to become a dead end. The robot moves back through the only possible path and then removes this new dead end. This procedure repeats as required.
6. Upon returning to a node that does not have to be removed, the robot once again determines the node with the most paths leading into the unknown and moves to that node.
7. The robot continues through the maze until it eventually reaches the exit…