Mobile Robot Control 2024 HAL-9000
Group members:
| Name | student ID |
|---|---|
| Salim Achaoui | 1502670 |
| Luis Ponce Pacheco | 2109417 |
| Nienke van Hemmen | 1459570 |
| Mohamed Elbehery | 1035058 |
| Aniek Wigman | 1463535 |
| Max Hage | 1246704 |
| Max van der Donk | 1241769 |
Exercise 1: Non-crashing robot
For the first exercise, the goal was to ensure that the robot does not move through walls in the simulation and not crash into the walls in both the simulation and the real world. To solve this matter, there were multiple solutions. The first solution collects all of the data from the lasers and stops the robot when it reaches a wall. A second solution also uses this notion but instead of stopping the robot, the robot turns away from the wall. These solutions were then tested on the robot in real life. After testing, it became clear that, although stopping the robot was not an issue, the robot was not able to move along a wall in parallel. This issue occurred since the sensor data was taken uniformly. So on all sides, the robot would stop with the same threshold. Therefore, a third solution was made that took the orientation of the sensor data into account for the robot to move alongside a wall. The details of the solutions will now be covered in more detail.
Solution 1
For the first solution, we utilize the laser data that the robot has. This contains data as to how far a wall or object is to the robot at a certain angle. For each angle, we check whether the robot is too close to an obstacle, thus within range x. If it is, it stops moving. Else, it keeps on going forward.
Solution 2
For the second solution, the first solution was expanded. Instead of just stopping, the robot now rotates until no obstacle is close to the robot anymore, and it moves forward again.
Solution 3
This solution is also an expansion of solution 1. In this expansion, the size of the robot is taken into account aswell. This solution was created after testing the robot physically. We came to the realisation that the size of the robot is not taken into account. Therefore, in the script an offset was included such that the body of the robot does not bump into the wall. using the line: scan.ranges[i] < minDist + robotWidth*abs(sin(currentAngle) we introduce an offset by adding the sinusoid of the current angle, which is approximately the circular body of the robot. Because the laser of the robot is approximately in the middle of its body, the sinusoid creates a proper offset to not bump into a wall anymore.
For local navigation, 2 different solutions had to be introduced for the restaurant scenario. We have chosen for artificial potential fields and vector field histograms because these solutions seemed the most robust to us. In this parahraph the 2 solutions will be explained.
Artificial potential fields
Artificial potential fields are self-explanatory: they portray the potential fields around an object. A field can either be repulsive or attractive. The reason for being artificial is because these fields do not exist in the real world. In the real world, an object does not push the robot away or pull the robot towards it. In a simulation, however, artificial potential fields can be drawn such that a robot avoids certain objects and gravitates toward others. In this particular case, the robot is drawn towards the goal and repulsed by obstacles that are in its way. The distance between the robot and the goal or obstacle dictates the strength of the field around it. When an obstacle is close, for example, the repulsion force should be higher than the attraction force and high enough to repulse the robot away from the obstacle. This dependency on distance can be seen in the formulas for the two fields. For the implementation the following source was used [1]
The artificial attraction potential is dependent on an attraction constand and the distance between the robot and the goal.
[math]\displaystyle{ U_{\text{att}}(x) = \frac{1}{2} k_{\text{attr}} \rho^2 (X, X_g) }[/math]
With the following:
- [math]\displaystyle{ K }[/math]: positive scaling factor.
- [math]\displaystyle{ X }[/math]: position of the robot.
- [math]\displaystyle{ X_g }[/math]: goal of the robot.
- [math]\displaystyle{ \rho(X, X_g) = \| X_g - X \| }[/math]: distance from robot to goal.
This is used in super position with the repulsion field created with the following formulas:
[math]\displaystyle{ U_{\text{att}}(x) = \frac{1}{2} k \rho^2 (X, X_g) }[/math]
The repulsive potential field is described by:
[math]\displaystyle{ U_{\text{rep}}(X) = \begin{cases} \frac{1}{2} \eta \left( \frac{1}{\rho(X, X_0)} - \frac{1}{\rho_0} \right)^2 & \text{if } \rho(X, X_0) \leq \rho_0 \\ 0 & \text{if } \rho(X, X_0) \gt \rho_0 \end{cases} }[/math]
- [math]\displaystyle{ \eta \gt 0 }[/math]: positive scaling factor.
- [math]\displaystyle{ \rho(X, X_0) }[/math]: the minimum distance (robot and obstacles).
- [math]\displaystyle{ \rho_0 }[/math]: distance influence imposed by obstacles; its value depends on the condition of the obstacle and the goal point of the robot, and is usually less than half the distances between the obstacles or shortest length from the destination to the obstacles.
Using these formulas the following artificial potential fields were created for all maps.
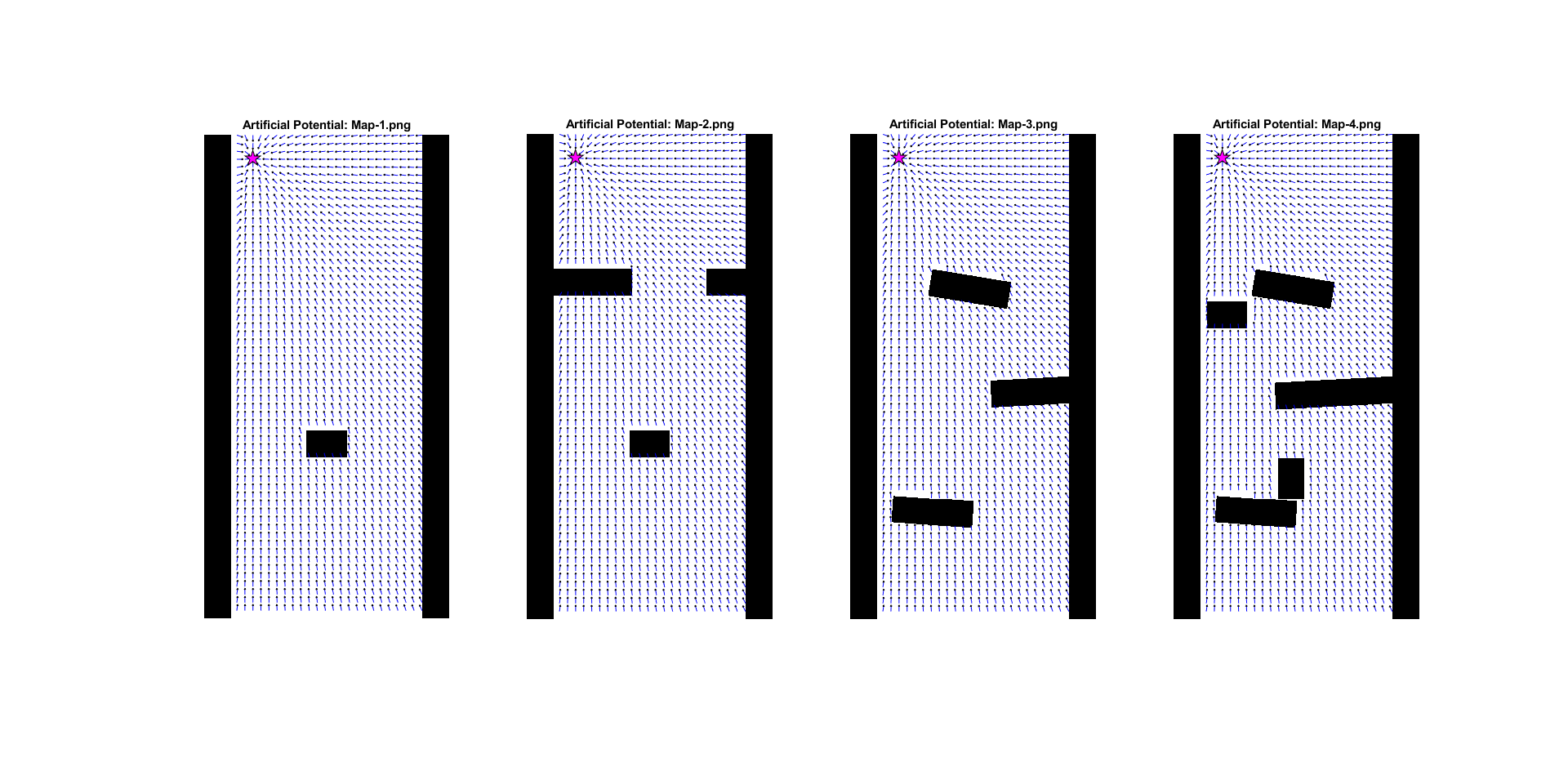
From this figure the weakness of the artificial potential method becomes apperent the 'local minimum'problem. There are methods to try and deal with them but this is a fundemental problem with the technique.
For the implementation not U is used but F to drive the robot into the direction of the of the potential: The attractive potential field function is described by:
[math]\displaystyle{ F_{\text{att}} = - \nabla [U_{\text{att}}(X)] = - k \rho (X, X_g) }[/math]
The repulsive force field is described by:
[math]\displaystyle{ F_{\text{rep}} = \nabla [U_{\text{rep}}(X)] }[/math]
<math> F_{\text{rep}}(X) = \begin{cases} \eta \left( \frac{1}{\rho(X, X_0)} - \frac{1}{\rho_0} \right) \frac{1}{\rho^2(X, X_0)} \hat{\rho}(X
Vector field histogram
*insert explanation for how this method works*
for vector field histograms, 2 major components had to be created. Firstly, the translation from the laser data to a map that contains the coordinates of the obstacles together with a certainty value and a polar histogram, from which a minima should be chosen as direction to continue moving.
Obstacle map
Polar Histogram
- ↑ Matoui, F., Naceur, A. M., & Boussaid, B. (2015). Local minimum solution for the potential field method in multiple robot motion planning task. Conference Paper presented at the 2015 IEEE/ACIS 14th International Conference on Computer and Information Science (ICIS). doi:10.1109/STA.2015.7505223. Retrieved from [ResearchGate](https://www.researchgate.net/publication/307799899).