Embedded Motion Control 2013 Group 11
Group Members
| Name: | Student id: | Email: |
| Justin Wildschut | 0617495 | j.a.wildschut@student.tue.nl |
| Jeroen Zegers | 0638172 | j.c.zegers@student.tue.nl |
| Alex Andriën | 0652965 | a.r.p.andrien@student.tue.nl |
| Talha Ali Arslan | 0867550 | talhaaliarslan@gmail.com |
| Leroy Hazeleger | 0651762 | l.hazeleger@student.tue.nl |
Discussion and Possible Solutions
Program Structure
We designed a program structure to divide the tasks, make the program more transparant and easier to debug. The program is divided in the following nodes, of which the workings are explained below:

The nodes and topics are described in the following document: File:EMC Main.pdf
Smoothing Node
Here, the raw laser data is smoothened using a moving average. This is done by averaging each value from the laserscanner with its neighbours, which leads to data with less noise in it, which is sent to the Averaging node.
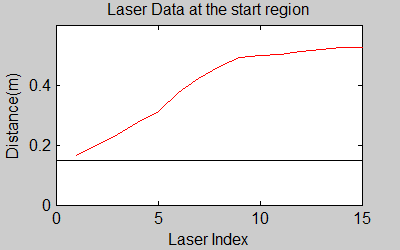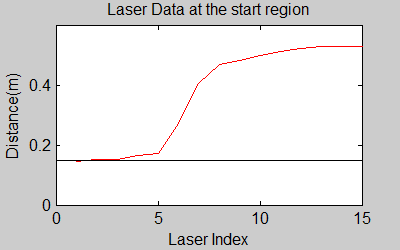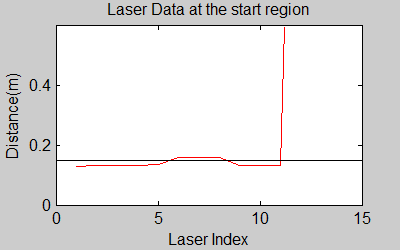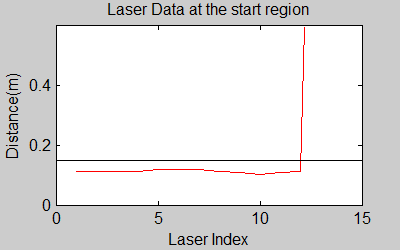
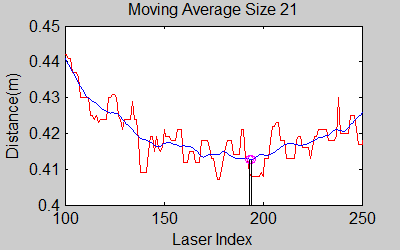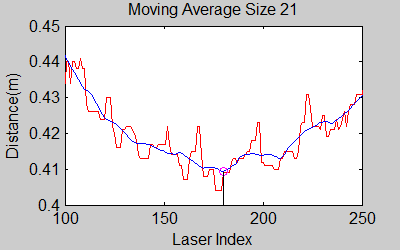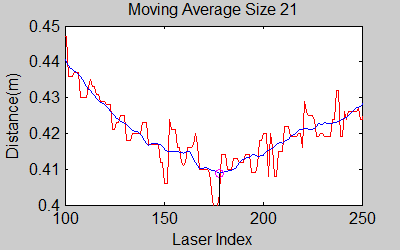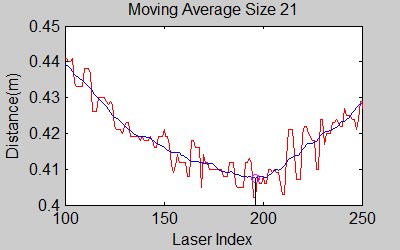

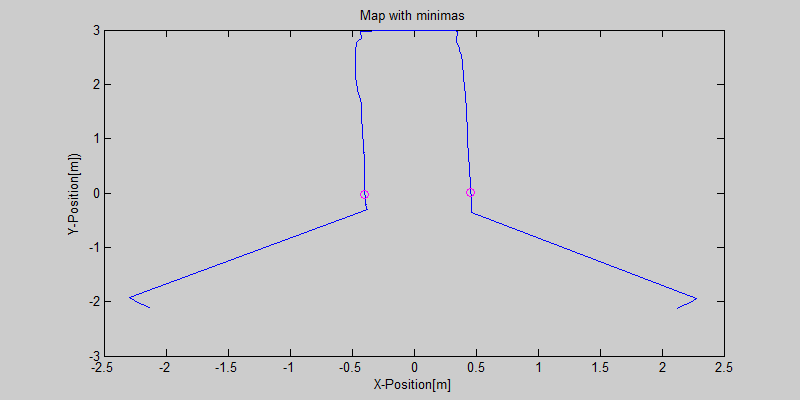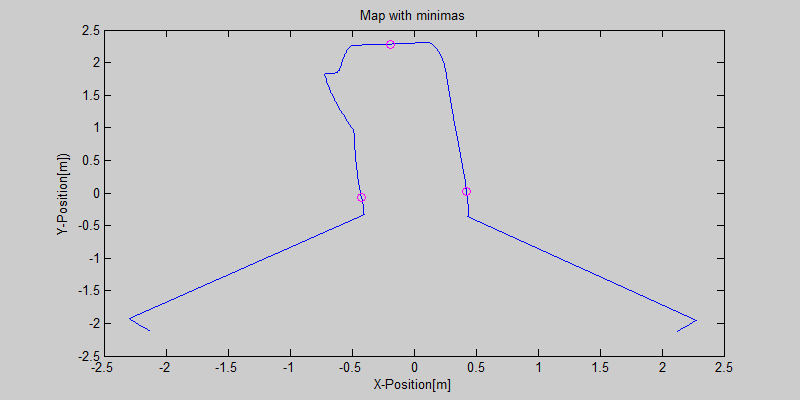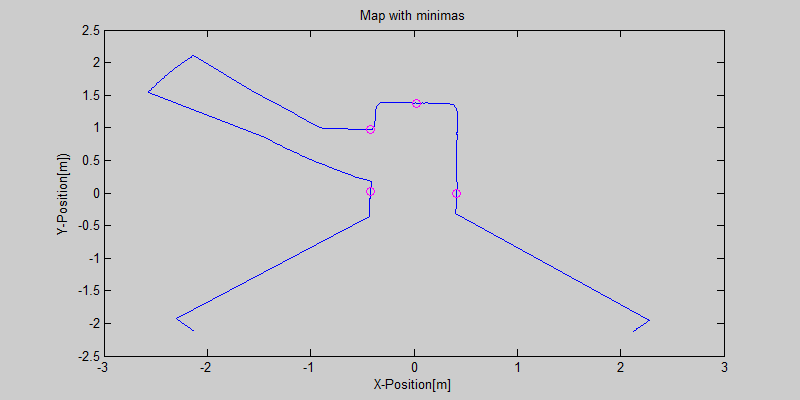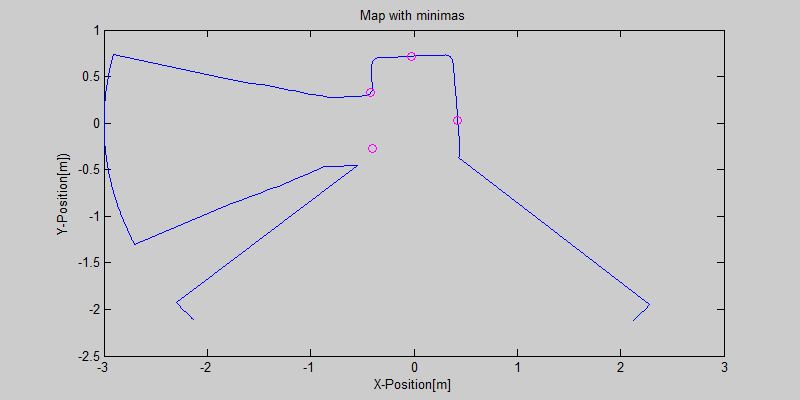
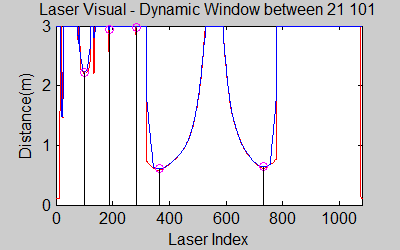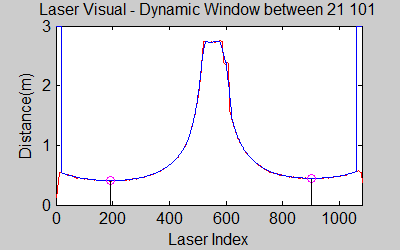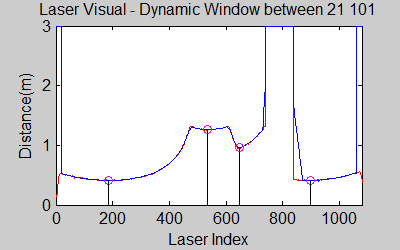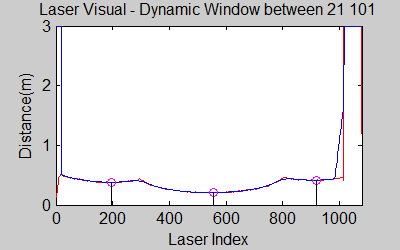
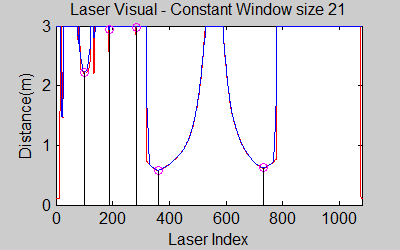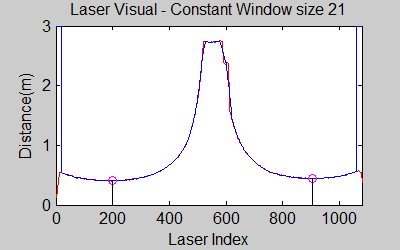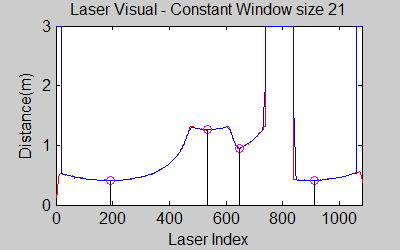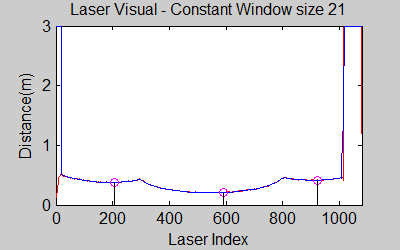
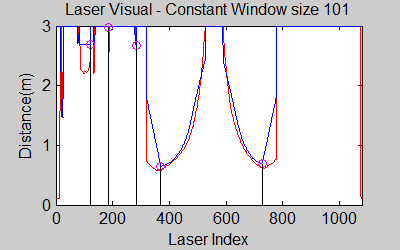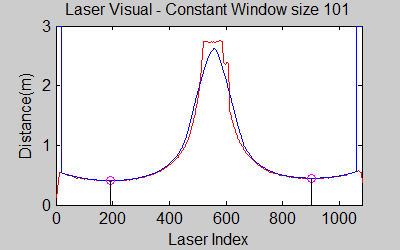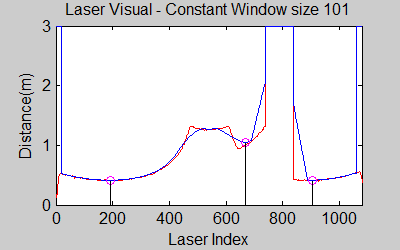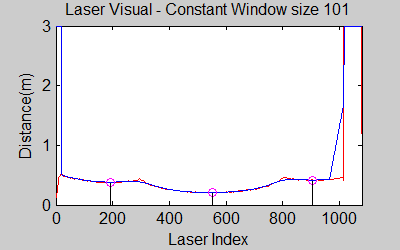
The smoothing is done by applying the moving average method in a variable window size. In this method, moving average at every index is calculated by taking the sum of 'window size' number of elements to the left and right (combined) of that point and dividing it by the window size (i.e. if the window size is 21, 10 points to the back, 10 points to the front and the current point is taken into account). We first started with a constant window size, but there were problems. Because the resolution of laser readings is high over small portions at close distances and low over large portions at large distances, we had to adjust the moving average window size accordingly. In these gifs on the upper left and center, you will see what happens if we use a small and large window size at close distances (Look at with small window size how the minima index changes rapidly and how smoothened the data is, and at large window size, look at how the data is smoothened and there not that much rapid change in minima location as with smaller window size, but there is still movement and this will be overcome in the next node 'Averaging Node').
One of the first assumptions was that the laser data below a magnitude of 0.15 m is due to the body of the robot. This is only correct for large distances. In the simulation this holds everywhere but in the real world, we discovered that at close distances first indices of the laser read distances 'between' the actual distance and 0; they look like an interpolation between 0 and those distances and we do not know why this happens; we guess that it may be due to the white shiny surface of the robot case that beams can reflect and be effective at close distances or it may just be a bug of the laser. So; because we depend our smoothing of laser data and determination of local minimum and maximum distances based on these start and finish indices, we should no longer use a dynamic start index and based on real world testing, we should constantly avoid first and last (~approximately) 20 indices which are around 18 in the simulation. We can increase these values based on readings (if a reading below 0.15m still comes after 20th index, we may shift starting index to that value but it should never be below 20). This gif file on the upper right shows the phenomena; where at first the distance to the wall is close, and when the distance increases the problematic readings goes below the line of 0.15 m (black) which was our previous assumption.
The gif pictures below show the whole data and the effect of window size on smoothing. Basically it is seen that with small window size, the smoothened data resembles the original more (not oversmoothened) but at close distances location changes too rapidly and even multiple maximas are found close to each other in some instances. Using a larger window size gives advantage at close distances and flat surfaces, but you can see in the middle gif that data is over smoothened and some corners to the sides are dislocated too much. Below right show a dynamical window result, at distances above a certain distance constand window size is used but between a preferred distance region, window size is proportionally changed between 21 and 101 in this case. Using a very large window size is also not preferable because it increases computation time. Because we use dynamical window, we cannot use a moving array which would solve that problem actually.
How the local minimum values are found is explained in the 'DeterminePosition Node' part.
Averaging Node
In contrary to the Smoothing node, which averages over all the laser data from a single time instance, this node averages the already smoothened data over several time steps. This is necessary because if there is a disturbance in a single timestep (a large dust particle in front of the laser for instance), we don't want the program to detect things that aren't there. The Averaging reduces the effect of such disturbances. The smoothened, averaged data is then sent to the Determine Position node.
In the visuals above, one can see that averaging helps reduce the oscillation of the minimas.
Determine Position Node
Here, the smoothened and averaged data is analysed. The minima and maxima of the laser data are determined, as well as their corresponding indices. This data is sent to the Detect Crossing node.
In this node, every data point from the Averaging node is checked according to its distance and index, relative to the other points within a constant window, where the current point is in the center. Also local maximas or minimas next to each other who have same distances are avoided and only one is taken into account, because from the smoothened and averaged data, there can be points next to or close to each other with same distance value.
Result of this node can be seen in the gif pictures in 'Smoothing Node' and 'Averaging Node' where local minimas are plotted with a circle and a vertical line.
Detect Crossing Node
As is presented in the program structure above there is a node which detects the crossings in the maze. This node detects at which moment Pico is at the middle of a cross-section and if there is a side-path on its left and/or right and/or a path in front. These different type of cross-sections are detected using the positions of the minima in the laser-data. The positions of these minima are found in the 'Determine Position' node and send via a topic to this 'Detect Crossing' node. The principle of this function is illustrated using the pictures below.
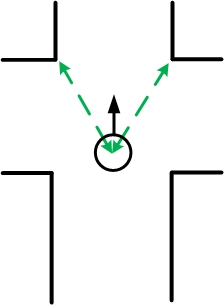
Suppose the robot approaches a T-crossing like in the picture below and that we want the robot to go left.

The left picture above shows the moment at which Pico arrives at the middle of an intersection. If two minima are within the red area's we know that the robot is approximately in the middle of the T-crossing (assuming that the width of the corridor and the side-path are approximately equal). The 'Detect Crossing' node will give a message to the 'Decision Making' node that it is in the center of an intersection and which options there are to take (left, straight or back). If the 'Decision Making' node decides to make a turn left, the robot will turn left untill the minima are in the regions as is depicted in the right picture above, The detect crossing sends a message to the 'Decision Making' node when the minima are in these regions and thus the turn in made.
For other types of intersections, the node will search for minima in different combinations. Each type of intersection has its own configuration of minima.
Decision Making Node
The structure of this node can best be explained using a program flow diagram as depicted below.
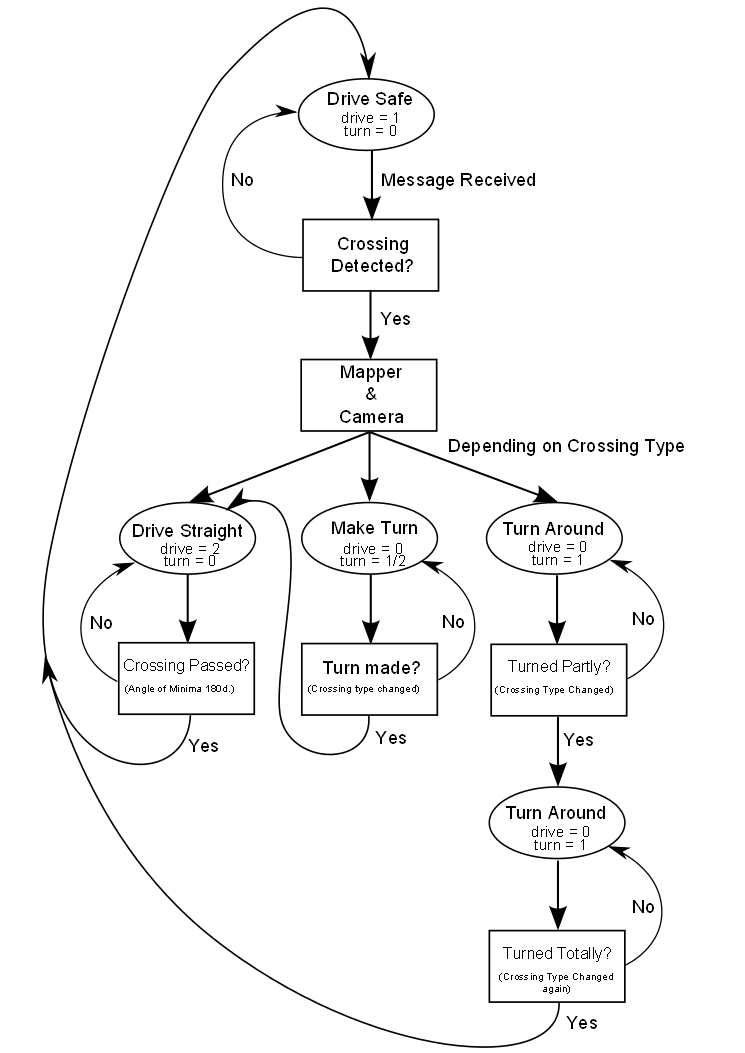
Mapper
Mapper helps the robot remember its options and its way back from dead ends; it will be explained in detail, later.
Drive Safe Node
The Drive Safe node makes sure that PICO drives safely throughout the whole maze. This means that PICO drives safely between walls so that it does not hit a wall and drives optimally through the pathway, it detects when it is entering a crossing and drives safely and straight to the middle of the crossing, and after PICO made the correct turn it exits the crossing safely and straight. After it exits the crossing, it continues to drive safely between walls.
The Drive Safe node is divided into four states: Normal Driving, Enter Crossing, Exit Crossing and Safety Driving. The Decision Making node determines if the Drive Safe node should be in the Normal Driving state,in the Exit Crossing state or PICO should do nothing. It publishes a Drive message of 1 if PICO should drive safely between walls (Normal Driving state), publishes a Drive message of 2 if PICO exits a crossing (Exit Crossing state) or publishes a Drive message of 0 if PICO should stop moving so that a turn can be made. Within the Drive Safe node, it is determined if PICO is actually between walls (Normal Driving state, Drive message 1), enters a crossing (Enter Crossing state, Drive message 1) or perform a ` special' maneuver to prevent collision (Safety Driving, Drive message 1). To determine the state in which PICO is, the message published by the Determine Position node is used which tells us where the minimum distances to the wall are located (index between 0 - 1081) and provides the distance to that minimum. Since we are interested only in the local minima, i.e. minima below a certain threshold, only the minimum distances below the threshold are considered in the Drive Safe node. Below, the different parts are explained in more detail.
Note that all thresholds are tuned during the real-time experiments
Normal Driving
PICO is in the `Normal Driving' mode if PICO is located between walls. In order for PICO to take the turns correctly, PICO should remain approximately in the middle of the path with its forward position parallel to the walls before it will be in the `Enter Crossing' mode. To determine when PICO is located between walls, we know that there are at least two minima which are approximately 180 degrees apart (approximately since the noise disturbs the Determine Position node). If those two minima are indeed approximately 180 degrees apart PICO is between walls, and if this is not the case (the angle between the two minima differs to much with a certain threshold) PICO enters a crossing. Also if one of the minima becomes to small, PICO goes into the Safety Driving node.
The two minima (index and distance, indicated by the red lines) are used to determine the width of the path (orange line), the position from the middle of the path (difference between the green and blue line, left from the blue line is negative) and the angle between the forward position and the right wall and the left wall (purple lines). Those are depicted in the figure below.
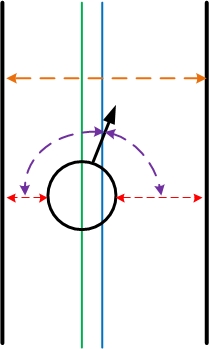
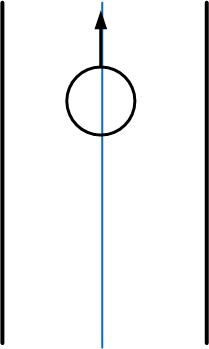
The width of the path is determined by summation of the distances of the two minima.
[math]\displaystyle{ \frac{}{}widthPath = distance_{left} + distance_{right} }[/math]
The position from the middle of the path is determined by dividing the width of the path by 2 and subtracting the distance to the right minimum.
[math]\displaystyle{ posFromMiddle = \frac{widthPath}{2} - distance_{right} }[/math]
Using the minimum angle and the angle increment, the angles of the two minima [math]\displaystyle{ \theta_{left} }[/math] and [math]\displaystyle{ \theta_{right} }[/math] are determined.
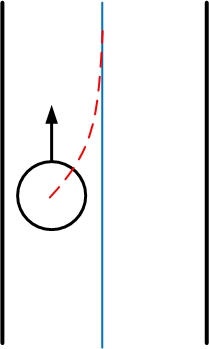
What we want is that PICO drives in the middle of the path and if not, it drives optimally to the middle of the path. Therefore we would like PICO to drive to the middle of the path by following a exponential decay towards to middle of the path. The exponent decay is shown by the red line in the figure above.
[math]\displaystyle{ \frac{}{}posFromMiddle(t) = posFromMiddle_{int} * e^{\beta t} }[/math]
Since we can only control the linear and angular velocity, the slope of the exponent in each point is determined
[math]\displaystyle{ \frac{d}{dt}posFromMiddle(t) = \beta * posFromMiddle_{int} * e^{\beta t} }[/math]
and from this exponent the desired netto angle of PICO is determined.
[math]\displaystyle{ \theta_{desired} = sin(\frac{\beta*posFromMiddle}{\sqrt{1+\beta^2*posFromMiddle^2}}) }[/math]
The actual netto angle is determined using the following equation
[math]\displaystyle{ nettoAngle = \frac{\theta_{left} + \theta_{right}}{2} }[/math]
The angular velocity is then calculated is the actual netto angle minus this desired netto angle and multiplied with a constant, resulting in an exponential decay towards the middle of the path.
[math]\displaystyle{ \frac{d}{dt}\theta_{z} = constant*(nettoAngle - nettoAngleDesired) }[/math]
Of course [math]\displaystyle{ \beta }[/math] can be chosen very high so that PICO returns quickly to the middle of the path, however from real-time experiments was observed that PICO has an overshoot due to a certain delay. Therefore [math]\displaystyle{ \beta }[/math] and the constant are tuned so that PICO moves to the middle of the path without oscillating around the middle.
Entering Crossing
When the two minima do not make an angle of approximately 180 degrees and PICO was in the Normal Driving state before, PICO enters a crossing. From the location of the different minima that are observed can be determined what type of crossing it enters.
T-crossing, left turn or right turn
If there is one minimum detected approximately at index 540 (within the threshold of course), we know that there is a wall in front of PICO. The only thing we want is that PICO drives towards this minimum so that drives straight into the crossing and can detect a crossing accurately using the DetectCrossing node. So the angular velocity is adapted so that the minimum will be detected around index 540 the whole time. The figures below show the different crossing when it should go to the minimum at index 540. So we correct the angle of PICO, for instance if the minima is at index 580, we know that PICO is oriented to the left, and we give it an angular velocity to the right.
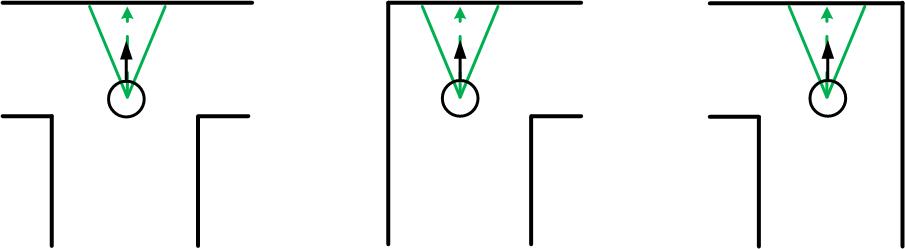
Left turn or right turn with a straight path
If there is no minimum approximately at index 540, and if there is one minimum detected approximately at index 180 (right), or one minimum detected approximately at index 900 (left) and not both at the same time of course otherwise we are between walls, then we know that PICO enters a crossing where you can turn right or straight and respectively left or straight. Since the width of the path can not be measured in the crossing, the old width of the path is remembered and the same strategy is used as in the Normal Driving state to drive to the middle of the path and to drive straight with respect to the wall (right or left).
Three-way crossing
If the T-crossing, left turn, right turn, left turn or right turn with a straight path do not occur, then PICO enters a three-way crossing. Now we need to use the two minima which are in front of PICO but the number of minima can vary between 2, 3 or 4 minima in the threshold. Also the index of two minima in front of PICO will change when PICO enters the crossing. Therefore, depending on the number of minima in the threshold, the right minima are selected and the angular velocity is changed such that the distances to these minima become equal. So if the left minima of the two is further away than the right minima, then PICO should be oriented to the left and should drive forward.
Exiting Crossing
When PICO is entering a crossing, a Drive message of 1 is published by the Decision Making node. At a certain point, the Detect Crossing node detects a crossing and the Decision Making node publishes a Drive message of 0 and PICO is will make a turn accordingly. During the Drive message of 0, PICO does not drive, and only turns. When the turn is finished, a new Drive message of 2 is published by the Decision Node and PICO is in the Exit Crossing state.
In the Exit Crossing state, the same method as in the Enter Crossing state could have been applied. However the problem with that is that when PICO turns, the width of the new path it will enter can be different from the path it came from and is unknown. Also the position from the middle is unknown and therefore the algorithm as used previously cannot be used. It can only be used if it is guaranteed that the width of the new path is equal to the old width of the path.
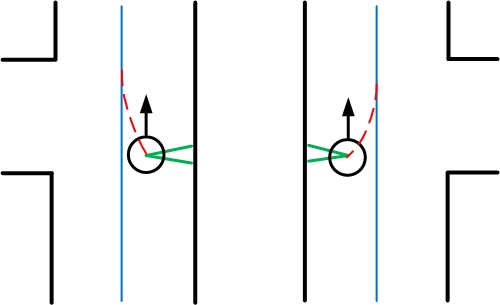
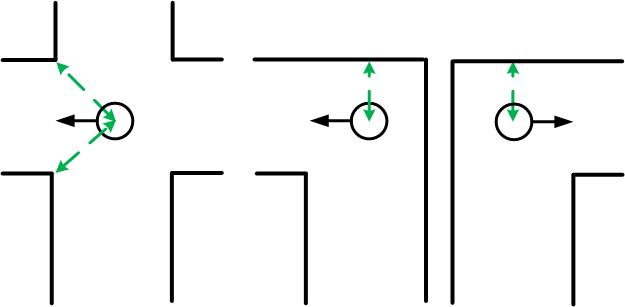
When PICO made the turn, three different situations can occur: a left + straight crossing can be seen, a right + straight crossing can be seen, or a three-way crossing can be seen. These are given in the figures below. The Detect Crossing node made sure that PICO stopped in approximately the middle of the intersection. Therefore what we like to have is that PICO moves straight into the new path, but due to the turn it made, the back wheels are orientated perpendicular to the new driving direction. Therefore we need a new control strategy which corrects PICO if it does not move straight into the new path. Depending on the minima it detects, the different situations occur and have different strategies. If a left + straight crossing can be seen when PICO made a left turn, PICO should follow the right wall since at index 180 a minimum will be seen. By keeping the index of this minimum at index 180 PICO can move straight into the new path. If the minimum is detected at for instance index 200, PICO is oriented in the direction of the right wall and the angular velocity should be positive. When there are two minima within the theshold which are 180 degrees across each other, then PICO is in the path ,thus PICO is between walls and a Drive message of 1 is published by the Decision Making node. PICO can continue in the Normal Driving state.
The same strategy is used for the right + straight crossing, which can seen when PICO made a right turn before. A minimum at approximately index 900 can be seen and should stay at index 900.
For the three-way crossing the same strategy as in the Enter Crossing state is used: A minimum at approximately index 360 and a minimum at approximately index 720 can be seen, and those distances are kept equal by adjusting the angular velocity. Those minima will change index, but rather than looking for the minima at those indexes, it is checked what the indexes are of those two minima.
Safety Driving
Filtering and Processing Laser Data
20 Sept 2013
By applying a set of filters, laser data is processed to give information which are easier to interpret for path planning. By detecting certain features of the environment, we now deal with smaller amount of data which are transferred by custom messages that can be modified.
At first, the filter process was created as a node and it got more complex as new stuff were added. So; for ease of programming,reading and debugging the code, we decided to split up some parts. Then it became much simpler, more fixes were done because it was easier to notice them now and the overall functionality of the processes increased. It was discussed that one down-side of creating more and simpler nodes is the possible lag between the nodes. So, we decided we are going to check and measure nodes' communication, how well they are synced and we are also not going to over-simplify and create too many nodes. But we are positive that separating the needed tasks may reduce the reaction time if the nodes are synced well; by using functions and options like ros::spin(),ros::spinOnce(),ros::Duration().sleep()(to save CPU) and message queues for publishing and subscribing.
After visualizing the environment as we wanted to; we now focus more on tasks of the robot as some of the tasks have to be carried out at all times (e.g. obstacle avoidance) and others have to be completed upon requests (e.g. change in trajectory due to decision making).
Laser data visualized
18 Sept 2013
The data from the laser can be interpreted as points given in a polar coordinate system, these points can be transformed to a cartesian coordinate system. This visualisation helps to create a strategy for detecting walls and corners.
ROS Nodes and Topics
17 Sept 2013
With ROS, one can use nodes and topics to create simpler and easy-to-handle structures. Usage of nodes is very useful when multiple tasks have to be done simultaneously. For this project, a 'Master' node, a 'Movement' node and a 'Vision' node can be created to perform given tasks as solving a maze and recognizing signs, which have to be done simultaneously and which are at times independent of each other. For the corridor competition, the task is simple; so the use of multiple nodes and especially the 'Vision' node will not be necessary. However, for the second competition goal of which will be solving the maze, these nodes can be implemented to perform recognition of signs and to solve the maze. Here is one of the first drafts of the nodal structure of the program:
Useful Things
Hardware info
Technical info about the laserscanner can be found in this document. Mostly to satisfy your curiosity, not specifically needed for programming. Hokuyo Laser Scanner
Creating a different map
Using GIMP Image Editor
1. Download GIMP Image Editor from the Software Center
2. Open the existing map ("maze.pgm") in '/home/s080482/ros/emc/general/gazebo_map_spawner/maps' with GIMP
3. Edit the map how you want it to be. Scroll all the way down in the 'Brushes' box in the bottom right of GIMP. Then there is a square on the second last row on the far right, called ' square (5x5)(5 x 5). (make sure you have this one and not one with 'blur'. Also select the 'Pencil Tool Hard Edge Painting Using a Brush' in the top left box.
4. Now just delete blocks and at add them were you want. Zooming in helps. You can switch color on the top left as well.
5. Also if you look closely, you can see a grey dot in the bottom center. I think this to mark the point where the robot spawns. I suggest we leave it where it is and edit the maze around it.
6. Save the map in the same folder but with a different name.
7. Go to the folder '/home/s080482/ros/emc/general/gazebo_map_spawner/scripts' and open spawn_maze in a text editor.
8. Change the name of the map in needs to load, i.e. change the OWN_MAP in the text below to your own map name.
rosrun gazebo_map_spawner map_spawner `rospack find gazebo_map_spawner`/maps/OWN_MAP.pgm
9. Now simply spawn the maze in exactly the same way as you did before, so with exactly the same commands!
Using Gazebo Model Builder
1. Open Gazebo
2. Go to 'Edit', 'Model Builder'.
3. You will see a 2-D image and 3-D world under it. Choose 'Add Wall' and start drawing walls on the 2-D image.
4. Check the locations and distances from the 3-D world.
5. Hit 'Done', save it to a file 'example.sdf'. Close 'Model Builder'. The model should spawn in the world.
6. Go to 'File', 'Save As'; again save as 'example.sdf'.
7. To load, go to the save folder and hit command:
gazebo example.sdf
Teleop Controller for Pico
To be able to move the robot around manually and easily is very useful when testing simple things in the algorithm. Here you can find the teleop controller for PR2:
And here is the revised version of the teleop controller for our robot pico:
/*
This code lets you move the jazz robot using your keyboard.
This is obtained from a sample code for pr2 from this link:
http://wiki.ros.org/pr2_simulator/Tutorials/Teleop%20PR2%20arm%20in%20simulation
It basically goes into a loop, where the terminal is set for user-input kind of operation
and everytime a button is pressed, velocities are published as the cmd_vel topic for pico.
--emc11
*/
#include <termios.h>
#include <signal.h>
#include <stdio.h>
#include <stdlib.h>
#include "ros/ros.h"
#include "geometry_msgs/Twist.h"
#define KEYCODE_A 0x61
#define KEYCODE_D 0x64
#define KEYCODE_S 0x73
#define KEYCODE_W 0x77
#define KEYCODE_Q 0x71
#define KEYCODE_E 0x65
class teleop_pico_keyboard
{
private:
geometry_msgs::Twist cmd_msg;
ros::NodeHandle n;
ros::Publisher cmd_pub;
public:
void init(){
cmd_pub = n.advertise<geometry_msgs::Twist>("/pico/cmd_vel", 1000);
cmd_msg.linear.x=0.0;
cmd_msg.linear.y=0.0;
cmd_msg.linear.z=0.0;
cmd_msg.angular.x=0.0;
cmd_msg.angular.y=0.0;
cmd_msg.angular.z=0.0;
cmd_pub.publish(cmd_msg);
};
~teleop_pico_keyboard() { };
void kloop();
};
int kfd = 0;
struct termios cooked, raw;
void quit(int sig)
{
tcsetattr(kfd, TCSANOW, &cooked);
exit(0);
}
int main(int argc, char **argv){
ros::init(argc, argv, "jazz_teleop_t");
teleop_pico_keyboard tpk;
tpk.init();
signal(SIGINT,quit);
tpk.kloop();
return 0;
}
void teleop_pico_keyboard::kloop()
{
char c;
bool dirty=false;
ros::Rate loop_rate(5);
// get the console in raw mode
tcgetattr(kfd, &cooked);
memcpy(&raw, &cooked, sizeof(struct termios));
raw.c_lflag &=~ (ICANON | ECHO);
// Setting a new line, then end of file
raw.c_cc[VEOL] = 1;
raw.c_cc[VEOF] = 2;
tcsetattr(kfd, TCSANOW, &raw);
puts("Reading from keyboard");
puts("---------------------------");
puts("Use 'WS' to forward/back");
puts("Use 'AD' to rotate left/right");
//puts("Use 'QE' to ...");
while(ros::ok())
{
// get the next event from the keyboard
if(read(kfd, &c, 1) < 0)
{
perror("read():");
exit(-1);
}
switch(c)
{
case KEYCODE_W:
cmd_msg.linear.x = 1.0;
cmd_msg.angular.z = 0.0;
dirty = true;
break;
case KEYCODE_S:
cmd_msg.linear.x = -0.5;
cmd_msg.angular.z = 0.0;
dirty = true;
break;
case KEYCODE_A:
cmd_msg.angular.z = 0.5;
cmd_msg.linear.x = 0.0;
dirty = true;
break;
case KEYCODE_D:
cmd_msg.angular.z = -0.5;
cmd_msg.linear.x = 0.0;
dirty = true;
break;
// You can use these for different tasks
// case KEYCODE_Q:
// dirty = true;
// break;
// case KEYCODE_E:
// dirty = true;
// break;
}
if (dirty == true)
{
cmd_pub.publish(cmd_msg);
}
}
}
Just create a ros package dependent on roscpp and geometry_msgs, compile and run it in a seperate terminal. As an example; by pressing 'W' in the terminal, you will move the robot forward in the simulator.