Verslag group 14

Return PRE2017 3 Groep14

Dingen die nog in het verslag moeten

• Wat kan er beter aan het programma, hoe uitbreiden, wat hebben wij niet meer kunnen doen maar willen we eigenlijk wel
• relatie tussen onderzoek en hoe het eruit ziet en hoe het werkt( wat komt er uit het literatuur onderzoek en hebben we gebruikt in de praktijk)

Introduction

Slim In Rekenen

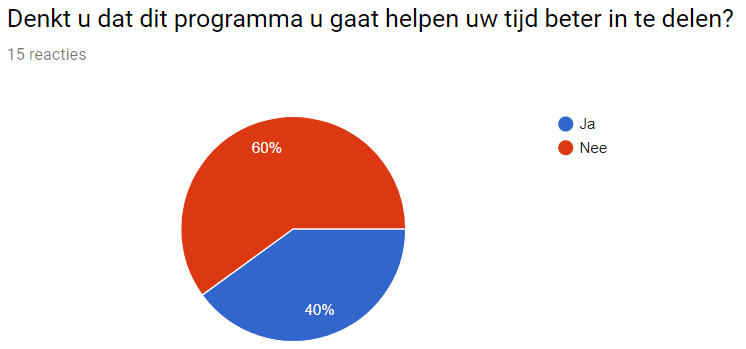
For the course Robots Everywhere from the Technical University of Eindhoven, a project about some form of robotics needed to be made. The only explanation given was that robotics has to be part of the project in some way and that a product needed to be delivered at the end. Because of the huge amount of freedom in this course, for this particular project it was decided to create a smart quizzing program for in class. The program can be used in groups 3 and 4 from schools with a traditional educational tactics, all research is focused on these schools in the Netherlands. Simple mathematics is the subject that this quiz will cover, so addition, subtraction, multiplying, and division. The purpose of the program is easily identifying students that need some extra teacher attention, while stimulating all students on an individual level. The way in which this is done is by finding the child’s knowledge boundary based on his or her answers to the previous questions. This way, the child will get questions that are still challenging enough to be interesting, but not too hard that the pupil will give up. As a quizzing program will be started at the same time for a whole class, but all pupils soon have an individual test, it is a perfect combination of individualism while working as a class so nobody feels left out. All questions in the test are multiple choice to make it easier for the children to input their answers. The teachers will be able to see from the results which children have mastered the subjects sufficiently and are ahead of the program, but also which pupils lack behind. Because these results will be visible very quickly, the teacher knows sooner which children will need some extra attention to catch up. This extra attention can then be given when the teacher sees fit. To test whether or not teachers think the program could make an actual difference in their teaching programs, an questionnaire was send to 50? elementary school teachers. The questionnaire focused on their opinions and whether they had tips to keep in mind while designing the program. An important question is whether or not they think the program will help them plan their time better, as this is our main goal?. The following report is an elaborate documentation about the program, the questionnaire and the results from this.

Problem description

The purpose of our program is to quickly recognize which children need extra help on a specific topic and to customize the test to each child, such that they can train specific topics on their own level. Quickly recoginizing the children will help the teacher to immediately step in. For example at the start of the year teachers do not know the weaknesses of the children, but our program can find them immediately after 1 test. Furthermore the personalised test ensures that the children will not lose interest, due to the questions being to easy, and ensures that they will not feel left out, due to always getting the questions wrong. These personalised questions are determined on the answers of previous questions.

Our program is now focussed on children in the third and fourth grade of the elementary school in the Netherlands using a tradional education system. The test consists of mathematical questions, that are divided by subject, for example multiplication tables or adding numbers up to 20. These choices were made to ensure an easy starting point for the program.

Objective

Develop a smart quiz program for a computer that can assess knowledge levels of the pupils, to give the teacher a better view on his pupils, and ask questions to the pupils on their personal boundary, so they learn effectively.

Users

The users of the program will be the pupils of the third and fourth grade of the elementary school in the Netherlands using a tradional education system, the parents and teacher of these pupils. The users will have the following requirements:

• The pupils want:
  • A program that stimulates their imagination
  • A test that remains interesting throughout the whole session
  • A test that does not make them feel dumb or left out

• The parents want:
  • A test that stimulates their children to learn and to perform the best they can.
  • Their children to be happy
  • Check their children's progress
  • The privacy of their children to be guaranteed

• The teacher wants:
  • A test that motivates the pupils to learn and to perform the best they can
  • The system to match the curriculum, meaning the teacher has to change the settings of each test
  • To check the progress of each pupil in an easy way
  • To divide his or her time in the best way over all the pupils

For the program we did not put our focus on privacy, because this is only a small part of our program. The program will not contain an interface for the parents, due to fact that the goal only incorporates the pupils and the teachers. However this could be added later on if desired. Almost all of the other the requirements will be implemented in our program by the use of the traditional didactic system.

Intelligent Quiz System

Given a set of questions, the quiz master will test the knowledge of a child, and help the child improve by asking the right questions at the right time. We will build an application that selects the next question to ask the child, based on the previous answers the child gave to previous questions. The quiz will find the knowledge level of the child and ask questions at the child's knowledge boundary so he can still learn from the question but will not be overwhelmed.

The quiz master has to:

• Find out the level of knowledge the child has, and ask questions that are on the 'edge' of a childs knowledge in order to improve their knowledge.
• Generate new questions.

In order to do so, we must:

• Define distance (or question similarity) between questions, which questions are of similar difficulty. So cluster questions based on their difficulty. Note that this will vary per child.
• Simulate the (increasing/decreasing) knowledge of different children. (To be able to train our app.)
• Construct a (large enough) data set to use parts of it for training and validation.
• Find out what the next right question would be. Our app should do this, based on the question similarity for a certain child.

Desk research

Didactic systems

In the book, het didactische werkvormenboek , a few important aspects of teaching are found.

• The best way for pupils to take in information is when they read and/or see it.
• When asking questions, there need to be both open questions and closed questions.
• Make sure pupils work with the whole class, but also occasionally in smaller groups or on their own.
• Switching between teaching tactics stimulates learning. An example could be switching between a game and simple sums.

For our project we chose to focus on a traditional education system instead of a constructive education system. This means that we will keep in mind that

• The teacher largely decided on the curriculum and order in which subjects are taught.
• The focus lies on teaching the whole class at once.
• There is a curriculum in which some subjects are more central than others.
• Learning is an individual activity.
• Pupil’s progress is checked by means of tests.

The use of computer programs in dutch education

From a government study , the following things became clear:

• Separating the class in smaller groups in year 3 has a positive effect on the pupils’ performances as it causes more interaction.
• More than 90 percent of the teachers in primary education use computers to teach. According to them using ICT can contribute to a more efficient, effective and likeable education.

The next article shows us that education often does not seem to fit the natural, experimental learning process that children have. In games it is possible to naturally lean, which is why using games can be relevant for primary education. There would have to be a good balance between playing and effectively learning, to make sure that the advantages of learning in a fun way are not lost. This means the following things need to be taken into account when asking questions:

• The information should not be presented in a way that is too abstract, make sure it speaks to the children’s imagination.
• There needs to be a lot of repetition.
• Important information should be taught in more than one way.
• Take some time, it should not be taught too fast.
• Use realistic characters.
• Use animation, childlike dialogues, interaction and direct feedback.
• Do not punish children for making mistakes.

Individual or in the class

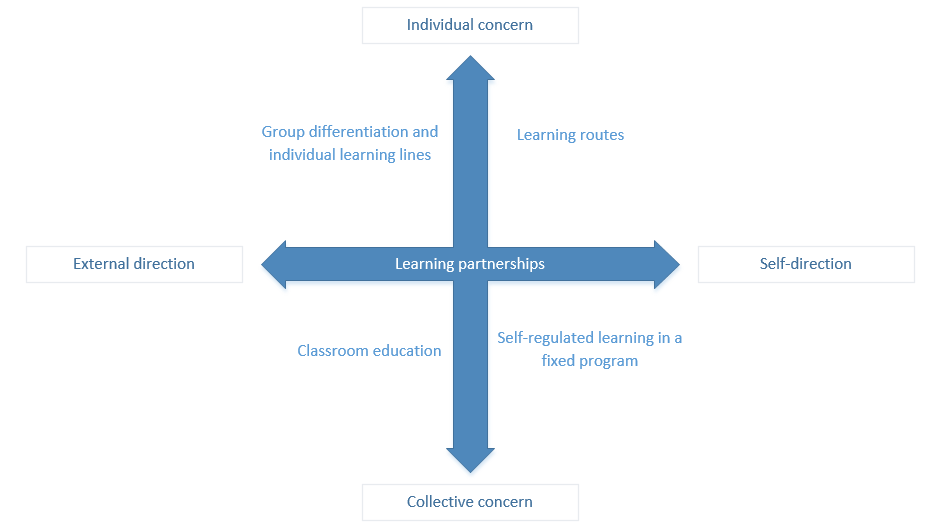
• As we can see in the following article , the program is part of groupdifferentiation with individual learling lines. This means that there is quite some form of external regie but with focus on the individuals. Consequently, the teacher has some set goals and subjects on which the pupils need to work, and they will work on these subjects when the teacher tells them to. However, as the program will ask questions on their personal knowledge levels, the individuals are also taken into account. This is a perfect combination of working with the class while working on one’s own.

Artikel over papier of digitaal

• As indicated in the following atricle using computers instead of paper to administrate achievement tests in elementary schools is supported. Using computers has multiple advantages such as being able to use an adaptive technology, which is the goal for the finished program. On the other hand, it is possible that children experience computer anxiety resulting in lower achievements, but for this project it is assumed that this will not be the case as most children these days work with computers from very early on.

Op het niveau van de les zijn de volgende beïnvloedbare factoren geïdentificeerd.  Ten eerste blijkt uit de internationale en Nederlandse literatuur dat alle onderzochte interventies gericht op instructie- en werkvormen effectief zijn. Daarbij is het niet goed mogelijk om werkzame elementen te identificeren omdat de verschillende effectieve interventies soms tegenstelde uitgangspunten hebben, zoals interventies gericht op directe instructie of juist constructivistische instructie. Bovendien zijn er zeer weinig studies die dit soort verschillende instructievormen rechtstreeks met elkaar vergelijken. Het voornaamste beeld dat rijst is dan ook dat ‘iets manipuleren aan instructie- en/of werkvormen werkt’. Dit sluit ook aan bij de conclusie van het eerdere rapport van de KNAW (2009) dat het (destijds) beschikbare Nederlandse onderzoek geen eenduidig beeld oplevert over de relatie tussen rekendidactiek en rekenvaardigheid, maar wel dat ‘iets doen’ aan de rekenles helpt.  Ten tweede heeft het toepassen van technologische hulpmiddelen, zoals oefenprogramma’s op de computer of tablet, en niet-technologische hulpmiddelen zoals driedimensionale materialen een positieve relatie met rekenprestaties. Dit blijkt uit zowel internationaal als Nederlands onderzoek, zoals naar het gebruik van mini-games en de programma’s Snappet en Rekentuin. Omdat het niet duidelijk is in hoeverre het toepassen van hulpmiddelen gepaard ging met extra aandacht of onderwijstijd voor rekenen is nader onderzoek gewenst naar wat precies het positieve effect teweeg brengt: het hulpmiddel of enkel ‘iets toevoegen’ aan de rekenles.  Ten derde heeft formatieve toetsing, het gebruik van toetsgegevens om het leerproces te verbeteren, een positieve samenhang met rekenprestaties. Dit werkt zowel middels feedback aan de leerkracht, bijvoorbeeld via digitale leerlingvolgsystemen, als middels feedback aan de leerling per gemaakte opgave.  Ten vierde bleek het differentiëren in niveaugroepen (homogeen of heterogeen) in internationaal onderzoek positief samen te hangen met rekenprestaties. Daarbij is het wel belangrijk om op te merken dat nader onderzoek gewenst is naar de specifieke en vergaande vorm van differentiëren die in Nederlandse rekenmethoden gebruikelijk is waarbij vaak gebruik wordt gemaakt van drie niveaugroepen (zie bijvoorbeeld Van Zanten & van den Heuvel-Panhuizen, in druk).

Articles about the layout of the test

How to implement feedback

• In this article it becomes clear that attributional feedback to children is useful as it is an effective way to promote rapid problem solving, self-efficacy, and achievement. This is probably because children have a sense of how well they are doing and attributional feedback helps to support these self-perceptions and validates their sense of efficacy. Because of this, the children will stay motivated to work on leading to a better performance in the end. The best way to do this is by giving them ability attributional feedback, so telling them they are either very smart, or not that good at math.
• Feedback in between The major findings evidenced in this research were the following:
  • Feedback was generally effective for learning, but more so on the lower level (identical) questions than on the higher level (reworded) ones;
  • Feedback information had greater impact in the absence of supporting text than with supporting text;

In this article they used several feedback methods such as knowledge of correct response (KCR), which identifies the correct response, and answer until correct (AUC). These two were shown to be the most effective.

When implementing these articles about feedback in our program the following decisions were made the KCR method with almost no supporting text except for the attributional feedback will be used.

How to construct mathematical questions

Bij het construeren van rekensommen is het belangrijk te weten hoe leerlingen context geven aan getallen en operaties op getallen. Dit artikel legt uit waar er allemaal opgelet moet worden. Hoofdrekenen is inzichtelijk rekenen met getallen, waarbij de waarde van de getallen bij de berekening in beeld blijft en handig gebruik wordt gemaakt van parate kennis, eigenschappen van getallen en bewerkingen en de onderlinge relaties. Globaal worden twee varianten van hoofdrekenen onderscheiden: het mét het hoofd rekenen en het úit het hoofd rekenen. Er zijn drie grondvormen van hoofdrekenen:

• het rijgend hoofdrekenen, bijvoorbeeld: 36 + 12 [math]\displaystyle{ \rightarrow }[/math] 36 + 10 [math]\displaystyle{ \rightarrow }[/math] 46 + 2 = 48;
• het splitsend hoofdrekenen, bijvoorbeeld: 36 + 12 [math]\displaystyle{ \rightarrow }[/math] 30 + 10 = 40 [math]\displaystyle{ \rightarrow }[/math] 6 + 2 = 8 [math]\displaystyle{ \rightarrow }[/math] 40 + 8 = 48;
• het gevarieerd of handig hoofdrekenen, bijvoorbeeld compenseren: 73 – 29 [math]\displaystyle{ \rightarrow }[/math] 74 - 30.

Modellen en schema’s spelen een rol bij de overgang van contextgebonden naar formeel redeneren en rekenen; het horizontaal mathematiseren. De getallen tot honderd worden gestructureerd met het lijnmodel, bijvoorbeeld de (lege) getallenlijn en het groepjesmodel.

Er zijn globaal drie didactische aanpakken te onderscheiden: kolomsgewijs leren rekenen, leren cijferen via progressief schematiseren en regelgeleid leren cijferen, leren aan de hand van de regels. Daarbinnen zijn variaties mogelijk.

• 1 a 2 artikelen wanneer is een rekenvraag moeilijk
• 1 artikel over hoe moeten we de score aanpassen

From these articles we can conclude that we want to focus on learning in a likeable way, using a computer program. We will do this by asking simple maths questions using fun pictures of animals. This way we hope to intrinsically motivate the children to play with our program. Other things we will implement is that we want to make sure it will not go too fast and we can use child-friendly language.

Program

Questions

We have 3 types of questions:

• Flock questions, where children can add or subtract two flocks of pigs, cows, or chickens.
• Animals with small blackboards which have simple additions or subtractions on them.
• Timeline questions where there are animals standing next to each other with numbers on their blackboards and one number is missing.

According to this website students from our target audience should be able to do the following things at the end of the school year:

• Group 3 can add and subtract from 0 to 20.
• Group 4 can multiply and add and subtract from 0 to 100.

For this reason exactly, we made sure the teacher can change the settings of the program to fit the needs of the current group. The teacher can choose between addition, subtraction, multiplying, and dividing on the range [x, y] or a combination of these operations. Furthermore, the teacher can input the maximal number of arguments each questions can have, how many questions there are in a session, whether the questions will be done with integers or decimals, and whether the program will go through a session automatically or manually. All questions are multiple choice to make it easier for the young children to reply.

Voeg hier plaatjes toe van de drie type vragen die we hebben

Score

The score of a child is determined by the following function:

[math]\displaystyle{ score = score+\frac{The Current Time}{The Total Time} }[/math]

here the total time and the current time are the times of that question

Border of the three groups

Teacher Interface

Description with pictures of all the things the teacher can adjust and see

Before Starting a Quiz

Interface of the teacher before the quiz starts

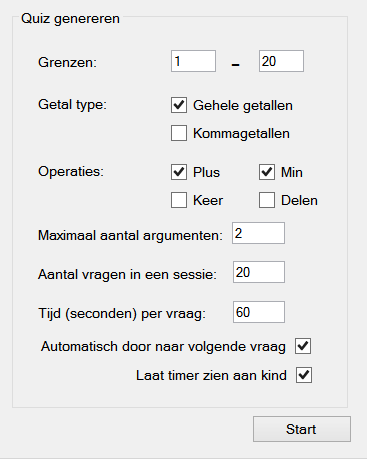
When the teacher starts a new quiz they will see a form on which they can adjust the settings for the quiz. When clicking the 'start' button, the program will generate exactly as many unique questions as the teacher requested in the category they provided. The form on the right will generate 20 questions. The numbers in each question (both the numbers in the question itself and its answer) will be within the range [1, 20], and this while be integers. The operations in this question set will only be addition and subtraction. The nubmer of questions for each operation will be random, so there might not be 10 addition and 10 subtraction questions. The maximum number of arguments of each question in this quiz will be two, which means that each question will be of the form x + y. When the children answer the questions in this quiz, they will have 60 seconds for each question. When these 60 seconds are over and a child has not answered the question, the question will be handled as answered uncorrectly. The upper of the last two checkboxes controls if the quiz automatically continues to the next question after all children have answered or time is up, or if the teacher manually has to start the next question. The last checkbox controls whehter the children get to see the timer for each question.

Child interface

Description with pictures of all the things the children can adjust and see

Results

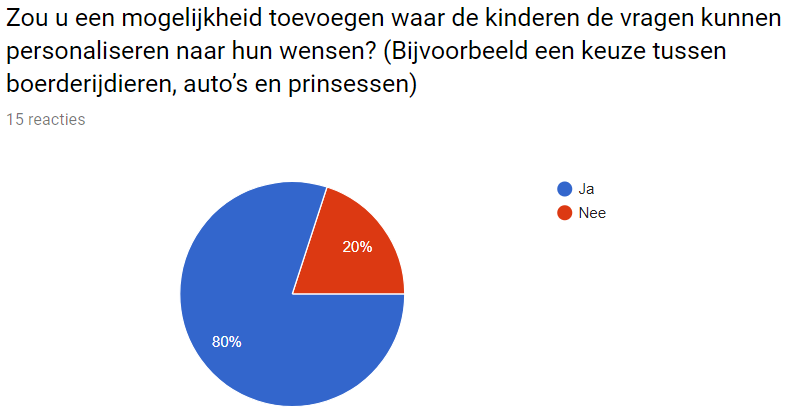
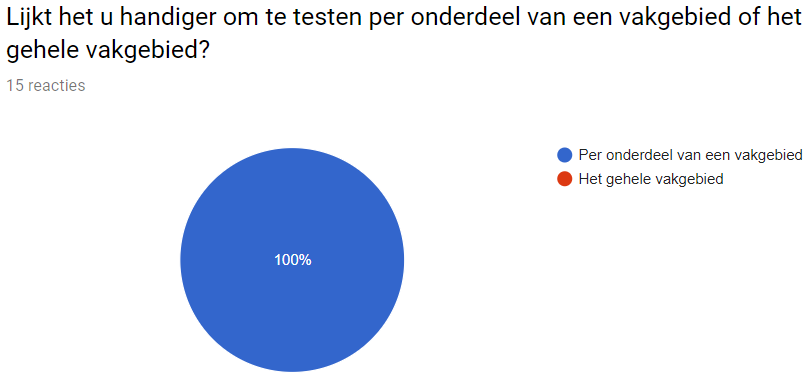
Survey

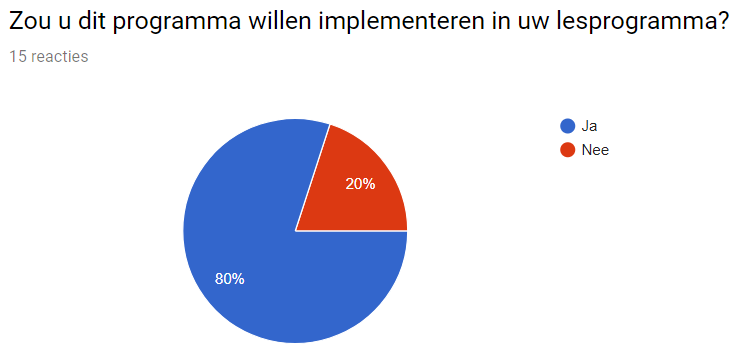
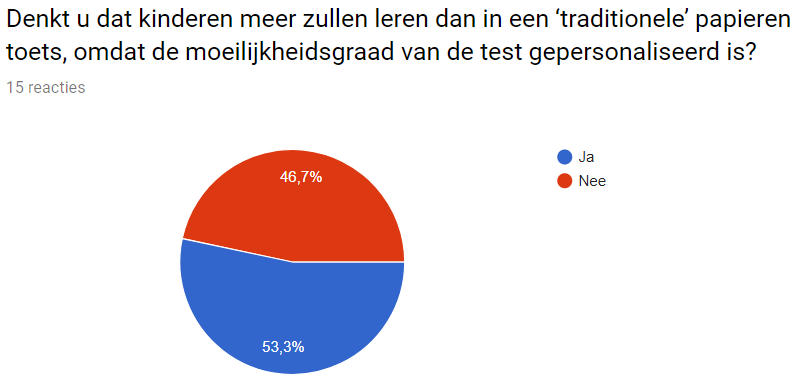
The purpose of the survey will be the following:

• look if there is demand for our program
• look if the program can be implemented
• look if teacher will find it a fun new addition to their class
• important features the program should have according to teachers

Results