Mobile Robot Control 2020 Group 2
Mobile Robot Control 2020 Group 2
Group members
Marzhan Baubekova - 1426311
Spyros Chatzizacharias - 1467751
Arjun Menaria - 1419684
Joey Verdonschot - 0893516
Bjorn Walk - 0964797
Bart Wingelaar - 0948655
Design Document
Design document for the escape room challenge can be found here:
File:Mobile Robot Control Design Document Group2.pdf
Escape Room Challenge
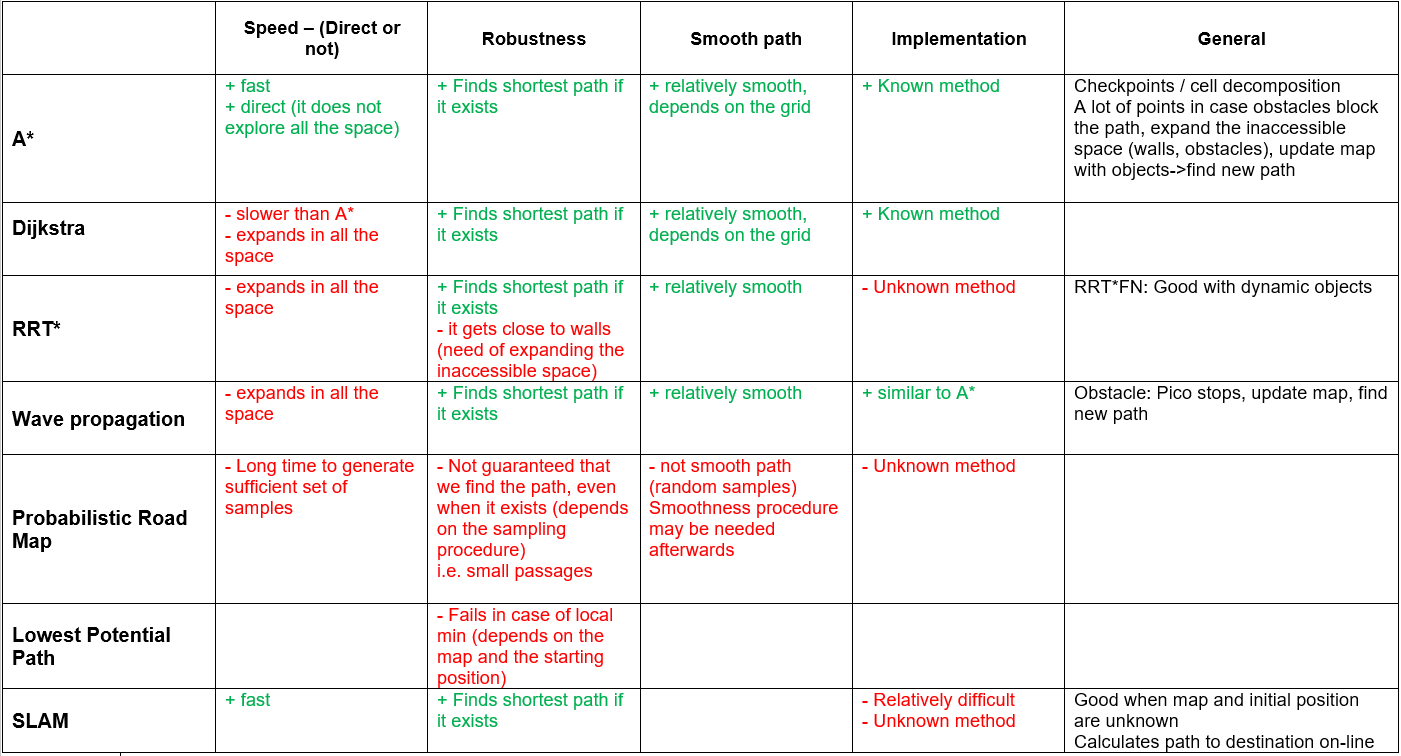
The software is based on a finite state machine. The robot starts in a certain state, and based on certain conditions it can go to some next state. These states will be followed until the final state is "Finished". While going through these states, the robot also communicates with the world model. This world model contains important information, for example the direction of the exit when identified or the distance to a wall. This information is also shared with the classes. These classes determine the actual actions of the robot. The SafetyMonitor will retrieve for example the distance to a wall and determine if the distance is larger than a certain threshold. If the wall is too close, the SafetyMonitor will tell the robot the move away form the wall to get some clearance. The detection class retrieves the laser data and determines the distances to walls or finds the exit. These parameters are then stored in the world model. Drive control determines the movement of the robot. Path planning is not used int the escape room but will be used for the hospital challenge.
At the start of the escape room challenge the robot will scan from the initial position. The scan is then analyzed to determine if the exit can be seen from this initial scan. If the exit can already be seen, the robot will move in the direction of that exit until it gets close to the exit. If the exit can not be seen, the robot will rotate approximately 180 degrees to do a second scan. If the exit can now be seen, the robot will move in the direction of the exit. If in the second scan the exit can still not be identified, the robot will move to the closest wall found in the two scans and start a wall following algorithm.
When the exit is found from one of the initial scans, the robot will rotate to face the right direction towards the exit. It will then start to move forward towards the exit. When it gets close to a wall the robot assumes it is near the exit and start and alignment procedure. This alignment procedure makes sure that the robot will enter the hallway approximately in the middle to steer clear of the walls. When the alignment is done the robot will start the exit entering procedure.
The wall following algorithm makes the robot move in a clockwise direction. When it gets close to a corner it will rotate approximately 90 degrees and use the wall to the left to align to an almost perfect 90 degrees. When it suddenly sees a jump in the distance of the wall to the left, it detects this as the exit. The robot scans a larger part of the wall while driving to identify this gap. This also means that if it is only a small slit in the wall, it will ignore this. When the robot has then moved forward so that it is standing in front of the gap, it will rotate to face the gap. It will then align so that it is standing approximately in the middle of the gap and start the exit entering procedure.
The exit entering procedure makes sure the robot slowly drives forward until it is somewhat into the hallway. While it is doing this, it is scanning for walls to the left and right of the robot to make sure it will not hit any walls. If the robot gets to far out of the middle line of the hallway, it will reposition itself towards the middle. While in the hallway the procedure is quite similar with respect to aligning to the middle line of the hallway. In the hallway the robot will also align to be parallel to the left wall of the hallway. This is done to make sure the robot can not get to close to this wall. Combined with staying in the middle line of the hallway, this ensures that the robot will not hit any of the walls in the hallway.
While in the hallway the robot will also scan ahead slightly to the left and right. This is done to determine when the robot has crossed the finish line. When the robot no longer sees walls in the front left and right direction, it will assume that it has crossed the finish line.
A flow chart of finite state machine is shown below:
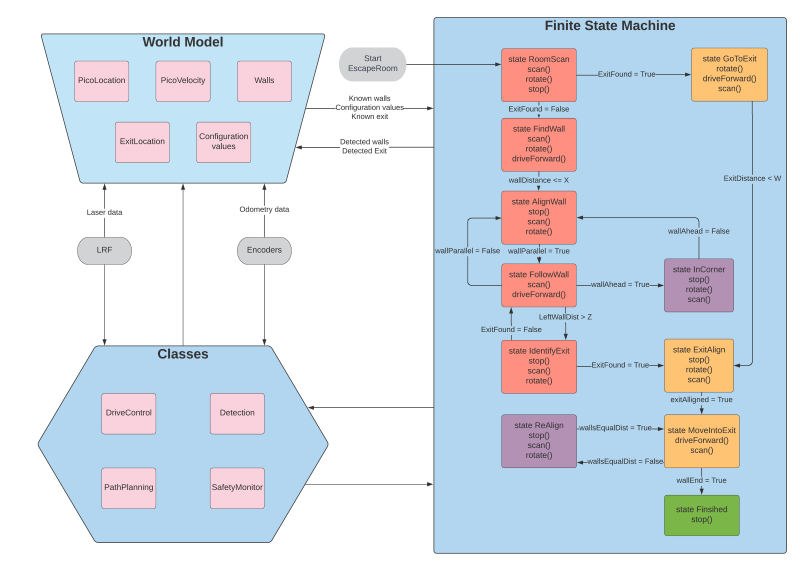
In the live Escape Room challenge the robot did not finish. In the first attempt this was due to the fact that the robot started close the the wall. This scenario was not tested. The robot starts by scanning the room and trying to find the exit. When an exit is found the robot moves towards it. However, the criteria for the robot to determine that it was close to the exit was if a wall is nearby. This criteria works if the robot starts clear of the walls and can drive straight to the exit. Since the robot started close to a wall in the challenge, it immediately thought it was at the exit and tried to allign with the hallway. This obviously did not work since there was no hallway.
The second attempt was a simple wall following algorithm. However, again a specific case was not tested making the robot still not finish the challenge. In this case it was the situation where the exit was very close to a corner. When the robot gets to a corner it is supposed to rotate approximately 90 degrees, and then use the wall to the left to align with the wall. Now that the exit was close to the corner, it could not detect the wall to align with, and the software got stuck in a loop.
The first code was fixed by changing the criteria for when the robot assumes it is close to the exit. Now the distance to the exit is measured at the 20Hz sampling rate. This distance was already calculated in the original code, however it was not stored and used. Now that it is used, the robot will only start the alignment procedure for the hallway when this distance is below a threshold. The robot will also move away from the wall slightly after the scanning to ensure safety margins. This was already in the code, but was not executed since the robot never started moving but immediately thought it was at the exit. The result is now that the robot escapes the room in 19 seconds and stops right after crossing the finish line and speaks "I have finished". The results is shown below:
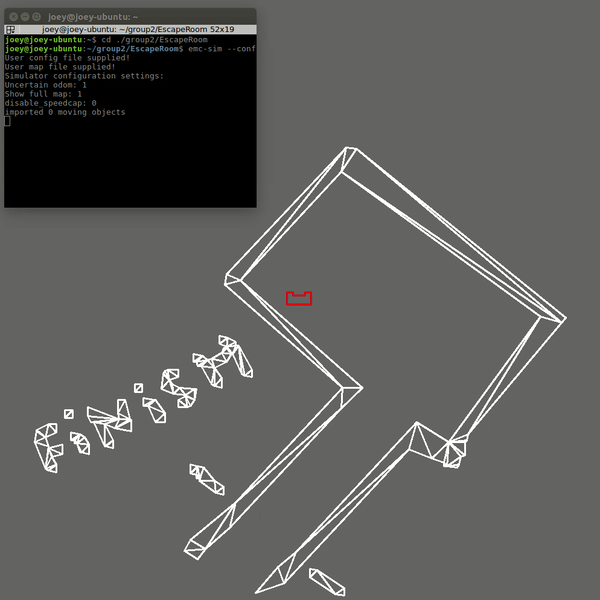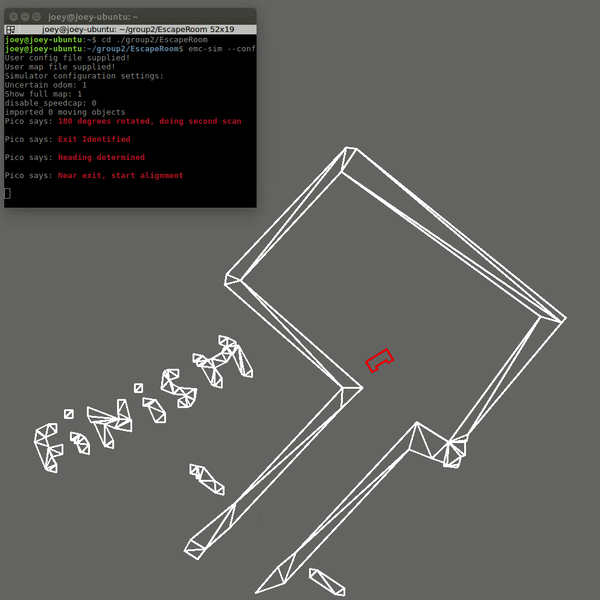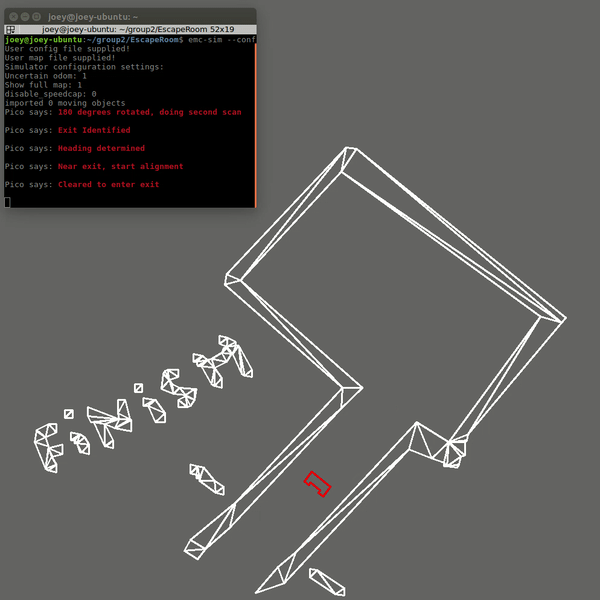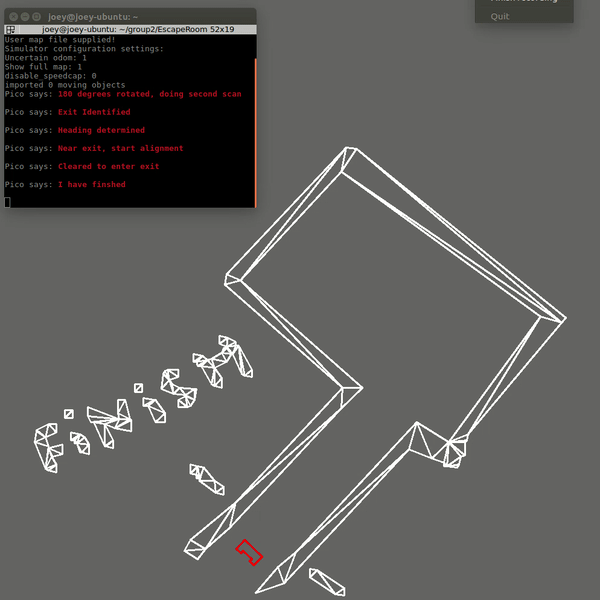
Hospital Challenge
Path Planning
The algorithm that is chosen for the path planning is an A* algorithm. Before proceeding to algorithm, it is essential to transform map to a binary grid map. This step is done in Matlab and later translated to C++. There are two heuristic functions which are tested, namely diagonal and euclidean. Pathplanning with 2 heuristics.
For the selection of the algorithm used for pathplanning a table of pros and cons has been formulated, which includes the computer performance index. A* is given an index number of 100. The walls and Dijkstra compute indices are an educated guess. The others are based on the amount of nodes used in a study
| Algorithm | Compute index |
|---|---|
| A* | 100 |
| Rapidly-exploring random tree | 100 |
| Potential field algorithm | 40 |
| Dijkstra | 100 or higher |
| Wall following | 100000 |
| Wave propagation | 100 or higher |
In addition, several algorithms are compared with respect to the convergence speed, the robustness of the method, the smoothness of the resulted path, the difficulty of the implementation and the sufficiency for the hospital challenge. The results are demonstrated in the table .........
Localization
For the successful navigation it is important that the robot is aware of its current location. After considering known algorithms such as Markov localization, Kalman filter and partilce filters, it has been chosen to implement the line segment based localization. (Why?? restricted in time, experience, identification of landmarkes is problematic and etc.)
First, the algorithm requires features extraction and the most important features in the robot's environment are the straight lines and corners. These features are used to build a local map from laser data. To extract corners the following problem should be solved. It consists of two subproblems, namely segmentation, which deals with the number of lines and correspondence of data points to lines, and corner definition, which answers how to estimate corners from segmented lines. To solve the segmentation, the split and merge algorithm is used, which is a recursive procedure of fitting and splitting. Then the corners are defined at the location where splits happens in the split and merge algorithm.
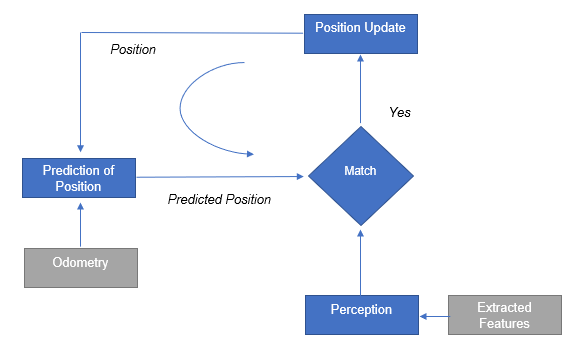
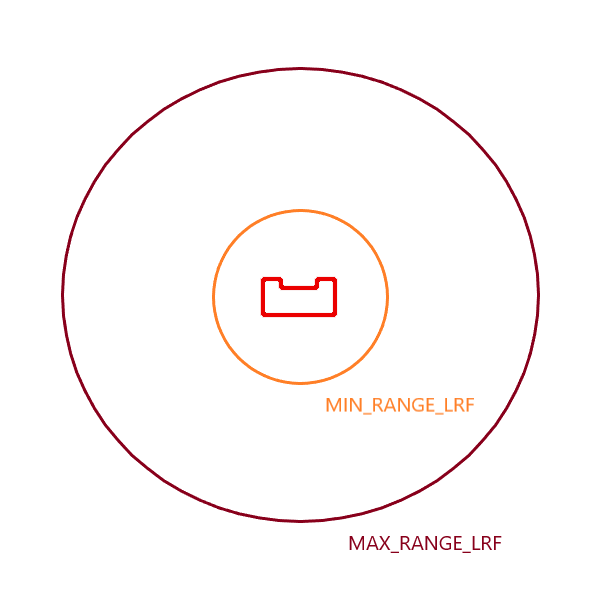
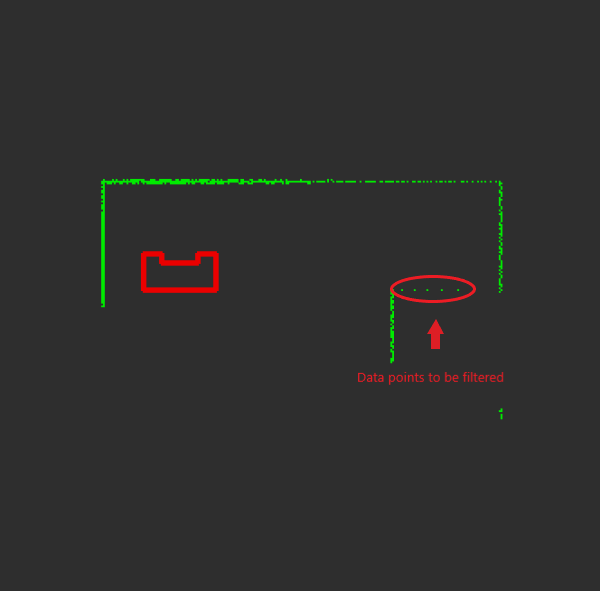
| Split and Merge Algorithm: |
|---|
| Initialize segments set S. |
| 1. Filter LRF outliers by setting thresholds MAX_RANGE_LRF and MIN_RANGE_LRF. |
| 2. Convert LRF data to cartesian coordinates. |
| 3. Calculate the distance between two cartesian points and check if it is within threshold DUMP_DIST. |
| 4. Check for a jump in LRF ranges of the filtered data set and if the jump is bigger than threshold CLUSTER_MARGIN-> make segmentation |
| Split |
| 1. Fit a line to begin and end point in current set S. |
| 2. Find the most distant point to the line using heron's formula. |
| 3. If distance > threshold LSE_MARGIN, then split and repeat with left and right point sets. |
| Merge |
| 1. If two consecutive segments are close/collinear enough, obtain the common line and find the most distant point. |
| 2. If distance <= threshold, merge both segments. |
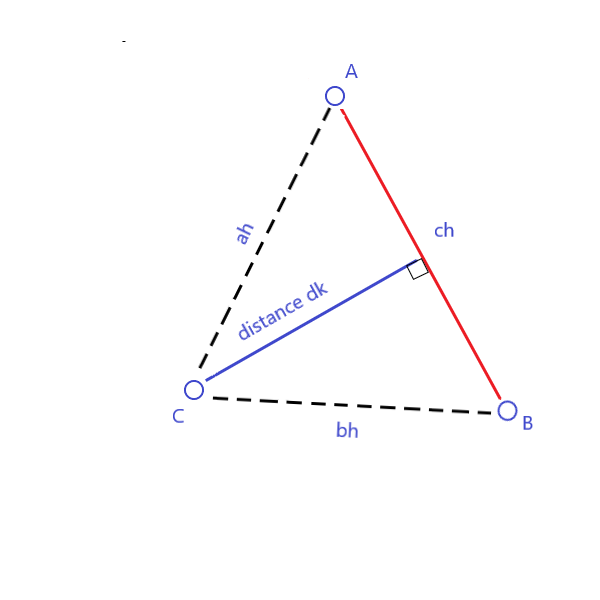
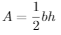
In our case the base b is ch and h is a distance-to-be-found dk. Area A is calculated by Heron's formula since all three distances ah, bh and ch can be found. To calculate area, define first
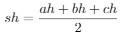
then
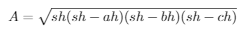
Finally, the distance can be calculated:
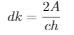
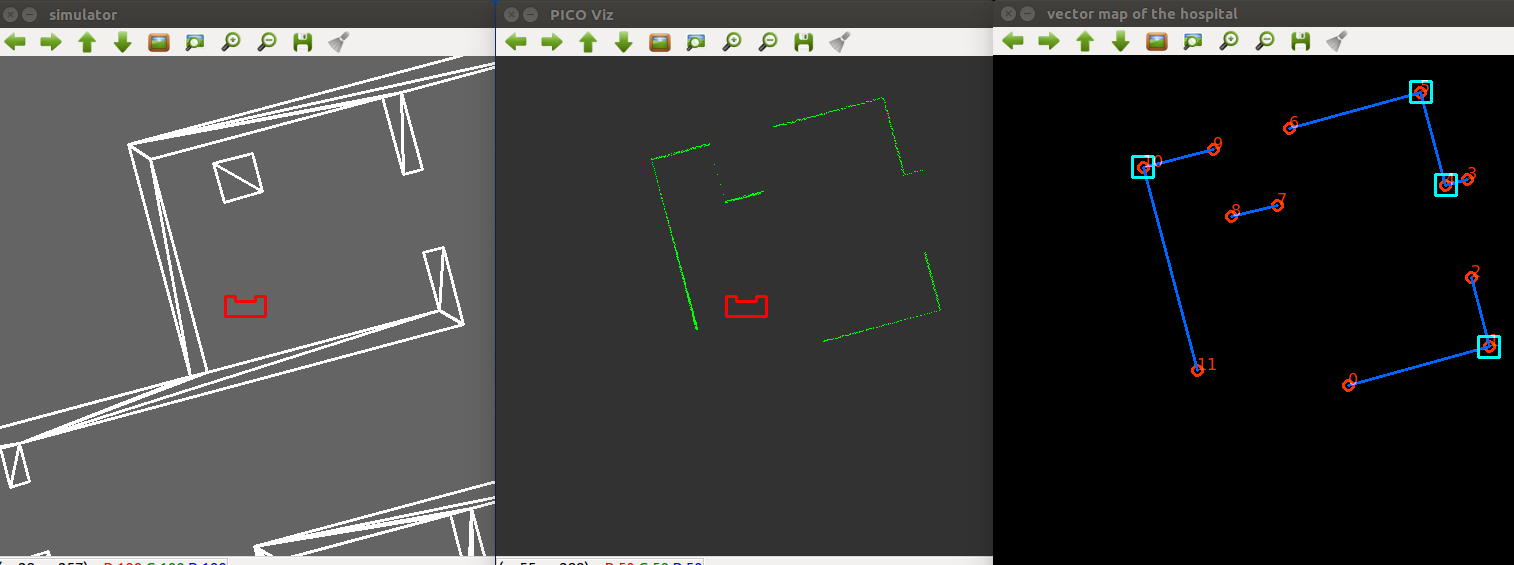
Visualization
Logs
| Meeting # | Date and Location | Agenda | Meeting notes |
|---|---|---|---|
| 1 |
Date: 28-04-20 Time: 10:00 Platform: MS Teams |
|
|
| 2 |
Date: 01-05-20 Time: 14:00 Platform: MS Teams |
|
|
| 3 |
Date: 05-05-20 Time: 10:00 Platform: MS Teams |
|
Work division
|
| 4 |
Date: 11-05-20 Time: 11:00 Platform: MS Teams |
|
Work division
|
| 5 |
Date: 18-05-20 Time: 11:00 Platform: MS Teams |
|
Work division
|
| 6 |
Date: 22-05-20 Time: 14:00 Platform: MS Teams |
|
Work division is the same
|
| 7 |
Date: 26-05-20 Time: 11:30 Platform: MS Teams |
|
Work division is the same
|
| 8 | 5 | 10 | 15 |