Embedded Motion Control 2013 Group 10
Group Name
Team Picobello
Group Members
| Name: | Student id: | Email: |
| Pepijn Smits | 0651350 | p.smits.1@student.tue.nl |
| Sanne Janssen | 0657513 | s.e.m.janssen@student.tue.nl |
| Rokus Ottervanger | 0650019 | r.a.ottervanger@student.tue.nl |
| Tim Korssen | 0649843 | t.korssen@student.tue.nl |
Corridor Challenge
Positioning
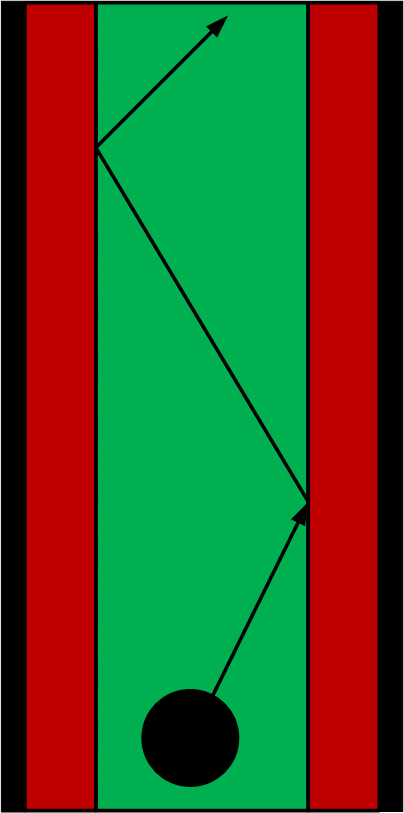
To remain in the center of the corridor and avoid hitting the wall the position is continuously checked and controlled. This is visualized in the picture below. The black area is the wall, the red area is close to the wall and should be avoided and the green area is the area where it is safe to drive. The robot drives forwards until it drives into the red area. Whether the robot is inside the red area is determined directly from the laserdata. If it is in the area it makes a slight turn (about 5 degrees) into direction of the green area and then again drives in forward direction.
Wall Avoidance
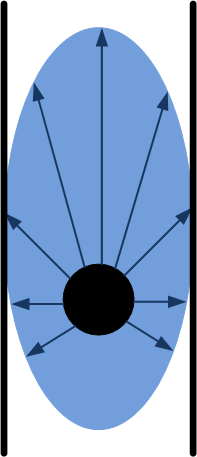
Wall avoidance has the highest priority at all times and is therefore active a all times. Wall avoidance measures distance in all possible directions. Once one distance becomes too small the “wall avoidance node” overrules all other nodes and commands the robot to stop. The threshold for the distance is not just a scalar. Since the robot has some velocity in forward direction, more space is required in forward direction of the robot than sideways. Therefore the threshold has an elliptic profile as shown in the figure.
Noise reduction
To reduce noise a Gaussian filter is added. [math]\displaystyle{ G(x)=\frac{1}{\sqrt{2 \pi}}e^{\frac{-x^2}{2 \sigma^2}} }[/math]
This Gaussian function is used to make a 9x1 Kernel. So that every point is the weighted averaged of 9 measurements. This results in the following kernel for [math]\displaystyle{ \sigma=2 }[/math]:
g = [0.0276 0.0663 0.1238 0.1802 0.2042 0.1802 0.1238 0.0663 0.0276]
So that the sum(g) = 1.
Corner detection
If there is a corner there is a sudden bump in the obtained laserdata. The location of this bump can be determined with the gradient of the laserdata. Since we still want to filter the data a kernel is used based upon the gradient of the Gaussian. [math]\displaystyle{ \nabla G(x)=\frac{-x}{\sigma^2}\frac{1}{\sqrt{2 \pi}}e^{\frac{-x^2}{2 \sigma^2}} }[/math]
Resulting in the following kernel for [math]\displaystyle{ \sigma=2 }[/math]:
dg=[0.1353 0.2435 0.3033 0.2206 0 -0.2206 -0.3033 -0.2435 -0.1353]
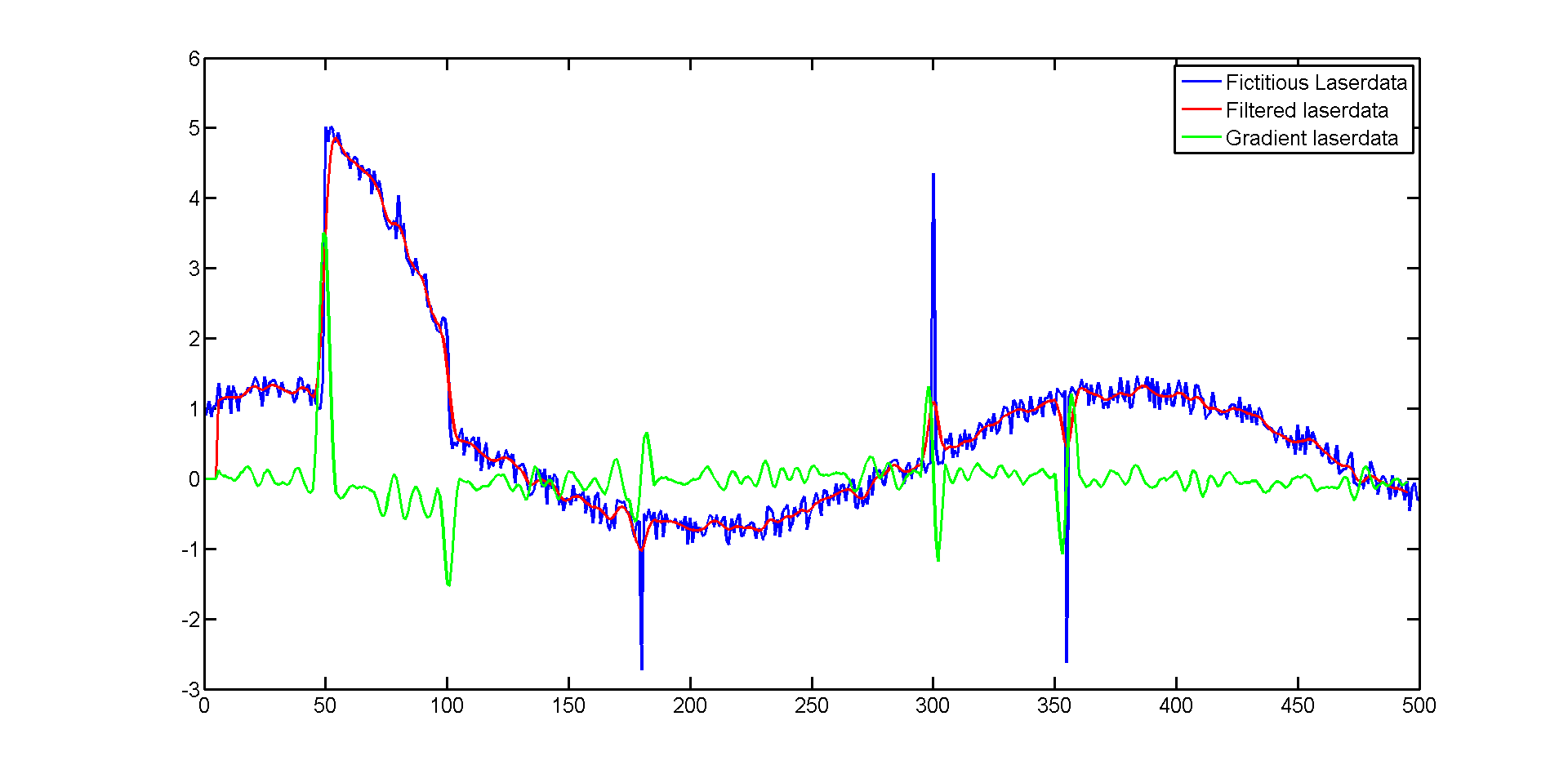
The way corners are detected can be visualized using some fictitious laserdata. We see some laserdata with both white noise as well as salt and pepper noise. The Gaussian filters the noise reasonably. The size of the kernel should be tuned. A larger kernel results in less noise, but results in more loss of data. The green line shows the gradient of the laser data. If a proper threshold is chosen this can be used to determine a bump in distance and thus a corner.
Corner movement

If there is a sideway, two corners are detected. The distance and corresponding angle towards each of those corners are sent towards the “go-around-corner-node”. Once theta1 is about + or – 90 degrees this nodes takes the following steps:
- Drive forward until L1=L2
- Turn towards corner until theta1 = theta 2
- Drive forward until theta1 > 90 degrees and theta2 < 90 degrees.
While performing these steps “wall-avoidance” keeps running. In the next stadium of programming this node should become more robust and should constantly update and control the position.
Maze
Mapping
There are two different information sources used for mapping and path determination. First of all the laserdata, which is first filtered by a Gaussian filter as explained above. Next it is used to determine possible edges. The tool used for this edge detection will probably be the Hough transform. By fitting edges of the highest probability through the laserdata a map is generated.
The second source of information is the odometry. Merely the odometry is not a sufficient tool to determine the position, because of deviations in sensordata due to effects like slip. However the odometry is a fairly easy to use tool and therefore we only use the odometry to determine an estimate of the position. This estimate is used as an initial guess to determine the “real” position, based on the laser data. This initial guess is used to fit the laserdata on the old map, which can be used to determine the real position.
Once there the position estimation and mapping are completed maze solver algorithm will be written. It should search for open and closed contours, which are respectively accessible and not accessible. One of the current ideas is to place “ficititious walls” to cover an area with a closed contour, so that an area is treated as not accessible. This will finally result in a one way corridor from entrance to exit.