This is the Wiki-page for EMC-group 3.

Checklist Wiki contents

		$[math]\displaystyle{ {{Check}} }[/math]$
1.1	Overview software architecture and approach
1.2	How does it map to the paradigms explained in this course?
2.1	Description why our solution is awesome (nice images)
2.2	Why unique/ what are we proud of?
3.1	What difficult problems and how solved?
4.1	Evaluation maze challenge (well/wrong/why/improvements?)
5.1	videos / gifs / animations / diagrams / pictures
6.1	Link to interesting pieces of the code (use snippet system like https://gist.github.com)
6.2	Comment the code and add introduction/explanatory
6.3	Make seperate section called 'code'

Group members

Name	Student number	Email
Max van Lith	0767328	m.m.g.v.lith@student.tue.nl
Shengling Shi	0925030	s.shi@student.tue.nl
Michèl Lammers	0824359	m.r.lammers@student.tue.nl
Jasper Verhoeven	0780966	j.w.h.verhoeven@student.tue.nl
Ricardo Shousha	0772504	r.shousha@student.tue.nl
Sjors Kamps	0793442	j.w.m.kamps@student.tue.nl
Stephan van Nispen	0764290	s.h.m.v.nispen@student.tue.nl
Luuk Zwaans	0743596	l.w.a.zwaans@student.tue.nl
Sander Hermanussen	0774293	s.j.hermanussen@student.tue.nl
Bart van Dongen	0777752	b.c.h.v.dongen@student.tue.nl

General information

This course is about software designs and how to apply this in the context of autonomous robots. The accompanying assignment is about applying this knowledge to a real-life robotics task.

The goal of this course is to acquire knowledge and insight about the design and implementation of embedded motion systems. Furthermore, the purpose is to develop insight in the possibilities and limitations in relation with the embedded environment (actuators, sensors, processors, RTOS). To make this operational and to practically implement an embedded control system for an autonomous robot, there is the Maze Challenge. In which the robot has to find its way out in a maze.

PICO is the name of the robot that will be used. Basically, PICO has two types of inputs:

The laser data from the laser range finder
The odometry data from the wheels

In the fourth week there is the "Corridor Competition". During this challenge, students have to let the robot drive through a corridor and then take the first exit (whether left or right).

At the end of the project, the "A-maze-ing challenge" has to be solved. The goal of this competition is to let PICO autonomously drive through a maze and find the exit. Group 3 was the only group capable of solving the maze.

Design

In this section the general design of the project is discussed.

Requirements

The final goal of the project is to solve a random maze, fully autonomously. Based on the description of the maze challenge, several requirements can be set:

Move and reach the exit of the maze.
The robot should avoid bumping into the walls.
So, it should perceive its surroundings.
The robot has to solve the maze in a 'smart' way.

Functions & Communication

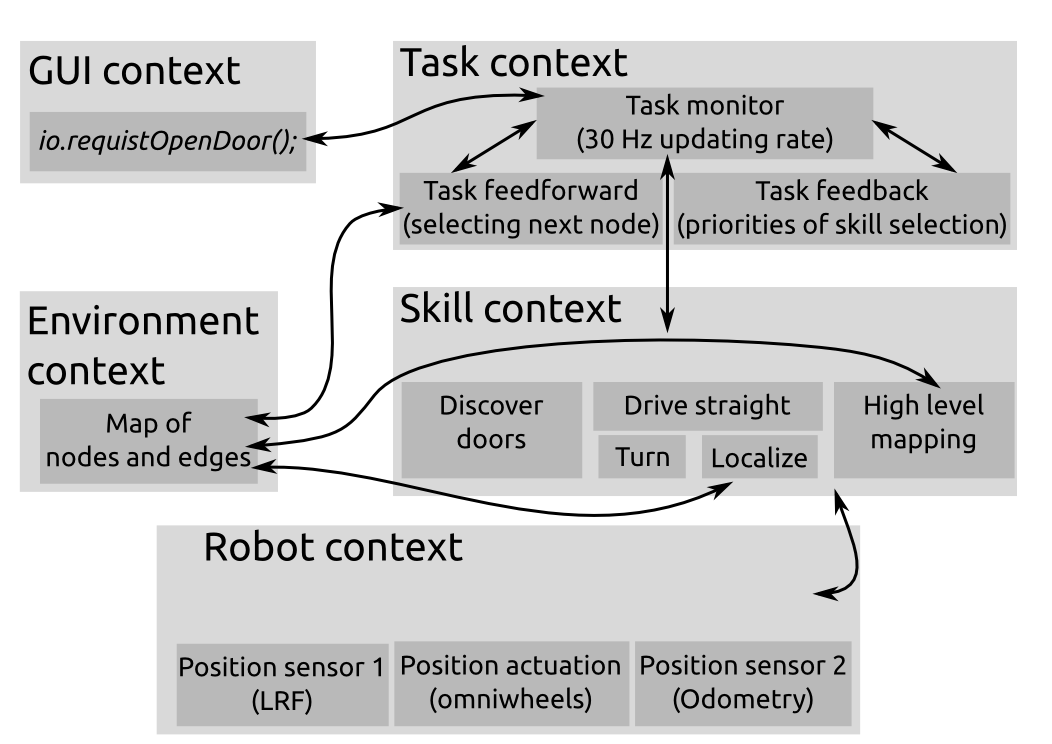
Blockdiagram for connection between the contexts

The robot will know a number of basic functions. These functions can be divided into two categories: tasks and skills.

The task are the most high level proceedings the robot should be able to do. These are:

Determine situation
Decision making
Skill selection

The skills are specific actions that accomplish a certain goal. The list of skills is as follows:

Drive
Rotate
Scan environment
Handle intersections
Handle dead ends
Discover doors
Mapping environment
Make decisions based on the map
Detect the end of the maze

Software architecture

Static LRF

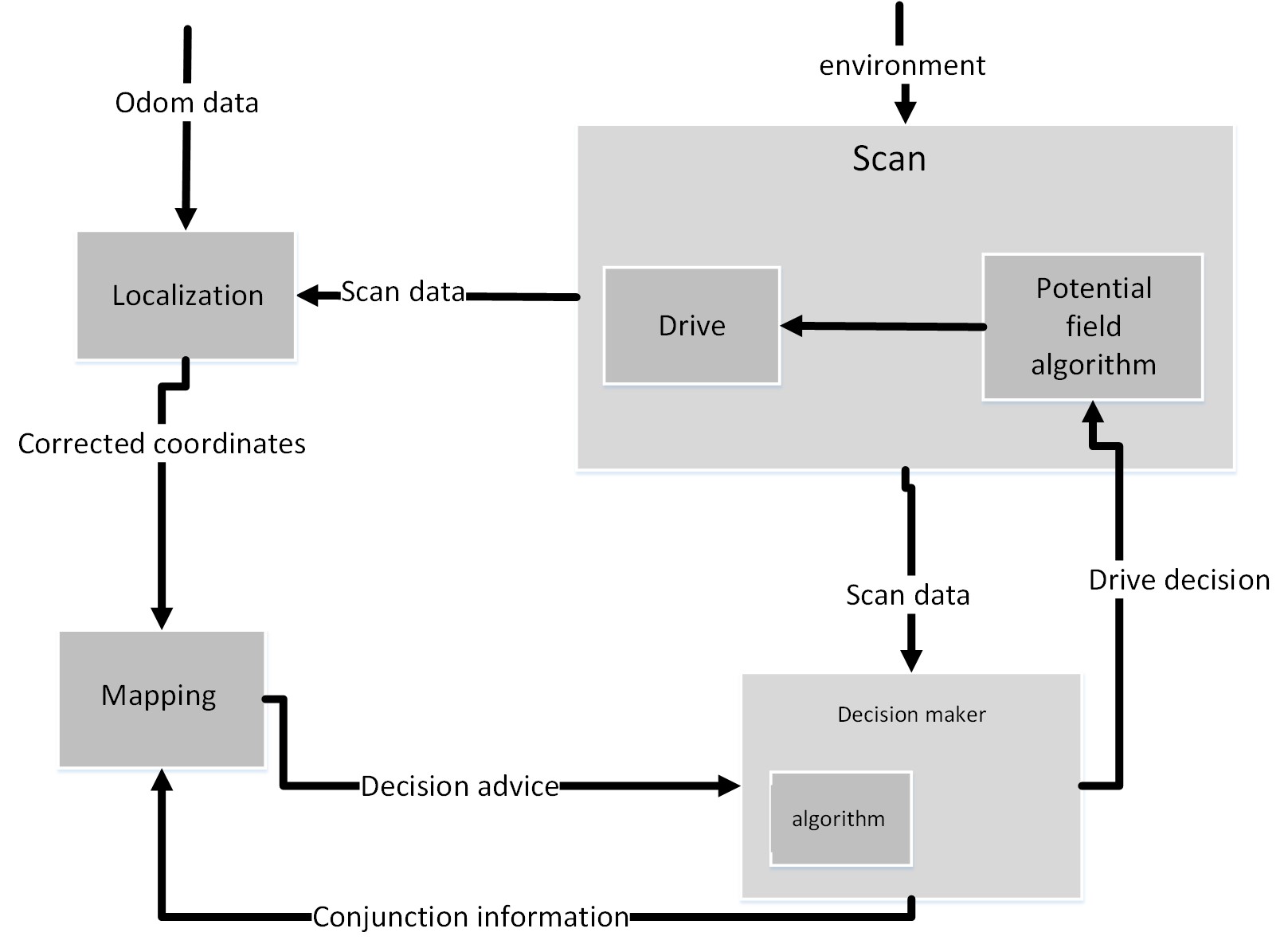
To solve the problem, it is divided into different blocks with their own functions. We have chosen to make these five blocks: Scan, Drive, Localisation, Decision and Mapping. The figure below shows a simplified scheme of the software architecture and the cohesion of the individual blocks. In practice, Drive/Scan and Localisation/Mapping are closely linked. Now, a short clarification of the figure will be given. More detailed information of each block will be discussed in the next sections.

Lets start with the Scan block:

Scan receives information about the environment. To do this it uses his laser range finder data.
Based on this data Scan consults its potential field algorithm to make a vector for Drive.
Drive interprets the vector and sends the robot in that direction.
Together the LRF and odometry data determine the traveled distance and direction. Localisation saves this in an orthogonal grid.
Mapping consults these positions to 'tell' Decision at what interesting point the robot is. For instance, this can be a junction or a dead end.
Then it should know if the robot has been there before. Based on that, Decision can send a new action to Scan/Drive.
Now the new vector is based on the environment data and the information from Decision. In this way, the robot should find a strategic way to drive through the maze.

Calibration

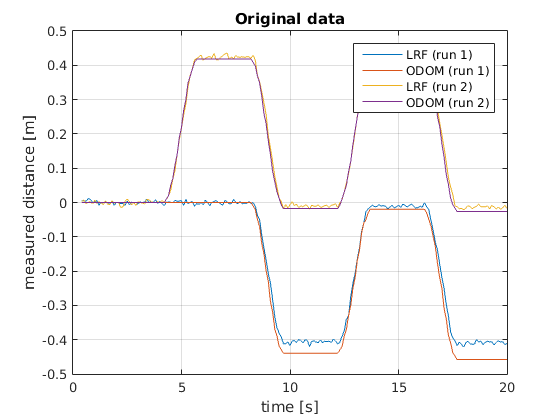
Figure 1 - Calibration: Difference between odometry and LRF

In the lectures, the claim was made that 'the odometry data is not reliable'. We decided to quantify the errors in the robot's sensors in some way. The robot was programmed to drive back and forth in front of a wall. At every time instance, it would collect odometry data as well as laser data. The laser data point that was straight in front of the robot was compared to the odometry data, i.e. the driven distance is compared to the measured distance to the wall in front of the robot. 'Figure 1 - Calibration' shows these results. The starting distance from the wall is substracted from the laser data signal. Then, the sign is flipped so that the laser data should match the odometry exactly, if the sensors would provide perfect data. Two things are now notable from this figure:

The laserdata and the odometry data do not return exactly the same values.
The odometry seems to produce no noise at all.

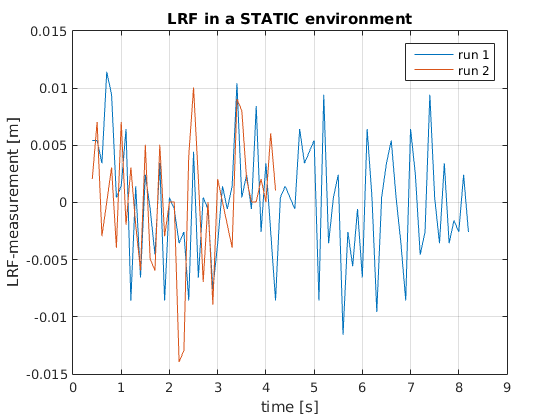
Figure 2 - Calibration: Static LRF

The noisy signal that was returned by the laser is presented in 'Figure 2 - Calibration'. Here, a part of the laser data is picked from a robot that was not moving.

The maximum amplitude of the noise is roughly 12 mm.
The standard deviation of the noise is roughly 5.5 mm
The laser produces a noisy signal. Do not trust one measurement but take the average over time instead.
The odometry produces no notable noise at all, but it has a significant drift as the driven distance increases. Usage is recommended only for smaller distances (<1 m)

Software implementation

In this section, implementation of this software will be discussed based on the block division we made.

Brief instruction about one block can be found here. In addition, there are also more detailed problem-solving processes and ideas which can be found in the sub-pages of each block.

Drive block

CP of Drive

Basically, the Drive block is the doer (not the thinker) of the complete system. The figure shows the composition pattern of Drive. In our case, the robot moves around using potential field. How the potential field works in detail is shown in Scan. Potential field is an easy way to drive through corridors, and making turns. Important is to note that information from the Decision maker can influence the tasks Drive has to do.

Two other methods were also considered: Simple method and Path planning. Especially, we worked a lot of time on the Path planning method. However, after testing, the potential field was the most robust and most convenient method.

Scan block

Composition pattern Scan

The block Scan processes the laser data of the Laser Range Finders. This data is used to detect corridors, doors, and different kind of junctions. The data that is retrieved by 'scan' is used by all three other blocks.

Scan directly gives information to 'drive'. Drive uses this to avoid collisions.
The scan sends its data to 'decision' to determine an action at a junction for the 'drive' block.
Mapping also uses data from scan to map the maze.

PICO moves always to the place with the most space using its potential field. However, at junctions and intersections the current potential field is incapable of leading PICO into the desired direction. Virtual walls are constructed to shield potential path ways, than PICO will move to its desired direction which is made by the decision maker. To create an extra layer of safety, collision avoidance has been added on top of the potential field. Also, the scan block is capable of detecting doors, which is a necassary part of solving the maze. More detailed information about these properties:

Potential field
Detecting junctions/intersections
Virtual walls
Collision avoidance
Detecting doors

Decision block

Composition pattern Decision

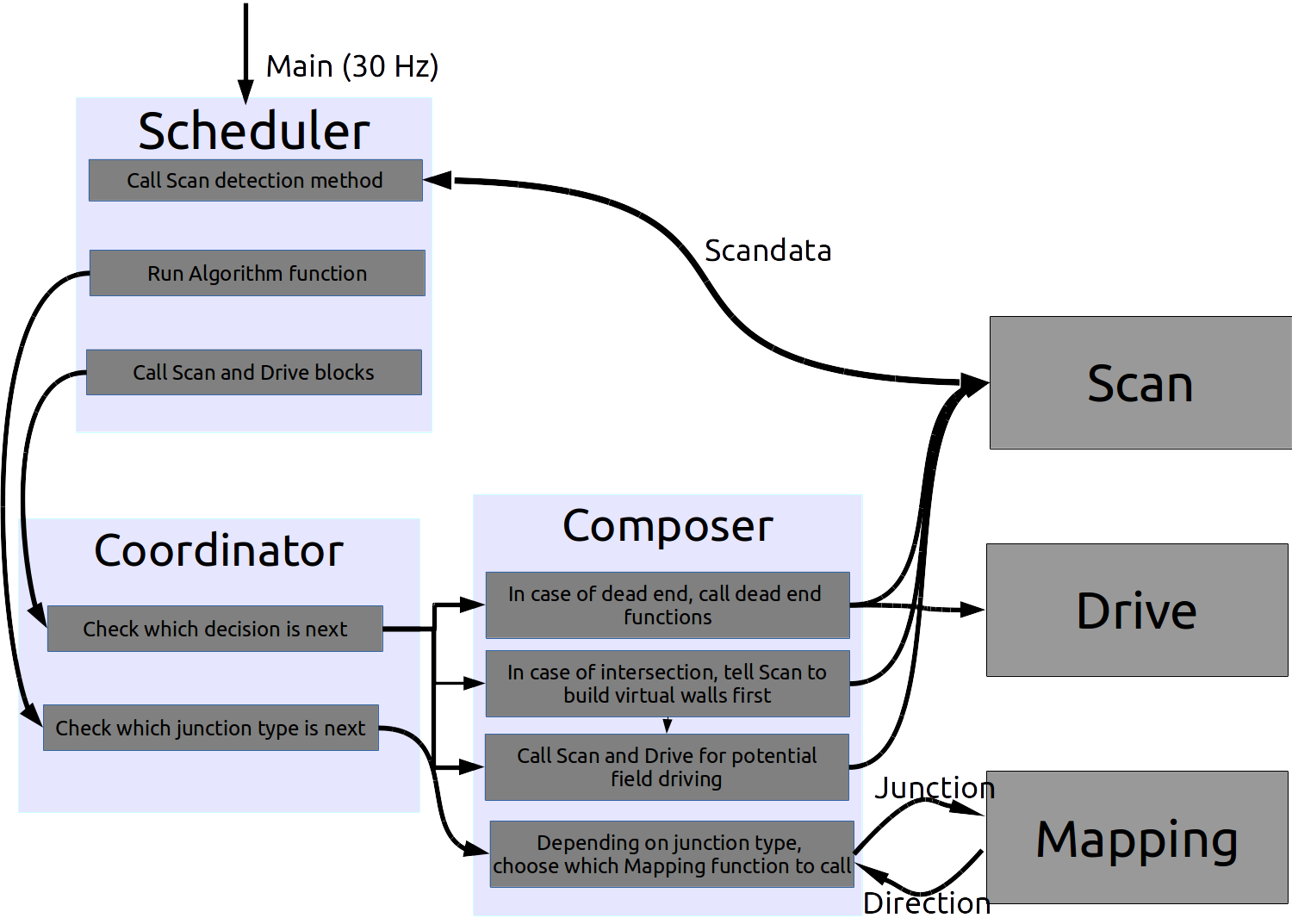
The Decision block contains the algorithm for solving the maze. It can be seen as the 'brain' of the robot. It receives the data of the world from 'Scan'; then decides what to do (it can consult 'Mapping'); finally it sends commands to 'Drive'.

Input:

Mapping model
Scan data

Output:

Specific drive action command

The used maze solving algorithm is called: Trémaux's algorithm. This algorithm requires drawing lines on the floor. Every time a direction is chosen it is marked bij drawing a line on the floor (from junction to junction). Choose everytime the direction with the fewest marks. If two direction are visited as often, then choose random between these two. Finally, the exit of the maze will be reached.

Mapping block

Map&solve algorithm

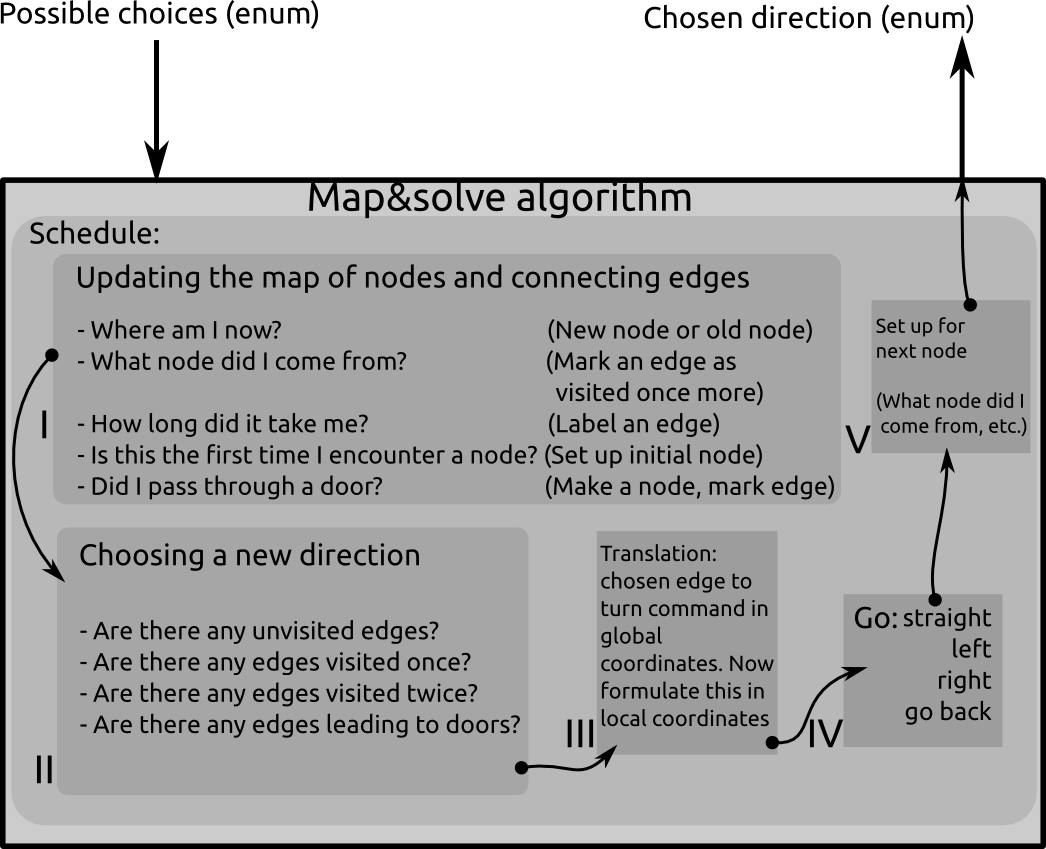
The mapping block will store the corridors and junctions of the maze. Therefore, the decision block can consider certain possiblilities, to ensure that the maze will be solved in a strategic way.

As is said in the previous paragraph, the Tremaux algorithm is used: .

The maze will consist of nodes and edges. A node is either a dead end, or any place in the maze where the robot can go in more than one direction. an edge is the connection between one node and another. An edge may also lead to the same node. In the latter case, this edge is a loop. The algorithm is called by the general decision maker whenever the robot encounters a node (junction or a dead end). The input of the algorithm is the possible routes the robot can go (left, straight ahead, right, turn around) and the output is a choice of possible directions that will lead to solving the maze.

The schedule looks like this:

Updating the map:

Robot tries to find where he is located in global coordinates. Now it can decide if it is on a new node or on an old node.
The robot figures out from which node it came from. Now it can define what edge it has been traversing. It marks the edge as 'visited once more'.
All sorts of other properties may be associated with the edge. Energy consumption, traveling time, shape of the edge... This is not necessary for the algorithm, but it may help formulating more advanced weighting functions for optimizations.
The robot will also have to realize if the current node is connected to a dead end. In that case, it will request the possible door to open.

Choosing a new direction:

Check if the door opened for me. In that case: Go straight ahead and mark the edge that lead up to the door as Visited 2 times. If not, choose the edge where you came from
Are there any unvisited edges connected to the current node? In that case, follow the edge straight in front of you if that one is unvisited. Otherwise, follow the unvisited edge that is on your left. Otherwise, follow the unvisited edge on your right.
Are there any edges visited once? Do not go there if there are any unvisited edges. If there are only edges that are visited once, follow the one straight ahead. Otherwise left, otherwise right.
Are there any edges visited twice? Do not go there. According to the Tremaux algorithm, there must be an edge left to explore (visited once or not yet), or you are back at the starting point and the maze has no solution.

Translation from chosen edge to turn command:

The nodes are stored in a global coordinate system. The edges have a vector pointing from the node to the direction of the edge in global coordinates. The robot must receive a command that will guide it through the maze in local coordinates.

The actual command is formulated

A set-up is made for the next node

e.g., the current node is saved as a 'nodeWhereICameFrom', so the next time the algorithm is called, it knows where it came from and start figuring out the next step.

Localisation block

The purpose of the localisation is that the robot can prevent itself from driving in a loop for infinite time, by knowing where it is at a given moment in time. By knowing where it is, it can decide based on this information what to do next. As a result, the robot will be able to exit the maze within finite time, or it will tell there is no exit if it has searched everywhere without success.

The localisation algorithm is explained in on the Localisation page; by separating and discussing the important factors.

Code

This section highlights several interesting parts of our code.

...

A-maze-ing Challenge

In the third week of this project we had to do the corridor challenge. During this challenge, we have to let the robot drive through a corridor and then take the first exit (whether left or right). This job can be tackled with two different approaches:

Make a script only based on the corridor challenge.
Make a script for the corridor challenge but with clear references to the final maze challenge.

We chose the second approach. This implies that we will have to do some extra work to think about a properly structured code. Because only then the same script can be used for the final challenge. After the corridor competition, we can discuss about our choice because we failed the corridor challenge while other groups succeed. But most of these group had selected approach 1 and we already had a decent base for the a-maze-ing challenge. And this was proving its worth later..

For the a-maze-ing challenge we decided on using two versions of our software package. In the first run (see section Video's further down on the page), we implemented Tremaux's algorithm together with a localiser that would together map the maze and try to solve it. Our second run was conducted with the Tremaux's algorithm and localisation algorithm turned off. Each time the robot encountered a intersection, a random decision was made on where to go next.

Run 1

The first run is taped on video and can be seen here. The robot recognizes a four-way cross-section and decides to turn to the left corridor. It then immediately starts do chatter as the corridor was more narrow than expected. Next, it follows the corridor smoothly until it encounters the next T-juction. The robot is confused because of the intersection immediatly to its left. After driving closer to the wall, it mistakes it for a door. Because it (of course) didn't open, it decides to turn to right and explore the dead end. In the part between 20 seconds and 24 seconds in to the video, the robot is visibly having a hard time with the narrow corridor. It tries to drive straight but also evade the walls to the left and to the right. It recognizes another dead-end and turns around swiftly. It crosses the T-junction again by going straight and at 43 seconds it again thinks it is in front of a door. After ringing the bell, it waits for the maximum of 5 seconds that it can take to open the door. Now, it recognized that also this is a dead-end and not a door. After turning around it drives back to the starting position. Between 1:11 and 1:30, it explores the edges that he has not yet seen. Here, the Tremaux's algorithm and the localiser 'seem' to be doing their job just fine. Unfortunately, as can be seen in the rest of the video, something went wrong with the other nodes to be placed. It decides to follow the same route as the first time, fails to drive to the corridor with the door in it and eventually got stuck in a loop.

Main reason for failure is thought to be the node placement. The first T-junction that the robot encountered made PICO go into its collision avoiding mode, which might have interfered with the commands to place a node. It is also possible that this actually happened, but that the localization went wrong because of all the lateral swaying to avoid collisions with the wall. It was clear that the combination of localisation, the maze-solving algorithm and the situation recognition by LRF was not yet ready to be implemented as a whole. Therefore, we decided to make the second run with a more simple version of our software, running only the core-modules that were tested and found to be reliable.

Run 2

For the second run, we ran a version of our software without the Tremaux's algorithm implemented and with the global localiser absent. These features were developed later in the project and were not finished 100%. For this run, a random decision was passed to the decision maker every time it asked for a new direction to head to.

The second run can be seen here. Again the robot immediately decides to go left. Note that the first corner it takes in the corridor, between 0:02 and 0:04 are exactly the same. This is because the robot is driven by separate blocks of software. The blocks that are active during the following of a corridor were exactly the same for both runs. At 00:7, the collision detection works just in time to prevent a head on collision with the wall in front of PICO at the T-junction. Now, a random decision is made to go left, followed by a right turn in to the corridor with the door. It recognizes the door in front of it exactly as expected and stops to ring the doorbell. Although the door started moving immediately after ringing the bell, the robot is programmed to wait for five seconds until it is allowed to move again. During these five seconds, it used the LRF to check if the door moved out of its way. After the passage was all clear, the robot started exploring the new area. Now, the robot drives in to the open space. Note that, between 0:30 and 0:36, the robot made a zigzag manoeuvre. When it first drives into the open space, the potential field points at the center of this open space. Between 0:36 and 0:46 it drives in 'open space mode'. This means that the robot will drive to the nearest wall and starts driving alongside of it. It should thereby always find a new node where a new decision can be made. By doing so, it drives into a corridor. Note that at 0:47, the normal 'corridor mode' started working again. The potential field method will direct the robot towards the middle of the corridor. This explains the sharp turn it made at 0:47. After hearing the presenter ask to 'Please go left... Please go left?!?', the robot makes another random decision. As luck would have it, the random decision was indeed to go left. It slightly overturns, but the collision detection saves PICO from crashing into the wall yet again at 1:06. At 1:10, the well earned applause for PICO started as he finished the maze in a total time of 1:16!

Experiments

Seven experiments are done during the course. Here you can find short information about dates and goals of the experiments. Also there is a short evaluation for each experiment.

Files & presentations

Initial design document (week 1): File:Init design.pdf
First presentation (week 3): File:Group3 May6.pdf
Second presentation (week 6): File:Group3 May27.pdf
Final design presentation (week 8): File:EMC03 finalpres.pdf

Videos

Experiment 4: Testing the potential field on May 29, 2015.

https://youtu.be/UAZqDMAHKq8

Maze challenge: Tremaux's algorithm, but failing to solve the maze. June 17, 2015.

https://www.youtube.com/watch?v=fzsNA2OUwww

Maze challenge: Winning attempt! on June 17, 2015.

https://www.youtube.com/watch?v=UHz_41Bsi7c

Embedded Motion Control 2015 Group 3

Contents

Checklist Wiki contents

Group members

General information