FINAL REPORT The Iron Giant

Group members:

Caption
Name	student ID
Marten de Klein	1415425
Ruben van de Guchte	1504584
Vincent Hoffmann	1897721
Adis Husanović	1461915
Lysander Herrewijn	1352261
Timo van der Stokker	1228489

Component selection Restaurant challenge

Is the choice of components motivated by the challenge?
Are the components adapted to the requirements of final challenge?
Does the wiki show an understanding of the algorithms in the component?

Experimental validation of the components

Are the components tested individually?
Are the experiments performed a suitable approximation of the conditions of the final challenge?
Are the conclusions drawn supported by the results of the experiments?

System design for the final challenge

Is the design presented complete?
Is the design communicated clearly?
Are design choices motivated by the final challenge?

Experimental validation of system design

Are the experiments performed a suitable approximation of the final challenge?
Are the conclusions drawn supported by the results of the experiments?

Evaluation Restaurant challenge

Is the behaviour during the final challenge explained?
Is this behaviour linked back to the designed system?
If applicable, is an adjustment to the design proposed?

Localization exercises improvement

Assignment 0.1 Explore the code framework

How is the code is structured?

The code is the implementation of a particle filter using either uniformly or gaussian distributed samples. The code of the particle filter consists of multiple classes, which are data structures that also include functionality. These data structures are linked to each other to divide functionality to segments which can be tested individually. The base of the particle filter structure is the identically named ParticleFilterBase. The base is the collection of the whole particle filter structure and thus of the particles. The ParticleFilter is the in the back-ground running code of the particle filter base structure which actually performs the particle tasks such as initialization, updating and resampling. Both classes work with a sub-class called particle. The particle class is the class of a single particle which consists of the location and weight of the particle. The class has functionality to update the position of the individual particle, get its likelihood, set its weight and initialise.

What is the difference between the ParticleFilter and ParticleFilterBase classes, and how are they related to each other?

The ParticleFilterBase class is like a basic framework for implementing particle filtering algorithms. It contains functions such as particle initialisation, propagation based on motion models, likelihood computation using sensor measurements, and weight management. Furthermore, the class ParticleFilterBase provides implementations that can be extended and customized for specific applications. It remains flexible by providing methods to set measurement models, adjust noise levels, and normalize particle weights, allowing it to be used effectively in different probabilistic estimation tasks.

On the other hand, the ParticleFilterclass builds upon ParticleFilterBase. ParticleFilter extends the base functionality by adding features such as custom resampling strategies, more advanced methods to estimate the state of a system, and integration with specific types of sensors. By using ParticleFilterBase as its foundation, ParticleFilter can focus more on the specific choice of filtering, enabling efficient reuse of core particle filter components while providing unique requirements of different scenarios or systems. This modular approach not only improves code reusability but also makes it easier to maintain and adjust particle filtering systems for different applications, ensuring robustness in probabilistic state estimation tasks.

How are the ParticleFilter and Particle class related to each other?

The ParticleFilter and Particle classes collaborate to implement the particle filtering algorithm. The ParticleFilter manages a collection of particles, arranging their initialization, propagation, likelihood computation, and resampling. In contrast, each particle represents a specific hypothesis or state estimate within the particle filter, containing methods for state propagation, likelihood computation, and state representation. Together, they determine the probabilistic state estimation by using the multiple hypotheses of the particles and probabilistic sampling to approximate and track the true state of dynamic system based on sensor data and motion models.

Both the ParticleFilterBase and Particle classes implement a propagation method. What is the difference between the methods?

The ParticleFilterBase::propagateSamples method ensures all particles in the filter move forward uniformly and in sync. It achieves this by applying motion updates and noise consistently to every particle, thereby keeping coordination in how they update their positions. This centralised approach guarantees that all particles stick to the same movement rules, effectively managing the overall motion coordination for the entire group.

On the other hand, the Particle::propagateSample method focuses on updating each particle individually. It adjusts a particle's position based on its current state and specific motion and noise parameters. Unlike ParticleFilterBase, which handles all particles collectively, Particle::propagateSample tailors the movement update for each particle according to its unique characteristics. This allows each particle to adjust its position independently, ensuring flexibility in how particles evolve over time.

Assignment 1.1 Initialize the Particle Filter

Initialization of particle filter

What are the advantages/disadvantages of using the first constructor, what are the advantages/disadvantages of the second one?

In which cases would we use either of them?

The first constructor places random particles around the robot with an equal radial probability (uniformly distributed). Each particle has an equal chance of being positioned anywhere around the robot, with completely random poses. This method is particularly useful when the robot’s initial position is unknown and there is no information about its location on the global map. By distributing particles randomly, the robot maximizes its likelihood of locating itself within the environment. The key advantages of this approach include wide coverage and flexibility, making it ideal for scenarios where the robot's starting position is completely unknown. However, the disadvantages are lower precision due to the wide spread of particles and higher computational demands, as more particles are needed to achieve accurate localization.

In contrast, when the robot’s position and orientation are known, the second constructor is more effective. This method initializes particles with a higher probability of being aligned with the robot's known state, placing more particles in at the location of the robot and orienting them similarly (gaussian distributed). This concentrated placement allows for more accurate corrections of the robot’s position and orientation as it moves forward. The advantages of this approach include higher precision and efficiency, as fewer particles are needed for accurate localization. However, it has the drawback of limited coverage, making it less effective if the initial guess of the robot’s position is incorrect. Additionally, it requires some prior knowledge of the robot’s initial position and orientation. This constructor is best used when the robot has a general idea of its starting location and direction.

Particle cloud with green arrow average

Assignment 1.2 Calculate the pose estimate

Interpret the resulting filter average. What does it resemble? Is the estimated robot pose correct? Why?

The filter calculates a weighted average across all particles to estimate the robot's state, including its position and orientation. Particles that align closely with sensor data receive higher weights, allowing the particle swarm to adapt to sensor readings. As the filter operates over time, the estimated pose gradually aligns more closely with the actual pose of the robot. However, some discrepancy in pose may persist due to the finite number of particles, which limits the filter's ability to fully represent the pose space. Iterating through the particle swarm with noise can enhance the accuracy of the estimated robot pose over successive iterations.

The resulting filter average, determined in ParticleFilterBase::get_average_state(), represents the estimated pose of the robot based on the weighted distribution of particles in the particle filter. This average pose represents the center of mass of the particle cloud, which approximates the most likely position of the robot according to the filter's current state. The alignment of the robots pose and the the average state of the particle cloud depends on several factors:

Particle Distribution: The particles should be distributed in a way that accurately reflects the true probability distribution of the robot's pose, then the estimated pose is likely to be correct or close the actual robot position.
Particle Weighting: The accuracy of the estimated pose of the robot depends on the weights assigned to the particles which represent their likelihood w.r.t. being at the robots pose. Particles with a higher weight contributed more to the average pose calculation, where the more probable poses are given more importance.
Model Accuracy: Another effect on the accuracy of the average state is how accurate the motion model (which is used to propagate particles) and the measurement model (used to update the particle weights) are. These models should accurately reflects the robot's actual movement and sensor measurements, then the estimated pose is more likely to be correct.

Currently, there is a difference between the average state and the actual robot position. This differences comes from several factors. Firstly, all particles have been assigned the same weight, which prevents the filter from properly reflecting the likelihood of different poses. In a correct setup, particles with higher weights should have more influence on the average pose calculation, accurately representing more probable robot poses.

Furthermore, the motion and measurement models essential for incorporating the robot's movement and sensor measurements have not yet been implemented in the script. These models are crucial for accurately updating particle positions and weights based on real-world data. Without them, the estimated state cannot accurately reflect the robot's actual movement and the measurements from its sensors.

Imagine a case in which the filter average is inadequate for determining the robot position.

The filter average assumes that the robot position is the average of all particle positions. This works well if all particles form a single cloud with a gaussion distribution which is the case if a large number of particles is used. Using a very small amount of particles could result in a less accurate sampling of the distribution. The filter average could be less useful if instead of a single gaussion particticle cloud, multiple clusters are formed. All clusters represent a possible location of the robot, and averaging of the particles then would result in a position in between the clusters where much less particles exist. Then a location is chosen which is less likely compared to inside one of the particle clusters. Identifying the clusters and computing the most likely cluster might in this case be a more suitable method compared to averaging.

Assignment 1.3 Propagate the particles with odometry

Why do we need to inject noise into the propagation when the received odometry information already has an unknown noise component?

When injecting noise during propagation, it is accounting for the fact that odometry data already has some unknown noise due to various factors like uncertainties due to factors like sensor inaccuracies, wheel slippage, or environmental conditions affecting the robot's movement. This additional noise helps the particle filter better represent the uncertainty in the robot's movement. It prevents the filter from becoming too confident in a single, potentially incorrect robot pose estimate. By adding noise, it allows the filter to explore different possible positions and corrent for the original noise in the measurement.

What happens when we stop here, and do not incorporate a correction step?

If the correction step is not incorporated, the particle filter cannot improve its estimates using actual sensor measurements. This means it only relies on predicted positions based on noisy odometry data. Over time, without corrections, errors and uncertainties in the odometry accumulate. The filter doesn't adjust its estimates to match what the sensors actually observe. As a result, the robot's estimated position could drift further away from its actual position because it doesn't course-correct based on real sensor data.

In the following link the resulting moving particle cloud is shown:

Simulation Localization Moving particle cloud

Assignment 2.1 Correct the particles with LiDAR

What does each of the component of the measurement model represent, and why is each necessary.

The measurement model consists of three main components: data, prediction, and additional parameters from lm. data represents the actual measurement obtained from the robot's LiDAR sensor. prediction refers to the measurement generated by a raycasting algorithm, which corresponds to what the LiDAR measurement would be if the robot were positioned exactly at the particle's pose. The likelihood of the particle accurately representing the robot's position is determined by four components:

Gaussian Likelihood: Represent the likelihood that the actual sensor measurement (data) matches the predicted measurement (prediction) under a Gaussian distribution assumption. This part is necessary as it captures the uncertainty in sensor measurements due to noise and provides a probabilistic measure of how closely the predicted and actual measurements align.
Maximum Range Check: Represents a scenario where the actual measurements exceeds the maximum permissible range (lm.max_range). This is necessary as it assigns a probability (lm.max_prob) to sensor readings that fall beyond the pre-defined sensor's range, accounting for scenarios where measurements are unreliable or uninformative due to range limitations.
Random Value Check: Represents the probability of random sensor readings with the pre-defined permissible range (0 ≤ range <lm.max_range). This is necessary as it assigns a probability (lm.rand_prob) to random measurements within the max range, recognizing the possibility of unpredictable sensor behaviour or noise.
Short Measurement Probability: Represents the likelihood of the measurements that are shorter than expected compared to the prediction. This is necessary as it assigns a probability (lm.short_prob) which models the decay in measurement intensity over distance, which are for measurements that are shorter than predicted due to physical or environmental factors.

With each particle having N >> 1 rays, and each likelihood being ∈ [0, 1], where could you see an issue given our current implementation of the likelihood computation.

All likelihoods per particle are multiplied with each other. This results in total likelihood being ∈ [0, 1]. However, when one of the components is not weighted properly, it would not contribute significantly enough to the final likelihood value as it should be. Especially, considering the short measurement probability component, when it is set too high, the particles close to a wall will get a large sum of small measurement contributions. These particles might overshadow some particles which were correct based on hits.

Assignment 2.2 Re-sample the particles

What are the benefits and disadvantages of both the multinomial resampling and the stratified resampling?

Multinomial resampling:

Benefits:
- Proportional sampling: It directly samples the particles according to their weights, making sure that all the particles with a higher weight are more likely to be selected which represent regions of higher probability density in the state space.
- Efficiency: It is computationally quite efficient when dealing with a large number of particles (N).
Disadvantages:
- Reduced particle diversity: It can lead to a reduction to diversity in the particle set, as only a few particles have significant weights while the majority have negligible weights. The reason for this is because the particles with lower weights are less likely to be selected.
- Handling weight variety: It can struggle when there is a large variety in particle weights. If there are some particles with a much larger weights than other, the multinomial resampling method may not effectively distribute the particles to accurately represent the lowest distribution.

Stratified resampling:

Benefits:
- Improved particle diversity: It approaches the particle diversity much better compared to the multinomial resampling method by making sure that there is a more uniform spread of particles across the weighted distribution. The method divides the cumulative distribution function (CDF) into strata and then selects the particles more uniformly from each stratum which results in more diversity.
- Handling weight variety: When there is a significant variety in particle weights the stratified resampling method handles it well. By stratifying the CDF, it makes sure that even particles with a lower weights has a chance to be selected.
- Stable estimation: By making sure to have a diverse set of particles, the stratified resampling method provides a more stable estimation of the lower distribution. This helps in reducing the variance in the weights and improve accuracy of the filter.
Disadvantages:
- Complexity: Implementing the resampling method requires more effort compared to multinomial resampling due to the use of the CDF into strata and sample from each stratum accordingly. This adds extra complexity which increases the implementation time.
- Efficiency: The process of stratification can be more computational intensive compared to the multinomial resampling as the additional operations are involved in stratifying the CDF which may have an effect on performance where high-frequency is necessary.

With each particle having N>> 1 rays, and each likelihood being ∈ [0, 1] , where could you see an issue given our current implementation of the likelihood computation?

All likelihoods per particle are added up and then normalized with the amount of beams that are used to calculate the system. This results in the equal weighting of all rays to the final likelihood of the particle. This could dilute the impact of important rays where for example an obstacle is detected by only a few rays where the rest of the rays do not detect this obstacle.

Assignment 2.3 Test on the physical setup

At the original deadline the localization was not properly tuned and tested. After the submission of the exercises this is still executed which resulted in the knowledge described below.

How you tuned the parameters:

Multiple parameters are adjusted while testing the localization, namely: the propagation parameters, the number of particles, the hit probability, hit sigma, random probability and finally also the resampling is tuned. The parameters are first tuned in simulation where not only the basic simulation maps are taken but also slightly altered simulation maps with additional obstacles, altered walls and multiple starting positions. The parameters are tuned by trial and error to understand which parameters should be improved and which parameter is already sufficient. Then, the localization is also tested on the real setup.

Number of particles: The number of particles has a strong effect on the running time of the filter. If the number of particles becomes too low the accuracy of the filter is significantly effected. Therefore the maximum number of particles possible to still achieve a 5 Hz bandwidth is chosen.
Hit probability: The hit probability is slightly reduced which showed improved behaviour for unmodeled obstacles.
Hit sigma: The standard deviation is slightly increased which showed better behaviour for unmodeled obstacles.
Short lambda: The lambda parameter was also increased to account for nearby obstacles which are not in the map but this did not showed improved results and was changed back to the initial value.
Random probability: The random probability is slightly increased on the real setup which showed some improved behaviour on the real setup where more measurement errors occured.
Resampling threshold: The resampling threshold was also increased a factor 10 and the resampling scheme was set to effectiveParticleThreshold. This improved the computational efficiency significantly. The threshold was in the end reduced a bit due to a larger particle cloud forming than desired.

How accurate your localization is, and whether this will be sufficient for the final challenge.

The localization is quite accurate. While moving, the localization is at most a 10 centimeters behind the real location on the real setup (video at the end). When standing still the localization seems to be even within the few centimeter range. This allows the robot to follow a path easily if the threshold range if set larger than 10 centimeter.

How your algorithm responds to unmodeled obstacles.

The localization algorithm is sensitive to unmodeled obstacle. If there exists a very large flat wall like obstacle the localization will quickly get away from its actual position. This is expected because the disturbance is very significant. The algorithm is also quite sensitive if a wall is removed which is not removed from the map. This also leads to the robot quickly moving further away from its actual position. The robot localization is not very sensitive to smaller obstacles, small mismatches between the real room and simulated map or obstacle which have round geometries like bins and chair legs. This makes the localization robust enough for the final challenge where additional obstacles are placed but no large walls are added or removed.

Whether your algorithm is sufficiently fast and accurate for the final challenge.

The number of particles are first set to 2500 where the simulation is unable to keep up with the framerate of 5 Hz. The results in the particles lagging behind as shown in the simulation video. When the robot stops again it is clear that the particles are following the robot quite well but this is not very feasible for the real setup.

Simulation Localization Multinominal 2500 Particles

Simulation Localization Stratified 2500 Particles

Reducing the number of particles to 300 results in the simulation being able to follow the robot much better. The video of multinominal resampling shows that the green arrow is closely following the robot and is at most one timestep behind. When stopping the green arrow overlays within one timestep again with the robot. In these simulations this still looks a little bit buggy but after including all improvements described above this resulted in a very fast and accurate localization discussed in the next section.

Simulation Localization Multinominal 300 Particles

Simulation Localization Stratified 300 Particles

Localization for final assignment

The algorithm works fast and accurate such that the estimated position follows closely to the robot. This is verified on the real setup as shown in the video in the link below.

Localization test on HERO

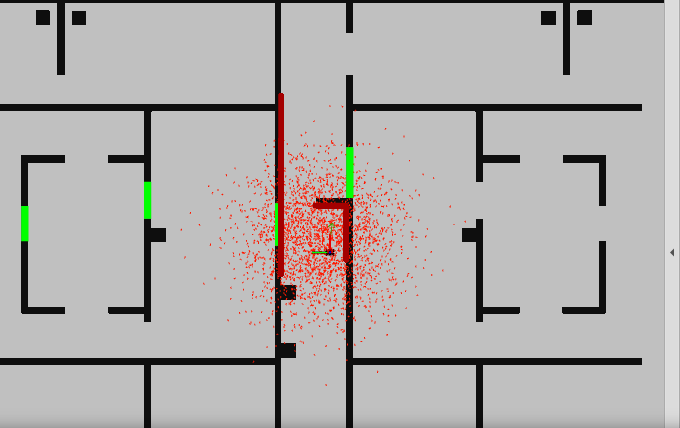
Although somewhat difficult too see, HERO has the difficult task to locate itself even though one of the larger walls is removed at the start. HERO glitches forward because it thinks it is already further along the hallway but as soon as hero actually reaches the end of the hallway it finds itself back and moves without any problems through the remainder of the map. Clearly shown in the final shot of the video is the laser data mapped over the RVIZ map showing a close approximation.

Introduction

State flow

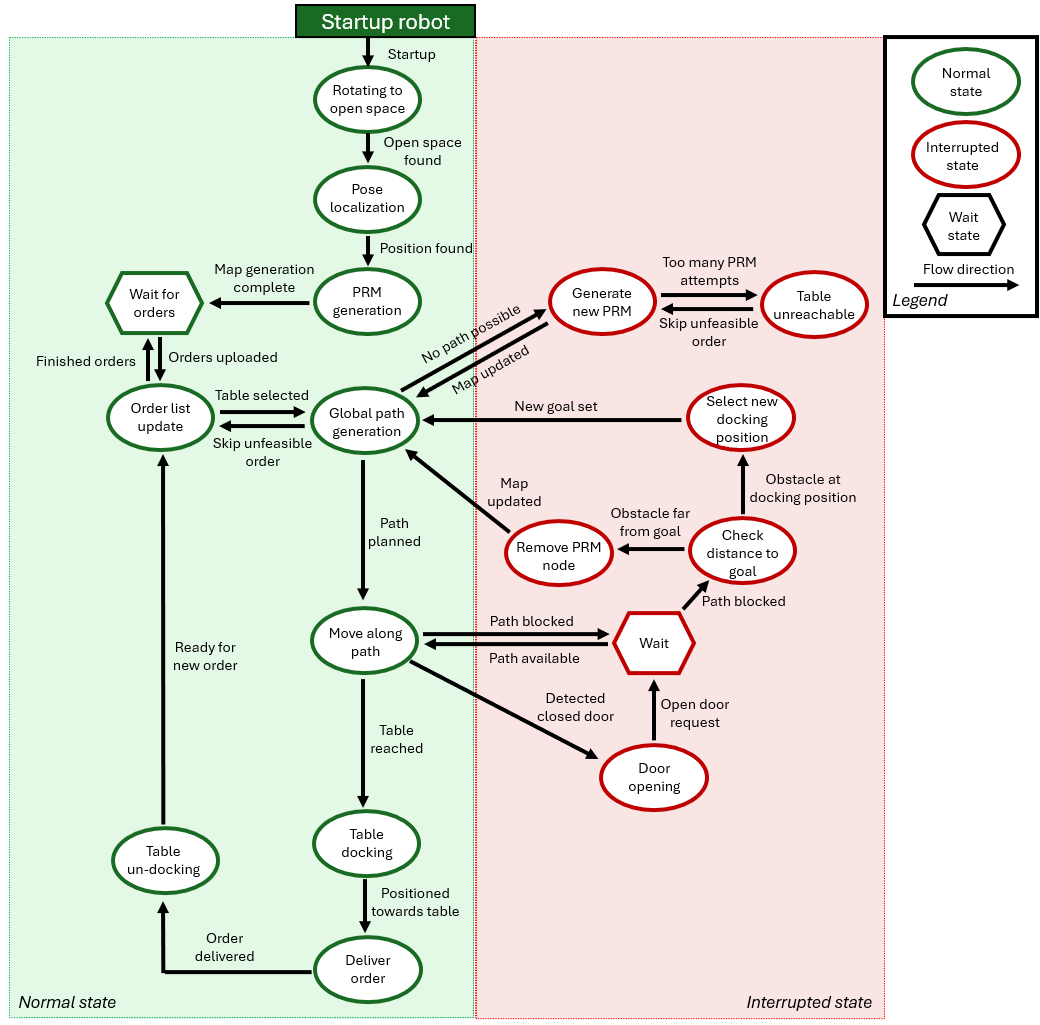
The state flow diagram, representing the state machine created to tackle the Mobile Robot Challenge. One can make a distinction between the normal and the interrupted states.

The state flow of the robot is shown in the figure on the right. The robot code works identical to this state flow by implementing a state machine in c++. This allowed us to debug the robot very efficiently and ensure that separate components worked most efficiently. The components of the state flow will be elaborated here. The specific inner working of the functions and states is described further on in the wiki. Furthermore, the numbered states are the states are written in the code, these are not completely one to one as described in the figure describing the states of the robot.

Robot startup

These states are only called when the robot starts up and are not revisited.

1: The first state initializes pose finding by rotating the robot.

2: In the second state, the robot tries to localize itself for 10 timesteps. It will go back to the state 1 when the timesteps have not been exceeded.

3: The final startup state initializes the PRM.

Normal states

When the robot does not encounter any hurdles, this sequence of states is followed to deliver all plates. Naturally, dynamic changes in the environment call for adaptive behavior indicated by the interrupted states.

4: From state 3, we move to state 4 in which the robot updates the order list.

5: In this state the A* function is called to find a path based on the PRM and the order list. If no path can be found we enter our first interrupted state; 10.

6: State 6 is the movement state with the most potential interruptions. The robot can find encounter several situations in which the robot will go to an interrupted state. XXXXX

Interrupted states

10: State 10 is called when no path can be found to the table. In this case, the introduced obstacles in the map are removed by reinitializing the PRM from the starting restaurant map. We go back to state 4.

Code buildup

The final main code updates each loop the laser, odometry data and it updates the localization. Then it enters the state machine where it goes to the state specified. In this state the corresponding tasks are executed and either a new state is specified or the same state is kept for the next loop. Then the poseEstimate of the robot is updated and the velocity is send to the robot. Then the loop ends and the next loop is started if the cycle time is completed.

Data flow

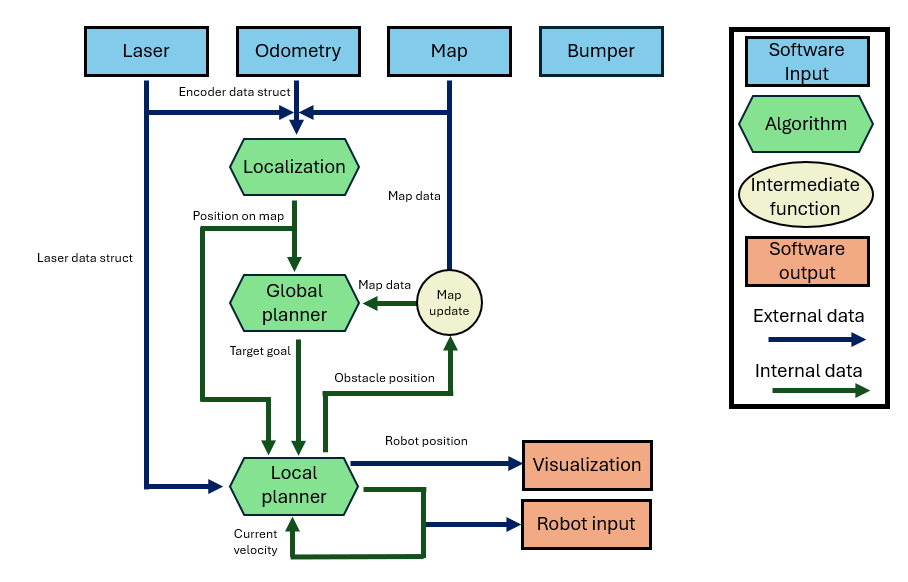
The data flow is an important part of the code functionality. Therefore, a data flow diagram is created which clearly shows how inputs are connected to algorithms which output information to the robot. The data flow diagram is shown in the figure on the right.

There are three main input originating from the robot and one input originating from the user. Important to notice is that the Bumper input is not connected. This component had simulation software bugs, which hindered the functionality of the sensor. The bumper sensor has the added value of measuring if the robot hits an obstacle which is not detected by the laser sensor. This makes the sensor very valuable and therefore still displayed in the data flow.

Explain data structure

Components

DWA Overview

DWA vision range (The image is adapted from MRC Introduction lecture)

Local Planner

In the exercises of the local planner both the dynamic window approach (DWA) and the vector field histogram (VFH) were developed. These two methods were then also combined with the global algorithm. The choice was made to use DWA for the final challenge due to some very undesired robot behaviour after implementing the VFH in combination with the global planner. The robot kept hitting obstacles and the group was unable to resolve these issues with the developer of the VFH being in another country. The biggest advantage of our DWA algorithm was the ability to not hit chairs with the help of the path generation component that calculates the distance to an obstacle for each laser measurement.

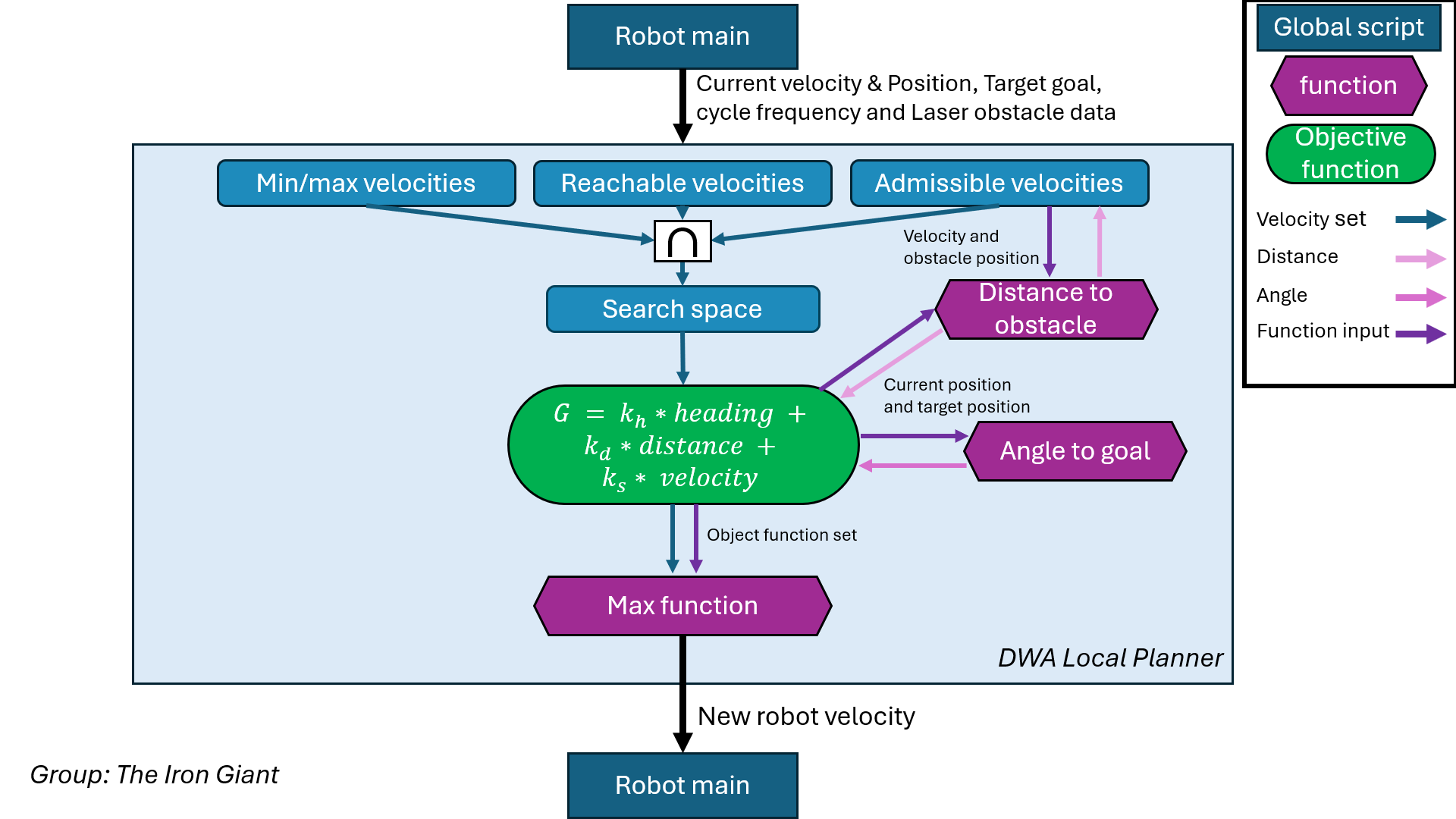
Some changes have been made to the DWA alorithm to ensure that the local planner is robust and efficient. The algorithm still consists of the same components as described in the exercises and as shown in the DWA Overview figure on the right. The improvements are made by tuning the parameters as well as increasing the vision range.

The tunable parameters of the DWA consists of parameters in the objective function, the velocity and acceleration of the robot and the stopping distance. The parameters of the objective function are tuned to aim more direct on the setpoints generated by the global planner and get less deviated by the distance to obstacles. This reduces the obstacle avoidance functionality of the DWA slightly but ensures that the DWA has improved performance for many setpoints close together. Since the obstacle avoidance is now taken on by a seperate algorithm this improves the total performance of the robot. The velocity of the robot was slightly reduced and the acceleration parameters are lowered while the deceleration parameters are kept the same which resulted in a smoother but still safe navigation.

Increasing the vision range of the DWA algorithm was also an important change to the algorithm for the final challenge. The algorithm took only part of the range of laser measurements into account to improve the speed of the algorithm (shown in the DWA vision range figure on the right). This worked well on the Rossbots and was also tested on HERO with a single target setpoint. However, while testing the complete system HERO started to hit edges of wall when turning in a corner. The DWA algorithm could not see these edges as shown in brown in the figure on the right. The main reason why the reduction of sensor data could not work has to do with the location of the lidar sensor. The Rossbots have a lidar sensor more in the middle of the robot where HERO has its lider on the front of the base. Since the DWA only allowes the robot to move forward this problem would have been less of an issue if the lidar would have been in the middle of the robot.

Local planner - Ankle detection

We detect ankles, or in our case also chair legs, by the lidar's interaction with circular objects. Generally, when a circular object is detected by the lidar, we see a ‘V’ shape, with the point of the V pointing towards the robot and both tails of the ‘V’ can be seen as lines on both sides of the leg. As if a parabola is wrapping around the leg of a chair or human. This is not the case for objects with straight lines, only circular objects. We use this property to detect our ankles. The behaviour of these parabola is that there are several consequent laser data scans that approach the robot followed by several consequent laser data scans that move away from the robot. We give a condition that detects ankles if within a certain vision bracket of the robot enough laser scans increase and decrease in succession between a minimum and maximum value. While walls that are slightly tilted from the robot does show the behaviour of points either getting closer or further away, we never see a wall that shows both. Only very pointy walls directed at the robot show this behaviour, which are not used in the restaurant setup. By looking only at brackets of the robots vision, we exclude behaviour where the robot detects ankles when the robot detects laser points moving away quickly from the very left side of its vision and approaching from the right side of its vision. Finally, only a limited vision slice of about 90 degrees in front of the robot is included in the scan and only points closer than 50 cm to the robot are processed.

Ankle detection video final challenge

Global planner

The global planner as its name implies is the component focused upon the planning of the global path. The path is created using the two sub-components, the PRM that generates an graph to plan a path over and the planner that uses the graph to plan the optimal path towards the intended goal. Together these components provide an optimal path towards a goal within the known map.

PRM

Planner

obstacle avoidance sim

Rerouting and navigation video final challenge

Reniew global route sim

Resetting map video final challenge

Localization

The localization of HERO has three important components. The initialization of the angle of HERO with the initialization of the filter, the localization performance with obstacles and localization with door opening.

Initialization of angle

Hero can start in any angle in his starting box. The filter is given an initial guess angle and standard deviation which can both be adjusted. Increasing the standard deviation of the angle to pi allows the robot to better find its angle but has the downside that the robot glitches easier to other points. A simple solution was to provide HERO with a better initial guess. Providing HERO with an initial guess which is accurate within 45 degrees allowed the localization to keep the standard deviation of the angle much smaller than pi.

HERO is initialized by reading the laser sensors from -pi/2 to pi/2. The number of measurement points within this measurement angle and with a range smaller than 1.2 meters are counted as wall hits. HERO is facing the empty hallway direction if the number of wall hits are lower than a predetermined number of hits. HERO is facing a wall if this predetermined number of hits is exceeded. Rotating HERO always in one direction (Counter-Clockwise) until HERO is no longer facing a wall ensures that HERO is approximately looking at the empty hallway. Then setting the initial guess of the particle filter in the direction of the hallway and slowly rotating HERO for a few more seconds results in a significantly high success rate of initialization (1 fail in approximately 40 attempt with the practical setup, 0 fails in approximately 100 attempts with the simulation).

Localization with unknown obstacles

Door opening

In the final restaurant challenge, there's a door on the map that HERO can open. However, when HERO opens the door, there's a noticeable difference between the world model and what HERO observes with its sensors, causing localization to become inaccurate. To restore accurate localization, the world map needs to be updated so that HERO can once again correctly perceive its environment.

The implementation of this update involves HERO moving towards the door. Once HERO reaches the door, it stops its movement and requests the door to be opened. Upon opening, HERO identifies the change and updates the world model accordingly. After updating the world model, HERO resumes its task with the updated world model.

nieuwe map zonder deur ingevoegd
Oude map deur als muur
Nieuwe map deur als gat

When the robot sees an object in front of it, it will stop and it will wait for the object to move or add the object to the map, as described in SECTION PREVIOUS. However, before this happens it will check if the robot encountered an obstacle near the door. It will look at the edges between its previous path node, its current node and the target node to see if either of those edges passes a door. If this is the case, it has already positioned itself to the door and it has already seen the door is closed. Otherwise, it would not have stopped. It is programmed to ask for the door to be opened and will then wait 10 seconds. After these 10 seconds, it will check if the door has been opened. It does this by counting how many laser point scans in a small angular section in front of the robot are measured with a range of less than 50cm. If less than 20 points are found, the door is considered open. For the localization, it will now load in the map with an open door. Instead of the starting map in which the door is closed. At first, this was not done and the robot would often lose its location for the entire run when it moved through the door. As it thought it had warped through the door. During these 10 seconds of stationarity, it also does not update its localization; it is in a complete waiting state. Although the door being left unopened was not part of the challenge, it was implemented that the robot would not update its map if it noticed the door is still closed after 10 seconds. In this case it would remove nodes around the door and regard this path as blocked. It would then reroute to find another way. As described in SECTION PREVIOUS, if no paths are possible it would route its path again without obstacles. If this finally also does not work, so when the door is again left unopened and no routes are available, it moves on the the next plate.

Initalization in simulation

Initialization video final challenge

Table order

This section outlines the algorithm implemented to manage the table order and locations at these tables in the restaurant. The robot follows a predefined list of tables, navigates to specified locations, announces successful deliveries, and handles cases where tables or specific locations are unreachable. The process ensures systematic and efficient delivery, providing status updates and handling new orders as they are received

New Order Handling

When a new order is received, the system checks if there are remaining orders to be processed. If there are, it retrieves the next table from the tableList and resets the location_index to 0, indicating that the robot should start with the first location of the current table. The new_order flag is then set to false, and the index for the next table is incremented. If all orders have already been processed, the robot stops moving, announces that all orders have been delivered, and exits the process.

Existing Order Handling

If the robot is not starting a new order, it continues processing the current order. The system checks if there are more locations to try for the current table. If there are, it increments the location_index to move to the next location. If all locations for the current table have been tried, the system checks if there are more tables to process. If there are, it retrieves the next table from the tableList, resets the location_index, and continues. If no more tables are left, the robot stops, announces that the table is not reachable, and exits the process.

Table and Location Update

For each order, the system retrieves the current table's details from a predefined list that includes the table's coordinates. The robot then updates its target location to the next position for the current table. This information is printed for debugging and tracking purposes, ensuring that the operator can monitor which location the robot is moving towards next.

Docking update sim Docking points video final challenge

Table docking

Table docking and turn sim

Table docking and turning video final challenge

Dynamic object

From the ‘move along path’ state, the robot may encounter an obstacle. There are a few consequences and checks when this happens. Every time it recalculates its speed and rotation, it uses the lidar data to check if circular objects are close to the robot in its path. If it notices a circular object in its path, it will increase the DWA’s safety distance. The main goal for increasing the safety distance is to assure that feet from bystanders are not hit by the robot. While the robot can see ankles, it is unable to detect feet which lie below the lidar’s height.

RemoceArea function application

Path blocking

In this section the functions of how a blocked path is registered and recalculated is described. A path is seen as blocked when an object is registered through the lidar denying acces to a node within the path. Some time is taken as to recognize whether the registered object is dynamic and therefore will be removed within some time or static and therefore remain. When a path is registered as blocked and determained the object to be static, the robot will remove the nodes within the path and recalculate its route.

Providing of point

Disconnect nodes around point

Provided a point with X and Y coördinates and a range, all nodes within the circle around the provided point will be disconnected. Visible with the image on the right. The nodes are disconnected by removing the connections of the nodes but keeping the nodes still. For, removing the nodes would result in index missalignments, causing the whole PRM graph to be wrong. As said these disconnections happens within the PRM, therefore, whenever a new route is calculated these nodes will never be reached unless a new PRM is generated.

Route update

obstacle avoidance and adding sim Obstacle avoidance and adding obstacle to map video final challenge

Door opening

Door opening sim

Door opening video final challenge

Testing

simulation run

Final challenge

Final challenge video angle 1

Final challenge video angle 2

Conclusion & Recommendations

WEEKLY EXERCISES

Week 1: The art of not crashing

Think of a method to make the robot drive forward but stop before it hits something.

These exercises were performed individually by the members leading to different outcomes.

There were a lot of similarities between the answers. Every group member used the laser data to determine if objects were close. All members invented a way to loop over the laser range data and check the individual values to see whether that value was lower than a safety threshold. If an object came close enough to the robot, in all cases a signal would be sent to the motor to stop moving forward. However, the way members determined whether an object was in front differed per member;

Ruben decided to not loop over all laser ranges but only check the ones in front of the robot. To determine which laser data actually represents the area the robot is going to drive to, a geometric calculation is executed, using the arc tangent of the required safety distance and the width of the robot to determine the maximum angle the laser data needs to check. After checking whether objects are not too close, it adds a geometric term to make sure the safety distance is consistent when looking at a line parallel to the driving direction. So the beams to check in front of the robot is not shaped like a circle due to the LiDAR.

Lysander made his robot start turning when an object was detected. In the next loop the robot would therefore get different laser scan data and after a few loops the object might be outside the angles the laser scanner can check and so it will drive forward again as it has turned away from the obstacle.

For all members the laser data was read.
A loop was created over the data to either pick out the smallest laser scan distance.
- In Ruben's case, the angles of the laser data were also used to select which specific laser beams should be included when determining it is safe enough to drive into a certain direction.
If one out of the (selected) beams measured a point smaller than the safety distance the robot stops.

Run your simulation on two maps, one containing a large block in front of the robot, the second containing a block the robot can pass by safely when driving straight.


Name	Code	Video exercise 1	Video exercise 2
Lysander Herrewijn	Code	Screen capture exercise 1	Screen capture exercise 2 map 1 Screen capture exercise 2 map 2
Adis Husanovic	Code	Screen capture exercise 1	Screen capture exercise 2 map 1 Screen capture exercise 2 map 2
Marten de Klein	Code	Screen capture exercise 1	Screen capture exercise 2 map 1 Screen capture exercise 2 map 2
Ruben van de Guchte	Code	Screen capture exercise 1	Screen capture exercise 2
Vincent Hoffmann	Code	Screen capture exercise 1	Screen capture exercise 2 map 1 Screen capture exercise 2 map 2
Timo van der Stokker	Code	Screen capture exercise 1	Screen capture exercise 2 Map 1 Screen capture exercise 2 Map 2

All runs stop in time in front of the walls for exercise 1 and for map 1 in the second exercise. However, for the second map, only Marten's, Adis' and Ruben's code caused the robot to drive by the obstacle as it was safe. Adis and Marten implemented a safety distance small enough such that the robot drove past the obstacle. Ruben's method is more dynamic and suitable in a wider range of cases. It it also better at looking at upcoming obstacles further away. The direction in which the robot is not allowed to drive if a laser point is closer than its safety distance becomes smaller as the robot gets closer to a gap. We deemed this preferrable, as the robot should be able to navigate smaller corridors. So, a more dynamic approach should be implemented for the local navigator.

Practical demonstration

The laser received less noise than we expected, it is fairly accurate with its measurements. However, only items at a certain height of the laser can be seen, as the laser only works on its own height. For example, when standing in front of the robot, the laser could only detect our shins as two half circles (the front of the legs).

When testing our don't crash files on the robot, it stood out that the stopping distance needed to include the distance from the measuring point (the LiDAR) to edge of the robot. This was measured to be approximately 10 cm. After changing this the robot was first tested on a barrier as seen in Robot stopping at barrier.

Next, we let a person walk in front of it to see if the code would still work. Fortunately, it did, as can be seen in Robot stopping at passing person.

Finally we tested Lysander's code that turns the robot when it sees an obstacle, and then continues. This gives an indication of the blind spot of the robot. As it will only drive if everything it sees within its vision range is not within its safety distance. This can be seen in Robot stopping and turning at feet.

Week 2: Local Navigation

A theoretical view of the VFH technique, the numbers are made up and only for illustration purposes. The robot counts the amount of beams that hit an objects within its LiDAR in a certain angular bracket. The range of angles is what we have approximated based on our tests [-110°, 110°].

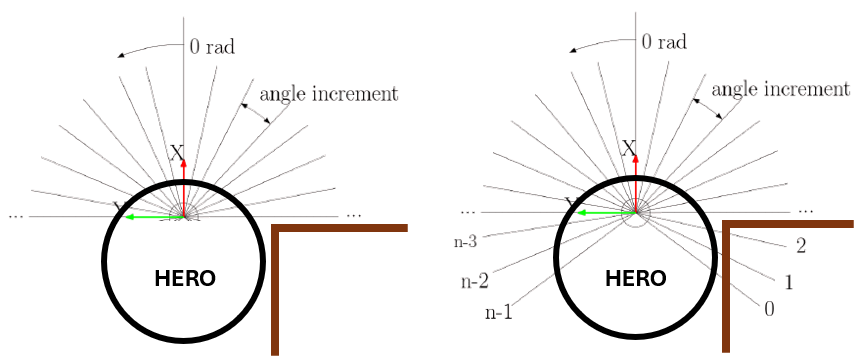
Vector field histogram (VFH)

Implementation:

The simplified vector field histogram approach was initially implemented as follows.

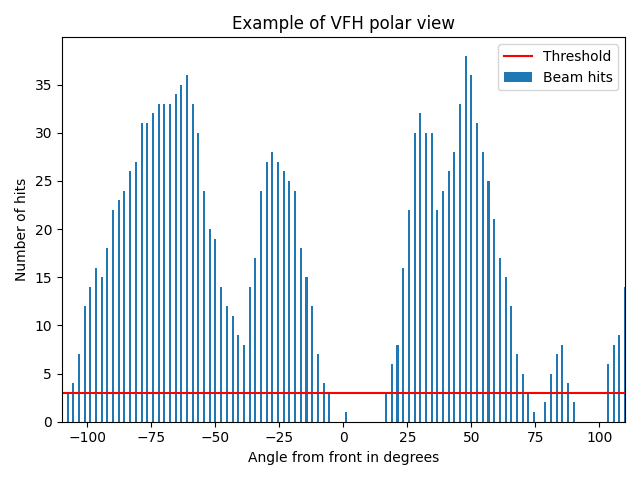
The robot starts out with a goal retrieved from the global navigation function, its laser data is received from the lidar and its own position, which it keeps track of internally. A localization function will eventually be added to enhance its ability to track its own position. The laser data points are grouped together in evenly spaced brackets in polar angles from the robot. For the individual brackets, the algorithm checks how many LiDAR points' distance is smaller than a specified safety threshold distance. It then saves the number of laser data points that are closer than the safety distance for every bracket. This is indicated by the blue bars in the plot to the right.

Next it calculates the direction of the goal by computing the angle between its own position and the goal position. It then checks whether the angle towards the goal is unoccupied by checking the values of the bracket corresponding to that angle. A bracket is unoccupied if the amount of LiDAR hits within the safety distance are fewer than the threshold value. Additionally, some extra neighboring brackets are checked depending on a safety width hyperparameter. The goas of the safety width is to make sure the gap is wide enough for the robot to fit through. If the direction towards the goal is occupied, the code will check the brackets to the left and to the right and save the closest unoccupied angle at either side. It then picks whichever angle is smaller, left or right. and sets that angle as its new goal. If we look at our example histogram, we can see that the forward direction to the goal is open. However, depending on the amount of safety brackets, its behavior might change. In our case, we use 100 brackets as is shown in the example histogram. In some cases, we have used about 5 safety brackets. In the example case, the robot would steer slightly to the positive angle direction (to the right) to avoid the first brackets left from x=0 above the safety threshold.

Afterwards it compares its own angle with the goal angle and drives forwards if it aligns within a small angular margin towards the direction of the goal. The global navigator keeps track of the position of the robot and updates the goal if the robot is close enough to its current goal.

This initial implementation had some oversights and edge cases that we came across when testing using the simulator and the real robot. The first issue arose when the system was tested to turn a corner after driving next to an obstacle. At this small distance the cone of laser data that needs to be checked is very large. Though if this cone were used to look at larger distances, the robot would discard routes it could easily fit through. This was fixed by performing a second check on the laser data at the side the robot is turning to and if this check finds an object moving forward a bit more before turning. This solved our problem where the robot would steer into objects or walls too early.

Advantages:

Implementing VFH for navigation is relatively straightforward, requiring basic processing of LiDAR data to compute the histogram of obstacles' directions.
VFH can generate smooth and collision-free paths for the robot by considering both obstacle avoidance and goal-reaching objectives
VFH is computationally efficient and robust to noisy sensor data

Disadvantages:

VFH may have difficulty distinguishing overlapping obstacles, especially if they are close together and occupy similar angular regions in the LiDAR's field of view. This can be solved by taking a small distance at which LiDAR points are taken into account.
In complex environments with narrow passages or dense clutter, VFH may struggle to find feasible paths due to the limited information provided by the LiDAR sensor and the simplicity of the VFH algorithm.
VFH performance can be sensitive to parameter settings such as the size of the histogram bins or the threshold for obstacle detection. Tuning these parameters for optimal performance may require extensive experimentation.

Possible failure scenarios:

A possible failure scenario encountered in testing was that the robots orientation deviated so far from the goal that it became unable to directly check the direction the goal was in. So, if the robot has to turn so far that the goal is in the 'blindspot' of 360-220=140 degrees, the robot would assume there is an available path in that direction and rotate towards it. After rotating that direction it would see that it is occupied and turn the other way towards space it could move to and this cycle would repeat.
- Solution: This problem could be solved by implementing an internal representation of the points that were detected before as was done in Borenstein, J., & Koren, Y. (1991). In our implementation we instead chose to solve this by making sure there are no such challenges in the path by choosing more intermediate goal points in the global navigator.

Another possible failure scenario presents itself when the robot needs to drive more than 90 degrees away from its goal. In this case driving away actually puts the robot further from its goal and as it has no memory will forget that there is an obstacle that caused it to need to turn this way in the first place. And after driving such that the obstacle exits its detection range, it will try to turn back. This will cause the robot to cause its behavior to loop between driving away and towards the obstacle.
- Solution: We again avoid this failure case by only letting the local navigator handle simple paths towards intermediate goals.

Implementation of local and global algorithms:

The global and local planner can be easily connected via a main script. In the main script the global planner is called first generating a set of target goals. Then the local planner is called and only given the first target goal. The main script keeps track of the distance from the robot to the target goal and if this distance is smaller than a given value the local planner is given the next target goal until it reaches the final target goal and the main velocity is set to zero. In case a target goal is not reachable (e.g. the distance to the target goal does not reduce for a given time) the global planner should be called again with an updated map.

Demonstrations:

Simulation:

The simulations show how the robot navigates through the maps. There are a few things to notice. Firstly, the robot is not very dynamic, it can only turn when standing still. If the direction the robot is facing is safe it will drive forward. Otherwise it will turn. In the case the VFH will be used in the final challenge, a distinction must be made such that the robot does drive forward during turning if no object is directly in front of it. Furthermore, we can see how the VFH finds local minima and manages to escape it by turning around and exploring the other side. This happens, for example, in map 3 after turning past the first corner. The settings are such, that the robot can pass the small corridor on map 4 after the first corner. As we selected only a few safety brackets to pass this corridor, we can see that the robot cuts corner fairly tight in the simulation. For the real life scenario, this should be adjusted to attain a bigger safety margin around corners.

Simulation Demonstration Video MAP3 VFH

Simulation Demonstration Video MAP4 VFH

Practical demonstration:

The first obstacle show the robot nicely passing an obstacle relatively tightly. It moves on and does not stop and turn, knowing it will make it. For the second object, he stops, turns, drives and repeats this a few times before he passes the corner. This is an example when driving forward in combination with turning could give a more smooth and also faster result. All in all, the VFH has proven to be a reliable method in avoiding obstacles.

Experimental Demonstration Video VFH

Dynamic Window Approach (DWA)

Implementation:

The DWA algorithm is a velocity based algorithm based on maximizing an objective function. The general overview is shown in the figure to the right.

The algorithm starts by defining the velocity and acceleration constraints, such as velocity and acceleration limits, bracking accelerations and safety distances. It then creates a set of possible velocities, creating a grid from minimum to maximum allowable velocities in discrete steps. Then, the velocities that are not reachable within a single time step, based on the current velocity and acceleration limits, are filtered out. Each remaining velocity in the set is checked for potential collisions with obstacles detected by the laser sensors. If the combination of the forward and angular velocity would result in a collision, it is removed from the set. This is done by calculating the distance to obstacles and comparing it with the robot’s stopping distance. The distance to an abstacle is calculated based on the curved trajectory it will follow. Is the velocity only forward and not rotational then the distance is simply calculated based on the shortest distance.

A pointing system is used in order to determine which combination of the forward and angular velocity suits the best at each step. For each feasible velocity, a score is computed based on three criteria in objective function. The first one is the heading towards the goal, the second one is the forward velocity, and the third one is the distance to the nearest obstacle. The weights for these criteria are defined to balance their importance where each individual criteria is first normalised. The weights are tuned based on the performance in simulation and experiments.

Finally, the robot’s velocity is updated with the highest-scoring velocity, resulting in the robot to move in a safe and smooth manner.

Advantages:

Effective at avoiding obstacles detected by the LiDAR sensor in real-time. It dynamically adjusts the robot's velocity and heading to navigate around obstacles while aiming to reach its goal.
Focuses on local planning, considering only nearby obstacles and the robot's dynamics when generating trajectories. This enables the robot to react quickly to changes in the environment without requiring a global map.

Disadvantages:

Can get stuck in local minima, where the robot is unable to find a feasible trajectory to its goal due to obstacles blocking its path. This can occur in highly cluttered environments or when the goal is located in a narrow passage.
Does not always find the optimal path to the goal, especially in environments with complex structures or long-range dependencies.
The performance can be sensitive to the choice of parameters, such as the size of the dynamic window or the velocity and acceleration limits of the robot. Tuning these parameters can be challenging and may require empirical testing.

Possible failure scenarios:

A possible scenario is a target position inside a wall. In this case the robot will never reach the target position because the required velocity to reach the target will be ommitted from the velocity set. Instead it will either stop as close as possible to the target position when no velocities are feasible anymore due to collision risk or the robot will keep moving around the target position trying to minimise the heading angle.
- Solution: ensuring that a target position is never inside a wall could be a method, however this only works for known obstacles. If the target position is part of a set of target positions the robot could try to skip this target position and immediately go to the next position, with the risk of getting stuck in a local minima. The best solution is giving the global planner a signal with an updated map and letting it create a new set of target positions.
A second possible scenario is that the target position is inside the radius of curvature of the robot resulting in a circling motion of the robot around the target without ever reaching the target.
- Solution: this scenario can be fixed by tuning the parameters of the algorithm. Ensuring that the heading angle is more important that the forward velocity is a method of avoiding getting stuck in a radial loop. However, when the target is still far away this is less desired because obstacle avoidance works better with a high score on the forward velocity. A solution would be to create a somewhat dynamic parameter setting where if the robot is located far away from the target it uses different values for the tuning parameters compared to when it is close to the target.
A third possible scenario is that odometry data is not correct resulting in a wrong calculation of the desired heading angle. This would result in the robot targetting a different goal location.
- Solution: A solution is to reduce the acceleration values to reduce the robot slipping. This makes the robot slightly slower but better controlled. Another solution which will be implemented later will be the addition of a localization algorithm that ensures that the robot has a higher positional accuracy.

Linking global and local planner:

The global and local planner can be easily connected via a main script. In the main script the global planner is called first generating a set of target goals. Then the local planner is called and only given the first target goal. The main script keeps track of the distance from the robot to the target goal and if this distance is smaller than a given value the local planner is given the next target goal until it reaches the final target goal and the main velocity is set to zero. In case a target goal is not reachable (e.g. the distance to the target goal does not reduce for a given time) the global planner should be called again with an updated map.

Demonstrations:

Simulation:

In the first video, the robot moves away from the first obstacle to the right. Then it turns back left before it has passed the obstacle. This has to do with the method of only looking in a cone in front of itself and it first does not see the walls beside himself since the hallway is quite wide. When the robot gets closer to the obstacle it again turns right and passes it with a safe distance between itself and the obstacle. Then it rotates itself to the opening and drives in a smooth motion to its final destination.

In the second video, the robot smoothly moves away from its first obstacle. Then it turns back left to move away from the second obstacle. After the second obstacle it orients itself back to the goal and chooses to go around the third obstacle on the right. In some simulations it chose the other direction, this is purely based on where it sees an opening first. Overal a safe distance is held and the obstacles are already taken into account from quite far away.

Simulation Demonstration Video MAP2 DWA

Simulation Demonstration Video MAP3 DWA

Practical demonstration:

In the video, the robot smoothly moves towards its goal, adjusting its path as needed when it encounters obstacles. At the start, the robot moves towards the goal until it meets a wall, then it turns in the right direction to avoid the obstacle. After turning, it keeps moving parallel to the wall. Approaching a corner formed by two walls, the robot slows down, ensuring it has enough space to make a left turn. There is enough space available for the robot to fit through the left gap so it turns there. After turning left, the robot again moves forward parallel to the wall while keeping a safe distance from the adjacent wall. When it completed it last turn around the wall, the robot arrived at its destination accurately enough and stopped smoothly.

Experimental Demonstration Video DWA

Week 3: Global Navigation

The goal of this project is to reach a certain destination. In order to reach the destination, a plan must be made which the robot will follow. This larger scale plan is called the global plan. This plan is made through the global planner. The global planner that is used throught this project is A* which will find the most optimal path for a graph. To create the graph on which a path is planned, the function Probablistic Road Map (PRM) is used. This function generates a random generated graph for a map. So, by combining these functions a optimal path can be generated for a given map.

Efficiently placed nodes

How could finding the shortest path through the maze using the A* algorithm be made more efficient by placing the nodes differently? Sketch the small maze with the proposed nodes and the connections between them. Why would this be more efficient?

The approach of placing nodes only at locations where the robot can change direction, known as "corner-cutting" or "graph-pruning," is an efficient way to implement the A* algorithm for finding the shortest path through a maze. By reducing the number of nodes and connections that need to be explored, this method significantly reduces the computational complexity and search space. It eliminates redundant paths, simplifies connectivity representation, improves memory efficiency, and generates smoother paths by allowing the robot to move directly between corner nodes. The efficiently place nodes can be seen in the figure on the right.

Would implementing PRM in a map like the maze be efficient?

PRM works best in open spaces as it generates random points. In a maze PRM likely does not generate points at the turning points. Additionally, PRM is not ideal for narrow hallways for points are just as likely to be generated near walls. Causing unwanted wiggle movements by the robot as is moves from point to point. Furthermore, placing a point within a narrow hallway is very difficult for many missplaced points will likely happen before PRM finally finds the specific coordinate where a point can be placed. So, PRM will fail a lot in trying to place points in hallways, therefore, being a less ideal. As for the maze is basically multiple narrow hallways, the PRM algorithms will be much less efficient.

What would change if the map suddenly changes (e.g. the map gets updated)?

If the map suddenly changes, meaning that after the initial path is made the map gets updated, the robot will keep following the path that it initially obtained from the A* algorithm using the original map. Meaning it will try to keep following the points the global path has determined, but still try to avoid obstacles with the local navigator. So, the local navigator tries to reach a distance of 0.2 meters away from the points determined by the glocal path while avoiding obstacles. As the global path is outdated, the eventual path the local navigator takes will probably end up being stuck in a local minima in an unexpected corner for example.

How did you connect the local and global planner?

The global and local planner are connected via a main script. In the main script the global planner is called first generating a set of points using PRM, then A* is used to determine target goals in the set of points. Then the local planner is called and only given the first target goal. The main script keeps track of the distance from the robot to the target goal and if this distance is smaller than a given value the local planner is given the next target goal until it reaches the final target goal and the main velocity is set to zero. This implementation still assumes that the global planner knows the map quite well and that there are no stationary unknown obstacles which hinder the path of the robot.

Test the combination of your local and global planner for a longer period of time on the real robot. What do you see that happens in terms of the calculated position of the robot? What is a way to solve this?

The misalignment between the real robot's position and its calculated position is caused by factors like wheel slippage and odometry inaccuracies. This leads to navigation errors. Localization techniques, such as particle filters, estimate the robot's actual position within the global map by updating pose hypotheses based on sensor data. Integrating localization with planners improves navigation accuracy, enables path planning from the correct position, and allows recovery from accidental displacements.

Node map when using PRM

Run the A* algorithm using the gridmap (with the provided nodelist) and using the PRM. What do you observe? Comment on the advantage of using PRM in an open space.

The observed difference between the routes generated by the A* algorithm using a gridmap representation versus a probabilistic roadmap (PRM) is notable. With the gridmap approach, the robot's path is constrained to horizontal and vertical movements along the grid cells, resulting in a stair-step pattern. While this ensures obstacle avoidance, it can lead to longer and less efficient paths, particularly in open spaces or environments with sparse obstacles.

In contrast, the PRM approach offers a significant advantage. By representing the environment as a graph with nodes denoting collision-free configurations and edges representing feasible paths between them, the A* algorithm can find more direct and diagonal routes through the roadmap. This allows the robot to take shortcuts through open areas, minimizing unnecessary turns or detours. Consequently, the paths generated by the PRM approach are typically shorter and have fewer intermediate waypoints to follow, simplifying navigation and control. Additionally, when generating the node map for PRM, the walls are also inflated to avoid nodes being placed too close to walls. The advantage of the PRM is particularly apparent in open spaces, where it enables the robot to take the most direct routes possible, leading to faster navigation, reduced energy consumption, and potentially smoother trajectories. The comparison can be seen in the figure on the right.

Comparison between using a grid map or using a probabilistic road map for the A* algorithm

Simulation results

VFH local + global planner simulation

The VFH is a strong contender for the final challenge due to its strong obstacle avoidance. Incorporating VFH with the global planner was easily initially. However, it turned out there were still major issues. The robot would traverse the corridor well, and the center of the map built in by walls, but it would not correctly follow the global planner. The local planner could be created such that it would drive to the goal just by avoiding walls.

The reported simulation is a debugged version where we can see the VFH local planner nicely follows the nodes of the global planner, which switches to the next node when the robot is closer than 20cm to the node. However, it is not completely debugged yet. Due to an implementation of the arctangent function (atan) the desired angle would flip 2 pi and the robot would turn completely before driving onward. This happens when position_x-goal_x>0 flips to position_x-goal_x<0, or for the y-direction. We will attempt to fix this before the final challenge. If this is fixed, the goal is to add a script that allows the robot to drive forward and turn when no objects are in front of it. Making its trajectory more smooth. It does eventually reach the goal in the simulation. The practical demonstration shows an older version where the goal is incorrect due to similar mistakes in the calculation of the goal and its position.

DWA local + global planner simulation

When used in the simulation, it can be observed that the DWA effectively guides the robot to follow the globally planned path while smoothly navigating around obstacles and avoiding collisions with walls. As the robot approaches a wall or obstacle, the DWA algorithm continuously evaluates the robot's velocity and steering commands within a dynamic window of admissible values.

By continuously reevaluating the robot's commands and choosing the optimal velocity and steering angle, the DWA ensures that the robot slows down and adjusts its trajectory when approaching obstacles or walls. This behavior can be observed in the video, where the robot smoothly decelerates and turns away from walls as it gets closer to them. The DWA's ability to adapt the robot's motion in real-time based on its current state and surroundings allows for safe and efficient navigation, even in cluttered or dynamic environments.

Practical demonstration

VFH local + global planner practical demonstration

The issue where the robot thinks it has reached its destination halfway through the path is likely caused by an incorrect implementation of the arctangent function (atan) used for calculating the robot's orientation or heading. However, if this function is not implemented correctly, particularly in handling the signs of the displacements or the quadrant mapping, it can result in the calculated angle flipping or being off by 180 degrees (or any other multiple of pi radians).

This error in angle calculation can propagate through the robot's motion model, causing the robot to think it is facing the opposite direction or at a completely different location on the map than its actual position. For example, if the angle calculation flips by 180 degrees midway along a straight path, the robot's perceived orientation will be inverted, and it may interpret its current position as the endpoint or destination, even though it has only traversed half of the intended path. The simulation shows a debugged version of the same VFH method. Earlier simulation attempts moved the robot to exactly the same endpoint in the simulation as for the world map test.

DWA local + global planner practical demonstration

Initialy the robot follows the right path and nicely goes around the first corner. After that, the large distance creates a coordinate displacement causing the robot to overschoot close to the wall. Notice in that moment the DWA local navigator recognizes the wall, slows down and slowly approaches the path point to a satisfying distance. After that is continues to follow the path, where after the corner the robot overshoots again due to missplacement and retries to reach the path point. This misses into the chairs what the local navigator finds hard to recognize. There the video ends.

Week 4 & 5: Localization

Assignment 0.1 Explore the code framework

How is the code is structured?

The code for this assignment is structures as multiple classes. Each object or component has its own class and functions that can be used to change aspects on about itself.

What is the difference between the ParticleFilter and ParticleFilterBase classes, and how are they related to each

other?

The particle filter base provides the base functionalities of a particle filter, like setting noise levels and returning position lists. The particle filter script provides the larger functions and connects the particle filter to other classes that need to work with the same data, like the resampler. The ParticleFilter runs the system on a high level by calling more basic functions form ParticleFilterBase.

How are the ParticleFilter and Particle class related to eachother?

The ParticleFilter creates the Particles that are used in the particle filter. When operations need to be done on an individual particle the ParticleFilter calls the functions inside the Particle class.

Both the ParticleFilterBase and Particle classes implement a propagation method. What is the difference between the

methods?

The ParticleFilterBase propagation method ask all individual particles to run their propagation function. The Particle's propagation does the actual propagation. The ParticleFilterBase function just provides a single command to let all these particles perform their operations.

Assignment 1.1 Initialize the Particle Filter

Initialization of particle filter

The first constructor places random particles around the robot with an equal radial probability. Each particle has an equal chance of being positioned anywhere around the robot, with completely random poses. This method is particularly useful when the robot’s initial position is unknown and there is no information about its location on the global map. By distributing particles randomly, the robot maximizes its likelihood of locating itself within the environment. The key advantages of this approach include wide coverage and flexibility, making it ideal for scenarios where the robot's starting position is completely unknown. However, the disadvantages are lower precision due to the wide spread of particles and higher computational demands, as more particles are needed to achieve accurate localization.

In contrast, when the robot’s position and orientation are known, the second constructor is more effective. This method initializes particles with a higher probability of being aligned with the robot's known state, placing more particles in front of the robot and orienting them similarly. This concentrated placement allows for more accurate corrections of the robot’s position and orientation as it moves forward. The advantages of this approach include higher precision and efficiency, as fewer particles are needed for accurate localization. However, it has the drawback of limited coverage, making it less effective if the initial guess of the robot’s position is incorrect. Additionally, it requires some prior knowledge of the robot’s initial position and orientation. This constructor is best used when the robot has a general idea of its starting location and direction.

Particle cloud with green arrow average

Assignment 1.2 Calculate the pose estimate

The filter takes a weighted average over all particles to estimate its state; the position and orientation of the robot. The particles that are in line with the sensor data receive a larger weight. This way, the particle swarm adjusts itself to the sensor data. Over time, the pose estimated by the particle swarm is getting in line with the actual pose of the robot. However, there remains a discrepancy in pose. This is caused by the limited amount of particles, disallowing a complete representation of the pose. Iterating over the particle swarm with noise will help improve the estimated pose of the robot over time.

When the sensor data provides insufficient feedback, for example when the robot is in open space, the pose estimate is impossible to predict accurately. For this, more information on the surroundings of the robot is required.

Assignment 1.3 Propagate the particles with odometry

Why do we need to inject noise into the propagation when the received odometry information already has an unknown noise component?

The noise of the odometry data is unknown. By manually adding noise to the odometry data, we can better represent uncertainties in the robot's movement model. This helps in capturing deviations from the expected path. Additionally, it is important to keep refreshing the particles to have a broad coverage of the environment. If we would not, we risk that not enough exploration of the surrounding causes or particles to converge to an incorrect state. Which makes it harder to correct the robot's real location and orientation.

What happens when we stop here, and do not incorporate a correction step?

When we start moving we need to keep adjusting for the environment. New sensor data must be continuously fed to the filter to approximate its state. If this is not done, we could not readjust our position and correct for odometry errors accumulated over time. If we are stationary, the filter's particles would also diverge from their true state over time. If we do not keep adding correction steps, we would simply accumulate errors over time. Noise and inaccuracies would over time cause increasingly worse state estimates.

In the following link the resulting moving particle cloud is shown:

Simulation Localization Moving particle cloud

Assignment 2.1 Correct the particles with LiDAR

What does each of the component of the measurement model represent, and why is each necessary.

The measurement model uses data, prediction and some additional measurement model data named lm. The data is the actual measurement acquired from the LiDAR of the robot. The prediction is the measurement the raycast algorithm provides and what the data would be if the robot were to be at the exact position of the particle.

The likelihood of the particle being the correct position is called likelihood en is represented by four components:

First, A probability of measuring the expected prediction. or in other words if the particle is right this part will give a high contribution to the total chance.

Secondly, there is a chance the LiDAR has an error or the measurements happens to reflect of something and does not return properly. To accommodate the chance of this happening a component is added that represents a chance of getting a maximum value as a reading.

Third, there is always a chance of an especially large dust particle or some other form of interference to block the measurement. This chance is modeled by an exponential decay from zero untill the predicted measurement.

Lastly, there is always a chance an error in some system replaces a measurement with a random value. Therefore there is a small probability added across the entire possible range of measurement values.

With each particle having N >> 1 rays, and each likelihood being ∈ [0, 1] , where could you see an issue given our current implementation of the likelihood computation.

All likelihoods per particle are summed up and normalized with the amount of beams that are used to calculate the system. This puts the value between 0 and 1 just like the individual likelihoods. An issue could arise when components of the measurement model are not weighted properly and would not give a decisive difference. Additionally when adding the likelihoods of all the particles together careful consideration of the weights of the short component. Setting it too high would let the a particle close to a wall get a big sum of small short contributions which might overshadow some position that gets some hits correct.

Assignment 2.2 Re-sample the particles

What are the benefits and disadvantages of both the multinomial resampling and the stratified resampling?

The multinomial sampling method always has a chance that the new particles are biased to an example particle due to the randomness with which the new particles are divided over the possible example particles. The stratified method takes away this randomness by dividing the new particles equally but weighted over the example particles.

With each particle having N>> 1 rays, and each likelihood being ∈ [0, 1] , where could you see an issue given our current implementation of the likelihood computation?

A high amount of particles with a high amount of beams will need a lot of computation power. This might not be available and slow down the robot.

Assignment 2.3 Test on the physical setup

While testing on the physical setup in the last session the algorithm was not fully working. The day after the testing on the physical setup the algorith does work. Therefore, we have chosen to show the simulation videos instead. Reducing the number of particles significantly ensures that the code is running smoothly within the desired timestep. The other parameters of the algorithm do have some effect on the algorithm but the simulation does not improve very significantly by tweaking these parameters from the default. This might change when the algorithm is also tested on the physical setup.

Multinominal resampling

The number of particles are first set to 2500 where the simulation is unable to keep up with the framerate of 5 Hz. The results in the particles lagging behind as shown in the simulation video. When the robot stops again it is clear that the particles are following the robot quite well but this is not very feasible for the real setup.

Simulation Localization Multinominal 2500 Particles

Reducing the number of particles to 300 results in the simulation being able to follow the robot much better. The video of multinominal resampling shows that the green arrow is closely following the robot and is at most one timestep behind. When turning at its position the arrow does lag behind a timestep which seemed to improve a little bit by tuning the propogation parameters.

Simulation Localization Multinominal 300 Particles

Stratified resampling

Similar results are found using stratified resampling. With 2500 particles, the simulation struggles to maintain a 5 Hz framerate, causing the particles to lag behind the robot's movements. However, when the robot stops, the particles accurately represent the robot's position.

Simulation Localization Stratified 2500 Particles

Reducing the number of particles to 300 significantly improves simulation performance, as seen with multinomial resampling. The green arrow, representing the robot's estimated position, follows the robot more closely and consistently.

Simulation Localization Stratified 300 Particles

Localization for final assignment

The algorithm works fast and accurate such that the estimated position follows closely to the robot. In the final assignment the script is run at 10 Hz instead of 5 Hz which means that the number of particles has to be reduced a bit more or the script has to be made more efficient. We still have to test the algorithm with unmodeled obstacles in the practical setup but it shows promising results in the simulation.

Mobile Robot Control 2024 The Iron Giant

FINAL REPORT The Iron Giant

Localization exercises improvement

Assignment 0.1 Explore the code framework

Assignment 1.1 Initialize the Particle Filter

Assignment 1.2 Calculate the pose estimate

Assignment 1.3 Propagate the particles with odometry

Assignment 2.1 Correct the particles with LiDAR

Assignment 2.2 Re-sample the particles

Assignment 2.3 Test on the physical setup

Localization for final assignment

Introduction

State flow

Robot startup

Normal states

Interrupted states

Code buildup

Data flow

Components

Local Planner

Local planner - Ankle detection

Global planner

PRM

Planner

Localization

Initialization of angle

Localization with unknown obstacles

Door opening

Table order

New Order Handling

Existing Order Handling

Table and Location Update

Table docking

Dynamic object

Path blocking

Providing of point

Disconnect nodes around point

Route update

Door opening

Testing

Final challenge

Conclusion & Recommendations

WEEKLY EXERCISES

Week 1: The art of not crashing

Practical demonstration

Week 2: Local Navigation

Vector field histogram (VFH)

Implementation:

Possible failure scenarios:

Implementation of local and global algorithms:

Demonstrations:

Dynamic Window Approach (DWA)

Implementation:

Possible failure scenarios:

Linking global and local planner:

Demonstrations:

Week 3: Global Navigation

Simulation results

Practical demonstration

Week 4 & 5: Localization

Assignment 0.1 Explore the code framework

Assignment 1.1 Initialize the Particle Filter

Assignment 1.2 Calculate the pose estimate

Assignment 1.3 Propagate the particles with odometry

Assignment 2.1 Correct the particles with LiDAR

Assignment 2.2 Re-sample the particles

Assignment 2.3 Test on the physical setup

Multinominal resampling

Stratified resampling

Localization for final assignment

Navigation menu

Search