Viotar

	Viotar project groep William Schattevoet David Duwaer Eric Backx Arjan de Visser
	Welkom op de pagina van de Viotar project groep, op deze pagina zullen we de voortgang van ons minorproject bij gaan houden. Waar de meeste minorprojecten vooraf vastgestelde opdrachten zijn is het Viotar project bedacht door een deel van de groep. Het project is voortgekomen uit het persoonlijk onbehagen dat de klassieke viool tijdens het spelen opwekte en het doel is daardoor het maken van een nieuw soort instrument wat wel de voordelen maar niet de nadelen van dit instrument heeft. Deze pagina zal vrijwel dagelijks bijgewerkt worden met de nieuwe bevindingen en resultaten. Motivatie De afgelopen eeuw zijn elektrische instrumenten immens populair geworden, de elektrische gitaar is hier een goed voorbeeld van. Elektrische strijkinstrumenten zijn echter nooit echt aangeslagen. Dat roept de vragen op waarom dit zo is. Er zijn verschillende gebreken aan deze electrische strijkinstrumenten aan te wijzen die de achterblijvende populariteit kunnen verklaren. De bestaande elektrische strijkinstrumenten zijn trouw gemodelleerd naar de traditionele akoestische familie van strijkinstrumenten, waarvan de bekendste instrumenten de viool, de altviool, cello en contrabas zijn. Deze traditionele instrumenten hebben echter verschillende nadelen die de nieuwe electrische modelen dus ook hebben: Heel moeilijk te bespelen (slechte combinatie van strijkdruk en snelheid resulteert in een lelijk “krassend” geluid) Beperkt bereik, om het volledige spectrum te dekken van toonhoogte moeten meerdere instrumenten gebruikt worden (i.e. viool hoog, cello laag en contras daaronder) Akkoorden zijn onmogelijk om te spelen, hooguit snaren tegelijk. Onprettige ergonomie Dit motiveert het maken van een elektrisch strijkinstrument dat geen van deze gebreken ondervind. Onder andere betekent dit dat er dus akkoorden op gespeeld moeten kunnen worden. Met andere woorden, er moeten meer dan 2 snaren tegelijk bespeeld kunnen worden. Deze eis kan worden uitgebreid zodat íedere combinatie van snaren tegelijk gespeeld moet kunnen worden, zoals dit bij de elektrische gitaar het geval is. Dit sluit het gebruik van een strijkstok zoals bij de traditionele strijkinstrumenten uit. Hierdoor kan de oorspronkelijke ergonomie van deze strijkinstrumenten worden losgelaten, en kan men een betere ergonomie ontwerpen. Ook moet het nieuwe instrument makkelijk bespeeld kunnen worden. Wat strijkinstrumenten moeilijk maakt is het feit ze “goed” moeten worden bestreken (de goede combinatie van druk en snelheid) om überhaupt een goede toon te krijgen. Het nieuwe instrument moet deze verantwoordelijkheid in feite overnemen, dus het instrument moet “zelf” verzorgen dat er altijd sprake is van de goede combinatie van strijksnelheid en druk. Deze eis in combinatie met het feit dat alle snarencombinaties tegelijk gespeeld moeten kunnen worden, doet denken aan een soort mechaniek dat het bestrijken van de snaren gaat verzorgen. Dit laatste in combinatie met de eis dat het ergonomisch moet zijn en een groot bereik moet hebben, maakt een elektrische gitaar een goed model om vanuit te gaan. Het doel is om een elektrische gitaar om te bouwen tot een instrument met bovengenoemde eigenschappen. Programma van eisen Vanuit de zojuist genoemde eigenschappen waar de viotar aan zou moeten voldoen zijn de volgende (kwalitatieve) eisen geformuleerd: Het geluid bestaat uit een door de snaren gegenereerd en elektronisch verwerkt signaal. De snaren kunnen in alle combinaties simultaan bespeeld worden. Op ieder tijdstip in een gespeelde noot is de amplitude van de noot varieerbaar van het minimaal tot het maximaal mogelijke op de snaar. De onder- en bovengrens worden opgelegd door de mogelijkheid om bij een bepaalde lage of hoge strijksnelheid en/of druk nog Helmholtz-trilling te kunnen genereren. Het mechaniek en de user-interface laten het toe dat er 18 verschillende noten per seconde op één snaar worden gespeeld. Het mechaniek en de user-interface laten het toe dat er 18 verschillende noten per seconde op verschillende snaren achter elkaar worden gespeeld. De snaar maakt bij aanstrijking een Helmholtz trilling, ongeacht het niveau van de speler. Het instrument moet net als bij strijkinstrumenten vrij “tokkelbaar” zijn: Als de gebruiker niet aan het strijken is, moet de ruimte boven de snaren volledig vrij zijn, en onder de snaren moet tussen de 5 en de 15cm van de brug, 5mm onder de snaren vrij zijn. Het bereik moet vanuit het gebied van de bas tot in de sopraan reiken: De laagste noot lager zijn dan E4, en de hoogste noot moet hoger zijn dan A5. Stappenplan Voor de aanpak van dit probleem is een stappenplan gemaakt, aan de hand van dit stappenplan is ook de planning gemaakt die later op de site zal komen. Concept Wat we willen Waarom (motivatie) Definitie Ontwerpeisen Ontwerp Literatuurstudie Model Regelaar + mechanieken Experimenteren met regelaar met verschillende mechanieken -> mechaniek kiezen Ergonomie Experimenteren met verschillende ergonomische alternatieven Definitief ontwerp Voorbereiding Inkopen voor prototype Productie Prototype Evaluatie Planning De tijdsplanning van het Viotar project. 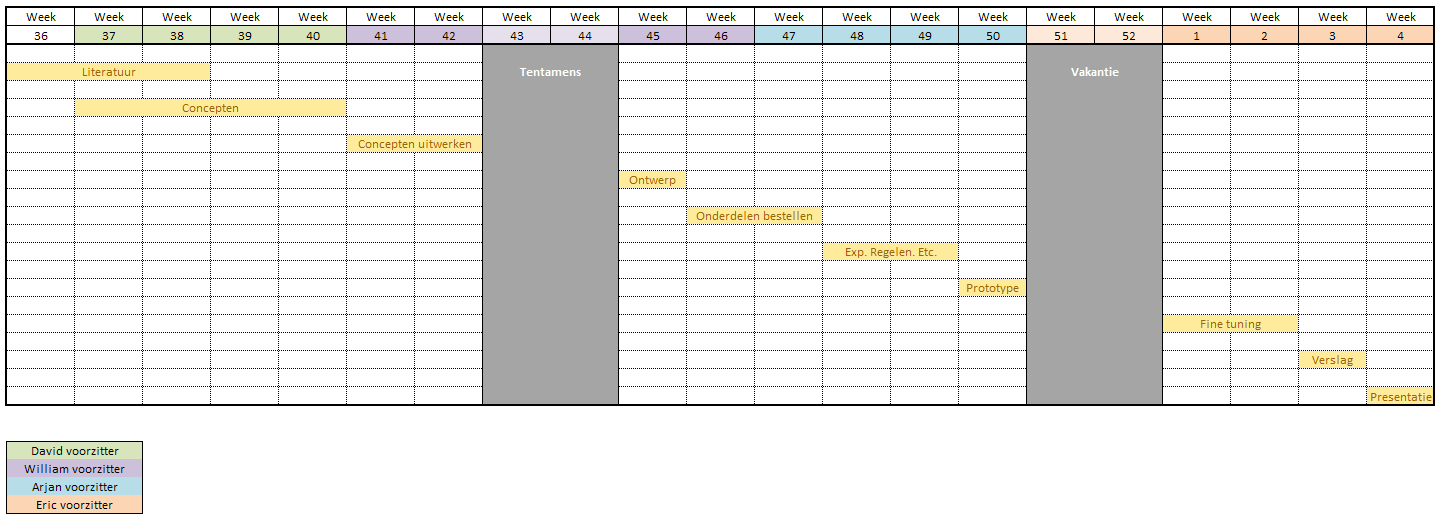Taakverdeling Tijdens de komende weken van het project zal er vooral in 2 verschillende groepen gewerkt gaan worden. De ene groep, bestaande uit David en Eric, zal zich vooral bezig houden met het maken van een matlab model. De andere groep, bestaande uit William en Arjan, zal zich vooral bezig gaan houden met de testopstelling. Arjan zal zich ook bezig gaan houden met het bijhouden van deze wiki om onze voortgang voor iedereen inzichtelijk te houden. Werking van de viool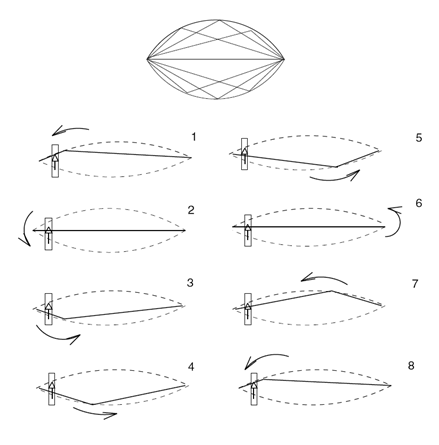 Figuur 1: Het doorlopen van een complete Helmholtz trilling. Om een electrisch strijkinstrument te kunnen maken is het allereerst belangrijk om te weten hoe een strijkinstrument zijn geluid produceerd. Daarom zal dit hier kort uigelegd worden. 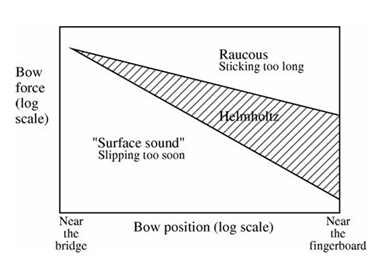Anders dan bij het tokkelen op een gitaar, levert het strijken op een viool geen staande golf op. De trilling die bij het strijken van een viool wordt opgewekt is, in tegenstelling tot de trilling op een gitaar, ook niet lineair. Er ontstaat bij juist aanstrijken van een snaar een zogenaamde Helmholtz trilling. Bij deze trilling beweegt de snaar in een “V”-patroon, ook wel Helmholtz hoek genoemd.. Dit houdt in dat de snaar wordt ‘opgedeeld’ in 2 rechte segmenten die bij elkaar komen in een scherpe hoek. Deze scherpe hoek beweegt rond gedurende de toon. Hoe de snaar er tijdens deze beweging uitziet is te zien in figuur 1. De Helmholtz beweging wordt veroorzaakt door twee verschijnselen op het contactoppervlak tussen de boog en de snaar die ‘stick’ en ‘slip’ worden genoemd. Tijdens de ‘stick’ periode blijft de snaar aan de boog plakken waardoor deze wordt meegenomen. Gedurende de ‘slip’ periode glijdt de snaar weer terug langs het boogoppervlak. ‘Stick’ vindt plaats wanneer de Helmholtz hoek zich tussen de boog en je hand bevindt (rechts van de boog in figuur 1), ‘slip’ vindt plaats wanneer de Helmholtz hoek zich tussen de boog en de brug bevindt (links van de boog in figuur 1). De moeilijkheid van het bespelen van een viool zit hem in het feit dat deze Helmholtz beweging alleen plaatsvindt onder de juiste combinatie van snelheid en druk op de boog. Als er in verhouding te zacht met de boog op de snaar gedrukt wordt, zal deze teveel over de snaar slippen. Wordt er echter teveel druk uitgeoefend op de boog dan zal er teveel ‘stick’ optreden. Tevens van invloed is de positie van de boog ten opzichte van de brug van de viool. Het gebied waarin een Helmholtz trilling optreedt bij constante strijksnelheid wordt weergegeven in een zogenaamd Schelleng diagram (zie figuur 2). In dit diagram is te zien hoe hard er minimaal en maximaal gedrukt mag worden om in het Helmholtz gebied te blijven, als functie van de afstand tot de brug. Figuur 2: Schelleng diagram dat het Helmholtzgebied aanduidt. Model Model voor de frictiecurve Om de resultaten van eventuele experimenten te kunnen voorspellen en het maken van een regelaar makkelijker te maken zal een model gemaakt worden van de Helmholtz trilling van de snaar. Dit model word in matlab gemaakt en de theorie achter het model word in het volgende stuk besproken. Eenvoudige benadering In simpele modellen van de interactie tussen boog en snaar, wordt ervan uitgegaan dat de wrijvingskracht tussen beide alleen afhangt van de relatieve snelheid van de snaar ten opzichte van de boog. Het verband heeft volgens deze modellen een exponentiële vorm zoals in onderstaand figuur 3. Hierin is v de snelheid van de snaar en vb de snelheid van de boog. Deze wrijvingskracht op het interactievlak tussen boog en snaar is te berekenen volgens: Waarbij µ de wrijvingscoëfficiënt is en fb de kracht waarmee de boog op de snaar wordt gedrukt. 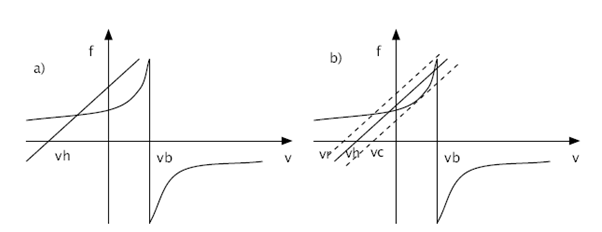Figuur 3: a) Het verband tussen de relatieve snelheid van de snaar, t.o.v. de boog, en de wrijvingskracht. b) Release velocity vr en capture velocity vc . Er zijn verschillende modellen voor de wrijvingscoëfficiënt. Het hyperbolische model wordt gegeven door de relatie: 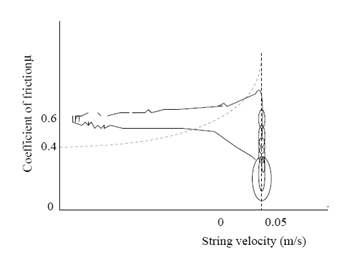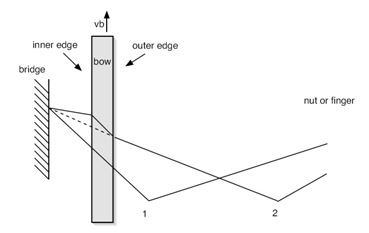Hierin is v0 de initiële boogsnelheid, µd de dynamische frictiecoëfficiënt en µs de statische frictiecoëfficiënt. In de meeste modellen wordt µd = 0.3 en µs = 0.8 gebruikt. Het exponentiële frictiemodel wordt gegeven door: Figuur 4: Het verband tussen snaarsnelheid v en wrijvingscoëfficiënt µ volgens het model (gestippeld) en volgens experimentele bepaling (getrokken). Figuur 5: Schematische weergave van het strijken van een snaar. De gestippelde lijn in situatie 2 geeft de werkelijke situatie weer, de getrokken lijn geeft de versimpelde voorstelling waarin zonder slip gestreken kan worden. In figuur 3 is tevens een verband weergegeven tussen de kracht die op de snaar wordt uitgeoefend en de snelheid die de snaar hierdoor krijgt. Dit dynamische gedrag van de snaar is volgens experimenteel onderzoek in benadering lineair. In figuur 3 b) zijn ook de release velocity vr en de capture velocity vc getekend. Dit zijn de snelheden waarbij de snaar respectievelijk losgelaten en meegenomen wordt door de boog. Dit kan als volgt worden uitgelegd. Als de snelheid van de snaar toeneemt, zal deze over de boog blijven slippen totdat de capture velocity vc is bereikt. Op dat moment blijft de snaar aan de boog plakken (‘stick’) waardoor de snaarsnelheid een sprong maakt naar de boogsnelheid vb. De snaar zal blijven plakken totdat deze de release velocity vr bereikt. Dit betekent dus dat de oplossing van de krachtsvergelijking een andere route over de grafiek volgt als de relatieve snelheid toeneemt dan wanneer deze afneemt. Frictiemodel vs. Experiment In het eenvoudige model dat in figuur 3 is afgebeeld, is ervan uitgegaan dat de wrijvingskracht alleen afhangt van de relatieve snelheid tussen de boog en de snaar. Uit metingen is echter gebleken dat het verband niet zo eenvoudig is. De gestippelde lijn in figuur 4 laat het verband tussen snaarsnelheid en wrijvingscoëfficiënt zien zoals dat uit het bovengenoemde model komt. De getrokken lijn geeft het werkelijke verband, welke experimenteel is bepaald. Uit deze figuur blijkt duidelijk dat de klassieke benadering niet klopt. Verklaringen voor fouten in het frictiemodel Een van de verklaringen hiervoor is dat de temperatuur van het interactievlak een sterke invloed heeft. De verklaring hiervoor is dat als de snaar een relatief kleine snelheid heeft ten opzicht van de boog, de contactlaag afkoelt door geleiding naar het materiaal buiten het contactgebied. Hierdoor nemen de schuifsterkte en de wrijvingscoëfficiënt op het contactgebied toe. Zodra er meer ‘slip’ plaatsvindt, warmt het contactgebied op door de arbeid die tegen de wrijving in wordt geleverd. Door deze warmteproductie wordt de hars in het contactgebied zachter en neemt de wrijvingscoëfficiënt snel af. Een ander verschijnsel dat veel invloed blijkt te hebben op de wrijvingskracht tussen boog en snaar, is de zogenaamde bow hair-compliance. Deze afwijking wordt veroorzaakt door het feit dat de boog niet op één punt contact maakt met de snaar, zoals verondersteld in het klassieke model, maar een contactgebied heeft. Het verschil is dat het voor een contactpunt wel mogelijk is dat de snaar zonder ‘slip’ de boog volgt, terwijl dit voor een contactgebied niet mogelijk is. In figuur 5 wordt aangegeven waarom dit niet mogelijk is. Situatie 1 is hierbij de uitgangssituatie. Hierin staat de boog op de snaar en is de snaar geëxciteerd. Een tijdsinterval later (situatie 2) is de boog met een snelheid vb omhoog bewogen en is de snaar door ‘stick’ gedrag meegenomen. De gestippelde lijn geeft de situatie weer zoals deze in werkelijkheid optreedt. De getrokken lijn geeft weer hoe vorm van de snaar zou moeten zijn als de snaar zonder enige vorm van ‘slip’ meegnomen zou zijn. Het moge duidelijk zijn dat deze situatie niet optreedt en er dus nooit geheel zonder ‘slip’ gestreken kan worden. Uit experimenten is echter wel gebleken dat de simpele voorstelling van de wrijvingscurve voldoende is om te kunnen simuleren wat de invloed is van het veranderen van wrijvingssnelheid en –druk op het al dan niet plaatsvinden van een Helmholtz beweging. Voor de toepassing van ons computermodel zal de wrijvingscurve zoals deze in figuur 3 is voorgesteld dus wel voldoen. Computermodel Variabelen Er zijn 3 waarden in te stellen in het model. Dit zijn de snelheid van de boog (vb), de druk die met de boog op de snaar uitgeoefend wordt (Fb) en als laatste een factor die de afstand tussen de boog en de kam ten opzichte van de lengte van de snaar aangeeft (beta). Werking van het programma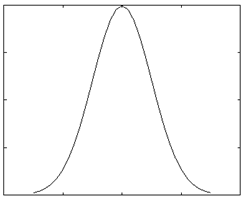 Figuur 6: De symmetrische Gauss-kromme. In het programma wordt het simulatiegebied opgedeeld in n intervallen, met een grootte dt. Het programma doorloopt voor elke tijdstap dt een loop waarin met behulp van bekende waarden voor de positie, kracht en snelheid uit het verleden de nieuwe waarden voor deze grootheden bepaald kunnen worden. Van belang hierbij is dat de snelheid waarmee een op de snaar uitgeoefende kracht zich door de snaar beweegt bekend is. Zo kan er op tijdstip i altijd terug gekeken worden in de geschiedenis welke krachten uit het verleden op tijdstip i teruggekaatst zijn en dus weer van invloed zijn op de beweging van het gesimuleerde punt. Om de exacte werking van het model te illustreren, zal hieronder de loop van één tijdstap doorlopen worden. Het model zelf is ook bijgevoegd. (Let op! Het model is nog niet werkend of voorzien van commentaar). De snaar wordt bekeken op positie x op tijdstip i. Trillingen die op positie x veroorzaakt worden, gaan via de snaar naar de uiteinden van de snaar, van waar ze teruggekaatst worden naar positie x. Op tijdstip i wordt eerst uitgerekend op welk tijdstip de trillingen die op dat moment terugkomen op positie x uitgezonden werden. Dit is dus een tijdstip in het verleden. Aangezien de snelheid waarmee de golf zich voortplant geen meervoud is van dt, zal er meestal geïnterpoleerd moeten worden tussen twee tijdstippen. Omdat trillingen die nog niet helemaal teruggekeerd zijn, of juist alweer voorbij positie x zijn ook invloed hebben op de beweging op positie x, wordt er ook rekening gehouden met deze trillingen. Met behulp van een symmetrische Gauss-kromme (zie figuur 6) wordt de invloed van deze trillingen uitgerekend en opgeteld bij de trilling die precies op tijdstip i is teruggekeerd. Al deze trillingen zijn in feite krachten die van invloed zijn op de snaarsnelheid v op tijdstip i. Met behulp van het frictiemodel kunnen de resulterende kracht omgezet worden in een nieuwe snaarsnelheid. Dit is dus de snaarsnelheid vi op tijdstip i. Als deze loop voor alle tijdstappen doorlopen is, is er dus een vector v gemaakt met daarin voor elke tijdstap i de bijbehorende snelheid vi. Uit deze snelheidsvector kan eenvoudig de positievector u bepaald worden door middel van integratie over alle tijdstappen dt. Als de complete trilling van de snaar bekend is (positie als functie van de tijd), kan door een fouriertransformatie toe te passen een powerspectrum gemaakt worden waarin de amplitude verhoudingen te zien zijn in het frequentiedomein. Problemen Het grootste probleem tot nu toe is dat de frequentie van de snaartrilling steeds afhankelijk blijkt te zijn van de strijksnelheid en –druk. In de werkelijkheid is dit niet het geval en wordt de frequentie slechts beïnvloed door de lengte van de snaar. Met het variëren van de strijksnelheid en –druk wordt in werkelijkheid alleen de amplitude en dus de luidheid van de trilling beïnvloed. Dit probleem wordt waarschijnlijk veroorzaakt door een ander probleem. Namelijk het modelleren van de snaarstijfheid, dus welke kracht de snaarstijfheid genereert als functie van de tijd. Hiervoor moet nog een oplossing gevonden worden. Analyses met het model Met behulp van het werkende model kan een Helmholtz trilling gegenereerd worden. Deze trilling kan daarna geanalyseerd worden met behulp van matlab. Het model herkent een trilling en kan deze klassificeren in een aantal groepen. Uit alle gemodeleerde trillingen is een zuivere Helmholttrilling gepakt, deze ziet er uit als in de figuur hier onder.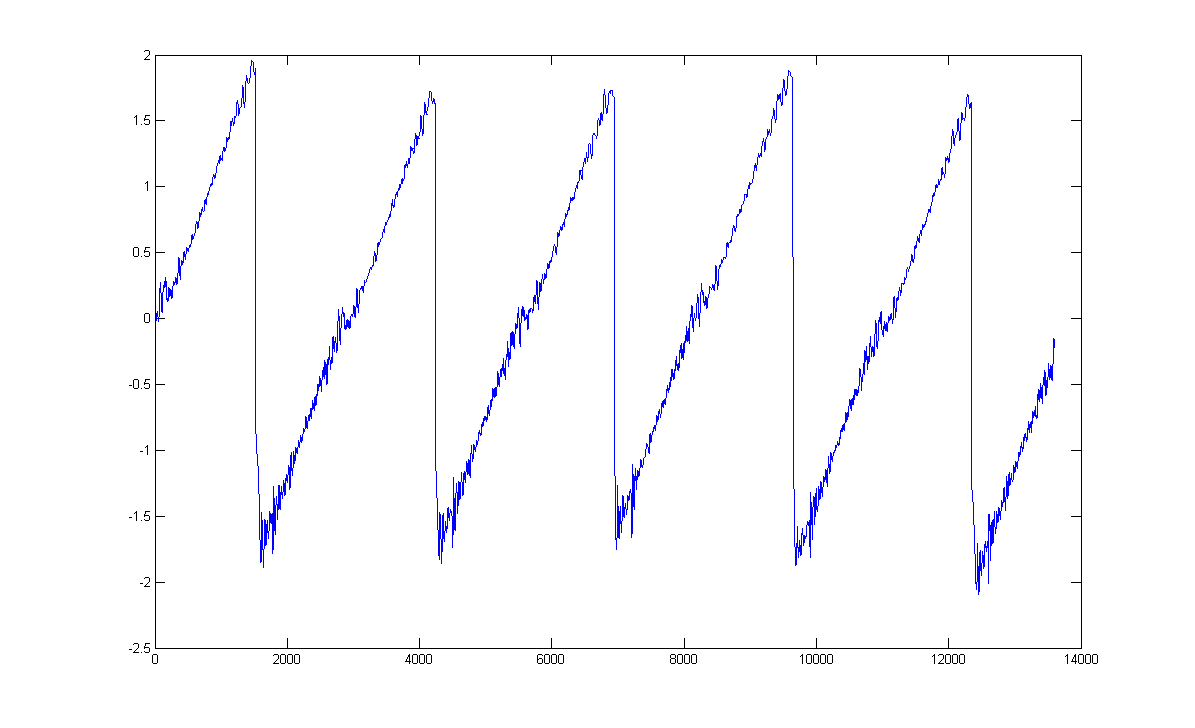 Figuur X: Een gegenereerde Helmholtz trilling. Van deze trilling is daarna het frequentiedomein geplot doormiddel van een discrete Fourier transformatie om meer inzicht te krijgen in de belangrijke frequenties in een Helmholtztrilling. Het resultaat hiervan is te zien in onderstaande figuur. 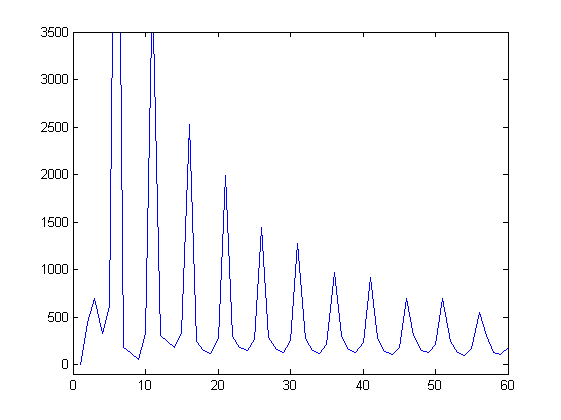Figuur X: Het frequentiedomein. Octrooionderzoek Viotar Het ontwerp Zoals gezegd is de viotar ontworpen om nieuwe mogelijkheden te creëren op het gebied van strijkinstrumenten. Het belangrijkste uitgangspunt van het ontwerp is dat de strijkdruk en -snelheid continu geregeld worden door het systeem. Dit houdt in dat de speler dit zelf niet hoeft te kunnen regelen, waardoor het instrument bereikbaar wordt voor een grotere groep musici. Tevens maakt dit ontwerp het mogelijk om akkoorden te spelen, wat bij een traditioneel strijkinstrument praktisch onmogelijk is. Om aan deze eisen te voldoen, is ervoor gekozen om af te zien van de klassieke strijkstok. In plaats daarvan zullen de snaren aangestreken worden door strijkwieltjes. Iedere snaar heeft een eigen strijkwieltje. Deze worden elk door een eigen elektromotor aangedreven, zodat de strijksnelheid van iedere snaar onafhankelijk geregeld kan worden. Om de strijkdruk continu te kunnen regelen, is ieder strijkwieltje tevens gekoppeld aan een lineaire actuator. Bestaande octrooien Gebruikte ECLA-codes in het onderzoek Om te onderzoeken welke octrooien er al bestaan op dit gebied, is op verschillende ECLA-codes en trefwoorden gezocht. De volgende combinaties van ECLA-codes en trefwoorden zijn gebruikt: G10 + String strike G10 + Bow wheel G10 + Violin string bow G10 + Mechanical bow G10D + Violin bow G10F + Violin G10F + Bow Geselecteerde octrooien Uit de resultaten zijn een aantal octrooien geselecteerd die mogelijk een raakvlak hebben met het ontwerp van de viotar. Deze selectie is in tabel 1 weergegeven. Er is gekozen voor deze octrooien omdat ze een kenmerk gemeen hebben met het ontwerp van de viotar. Het octrooi dat het meest overeenkomt met ons ontwerp is de onderste (US1425533 (A). Dit is het octrooi van zelf spelende viool van de gebroeders Mills verbeteringen op hun patenten US1028495 en US0807871. De aandrijving van van de snaren wordt gedaan aan de hand van wieltjes die dankzij een aangepaste viool in het platte vlak liggen. De aandrijfwielen zijn bevestigd aan hefbomen die de aandrijfwielen op de snaren drukken doormiddel van een relais. De aandrijving van dit patent komt sterk overeen met ons ontwerp, echter wordt de druk en de snelheid van het strijken niet continue geregeld, dit is waar wij afwijken. Dit patent heeft het tevens over een volledig automatisch bespeelde viool aangestuurd door rollen, waar wij uit gaan van een instrument waar je het bespelen zelf in de hand hebt. 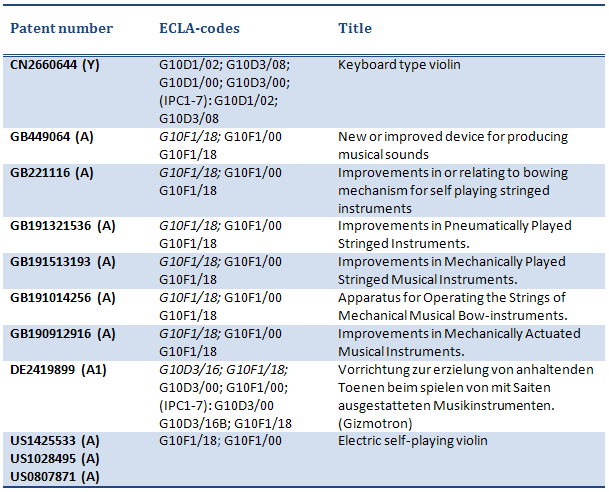Tabel 1: Geselecteerde octrooien uit zoekresultaten Viotar patenteerbaar? Uit het octrooionderzoek is gebleken dat het idee van de viotar niet geheel nieuw is. Er zijn elementen van de viotar die in bestaande octrooien zijn terug te vinden. Bijvoorbeeld het gebruik van strijkwieltjes in plaats van een strijkstok is niet nieuw. Ook het idee dat deze via elektrische aansturing op het bestrijken van een viool doormiddel van van bespeeld wordt met toetsen is in de octrooien terug te vinden. Wat echter niet terug gevonden is, is het idee om de strijkdruk en snelheid continu te regelen zodat er altijd zuivere tonen gespeeld worden. Op grond van deze resultaten zou het idee van regelen van strijkdruk en –snelheid mogelijk gepatenteerd kunnen worden. Het gebruik van strijkwieltjes in plaats van een strijkstok zal geen problemen opleveren, aangezien de gevonden octrooien reeds verlopen zijn. Opstelling http://www.tec-automatismes.com/anglais/electroaimants_3.php?idDoc=349&rech=false Interview met Eindhovense vioolbouwer Hendrik Zick Over de strijkstok Over het houten gedeelte van de strijkstok: Het material is brasilhout en dan het liefst pernambuco hout. Dat heeft zich bewezen op het gebied van stabiliteit en veerkracht. Bij het selecteren van het hout wordt gekeken naar de houtstructuur, hieruit kan opgemaakt worden of het goed te bewerken is. Na het uitzoeken wordt het hout in de goede vorm geschaafd. De stijfheid wordt emprisich en op gevoel getest. Daarna wordt de stok boven het vuur al ronddraaiend gebogen. Er word ook geprobeerd om de strijkstokken van carbon te maken maar vooralsnog met weinig succes, er is nog steeds een verschil te merken. Over de haren op de strijkstok Paardenhaar heeft een hele fijne oppervlaktestructuur, paardenhaar van schimmels, Mongools paardenhaar is wat ze willen hebben. Je voelt als je de haar in de lengterichting tussen de vinger en duim door trekt, hoe fijn de structuur is. Hoe meer je weerhaakjes hebt, dus hoe fijner de structuur is, en hoe beter die verdeeld is, hoe beter dat het haar is. Echter; een fijnere structuur houdt vaak ook in dat de haar dunner is, en dus slapper is (eerder breekt), en dat er meer haren nodig zijn op een strijkstok. De weerhaakjes op de paardenharen zijn goed om de hars vast te houden. Paardenharen zijn ook met kunststof nagemaakt maar dat is te horen, dat geeft een rauw geluid. Er zijn in de loop der tijd kunstmatige alternatieven voor de traditionele naaldboomhars bedacht, maar deze klinken toch anders en niet in iedereens ogen goed. Een ander soort hars geeft een andere klank. Verder zetten de paardenharen thermisch flink uit. De beste strijkstokbouwers waren de fransen, nog tot anderhalve eeuw geleden, die hebben het hout homogener gemaakt door een bepaalde behandeling aan het hout te geven, waardoor ze heel erg “stabiel” zijn. De wolfnoot Met name cellisten krijgen te maken met een fenomeen genaamd de wolfnoot. Op een bepaalde snaar (meestal de G-snaar) op een hoge positie zit dan een noot waarbij de toonhoogte hevig gaat schommelen, iets wat een speler wil vermijden. Deze wolfnoot is bij een strijkinstrument niet te voorkomen, men kan hem alleen onderdrukken door de resonanties bij deze noot te onderdrukken. Ook de speler kan de wolfnoot een beetje opvangen door de manier waarop hij strijkt. Hij is hierbij ook afhankelijk van de strijkstok. Een slechte goedkope strijkstok kan de wolftoon niet goed afvangen, omdat hij te “stijf” of “te stug” is, een goede strijkstok kan dat beter. Over het algemeen is de wolfnoot sterker bij een lagere snaarspanning. Een stalen snaar is normaal strakker gespannen, waardoor hij wat sneller “reageert”, dat wil zeggen, wat sneller van waveform verandert. Hierdoor is een wolfnoot vaak weer “sneller weg”. De bouw van een viool Rond het begin van de 19e eeuw werden violen “virtuozer”. Voor die tijd waren de halzen korter dan dat ze nu zijn. Mensen speelden toen alleen in lage posities op de viool, en het bereik was beperkt. Toen violisten als Paganini lieten zien dat er veel meer mogelijk was met een viool, gingen violen veranderen. Bestaande violen werden omgebouwd (nieuwe violen waren en zijn nog steeds erg duur) zodat de hals langer werd, zodat men op hogere posities kon spelen. Hierbij kwam ook een hogere snaarspanning kijken. Hierdoor kwamen ook andere eisen aan de constructie van de viool. Veel instrumenten klonken in het hogere (nieuwe) register niet, omdat daarvoor hogere resonantiefrequenties nodig zijn. Veel instrumenten van Stradivarius bleven echter wel goed klinken, en dat is waardoor ze zo beroemd zijn geworden. Het op klank brengen van een viool bestaat voor een groot deel uit het variëren van de dikte van het voor- en achterblad. Dit luistert heel nauw, de kleinste diktevariatie op een klein gebied op het blad leidt direct tot verandering in de klank. Je hebt goedkope instrumenten, die bijvoorbeeld in Rusland of China worden gebouwd, dat zijn blokken hout en die worden voorgefreesd zodat men een boven- of onderblad krijgt. De zowel de binnenwelving als de buitenwelving zijn dan bijna klaar. Je kunt daarna echter niet een blad geautomatiseerd op klank brengen, want elk stukje hout klinkt weer anders. Zou je uit dezelfde boom een net zo dik, hetzelfde georienteered blad halen uit bijna dezelfde plek in de boom, dan klinkt hij toch anders. Het hout is sterk inhomogeen. Daarom moet het op klank brengen voor iedere viool anders gebeuren. Dat is de reden dat goede instrumenten altijd handgemaakt zijn. Bij een meesterwerk van een viool is 80-85% handwerk. Je kunt een beetje voorfrezen maar de rest moet je met de hand doen. Bij het bouwen moet je doen wat het hout zegt en niet andersom. Als je ergens een goede frequentie uit een gebiedje kan halen moet je dat aangrijpen. Je kunt niet volgens een vast plan werken om bijvoorbeeld een Stradivarius na te bouwen, want het hout zal zich niet aan je vaste plan aanpassen. De toets van de viool is van esdoorn. Beuken is te “stug”, het wil niet zo makkelijk trillen (voor de klankkast) en daarom is men uitgekomen bij brasil. De vlammen op een elektrische gitaar zijn esdoorn. Esdoorn bemoeilijkt het krijgen van een goede klank, maar je kán er een betere klank mee krijgen omdat het hard is en een hoge eigenfrequentie heeft. Hogere eigenfrequenties is wat men meestal zoekt, omdat het hoge bereik van een viool dat vereist. Voor het bovenblad heeft men bewust een andere houtsoort gekozen: grenen. In nerven zijn donkere streepjes winterhout, lichte streepjes zomerhout. Dit andere hout is vanwege de klankkleur. Er zijn mensen die hebben geprobeerd bepaalde mineralen in de grondlaag van de lak te verwerken, en beweren dat dit de viool beter laat klinken. Zick doet dit af als onzin, omdat dit zou betekenen dat over het hele oppervlak van de viool hetzelfde moet gebeuren om hem “beter” te laten klinken, áls “beter” al een definieerbaar begrip is. Het tegendeel is namelijk waar: door de inhomogeeniteit van het hout moet voor de resonanties die de klank vormen te beïnvloeden ieder plekje op de viool anders worden behandeld. Wat zou Zick aan het ontwerp van een viool kunnen verbeteren? Hij zou niet weten hoe je het zou kunnen veranderen. Als je het groter maakt, wordt het een alt, dus dat wil je niet als je een viool bouwt. De vorm bepaalt de klank van de viool, dus als je een viool bouwt wil je dat dus ook niet veranderen. Het punt zit het dus in dat je als je een vióól bouwt, je niets anders van plan bent te bouwen; er zit geen verandering meer in het ontwerp, omdat de viool gedefinieerd is zoals ie nu is. Toch hebben mensen van alles geprobeerd, zelfs een uitschuifbare viool voor volumemodulatie, of een ander materiaal: van glas, plastic, messing, koper, alles was geprobeerd. Wat gebeurde alleen: de klank veranderde van kleur, het werd niet mooier. Als het mooier zou zijn, dan ok, maar dat werd niet zo gevonden. De “mooiheid” van een viool is veel te danken aan de vele boventonen die ontstaan door het (inhomogene) hout. De vele hogere harmonische zijn nog niet goed na te bouwen met een ander materiaal.