Water Transport Infrastructure

Group Members

Name	Student Id
Han Wei Chia	1002684
Hans Chia	0979848
Joost Roordink	1005406
Dennis Rizviç	1020540
Minjin Song	1194206
Thomas Gian	0995114

Subject

According to research, one in six people have no access to drinkable water. Even if they have a water source, it takes them hours of travelling long distances to reach it. This causes a harsh environment for humans to survive in. Current methods of transporting water require expensive infrastructure investments, which is often not affordable for areas where water access is limited (they often tend to be fairly poor). We want to see if robots replacing these is a viable option.

Objectives

Our objective investigate the viability of using a robot to replace the manual labor that millions of people need to do to have access to water, compared to other possible solutions to this problem.

Users

The main users are charities that help communities or even the communities themselves that have no convenient access to water in areas with a semi-arid or desert climate. We assume these areas can generate the amount of solar power needed to power the water transport robot for most of the day.

Approach

Before we start designing the robot, we'll gather information surrounding this subject. This is to get more in depth knowledge of the current water supply situation and solution that are already in use. After gathering information, we analyze whether a robot has an use case between the already existing solutions. Finally, finding a scenario that could fit the use case and start designing the robot according to scenario.

Milestones

• Find use Case between the already existing solution
• Design choices fully fledged out.
• Design made according to our design choices.

Deliverables

• Logbook
• Planning
• Final document (including code)
• Presentation
• Research paper of the infrastructure , With Advantages, disadvantages and cost comparisons.

Literature study

Summary of Literature's

Why does this problem need to be solved?

According to Graham et al, over 13 million women and 3 million children that are responsible for water collection in their household need to walk for more than 30 minutes. Note that these numbers are from only 24 countries in sub saharan africa, and the scale of the real problem is even larger than these numbers suggest. The paper also mentions various negative effects this has on these people. One of them is decreased hygiene. In the case of one particular disease(trachoma) has its prevalence almost doubled if water access is further away. Diarrhea also sees significant decreases if water collection time is reduced. Collection of water is also a physically demanding job. The negative effects of this are studied by Geere et al. in . They report that manual carrying of water results in a serious increase in spinal, neck and head pain. Children doing manual labour to fetch water has also been linked with decreased school performance. This is mostly linked to fatigue and lower attendance rates of children that need to carry water compared to those that don’t. Another major concern is the opportunity cost of the time women spend on getting water. Research done by Cairncross and Cuff that compared two villages with different access to water found that time saved by reducing travel times to water sources would be used on either other household tasks or used to spent more time with children. This is also backed by research done by Koolwal and Van de Walle, which finds that reduced travel times to water access improve children’s education rather than paid-market labour participation.

Water Access

Water Wells

Water wells have been used for ages in order to have access to groundwater as a source of water consumption. They are inexpensive and require little technology as it’s mainly manual labor in which every person can participate in. However, the costs and difficulty depend on the location of where the well is to be built. In areas where the groundwater level is deep in the ground and also what type of ground it is that provides stability of the surrounding earth will prove to be important factors.

cost of wells

The main advantage of wells is that there very cost effective ones there running, but the initial cost and the time required to make them can add up a lot.

The cost of a well being drilled can vary, depending largely on the depth of the well, the diameter of the hole and the materials needed for the job. Other factors can also affect the cost of the well, such as the quality of the pump, and all the other technology you want to attach to it, man hours needed for the job, transportation of materials and equipment.

Accurate information on drilling prices or costs in sub‐Saharan Africa is not easy to access. Systematic analysis is a challenge because there is poor, fragmented and non‐standardized record keeping of water supply projects and programmes in sub‐Saharan Africa as well as lack of transparency. Table 1 provides examples of estimated and actual borehole costs and prices, ranging from $2,000 to $500,000 ($120 to $1,271 per meter).

According to Water Wells for Africa, the average cost for building a well in Africa costs around $8,000, mostly in Malawi and Mozambique. According to the WaterPage.com, the cost of building a well with modern technology, using hydraulics for digging a well, will cost around $8,000 on average, without the cost of purchasing the hydraulics equipment. The lower cost, using Eureka Drill System or other small hydraulics, will cost around $1,500. The lowest cost of the three options, which is digging a borehole that are human operated without any mechanical equipment, will cost few hundred dollars to dig. However, these methods are only available if there is a water source available nearby underground. If the water source is located deeper, the costs will increase drastically as it will either require more manpower or more costs to use the hydraulic equipment.

Disadvantages

Digging a well can be risky as you will usually be digging deep in the earth, which might collapse depending on the type of ground you work on. This requires technical overhead to avoid construction failures. And once you have a well, they aren’t well known for their hygienic reputation. Wells are easily contaminated and increase the chance of spreading various waterborne diseases such as cholera. Although there are ways of preventing the well of becoming contaminated, like sealing the well head, cleaning it with chlorine solutions and periodically checking it, these wells all require knowledgeable maintenance from the local community that makes use of these wells. They will have to be educated to protect the drinking water. But the cleanup of the well’s water is quite expensive and difficult as well, since they will require chemical, physical and biological treatments. The local community won’t have the knowledge on which treatments to apply and this will require an expert to perform throughout cleansing on every well. Knowing all the difficulties and costs that come along with using a well, It might not always be the best option.

Pipelines

Pipelines are mostly used for transporting different kinds of fluids, including petroleum, water, and natural gas. In this research, we will look deeper into how water transport, especially transport of drinking water, works and how much it costs.

Advantages of pipelines below ground

The advantages of using pipelines for water transportation are low maintenance costs, stable fluid transportation through difficult terrains, and low energy cost. Pipelines normally lasts for about 50 years and have low probability of leaks during the lifespan Pipelines are hidden underground, so there are no physical limitations once the pipelines are built. Compared to other transport methods, such as over ground vehicles, water pipelines are much more cost efficient since water is transported by a pump that requires little energy to operate.

Advantage of pipelines above the ground

Due to the pipelines being above the ground, maintenance should be a lot easier than underground pipelines. The leaks are visible in the open air, so the process of finding and identifying leaks is a lot easier, which in turn makes maintenance easier as well.

Disadvantages of pipelines below ground

The main disadvantages of using pipeline for water transport is that it is difficult to find the source of leakage when it is known that the pipelines are broken. Although the probability of broken pipelines are low, the broken pipelines may take a long time to repair since it is buried underground. Also, the pipelines are inflexible in capacity once they are constructed since they have fixed pipe sizes that need to be compatible with other pipeline networks. The construction of pipelines are also limited to certain areas as they are buried underground and the constructors have to consider the environmental consequences of creating underground pipelines.

Disadvantages of pipelines above ground

Pipelines that are build above the ground, can cause visual pollution due to its massive size and length. Also, due to the pipelines being above the ground they are not protected against open air, water, wind and the weather in general. This can cause corrosion and erosion of the pipelines, which can lead to leaks and just a generally shorter lifespan. Also, the disadvantage of pipelines in general still hold.

Cost analysis

There are two types of water that can be used to create drinking water: Surface water and groundwater. Surface water is open to the environment and therefore exposed to human and animal activity, which causes surface water to be contaminated. To create drinkable water from contaminated water, it needs to be treated, but treatment of contaminated water comes with extra costs. Also, surface water often has more salinity than drinkable water, which causes the water to be unsafe for consumption. To reduce the salt in surface water to drinkable levels, the water needs to be desalinated. The process of desalination costs $1/m3 for seawater and $0.60/m3 for brackish water. Groundwater is often a lot less salt, which causes the desalination costs to be a lot lower. In some cases desalination is not even needed, which means that the costs of desalination will be non-existent. For further treatment, groundwater needs nothing more than filtration of sand and other small particles, so in terms of cost groundwater is the far superior option compared to surface water.

Transport of water by pipelines costs around $0.05-0.06/m3 for every 100 kilometer of horizontal movement and has about the same price for a vertical lift of 100 meters. This means that transport of water by pipeline to areas that require more vertical lift are more expensive, than areas where only horizontal movement is needed.

According to the Trans Africa Pipeline that constructed the water pipelines across sub-Saharan region of Africa, the project that involves about 6,000 km of pipelines with pipe monitors, desalination plant, water tanks, and water pumps cost about 9.9 billion US dollars to construct and estimated cost about 380 million US dollars per year to maintain those pipelines.

In the case of our scenario, installing 3km of water pipeline would cost $4.95 million, if the same method of calculation was used. If separate calculation were used, taking $4 million dollars for the pipeline itself, $1.5 million for one water tank and pump over 3 km of distance, $83,000 for solar panel to power the pump, and 40 million for monitoring system, will cost around $45 million in total. In this calculation, desalination plants and nuclear plants were taken out off the cost calculation since our scenario does not fit with using sea water for providing water. Maintenance of 3 km of pipeline will cost around $9,300 to $18,600 per year. For a 3 km setup of pipeline, $45 million dollars plus $18,600 per year does not seem to be cost efficient to support a population of 250 people.

Robot

Will a robot be accepted by the population in rural areas, that may not have any previous experience with robots?

The robot is intended to be used in areas where water access is a serious issue. These areas are often poor and have less access to technology in general. Therefore it might be an issue that the primary user group of these robots do not have any previous experience in encountering robots. One study that dealt with this issue is. In this study a remotely controlled robot was used to carry water in a rural village in India in order to observe the users reactions to this robot. The study reports that the robot was positively received by the population. It also noted that there seems to a strong cultural influence in what the robot was perceived to be, f.e. being seen as female despite it having a male voice. This means that the robot will need some degree of modularity in its appearance and interaction with users to adapt to any local customs that might affect its performance. It should be noted however that this study was carried out in India, so it can be disputed whether the results are applicable to rural areas in Africa.

The advantages of having a robot as a solution

In the list below, we’ll consider three other possible methods of assuring water for a community of people and compare them with the robot. The three methods are: building a well, building a pipeline network and transporting water to the community through vehicles such as planes, boats or trucks/ cars.

• The robot is instantly deployable. Pipelines, wells etc need to be build and often takes a long amount of time, while a robot can be build beforehand and be deployed instantly to places where it’s needed. This is an advantage over pipelines and wells since they have a much longer construction time. The main contester on this point would be to have a vehicle transport water towards the community. While transportation with vehicles would be faster, it also requires more manpower and more money (traveling cost) the longer this form of transportation persists. A robot on the other hand has no other costs or need for manpower next to maintenance and build cost, which can be done beforehand and might thus be a better option regarding money and manpower.

• The robot is reusable. If a better means of transportation of water is deployed, the robot can be reused at a different location where it is needed. Being instantly deployable and reusable means that the robot can be moved and deployed quickly at another location. This is a great attribute in case the robot is used as a temporary form of providing water. When the robot is no longer needed in a certain area, it can simply be moved to another location which only requires traveling time and the traveling cost.

• Sustainability. A robot which is able to power itself by sunlight is mostly or fully (depending on how it’s made) self-sustainable excluding maintenance. This is also a characteristic of wells or pipelines, but overall it is a huge advantage over transporting water by conventional means towards a place. Maintenance is the largest problem regarding the sustainability of the robot. Depending on how well the robot is build, the frequency of the maintenance would be increased or decreased. While maintenance is a problem with the robot, all structures, including the well and the pipeline, require some form of maintenance from time to time. Since the robot has not yet been fully built and tested, it is hard to give an estimate of the frequency of maintaining the robot and the time it takes to perform the maintenance and thus we can’t say if it would be more or less frequent or time-consuming than pipelines or wells.

• Automatic. Since the robot is automatic, just like a well or a pipeline, it helps people gather water and thus saving them time. A well and a pipeline can also fulfil this criterion if it is located relatively close to the community. Having the robot being fully automatic, the habitants of the area, will have more time which could possibly be spent on improving education or improving their settlement such as building better houses, creating a road, building a well or creating a pipeline network. It might be possible to let a person of that community do the maintenance depending on the complexity of the robot. If this would be possible, the sustainability of the robot would further improve.

• Deployability: the places it can be deployed. The robot has a couple of conditions to be deployed in a certain area. The first one would be strong long-lasting sunlight and the second would be that it’s able to traverse the area. While this is not an advantage, but more restrictions to the robot, it is possible that it would be the only viable option.
  • A pipeline without a pump requires there to be a decent foundation for the network and the starting position needs to be higher than the destination. If that’s not the cause, the pipeline would need a pomp which would consume energy based on the different in height.
  • For the construction of a well, there needs to be a large underground water source. Underground water is often salty to some degree and might thus not be drinkable water. The last problem with a well is the depth that the underground water source is located at. If the depth is too great, construction a well would be too difficult and thus not viable.
  • Transportation of water through boats, planes, trucks is close to always an option, the main problem with this form of transportation is that it’s time consuming, requires manpower and requires a lot of energy and thus money in the long-term. This method is more of a short-term method until they find something better and is most likely not viable in the long-term since the cost would increase each time you have to transport water.

In case all of the above methods are not viable, the robot might be the best idea to be deployed, if it satisfies the above-mentioned requirements.

From the list of advantages, we can conclude that the robot does have a few cases in which it outperforms the other methods. While the robot is not viable in every situation, it fulfils some niche cases in which the other methods are not optimal.

Technical Requirements

Component	Usage	Cost	Importance
Actuators (motors)	To move the robot to a specified destination	Depends on water storage	High
Microcontroller	The controller will be the autonomous brain of the robot, steering the other components.	Depends on how much processing power is required	High
Wireless communication module	The status of the robot will be accessible through this link with another device.	Medium	Medium
GPS module	For measuring the distance until it's destination and the robot's location will be reported upon request of the manufacturer.	Medium	High
PC connector	To provide the most reliable connection establishment with another device to view its status.	Low	High
Solar panels	Generates energy from sunlight during daytime.	Depends on actuator usage	High
Battery	As a last resort, when the robot fails to follow the desired commands.	Depends on power usage	High
Power switch		Low	High
External LEDs	To light up the environment in the dark for avoiding collision, depending on the sensor type.	Low	Low
Gyroscope	For areas with a lot of height differences it will provide data to the microcontroller that can be processed to avoid topping over.	Low	Medium
Frame	Provides structural support to all components.	Depends on size	High
Waterproof casing	To protect all electronic components from external (water)damage.	Depends on size	Medium
(Active) cooling block	To prevent the components of overheating by taking the generated heat and dissipating it.	Depends on size	Medium
Memory storage	Stores all measured data from other components and all actions that were made by the robot. Also provides information for future debugging.	Depends on amount of measuring components	Low
Water filter	Filters the external water before it is stored by the robot.	Depends on the filter itself	High
Water tank	Local storage of drinkable water by the robot.	Depends on size	High
Camera	To perceive the environment and to report its actions for future debugging.	Low	Low
Speaker	To fend off hostile animals	Low	Medium
Ultrasonic sensor	To detect ground in front of the robot	Low	High

Scenario

Country: Republic of the Niger

Population estimate: 21 million

Area: 1,267,000 km2

Prosperity ranking: 139th out of 149

Landscape:

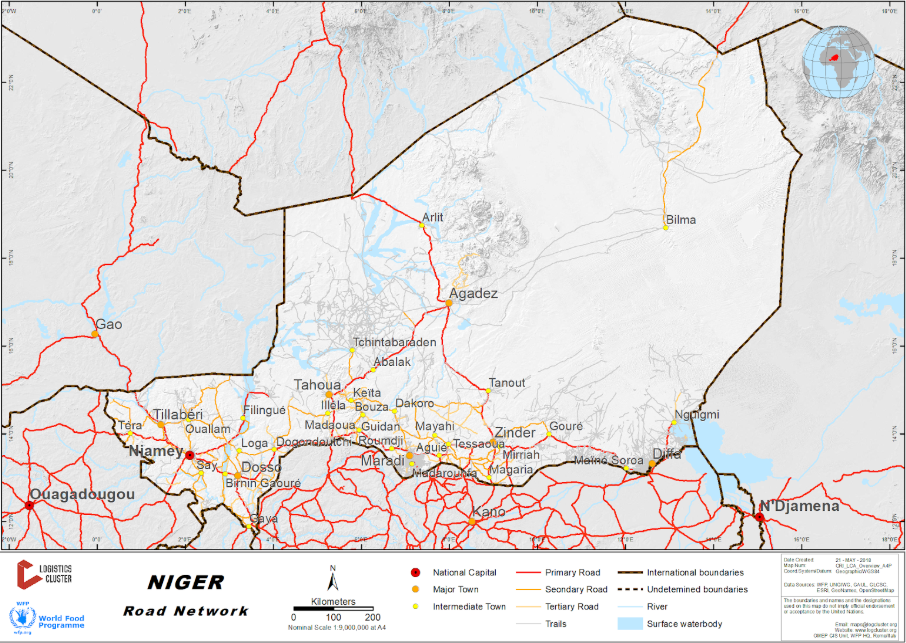
Groundwater located very deep in the ground. From around 50 to 250 meters below ground level

The north of Niger is covered by large deserts and semi deserts. The southern parts of Niger are naturally dominated savannahs Environmental issues in Niger include destructive farming practices as a result of population pressure. Illegal hunting, bush fires in some areas and human encroachment upon the flood plains of the Niger River for paddy cultivation are environmental issues. Dams constructed on the Niger River in the neighboring countries of Mali and Guinea and also within Niger itself are also cited as a reason for a reduction of water flow in the Niger River—which has a direct effect upon the environment. A lack of adequate staff to guard wildlife in the parks and reserves is another factor cited for loss of wildlife.

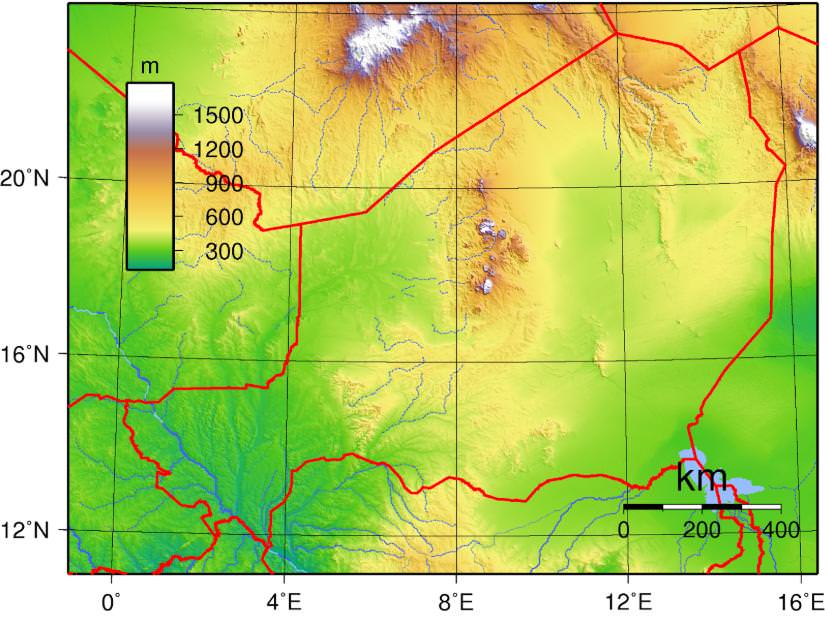
Surrounded by the vast Sahara desert, Niger is one of the least developed countries in the world. With intense droughts, poor soil conditions and the gradual spread of the desert, life is hard. The rainy season lasts from June to October during which 99% of the annual rainfall occurs with peaks in August, however it is still possible to have up to 10 days of drought during this month, making the distribution of rainfall extremely irregular. This is even more apparent in the north, where the the rainfall is unpredictable. Overall rainfall is below 100 mm and the potential evaporation is 2 to 3 meters per annum. During the rainy season, widespread hollows are transformed into temporary water pools and can act as a water source. The coolest months are November to February with a low mark of 19°C in December and the hot season from March to May has a mean maximum of 40°C. The Government faces many barriers to providing public services like clean water and toilets. The economy can barely fund infrastructure. And the extreme climate makes installation and maintenance a major challenge. However, the Republic of Niger has one of the best and macadamized road networks in sub Saharan Africa. This macadam is a type of road construction consisting of layers of small angular stones compacted in shallow lifts and it has a straight surface, which is an all weather road.

Primary roads are paved, secondary roads consist of lateral and gravel, tertiary roads generally consist of dirt. While the primary and secondary roads are more or less passable during the wet season, trails will practically become impassable. The terrain is predominantly sand dunes and desert plains in the south with hills in the north.

Soil in the northern Saharan region infertile. The Sahel, a region which forms a transitional zone between the Sahara and the region south, has thin white soils covered with salty deposits from intense evaporation that forms an infertile crust. The southern region however is cultivated, as the area has soils associated with uplands or extensive dunes or basins.

In rural areas, women perform arduous physical labor such as gathering firewood hand-processing food, fetching water from the well, and building and tending cooking fires. In rural areas, many families discourage girls from pursuing an education beyond primary school. At the one university, the University of Niamey, males predominate. Among some groups, particularly in the north, many families opposed all secular schools until recently, fearing them as sources of government control and cultural change.

Our Scenario plays in this Northern part of Niger. it can be from 19 to 48 degrees Celsius. There will be a water well 3 km distance from the community to the water source. The Community size consist of 250 people(Niger population is very thin in the north of the graph and thus small communities are more common)

Robot Design

Requirements

	Requirement text	Rationale	Verification/Testing	Dependency to requirements
R_0001	The robot can move through desert areas without obstruction.	This means that the robot is capable of moving in the target environments.	Assume we have a robot located in a desert. Let the robot move to some location in the desert. Observe whether the robot reaches its destination.	None
R_0002	The robot shall carry a local container of drinkable water.	This is necessary as the main goal of the robot is to transport water to those who need it.	Assume we have a robot carrying X amount of water stored in an enclosed object. After any arbitrary amount of time, observe whether the volume of water has remained the same.	None
R_0003	Upon reaching a water source, the robot shall filter the water before it stores the water in its local storage.	The water from the source might not be safely edible for humans, therefore it shall be filtered such that it is immediately available for consumption.	Assume we have a robot next to a littered water source. Let the robot filter the water and store it. Measure whether the stored water is safely drinkable for humans.	R_0002
R_0004	The robot shall generate energy locally through solar power.	The robot should be self sustainable and be able to operate at any time. In the targetted areas the likeliness of long daytime is very high.	Assume we have a robot in open air exposed to daylight. Measure whether energy is generated by the robot.	None
R_0005	When the robot's rate of energy generation exceeds that of energy usage, the excessive amount of energy shall be stored locally at the robot.	Stored energy shall be available for use during night time.	Assume we have a robot with an empty energy storage exposed to daylight. Measure whether the energy level remains at zero.	None
R_0006	During transit, the robot shall not collide with any objects.	The robot will be given a destination and it has to make it's way there by itself, here it's important to arrive there as fast as possible while making sure it won't collide with object in its route. So it has to be autonomous.	Give the robot a destination with a cushion in between its current position and destination. Observe whether the robot moves around the cushion instead of colliding with it.	R_0002
R_0007	The robot's appearance is noticable in any circumstance.	For the sake of the people in need of water, the robot has to be clearly visible to them.	Put the robot in the targetted environments at day and night and let a group of people spot the robot.	None
R_0008	When the robot is taking external damage, it will make a loud sound.	It is likely that the robot is being attacked by a wild animal, the sound might fend off the animal while it keeps moving towards it destination.	Assume we have a moving robot that will not topple over. Have a large animal or human attack the robot by pushing and shaking it. Observe the gyroscope values for spikes in a short timespan. Listen whether a loud sound is played.	None
R_0009	The robot's circuits and wires shall not be exposed to water.	This ensures some form of water resistance to avoid hardware failure.	Assume we have a robot exposed to heavy rainfall during an activity. Observe whether the robot still performs the activity as intended.	None
R_0010	The robot's water storage is sealed such that no changes can be made to its content, besides adding filtered water and tapping the stored water.	The safe water should remain as is, without external objects or fluids interacting with it to possibly modify it's drinkability.	Assume we have a robot with water stored. Cover the robot with sand and spray it with colored water. Observe whether sand or colored water has entered the storage.	R_0002
R_0011	The robot shall maintain operational in ambient temperatures up to 50 degrees Celsius.	Since the robot will be exposed in the desert where the temperatures can reach up to 48 degrees. Besides the robot itself will produce heat from the motors.	Assume the robot is in an environment where the ambient temperature is 50 degrees Celsius. Let the robot roam around for an hour. Observe whether the robot is operational.	None
R_0012	The robot shall transport 5000 liters of water in 24 hours.	The expected community size is 250 people, the minimum water requirement per person is 20 L according to research.	Assume we have a fully functional robot with a 3 km travel distance to a water source. Let the robot transport water between the source and destination continuously. After 24 hours, observe whether the transported amount of water has reached 5000 liters.	R_0001, R_0002, R_0003

Design choices

Energy Source

Choice of energy Source

For power source we have four main options: wind energy, solar energy, fossil fuels and grid power.

The electrification rate in Niger is very low. In rural areas it’s even effectively non-existent. This means that we will not be able to rely on grid power being present, which makes using it to power the robots impossible.

For fossil fuels we would need to set up the logistics required to supply the robots with said fossil fuel. This would also require ensuring that the locals are able to handle the fossil fuel in a safe manner since it is not possible to go there every couple of days to fill the fuel tanks ourselves. Additionally, as study doe by Szabó et al found that diesel is not as cost efficient as diesel is to provide off-grid power. These factors ensure that the usage of diesel fuel is not viable either.

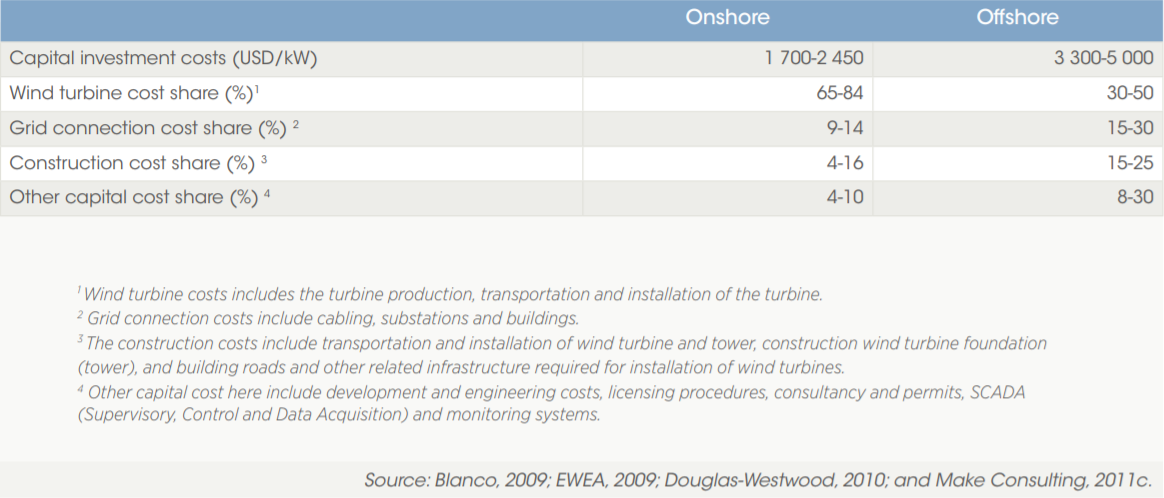
For wind power if onshore wind is considered, the capital investment that is needed per kW on a windmill is about $1700 to $2450 in 2009. This price is for large scale wind energy projects, consisting of hundreds of MW. The capital costs for small wind turbines are much more expensive ranging from $3000 to $6000 per kW. However, the amount of kW the wind turbines can provide is definitely not the same as how much kW the wind turbines will actually provide. The wind will not blow all the time, reducing the amount of kW actually produced by the windmills. Also the wind speed will also fluctuate a lot, meaning that the amount of kW it will produce is unreliable in shorter periods of time. For example it could be that the wind speed is below the cut in speed of the wind turbine for a whole day, meaning that no electricity will be generated for the entire day, because the wind speed has to be higher than the cut in speed to start generating electricity by turning.

The average wind speed in Agadez ranges from 7.4 mph to 11.7 mph, which is about 11.91 km/h to 18.83 km/h, depending on the time of the year. Making it quite an unreliable average wind speed all year round. On the wind density scale, a class 3 or above are considered good wind resources.

Considering that class 3 or above means an average wind speed of 13 mph or higher, the average wind speed in Agadez can’t be considered a good wind resource. So, wind energy is definitely not optimal in this region at all.

A disadvantage of using wind energy would be the loud noise that wind turbines make, disturbing nearby wildlife and people alike. The generation of wind energy would have to be at least 300 meters away to receive a level of constant noise of about 40 dB. Which is still some noise that people would rather not hear.

This leaves solar power as the only viable option to provide power. The main advantage of solar power is that this region is extremely sunny as was described in the scenario. It is also fairly low cost, and requires very little maintenance afterwards.

Neccesary solar area for certain power output

The main goal here is to have a rough watt/m^2 number to be able to make an estimate of how much space is needed to satisfy the energy needs of the robot. This is neccesary to be able to make a rough estimate of how much area our solar panels are going to use, which is an important factor in determining whether it is viable to put solar panels on the robots, or to use solar panels at all The solar panels have mostly been picked from the list given at to have some guarantee that they are within the price range we can afford for this robot. Note that we will not yet pick one specific panel here, since we would require knowledge of exactly how much space we have, what the dimensions of said space are, and how much power is actually needed in order to pick the cheapest panel that satisfies our needs.

From we can see that we can expect an efficiency of something in the range of 16-18%.

In Niger, we have an average daily irradiance of about 6 to 7 kwh/m^2

Using E=A*r*H*PR, where E is energy, A is the solar panel area, r is the efficiency, H is the solar irradiance and PR is a factor accounting for various electrical losses(usually taken at 0.75), we can calculate that the daily energy per square meter is, depending on the exact solar panel and irradiance used, between E=A*0.16*6*0.75=A*0.72kwh and E=A*0.18*7*0.75=A*0.945kwh.

This gives the following lower and upper bounds on the performance of a solar panel(note that this is an average over the entire day, which includes the night and evening bringing the average down): 0.72*3600000/(24*3600)=30w/m^2 0.945*3600000/(24*3600)=39w/m^2

We can also use the kwh/kwp map given in. The panels listed in and give a nominal power within a range of 250 to 300 wp. In northern Niger we get a daily kwh/kwp production in the range of 5 and 5.5. This then gives a worst case of 5*0.25=1.25 kwh/day and a best case of 5.5*0.3=1.65 kwh/day.

However, these wp figures are for the entire panel, which is usually larger than 1m^2. For wp/m^2 we need to look at table 1. Note that each panel has several variants and we have rounded the area to make the numbers easier to read, so exact numbers may differ a bit.

With these numbers, we’re looking at a rough 160-180 wp/m^2 range for the panels. These number then give 5*0.16=0.8 kwh/day and 5.5*0.18=0.99 kwh/day as lower and upper bounds. Note that these numbers are roughly the same as those found earlier, so the conversion to w/m^2 will give the same results.

Panel	ALLMAX framed 60 cell	330|335P-FG	295|300MS-FG	275|280P-FG	SUNIVA OPTIMUS
wp/m^2	180	165	150	180	165

Additionaly, we have also calculated how much energy we expect to need for various different speeds. This was done in an external latex file since it involved quite a bit of mathematics/physics. (NOTE TO TUTORS: not entirely finished yet but for the most part done.) https://v2.overleaf.com/read/nhdhyhfjkjrd

Energy Reliability

Unfortunately solar power isn't always 100% reliable as an energy sources. If there happen to be some clouds the production for solar panels will go down dramatically, so a prolonged period of clouds could result in the robots failing to function. Now we seek to determine how long the robot needs to be able to operate without being able to charge. Combined with the calculations for energy usage, this will determine how large the battery in a robot needs to be. The region the robot is to be deployed is covered by clouds 40% of the time. Note that this is in the worst month of the year, usually we are looking at a coverage of around 35%(getting as low as 25% in the best months).

We define the failure rate of the robot as the number of days it is not able to function because of a lack of energy. This is a number we want to keep low whilst also keeping the size of the battery and and the solar panels reasonable.

In order to get a rough estimate of the failure rate of the robot with this information, we make the following model:

• We keep track of a variable energyAvailable that tells us for how many days we have energy left in the robot.
• We will assume the robot can only have enough energy stored for dMax days(limited by the size of the batteries), and must have at least enough for 0 days(can’t use any energy at that point since there is none).
• For every day, there is a chance p for the day to be cloudy.
• On every day the robot uses energy for 1 day. So we need to reduce the variable by 1, with a minimum at 0 since we can’t use energy if there is none.
• If a day is not cloudy the robot will generate enough energy for x days, with a maximum of dMax since the batteries can’t charge if they’re full. Note that this number x includes the energy it uses on the day itself.
• Note that the subtraction and addition are executed simultaneously, so for a non-cloudy day we add x-1 energy(subject to the maximum).
• On every day we check if the robot is at 0 energy. If so, the robot did not function on that day.
• The failure rate is then given by the precentage of days the robot did not function.

Note that since x can be any real number, this model is effectively a bounded random walk with continuous step sizes.

We still need to determine what value to use for x. The robot needs on average Eused units of energy per day. To meet this energy need, the robot generates energy for [math]\displaystyle{ E_{used}*(1+safetyMargin) }[/math] units of energy per day on average. However, the robot only generates energy on [math]\displaystyle{ (1-p) }[/math] fraction of days(since the other p are cloudy). If we take Egen to be the amount of energy the robot generates on the non-cloudy days, we get

[math]\displaystyle{ E_{gen}*n_{days}*(1-p)/n_{days}=E_{average}=E_{used}(1+safetyMargin) }[/math]

So [math]\displaystyle{ E_{gen}*(1-p)=E_{average}=E_{used}(1+safetyMargin) }[/math]

Which gives x[math]\displaystyle{ x=E_{gen}=E_{used}(1+safetyMargin)/(1-p) }[/math] Since the model uses the average energy useage of 1 day as the unit of energy, we can take [math]\displaystyle{ E_{used}=1 }[/math], giving x=(1+safetyMargin)/(1-p)

In the interest of avoiding potentially extremely complex behaviour, we use mathematica to simulate the model for us.

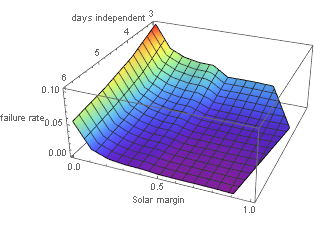
the 0 to 1 axis is margin and the 0 to 100000 is failures per 1000000, the 3 to 5 is the battery duration. This shows the results of the simulation. As can be seen, adding extra batteries and increasing the margin decreases the failure rate(as could be expected). note that in the flat,blue part of the graph there is no benefit to increasing the margin even further. This is because at that point to robot almost always charges fully between cloudy periods, so the failure rate is mostly determined by the probability of getting a lot of cloudy days in a row. This is also the reason why 1 and 2 days have been left out, as they do not reach an acceptable failure rate even for a massive margin(2 goes to about 0.09).

It should also be noted that a small margin already makes a massive difference in reliability. The reason this happens becomes a lot clearer if we consider the model without the upper and lower bounds on energy stored. If we then take the margin to be 0, we expect to generate exactly the amount of energy we need, so the overall mean would remain at its starting point and a dip below 0 is fairly likely to happen. If we were to take a margin that’s larger we generate more energy than we need. This means that the expected value of the energy gain each day is positive, so the total amount of energy would keep going up, which makes a dip below 0 far less likely. Of course, the model does include an upper and lower bound, so we can’t actually grow off into infinity, but even a small expected gain still seriously improves the failure rate.

Note that the lowest failure rates in the graph are at about 0.01. As we will see in the document on energy calculations, taking the battery size at 3 days with an extra solar area of 0.3(so we take 1.3 times the area needed to break even on average) gives reasonable results in terms of mass and solar area required. Using these numbers we get a failure rate of 0.046. Note that following the definition of failure rate, this is only the percentage of days the robots do not function. As we noted earlier, the most cloudy period of the year falls in the rain season, so it is not unlikely the village will have access to other water sources in that period. It should also be noted that this gives a similar rate as the energy sources given in , which designs around a failure rate of 0.05

So using these numbers, the robots will not function on 4.6% of the days. This means that the people will need to walk for their water 365*0.046=16.8 days per year. Whilst this is not a perfect solution, better failure rates start demanding higher costs from the robot(see the formula for battery size in the energy calculations) and this is still far, far better than having to walk 365 days per year. Note that batteries are expensive, so increasing the duration the robot needs to last without supply would come at a steep cost. Another thing to consider is that the model assumes that the panels do not produce anything at all when it’s cloudy, which is not the case in reality, so we expect that the robot will be able to do a bit better than this in practice.

Number, speed, size and energy consumption of the robots

The energy consumption of our robots is closely linked to how many robots we use, how fast they are and how large they are. In order to see what kind of robots would be viable a detailed analysis has been made to determine how exactly the needed solar power depends on these variables. Or course energy consumption is not the only design consideration that affects this, since a gigantic robot would have problems navigating the terrain and a miniscule robot would get crushed of someone happens to step on it. However, energy consumption is a neccesary and leading variable to consider since if the robot needs too many solar panels it will no longer be viable to use.

A basic energy model

The robot’s task is to move [math]\displaystyle{ s_{well} }[/math] meters to the well, and then take [math]\displaystyle{ m_{water} }[/math] kg back over the same distance to the village. In terms of energy the main costs will be from rolling friction and, depending on the speed, air friction. In addition, there will also be an energy cost for operating the boardcomputer and other electronics, but these are fairly small compared to the energy needed to move the robot so we will ignore this to keep the calculations a bit easier. TODO: do a quick sanity check to see if this is actually correct/can be ignored.

Another factor that will be ignored is height. The energy cost of climbing a hill [math]\displaystyle{ g*h*m_{total} }[/math] is recouped as we go down the hill on the other side. This of course only holds if the robot is actually able to reach the top of the hill, but that is outside the scope of these energy production calculations. The other height difference we need to consider is that between the village and a pump since the weight of the robot changes at those points. It's a benefit if the pump is higher and a loss of the village is higher. However, this factors is effectively impossible to consider in these calculations since it needs a detailed knowledge of which exact hills we will encounter at what point in the route. This will differ wildly between locations. It should also be noted that the impact of this on actual running costs is fairly small. If we assume a 10 meter height difference(village being higher), and we need to carry 5000 liters of water per day as is the scenario, we need an extra [math]\displaystyle{ 5000*10*9.8/3600000=0.14 }[/math] kwh of energy per day for the total energy used by all robots. As we will see, this is a fairly insignificant amount of energy compared to the total, so we will ignore it to simplify calculations

We will also be ignoring the energy needed to accelerate the robot/change the speed of the robot. The amount of energy this requires is [math]\displaystyle{ E_k=\frac{1}{2}m*v^2 }[/math]. If we were to assume the robot weighs 10000 kg and needs to move at a speed of 7 m/s(further on in this document we will see that this is already faster than what is actually needed for our requirements), we need [math]\displaystyle{ E_k=\frac{5000*7^2}{2*3600000}=0.03 kwh }[/math]. Compared to the energy costs we will find this does not make a large impact on the total amount of energy, so we will ignore this to simplify the calculations.

The rolling friction force is(assuming the worst case scenario of a level surface) [math]\displaystyle{ F_{roll} = c_{rr} * F_n = c_{rr} * m_{total} * g }[/math] Note that while [math]\displaystyle{ c_{rr} }[/math] and [math]\displaystyle{ g }[/math] are constant, [math]\displaystyle{ m_{total} }[/math] is not since the water tank will be empty on the way towards the well and filled on the way back. So the energy lost to rolling friction in a single trip will be [math]\displaystyle{ E_{roll} = f * s = f_{roll,empty} * s_{well} + f_{roll,full} * s_{well} = c_{rr} * g * s_{well} * (2 * m_{robot} + m_{water}) }[/math]

If we assume that the watertank will maintain the same shape regardless of its content the air friction will be constant throughout the ride(assuming constant speed). We then get [math]\displaystyle{ f_{air} = \frac{1}{2} * CdA* p * v^2 }[/math], where [math]\displaystyle{ p }[/math] is air density and [math]\displaystyle{ CdA }[/math] is the air drag coefficient times the frontal surface area. Multiplying(integrating) with the distance we need to travel in a trip, we get [math]\displaystyle{ E_{air} = \frac{1}{2} * s_{well} * CdA * p * v^2 }[/math] Note that that while it is possible to use different speeds for different parts of of trip, that would not be energy efficient since the speed is squared in this equation.

This then places the total energy used in a trip to and from the well at [math]\displaystyle{ E_{needed} = s_{well} * (c_{rr} * g * (2m_{robot} + m_{water}) + \frac{1}{2} * CdA * p * v^2 }[/math] This is of course only the energy output that's needed to keep the robot moving, and does not yet take into account the efficiency of the motor. This then gives [math]\displaystyle{ E_{used} = \frac{s_{well} * (c_{rr} * g * (2m_{robot} + m_{water}) + \frac{1}{2} * CdA * p * v^2}{e_{motor}} }[/math]

Estimating the variables

In order to actually use this formula we will need to find values for the variables. Some of them are constants(either physical or from the scenario) and will be fairly easy to fill in, but parameters that relate to the mass and speed of the robot

For the gravitational acceleration [math]\displaystyle{ g }[/math] we can take the usual value of [math]\displaystyle{ g=9.8 }[/math]

From the scenario we already know that [math]\displaystyle{ s_{well}=3000 }[/math] meters and [math]\displaystyle{ m_{water}=5000 }[/math] kg(assuming a denstity of 1 kg/l for the water).

The rolling coefficient [math]\displaystyle{ c_{rr} }[/math] is primarily determined by the tires used and by the terrain we're moving over. For the scenario we will be moving across solidground. This can be best modeled as solid sand in our scenario, which gives a rolling coefficient of </math>0.06</math>. Note that this is significantly higher than moving over more agreeable surfaces such as tarmac, where the rolling coeficient is usually a factor 10 or more lower.

The drag coefficient of a pickup truck is about 0.47. For the frontal area we assume we have a a box using a square water tank. Then the frontal area is [math]\displaystyle{ (m_{water}/1000)^{2/3} }[/math]. This then gives [math]\displaystyle{ cda=0.47(m_{water}/1000)^{2/3} }[/math].

Relation between water per trip, speed and number of robots

We need to make at least [math]\displaystyle{ n_{trips,needed} = \frac{m_{required}}{m_{water}} }[/math] trips to the well per day to ensure that enough water is transported to the village.

To see how fast a robot needs to be to make this target, we need to consider that the robot will not be moving 24/7. It will need to spend time filling and unloading, during which it is not moving, and it might also be possible the residents don’t want to have the robot moving during the night. Here we also need to start considering the possibility of using multiple smaller/slower robots instead of a single large/fast robot. We let [math]\displaystyle{ p_{idle} }[/math] be the fraction of time a robot spends doing things that are not moving. Using [math]\displaystyle{ s=v*t }[/math], we then get [math]\displaystyle{ n_{trips,achieved}=\frac{n_{robots}s_{driven}}{2s_{well}}=\frac{n_{robots}v_{average}*24*3600*(1-p_{idle})}{2s_{well}} }[/math] The factor 2 for [math]\displaystyle{ s_{well} }[/math] is there because [math]\displaystyle{ s_{well} }[/math] is only the distance to the well, which is half the distance we need to travel. So the number of achieved trips needs to be at least the number of required trips, we get [math]\displaystyle{ \frac{n_{robots}v_{average}*24*3600*(1-p_{idle})}{2s_{well}}\geq m_{required}/m_{water} }[/math] So we need to ensure that the speed we pick satisfies this inequality if we want to be able to reach the necessary amount of water each day.

For [math]\displaystyle{ {p_{idle}} }[/math] we take 20% as an upper limit for the time the robot is either loading or unloading its water tank. This is fairly high so it should ensure that are on the safe side. However, we also need to consider the robot cannot function during the night for a variety of reasons, such as people wanting some quiet during the night, so we will only be able to operate for 16 hours a day. Adding the loading times to this gives us 12.8 hours of movement, giving a [math]\displaystyle{ p_{idle}=0.45 }[/math].

If we seek to minimize energy needs, we will want to minimize speed as much as we can, so we will be taking the inequality we found earlier and use as an equality. Rewriting it to get the needed [math]\displaystyle{ m_{water} }[/math] for a certain speed and idle time we get [math]\displaystyle{ m_{water}= \frac{m_{required}*s_{well}}{n_{robots}v_{average}*24*3600*(1-p_{idle})} }[/math] Using various possible combinations of possible speeds and idle times, we get table 1. Note that not all speeds and volumes are necessarily achievable.

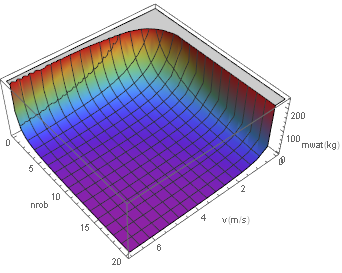
If we graph this with multiple robots, we get the following graph(note that the origin is in a nonstandard position to better show the graph):

Note that behaviour is determined by the divisions by both [math]\displaystyle{ v }[/math] and [math]\displaystyle{ n_{robots} }[/math]. This means that while it may be worthwhile to increase the number of robots or speed to keep away from the asymptotes we're seeing in this graph, but there aren't any real benefits to really large values if we consider the size of the water tank.

Estimating the mass of the robot

The hardest variable to estimate is the mass of the robot. This mass is the sum of each individual mass of various parts of the robot, but the mass of some parts of the robot is determined by the total mass of the robot. This results in a very hard to solve system of equations. The mass of the robot is determined by:

• Frame
• Wheels
• Motor
• Battery
• (unloaded) water tank
• Electronics

Note that the solar panels are ignored because we will find that the mass of the battery is too large to put on the robot in its entirety. This will result in having a charging station seperate from the robots. Moving (part of) the batteries off the robot will also result in the solar panels being moved off the robot as well, so they are then no longer relevant to determine the mass of the robot.

Electronics are going to give a fairly marginal addition to the mass of the robot in comparison to other factors, so we will ignore it. The weight of the water tank will be purely dependent on the volume of water we want to carry. Using the tanks available at tanks direct we get the following weights:

• A 5000l tank weighs about 120 kg, giving [math]\displaystyle{ 0.024 }[/math] kg/l
• A 1250l tank weighs about 35 kg, giving [math]\displaystyle{ 0.028 }[/math] kg/l
• A 227 l tank weighs about 6 kh, giving [math]\displaystyle{ 0.026 }[/math] kg/l
• A 100l tank weighs about 2.5 kg, giving [math]\displaystyle{ 0.025 }[/math] kg/l

So it seems the weight of the water tank is about linear in the weight we need to carry for about 0.025 kg/l.

The rest of the masses will be a lot harder to get a good estimate of since they are all interdependent:

• The mass of the wheels will depend on how much weight they need to carry.
• The mass of the motor will also depend on how much mass they need to move.
• Similarly, the mass of the batteries will depend on how much energy is needed in 1 trip, which will depend on the total mass as well.
• The mass of the frame will mostly depend on how much volume it needs to encase.

This results in a lot of masses that are interdependent on each other. The general approach is to try and derive a series of formulas for each of these masses in terms of the other masses, speed and the already known constants. Then we will try if Wolfram Mathematica is capable of finding a solution for these formulas in terms of speed(which should be possible since this will give 4 equations and 5 unknowns, with one of them being speed).

Battery mass

First the mass of the batteries. This will need to be enough for the robot to last [math]\displaystyle{ {d_{endep}} }[/math] days without a power source, with an extra security buffer in case conditions get a bit worse and to take the ignored factors in energy calculations into account. We will have some energy-density [math]\displaystyle{ \rho_{energy}\ j/m^3 }[/math] for the battery. We know we will need [math]\displaystyle{ E_{used}*b_{sec} }[/math] to move the robot for a single roundtrip to and from the well, where [math]\displaystyle{ e_m }[/math] is the efficiency of the motor(roughly [math]\displaystyle{ 0.80 }[/math] ) and [math]\displaystyle{ b_{sec} }[/math] is the security buffer which we will take as [math]\displaystyle{ 1.15 }[/math]. We need to do [math]\displaystyle{ n_{trips,achieved} }[/math] trips to the well per day, and do it for [math]\displaystyle{ d_{endep} }[/math] days. So then the total energy we need to store in the battery is [math]\displaystyle{ d_{endep}*n_{trips,achieved}*E_{used}*b_{sec} }[/math]
We then get [math]\displaystyle{ m_{battery} =\frac{d_{endep}*n_{trips,achieved}*E_{used}*b_{sec}}{\rho_{energy}} }[/math]
[math]\displaystyle{ =\frac{[s_{well} * (c_{rr} * g * (2m_{robot} + m_{water}) + \frac{1}{2} * CdA * p * (v_{empty}^2 + v_{full}^2))]*e_{motor}*d_{endep}*n_{trips,achieved}*b_{sec}}{\rho_{energy}} }[/math]
[math]\displaystyle{ =\frac{[s_{well} * (c_{rr} * g * (2(m_{motor}+m_{frame}+m_{battery}+m_{wheel}+m_{tank}) + m_{water}) + \frac{1}{2} * CdA * p * (v_{empty}^2 + v_{full}^2))]*e_{motor}*d_{endep}*n_{trips,achieved}*b_{sec}}{\rho_{energy}} }[/math]
Note that, other than the four masses, everything is either a constant of dependant on [math]\displaystyle{ v }[/math]. For energy density we can take li-ion batteries to get [math]\displaystyle{ 612000 }[/math] j/kg

Motor mass

Then the motor: in order to keep a robot of mass [math]\displaystyle{ m_{total} }[/math] moving at speed [math]\displaystyle{ v }[/math], the motor must have a power of [math]\displaystyle{ p(m_{total})=v*(f_{roll}(m_{total})+f_{air}(m_{total}))=v*(c_{rr} * m_{total} * g+\frac{1}{2} * CdA* p * v^2) }[/math]. Note that in this case we are only interested in keeping the robot moving at all times, rather than energy. This worst case scenario will happen with the tank filled, which is why we are using [math]\displaystyle{ m_{total}=m_{robot}+m_{water}=m_{motor}+m_{frame}+m_{battery}+m_{wheel}+m_{tank}+m_{water} }[/math] here. However, we also need to take into account that the robot needs to be able to move up a hill. For a 5% hill we would need [math]\displaystyle{ m_{total}*g*v*perc }[/math] extra power, where [math]\displaystyle{ v }[/math] is the horizontal speed and [math]\displaystyle{ perc=0.05 }[/math] is the percentage of the hill. This then gives [math]\displaystyle{ p_{motor}=v*(c_{rr} * m_{total} * g+\frac{1}{2} * CdA* p * v^2)+m_{total}*g*v*perc }[/math]

Then we will need to get some estimate for the mass of the motor if we need some certain power output. For this we can simply take the power to weight ratio of the motor of an electric car given at $https://en.wikipedia.org/wiki/Power-to-weight_ratio$, which gives a weight to power ratio of [math]\displaystyle{ \frac{1}{80} }[/math] kg/w. This then gives in a mass formula for the motors: [math]\displaystyle{ m_{motor}=\frac{p_{motor}}{80} }[/math]

Wheel mass

Continuing with the wheels. For this we need to consider the needed groundclearance. This will be about 5 inches above the ground as we will argue later. This means that the wheels will need to have a minimum size no matter how large the robot is. We can use giving us 4kg of mass in the wheels. These wheels have a load limit of around 540 kg. We will see in a moment that this will be more than enough for every size of robot we could seriously consider. Note that this means that the mass of the wheels is not dependent on the mass of the robot in our model. This is because by the time these wheels no longer apply the mass of the robot is alread fairly large. Ignoring what kind of wheels we would need for larger robots makes the model less powerful and less predictive for larger robots, but does make the model a lot simpler to handle.

It should also be noted that the mass of the wheels is only a fairly small contribution to the vehicle for heavier vehicles. One example of such is the Toyota Tacoma, where the ratio of wheel mass to total car mass is about 0.02 depending on the exact model used.

Frame mass

This leaves only the frame. We will model it as a simple square box with set thickness. The robot will likely not be box shaped, but this should give us a rough idea of much material we will need for our robot. If we have a given mass of water we need to be able to transport, we would need at least [math]\displaystyle{ (m_{water}/1000)^{\frac{2}{3}}*6m^2 }[/math] just to encase a square water tank. Note that this assumes we can't compress the water in the tank to achieve a better density than [math]\displaystyle{ 1 kg/l }[/math]. Since we need to be able to carry more than just the water tank, we will increase the length of the vehicle by a factor 2 as an absolute worst case estimate, giving us [math]\displaystyle{ (m_{water}/1000)^{\frac{2}{3}}*10m^2 }[/math] of surface area. For the thickness of the hull we will for now use [math]\displaystyle{ 1 cm }[/math]. For comaprison, the Mark V tank from ww1 had a thickness of 16 mm, so our 1 cm should be enough of an upper limit to deal with anything it can encounter. We then have a material volume of $surface*thickness$. If we then multiply by the density we get the mass of the frame. Using the alluminium alloy we are currently considering to use, we have a density of [math]\displaystyle{ 2700kg/m^3 }[/math].

Resulting mass

So now we have 4 equations for the masses we're missing, all dependent on each other. These equations are, using [math]\displaystyle{ m_{total}=m_{frame}+m_{motor}+m{wheels}+m_{battery}+m_{tank}+m_{water} }[/math]:

• [math]\displaystyle{ m_{frame}=density*thickness*(m_{water}/1000)^{2/3}*10 }[/math]
• [math]\displaystyle{ m_{motor}=\frac{v*(c_{rr} * m_{total} * g+\frac{1}{2} * CdA* p * v^2)+m_{total}*g*v*0.05)}{80} }[/math]
• [math]\displaystyle{ m_{wheels}=4 }[/math]
• [math]\displaystyle{ m_{battery}=\frac{[s_{well} * (c_{rr} * g * (2(m_{motor}+m_{frame}+m_{battery}+m_{wheel}+m_{tank}) + m_{water}) + \frac{1}{2} * CdA * p * (v_{empty}^2 + v_{full}^2))]*e_{motor}*d_{endep}*n_{trips,achieved}*b_{sec}}{\rho_{energy}} }[/math]

And additionally also [math]\displaystyle{ m_{tank}=0.025 m_{water} }[/math]

It should be fairly obvious that it is not viable to solve this system by hand. However Wolfram Mathematica is still capable of solving this system for the 4 masses. We then get multiple solutions for this system. All except one of these solutions require complex numbers, so we can safely dismiss those as a result of the complexity of the system rather than being real world solutions. There is only one real valued solution to the system:

[math]\displaystyle{ \frac{(-80.2574 - 341.103 v - 20.3404 n_{rob} v + n_{rob}^{1/3} v^{ 1/3} (-653.393 - 2.84217*10^{-14} v - 0.173981 v^3))}{(n_{rob} v (-5.08511 + 1. v))} }[/math]

This formula gives the following graph:

This was graphed with [math]\displaystyle{ d_{indep}=3 }[/math]. Using other values for [math]\displaystyle{ d_{indep} }[/math] does not give a qualitatively different graph. Most striking is that the mass of the robot gets really high as we get to speeds even as low as 4 m/s. This is because a larger robot takes more energy. But to remain operational for 3 consecutive days we will need to have larger battery, which in turn leads to more energy consumption because the robot is now even larger.

If we were to remove the factor [math]\displaystyle{ d_{indep}*n_{trips} }[/math] from the battery mass(so remove the battery from the robot except for what we need for a single trip), we get the following graph and formula instead:
[math]\displaystyle{ \frac{(-1085.56 - 631.313 v + n_{rob}(-237.477 - 8.88178*10^{-16} v) v + n_{rob}^{1/3} v^{ 1/3} (-12233.5 - 0.0812779 v^2 - 0.188417 v^3))}{(n_{rob} v (-58.8986 + 1. v))} }[/math]

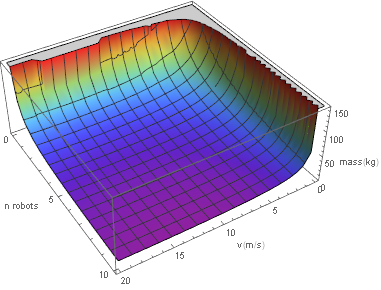
In this graph we more reasonable behaviour since the size of the battery is no longer exploding. The increase near [math]\displaystyle{ v=0 }[/math] and [math]\displaystyle{ n_{robots}=0 }[/math] is caused by the division we see in the formula. The formula does still eventually deal with battery size getting large, but this happens at much larger speedsthan we get if we were to put the battery on the robot itself. Note that this also means that our ignoring of the mass of the solar panels is justified since those will no longer be on the robot either. This does mean that we will need to set up a seperate charging station in order the charge the robots since they will not last 3 days on the batteries for just a single trip.

Results from the calculations

At this point all our variables in are known, except for [math]\displaystyle{ v }[/math] and [math]\displaystyle{ n_{robots} }[/math]. These are parameters where optimization through formulas is no longer doable. It should also be noted that for these parameters(and the variables that depend on them), other concerns than just optimizing energy are relevant.

Note that the energy derivation only considers a single trip to the well. if we want to know the total amount of energy we additionally need to multiply by [math]\displaystyle{ n_{robots} }[/math] and be [math]\displaystyle{ n_{trips} }[/math](since [math]\displaystyle{ n_{trips} }[/math] is the number of trips a single robot needs to make).

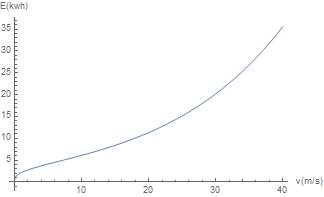
For analysis purposes we first limit ourselves to a single robot(so [math]\displaystyle{ n_{robots}=1 }[/math]). This gives the following graph:

The graph can be divided into 3 sections: the start, the roughly linear middle, and the the quadratic tail. At extremely low speeds the energy needs of the robot will drop tremendously. A large part of the energy need that remains comes from the rolling friction caused by moving the weight of the water.

Note that the mass of robot can be approximated by [math]\displaystyle{ c*\frac{1}{v} }[/math] for small [math]\displaystyle{ v }[/math](with [math]\displaystyle{ c }[/math] a constant). This is a result of the constant we see in the numerator of our formula. The number of trips per day we achieve with this speed is linear in [math]\displaystyle{ v }[/math], since twice the speed results in twice the distance traveled. So we would then get [math]\displaystyle{ c*\frac{1}{v}*v }[/math] mass kilometers, meaning that the energy needed for the rolling friction can be approximated with a constant for very small [math]\displaystyle{ v }[/math]. Note that this is only an explanation of why the model gives this behaviour, and it does not mean that the model this behaviour is correct. The most likely explanation for why these factors come together like this is that one or more of the assumptions we have based our mass estimate on fails for small [math]\displaystyle{ v }[/math]. Note that the air resistance is negligible at these speeds so can be ignored in our analysis here.

In the middle section our energy need goes up roughly linearly. This is because air resistance does not yet play a significant role in this part of the graph. The increase in energy will come purely from needing to do more trips whilst mass doesn't go down by a similar factor, leading to more mass kilometers and a higher energy cost.

In the tail of the graph air resistance starts playing a more dominant role, leading a quadratic graph.

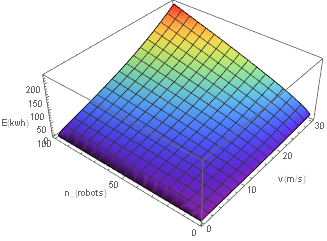
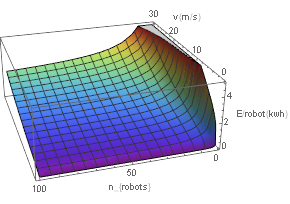
If we start considering the total energy needed by multiple robots we get the following graph:

It should be immediately obvious that more robots will result in higher energy costs. The reason for this can be found in our mass estimate. If we want to cancel out the factor [math]\displaystyle{ n }[/math] that accounts for the fact that we have $n$ robots, we would need our mass to decrease by at least a factor [math]\displaystyle{ n }[/math], but this does not happen. Instead the mass will tend towards a constant function in [math]\displaystyle{ v }[/math] as [math]\displaystyle{ n }[/math] gets larger because of the linear factors in the numerator. The quadratic and higher order factors in v would only make this get worse if we let [math]\displaystyle{ v }[/math] get even larger. Note that the same three stages of the graph can be seen as in the single robot example.

This graph shows the energy needed by just 1 robot if we have multiple robot(so the total energy divided by the number of robots. This graph shows that the energy we need for larger speeds goes up, while the energy needs for smaller robots go down. The reason the graph starts flattening for larger numbers of robots has to be found in the mass estimate: the linear factor in the numerator becomes constant after the division. This constant factor comes from the fact that our wheels give us a constant weight because of our minimum ground clearance. This also results in the other masses getting a constant factor because they are partially dependent on the mass of the wheels.

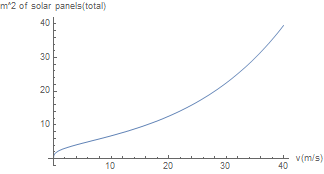
From earlier calculations we already know that 1 [math]\displaystyle{ m^2 }[/math] of solar panels corresponds to roughly 0.9 kwh per day. This graph shows us how much area of solar panels a single robot would need.

This graph shows the same basic behaviour as the energy graph as we would expect. This mostly shows that we can’t go very fast with our robots before the required solar area to power them starts exploding.

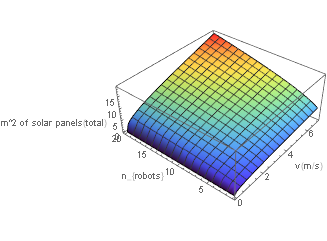
If we start considering multiple robots we get a graph similar to that of the energy graph for multiple robots as well

This shows that we need to avoid having too many robots or too fast robots since the energy needs go up quite a bit if we do so. The graph may seem to be slightly different form the energy graph, but that’s only because we zoomed in to exclude parts of the graph that weren’t going to give us a reasonable area because of needing too much energy. Note that in reality we can only deploy a whole number of robots, so not every point in the graph is necessarily possible in reality. Note that whilst our energy needs drop dramatically near v=0, using this would result in massive robots as can be seen in the water and robot mass graphs we’ve shown earlier.

So there is a strong dependencies between the robots size, speed and number of robots. This has been expressed as a formula that determines the robots required size of speed and the number of robots are known. Using this formula and a series of other dependencies/constants we have derived how much energy the robots need to be able to function. From this we could derive how much area of solar panels we need to keep them functioning on a daily energy needs basis. However, some minor factors had been ignored in these calculations, and some of the constants were estimates that may not necessarily be 100% correct for the actual robot made. It would therefore be wise to add a margin of error to the solar area to compensate for this and ensure that we have enough solar panels even if the calculations are a bit off.

In terms of deciding what kind/how many robots to make, three graphs are relevant: The mass of the robot, the mass of the water carried and the solar area. The first two are a good indicator of how large the robot will be. We will want the robot to remain small since that makes it easier to maneuver the robot around in rough terrain. It also ensures that that the system of robots can scale to villages of different size or different distances to the well(note that the latter does need some consideration in terms of battery size if the distance is even larger). Having less robots also ensures that water supply doesn’t stop completely in case one of the robots breaks down.

The third graph we need to consider if the solar area we need to power the robot. If we use more energy we will need more batteries and solar panels, which increase the costs of the robot. This is something we obviously want to keep down as well.

Taking these factors into account, we decided to go for using 5 robots going at a speed of [math]\displaystyle{ 3 m/s }[/math]. The calculations then give a watertank of [math]\displaystyle{ 42l }[/math], a solar area of [math]\displaystyle{ 1.35m^2 }[/math] per robot(and [math]\displaystyle{ 6.8m^2 }[/math] in total).

Note that using more robots does not give an advantage since the size of the water tank is already small enough to allow scaling up and down fairly easily. With the distance of 3000 m to the well, each robot carries about 1000l per day, which gives a decent amount of flexibility. We do not want to make this flexibility in smaller steps since the solar area per robot is independent of the number of robots, so using more robots will rapidly increase the energy we need. Less robots would, however, result in losing too much of this flexibility. For, say, 3 robots we are already looking at 1666 l per day and also more disastrous effects in case a robot fails.

For speed the arguments are similar: higher speed would cost us more energy, less speed would make the robot get larger than we would want without giving us a significant decrease in the energy we need.

The mass estimate of a robot gives is [math]\displaystyle{ 41kg }[/math], of which [math]\displaystyle{ 0.51kg }[/math] batteries in the robot for these numbers. We need to do 24 trips in a day per robot, have 5 robots and need to last for 3 days without charging. The needed energy for a single trip is 0.05 kwh. This means that the charging station needs to have 0.05*24*5*3=18 kwh of capacity. We get a needed motor power of a bit less than 350w(including the extra power needed to go up inclines). This seems fairly small, but we should consider that the robot moves at low speeds and is fairly lightweight.

Solar Panels

Note that since the panels are no longer on the robot we don’t need to worry as much about minimizing area so long as it stays within somewhat reasonable bounds(i.e. not needing 10000 m^2 of something similar). We also don’t need to be concerned with the weight as much since we don’t need to carry them to and from the well.

From the energy calculations we found we need about 6.8m^2 of solar panels with 180 wp/m^2 or a different setup with an equivalent wp. However, this did not yet take the margin from the reliability calculations into account. This gives some some 6.8*1.3=8.8m^2 of panels. With this wp/m^2 we will need 1590wp. Note that we should also take into account the battery round trip efficiency of the powerwall, so we will need 860/0.9=990 wp

One option we have is to use the ALLPOWERS 100w bendable solar panel[3]. This gives us 100wp for 0.55m^2. It Costs $170,-. Since this only gives us 100wp, we will need to use 6 of these for a total cost of $1530,- price of $1.7/wp

A similar option is given at [4], giving us 100wp for 0.6m^2 at $179,-. Note however that this panel is slightly more expensive for the same amount of wp. $1.79/wp.

Another option is to use the panel given at [5]. This gives a 275 wp panel of 1.6m^2 for €132,-=$153,-. This will then give a price of $0.55/wp, leaving a total price of +-$875,-. The area needed would be 1590/275*1.6=9.2m^2. Unfortunately, we can’t use a partial solar panel, so we would then end up with 6 panels for $900,- and 9.6m^2. The then gives us 1650 wp in total.

However, this does not yet take degradation of the panels into account. The warranty guarantees that these panels will degrade at by at most 2.5% in the frist year, and then by 0.7% per year adter that. With 6 panels we would hit 1590wp after just 2 years, so we will a seventh panel to compensate, brining our starting wattpeak to 1925wp, and giving us 1925*0.975*0.993^23=1596 wp after 23 years. So these panels would then need to replaced after 23 years. Note that by that time technology will likely have improved quite a bit, so the panels will less expensive by that time.

Battery

For the batteries of the charging station we need a capacity of 19 kwh as we saw in the energy calculations. A problem is however that batteries are fairly expensive. This will mean that the batteries form a large part of the costs of our water transport system.

From [7] we can see that the best batteries for home use(which have capacities that are somewhat similar to what we are going to need) reach somewhere around $500 to $600/kwh of storage. Using these numbers we will then get a price of $9500 to $11400 for the batteries of the charging station. Note that batteries for cars are currently experiencing a rapid price drop[6]. They are already significantly cheaper than the home batteries(costs for this type of battery are at around $200,- per kwh), and are expected to come down to $100,- per kwh in 2025. Unfortunately, the batteries used in cars are not available for purchase separately from the car they’re in. However, this does indicate that the price of batteries that we can use are also going to come down rapidly.

For an actual installation we can use right now we have the following options:

Tesla power wall with capacity of 13.5 kwh for $7553(6500 euro)[9]. This gives a $481,-/kwh price tag. However, this size of 13.5 kwh doesn’t scale well into our 19 kwh needs, we are going to need two power walls for $15000,- to ensure we reach our needed capacity. Note that this give a capacity of 27 kwh, so this immediately gives us a lot more than we need after installation. This battery has a round trip efficiency of 90% The powerwall is guaranteed to remain above 70% of its capacity for at least 10 years as is stated in their warranty TODO find a proper link to the warranty, can only find direct download from google if it’s charged purely through solar power as we will do. This would mean that option to use two powerwalls will be at 18.9 kwh after 10 years.

With the LG Chem RESU 10.0H battery we get a capacity of 9.3 kwh for $6225(5357 euros)[9] giving $669,-/kwh. We would need three of these to reach at least 19 kwh(which would result in a capacity of 27.9 kwh), giving a total price of $18675,- Note that using two would put us barely short of the 19 kwh target(18.6 kwh). Doing that would cost $12450,- This battery has round trip efficiency of 95%, which is better than that of the powerwall. If we consider degradation the battery is warranted to have 80% of its original capacity after 10 years. The option of using two of these would then result in needing to replace the battery very often, which is not a serious option. The option of using three batteries would put us at 22.8 kwh after 10 years. Unfortunately, no guarantees are given after these 10 years. Using three of these puts our price quite a bit above the option of using powerwalls, so this option can be discarded.

Within the same family we also have the LG Chem RESU 3.3, giving 3.3 kwh $2905(2500). This then gives a pretty bad $880,-/kwd hour price. This can however be used in addition to the previously mentioned LG Chen RESU 10.0H to deal with it being slightly below the target. One of these batteries added to the two 10.0H batteries gives 21.9 kwh for $15355,- Note that this results in a similar price for less capacity compared to the tesla power wall, so this option can be discarded.

taken two of these and putting them in serie will give 24 v, max 10A and 10ah each gives 240 w and 240wh, which is significantly more than we need(should be enough for 3 rides and some). This results in a battery mass of 1.5 kg, which is significantly more than our estimate of 0.4 kg, but isn’t enough of a difference to make the robot stop functioning, especially since this has a greater capacity then we need. Charging speed of these packs takes about 4 hours, so we will need to be able to switch the batteries automatically? 3 rides will not take more than 3 hours(including stops in between waiting for villagers picking up the water). This means we need 4 of there per robot, 20 in total for a total price of $3000,-

Locomotion

With the given scenario, there are 5 possible methods of locomotion in the desert. Although not all of them are suitable for this scenario, they give good comparison of which of the aspects will work best in the desert.

The tires are the most common types of locomotion for a vehicle in any road conditions. Different types of tires are available for different terrain conditions, whether it is on hardgrounds like asphalt or soft grounds like sand or dirt. Since it is the most common type of locomotion on vehicles, it is very easy to find replacements, even with specialized tires. In comparison to other methods of locomotion, tires are cheaper and simpler to maintain since it only requires tire replacements a tire punctures. However, conventional tires may not work well with soft grounds, which requires more expensive specialized tires.

The second option to solve the locomotion is the tank tracks, which is used mostly for heavy all terrain vehicles. Tank tracks are easily maneuvered in any road conditions, whether it is hard or soft grounds. However, the cost to operate tank tracks in the vehicle is very expensive in terms of energy and money. Tank tracks require higher power input since tank tracks are usually heavy. Tank tracks replacement when damaged or broken down is not simple, so the maintenance costs are high in money and time.

The newly discovered method of locomotion in the desert is a screw propelled locomotion. The way this works is that two or four screws are attached to the vehicle to maneuver through soft grounds. When four screws are attached for locomotion, the maneuverability of the vehicle significantly increases compared to that of the vehicle with two screws. Just like some vehicles with tank tracks, this vehicle is also amphibious. However, further research is needed to implement this locomotion since some of the vehicles that used this type of locomotion are from the 20th century. This locomotion may not work well if it is going through normal road infrastructure. Maintenance can also be expensive as screws need to be design in accordance to the given ground conditions.

A combination of ski and small tracks were also discussed for the locomotion of the robot. This is already adapted in snowmobiles, which maneuvers through snows very effectively. If parts in snowmobiles for locomotion are redeveloped in such a way that it adapts to soft grounds with higher temperature, this locomotion seems to be the most plausible method. However, this requires further research on soft grounds other than snow as this method requires reconfiguration of snowmobiles. Furthermore, it takes both positives and negatives of the tank tracks to a smaller degree.

The last method of common locomotion on the ground is railways. Railways are one of the fastest ways of moving in the ground with its fixed yet direct railways that cause little accidents. If enough infrastructures are developed, it is possible for longer and more efficient travels to be performed by the robots. However, its biggest issue is that it requires expensive and time consuming infrastructure installation even on short distance travels. Railways on soft grounds may not perform well as the railways need to be installed on hard grounds. Furthermore, the routing of this locomotion is very limited once it is installed on the ground. The maintenance cost may be cheaper as it is more durable than some of the locomotion methods mentioned above, but once it requires maintenance, it will take lots of time and money.

Wheel

To determine the diameter of the wheel size of our robot, we will refer to the already existing Smart fortwo, since the design of our robot will be close to its design. Although this car operates in 3 wheels in a shape for more solar energy generation, this gives us a good estimate of how big our wheels should be in order to deliver about 50 liters of water per day per robot which equates to 50 kg of water.

The wheel size of a vehicle depends on the load capacity of the vehicle, motor torque, and speed of the vehicle. As the wheel gets bigger, the load capacity and motor torque will increase, but the speed will decrease as a result of more energy usage for increased motor torque. Since speed of the vehicle is not the priority and the load capacity is mostly determined by the amount of water for one robot, wheels could be smaller compared to normal cars.

The current model of Smart fortwo coupe has wheel size of 15 inches (38.1 centimeters) in diameters and 5.5 inches (13.97 centimeters) in thickness, with load capacity of 260 kg and 1150 kg maximum weight allowed. Considering how much less the robot will weight and carry in comparison to this vehicle, it is safe to assume that the wheel size in diameters can be less than 15 inches1

Based on this information, with 50 liters of water as load capacity and about 3 m/s for the average speed of the robot, it is safe to assume that the size of the wheels can be within the range from 8 to 10 inches in diameter and 3 to 4 inches in thickness.

Ground Clearance

The ground clearance of the robot will be determined by the environment that the vehicle will operate in as well as the wheel diameter. For example, a race car on a track that requires high speed will have lower ground clearance because the car needs to be as low as it can to reach the least amount of air resistance against the car. However, the speed of our vehicle is not the emphasis and therefore low ground clearance is not required. Since the ground condition on which the robot will be driving in on will be mostly plateau with some areas of desert, the ground clearance is expected to at least avoid small obstacles. Off Road vehicles tend to have high ground clearance since they face obstacles more often than normal vehicles.

In this case, a small sized vehicle will be defined as cars with petroleum engines of 1.0 liters capacity with 4 to 5 people at maximum capacity. Small sized vehicles, such as Ford Figo, Honda City, Suzuki Swift, and Hyundai i10, has 168mm, 165mm, 170mm, and 165mm ground clearance, respectively. Their respective wheel sizes are 17 inches, 15 inches, 18 inches, and 16 inches in diameters. In consideration to some of obstacles that the robot may face, the ground clearance of the robot should be around 5 to 6 inches off the ground.

Braking

The most common types of braking in vehicles are using disc brakes and motor reversal. Disc brakes are useful when a vehicle needs to be stopped at a great speed. However, our vehicle will operate at most 3 m/s, which is not a high speed compared to that of normal vehicles. Therefore, it is efficient to use just motor reversal as a method of decreasing speed and stopping the vehicle.

Colour

Colouring might be an important aspect in increasing the success rate of the robot by avoiding animals by either using aposematism or camouflage. Aposematism is the means to prevent an attack of animals by giving them a warning signal. These warning signs often indicate being toxic, venomous or having means to protect itself such as sharp teeth. They signal having these traits by having a colour which is easy to detect such as bright colours. Most often the brighter the colour, the more dangerous the animal is. Camouflage is the means to avoid an attack of an animal by making it hard to notice itself. In a similar manner, our robot could have colours which are easy to detect to try and imitate being a noxious prey and thus avoiding aggressive animals such as lions. However even if our robot inmates a noxious prey, there is no guarantee that all animals will leave it alone. There even exists various animals which ignore aposematism in Niger such as the honey badger which has a strong resistance against toxins and eats various venomous and toxic animals. Another option is for our robot to get a colour to blend in the environment so that it wouldn’t get spotted easily. This colour might allow the robot to completely avoid all interactions with animals, but in case the robot gets spotted, it will most likely be seen as prey by carnivores. Another downside of having the robot’s colour blend in with the environment is that if needed, it will be hard to find the robot, while bright colours will make it easier to find the robot. (for example when it is stuck somewhere and you have to find it) . Overall both colours have positive effects and negative effects, but overall colours which are easy to detect will be more useful in our scenario. In both cases there is still a risk whether our robot will get attack or not, but the main advantage aposematism has over camouflage is that it will be easier to find the robot in case something goes wrong. For the actually colour that our robots will have, it will most likely be white and black(similar to the honey badger which residence in that area) . This is because in Niger there are close to no places that blend in with this colours thus trying to use aposematism to prevent attacks. Naturally, other bright colours such as green are also possible.

pick-up and drop-off mechanic

In our scenario we have a water well. Our robot needs to be able to draw out water from this well. The easiest way to acquire this is by pumping the water out of the well into the robot. For pumping out the water we have two possibilities of how to obtain this. The first would be to station the water pump on top of the robot together with a tube to suck out the water and have the robot carry this around. The second option would be to place an automatic water pump on top of the water well. The problems with the first option are that the robot would constantly need to carry the pump which adds up to the weight and this the amount of energy consumed and that every single robot would need his own pump to function. In case there are multiple robots assigned to the same water well, it would mean that every robot would need his own pump which might make the cost unnecessary higher. Because of these reason it might be beneficial to have a pump separate from the robot which is stationed at the water well. The down side of this method would be that it would increase the time that a robot would be functional after deployment. The time from deployment till functionality would thus only depend on the time it takes to install the automatic pump onto the water well.

Pick-up

By placing the water pump at the well we can modify the design of the pump in such a way that it is able to pump water into the robot. If we look at the current design of wells, whether the water is stored into a container or comes straight out of the well. They all have an something in common in the design. The water outlet attached to it always drops the water straight downwards. There is one major design choice to be made. The first option is to modify the robot that it is able to get water from the water outlet. By doing this their will be less trouble during the implementation of the robots itself. It can get water from any water outlet, but this is an very difficult task as there are more design for an water outlet. Creating a mechanism for the robot to be able to get water from any water outlet will be highly complicated. The second option is to modify the water outlet according to the robot. By doing this their will be more trouble during the implementation, as we would need to make adjustments to the water outlet. This of course comes with a tradeoff that there is no need to invest a lot of time and money into solving the problem unlike the first option.

In our scenario we chose to work out the second option since there is no clear estimate of how fast this would be solved. The time and research cost could be more wisely spend on other components of the robot. For example the highly complicated issue NASA had in which they spend millions of dollars into finding the solution on how to write with a pen in space. The solution they came up with was very pricy and not that reliable, while the russians just used a pencil.

Drop-off mechanic

For the drop-off mechanic, a simple faucet at the bottom of the water container of the robot should be sufficient. Since people have been living in the village described in our scenario, they should have some means to hold water, since they need to have something that they used to transport water in. Because of this, a faucet to let the water flow out of the water container into their means to hold the water should be sufficient. Ideally the robot would be emptied immediately and start gathering water again, but in case all the water storage is full or everyone is unable to use the faucet (for example sleeping), the robot will wait till the water container is empty before it goes to gather more water. To avoid this, it might be beneficial for the villagers to construct a water tank, during their newly gained free time, in which the robot will drop-off the water. Although it might not be viable for villagers to construct a safe water tank without sufficient knowledge of how to create one and how to maintain the tank to avoid pollution of the water.

Cooling

most of our components for the robot need no cooling, as they produce almost no heat.

• Controllers
  • GPS modules
  • Wireless communication module
  • Memory storage
• Sensors
  • Gyroscope
  • Ultrasonic sensors
• Power Switch

The only thing that produces a lot of heat is, the motor itself. When electrical vehicles are considered, a thermal-management system is very important. Cooling the electric motor boosts its performance, which allows for smaller motors to be used. Smaller motor weigh less, so the total weight of the vehicle will be less as well and results in better overall energy efficiency of the vehicle.

```From the energy calculation we need an 175 W motor. When looking through motors that would fit our needs, there was nothing that would exactly fit our need, as most rpm where to high or too low. The best option that i came across where electrical scooter motors. These motors are small enough to fit in our robot and very affordable. Only downside it that their Rpm is unnecessary high for our robot. 24 Volt 200 Watt MY1016 Electric Motor, it cost 34~ euro with a efficiency of at least 74%.```

With this we can calculate how much energy it loses through heat. 200W*0.26(26% wasted)= 52W. 52W is lost through the process of converting electrical energy to mechanical energy. Most of this is converted into heating the surroundings. We give a rough estimate that at least 50W is converted to heat. 50w is approximately 170.6 btu/hr. This means that in 1 hour, 1 pound of water will be raised by 170.6 fahrenheit(95 °C) in an hour or 2.84 fahrenheit(1,58°C) in a minute. The water tank on its own can already act as a passive cooling block.

Transport system

The robot will use a GPS for tracking it's position while it moves towards its destination. The location of the destination is input as GPS coordinates. There are two possible ways for a robot to create a path. The first one is that a path is already present, this path will most likely be created by the villagers and the robot will try to follow it. The second is that there is no path present, in this case the robot will turn until the front faces towards the destination which afterwards the robot will try to move directly towards. To make sure the robot does not deviate from its path, every x traveled meters the GPS is used to check whether the location from the robot is still on its path. The robot will keep moving on its path until it either reaches the destination or something is hindering the robot from continuing.There are multiple things that can hinder the robot from continuing it’s path, each creating a different response from the robot to solve it. Here’s a list of things that the robot might encounter and how it should react.

Rocks, debris or plants on the path.

When encountering these things, the first thing the robot will have to do is to decide the gravity of its situation based on the height and width, the robot will chose if it will more around it or go over it. In case the rocks, debris and plants are small enough such that they won’t hinder the robot from going easily over it,the robot will decide to go over it. If that is not the case, the robot will have to move around it and thus changing it’s path. Using it’s sensors it will move around it and after the obstacle is no longer present, it will use it’s GPS to form a new straight path towards the destination.

Cliffs

A cliff can be a problem which the robot will have to avoid. The main problem with a cliff however is the detection of it using a sensor. At the bottom of the cliff, the cliff will be detected as a large wall and will thus be treated the same as a rock which the robot will not be able to travel over it. Detecting an cliff at the top will be more difficult since the ground will simply stop. For this reason the robot will have a ultrasonic sensor dedicated to detecting the ground in front of the robot to avoid such situations. When the robot has detected a cliff which hinders him from continuing on it’s path, it will again move around it and once it has accomplished this, create a new path and continue on it.

Damage by external factors, such as wild animals

It is possible that the robot will be attacked by animals while on-route. This can be known by using the gyroscope values, attacks will cause some form of shaking to the robot which are visible as spiking values in the gyroscope measurements. To fend off animals, the robot will be equipped with a speaker that will play a loud sound when threatened. It will also be possible to play the sound of a lion or tiger to scare off most animals, but this sound might attracted lioness or tigress which can worsen the situation.It will also save the GPS location of where the attack happened for avoidance in the future.

Once the robot reaches the destination coordinates according to its GPS, depending on the size of the water source it might not see where to retrieve water from. Small sources as wells might be missed as the GPS usually has a radius of approximately 5 meters, in cases like these we would require a more precise location for the robot to reach the well. Possible solutions are including a camera in the robot to detect the well on its own or a signal transmitter could be placed on the well. Using a camera will require more processing power to run a detection algorithm, while using a signal transmitter will need the overhead of having one installed at the destination well. To get back to the village, the robot will basically have the source coordinates input, assuming that it started moving from the village, and it will move towards it as described above how it moves to a destination.

Microcontroller

In some sense our robot is a form on a self-driving car, since it has to autonomously drive to the inputted GPS coordinates and gather water while avoiding obstacle collision. While self-driving cars are meant for actual traffic roads with a lot of dynamic external factors, in our scenario the robot only has to avoid collision by driving over low obstacles or moving around them which will greatly simplify the processing work required.

The current hardware market for self-driving cars is dominated by NVIDIA's computing platform which have end-to-end AI learning systems that are partnered with major car manufacturers. However, these components require larger power supplies of 500 Watts and the processing units will provide much more computing than necessary. The pricing will also not be budget friendly as these are the latest and greatest computing engines available on the market as of now. Therefore we will look at open-source for self-driving as the best option.

Since our robot is a “dumbed down” variant of self-driving cars, the actual code needed will be simpler and less. The computing engine won’t have to run complex calculations and is limited to only controlling the motors, reading the sensor values, detect and decide what action it should take. It should be possible to build the hardware with desktop components which are more than capable of providing a sufficient computing system. The general components such as processor, motherboard, internal memory, storage and power supply will be needed, but they are widely accessible. However the connections that are to be made are not plug and play since there are no built-in connectors for adding external motors, cameras etc. These would need a custom circuit attachment and specialized drivers to work.

Another option is to make use of embedded-computing platforms as Raspberry and Arduino, which have a large variety of low-cost, low-power reliable hardware. The available connections are easily accessible with custom jumper wires and that makes the construction difficulty and cost lower compared to using desktop components. Taking examples of both platforms, the Arduino UNO and Raspberry Pi 3 are both smaller cheaper hardware that are capable of running obstacle avoidance algorithms, which will be most computational intensive requirement in for our robot. Both are readily available for under $35 and if desired the faster larger boards can be used instead.

There are important differences between the two though, the Raspberry Pi is essentially a fully functional computer with memory, graphics driver and operating system while an Arduino as a micro-controller mainly runs one task. The Arduino’s main purpose is simply to respond to various sensor readings where a full operating system for these tasks would require unnecessary overhead.

Conclusively, we see that the use of one of the most prominent embedded-computing platforms will satisfy our needs and will also have the lowest cost and better easy of use. Therefore we will consider the Arduino Uno rev3 for our robot.

Communication module

The Raspberry Pi 3 has both built-in Ethernet port and Wireless N connectivity, while the Arduino doesn’t have any built-in network connectivity and requires an external communication module. This however allows modularity and freedom of communication type selection as the wiring and setup is straightforward.

If we consider the use of a Bluetooth Low Energy (BLE) module to avoid having a robot collide with another en route since we employ the use of multiple robots that will likely follow the same path. Once the robots are within each other’s range and are detected in the Bluetooth module, then they are within close proximity. Compared to the Classic Bluetooth, BLE is intended to provide significantly reduced power consumption and cost while maintaining a similar communication range of about 10 meters.

When we want to connect to our controller board, we can simply connect through the built-in USB port of the Arduino, therefore with the use of this system we would not require a seperate PC connector. The power switch can be custom made depending on the placement of the batteries and the cost would be neglectible as you would only need some wires and a button or switch.

GPS

We require a cost effective, yet high-performance GPS module that is compatible with the Arduino and has a low power usage. Here we consider the NEO-6M module that is designed for use with passive and active antennas. We will use a passive antenna since it won’t require additional energy use and it boosts the GPS signal. The horizontal accuracy of 2,5 m is achievable due to the open air scenario which all of our robots will be located in along with an antenna.

Gyroscope

For the gyroscope we have an accurate 16-bits analog to digital conversion sensor that also includes an accelerometer in one. It is inexpensive and easily reads raw measured data, the processing can be done with an existing library.

Sensors

Collision avoidance is one of the most basic tasks in mobile robotics that ensure safety of the robot as well as the objects and users around it. In order to avoid obstacle collision, we need external sensors that can scan the environment around the robot to gather spatial information. Here we take two kinds of obstacle detection, front-facing in the direction the robot is moving and sideways to avoid scraping the sides against an object. There are a lot of sensors available for obstacle detection such as ultrasonic, infrared, camera and laser based sensor systems (LiDAR). However, each sensor has its own pros and cons in terms of accuracy, constraints, power usage and price.

Ultrasonic sensors send out high frequency pulse and then times how long it takes for the echo of the pulse to reflect back. They are commonly used in drones for detecting ground and the response time is limited as the speed of the pulse is equal to the speed of sound. Ultrasonic sensors are not affected by ambient light and offer highly accurate and stable readings.

IR sensors detect an object’s distance with infrared radiation, once the beam detects an object the light beam will return due to reflection.

They have a low cost and are widely used for measuring distances. The response time is faster than ultrasonic sensors and in addition the power consumption is lower as well. Using an active IR sensor, it is both an emitter and detector that works with reflective surfaces. There are two categories for IR sensors, retro-reflective and diffuse reflection sensors. Retro-reflective are made for harsh environment conditions and have a larger detection range compared to diffuse reflection sensors, which fits our scenario. However, the performance of IR in general is limited by its poor tolerance to light reflections such as ambient light or bright colours. It is also influenced by the radiation for sunlight, taking these limitations in consideration we see that the desert plains contain all these negative environmental factors. Therefore the use of IR for front-facing object detection is not optimal. However for closer proximity detection in the sides of the robot, it would be a good choice as the light reflections are easier to detect.

Stereo camera vision works similarly to human vision as in sensing the environment in 3D by using the combination of 2D images at slightly different viewpoints to calculate depth information. However, it won’t perform well under certain environment conditions such as poor lighting, glass surfaces and areas with a lot of light reflaction in general. As their use is limited to in-doors areas, we cannot make use of them in our scenario.

LiDAR sensors calculate distances and objects by measuring the time it takes for a short laser to travel from the sensor to an object and back by the speed of light. This is the most advanced way for obstacle detection that provides the most spatial information, however it is also the most expensive one in terms of costs and power consumption since they are made for more complex purposes in traffic whereas we only require simple avoidance of walls, debris etc. Hence, we will not make use of this sensor.

	Ultrasonic	IR	Camera	LiDAR
Model	HC-SR04	GP2Y0A02YK0F	OV7670	TFMini*
Price	$1	$15	$20	$40
Power supply	+5V DC	+5V DC	+3V DC	+5V DC
Current	15 mA	33 mA	120 mA	800 mA
Range	2-400 cm	20-150 cm	~150 cm	30-1200 cm

• This product uses LED instead of laser light, which causes the significantly lower price compared to regular LiDARs

Water tank content detection

We would need sensor to know whether the water tank is full or empty, there are different options for this. Load sensors, also known as strain gauge, sense the force by deformation on the component. The SEN-10245 sensor is capable of measuring up to 50kg and costs $10.

Another option is to use ultrasonic level transmitters to measure the distance between the transducer and surface using the time required for a sound pulse to travel. The speed of sound will be affected by the temperature of the air inside the tank however, but this will be compensated for if the sensor is located inside the tank. Therefore it is limited to the atmospheric pressure measurements in the air.

Similarly, there are also infrared and laser level transmitters to measure the water levels. The cost of these sensors however are around $1000, which is rather expensive to employ for each robot. Therefore we will make use of load sensors instead, as they fit our needs and are within a very budget friendly price range.

Conclusively, we will opt for the load sensor that meets our filled water tank weight and has a low cost as well.

Durability

As the water transportation robot is expected to function in sub-Saharan Africa, it is certainly required for the robot to have a certain degree of sand erosion resistance. For this purpose materials and coatings can be deliberately selected to improve sand erosion resistance.

Options for the materials of the base frame :

• Aluminium: Has been known as a light and strong material. A lower weight of the robot results in less power consumption for the movement which makes it quite a desirable option. Aluminium should be a good choice for the base frame or at least to supplement it. Aluminium alloys have more advantages, but have a higher production cost attached to it.
• High strength steel: Is the base choice of material for automobile bodies due to its strength, ductility and low cost. Knowledge of the material, processing properties and efficient design of steel are all well-explored. However, the material itself is heavy resulting in more fuel consumption. Also, the strength of this material is likely not to be well-utilised in the robot, since crashes are unlikely to happen and the crashes that will happen will be at low speed.
• Magnesium: Very lightweight material, which sees some usage in automobile industries already due to its malleability cutting down costs of production. One of the downsides is that there is not much magnesium production which limits supply. Also it doesn’t enjoy the creep resistance that aluminium does have.

As the robot is expected to function for a long time without maintenance it becomes quite clear that it needs the remain functional even if some components fail. To achieve this, the number of vital components needs to be reduced, also these components need to be well-protected and fail proof. For this purpose, designing components to be less reliant on another seems to be a valid strategy. A few examples of this concept would be:

• Separating power sources for different components, more important parts would have their battery placed in more protected areas.
• Multiple of the same component, if a critical component were to fail, then a backup component would be able to continue, ensuring that the robot keeps doing its job. Also, if multiple of the same component are in use at the same time, it should be designed in such a way that if one of them fails, the other components would be able able to make up the difference.

Also, creating fail safes for many different situations is also needed to improve the durability of the robot.

General properties of aluminium and its alloys are:

• Low density compared to steel: 2.7 g/cm^3 compared to 7.83g/cm3
• Low density coupled with high strength in some of its alloys makes it a great material to create strong, but lightweight vehicles and by extension robots as well.
• Aluminium resists progressive oxidization, which causes steel to rust. When aluminium is exposed to oxygen it forms a thin, colorless and transparent inert aluminium oxide film that blocks further oxidation. So, the discoloration and flaking that is common with iron or steel does not occur with aluminium.
• Resists all sorts of corrosion when properly alloyed and treated.
• Great electrical thermal and electrical conductivity, but can be alloyed to have great electrical resistivity.
• Aluminium is non-ferromagnetic, non pyrophoric and non-toxic. Non-toxic is important, since the robot has to transport water.
• Can easily be fabricated into any form. There is no limit to the different shapes in which aluminium can be shaped.

Price of aluminium as of 07-06-2018 is $2317/tonne. So 2317/1000 = $2.317/kg

Aluminium alloys

• Alloy 3003
  • A widely used general purpose alloy with its major alloying element being manganese. Is used in moderate-strength applications requiring good workability. Price as of 07-06-2018 is $ 1.90/lb of Aluminium 3003-H14-Sheet. 1.90/0.45359237 = $4.189/kg. 4.189/2.317 = 1.8079. Which is an 80.79% increase in price compared to pure aluminium.
• 5xxx series:
  • Aluminium alloy thats contains the major alloy element magnesium.The major benefit of these alloys is its corrosion resistance, which is better than all other types of alloys. The drawbacks of this aluminium alloy is its safe operating temperature, if the alloy contains over 3.5% magnesium, which shouldn’t rise above about 65 degrees Centigrade to avoid stress-corrosion cracking. Alloy 5456 is often used a storage tank or pressure vessel for this purpose. This alloy also has high weld efficiency and joint strength.
• 6xxx series:
  • Aluminium alloys that contains major alloy elements silicon and magnesium and are heat-treatable. Are not as strong as 2xxx or 7xxx alloys, but have good formability, weldability, machinability and corrosion resistance with medium strength.
• Alloy 6061
  • The general purpose 6xxx series alloy, which is used in a broad range of structural applications and welded assemblies. Such as truck components, railroad cars, automotive parts, machine parts, aircrafts etc. Has 42 ksi tensile strength and 36 ksi yield strength. Price of aluminium alloy 6061 t6 sheets: $2200-$2300/tonne, so $2.20-$2.30/kg. Has a density of 2.70 g/cm^3. According to Laguna-Camacho et al. aluminium 6061 is the more erosion resistant than AISI 304, AISI 316, Brass, AISI 420, AISI 1018, Copper and AISI 4140. According to Algahtani et al. erosion performance of aluminium alloys can be highly increased using different surface treatments. PEO, HA and PSC coatings were tested on erosion protection, with PEO coating giving the best erosion protection.
• Alloy 6151
  • Has 44 ksi tensile strength and 37 ksi yield strength, is used in the automotive industry due to being able to make intricate forgings for automobiles with this alloy.
• Alloy 6205
  • Has as benefit a high impact resistance. If the speed of the robot reaches a certain point, this alloy could be used to counteract crashes in case they happen.
• Alloy 7150
  • Aluminium alloy that contains zinc as major alloying element.

Has 84 ksi tensile strength and 78 ksi yield strength. It is used in aircrafts and other structures, requiring high strength. This strength comes with the disadvantage of reduced resistance to stress corrosion cracking.

Magnesium Alloy:

The density of magnesium is around 1.8g/cm^3, making the lightest material of the available materials for the frame. Magnesium alloy with silicon has high creep resistance but may decrease corrosion resistance if iron is found. Magnesium itself has a poor corrosion resistance and is weak to stress concentration. Magnesium is resistant to progressive oxidation with oxide layer formed while the metal is heated. However, when the temperature reaches about 450 degrees celsius, the layer is destroyed and magnesium begins to melt. Magnesium has lower electrical conductivity, but has higher damping performance than aluminium. Magnesium is non toxic and diamagnetic. The main advantage of magnesium is the high weight per strength ration due to its low density compared to other available frame materials. Magnesium also has high fatigue limit and is very easy to recycle.

Alloys:

• AZ91D
  • AZ91D is the most commonly used magnesium alloy that has 33.4 ksi tensile strength and 23.2 ksi yield strength. AZ91D is widely used in many of current automotive parts such as transmission case, steering box and subframe. Its main advantages are room temperature strength, high die-castability, and corrosion resistance.
• AM60, AM50, AM20
  • AM60 is used for wheels in Porsche, while AM50 and AM20 are used for seat frames in Mercedes Benz. Their advantages are high ductility and good impact strength. These alloys have tensile strength of 35 ksi, 33 ksi, and 30 ksi and yield strength of 18 ksi, 18 ksi, and 13 ksi, respectively.
• AZ31
  • AZ31 was experimented by Morteza Kiani and 3 others from KeAi as one of the components to replace steel parts in original body frame of a car to optimize the weight of a car to minimum. The experiment resulted in 54.5 kg of weight reduction with similar crashworthiness to that of the original frame. AZ31 has tensile strength of 37.7 ksi and yield strength of 29 ksi.

Conclusion on materials to use:

Based on the information of all the listed materials in this section, Aluminium alloy 6061 is the prime candidate to use as base material for the robot, due to its erosion and corrosion resistance, strength, low density, availability and multi-functionality. By using a PEO coating the erosion resistance will be improved even more, making it the best option in a desert environment. Magnesium alloys can be used to supplement the robot due to its lighter weight than aluminium, resulting in a lower total weight of the robot, which causes energy consumption for movement to lower. However magnesium alloys are a lot more expensive, which results in a higher production cost per robot.

Waterproofing

The patent US5536904A describes a way of waterproofing wires and a way that delivery of water to a branch wire from a main wire connected to a non-watertight terminal can be prevented. This is assuming that the terminal is non-watertight though, because the terminal can be waterproof as described by the patent US5532433A and the patent US20010003687A1 gives a way to waterproof the terminal connection portion of sheathed wire. In conclusion the wiring can be made waterproof according to these patents.

Design

Placement

The idea behind placing the components to the robot is to avoid damages from both internal and external causes. Internal causes are incidents related to overheating components that would cause breaking of the components at the extreme case and the significant decrease in robot performance in terms of how much water can it transport within an hour. External causes can include harsh weather conditions, attacks from wild animals, and unexpected terrain conditions.

In most cases of road vehicles, the engines are placed in front of the vehicle for easy access for maintenance. Batteries for powering up electronic components within the vehicle are also placed near the engine for easy maintenance. The controller unit, such as engine control unit, is placed a bit closer to passenger seats rather than being close to the engine and battery.

In case of our robot, we have several components that will affect the movement and communication with other robots. The motor will be placed on front and top of the frame of the robot, along with the battery for powering components. The components will have waterproof casing around them so the water will not leak into the components. Since motor will have a cooling solution to prevent overheating, placing battery next to the motor should not create a heating problem. The water tank will be placed above the core components on top of the waterproof casing. The controller unit will be placed on the center of waterproof casing under water tank, along with gyroscope, wireless communication module, memory storage, and gps module. Ultrasonic sensors will be placed in front of the robot, one facing the ground to detect any dangerous ground conditions and one facing front for which ground can it go over.

When designing a robot that satisfy our requirements and accomplish the necessary task, it is important that we have correct design decisions and thorough research. Each component of the robot was chosen based on the efficiency of components with respect to specified requirements of the robot.

Firstly, we chose to use Aluminum alloy 6061 as the material of the frame and hull of the robot. Aluminum alloy 6061 is widely used in automobile and aerospace industries that they use it to build chassis and frame of cars as well as wings and fuselage of aircrafts. The main advantages of using this alloy were corrosion resistance, high weldability, good strength, and cost efficiency. Some other alloys, such as magnesium alloys, also have been discussed, but were discarded due to high material costs as well as weak corrosion resistance. The design of the frame was based on the existing water tank trailers, which provided stability of the water tank during movement.

The water tank is the next main component to discuss as it is the key to achieve our goal, which is to deliver 50 liters of water per trip. The dimensions of the frame will be determined by the dimensions of the water tank itself, which is 500 mm in length, 400 mm in width, and 250 mm in height. This way, the water tank will sit on the center top of the frame for well distributed center of mass. The filling and emptying of water tank also needs to be implemented so that the robot can actually load and deliver water to the villagers. In the hull, there will be a casing where the water pipes will be protected for filling in water with valves for securing the water tank. At the bottom back hull of the robot, water tap will be installed with water pipe going towards the tap so that villagers have no difficulties using the robot for water.

Next, the decisions on ground clearance and wheel sizes were based on the researches of commercial vehicles. Because the robot has lighter weight and is smaller than normal gasoline based vehicles, we took account into currently existing wheel sizes and ground clearances and made our decisions based on terrain conditions and load weight. Small gasoline based vehicles had their wheel sizes ranging from 380 mm to 460 mm, while ground clearance was between 150mm to 200mm. In these vehicle researches, we noticed that the ground clearance was approximately about the radius of the wheel size. Given the ground condition of our scenario and the weight of the load, we came to conclusion that 254 mm in diameter with 102 mm in thickness was the right size to handle the weight while going over possible ground obstacles. As a result of chosen wheel size, the ground clearance of 127 mm was deemed sufficient for the robot.

For the locomotion of the robot, we decided to use two motors that will be located on each side of the robot. The motors will be placed on lower part of the robot for lower center of mass and closer access to the wheels for better power delivery. The way this method works is that two motors will give same amount of power output to the wheels via chassis in which gears deliver power to the wheels instead of motors giving direct power to the wheels. When the robot needs to maneuver to avoid obstacles, each motor will give different power output and direction depending on the direction of which it needs to head. Other options were to use tank tracks and screw propelled locomotion, but both of the methods cost more power and time on maintenance. The motors will be held in cylinders that wrap around the motor, which will act as heat sinks in case of overheating. The copper heatpipes will be placed inside the angled support bars of the cylinders, which will transfer heat from the water tank to the motors.

Now that the decisions on the body has defined, we discussed the choice and placement of the smaller components that will be the brain of the robot. For the computation, we decided to use Arduino Uno as the main unit of computation, along with several sensors, such as GPS sensors for accurate location of the robot, gyroscope for detecting whether the vehicle has rolled over, bluetooth for communication among the robots, ultrasonic sensors for obstacle avoidance, and infrared for side collision avoidance. The battery of the robot will be placed at the back of the robot with casing around itself inside the hull so that the battery is not damaged in case of internal failures. In case charging station does not provide enough powers, solar panels will be placed for charging up additional power during operation.

Placing sensors on the robot is crucial to whether the robot will successfully deliver water while meeting the requirements. The ultrasonic sensors were placed in front of the robot for better obstacle detection with longer range than other sensors for the option. The angle of which the sensor should face was based on the angle calculation by taking arccos of ground clearance and the range of sensors, which were 127 mm and 4000 mm, respectively. As a result, 88 degrees towards the ground was found to be optimal angle at which the ultrasonic sensor should face to avoid obstacles. On the sides, two IR sensors were placed on bottom center of the hull for any wall detection so that the robot would not scrape itself to the wall. The sensors has to be placed above the wheels as it may detect wheels as obstacles on the sides. Arduino Uno, GPS, and gyroscope were placed on the front of the water tank inside the hull for easy accessibility for maintenance and to all components. For better signal reception, two GPS antennas were placed on front top of the side hulls.

In addition to motors and sensors for better maneuverability and obstacle avoidance, several devices were implemented. First, the idea of Aposematism was implemented into the color of the robot in case of animal attacks. Given the scenario in which our robot will operate in, it is possible that the robots may face wild animals. With the idea of Aposematism, the color of the robot can easily scare away wild animals, thus avoiding external damages to the robot. The color of the robot will be with black on top half and white on the bottom half, which is ideal for both scaring away the animals as well as easy discovery of the robot for human eyes. The speakers at the back of the hull will also aid with Aposematism for protection against wild animals by emitting sounds that will cause wild animals to be away from the robot. Finally, the cased emergency button will be placed for cases when the robots need immediate shutdown by the users. The case will protect the button from accidental activation as well as external damages from environment.

Weight and Cost of frame and hull

Frame Volume Volume (in m3):

• Radius 0.03m alloy hollow cylinder: 0.03*0.03*3.14*1.12-(0.02*0.02*3.14*1.12)=0.0017584(x3)
• Radius 0.03m alloy hollow cylinder: 0.03*0.03*3.14*0.76-0.02*0.02*3.14*0.76=0.00214776-0.00095456=0.0011932(x4)
• Radius 0.03m alloy hollow cylinder: 0.03*0.03*3.14*0.36- (0.02*0.02*3.14*0.36)=0.00101736 -0.00045216 = 0.0005652 (x4)
• Radius 0.02m alloy hollow cylinder: 0.02*0.02*3.14*0.16-0.01*0.01*3.14*0.16=0.00020096-0.00005024=0.00015072(x8)
• Radius 0.02m alloy hollow cylinder: 0.02*0.02*3.14*0.09-0.01*0.01*3.14*0.09=0.00011304 - 0.00002826 =0.00008478 (x8)
• Radius 0.02m alloy hollow cylinder: 0.02*0.02*3.14*0.58-0.01*0.01*3.14*0.58=0.00072848-0.00018212=0.00054636(x2)
• Plate for components: 0.50*1.02*0.015=0.00765

Total: 0.0052752+0.0047728+0.0022608+0.00120576+0.00067824+0.00109272+0.00765=0.02293552 m3

Frame Cost and Weight

• Density: 2.7g/cm3=2700kg/m3
• Weight: 2700kg/m3*0.02548552 m3=61.925904 kg
• Rate: $2.25/kg
• Cost: $2.25/kg * 61.925904kg=$139.33

Hull Volume Volume (in m3):

• Side hull: (0.40*1.19-((2*(0.06*(0.15+0.25)/2))+((0.15*0.10)/2))*0.01=(0.476-(0.024+0.0075))*0.01=0.004445(x2)
• Front hull: 0.01*0.18*0.76+0.01*0.30*0.76=0.001368+0.00228=0.003648
• Back hull: 0.01*0.40*0.76+4*(((0.31*0.12)/2)*0.01)+2*(0.34*0.12*0.01)+ 3*(0.12*0.12*0.01)= 0.00304+0.000744+0.000816+0.000432=0.005032
• Top hull: 0.76*1.04*0.01=0.007904

Total: 0.00889+0.003648+0.005032+0.007904=0.020232 m3

Hull Cost and weight

• Weight: 2700kg/m3*0.020232m3=54.6264kg
• Cost: $2.25/kg * 54.6264kg=$122.91

Total Cost and Weight

Cost: $139.33+$122.91 = $262.24 Weight: 61.925904kg+54.6264kg=116.552304kg