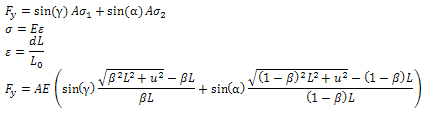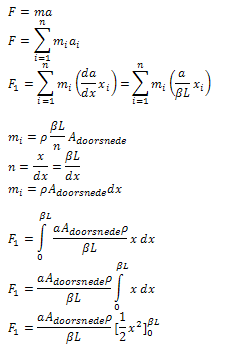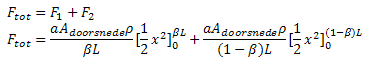Viotar/ Ways To Exite The String

Viotar project group William Schattevoet David Duwaer Eric Backx Arjan de Visser Subpages: Main page Patent Research Working of the violin Software Design (Quantifying the signal we want to see) Hardware Design Interview met Eindhovens vioolbouwer Hendrik Zick Ways to exite the string Model Overview: There are several possibilities to exite the string of the viotar. The only criteria is that is has to set in motion an Helmholz vibration, and that the Viotar has to remain playable with a normale guitar playing technique. From a list of possibilities four have been chosen that has to be further researched. We will look at the feasability of construction and if it is possible to meet the design requirements. The four subjects that will be researched are: Electro-magnet Piëzo-element Bowing wheel Bowing belt The findings of the research will be made into small reports, which will be used to choose a the method of exitation we are going to research in depth. Exitation by Elektromagnet Principle Another way to exite the string is by using an electromagnet force on the steel strings. This force is created by the flow of current through a coil wrapped around a magnetizable core, creating an electro magnet. The force can be controlled by changing the current that flows through the coil. Because current can be controlled by speeds in the order of several Gigahertz, the flow can be controlled very rapidly. 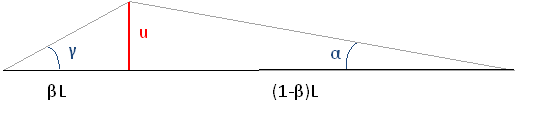Estimation for the maximum bow force on the string In figure x shows the string on the moment it's being exited by the violin bow. The displacement of the string is called 'u', creating two angles α and γ. The string will be exited on position βL. Figure x: De snaar geëxciteerd over afstand u De kracht in y-richting kan berekend worden volgens: De grootste kracht die op een snaar komt is de kracht op een korte, dikke snaar. Er wordt aangenomen dat de lengte van deze snaar 20 cm is en de diameter 0.25 mm. De kracht die op deze snaar komt te staan bij een uitwijking van 0.5 cm is ongeveer 40 N. Schatting voor de maximaal uitgeoefende dynamische kracht op de snaar Aangezien de snaar niet statisch uitgerekt wordt maar continu in beweging is, is de statische kracht die hierboven staat uitgewerkt niet de enige kracht waar rekening mee moet worden gehouden. De snaar moet namelijk volgens een vooraf gedefinieerd patroon gaan trillen, waardoor grote snelheidsveranderingen een rol gaan spelen. Volgens de tweede wet van Newton kan de kracht die nodig is om een massa een versnelling te geven te berekenen volgens F=m*a. Aangezien de versnelling van de snaar lineair varieert over de snaar, moet voor elk segment van de snaar afzonderlijk worden berekend wat de versnelling en dus de benodigde kracht is. Hiervoor wordt de snaar opgedeeld in twee stukken, namelijk het stuk βL en het stuk (1-β)L. Dit levert voor het stuk βL: Voor het stuk (1-β)L geldt: Waarin: a = de versnelling van de snaar op positie βL Adoorsnede = Het doorsnedeoppervlak van de snaar ρ = De dichtheid van de snaar De totale kracht die geleverd moet worden door de elektromagneet om de snaar te versnellen, wordt dus gegeven door: Dit levert een kracht op ter grootte van 6,25 N voor de volgende parameters: a = 500 m/s2 Adoorsnede = 5 ∙ 10-6 m2 ρ = 8 ∙ 103 kg/m3 De maximale totale kracht, dus de kracht de geleverd moet worden om bij een grote uitwijking de snaar een grote versnelling te geven, is de som van Fy en Ftot. Dit betekent dat de totale benodigde magnetische kracht ongeveer 50 N bedraagt. Haalbaarheid Volgens de berekeningen is een elektromagneet die een kracht levert van 50 N voldoende om de snaar in een gewenste trilling te krijgen. Elektromagneten die deze kracht leveren, zijn te koop. Een probleem zou echter kunnen zijn dat de magneet te breed is in verhouding tot de afstand tussen de snaren, omdat er dan niet genoeg ruimte is om voor iedere snaar een magneet te plaatsen. Dit zou echter opgelost kunnen worden door de elektromagneten zelf te maken. De kracht van de elektromagneet is namelijk alleen afhankelijk van het aantal windingen en de stroom die door de windingen gaat. Aangezien er voldoende ruimte onder de snaren is, zou een elektromagneet gemaakt kunnen worden die dun en langwerpig is. Tevens zou de magneet van de ene snaar de andere snaar kunnen verstoren aangezien het magneetveld te dicht bij de naastliggende snaren kan liggen. Hier is echter ook wel een oplossing voor te vinden. Bijvoorbeeld door een scherm tussen de magneten te plaatsen, wat magnetische veldlijnen tegenhoudt. Een ander idee is dat iedere magneet compenseert voor de storing van de naastliggende magneten. Nadelen Ondanks dat het volgens de berekeningen en specificaties van bestaande magneten mogelijk zou moeten zijn om de snaar met een elektromagneet in de gewenste trillingsvorm te brengen, zijn er twee belangrijke nadelen aan dit concept. Het eerste nadeel is dat de snaar in dit ontwerp niet meer aangestreken wordt. Gevoelsmatig behoort het ontworpen instrument dus al niet meer tot de strijkinstrumenten, ondanks dat het wel hetzelfde geluid zal voortbrengen als een strijkinstrument. Waarschijnlijk het grootste minpunt aan dit concept is dat de synthese van het geluid erg onlogisch is. Om de snaar in de gewenste trillingsvorm te brengen, moet namelijk eerst deze trillingsvorm bekend zijn. Het verkrijgen van deze trilling zal geen problemen geven. Dit kan of uit een model komen, of opgenomen worden van een strijkinstrument. Maar als deze trilling eenmaal bekend is, is het erg onlogisch om dit via een elektromagneet, door de snaar, door een trillingsopnemer, en dan nog door een versterker te laten gaan, om het uiteindelijk af te spelen. Dit omdat het geluid eigenlijk al afgespeeld kan worden zodra de trillingsvorm bekend is. Conclusie De conclusie over dit concept is dat het hoogstwaarschijnlijk zal werken en dat de trillingsvorm vrij gekozen kan worden. Dit weegt echter niet op tegen het nadeel dat er niet meer gestreken wordt en met name tegen het nadeel dat er een erg onlogische route gevolgd moet worden terwijl dit totaal onnodig is. Actuatie door piëzo Principe Een piëzo actuator maakt gebruik van het verschijnsel dat kristallen van bepaalde stoffen uitzetten als er een spanning op komt te staan of omgekeerd, ze geven een spanning af als er druk op het kristal wordt uitgeoefend. De naam piëzo is dan ook afgeleid van het Griekse woord piezein, wat drukken betekent. Het concept voor actuatie door piëzo, is dat er aan de snaar een piëzo-element wordt gekoppeld, wat uitzet als er een spanning op wordt gezet. Het idee is dat door de spanning te variëren, de beweging van de snaar gecontroleerd kan worden, waardoor de gewenste trilling in de snaar kan worden gebracht. Haalbaarheid Als er naar de haalbaarheid van dit concept wordt gekeken, blijkt de combinatie van benodigde kracht en benodigde uitwijking een moeilijkheid te vormen. Piëzo’s zetten namelijk maar erg weinig uit, variërend van enkele micrometers tot soms tientallen micrometers. Er zijn wel piëzo-elementen op de markt die dienen als lineaire motor en een maximale uitwijking hebben tot soms wel 100 mm, maar deze leveren weer niet de benodigde kracht. Een andere mogelijkheid is zogenaamde piëzo stacks gebruiken. Dit is als het ware een serieschakeling van piëzo’s waardoor de maximale uitwijking toeneemt. Deze uitwijking is echter ook nauwelijks meer dan 1 mm. Nadelen Het belangrijkste nadeel van actuatie met piëzo’s is dat de uitwijking die ze geven niet groot genoeg is. Dit is deels op te vangen door een stack te gebruiken, maar zelfs dan is de uitwijking nog niet groot genoeg om de snaar in de gewenste trillingsvorm te brengen. Daarnaast is er in dit ontwerp geen sprake meer van een strijkinstrument. Conclusie Uit het voorgaande kan geconcludeerd worden dat het niet mogelijk is om de snaar in de gewenste trilling te brengen door middel van piëzo actuatoren. Tevens zou er dan geen sprake meer zijn van een strijkinstrument, wat ook een zwaar wegende factor is.   The bowing wheel 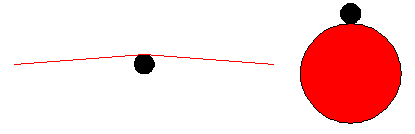Figure 1.1: Simple drawing of the bowing wheel with the string. Figure 1.2: In both drawings the black dot is the cross section of the string and the bowing medium is red. Left: with a bow the bow hairs tilt slightly towards the string around the bowing point. Right: the surface of the bowing wheel tilt away from the string around the bowing point. Figure 1.3: The bowing wheel rotating clockwise blocks the string from moving back when the string is deflected. One straightforward way to excite the string electronically is by using a “bowing wheel”, which contacts the string as shown in Figure 1.1. As we know from practice, exciting the string using stick-slip with a bow works. It is where the notion of a good-sounding bowing sound comes from in the first place, so this should be the reference of how the bow-string interaction should be. A good way to see how well a bowing wheel can produce a sound like this is to look into how far a bowing wheel can act like a bow, and determine what exactly marks the essential difference with a bow. Finally it should be determined if this difference will pose a problem. A set of properties of the bowing medium that influence the bow-string interaction has been assembled: The stiffness of the medium in z-direction The stiffness of the medium in y-direction The impulse response of the medium in z-direction The impulse response of the medium in y-direction All the surface properties of the medium (including the presence of rosin) The shape of the medium directly surrounding the point of contact with the string The bow’s stiffness in z-direction can be simulated using a bowing wheel by suspending the wheel in some way in z-direction. The bow’s stiffness in y-direction, coming from the longitudal stiffness of the bow’s hairs, corresponds with the rotational stiffness of the wheel in ϕ direction. The wheel can be suspended in this direction as well, so the bow’s stiffness in y-direction can be accounted for. The impulse responses in both y- and z-directions can be simulated in the control of the rotation of the wheel and the z-translation of the wheel, respectively. The surface properties can then theoretically match those of a mat of bow hairs when a mat of bow hairs is somehow applied to the outside of the wheel. This leaves only the property of the shape of the wheel to be compensated for. The wheel, as it is round, doesn’t have the same shape around the string as a bow. This is important because when the string transverses in y-direction (which will be the direction in which it will ideally vibrate), it keeps contact with a bow because a bow is almost straight, with the bow hairs actually tilting a bit towards the string around the bowing point, as in the left side of Figure 1.2. With a bowing wheel this is different, because it tilts away from the string around the bowing point, as shown in the right side of Figure 1.2. This does not necessarily mean that the string loses contact with the wheel. This is because the wheel is pushed against the string with a certain force, so the string will have a static positive deflection in z-direction and is pulled down by its terminations. Because of this, as the string transverses, the string will keep contact with the bowing wheel. However, the bowing wheel is not capable of moving in y-direction, so when the string is deflected in y-direction the situation will look like Figure 1.3. In this situation the string is actually pressing harder against the wheel because of its own urge to go back to a neutral position. This causes the friction force of the wheel to increase, probably resulting in a blockage of the system. This effect could hypothetically be prevented by the controller for the z-translation of the wheel. If the current friction force and normal force between the wheel and the string could be determined at every moment, the controller could “make sure” that these two stay at “natural” values (i.e. the same as when using a bow). This requires a constant reference for these both forces over the course of one vibration period, and a construction together with an actuator capable of following this reference with a total delay time including the sampling of the force measurements t_d that is much smaller than one vibration period, t_d≪T. This in addition with the sensors that are needed to measure the forces, makes bowing wheel a very unrealistic concept.