Input

Back to main page: PRE2015_3_Groep4

To the code: Code

To the output: Output

Brightness

The brightness is measured by a sensor inside the bedroom. In the simulation this will be represented by an integer light strength. The value is determined by superposing the sunlight that falls through the blinds and the light generated by our wake-up light. It is assumed there are no other light sources in the bedroom. It is also assumed that the window is always vertical and perpendicular to the suns rays.

The intensity of the sunlight is calculated based on the date and time. It is assumed the sky is clear, and there are no obstacles above the horizon.

The light coming from the wake-up light is regulated by the controller, giving an output strength, as a fraction of the full output strength( 250 lx ). These two values are then added to give the input brightness.

Temperature

The room is to be modeled as a 3x4x2.5m box filled with air, surrounded by outside air on one side and the house all other sides. This proved to be more difficult than thought, therefor we will start with a simpler, linear model for temperature change:

[math]\displaystyle{ dT = k*(T - T_\infty) }[/math]

With k a heat transition constant (estimated at k = -0.03), T the room temperature and T_∞ the temperature the room assumes when not regulated, 12°C. When the heating is on an additional term is introduced:

[math]\displaystyle{ dT_{heating} = h*(T_r - T) }[/math]

With h a convection constant (estimated at h = 0.02) and T_r the radiator temperature at 50°C

Sleep model

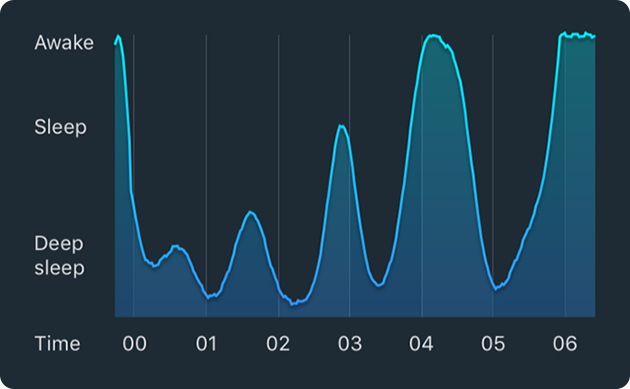
The Sleep Cycle App provides graphs to the user that show his measured sleep behavior during that night. Here's an example:

To model this pattern, we assumed that if the graph is split up in pieces with the peaks and valleys as cutting points, each piece will be sinusoidal with a random period and amplitude. Furthermore, we made the assumption that the period is normally distributed with mean 90 minutes or 5400 seconds (mean duration of one sleep cycle) and standard deviation 30 minutes or 1800 seconds. At first, we assumed that the amplitude is uniformly distributed, but people sleep deeper just after going to sleep and lighter just before waking up, so we had to come up with our own probability distribution. We decided to use the following probability density function:

[math]\displaystyle{ f(x) = rc \left( x - \frac{1}{2} \right) + 1 \qquad 0 \le x \le 1 \quad \and \quad -2 \le rc \le 2 }[/math]

[math]\displaystyle{ P(0 \le X \le x) = \int\limits_{0}^{x} f(x)dx = \frac{1}{2} rc \left( x^2 + \left( \frac{2}{rc} - 1 \right) x \right) }[/math]

So X is a fraction and the probability of X = x depends on the coefficient rc. How closer rc is to 2, how closer E[X] is to 1 and how closer rc is to -2, how closer E[X] is to 0. To get a random value for x, the second function needs to be rewritten, which gives:

[math]\displaystyle{ x = \frac{1}{2} - \frac{1}{rc} \pm \sqrt{ \frac{2}{rc} P(0 \le X \le x) + \frac{1}{rc^2} - \frac{1}{rc} + \frac{1}{4} } }[/math]

0 ≤ x ≤ 1, so for positive rc the ± becomes a + and for negative rc a -. If rc = 0, then this is a uniform distribution. If a value for P(0 ≤ X ≤ x) is taken from a uniform distribution with range [0,1], then a random value for x can be calculated. To model de transition from generally deep sleep to light sleep, the value of rc must decrease from 2 to -2 over time. For this we used the following function:

[math]\displaystyle{ rc = \frac{4}{1 + e^{\frac{t - 2,5T_{gem}}{20000}}} - 2 }[/math]

t is the time elapsed since going to bed and is represented by the number of ticks and Tgem is the mean duration of one sleep cycle and is in this case 90 minutes. A person needs an average of five complete sleep cycles for a good night's rest, so the point of inflection is 2.5*Tgem.

Script

globals [y
         Tgem
         start
         T
         p
         rc
         x
         R
         time
         stage
         test]

to Setup
  clear-all
  set y 100
  set Tgem (90 * 60)
  reset-ticks
end

to Go
  foreach [1 2] [
    set start y
    set T -1
    while [T < 0] [set T (random-normal Tgem 1800)]
    set p (random-float 1.0)
    set rc (4 / (1 + exp((ticks - (2.5 * Tgem)) / 20000)) - 2)
    ifelse rc > 0
      [set x (0.5 - (1 / rc) + sqrt((2.0 / rc) * p + (rc ^ -2) - (rc ^ -1) + 0.25))]
      [set x (0.5 - (1 / rc) - sqrt((2.0 / rc) * p + (rc ^ -2) - (rc ^ -1) + 0.25))]
    ifelse ? = 1
      [set R (x * start / 2)]
      [set R ((x - 1) * (100 - start) / 2)]
    set time (n-values (T / 2) [?])
    foreach time [
      set y (R * (cos (360 * ? / T)) + start - R)
      set stage ((y - (y mod 25)) / 25 - 3)
      set test (1 / (1 + exp(ticks)))
      tick
    ]
  ]
end

Result

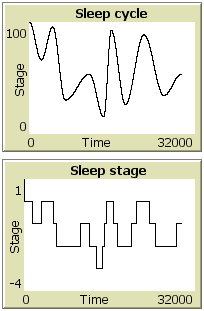
Running the script gives these two graphs:

The first graph shows how deep you sleep on a percentage scale and the second graph translates that to the sleep stage you're in. Stage 0 means being awake and corresponds with 100%-75% on the first graph. Afterwards come stages -1, -2 and -3 which correspond with 75%-50%, 50%-25% and 25%-0% respectively. They are actually stages 1, 2 and 3, the three stages of the sleep cycle. Stage 1 can also correspond with REM sleep, because they both behave the same based on the sound you make during those stages.