Input: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 12: | Line 12: | ||
[[File:sleepcycle_irregular_sleep.png]] | [[File:sleepcycle_irregular_sleep.png]] | ||
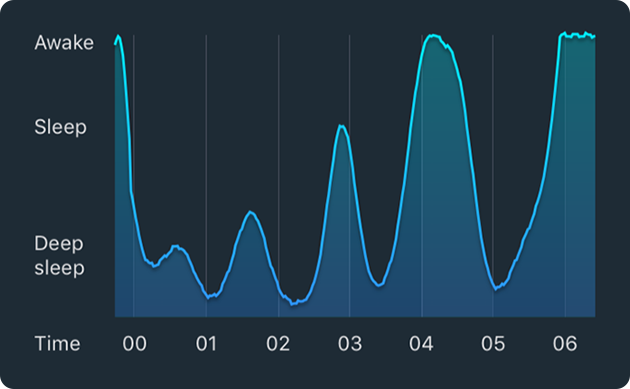
To model this pattern, we assumed that the peaks and valleys of the graph are sinusoidal with random periods, amplitudes and equilibriums. | To model this pattern, we assumed that the peaks and valleys of the graph are sinusoidal with random periods, amplitudes and equilibriums. Furthermore, we made the assumption that the period is normally distributed with mean 90 minutes or 5400 seconds (mean duration of one sleep cycle) and standard deviation 30 minutes or 1800 seconds. | ||
globals [y | globals [y | ||
Revision as of 17:26, 28 February 2016
Back to main page: PRE2015_3_Groep4
To the code: Code
To the output: Output
Brightness
Temperature
Sleep model
The Sleep Cycle App provides graphs to the user that show his measured sleep behavior during that night. Here's an example:
To model this pattern, we assumed that the peaks and valleys of the graph are sinusoidal with random periods, amplitudes and equilibriums. Furthermore, we made the assumption that the period is normally distributed with mean 90 minutes or 5400 seconds (mean duration of one sleep cycle) and standard deviation 30 minutes or 1800 seconds.
globals [y
Tgem
start
T
p
rc
x
R
time
stage
test]
to Setup
clear-all
set y 100
set Tgem (90 * 60)
reset-ticks
end
to Go
foreach [1 2] [
set start y
set T -1
while [T < 0] [set T (random-normal Tgem 1800)]
set p (random-float 1.0)
set rc (4 / (1 + exp((ticks - (2.5 * Tgem)) / 20000)) - 2)
ifelse rc > 0
[set x (0.5 - (1 / rc) + sqrt((2.0 / rc) * p + (rc ^ -2) - (rc ^ -1) + 0.25))]
[set x (0.5 - (1 / rc) - sqrt((2.0 / rc) * p + (rc ^ -2) - (rc ^ -1) + 0.25))]
ifelse ? = 1
[set R (x * start / 2)]
[set R ((x - 1) * (100 - start) / 2)]
set time (n-values (T / 2) [?])
foreach time [
set y (R * (cos (360 * ? / T)) + start - R)
set stage ((y - (y mod 25)) / 25 - 3)
set test (1 / (1 + exp(ticks)))
tick
]
]
end