Embedded Motion Control 2012 Group 5: Difference between revisions
| Line 80: | Line 80: | ||
'''Hough transform''' | '''Hough transform''' | ||
A hough transform interprets the data points of the LRF in a different way; each point in x-y-space can be seen as a point through which a line can be drawn. This line will be of the form <math>y=ax+b</math>, but can also be parametrized in polar coordinates. The parameter <math>r</math> represents the distance between the line and the origin, while <math>\theta</math> is the angle of the vector from the origin to this closest point. Using this parameterization, the equation of the line can be written as | [[Image:R_theta_line.png|150px]]A hough transform interprets the data points of the LRF in a different way; each point in x-y-space can be seen as a point through which a line can be drawn. This line will be of the form <math>y=ax+b</math>, but can also be parametrized in polar coordinates. The parameter <math>r</math> represents the distance between the line and the origin, while <math>\theta</math> is the angle of the vector from the origin to this closest point. Using this parameterization, the equation of the line can be written as | ||
:<math>y = \left(-{\cos\theta\over\sin\theta}\right)x + \left({r\over{\sin\theta}}\right)</math> | :<math>y = \left(-{\cos\theta\over\sin\theta}\right)x + \left({r\over{\sin\theta}}\right)</math> | ||
So for an arbitrary point on the image plane with coordinates (<math>x_0</math>, <math>y_0</math>), the lines that go through it are the pairs (<math>r</math>,<math>\theta</math>) with | So for an arbitrary point on the image plane with coordinates (<math>x_0</math>, <math>y_0</math>), the lines that go through it are the pairs (<math>r</math>,<math>\theta</math>) with | ||
Revision as of 11:19, 15 May 2012
Group Information
| Name | Student number | Build |
|---|---|---|
| Fabien Bruning | 0655273 | Ubuntu 10.10 on Virtualbox in OSX 10.7 |
| Yanick Douven | 0650623 | Ubuntu 10.04 dual boot with W7 |
| Joost Groenen | 0656319 | Ubuntu 10.04 dual boot with W7 |
| Luuk Mouton | 0653102 | Ubuntu 10.04 dual boot with W7 (Wubi) |
| Ramon Wijnands | 0660711 | Installed Ubuntu with wubi (included with the Ubuntu CD) |
Planning and agreements
Planning by week
- Week 1 (April 23th -April 29)
- Install Ubuntu and get familiar with the operating system
- Week 2 (April 30th - May 6th)
- Get the software environment up and running on the notebooks
- ROS
- Eclipse
- Gazebo
- Start with the tutorials about C++ and ROS
- Get the software environment up and running on the notebooks
- Week 3 (May 7th - May 13th)
- Finish the tutorials about C++ and ROS
- Install smartsvn
- Create a ROS package and submit it to the SVN
- Read chapters of the book up to chapter 7
- Make an overview of which elements of chapter 7 should be covered during the lecture
- Week 4 (May 15th - May 20th)
- Make lecture slides and prepare the lecture
- Finish the action handler
- Finish the LRF-vision
- Start with the strategy for the corridor competition
- Week 5 (May 21th - May 27th)
- Week 6 (May 28th - June 3rd)
- Week 7 (June 4th - June 10rd)
- Week 8 (June 11th - June 17rd)
- Week 9 (June 18th - June 24rd)
Agreements
- For checking out the svn and committing code, we will use Smartsvn
- Add your name to the comment when you check in
- Every Tuesday, we will work together on the project
- Every Monday, we will arrange a tutor meeting
Strategy and software description
Strategy
'Visual Status Report Because a picture is worth a thousand words.
ROS layout
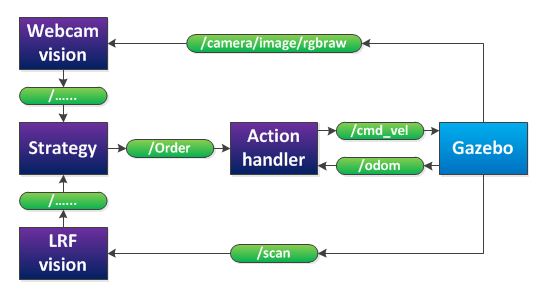
After a group discussing, we decided that our provisionally software layout will be as in the figure below.
The 'webcam vision' node processes the images, produced by the RGB-camera. It will publish if it detects an arrow and in what direction the arrow points. The 'LRF vision' node processes the data of the laser range finder. It will detect corners, crossroads and the distance to local obstacles. This will also be published to strategy. The 'strategy' node will decide, based on the webcam and LRF vision, what action should be executed (stop, drive forward, drive backward, turn left or turn right) and will publish this decision to the 'action handler' node. Finally, the 'action handler' node will send a message to the jazz-robot, based on the received task and on odometry data.
Action Handler
LRF vision
The Laser Range Finder of the Jazz robot is simulated in the jazz_simulater with 180 angle increments from -130 to 130 degrees. The range is 0.08 to 10.0 meters, with a resolution of 1 cm and an update rate of 20 Hz. The topic is /scan and is of the type sensor_msgs::LaserScan. The data is clipped at 9.8 meters, and the first and last 7 points are discarded, since these data points lie on the jazz robot.
The LRF data can be processed in multiple ways. Since it not exactly clear what the GMapping algorithm (implemented in ROS) does, we decided to write our own mapping algorithm. But first the LRF needs to be interpreted. Therefore, a class is created that receives LRF data and fits lines through the data. The fitting of lines can be done in two ways; a hough transform and a fanciful algorithm.
Hough transform
 A hough transform interprets the data points of the LRF in a different way; each point in x-y-space can be seen as a point through which a line can be drawn. This line will be of the form [math]\displaystyle{ y=ax+b }[/math], but can also be parametrized in polar coordinates. The parameter [math]\displaystyle{ r }[/math] represents the distance between the line and the origin, while [math]\displaystyle{ \theta }[/math] is the angle of the vector from the origin to this closest point. Using this parameterization, the equation of the line can be written as
A hough transform interprets the data points of the LRF in a different way; each point in x-y-space can be seen as a point through which a line can be drawn. This line will be of the form [math]\displaystyle{ y=ax+b }[/math], but can also be parametrized in polar coordinates. The parameter [math]\displaystyle{ r }[/math] represents the distance between the line and the origin, while [math]\displaystyle{ \theta }[/math] is the angle of the vector from the origin to this closest point. Using this parameterization, the equation of the line can be written as
- [math]\displaystyle{ y = \left(-{\cos\theta\over\sin\theta}\right)x + \left({r\over{\sin\theta}}\right) }[/math]
So for an arbitrary point on the image plane with coordinates ([math]\displaystyle{ x_0 }[/math], [math]\displaystyle{ y_0 }[/math]), the lines that go through it are the pairs ([math]\displaystyle{ r }[/math],[math]\displaystyle{ \theta }[/math]) with
- [math]\displaystyle{ r(\theta) =x_0\cdot\cos \theta+y_0\cdot\sin \theta }[/math]
Now a grid can be created for [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ r }[/math], in which all pairs ([math]\displaystyle{ r }[/math],[math]\displaystyle{ \theta }[/math]) are drawn. Now a 3D surface is created that shows peaks for the combinations of [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ r }[/math] that are good fits for lines in the LRF data.
The drawback of this method is that holes in the wall are difficult to detect, since the line is parametrized with [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ r }[/math] and has therefore no beginning or end. This problem can be fixed by mapping all data points to the closest line and snipping the line in smaller pieces. An advantage is that a Hough transform is very robust, and can handle noisy data.
Fanciful algorithm
We thought of an own algorithm for line detection as well. Since the data is presented to the /scan topic in array of points with increasing angle, the points can be checked individually if they contribute to a line. A pseudocode version of the algorithm looks as follows:
create a line between point 1 and point 2 of the LRF data (LINE class)
loop over all data points
l = current line
p = current point
if perpendicular distance between l and p < [math]\displaystyle{ \sigma }[/math] AND angle between l and p < 33 degrees AND dist(endpoint of l, a) < 40 cm
// point is good and can be added to the line
then add point to line
else false_points_counter++
end
if false_points_counter > 3
then end the line
decrease the data point index with 3
create a new line with the first two points
increase the line index with 1
end
end loop
LRF processed data
The output of the line detection algorithm is published on /lines, and the map-node is subscribed to this topic.