Embedded Motion Control 2015 Group 7

About the group

Student information

	Name	Student id	E-mail
Student 1	Camiel Beckers	0766317	c.j.j.beckers@student.tue.nl
Student 2	Brandon Caasenbrood	0772479	b.j.caasenbrood@student.tue.nl
Student 3	Chaoyu Chen	0752396	c.chen.1@student.tue.nl
Student 4	Falco Creemers	0773413	f.m.g.creemers@student.tue.nl
Student 5	Diem van Dongen	0782044	d.v.dongen@student.tue.nl
Student 6	Mathijs van Dongen	0768644	m.c.p.v.dongen@student.tue.nl
Student 7	Bram van de Schoot	0739157	b.a.c.v.d.schoot@student.tue.nl
Student 8	Rik van der Struijk	0739222	r.j.m.v.d.struijk@student.tue.nl
Student 9	Ward Wiechert	0775592	w.j.a.c.wiechert@student.tue.nl

Updates Log

03-06: Revised composition pattern.

Planning

Week 7: 1 June - 7 June

• 2 June: Revised Detection, correcting Hough Transform and improving robustness
• 2 June: Back-up plan considering homing of PICO (driving based on potential field)
• 3 June: SLAM finished, functionality will be discussed (will it or will it not be used?)
• 4 June: New experiment: homing, SLAM, ....
• Working principle of decision maker
• Add filter to Detection: filter markers to purely corners

Week 8: 8 June - 14 June

• 10 June: Final design presentation - design and "educational progress"

Week 9: 15 June - 22 June

• 17 June: Maze Competition

Introduction

Robots Pico and Taco

For the course Embedded Motion Control the "A-MAZE-ING PICO" challenge is designed, providing the learning curve between hardware and software. The goal of the "A-MAZE-ING PICO" challenge is to design and implement a robotic software system, which should make Pico or Taco be capable of autonomously solving a maze in the robotics lab.

PICO will be provided with lowlevel software (ROS based), which provides stability and the primary functions such as communication and movement. Proper software must be designed to complete the said goal, the software design requires the following points to be taken in account: requirements, functions, components, specifications, and interfaces. A top-down structure can be applied to discuss the following initial points.

Design

This software design is discussed in the following subsections. These sections will be updated frequently. The Components and specifications are no longer discussed in the Design, as similar information is present in the other subjects.

Requirements

Requirements specify and restrict the possible ways to reach a certain goal. In order for the robot to autonomously navigate trough a maze, and being able to solve this maze the following requirements are determined with respect to the software of the robot. It is desired that the software meets the following requirements:

• Move from certain A to certain B
• No collisions
• Environment awareness: interpeting the surroundins
• Fully autonomous: not depending on human interaction
• Strategic approach

Functions

Functions and requirements

To satisfy the said requirements, one or multiple functions are designed and assigned to the requirements. describes which functions are considered necessary to meet a specific requirement.

The function ’Build world model’ describes the visualisation of the environment of the robot. ’Path memory’ corresponds with memorizing the travelled path of the robot. ’Sensor calibration’ can be applied to ensure similar settings of both robots, so that the software can be applied for both.

Interface

Interface

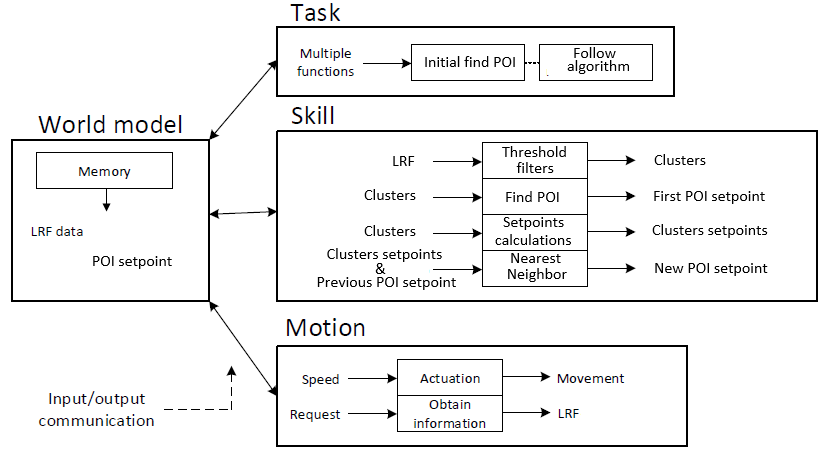
The interface describes the communication between the specified contexts and functions necessarry to perform the task. The contexts and functions are represented by blocks in the interface and correspond with the requirements, functions, components and specifications previously discussed.

The robot context describes the abilities the robots Pico and Taco have in common, which in this case is purely hardware. The environment context describes the means of the robot to visualize the surroundings, which is done via the required world model. The task context describes the control necessary for the robot to deal with certain situations (such as a corner, intersection or a dead end). The skill context contains the functions which are considered necessary to realise the task.

Note that the block ’decision making’ is considered as feedback control, it acts based on the situation recognized by the robot. However ’Strategic Algorithm’ corresponds with feedforward control, based on the algorithm certain future decisions for instance can be ruled out or given a higher priority.

To further elaborate on the interface, the following example can be considered in which the robot approaches a T-junction: The robot will navigate trough a corridor, in which information from both the lasers as the kinect can be applied to avoid collision with the walls. At the end of the corridor, the robot will approach a T-junction. With use of the data gathered from the lasers and the kinect, the robot will be able to recognize this T-junction. The strategic algorithm will determine the best decision in this situation based on the lowest cost. The decision will be made which controls the hardware of the robot to perform the correct action. The T-junction is considered a ’decision location’, which will be saved in the case the robot is not capable of solving the maze with the initial decision at this location. During the movement of the robot, the walls are mapped to visualise the surroundings.

Composition Pattern

Composition Pattern

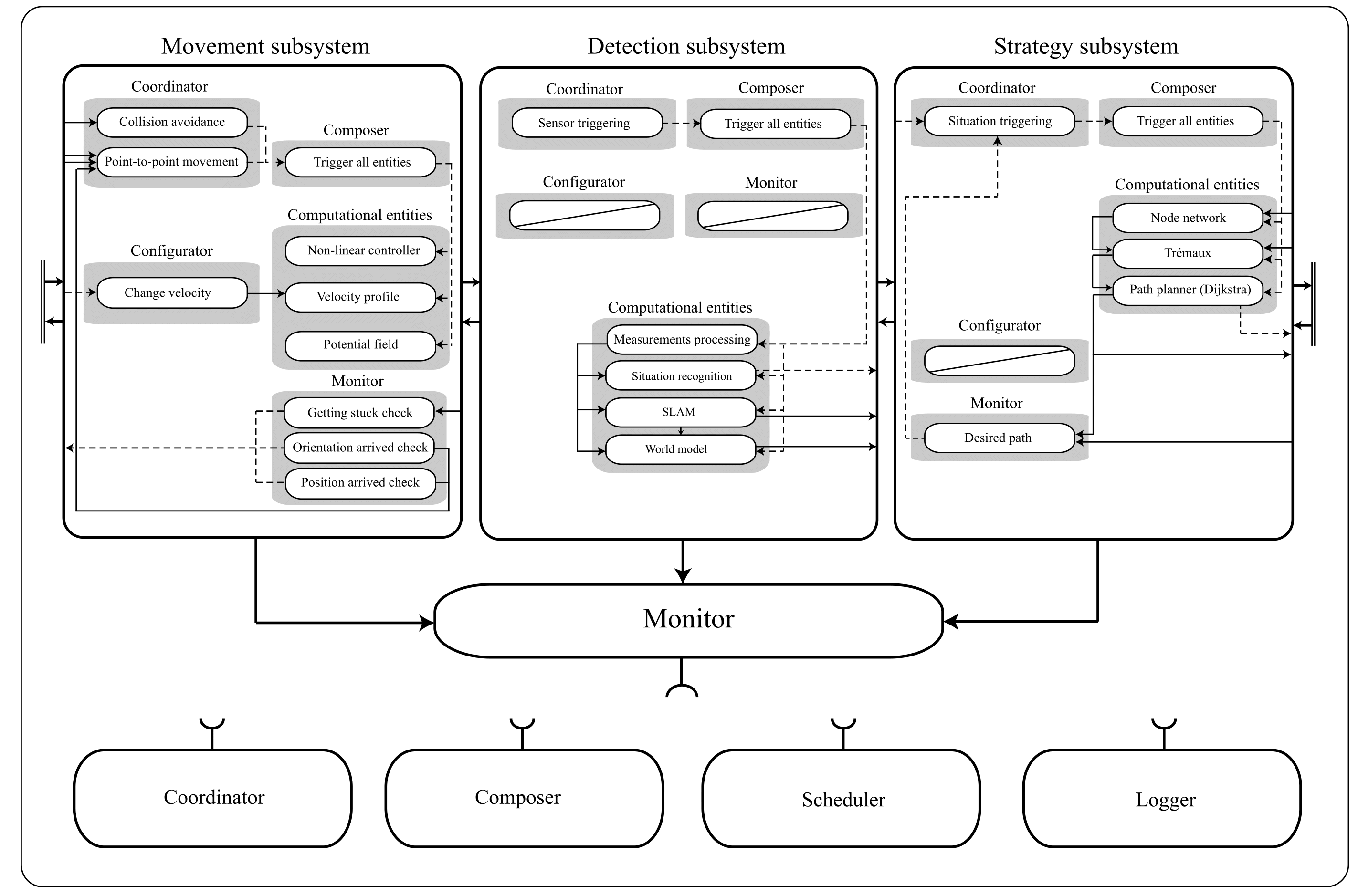
The structural model, also known as the composition pattern, decouples the behavior model functionalities into the 5C’s. The code is divided into five seperate roles:

• Computational entities which deliver the functional, algorithmic part of the system.
• Coordinators which deal with event handling and decision making in the system.
• Monitors check if what a what a function is supposed to accomplish is also realized in real life.
• Configurators which configure parameters of the computational entities.
• Composers which determine the grouping and connecting of computation entities.

The total structure is divided into three subsystems which will be discussed indivually: movement, detection and strategy.The collaboration between the subsystems is determined by the monitor, coordinator and composer of the main system. Note: the computational entities are discussed in the chapter "Software design".

In the current structure of the code, the three subsystems are combined in the C/C++ main file. This file handles the communication of the various subsystems by using the outputs of the various subsystems as inputs for other subsystems. The different subsystems are scheduled manually. First, the detection subsystem is called to sense the environment and recognise situations/objects. Also, the current location of the robot is determined using the Simultaneous Localization And Mapping (SLAM) algorithm. The strategy subsystem uses this information to make a decision regarding the direction of the robot. This subsystem has a setpoint location as output which in turn will be used by the movement subsystem. The movement subsystem uses the current location and the set-point location to control the velocity of the robot. Currently, there is no data logged in the main file. Also, there is no composing happening in the main file.

The detection subsystem is used to process the data of the laser sensors. It's main function is to observe the environment and send relevant information to the other subsystem and the main coordinator. As commissioned by the coordinator the composer simply triggers all computational entities, which are then carried out in the shown order. The computational entities are shortly explained, and further elaborated in the "Software Design".

• Measurement Processing: using Hough transform to convert LFR data to lines and markers.
• Situation Recognition: detecting corners, corridors and doors based on lines obtaing by Hough transform.
• SLAM: creating global coordinate frame in order to localize PICO in the maze.
• World model: gathering recognized situations and corresponding data.

The strategy subsystem is used for path planning. This subsystem receives edge, corridor and door as global coordinate data from the detection subsystem for the computational entities. When the detection subsystem recognizes a situation in the maze a discrete event is send to the coordinator of this system which will then triggers all computational entities via the composer. These then choose the best path to take, which is executed by the Movement subsystem. To perform accordingly, the following computational entities are designated:

• Node network: network containing all corners and junctions.
• Tremaux: determines which direction to choose at junctions.
• Path Memory: memorizes visited locations, sends information as discrete location data to world model.

Based on the computational entities a planned path is determined. This path is send to the monitor, together with the Point-to-point movement coordinater from the Movement subsystem. The monitor is applied to check whether or nor the path is followed as is desired.

The movement subsystem controls the movement of the robot, based on the input it receives from the other subsystems of the robot. The movement receives the current position of the robot, determined by the SLAM algorithm in the detection subsystem, together with the set point location, determined by the strategy subsystem, both in a global coordinate system. The movement subsystem calculates the robot velocity (in local x, y and theta-direction) so the robot will move from the current location (A) to to the set-point location (B), while avoiding collisions with object. To this end, three compu- tational entities are used.

• Non-linear controller: controlling x and theta velocity.
• Velocity profile: predescribing acceleration and maximum velocity
• Potential field: redirecting PICO for objects in the near proximity

Note that the configurator predescribes the maximum velocity, operating based on events raised by other subsytems. The monitor should assure that PICO arrived at the set-point location, otherwise raising an event to act on accordingly.

Software Design

[new intro following on 27-05 wrt new structure and subsystems: movement, detection, strategy]

Movement

The "movement" part of the software uses data gathered by "detection" to send travel commands to PICO. In the near future, a new "strategy" part of the software will be designed, which basically becomes the "decision maker" which commands the "movement" of PICO. An odometry reset has been implemented to make sure that the code functions properly every time PICO starts in real life.

The current non-linear controller has some sort of stiffness, which results in PICO slowing down too soon too much. This “stiffness” can be removed, so it just goes full speed all the time, but this is a bad idea. Due to the sudden maximum acceleration and deceleration which might result in a loss of traction, the odometry data could get corrupted and therefore the movement would not work properly. Instead, a certain linear slowing down is introduced when PICO comes within a certain range of its destination. It also slowly starts moving from standstill and linearly reaches its maximum velocity, based on a velocity difference.

Local coordinates

The main idea is to work with local coordinates. At time t=0, coordinate A is considered the position of PICO in x, y and theta. With use of the coordinates of edges received by "detection" point B can be placed, which decribes the position PICO should travel towards. This point B will then become the new initial coordinate, as the routine is reset. In case of a junction as seen in the figure multiple points can be placed, allowing PICO to choose one of these points to travel to.

The initial plan is to first allow PICO to rotate, followed by the translation to the desired coordinates. This idea was scrapped, because this sequence would be time consuming. Instead a non-linear controller was used, that asymptotically stabilizes the robot towards the desired coordinates.

Although the PICO has an omni-wheel drive platform, it is considered that the robot has an uni-cylce like platform whose control signals are the linear and angular velocity ([math]\displaystyle{ u }[/math] and [math]\displaystyle{ \omega }[/math]). The mathematical model in polar coordinates describing the navigation of PICO in free space is as follow:

[math]\displaystyle{ \dot{r}=-u \, \text{cos}(\theta)\! }[/math]

[math]\displaystyle{ \dot{\theta}=-\omega + u\, \frac{\text{sin}(\theta)}{r},\! }[/math]

where are [math]\displaystyle{ r }[/math] is the distance between the robot and the goal, and [math]\displaystyle{ \theta }[/math] is the orientation error. Thus, the objective of the control is to make the variables [math]\displaystyle{ r }[/math] and [math]\displaystyle{ \theta }[/math] to asymptotically go to zeros. For checking such condition, one can consider the following Lyapunov function candidate: [math]\displaystyle{ V(r,\theta) = 0.5 \, r^2 + 0.5 \, \theta^2 }[/math]. The time derivative of [math]\displaystyle{ V(r,\theta) }[/math] should be negative definite to guarantee asymptotic stability; therefore the state feedback for the variables [math]\displaystyle{ u }[/math] and [math]\displaystyle{ \omega }[/math] are defined as,

[math]\displaystyle{ u = u_{max}\, \text{tanh}(r)\, \text{cos}(\theta) \! }[/math]

[math]\displaystyle{ \omega = k_{\omega} \, \theta + u_{max} \frac{\text{tanh}(r)}{r} \, \text{sin}( \theta) \, \text{cos}( \theta),\! }[/math]

where [math]\displaystyle{ u_{max} }[/math] and [math]\displaystyle{ k_{\omega} }[/math] both are postive constants.

Potential field

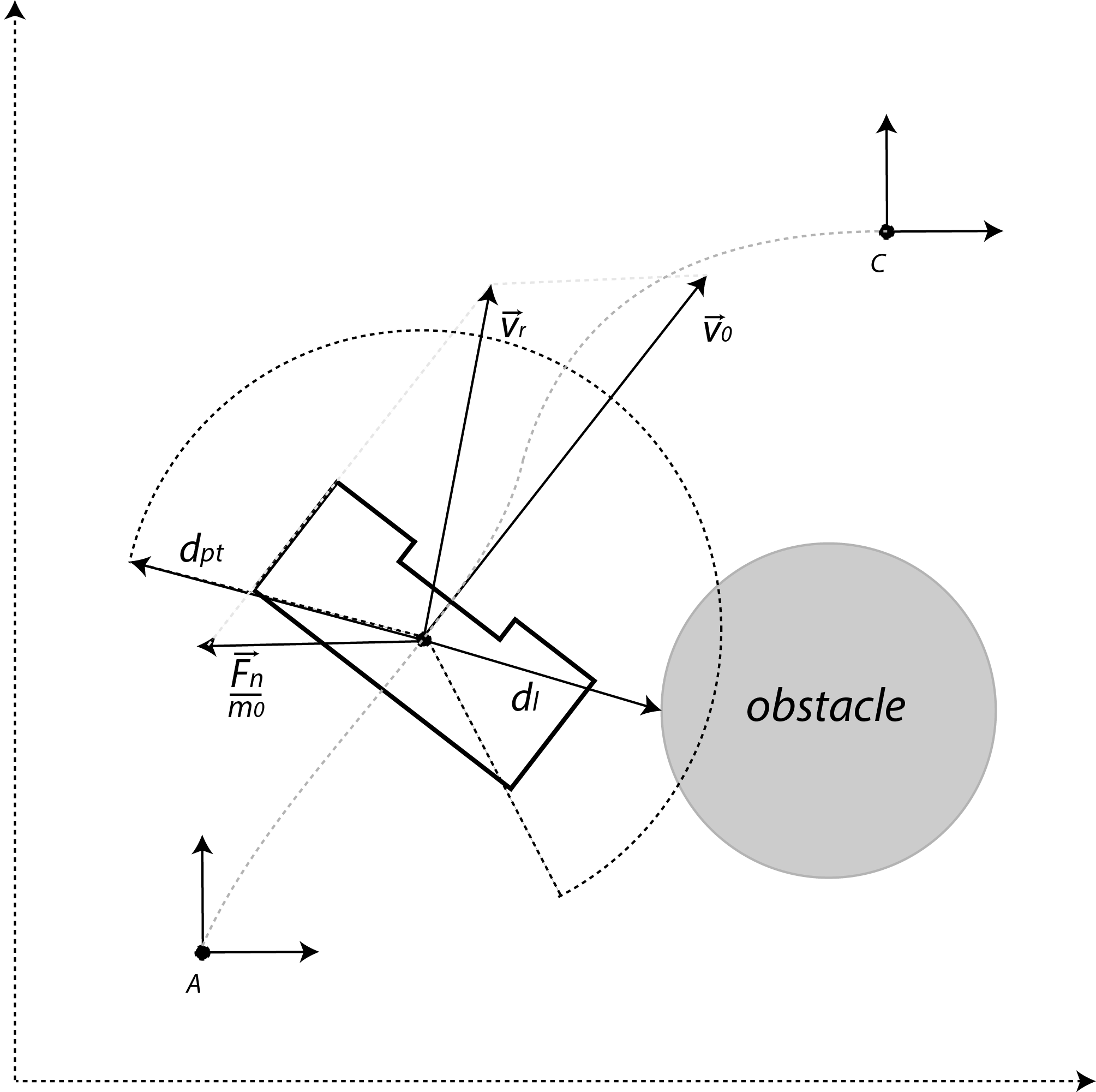
If PICO would be located at position A and would directly travel towards point C, this will result in a collision with the walls. To avoid collision with the walls and other objects, a potential field around the robot will be created using the laser. This can be interpreted as a repulsive force [math]\displaystyle{ \vec{U} }[/math] given by:

[math]\displaystyle{ \vec{U}(d_l) = \begin{cases} K_0 \left(\frac{1}{d_{pt}}- \frac{1}{d_l} \right) \frac{1}{{d_l}^2} & \text{if } d_l \lt d_{pt}, \\ ~~\, 0 & \text{otherwise}, \end{cases} }[/math]

where [math]\displaystyle{ K_0 }[/math] is the virtual stiffness for repulsion, [math]\displaystyle{ d_{pt} }[/math] the range of the potential field, and [math]\displaystyle{ d_l }[/math] the distance picked up from the laser. Moreover, the same trick can be applied in order for an attractive force

[math]\displaystyle{ \vec{V}(d_l) = \begin{cases} 0 & \text{if } d_l \lt d_{pt}, \\ ~~\,K_1 d_{pl}^2 & \text{otherwise}, \end{cases} }[/math]

where [math]\displaystyle{ K_1 }[/math] is virtual spring for attraction. Summing these repulsive force [math]\displaystyle{ \vec{U} }[/math] results into a netto force,

[math]\displaystyle{ \vec{F}_n = \sum_{i=1}^N \vec{U}(d_{l,i}) + w_i\vec{V}(d_{l,i}), }[/math]

where [math]\displaystyle{ N }[/math] is the number of laser data, and [math]\displaystyle{ w }[/math] a weight filter used to make turns. Assume that the PICO has an initial velocity [math]\displaystyle{ \vec{v_0} }[/math]. Once a force is introduced, this velocity vector is influenced. This influence is modeled as an impulse reaction; therefore the new velocity vector [math]\displaystyle{ \vec{v}_r }[/math] becomes,

[math]\displaystyle{ \vec{v}_r = \vec{v_0} + \frac{\vec{F}_n \,}{m_0} \, \Delta t, }[/math]

where [math]\displaystyle{ m_0 }[/math] is a virtual mass of PICO, and [math]\displaystyle{ \Delta t }[/math] the specific time frame. The closer PICO moves to an object, the greater the repulsive force becomes. Some examples of the earlier implementation are included:

Detection

The initial idea of edge detection will be replaced by a set of multiple detection methods: Hough Transform and SLAM. At this point edge detection is still in use, this will be become a part of the Hough Transform code.

Edge detection

File:Sketch edgedetec.png

Sketch of edge detection

An edge can be considered as a discontinuity of the walls perpendicular to the travel direction of PICO. This can be either an door (open/closed), a corner or a slit in the wall. At this stage only the detection of a corner will be implemented.

.

The edge is then defined as the position of the corner (relative to PICO). At every (time)step the relative distances (wall to pico)will be checked, based on LRF data. If at some point the distance between one increment of the LRF and the neighbouring increment exceeds a certain treshold, it can be considered as an edge point. This is further illustrated by the image. This primary idea is however not robust, therefore the average of neigbouring increments is checked. Robustness will be further improved later on.

Hough Transform

Geomtery in Hough Transform, source: Giesler et al(1998)

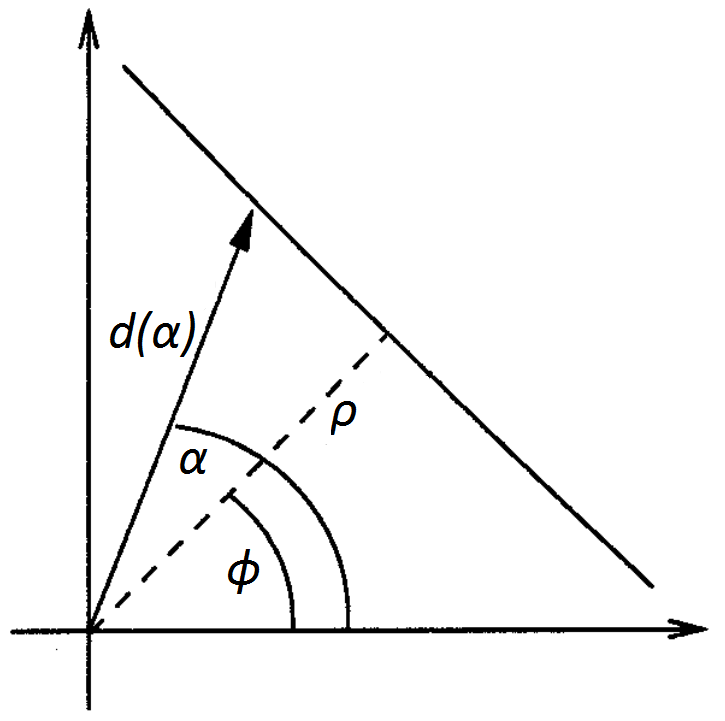
The Hough transformation is used to detect lines using the measurement data. The basic idea is to transform a single point into the parameter space of the set of infinite lines running through it, called the Hough space. In the polar coordinate system of the laser scan, a line through a data point is given by [math]\displaystyle{ \rho=d\cos(\alpha-\phi) }[/math] where [math]\displaystyle{ \rho }[/math] is the length of the orthogonal from the origin to the line and [math]\displaystyle{ \phi }[/math] is its inclination.

By varying [math]\displaystyle{ \phi }[/math] for each data point from 0 to 180 degrees, different [math]\displaystyle{ (\rho,\phi) }[/math] pairs are obtained. Laser points which are aimed at the same wall will yield the same [math]\displaystyle{ (\rho,\phi) }[/math] pair. To determine if a given [math]\displaystyle{ (\rho,\phi) }[/math] pair is a wall, [math]\displaystyle{ \rho }[/math] is discretized, and a vote is cast at the corresponding element for that [math]\displaystyle{ (\rho_d,\phi) }[/math] pair in an accumulator matrix. Elements with a high number of votes will correspond with the presence of a wall. The end-points of the walls are found using detected corners and the intersection points of the walls.

SLAM

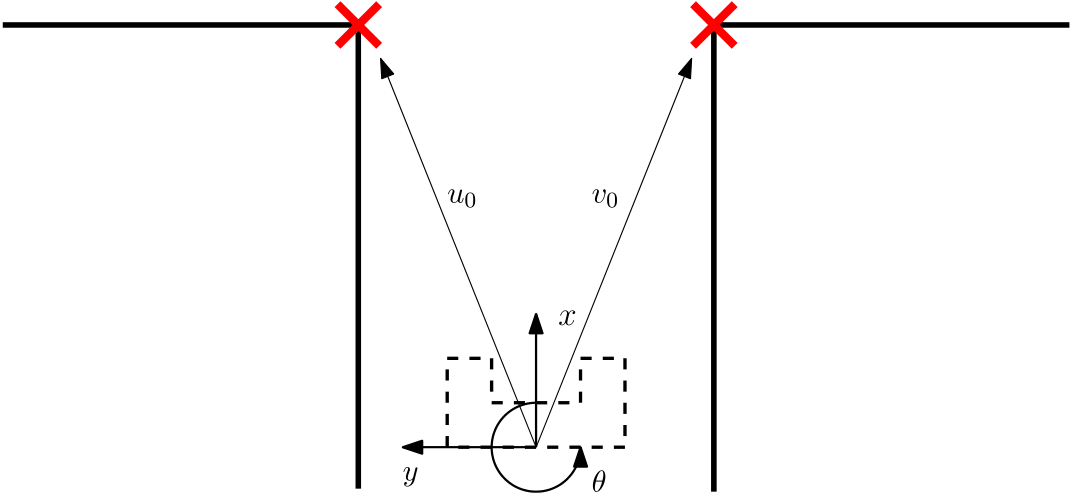
To determine the map of the maze and simultaneously the position of the PICO inside the maze, the odometry is used to make an initial guess. Due to the inaccuracy of the odometry data, the position must be verified and if necessary corrected with the laser measurements. In the figure to the right, the initial position of PICO is shown. Here the odometry data is [math]\displaystyle{ (x,y,\theta)=(0,0,0) }[/math] and exact. The data is verified with the laser measurements requiring landmarks, which in this case the are the corners denoted by the red crosses.

After a certain time step PICO is positioned at a different coordinate, resulting in an estimate and exact position. In the second figure to the right, the exact position of PICO is showed in black and the measured position of the PICO is given in blue. To correct the initial guess to the exact position the landmarks as determined earlier are used. The laser data at [math]\displaystyle{ t_k }[/math] is compared with the laser data at [math]\displaystyle{ t_{k-1} }[/math]. However, the laser data is not perfectly accurate aswell. Therefore, a trade off has to be made. To filter incoming data, laser sensors and odometry, an Extended Kalman Filter is used.

For the correct functionality of the SLAM method, landmarks are necessary. On the downside, the landmarks are not positioned similar with respect to PICO every time the laser measurement is performed. To connect the same landmarks of [math]\displaystyle{ t_k }[/math] and [math]\displaystyle{ t_{k-1} }[/math], the data of the odometry is used. An initial guess will determine an estimate for the range where the landmark will be positioned. In \autoref{fig:landmarkRegion} the region where the landmark must be in is showed. In this region there can be measured where the landmark is positioned exactly. All the new landmarks that are not in the region are not used for determine the exact position at [math]\displaystyle{ t_k }[/math].

To simultaneously locate and map the robot and its environment, the observations have to be filtered. An Extended Kalman Filter is used to filter the observation and update the position of the robot and its environment. The EKF has two input parameters. The first parameter is the robot's controls ([math]\displaystyle{ \mu_t }[/math]) which are the velocity outputs or the odometry reading. Second given parameter is the observations ([math]\displaystyle{ z_t }[/math]) which is in this case, the laser data. With this information, a map of the environment can be made and in this case this map will consist out of markers ($ m$). Second the path of the robot ([math]\displaystyle{ x_t }[/math]) can be calculated with the input and the EKF. This is done by comparing the certainty of the odometry with the certainty of the laser measurement. This comparison results in a Kalman gain. When the Kalman gain is equal to zero, the system uses the odometry data to update the positions. However, when the Kalman gain is large, the system uses the markers and laser data update the positions.