Embedded Motion Control 2015 Group 4

Authors: T. Cornelissen, T van Bommel, J. H. de Kleuver, M. Oligschläger, B. Hendrikx, P. Rooijakkers, T. Albers

Requirements and function specifications

Problem statement

The software design process starts with a statement of the problem. Although all the details of the assignment are not yet knwon at this point, we can best summarize the statement with the following sentence:

Design the software in C/C++ for the (existing) Pico/Jazz robot that enables to find the exit of an unknown and dynamically changing maze in minimal time.

Requirements

A (draft) list of the requirements contains the following points:

• Exiting the maze in minimal time.
• Avoiding damage of the robot and the environment.
• Robustness of pathfinding algorithm with respect to maze layout.
• Design software using modular approach.
• Implement algorithm using only available hardware and software API's.
• Manage code development with multiple developers.

Existing hardware interfaces

• The Pico/Jazz robot with customized inner workings and a robot operating system with C++ API's.
• A (still unknown) wheelbase layout of which the possible DoF/turning radius is a design constraint.
• A lasersensor and acoustic sensor of which the range-of-visibility is a design constraint.

Unknown design constraints

• Simulation environment for code testing?
• Location of sensors and wheels relative to robot fixed frame?
• What data can we extract form the sensors?
• What does the maze look like? How do the doors operate?

Main focus point in the first two weeks

• Learn basics of C/C++ and software development.
• Determine the layout of the robot and the possibilities of the sensors and wheel structure.
• Become familiar with the integrated development environment.
• Explore the possibilities of th API's (how much postprocessing of the aquired sensor data is necessary and what techniques must be learned?).

Software design strategy

The figure below shows the overview of a posible software layout. The skill functions can be assigned to different programmers that are also responsible for exploring the API's and gathering details about the hardware. The maze solving strategy can be handled separately and the supervisory controller is the brain of the robot combining all the information. File:Maze example.pdf

Laser vision

Compass function

This function measures the angular misalignment of the robot with it's environment. The compass function gives a valid estimate of the angular misalignment under the following assumptions.

Assumptions:

• The world consists of mainly straight lines.
• All the lines cross each-other approximately with an angle which is a multiple of the world angle (when for example all the angles are perpendicular then the is 90 degrees)
• The current misalignment of the robot with it's environment is small: [math]\displaystyle{ \theta_{robot}\lt \lt 0.5\cdot\theta_{world\,angle} }[/math]. This implies that the compass function is unreliable during large rotations.
• There are enough sample points (preferably in front of the robot) to ensure that lines can be detected in the so called trust area.
• The trust area is defined as a bounded square around the robot which is aligned with the robot frame. Only the samples in this square are used for the compass function calculations. As is shown in the figure below.

Compass function

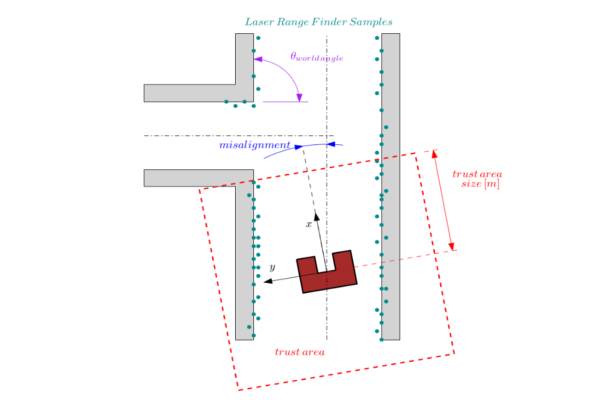
Approach:

We are searching for a reference line from which we can calculate the angular misalignment of the robot. This calculation proceeds in the following sequence: First the laser data is expressed in a orthogonal frame (fixed to the robot). A line through point [math]\displaystyle{ [x_i,y_i] }[/math] can be described in polar coordinates as [math]\displaystyle{ p(\alpha)=x_i \cos(\alpha)+y_i \sin(\alpha) }[/math] where [math]\displaystyle{ p }[/math] and [math]\displaystyle{ \alpha }[/math] are unknown parameters. We want to find a [math]\displaystyle{ \alpha\in[0,\pi] }[/math] and a [math]\displaystyle{ p\in [-p_{max},p_{max}] }[/math] where [math]\displaystyle{ p_{max}=\sqrt{(2\cdot trust\,area\,size)^2} }[/math] is half the trust area diagonal. The Hough transform [1] gives a procedure to find [math]\displaystyle{ p }[/math] and [math]\displaystyle{ \alpha }[/math]. The procedure is as follows: for each [math]\displaystyle{ [x_i,y_i] }[/math] in the trust area and [math]\displaystyle{ \alpha\in[0,\pi] }[/math] the value of [math]\displaystyle{ p(\alpha) }[/math] is calculated.

The calculated [math]\displaystyle{ p }[/math] values are round to the closest value in a discrete set. The Hough parameter space can in this case be interpreted as a 2 dimensional grid where the first axis represents the value of [math]\displaystyle{ \alpha }[/math] and the second axis the [math]\displaystyle{ p }[/math] value, where for each solution of [math]\displaystyle{ p }[/math] a value of one is added to the corresponding cell in the grid. The parameters of our reference line are the parameters that corresponds to the highest value in the Hough parameter grid.

The Hough transformation is shown in the following figure. The x and y values of the laser measurements are shown on the left. On the right the Hough space is shown, where the red line represents the current [math]\displaystyle{ \alpha }[/math] value of our reference line.

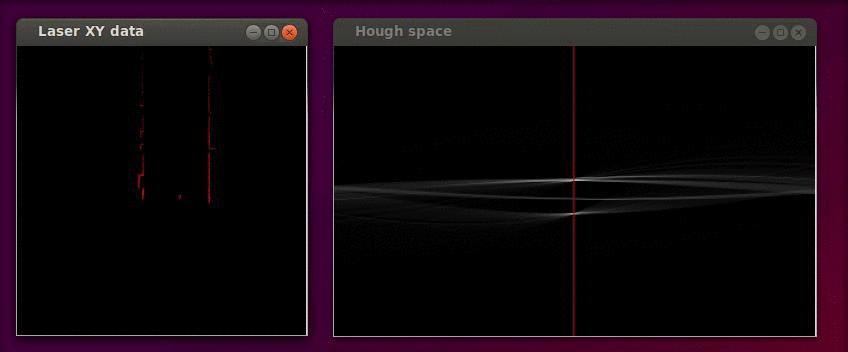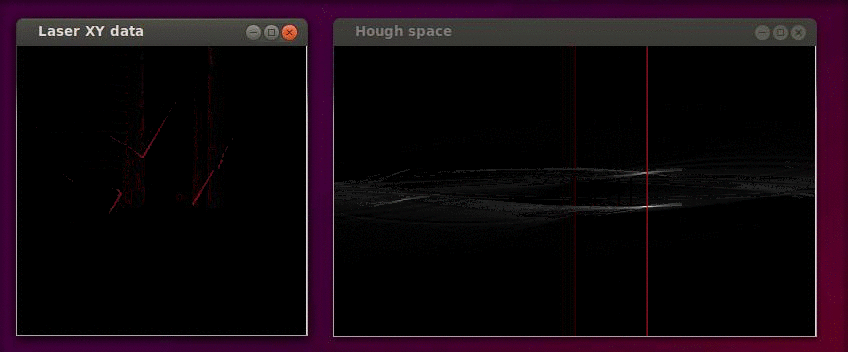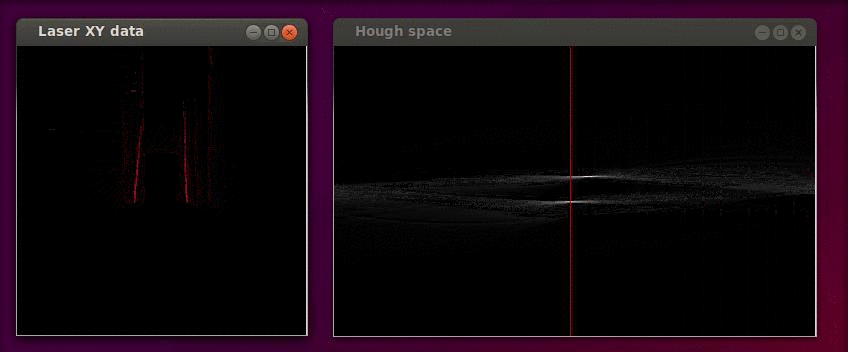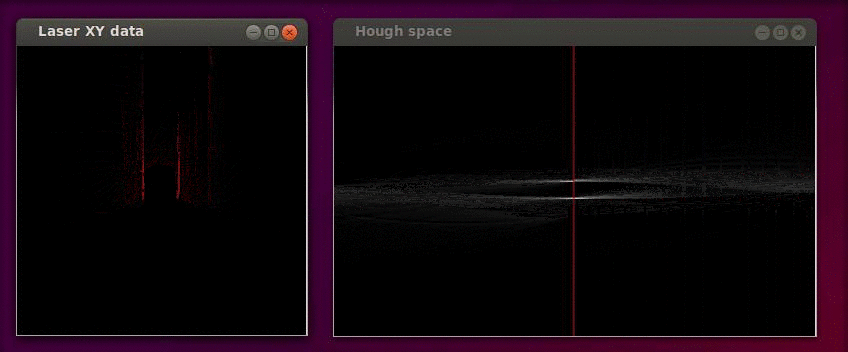
Only the [math]\displaystyle{ \alpha }[/math] parameter is in this case of interest. Since we assumed that the angular error of the robot with its environment is small we calculate the misalignment as the smallest difference between the parameter [math]\displaystyle{ \alpha }[/math] and a multiple of the world angle (in other words it does not matter for the result when we find a reference line parallel to the robot y axis instead of a line parallel to the y axis).

Applications:

The result of the compass function can be directly used to reduce the angular misalignment of the robot with its environment. This is accomplished in the form of a simple gain feedback control rule: [math]\displaystyle{ \omega_z=K_ze_z }[/math] where [math]\displaystyle{ \omega_z }[/math] is the rotation velocity, [math]\displaystyle{ K_z }[/math] is a control gain and [math]\displaystyle{ e_z }[/math] is the angular misalignment found by this function. The other application of the compass function is to align the mini map with the robot’s environment.