Viotar/Quantifying the signal

Introduction

The signal that we want from the string, somehow will have to be read out by the instrument. No matter how this is done, some sensor will provide a signal, in which the vibration we want from the string should be recognised. This recognising has to be done on a reliable, quantitative basis. More specifically, there has to be some kind of scalar quantity (which we'll define as the tonal quality Q) that gives us how far we really are from the ideal trajectory in the bow speed-force space, so a feedback loop can be made to let the system find this trajectory for itself. For this, an experiment will be done, and it's results will be analysed thoroughly.

Experiment plan

• Is the computer model of the bowed string accurate?

• Where does the "pleasant" sound come from that you hear when you stand next to the instrument when it's bowed? Is it mainly the vibration of the body that you hear? In that case it would origin mainly from the pressure variances of the string on the bridge, which translate into the body. On the other hand, it could be mainly the vibration of the string that you hear. In that case, the transversal wave as described by the computer model and measured by a laser sensor is dominant. The outcome of this will be important in the choice of what the capture and amplify exactly, when the instrument is done.

• What do these vibrations look like in the transversal wave of one point on the string?
  • The vibration we want (Helmholtz)
  • Raucous noise (bow pressed too hard against the string)
  • Surface sound (bow pressed too softly against the string)
• What do these vibrations look like in the variances of the pressure of the string on the piëzo element?
  • The vibration we want (Helmholtz)
  • Raucous noise (bow pressed too hard against the string)
  • Surface sound (bow pressed too softly against the string)

A measurement will be done for the low E-string and the high e-string, on the open string and the 1st, 12th and 13th fret. The open string and 1st fret measurements are needed to "shift" the signal in the frequency domain. Everything that shifts up according to the fret change is part of the vibration we want to measure, the rest is noise. With this principle we are hoping to be able to cancel the noise from the measurements. The 12th and 13th fret are done so that the same can be done for a much higher position (one octave up), because the waveform may have a different character there.

Goal of the measurement

In order to find out what a Helmholtz vibration and a noisy (in this case raucous) sound look like in the frequency domain, we did some experiments. We measure the vibration of the string in three ways. Firstly, we measure the transversal motion of the string, using a laser. This will be done because we need to know the vibration of the string at one single point, since the model also describes one point. Also the vibration at the bridge will be measured, using the existing piëzo’s. This is done because we want to know the difference between the vibration of the end of the string and the vibration at a single point somewhere in the middle of it. At last, we also measure the sound that you hear when the instrument is bowed, using a microphone. The main goal of these measurements is that we want to know how we can recognize a clear Helmholtz vibration in the frequency domain.

Measurement setup

The measurement with the laser will be done using a Lab Interface. For the measurements with the piëzo’s and the microphone, we will use a SigLab. The experiments will be done for two different strings, the A and B string. The string will be bowed at 4 different fret positions, being the open string, the 1st, 12th and 13th fret. All the measurements will be done twice to reduce errors.

Results

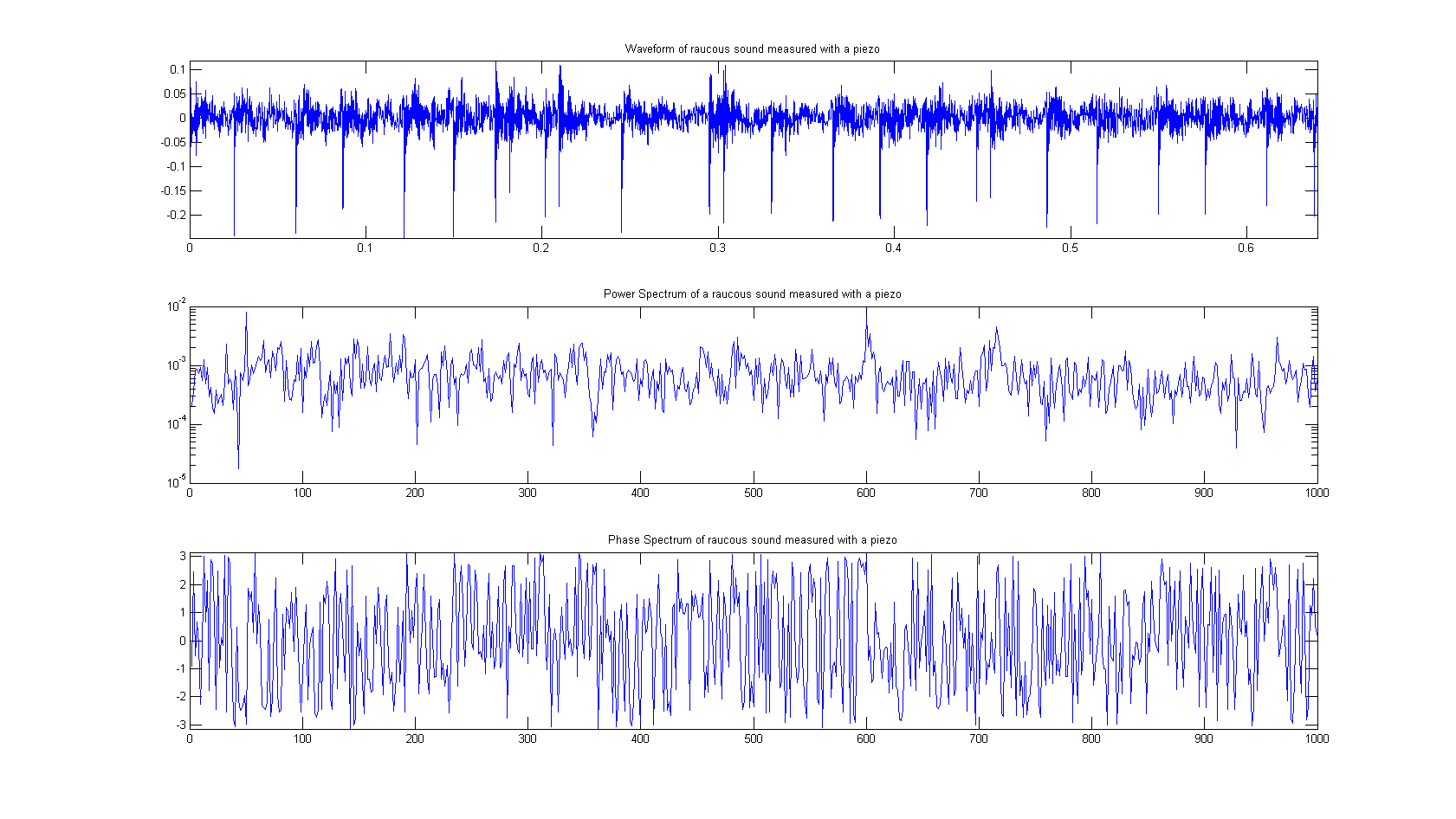
In figure 1 both the time and frequency domain results are given for what we call a raucous sound, which means that the string is sticking to much. This measurement is done using a piëzo. As can be seen from the power spectrum, there are no harmonic vibrations in this sound. It is all very chaotic and there is only noise.

Figure 1: The measurement results for a raucous sound

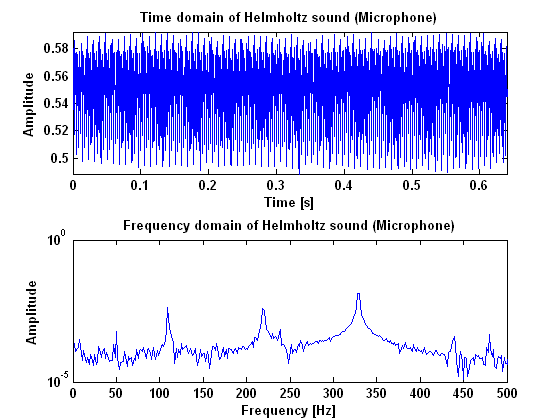
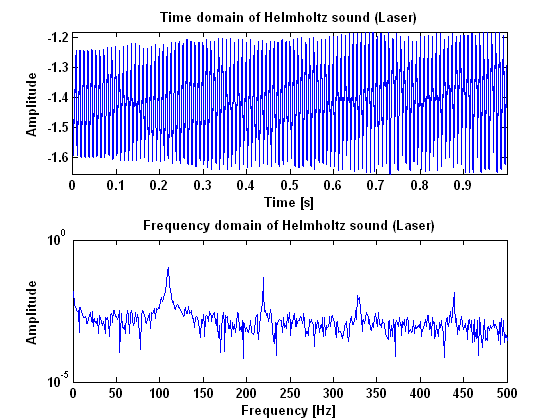
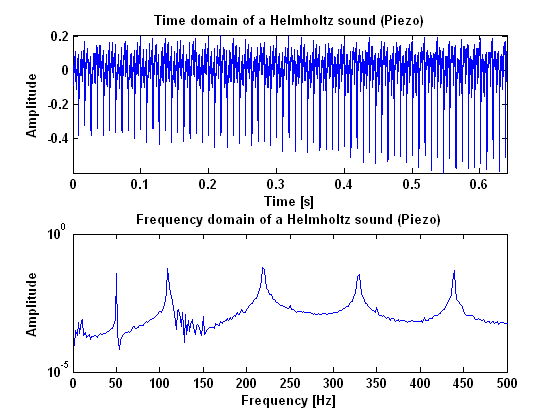
In figures 2, 3 and 4, the results are given for helmholtz vibration, measured with the microphone, the laser and the piëzo. As can be seen in these figures, a Helmholtz vibration gives clear harmonic peaks in the power spectrum. Especially the measurements done with the piëzo and the laser give a good result. Important to notice when the vibration is measured with the piëzo, is the peak at 50 Hz which is caused by the power supply. Besides that peak however, all the peaks appear in harmonic frequencies.

Figure 2: The measurement results for a Helmnholtz sound measured with a microphone

Figure 2: The measurement results for a Helmnholtz sound measured with a laser

Figure 2: The measurement results for a Helmnholtz sound measured with a piëzo

Analysing the results

The first goal was to cancel the noise from the measurements using the method explained in the previous paragraph. This proved to be impossible. The power spectrum of a measurement may be split up in two components: the 'noise' component, which stays the same when a higher note is played, and the 'harmonic' component, which shifts up when a higher note is played.

Probaby, Helmholtz is the only harmonic vibration that you can get from a string when you bow it. With a bow you can never get a normal standing wave as when you would pluck the string. Because of this, it is not necessary to quantify "how much" the measured vibration is the specific Helmholtz waveform. It may suffit to merely quantify how harmonic the measured vibration is. This can be done by detecting the fundamental frequency in the fft of the signal, and looking looking how many multiplications of this frequency are still in the signal. The more overtones, the sharper the Helmholtz, and therefore the better the tone.