PRE2018 3 Group14: Difference between revisions
| Line 221: | Line 221: | ||
[[File:Rotterdam_selected_roads.png|400px|thumb|right|Selected roads and measurement points in Rotterdam]] | [[File:Rotterdam_selected_roads.png|400px|thumb|right|Selected roads and measurement points in Rotterdam]] | ||
[[File:Raw DATEXII data.jpeg|400px|thumb|right|Selected roads and measurement points in Rotterdam]] | |||
== Maximum Flow Research == | == Maximum Flow Research == | ||
Revision as of 19:15, 20 February 2019
Group Members
| Name | Study | Student ID |
|---|---|---|
| Joost de Boer | Software Science | 1016745 |
| Yanic Dobler | Software Science | 1007100 |
| Leon Kersten | Software Science | 1006966 |
| Pietro Maschera | Psychology and Technology | 1220953 |
| Koen Vlaswinkel | Software Science | 1016271 |
Problem statement
Traffic management and prediction is a major concern and industry all over the world. City planers are always on the lookout for new methods, algorithms and procedures to guide the ever-growing car masses through the narrow streets of urban areas. These engineers focus mostly on developing means of controlling traffic light switching and while it is an important area to optimize, it has one looming downfall: It can only dictate the paste and rythm at which traffic flows through a specific intersection and not how traffic is split among possible intersections. Therefore to fully maximize the efficiency of the traffic network, an expert system which gives advice to city planners and administrators is needed. This software will find how the flow of the traffic can be optimized and it will give potential solutions as advice.
Objectives
- To evaluate the current state of the art on traffic advice.
- To evaluate the current state of the art of traffic light control based on actuators.
- To interpret real-life traffic data provided in real time to feed the simulation (below).
- To develop an algorithm to solve the aforementioned problem.
- To develop a traffic simulation showing the effects with and without the provided soltuion on heavy traffic in urban areas.
USE Aspects
Target users
Our project aims to provide motorized traffic advice to whoever is in control of the road network, hence the direct target user will be the city administrators or government, depending on the governmental structure of the country.
Users
The direct users of this product would be the ones who control the road network (i.e municipality or government) because they are the only ones who interact with the product. This is because the municipalities and the government are the ones who have a choice to listen to the expert system or ignore the advice given. However, road users such as car drivers will be an indirect user of this product too as any choice implemented by the road network controllers will affect the ones who use the road.
Society
Society could benefit from any modifications that is implemented to the road network based on the advice given by the expert system. This is because any optimization in the road network for vehicles, leads to less congested roads and hence a lower amount of total travel time. Therefore, most individuals will have more time for other activities and also save money with gas. From a broader point of view, less total travel time also means that pollution from cars will be reduced, meaning less damage towards the environment which is a good social impact as a whole. However, road networks might become more car-centric as the expert system only tries to optimize the traffic for cars. This may lead to negative consequences for other road users such as bikers and pedestrians, which might have to deal with issues such as but not limited to: crossing broader intersections, waiting longer at traffic lights and cars going faster on roads.
Enterprise
Enterprises could be hired by governmental departments to control the road network, while the goverment still owns the roads itself. Then these companies would be the users of this expert system. Also in cases for smaller private road networks, this software could be used.
Approach
Our approach will be based on mathematical and logical models with whom we aim to describe the traffic behavior around the vehicle and also derive the best possible advice for the individual vehicle. To do so we begin by understanding current models for traffic behavior and prediction. We then use this knowledge to formulate new models which fulfill our purpose. Using these models and real life traffic data a simulation is created, showing traffic with and without the created algorithm. The simulation will "probably" be made using openGL and java.
Planning
In short, we want to do a research on the topic of flow control in traffic situations and improve the flow by analyzing data and creating a software model. The research will be detailed further on the wiki.
There are two things that keep occuring each week, one before each meeting, and one at the end of the week. What is done at the start of each meeting is discussing work done that has been divided last meeting. What is done at the end of the week is a short evaluation meeting with the tutor to compare progress and discuss issues that might have come up. This will start in week 2, as week 1 is the introductory week, with no assigned meeting.
- Week 1:
- Brainstorm on the project idea and pick one idea.
- Elaborate on it by finding sources(indiviually, at least 5 per person).
- Divide the work for the first meeting and work on this individually. Make sure all of the points of the slides have been covered before the first meeting with the tutor.
- Week 2:
- Start researching with the found papers, looking for how flow control works currently and finding ways to help improve it.
- Look for databases of traffic data (in the Netherlands, or outside of it), which might be used in later research/in the software model.
- Search for algorithms or discuss and make one on our own.
- Week 3:
- Start work on a software model based on an algorithm found/created in week 2. Collectively implement a start for the algorithm using data.
- Keep on researching for databases to use and finalize on a choice for database to use in the software model.
- Write about the research that has been done in week 2.
- Week 4:
- Implement details of the software model and fix possible bugs. Discuss ideas that might improve the model, and implement the data reading such that we can get results on our improvement.
- Continue working on writing about the research done, and report on the software model on the wiki.
- Research for new studies/algorithms should not be needed after this point, as the software should be largely done.
- Week 5:
- Finalize the software model and process data from the database. If needed, fix bugs in the software model.
- Compare the data from the results and think of conclusions linked to the outcomes.
- Collectively look for reasons why the data behaves like how it is found.
- If there is time for it, start working on the questionnaire for the USE aspect.
- Week 6:
- Continue processing of the data and results of using the software model. The software model should be done at this point, because otherwise data will not be reliable for later.
- Find interesting results, and compare them to real life data. Couple the found results to USE: is it helpful in improving daily life? Done in the form of a questionnaire perhaps.
- Start with picking interesting topics to discuss about our results for the presentation in week 8.
- Week 7:
- Finalize a presentation about the work that has been done on the project.
- Finish conclusions on the results, and update the wiki accordingly. If it did not turn out to improve flow, explain why. Similarly, if it did improve flow, show how this was done.
- Week 8:
- Give the presentation for the tutors.
- Update the wiki with last information on the project.
Who does what
The general planning per person:
- Koen: Software model.
- Yanic: Database Analysis.
- Pietro: Research of the USE aspect.
- Leon: Theoretical Analysis of Algorithms.
- Joost: Data Analysis and Research of the Flow problem.
This planning will be updated weekly to include what everyone will have to do for the following week.
As of 11/2/2019, week 2:
- researching papers: Yanic, Pietro
- looking for databases: Koen
- searching for algorithms: Joost, Leon
Milestones
- Evaluation of both main topics completed
- Complete report on opportunities and threats of their co-operation.
- Interpret real life traffic data to feed the simulation
- Develop functioning algorithm for the problem.
- Having a simulation prototype making use of real life traffic data.
- Combining everything together to create a working simulation showing the positive effects of the algorithm on urban traffic.
Deliverables
- Research and literature study
- A flow control algorithm
- A model for simulating and testing our algorithm
- A functional simulation
- An analysis of the feasibility
- This wiki page on all our findings and processes
SotA
Previous Groups
| Subject and relevancy | Summary | Group |
|---|---|---|
| Vehicle intersection control
This could be interesting to see what final algorithm they have introduced to solve the problem. They only work on autonomous cars, even if a part of the algorithm is dedicated to traffic lights in order to have the best solution in an environment of both normal and autonomous cars. Moreover their project was mainly for research sake - no actual simulation. |
The idea is to design an algorithm that will use the benefits of autonomous cars on intersections with mixed traffic. | PRE2016 1 Groep2 |
| Traffic light solution
They have had kind of a similar idea to ours. They picked the ring of Eindhoven as a model and they used Netlogo as the software of simulation. They only focus on lights and green waves - no closing streets. |
One of the methods to improve traffic flow is through the use of green waving. Here cars can continuously get a serie of green lights when they drive at an appropriate speed. For this project it was decided to try to implement green waving in a ring system. This was modelled through the use of the program Netlogo, where eventually a ring of twelve crossings was achieved. | PRE2016 3 Groep11 |
| Pedestrian crossing
This can be interesting for a research point of view and the method the used, even if it involves only autonomous cars and pedestrians. They conducted interviews, questionnaires and asked to specialists to gather information. They looked also at experiments made from the big companies (Tesla and Volvo). |
The problems pedestrians face when crossing streets where autonomous vehicles drive and the other way around. Then we will look at numerous stakeholders and possible solutions. After that, questionnaires/interviews will be held with stakeholders to determine the needs of a system that offers a solution to the defined problem. After this, a design for our solution will be made and a prototype will show some of the working principles that need to be proven in order to give credibility to the final design. | PRE2017 3 Groep16 |
| Self-learning navigation software
This can be cool for the study of traffic jams that they made and the actual navigation system that could be something collateral to our project. |
Every day in the Netherlands people commute to work with their cars, and every day the same thing happens, traffic jams causing a lot of pollution and waiting time. Most of the time people are traveling a lot longer than necessary to reach their goal. This gave us the idea to create a system that will reroute this traffic through secondary roads to minimize the overall waiting time or maybe even prevent traffic jams. By doing a lot of user research we hope to create a user friendly system that will help the user and society with this problem. | PRE2016 3 Groep13 |
Traffic light SotA evaluation
The current industry standard on traffic light control varies a lot within areas, cities and countries. Most use a fixed, cyclic schedule which was determined by some software or a human engineer. Other, more sophisticated crossroads might employ a dynamic system which uses factors such as day of time, holidays and other trends to control the traffic light, but in essence it is still a system that repeats, at least partly. Current SotA research develops into two major directions:
- The development of traffic light control systems using sensors to determine traffic load on the relevant lanes. Based on the actuator data, the system would leave open busy lanes for a longer time to increase traffic flow and reduce congestion. [1] [2] [3]
- The development of prediction systems using big data and artificial intelligence which aim at predicting, with a high accuracy, the traffic behavior of the future. Using these predictions the traffic lights would then adjust its cycle to maximize traffic flow and reduce congestion. [4] [5] [6]
The first direction runs into a widespread issue of robotics, any type of sensor is vulnerable to noise and can occasionally provide false information. Distorted information would lead these systems to break and/or misbehave. Consequences could be at worst fatal. The second direction is more predictable and less error prone, but it remains to be seen whether traffic can truly be predicted with a high enough accuracy for the process of developing such an AI to be worth the resource investment necessary. Also any unforeseen change in traffic due to outside circumstances will render the prediction model useless.
There is one more type of approach which was found to be very interesting and potentially a great co-system for what we are developing. The idea is that each car, given a starting point and a destination, receives a virtual "budged" to perform its journey. Traffic lights all have spots in their lanes which incoming cars can "purchase" using previously mentioned virtual budged. A car can only enter the lane of a traffic light if it has purchased a spot for itself. Upon passing the traffic light, the spot can be sold again by the traffic light to another vehicle. The vehicles on-board software would constantly engage with the environment (traffic lights, toll gates etc.) in a virtual market place, trying to find the cheapest spots which allow for the quickest route. This system in particular is only believed to be implementable if self driving cars make up the majority of traffic, however the idea of being able to assign numerical values to routes based on demand is a valuable corner stone for our own algorithm, as it provides another numerical fix point which is determined by the system of traffic vehicles and not on a potentially falsified. [7]
State of the Art Traffic Congestion
Most researchers agree that the most effective way to fix congestion in cities is implementing tolled roads. These tolled roads should be priced based on marginal cost (including marginal social cost to account for externalities). Vehicles that carry high number of passengers such as buses should have a reduced price or be exempted from the charging system, as these vehicles should be encouraged. This is because, if more people use those type of vehicles, less vehicles overall are needed, and hence these vehicles help reducing congestion. An example of a country which already implements this system quite effectively is Singapore where automatic charging gates charge cars automatically the moment it drives onto a tolled road.
To fix traffic congestion however, good traffic congestion detection is needed. At the status quo this is done by tracking a set of cars (usually taxis) with GPS systems, and then checking the positions of those cars occasionally. Shared Nearest Neighbor Algorithm is often used to find congestion after those GPS systems are implemented. observation.
Other relevant State of the Art papers
Tettamanti et al. discuss a method of responding to real-time traffic using a signal split algorithm taking uncertainty into account. They try to minimize the queue length while doing so. [11]
Ge et al. look at how a traffic jam stabilizes and does both an analytical and simulation study. They derive that a three-car lookahead is enough for cooperative driving. [12]
Konishi et al. use a single-lane model and a lead car and following vehicles to observe traffic jam formation. When the speed of the lead car is varied, there are varying degrees of traffic jams. They derive a condition under which no traffic jam is formed. [13]
Davis adds reaction time (delay) to an already existing model to observe how driver delay impact the flow of traffic. In his modified model, traffic jams are caused primarily by driver reaction time. [14]
Koukoumidis et al. show how mobile phones can be used to reduce delays caused by traffic lights. Users receive the schedule of traffic lights ahead on their mobile phone and can adjust their speed so as to avoid coming to a complete halt. They evaluate SignalGuru, a service that collects and predicts the traffic signal schedule. [15]
Mellodge et al. discusses the details of a path following lateral controller implemented on a prototype car by using a kinematic model for a wheeled robot. The complete architecture of this is discussed and how it has been simulated. [16]
Ge proposes a new car-following model where the optimal speed is determined based on the velocity of the two cars in front of it. They also discuss the steady and error states and how they occur, including a state in which no traffic jam occurs. Moreover, a control scheme under which no traffic jam occurs is discussed. [17]
SUMO is an open source traffic simulation package including supporting tools. Krajzewicz et al. discusses the current state of the package as well as its major application and future developments. The current version is available as well. [1] [18] Traffic Control Test Bed is an open-source piece of software built on SUMO that allows traffic control systems to be evaluated and benchmarked against each other. [19]
MITSIM is another piece of software that was developed for modeling traffic networks, just like SUMO. It includes advanced traffic control, route guidance and surveillance systems. It simulates invididual vehicle movements. The current version is available as well. [2] [20]
Another open-source software developed for traffic networks is YatSim. This software focuses on testing consensus-based control strategies in urban road networks. By using a consensus-based control strategy, the traffic system requires agreement to guarantee several factors. [21]
A test bed for multi-agent control systems is presented by Van Katwijk et al. The test bed was created to aid research and two examples are discussed. [22]
Machine-to-machine communications can be used for road traffic management as well, as discussed by Foschini et al. Their design is built on top of existing production systems, unlike other proposals at the time. [23] A year later, another paper on this was published by Fernandes et al. They discuss mitigations for communication delays inherently present and simulations of intraplatoon information management strategies. They find that the effects of communication delays may be cancelled out by better communication. [24]
Van Arem et al. discuss the impact of cooperative adaptive cruise control on traffic flow. Cooperative adaptive cruise control is an extension of adaptive cruise control which also communicates with the predecessor by wireless communication. This allows a shorter following distance and a simulation executed by the authors show an improvement of the stability of the traffic flow and a slight increase in the traffic-flow efficiency. [25]
Papageorgiou et al. show how a reduced throughput can be achieved and a number of countering methods. They discuss these methods in three context: urban road networks, freeway networks and route guidance. [26]
Database analysis
Ever since we decided for our project and the simulation that comes with it, we were looking for traffic data sources which would allow us to supply our simulation with real life data. No member of our group had special connections to traffic data sources so our best chance was Google and the local municipality. The latter was not particularly helpful, so after some extensive google searches we found NDW. The NDW provides real-time, as well as historical traffic information. [3] [4] [5] The traffic data came in the DATEX II format, the European standard for traffic information. [6] After studying and understanding the essentials of the DATEX II scheme, it was possible to filter the data for the region around Eindhoven, the results were not what we expected. OpenStreetMap provides map data that we can use for visualization. [7] [8] [9] [10] Using this tool, a map of Eindhoven and all locations where traffic information is being collected was created.
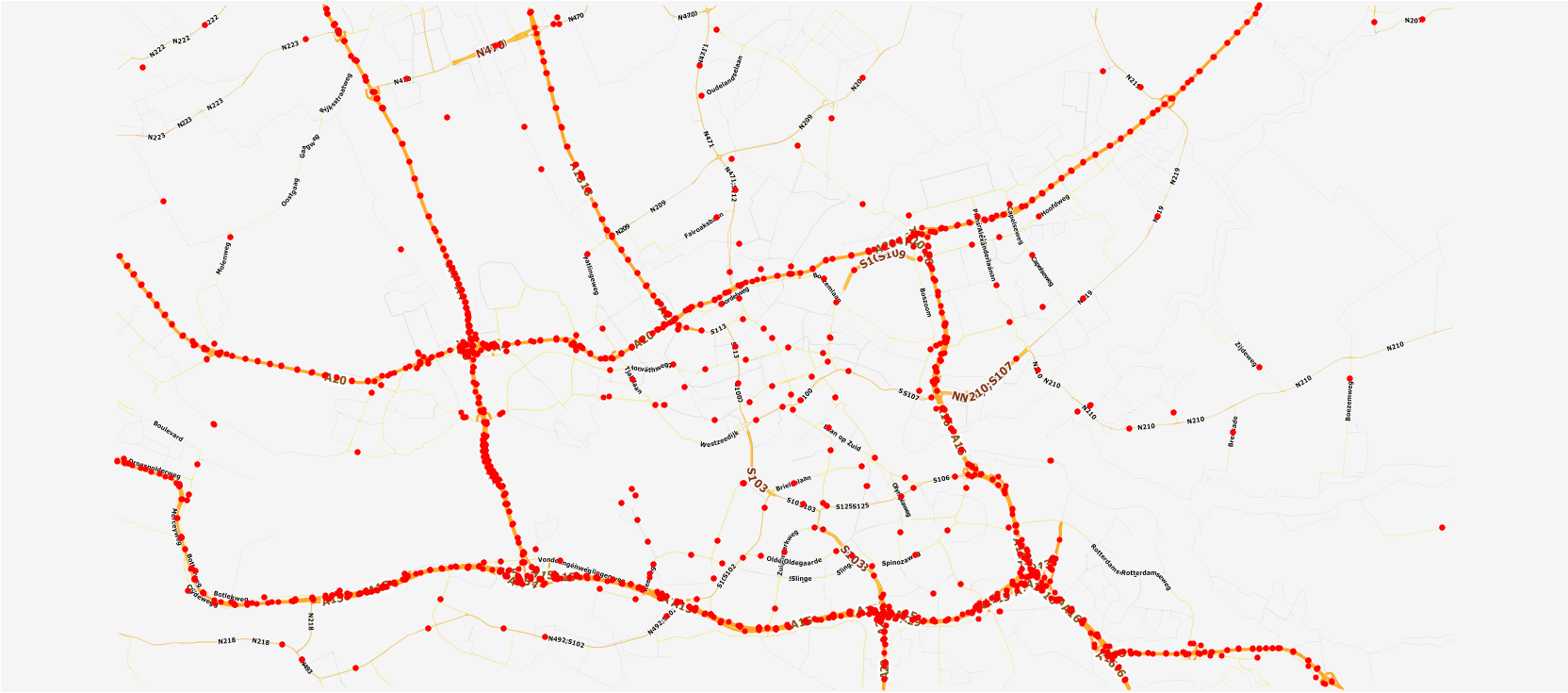
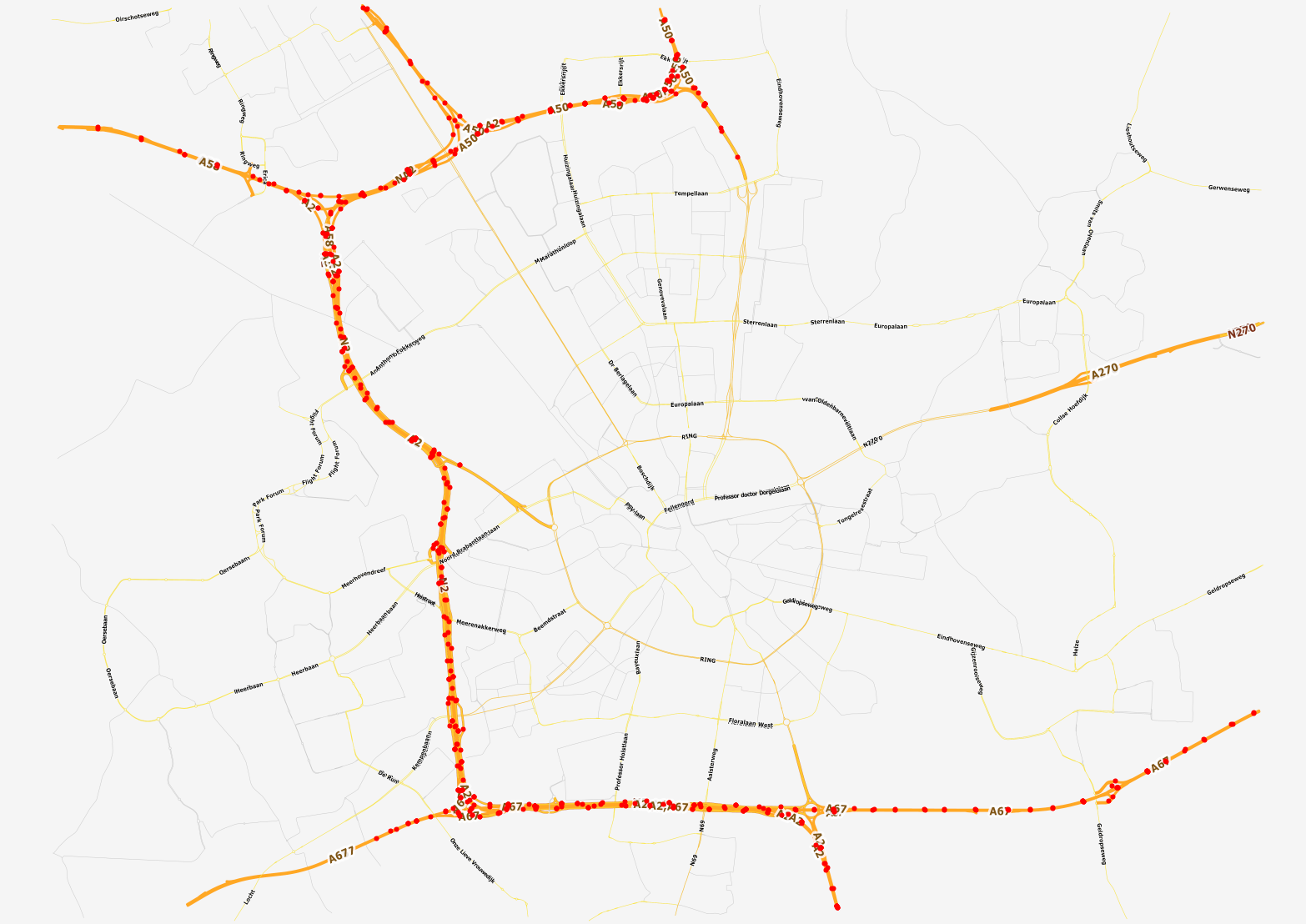
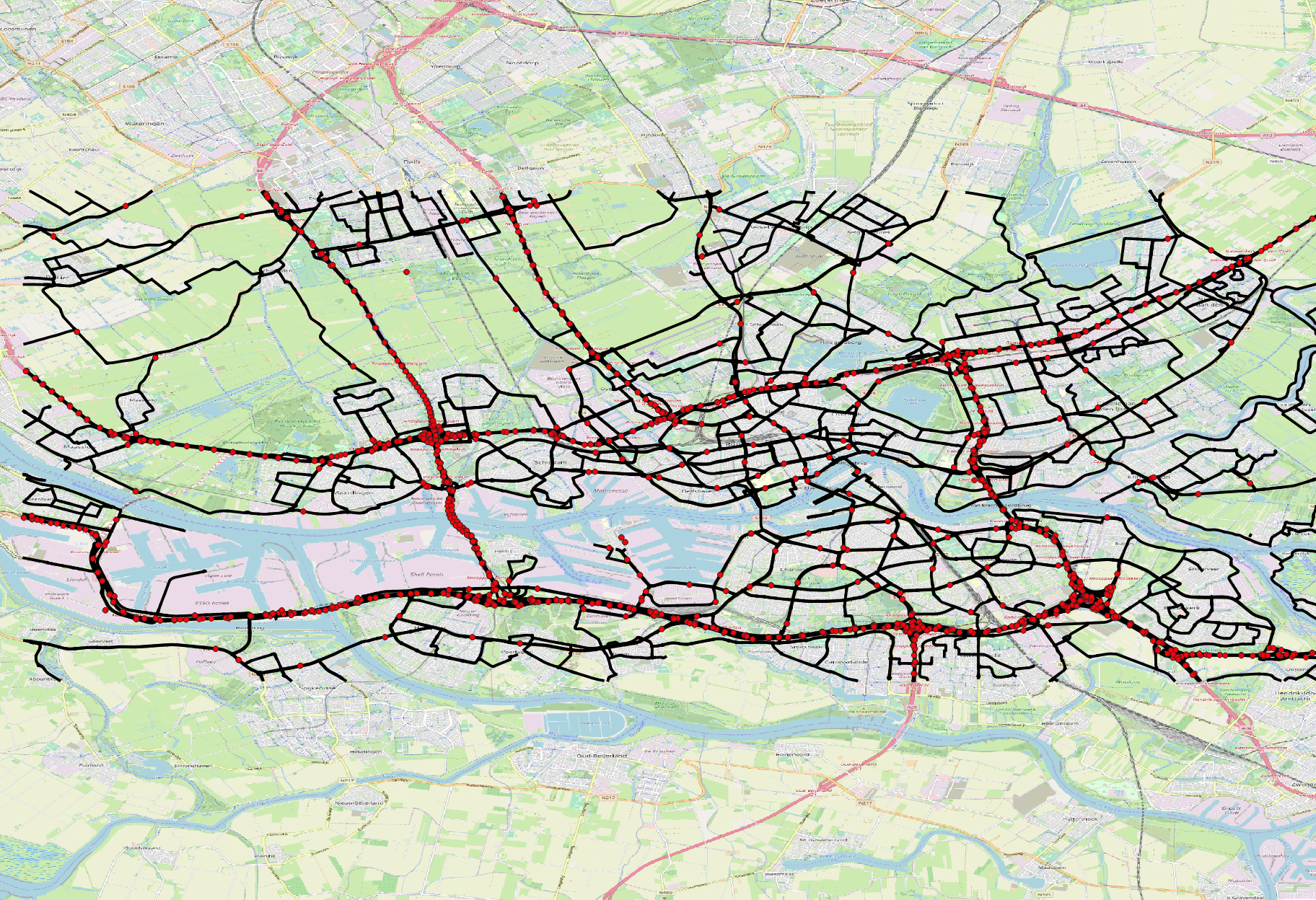

Maximum Flow Research
The problem we are looking at is considered an instance of the Maximum Flow Problem. This problem is defined as follows: “Find a feasible flow through a flow network with a single source s and a single sink t, such that the flow is maximum.” A flow network is defined as: “A directed graph where all edges have a capacity, and all edges receive a flow.”
The first known algorithm to solve this Maximum Flow Problem was created by Lester R. Ford Jr. and Delbert R. Fulkerson, and is called the Ford-Fulkerson algorithm.[1] Over the years there have been many improved solutions for the Maximum Flow Problem besides the Ford-Fulkerson algorithm. Some of the more notable ones are:
- Edmonds-Karp
- Dinic’s blocking flow algorithm
- push-relabel maximum flow algorithm
- Binary blocking flow algorithm
- Orlin's + KRT’s algorithm
All of the algorithms listed here will be explained below, and compared to each other to see which one fits best to our instance of the Maximum Flow Problem.
Ford-Fulkerson:
A greedy algorithm to compute the max flow in a flow network. The idea for Ford-Fulkerson is that, as long as there exists a path from source to sink, with capacities available on the edges in between, we can send flow along one of the paths. This is repeated until there exist no more available capacities. The paths that still have a capacity available are called augmenting paths. When no more augmenting paths can be found in the graph, the maximum flow can be found by adding the flow augmenting path and the flow already established in the graph together. There is no guarantee for this to happen though, therefore the only certain aspect is that it reaches a correct answer when the algorithm terminates. The runtime for this algorithm is O(E*max|f|), with E the number of edges in the graph and f the maximum flow in the graph.
Edmonds-Karp:
An implementation of the Ford-Fulkerson algorithm, which is largely the same as the other.[2] The only difference is that in Edmonds-Karp the search order for the augmenting path is defined. The way this augmenting path is chosen, is by choosing the shortest path with the available capacity. This path is found by applying a breadth-first search with a weight of 1 per edge. The runtime for this algorithm is O(V*E²).
Dinic’s (blocking flow) algorithm:
A variation on Edmonds-Karp, also applying the breadth-first search method, but instead of using it to find an augmenting path and sending the flow directly over it, we check if more flow is possible and construct a level graph out of it. We use BFS in a loop to construct this level graph. In a level graph we assign levels to all nodes, with the level being the shortest distance(read: smallest number of edges) of this node to the source. With this level graph, we can send multiple flows. This is the reason why Dinic’s algorithm performs better, as instead of only sending flow over one path, we send it over multiple at once. The runtime of this algorithm is O(V²*E).
A core concept of this is to make use of blocking flow, which means that an edge can not send more flow using the level graph, that is, there exist no more paths from s to t such that the vertices on the path have levels 0,1,2,... in this exact order. Blocking flow can be seen as maximum flow in greedy algorithms. One additional optimization that can be applied is the use of the dynamic trees data structure, which speeds up the computation of the maximum flow to O(V*E*log(V)) by making finding blocking flow in each iteration faster to be O(E*log(V)).
General push-relabel maximum flow algorithm:
This algorithm is similar to the Ford-Fulkerson algorithm, but changed up to improve the flow. Similar to the other algorithms, push-relabel also uses the residual graph to check additional possible flow in a network. It differs in the fact that it is checking the augmenting path for one vertex at a time only, instead of examining the entire residual network. As the name suggests, this algorithm computes maximum flows using two basic operations to perform its tasks.
If you consider the source to be the highest level, all following nodes will be a level below that, until you reach the bottom, the sink node. The “push” operation pushes the flow to the next vertex which needs to have a small height once the vertex that is currently being looked at has reached its capacity. If the flow gets trapped at some point in the graph, the vertex at which this happens will be “relabeled”, which means their height will be increased in the graph. The runtime of this algorithm is O(V²*E), but can be improved if certain conditions are met, or the algorithm is changed slightly. It can be O(V³) if the most recently active vertex is chosen to be looked at(using a FIFO selection rule), or O(V*E*log(V²/E)) if the algorithm builds limited size trees to calculate the height.
Binary blocking flow algorithm:
The algorithm uses an augmenting path and blocking flows, similar to Dinic’s algorithm, but it is applied differently. Goldberg believes this creates a fundamental improvement to calculate the maximum flow of a graph.[3] However, from practical experience, we can derive that the push-relabel method is in fact more practical than using blocking flows.
Whereas Dinic's algorithm uses only the concept of blocking flows, Goldberg's algorithm extends this concept to more general length functions, as that is what blocking flow is based on. The length function that is used in Goldberg's algorithm is more specifically a binary length function, which assigns arcs(edges) to be zero length if their capacity is large, and gives the arc unit length(which is defined to be 1) to small capacity arcs. This makes the binary length function adaptive, which is a crucial feature to improve the time bounds.
The runtime of this algorithm is O(E*min(V^(2/3), sqrt(E))*log(V²/E)*log(U)). The U here is the maximum capacity of the network. Other than that it’s fairly similar to the push-relabel algorithm with dynamic trees. They take the minimum of V^(2/3) and sqrt(E) because it is a proven runtime from Dinic's algorithm as long as there are unit arcs. You apply that on all edges, hence the *E part. The multiplication by log(V²/E)*log(U) is to find the blocking flows in the network, as can be found in the paper of Goldberg[3].
Orlin’s + KRT’s algorithm.
In a paper made by Orlin[4] ways are described to improve and solve the max-flow problem in O(V*E), as long as the requirement is met, being E <= O(V^(16/15-e)). Similarly through the combined effort of King, Rao and Tarjan, KRT’s algorithm solves the max-flow problem in O(V*E) if E > O(V^(1+e))[5]. Both of these runtimes have a value e in it, which denotes a positive constant integer value.
Orlin's algorithm solves the max flow problem in improvement phases. They then create an abundance graph, and use contraction to speed up the algorithm. This abundance graph is then used along with some of the arcs to contract it into a smaller max flow problem. This smaller max flow problem is then compacted by removing all nodes in the network that have either all incident arcs being abundant, or a very small capacity. Using all of this together, we can run the algorithm in an improvement phase for the max flow problem on this compact network to reduce the runtime to O(V*E+E^(31/16)*log²(V)), which, when using the special bound on the edges, can be reduced to O(V*E). There is a bottleneck in the algorithm, which is the time it takes to maintain the transative closure of the abundance graph, as can be found in Orlin's paper[4].
KRT’s algorithm is based on the randomized algorithm created by Cheriyan and Hagerup[6], which computes the maximum flow in a a graph to efficiently play a certain combinatorial game that arises during computation of the maximum flow. The algorithm of KRT is similar, but uses a more general version of the game described by Cheriyan and Hagerup. The strategy of KRT yields a deterministic algorithm for computing the maximum flow that runs in O(E*V*(log_((E/V)log(n))(n))). This can then be reduced to O(V*E) if the constraint is met that states that E > O(V^(1+e)).
Combining the knowledge of both improvements can allow for maximum flow problems to be solvable in O(V*E) time, if the conditions are met in terms of its edges. Whether it is useful for our problem will be discussed in the next section.
Which algorithm should we choose:
We will choose which algorithm to use based on their runtimes and method of implementation. Basing our software model on an algorithm with a faster runtime, will result in the model being easier to use for larger datasets in comparison to other algorithms with a higher runtime, which is what we are making use of in our instance of the maximum flow problem. If two or more algorithms have the same runtime, ease of implementation will be deemed more important, as it is less time consuming to fix errors or bugs in a simple software model when compared to an elaborate or complex one.
Based on the runtimes of the algorithms, the best one to pick would be Orlin’s + KRT’s algorithm, as O(V*E) is by far the best. However, it has some requirements that are not easily satisfiable by us in our project. The algorithm itself is mostly theoretical, which means it has not been implemented in software at all. Hence this algorithm is more difficult to implement and will probably not be chosen. Another reason for not choosing it, would be because it has strict requirements on the number of edges, which does not always happen in our instance of the Maximum Flow Problem. The more basic methods of Ford-Fulkerson and Edmonds-Karp are the general cases of how to implement maximum flow problems, but they are still on the slower side. Dinic’s and Goldberg’s blocking flow algorithms are already a lot faster, as the runtime is O(V*E*log(V)) instead of O(V²*E). As the number of vertices is always lower than the number of edges in a flow network, having the runtime depend more on the number of vertices than on the number of edges will make for a significant improvement, hence why Dinic’s algorithm would be prefered over Edmonds-Karp. Goldberg's binary blocking flow seems even better, but it has a major downside, namely that it is only having such a good runtime if all edges have a unit capacity of 1. As this is not the case in any real world scenario, this makes the algorithm unusable in our instance of the Maximum Flow Problem. The last algorithm, the general push-relabel algorithm, also has the same runtime as Dinic’s algorithm, can be sped up even more if the right data structure is being applied.
Therefore, the choice of what algorithm to pick, should be based on the implementation of either of them. If it is a feasible choice to utilize these data structures in our software model, then using the push-relabel algorithm should be the right way to go. If, however, it turns out to be difficult to implement, then it might be better to choose for Dinic’s algorithm, as it is a more simple model to implement than the push-relabel algorithm, while also having the same runtime.
- [1]https://www.cambridge.org/core/journals/canadian-journal-of-mathematics/article/maximal-flow-through-a-network/5D6E55D3B06C4F7B1043BC1D82D40764
- [2]https://dl.acm.org/citation.cfm?doid=321694.321699
- [3]http://cse.iitkgp.ac.in/~palash/2018AlgoDesignAnalysis/1998JACMGoldbergRao.pdf
- [4]https://dspace.mit.edu/openaccess-disseminate/1721.1/88020
- [5]https://ac.els-cdn.com/S0196677484710443/1-s2.0-S0196677484710443-main.pdf?_tid=de8d99a7-af58-49c7-ba1b-a1fd46923a4d&acdnat=1550486537_68a656a95b07f29badfbdba55857cdd2
- [6]https://www.researchgate.net/publication/3501919_A_randomized_maximum-flow_algorithm
Questions to town hall
In order to collect data directly from a source, we have chosen to ask some questions to someone in charge of traffic at the Eindhoevn town hall. After having being denied an appointment we decided to write an email. A first mail has been sent to the general information address, but no response has been received so far. The mail contained the following text:
"To whom it may concern,
We are a group of students involved in a project at TU/e. The project involves the analysis of traffic jams and flows. We would like to ask some questions about it to someone that is in charge of this field of operation. Would it be possible to have an email address or a phone number?
Thank you in advance, we hope to hear from you soon. Kind regards".
Following this email there would have been the list of desired questions with the description of the project. The questions are:
- What is the current method used by the town hall to handle traffic congestion? Is there an adaptive system or is it rule-based?
- Are you satisfied with the current management of traffic?
- In case of an accident how do you deal with the traffic? How about road construction?
- Do you apply any traffic limitation based on the level of pollution of an area?
- Is there a dedicated team to the traffic control? How does it work?
- Would you be open to use a computerized system to improve the traffic situation?
- To what level would apply the solutions provided by the software?
- With the advancement of technology also cars and traffic are evolving, what kind of plans do you have for the future?
If there will not be any kind of answer from the Eindhoven town hall, we will proceed with the forwarding of these mails to other town halls in the Netherlands.
References
- ↑ Ghazal, B., Elkhatib, K., Chahine, K., & Kherfan, M. (2016). Smart traffic light control system. In 2016 3rd International Conference on Electrical, Electronics, Computer Engineering and their Applications, EECEA 2016. https://doi.org/10.1109/EECEA.2016.7470780
- ↑ Salama, A. S., Saleh, B. K., & Eassa, M. M. (2010). Intelligent cross road traffic management system (ICRTMS). In ICCTD 2010 - 2010 2nd International Conference on Computer Technology and Development, Proceedings. https://doi.org/10.1109/ICCTD.2010.5646059
- ↑ Sundar, R., Hebbar, S., & Golla, V. (2015). Implementing intelligent traffic control system for congestion control, ambulance clearance, and stolen vehicle detection. IEEE Sensors Journal. https://doi.org/10.1109/JSEN.2014.2360288
- ↑ Le, T., Kovács, P., Walton, N., Vu, H. L., Andrew, L. L. H., & Hoogendoorn, S. S. P. (2015). Decentralized signal control for urban road networks. Transportation Research Part C: Emerging Technologies. https://doi.org/10.1016/j.trc.2014.11.009
- ↑ Lv, Y., Duan, Y., Kang, W., Li, Z., & Wang, F. Y. (2015). Traffic Flow Prediction with Big Data: A Deep Learning Approach. IEEE Transactions on Intelligent Transportation Systems. https://doi.org/10.1109/TITS.2014.2345663
- ↑ Lämmer, S., & Helbing, D. (2008). Self-control of traffic lights and vehicle flows in urban road networks. Journal of Statistical Mechanics: Theory and Experiment. https://doi.org/10.1088/1742-5468/2008/04/P04019
- ↑ Vasirani, M., & Sascha, O. (2009). A market-inspired approach to reservation-based urban road traffic management. In Proceedings of 8th International Conference on Autonomous Agents and Multiagent Systems. https://doi.org/10.1145/1558013.1558099
- ↑ Jain, S., Jain, S. S., & Jain, G. (2017). Traffic Congestion Modelling Based on Origin and Destination. In Procedia Engineering. https://doi.org/10.1016/j.proeng.2017.04.398
- ↑ He, F., Yan, X., Liu, Y., & Ma, L. (2016). A Traffic Congestion Assessment Method for Urban Road Networks Based on Speed Performance Index. In Procedia Engineering. https://doi.org/10.1016/j.proeng.2016.01.277
- ↑ Ye, S. (2012). Research on Urban Road Traffic Congestion Charging Based on Sustainable Development. Physics Procedia. https://doi.org/10.1016/j.phpro.2012.02.231
- ↑ Tettamanti, T., Luspay, T., Kulcsar, B., Peni, T., & Varga, I. (2014). Robust control for urban road traffic networks. IEEE Transactions on Intelligent Transportation Systems, 15(1), 385–398. https://doi.org/10.1109/TITS.2013.2281666
- ↑ Tettamanti, T., Luspay, T., Kulcsar, B., Peni, T., & Varga, I. (2014). Robust control for urban road traffic networks. IEEE Transactions on Intelligent Transportation Systems, 15(1), 385–398. https://doi.org/10.1109/TITS.2013.2281666
- ↑ Konishi, K., Kokame, H., & Hirata, K. (1999). Coupled map car-following model and its delayed-feedback control. Physical Review. E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics. https://doi.org/10.1103/PhysRevE.60.4000
- ↑ Davis, L. C. (2003). Modifications of the optimal velocity traffic model to include delay due to driver reaction time. Physica A: Statistical Mechanics and Its Applications. https://doi.org/10.1016/S0378-4371(02)01457-7
- ↑ Koukoumidis, E., & Martonosi, M. (2011). SignalGuru : Leveraging Mobile Phones for Collaborative Traffic Signal Schedule Advisory. In ACM MobiSys. https://doi.org/10.1145/1999995.2000008
- ↑ Mellodge, P., Abbott, A. L., & Vanlandingham, H. (2002). Feedback Control for a Path Following Robotic Car. Control.
- ↑ Ge, H. X. (2011). Modified coupled map car-following model and its delayed feedback control scheme. Chinese Physics B. https://doi.org/10.1088/1674-1056/20/9/090502
- ↑ Krajzewicz, D., Erdmann, J., Behrisch, M., & Bieker, L. (2012). SUMO - Recent Development and Applications of {SUMO - Simulation of Urban MObility}. International Journal On Advances in Systems and Measurements. https://doi.org/10.1080/08913810902952903
- ↑ Gao, B. and Anvari, B. and Tsotskas, C. and Franco, P. and Box, S. (2018), Developing an open source platform for the evaluation of intelligent traffic control algorithms, Proceedings of the 7th Transport Research Arena https://github.com/intelaligent/tctb
- ↑ Yang, Q., & Koutsopoulos, H. N. (1996). A microscopic traffic simulator for evaluation of dynamic traffic management systems. Transportation Research Part C: Emerging Technologies. https://doi.org/10.1016/S0968-090X(96)00006-X
- ↑ Dethof, A.M., Molinari, F. (2018). YatSim: an Open-Source Simulator For Testing Consensus-based Control Strategies in Urban Traffic Networks https://arxiv.org/abs/1810.11380
- ↑ van Katwijk, R. T., van Koningsbruggen, P., De Schutter, B., & Hellendoorn, J. (2005). A Test Bed for Multi-Agent Control Systems in Road Traffic Management. In Applications of Agent Technology in Traffic and Transportation. https://doi.org/10.3141/1910-13
- ↑ Foschini, L., Taleb, T., Corradi, A., & Bottazzi, D. (2011). M2M-based metropolitan platform for IMS-enabled road traffic management in IoT. IEEE Communications Magazine. https://doi.org/10.1109/MCOM.2011.6069709
- ↑ Fernandes, P., & Nunes, U. (2012). Platooning with IVC-enabled autonomous vehicles: Strategies to mitigate communication delays, improve safety and traffic flow. IEEE Transactions on Intelligent Transportation Systems. https://doi.org/10.1109/TITS.2011.2179936
- ↑ Van Arem, B., Van Driel, C. J. G., & Visser, R. (2006). The impact of cooperative adaptive cruise control on traffic-flow characteristics. IEEE Transactions on Intelligent Transportation Systems. https://doi.org/10.1109/TITS.2006.884615
- ↑ Papageorgiou, M., Diakaki, C., Dinopoulou, V., Kotsialos, A., & Wang, Y. (2003). Review of road traffic control strategies. In Proceedings of the IEEE. https://doi.org/10.1109/JPROC.2003.819610