Embedded Motion Control 2017 Group 10

Group Members

0773865	Tim Coerver
0953808	Pieter de Groot
0970955	Jos Terlouw
0973811	Bas Vermij
0972391	Roel Vromans
0975718	Corné van Haren

Initial Design

Link to the PDF version of the design document: PDF

Requirements

• Software easy to setup
  • Updated with one easy command, e.g. 'git pull'.
  • Software can be compiled using 'cmake' and 'make'.
  • One executable to start software.

• Autonomously solving the corridor challenge
  • Solving the corridor challenge has to be done within 5 minutes.

• Autonomously solving the maze challenge
  • Solving the maze challenge has to be done within 7 minutes.

• Avoiding collision
  • Do not bump into walls or doors.

• Recognize and open a door in the maze
  • There might be multiple dead ends in the maze, one of which is a door. The robot has to be autonomously open the door (by ringing a bell) to solve the maze.

• Detect corridors, corners, T-junctions and intersections
  • The maze and corridor challenge consists of several, corridors, corners, T-junctions and intersections. Various algorithms created in order to detect these.

• Navigate through corridors, corners, T-junctions and intersections
  • When corridors, corners, T-junctions and intersections are detected, the robot has to drive trough these. In order to do this, strategies have to be created for each of these.

• Detecting dead ends
  • The maze can contain dead ends, these have to be distinguished from doors.

• Detecting maze exit
  • The exit of the maze has to be detected in order to know when the maze is finished.

• Navigate open spaces
  • The maze can contain open spaced, when these are detected these has to be explored by navigating trough them.

Specifications

The specifications are related to the requirements specified above.

• The time to reach the end of the maze is 7 minutes.
• The time to accomplish the corridor challenge is 5 minutes
• The robot may not be idle for more than 30 seconds.
• When the robot find a door, it rings a bell and the door will be opened manually.
• Two attempts to solve the maze are allowed. Both attempts have to be finished within 7 minutes total.
• Two attempts are allowed to solve the corridor challenge. Both attempts have to be finished within 5 minutes.
• When the robot bumps into a wall the attempt is over.

Specifications of the maze

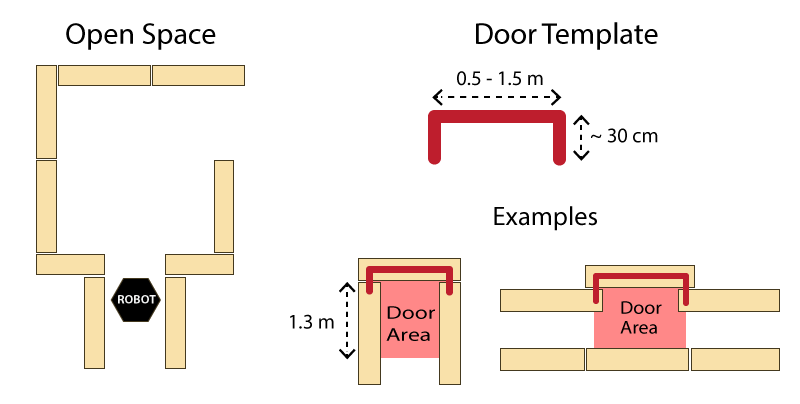
• All walls are positioned approximately perpendicular to one another.
• Open spaces might occur (as depicted in Figure 1 ).
• There may be loops in the maze, which means that some walls may not be connected to other walls.
• Walls are approximately parallel.

Doors and open spaces are specified as described by Figure 1.

Figure 1: Maze open spaces and door specifications

Functions

The functions are categorized in three different levels of complexity: Low, Mid and High level. An overview of the functions is given in Figure 2.

Figure 2: Function overview. The functions are grouped based on complexity as well as input/output type.

Components

The following components are accessible on the pico:

• Sensors
  • Laser Range Finder (LFR)
  • Wheel encoders (odometry)

• Actuators
  • Holonomic Base (Omni-wheels)

• Computer
  • CPU Intel i7
  • OS Ubuntu 14.04

Interface

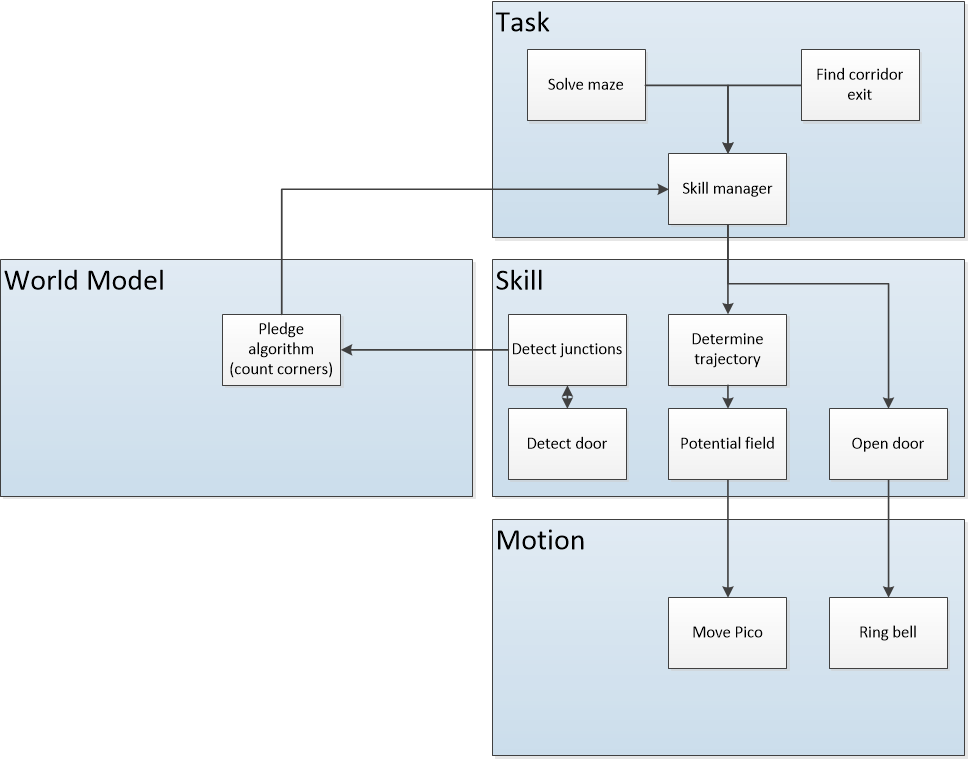
The interfaces between functions are shown in Figure 3. Here the functions are devided into: Tasks, Skills, Motion and World Model. The world model contains the functions that are used to keep track of Pico's surrounding. Tasks contains the functions on the highest level where the robot decides what it is going to do, like solve the maze. The skill block consists of all functions that make the robot perform lower level tasks such that the high level objective can be achieved. The motion block does the low level operations that make the skill functions work.

Figure 3: Interface overview of all functions needed by Pico to solve the maze and corridor challenge.

The Corridor Challenge

Corner mapping

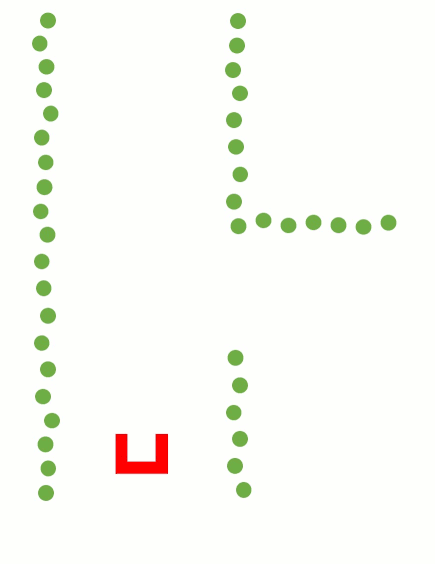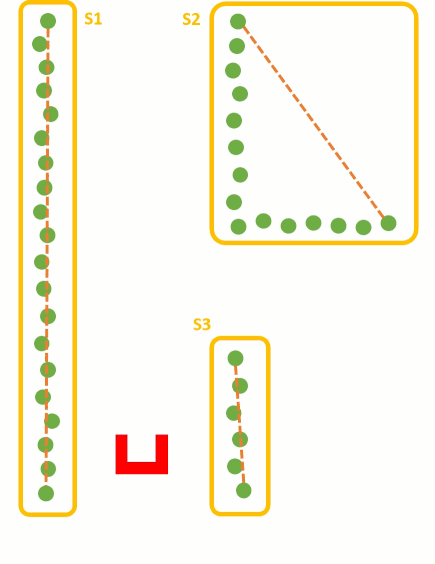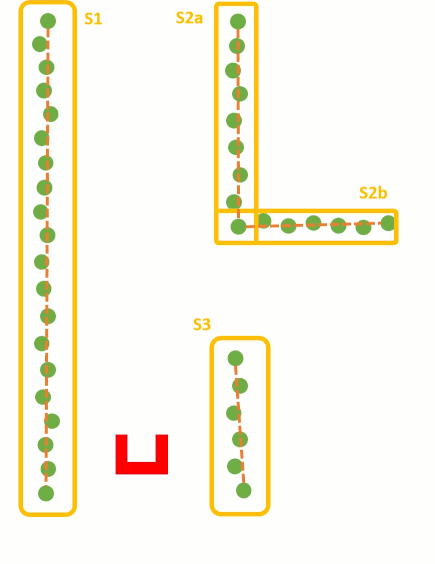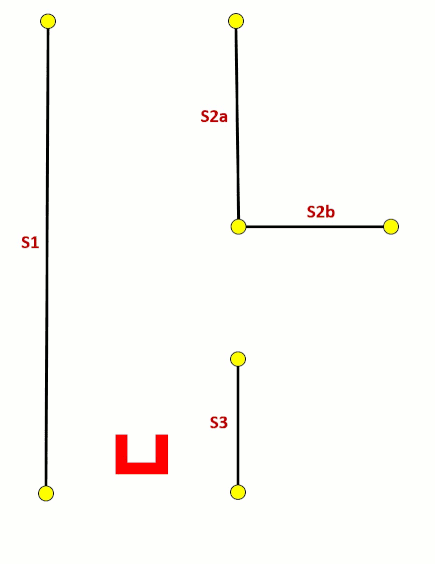
To detect corners and walls the Split and merge algorithm is used on the laser data. This algorithm contains the following procedure;

• 1. Laser data is transformed in x and y coordinates
• 2. The laser data points will split in segments
• 3. Within each segment the points between the first and last point will be check for the distance perpendicular to the line between the first and last point
• 4. If the maximum perpendicular point is above a set threshold (0.2 m), this point will set as a vertex within this segment.
• 5. Step 3 and 4 will be repeated until there are no new vertices are found.
• 6. Within each segment a line will be defined using the least squire method.
• 7. If two lines are connected with each other, the intersection will be used to define the vertex.
• 8. If there is not a connection with another line, the end point will be fitted on the line.

These steps are visualized in the figure below:

Dead end detection

The dead end detection method makes use of the Corner mapping method as described above.

The corner mapping returns the vertices's of the line segments it has found, and if the vertices's are connected to each other. This information is used by the corner detection to form vectors between these vertices's.

These vectors are then normalized so they can be used to determine the angle between them. If two vectors are connected, the angle is calculated using the following function

[math]\displaystyle{ \theta = \acos(v_i \dot v_{i+1}) }[/math]

Where [math]\displaystyle{ \theta }[/math] is the angle between the vectors and [math]\displaystyle{ v_i \dot v_{i+1} }[/math] is the inner product of vector i with i+1. If this angle is [math]\displaystyle{ 90\pm5 }[/math], the corner is marked perpendicular. The calculated angle does not give information on the sign. A vector pointing to the left or right result in the same angle (as the inner product between almost perpendicular vectors is approximately 0). In order to determine the direction of the turn, the vector [math]\displaystyle{ v_i }[/math] is rotated 90 degrees to the left. The inner product is then calculated again, if the result is positive, then the turn is to the left. If rotating the vector to the right results in a positive inner product, then the turn is to the right. All vectors are checked in this fashion, resulting in a list of left-, right- or no-turns.

Using the list of turns, possible dead ends can be identified. An important aspect of the list of vertices's is that it is generated in an anti clockwise direction. Therefore it is known that when two left turns follow after each other indicate a dead end candidate. Since the walls of the dead end candidate can be long, and therefore can just be a wall in the maze, further identification is done. The specifications of a dead end are given in the specifications above. There it is noted that the width of the dead end has to be within [math]\displaystyle{ 0.5 \lt width \lt 1.5 }[/math] [m]. So when a possible dead end is found, the width of that dead end candidate is checked. If it fails, the dead end is dropped. If it passes the minimum depth of 0.3 [m] is checked. If that also passes the dead end will be marked.

As all turns in the turn vector have been evaluated, the dead end closest to pico is returned from the dead end detection method for furher use in the state machine.

Matrix multiplication, matrix norms and inner products where used in this function to make the implementation easier. Here fore the Eigen library was used, this made working with matrices a lot more convenient (almost matlab like).

Challenge Result

Pico managed to finish the corridor challenge in 24 seconds, this got us the third place. As can be seen in die video on the straight the Pico wobbles a lot this is due to the over reactive implementation of the potential field. Without this wobbling we would possible end up in the first place.

Corridor challenge result showing a drunk pico making a perfect corner.

The Maze Challenge

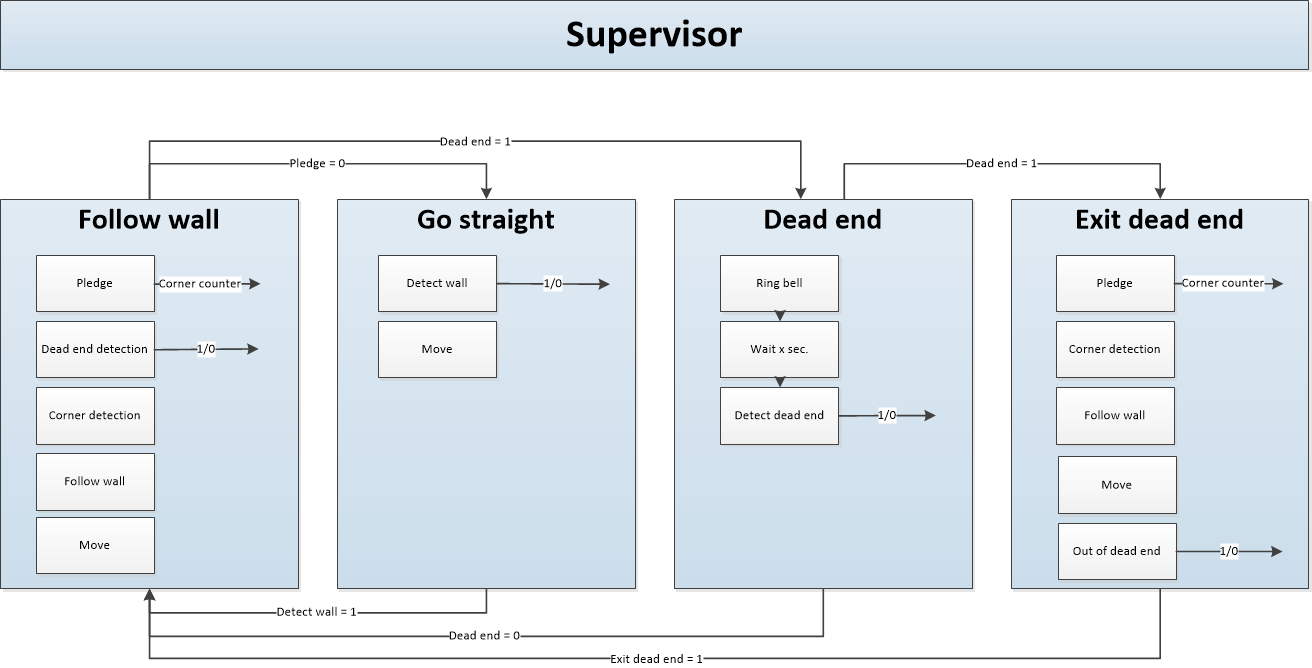
Final design

For the final desig the following stage machine is designed

Figure 4: State machine

Pledge

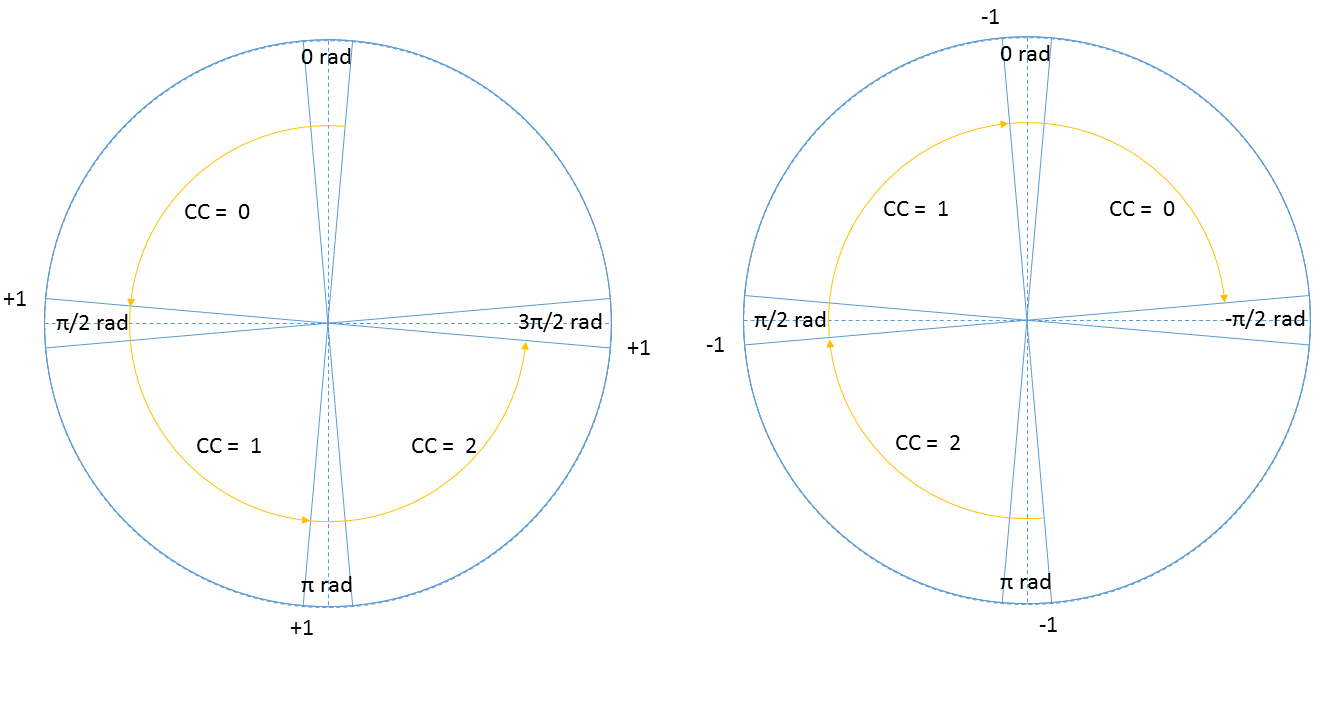
The Pledge algorithm is used to make a very simplistic global world map to solve the maze. The pledge algorithm uses relative angle movements to calculate the total rotation angle of the robot. Rotation clockwise has negative angle and rotation clockwise has positive angle. After the robot rotates pi rad, the OdometryData switches to a negative angle of -pi rad. The relative angle is in that case 2 pi rad. To compensate, 2 pi is subtracted leaving with only the relative angle. With this rotated angle, the taken corners can be calculated.

To make the pledge algorithm robust, a method is used where a corner is counted after the robot moved pi/2-delta rad and will hold this count till the robot moved another pi/2-delta rad as shown in Figure 5 (left circle). In between the robot can move freely without corners being added. The same holds for the robot rotating back where the corner counter is reduced only after the robot moved -pi/2+delta rad Figure 5 (right circle).

Figure 5: Pledge counter

Weekly Planning

- Final challenge