Viotar

	Viotar project groep William Schattevoet David Duwaer Eric Backx Arjan de Visser
	Welkom op de pagina van de Viotar project groep, op deze pagina zullen we de voortgang van ons minorproject bij gaan houden. Waar de meeste minorprojecten vooraf vastgestelde opdrachten zijn is het Viotar project bedacht door een deel van de groep. Het project is voortgekomen uit het persoonlijk onbehagen dat de klassieke viool tijdens het spelen opwekte en het doel is daardoor het maken van een nieuw soort instrument wat wel de voordelen maar niet de nadelen van dit instrument heeft. Deze pagina zal vrijwel dagelijks bijgewerkt worden met de nieuwe bevindingen en resultaten. Motivatie De afgelopen eeuw zijn elektrische instrumenten immens populair geworden, de elektrische gitaar is hier een goed voorbeeld van. Elektrische strijkinstrumenten zijn echter nooit echt aangeslagen. Dat roept de vragen op waarom dit zo is. Er zijn verschillende gebreken aan deze electrische strijkinstrumenten aan te wijzen die de achterblijvende populariteit kunnen verklaren. De bestaande elektrische strijkinstrumenten zijn trouw gemodelleerd naar de traditionele akoestische familie van strijkinstrumenten, waarvan de bekendste instrumenten de viool, de altviool, cello en contrabas zijn. Deze traditionele instrumenten hebben echter verschillende nadelen die de nieuwe electrische modelen dus ook hebben: Heel moeilijk te bespelen (slechte combinatie van strijkdruk en snelheid resulteert in een lelijk “krassend” geluid) Beperkt bereik, om het volledige spectrum te dekken van toonhoogte moeten meerdere instrumenten gebruikt worden (i.e. viool hoog, cello laag en contras daaronder) Akkoorden zijn onmogelijk om te spelen, hooguit snaren tegelijk. Onprettige ergonomie Dit motiveert het maken van een elektrisch strijkinstrument dat geen van deze gebreken ondervind. Onder andere betekent dit dat er dus akkoorden op gespeeld moeten kunnen worden. Met andere woorden, er moeten meer dan 2 snaren tegelijk bespeeld kunnen worden. Deze eis kan worden uitgebreid zodat íedere combinatie van snaren tegelijk gespeeld moet kunnen worden, zoals dit bij de elektrische gitaar het geval is. Dit sluit het gebruik van een strijkstok zoals bij de traditionele strijkinstrumenten uit. Hierdoor kan de oorspronkelijke ergonomie van deze strijkinstrumenten worden losgelaten, en kan men een betere ergonomie ontwerpen. Ook moet het nieuwe instrument makkelijk bespeeld kunnen worden. Wat strijkinstrumenten moeilijk maakt is het feit ze “goed” moeten worden bestreken (de goede combinatie van druk en snelheid) om überhaupt een goede toon te krijgen. Het nieuwe instrument moet deze verantwoordelijkheid in feite overnemen, dus het instrument moet “zelf” verzorgen dat er altijd sprake is van de goede combinatie van strijksnelheid en druk. Deze eis in combinatie met het feit dat alle snarencombinaties tegelijk gespeeld moeten kunnen worden, doet denken aan een soort mechaniek dat het bestrijken van de snaren gaat verzorgen. Dit laatste in combinatie met de eis dat het ergonomisch moet zijn en een groot bereik moet hebben, maakt een elektrische gitaar een goed model om vanuit te gaan. Het doel is om een elektrische gitaar om te bouwen tot een instrument met bovengenoemde eigenschappen. Programma van eisen Vanuit de zojuist genoemde eigenschappen waar de viotar aan zou moeten voldoen zijn de volgende (kwalitatieve) eisen geformuleerd: Het geluid bestaat uit een door de snaren gegenereerd en elektronisch verwerkt signaal. De snaren kunnen in alle combinaties simultaan bespeeld worden. Op ieder tijdstip in een gespeelde noot is de amplitude van de noot varieerbaar van het minimaal tot het maximaal mogelijke op de snaar. De onder- en bovengrens worden opgelegd door de mogelijkheid om bij een bepaalde lage of hoge strijksnelheid en/of druk nog Helmholtz-trilling te kunnen genereren. Het mechaniek en de user-interface laten het toe dat er 18 verschillende noten per seconde op één snaar worden gespeeld. Het mechaniek en de user-interface laten het toe dat er 18 verschillende noten per seconde op verschillende snaren achter elkaar worden gespeeld. De snaar maakt bij aanstrijking een Helmholtz trilling, ongeacht het niveau van de speler. Het instrument moet net als bij strijkinstrumenten vrij “tokkelbaar” zijn: Als de gebruiker niet aan het strijken is, moet de ruimte boven de snaren volledig vrij zijn, en onder de snaren moet tussen de 5 en de 15cm van de brug, 5mm onder de snaren vrij zijn. Het bereik moet vanuit het gebied van de bas tot in de sopraan reiken: De laagste noot lager zijn dan E4, en de hoogste noot moet hoger zijn dan A5. Stappenplan Voor de aanpak van dit probleem is een stappenplan gemaakt, aan de hand van dit stappenplan is ook de planning gemaakt die later op de site zal komen. Concept Wat we willen Waarom (motivatie) Definitie Ontwerpeisen Ontwerp Literatuurstudie Model Regelaar + mechanieken Experimenteren met regelaar met verschillende mechanieken -> mechaniek kiezen Ergonomie Experimenteren met verschillende ergonomische alternatieven Definitief ontwerp Voorbereiding Inkopen voor prototype Productie Prototype Evaluatie Planning De tijdsplanning van het Viotar project. 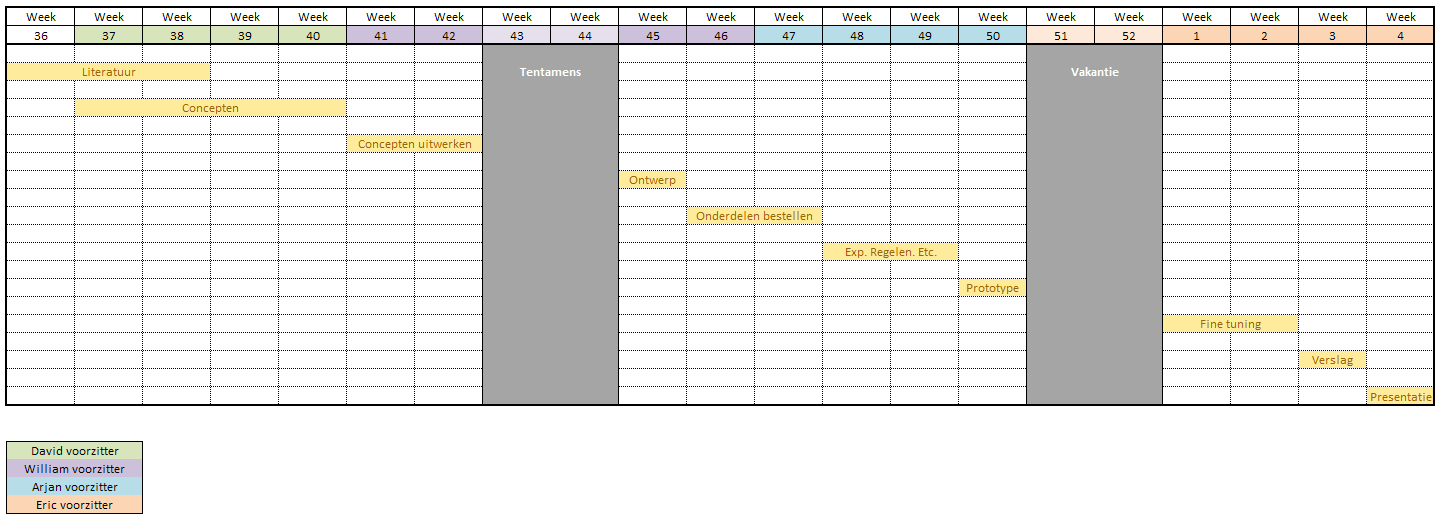Taakverdeling Tijdens de komende weken van het project zal er vooral in 2 verschillende groepen gewerkt gaan worden. De ene groep, bestaande uit David en Eric, zal zich vooral bezig houden met het maken van een matlab model. De andere groep, bestaande uit William en Arjan, zal zich vooral bezig gaan houden met de testopstelling. Arjan zal zich ook bezig gaan houden met het bijhouden van deze wiki om onze voortgang voor iedereen inzichtelijk te houden. Werking van de viool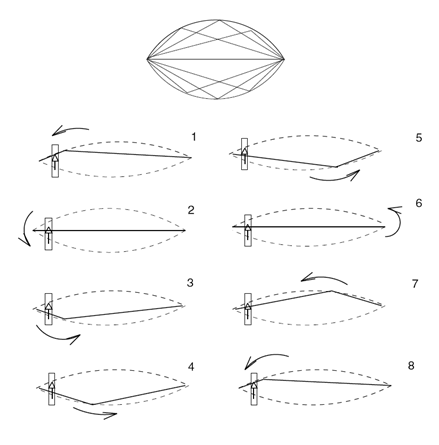 Figuur 1: Het doorlopen van een complete Helmholtz trilling. Om een electrisch strijkinstrument te kunnen maken is het allereerst belangrijk om te weten hoe een strijkinstrument zijn geluid produceerd. Daarom zal dit hier kort uigelegd worden. 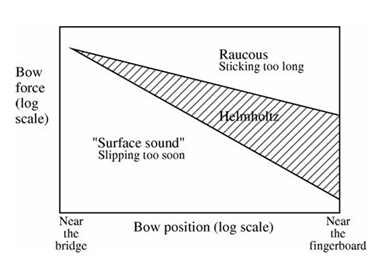Anders dan bij het tokkelen op een gitaar, levert het strijken op een viool geen staande golf op. De trilling die bij het strijken van een viool wordt opgewekt is, in tegenstelling tot de trilling op een gitaar, ook niet lineair. Er ontstaat bij juist aanstrijken van een snaar een zogenaamde Helmholtz trilling. Bij deze trilling beweegt de snaar in een “V”-patroon, ook wel Helmholtz hoek genoemd.. Dit houdt in dat de snaar wordt ‘opgedeeld’ in 2 rechte segmenten die bij elkaar komen in een scherpe hoek. Deze scherpe hoek beweegt rond gedurende de toon. Hoe de snaar er tijdens deze beweging uitziet is te zien in figuur 1. De Helmholtz beweging wordt veroorzaakt door twee verschijnselen op het contactoppervlak tussen de boog en de snaar die ‘stick’ en ‘slip’ worden genoemd. Tijdens de ‘stick’ periode blijft de snaar aan de boog plakken waardoor deze wordt meegenomen. Gedurende de ‘slip’ periode glijdt de snaar weer terug langs het boogoppervlak. ‘Stick’ vindt plaats wanneer de Helmholtz hoek zich tussen de boog en je hand bevindt (rechts van de boog in figuur 1), ‘slip’ vindt plaats wanneer de Helmholtz hoek zich tussen de boog en de brug bevindt (links van de boog in figuur 1). De moeilijkheid van het bespelen van een viool zit hem in het feit dat deze Helmholtz beweging alleen plaatsvindt onder de juiste combinatie van snelheid en druk op de boog. Als er in verhouding te zacht met de boog op de snaar gedrukt wordt, zal deze teveel over de snaar slippen. Wordt er echter teveel druk uitgeoefend op de boog dan zal er teveel ‘stick’ optreden. Tevens van invloed is de positie van de boog ten opzichte van de brug van de viool. Het gebied waarin een Helmholtz trilling optreedt bij constante strijksnelheid wordt weergegeven in een zogenaamd Schelleng diagram (zie figuur 2). In dit diagram is te zien hoe hard er minimaal en maximaal gedrukt mag worden om in het Helmholtz gebied te blijven, als functie van de afstand tot de brug. Figuur 2: Schelleng diagram dat het Helmholtzgebied aanduidt. Model voor de frictiecurve Om de resultaten van eventuele experimenten te kunnen voorspellen en het maken van een regelaar makkelijker te maken zal een model gemaakt worden van de Helmholtz trilling van de snaar. Dit model word in matlab gemaakt en de theorie achter het model word in het volgende stuk besproken. Eenvoudige benadering In simpele modellen van de interactie tussen boog en snaar, wordt ervan uitgegaan dat de wrijvingskracht tussen beide alleen afhangt van de relatieve snelheid van de snaar ten opzichte van de boog. Het verband heeft volgens deze modellen een exponentiële vorm zoals in onderstaand figuur 1. Hierin is v de snelheid van de snaar en vb de snelheid van de boog. Deze wrijvingskracht op het interactievlak tussen boog en snaar is te berekenen volgens: [math]\displaystyle{ (1.1) }[/math] Waarbij µ de wrijvingscoëfficiënt is en fb de kracht waarmee de boog op de snaar wordt gedrukt. 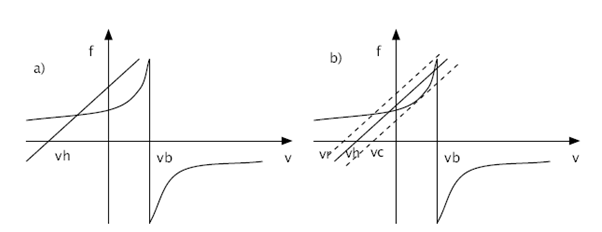Figuur 1: a) Het verband tussen de relatieve snelheid van de snaar, t.o.v. de boog, en de wrijvingskracht. b) Release velocity vr en capture velocity vc . Er zijn verschillende modellen voor de wrijvingscoëfficiënt. Het hyperbolische model wordt gegeven door de relatie: (1.2) Hierin is v0 de initiële boogsnelheid, µd de dynamische frictiecoëfficiënt en µs de statische frictiecoëfficiënt. In de meeste modellen wordt µd = 0.3 en µs = 0.8 gebruikt. Het exponentiële frictiemodel wordt gegeven door: (1.3) In figuur 1 is tevens een verband weergegeven tussen de kracht die op de snaar wordt uitgeoefend en de snelheid die de snaar hierdoor krijgt. Dit dynamische gedrag van de snaar is volgens experimenteel onderzoek in benadering lineair. In figuur 1 b) zijn ook de release velocity vr¬ en de capture velocity vc getekend. Dit zijn de snelheden waarbij de snaar respectievelijk losgelaten en meegenomen wordt door de boog. Dit kan als volgt worden uitgelegd. Als de snelheid van de snaar toeneemt, zal deze over de boog blijven slippen totdat de capture velocity vc is bereikt. Op dat moment blijft de snaar aan de boog plakken (‘stick’) waardoor de snaarsnelheid een sprong maakt naar de boogsnelheid vb. De snaar zal blijven plakken totdat deze de release velocity vr bereikt. Dit betekent dus dat de oplossing van de krachtsvergelijking een andere route over de grafiek volgt als de relatieve snelheid toeneemt dan wanneer deze afneemt. Model vs. Experiment In het eenvoudige model dat in figuur 1 is afgebeeld, is ervan uitgegaan dat de wrijvingskracht alleen afhangt van de relatieve snelheid tussen de boog en de snaar. Uit metingen is echter gebleken dat het verband niet zo eenvoudig is. De gestippelde lijn in figuur 2 laat het verband tussen snaarsnelheid en wrijvingscoëfficiënt zien zoals dat uit het bovengenoemde model komt. De getrokken lijn geeft het werkelijke verband, welke experimenteel is bepaald. Uit deze figuur blijkt duidelijk dat de klassieke benadering niet klopt. File:Verband2 Figuur 2: Het verband tussen snaarsnelheid v en wrijvingscoëfficiënt µ volgens het model (gestippeld) en volgens experimentele bepaling (getrokken).   Verklaringen voor fout model Een van de verklaringen hiervoor is dat de temperatuur van het interactievlak een sterke invloed heeft. De verklaring hiervoor is dat als de snaar een relatief kleine snelheid heeft ten opzicht van de boog, de contactlaag afkoelt door geleiding naar het materiaal buiten het contactgebied. Hierdoor nemen de schuifsterkte en de wrijvingscoëfficiënt op het contactgebied toe. Zodra er meer ‘slip’ plaatsvindt, warmt het contactgebied op door de arbeid die tegen de wrijving in wordt geleverd. Door deze warmteproductie wordt de hars in het contactgebied zachter en neemt de wrijvingscoëfficiënt snel af. Een ander verschijnsel dat veel invloed blijkt te hebben op de wrijvingskracht tussen boog en snaar, is de zogenaamde bow hair-compliance. Deze afwijking wordt veroorzaakt door het feit dat de boog niet op één punt contact maakt met de snaar, zoals verondersteld in het klassieke model, maar een contactgebied heeft. Het verschil is dat het voor een contactpunt wel mogelijk is dat de snaar zonder ‘slip’ de boog volgt, terwijl dit voor een contactgebied niet mogelijk is. In figuur 3 wordt aangegeven waarom dit niet mogelijk is. Situatie 1 is hierbij de uitgangssituatie. Hierin staat de boog op de snaar en is de snaar geëxciteerd. Een tijdsinterval later (situatie 2) is de boog met een snelheid vb omhoog bewogen en is de snaar door ‘stick’ gedrag meegenomen. De gestippelde lijn geeft de situatie weer zoals deze in werkelijkheid optreedt. De getrokken lijn geeft weer hoe vorm van de snaar zou moeten zijn als de snaar zonder enige vorm van ‘slip’ meegnomen zou zijn. Het moge duidelijk zijn dat deze situatie niet optreedt en er dus nooit geheel zonder ‘slip’ gestreken kan worden. File:Verband3 Figuur 3: Schematische weergave van het strijken van een snaar. De gestippelde lijn in situatie 2 geeft de werkelijke situatie weer, de getrokken lijn geeft de versimpelde voorstelling waarin zonder slip gestreken kan worden. Uit experimenten is echter wel gebleken dat de simpele voorstelling van de wrijvingscurve voldoende is om te kunnen simuleren wat de invloed is van het veranderen van wrijvingssnelheid en –druk op het al dan niet plaatsvinden van een Helmholtz beweging. Voor de toepassing van ons computermodel zal de wrijvingscurve zoals deze in figuur 1 is voorgesteld dus wel voldoen.