Embedded Motion Control 2012 Group 11: Difference between revisions

From Control Systems Technology Group
Jump to navigation Jump to search
Line 23: Line 23:




'''Week 1 and 2:'''
Due to major personnel changes the project was reset in week 7, and a brand new start was made. The results from this point on are reported in the section below.
-> Installed required software,
The project was split into two parts. The first part consists of the basic robot control algorithm. This includes the mapping of the laser data in combination with odometry. With this alignment functions and wall avoidance can be implemented, as well as recognition of corners and junctions. The recognition of a junction marks the jump to the second part of the algorithm: solving the maze. For the corridor competition it is enough to find the first exit and leave the corridor: in the maze the decision making will start at the detection of the junction. The basic robot control algorithm consists of three separate points: data acquisition and simplification of the data, detection of the environment and the response of the robot to the environment.
-> Fixed software issues, 2 members had to reinstall ubuntu 3 times plus some wireless network issues had to be fixed.


'''Week 3:'''
-> Finished all tutorials
-> Working on processing of a 2d map in Jazz simulator and Rviz to make the robot navigate autonomously. We are trying to measure distance in front of the robot in order to take decisions.


'''Week 4:'''
==Data acquisition and simplification==
-> The robot can now autonomously move through a given maze only using the LaserScan data.
The laser-output from the robot is given in polar coordinates. The first thing done was to make a conversion to Cartesian coordinates to get a better feeling of how to treat the data, and the possibilities this would give for simplification of the data. For this conversion the following data was used:
-> Given a corridor with exits, the robot is able to take the first exit.
-msg->ranges.size()
-msg->angle_min
-msg->angle_max
-msg->ranges[x]; x < ranges->size()
-msg->angle_increment
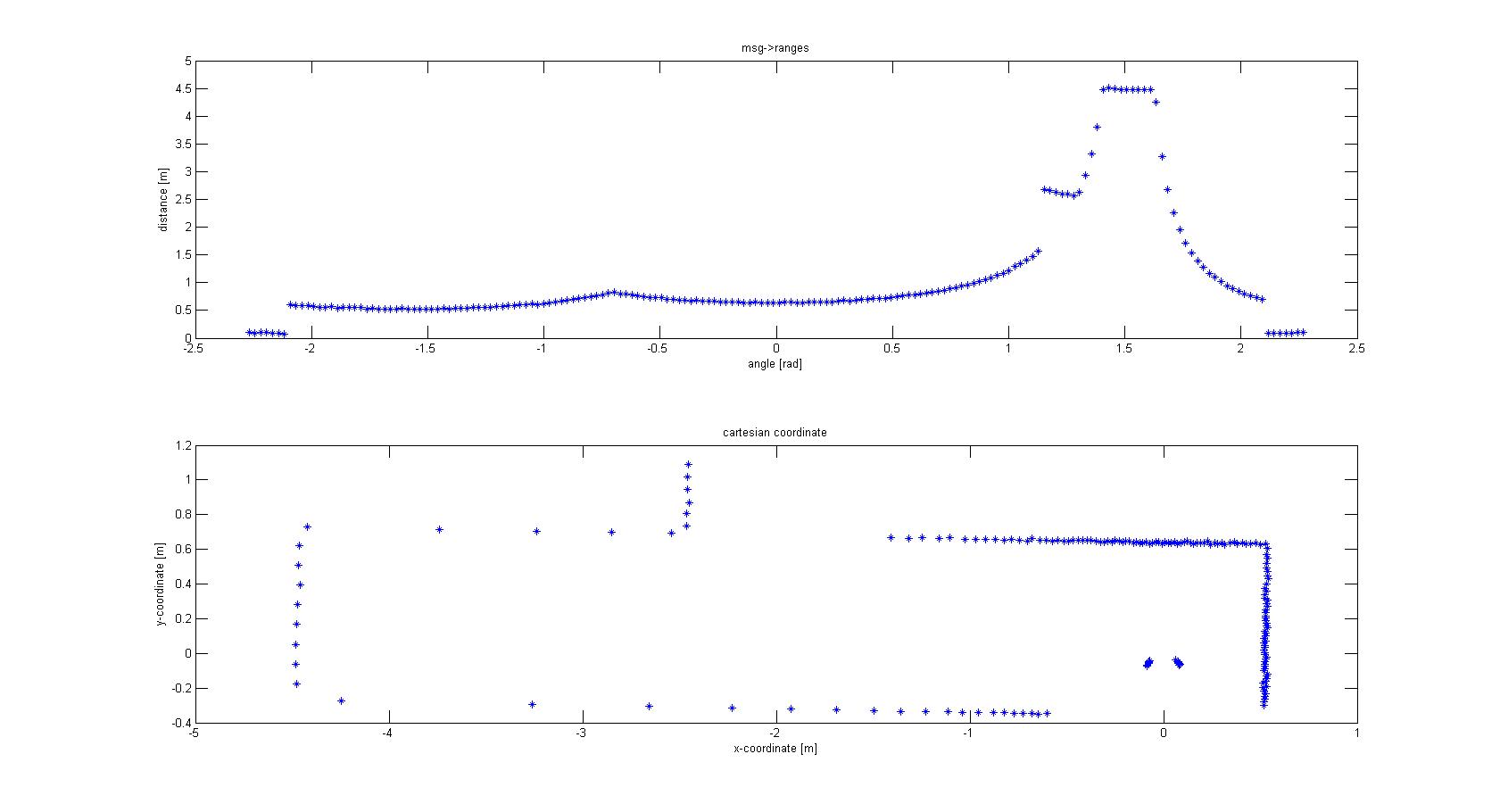
With basic algebra the conversion was made, which is shown in Figure 1.


'''Exit detection'''
[[File:conversion.jpg]] (Figure 1)
Two candidate algorithms were chosen In order to detect an exit. In the first algorithm, the sudden jump in the laser data is detected, and the robot keeps moving forward until half the width of the exit is traversed, and then the robot halts and turns by 90deg. In the second algorithm, the time required to traverse half the width of the exit is multiplied with the loop rate, and the corresponding laser data points are monitored before an exit is detected, and then similarly the robot halts and turns by 90 deg. To make this robust, both the algorithms were applied together.


[[File:exit.jpg]]
From the Cartesian plot some decisions can already be made. For instance, the data points that are plotted near the robot will have to be removed, since these are laser points that are projected on the robot itself. Furthermore we see a lot of points that are far away from the robot, all at a distance close to 10 meter. This is the maximum range of the laser points on the simulated robot, but on the real robot this might be different and can give a disturbing input. Therefore the data points which are relevant to the robot is limited to a range of TOO_FAR_TO_MAP meters, which is a static float to be fine-tuned to achieve good vision for the robot without large disturbances or processing time (limiting the data points you take into consideration when making decisions can speed up calculation times).  


'''Tasks for Week 5:'''
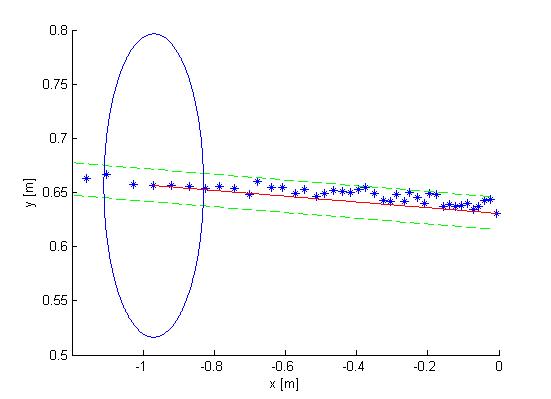
The next observation made from the Cartesian plot was that the data from the laser is actually quite noisy, as can be seen in Figure 2. The points do not align in a nice way, which can complicate decision making and mapping. One option is to make a fit over all the data points using basic functions for the walls instead of the points. This is also shown in Figure 2. If you assume that all the walls are straight (at least the walls are not substantially curved) you can use linear functions to represent the walls. If you do this in a correct manner you will only have to compare the robot position and orientation to the linear functions (i.e. only a zero order and first order constant a0 and a1) of these walls. Since you map only walls that are close to the robot this will reduce the input of your algorithms for wall avoidance from the number of laser points (over one thousand for the real life robot) to the first order functions of the walls (which will generally not exceed 8 wall segments, so 16 constants in total). A good motivation to continue developing an algorithm to do this.
-> Improve algorithm implementation to correct existing flaws
-> Develop an algorithm for arrow detection using Camera in rViz.
-> Work on methods to implement odometry data in the system.


[[File:FLOW 1.jpg]][[File:FLOW 2.jpg]]
[[File:data_fit.jpg]] (Figure 2)
 
   
'''Week 5'''
'''Mapping Algorithm'''
-> A new self aligning algorithm was implemented, and the robot is able to align itself in the simulator, given any initial angle and position inside the maze.
 
'''Alignment algorithm'''
 
'''Case1:''' Robot in the middle
The angle of inclination is calculated using trigonometry by calculating the minimum distance and the perpendicular distance to the walls, and the corresponding correction in angle is applied to the robot.
 
'''Case2:''' Robot closer to the wall (collision threshhold)
The angle of inclination is calculated similarly and the robot rotates by angle, which is the sum of the inclination angle and 90 deg, it then travels perpendicular to the walls until the mid-point is reached. The robot then makes 90 deg turn in the opposite direction, thereby aligning the robot onto the centre of the track.
 
[[File:align.jpg]] [[File:align2.jpg]]
 
'''Week 6'''
-> The algorithm was made more robust depending on less varying parameters. More complicated mazes were designed for later testing of the maze solving algorithm. The backbone structure of the maze solving algorithm was designed and partially implemented. The allignment and exit strategy were tested on the robot.
-> Working on publishing the odometry data using tf
 
'''Corridor competition:'''
The reason for failure to align and take the exit, was perhaps due to the lack of feedback from the robot, since odometry feedback was not implemented in the code. We are currently working on combining odometry data into the code to make the algorithm more robust.

Revision as of 22:59, 14 June 2012

Group Info

Group Members Email Student nr.
Christiaan Gootzen c.f.t.m.gootzen@student.tue.nl 0655133
Sander van Zundert a.w.v.zundert@student.tue.nl 0650545


Tutor Sjoerd van den Dries - s.v.d.dries@tue.nl


Due to major personnel changes the project was reset in week 7, and a brand new start was made. The results from this point on are reported in the section below. The project was split into two parts. The first part consists of the basic robot control algorithm. This includes the mapping of the laser data in combination with odometry. With this alignment functions and wall avoidance can be implemented, as well as recognition of corners and junctions. The recognition of a junction marks the jump to the second part of the algorithm: solving the maze. For the corridor competition it is enough to find the first exit and leave the corridor: in the maze the decision making will start at the detection of the junction. The basic robot control algorithm consists of three separate points: data acquisition and simplification of the data, detection of the environment and the response of the robot to the environment.


Data acquisition and simplification

The laser-output from the robot is given in polar coordinates. The first thing done was to make a conversion to Cartesian coordinates to get a better feeling of how to treat the data, and the possibilities this would give for simplification of the data. For this conversion the following data was used: -msg->ranges.size() -msg->angle_min -msg->angle_max -msg->ranges[x]; x < ranges->size() -msg->angle_increment With basic algebra the conversion was made, which is shown in Figure 1.

Conversion.jpg (Figure 1)

From the Cartesian plot some decisions can already be made. For instance, the data points that are plotted near the robot will have to be removed, since these are laser points that are projected on the robot itself. Furthermore we see a lot of points that are far away from the robot, all at a distance close to 10 meter. This is the maximum range of the laser points on the simulated robot, but on the real robot this might be different and can give a disturbing input. Therefore the data points which are relevant to the robot is limited to a range of TOO_FAR_TO_MAP meters, which is a static float to be fine-tuned to achieve good vision for the robot without large disturbances or processing time (limiting the data points you take into consideration when making decisions can speed up calculation times).

The next observation made from the Cartesian plot was that the data from the laser is actually quite noisy, as can be seen in Figure 2. The points do not align in a nice way, which can complicate decision making and mapping. One option is to make a fit over all the data points using basic functions for the walls instead of the points. This is also shown in Figure 2. If you assume that all the walls are straight (at least the walls are not substantially curved) you can use linear functions to represent the walls. If you do this in a correct manner you will only have to compare the robot position and orientation to the linear functions (i.e. only a zero order and first order constant a0 and a1) of these walls. Since you map only walls that are close to the robot this will reduce the input of your algorithms for wall avoidance from the number of laser points (over one thousand for the real life robot) to the first order functions of the walls (which will generally not exceed 8 wall segments, so 16 constants in total). A good motivation to continue developing an algorithm to do this.

Data fit.jpg (Figure 2)

Mapping Algorithm

Retrieved from "https://dsdwiki.wtb.tue.nl/index.php?title=Embedded_Motion_Control_2012_Group_11&oldid=2872"