Embedded Motion Control 2015 Group 3/Mapping: Difference between revisions
No edit summary |
|||
| Line 2: | Line 2: | ||
This page is part of the [http://cstwiki.wtb.tue.nl/index.php?title=Embedded_Motion_Control_2015_Group_3 EMC03 CST-wiki]. | This page is part of the [http://cstwiki.wtb.tue.nl/index.php?title=Embedded_Motion_Control_2015_Group_3 EMC03 CST-wiki]. | ||
= Mapping block = | |||
The mapping block contains a very high-level model of the world. The mapping has been created in such a way that only essential information is stored, in order to create a very flexible and modular world model. | The mapping block contains a very high-level model of the world. The mapping has been created in such a way that only essential information is stored, in order to create a very flexible and modular world model. | ||
| Line 9: | Line 9: | ||
[[File:Emc03 wayfindingCP1.png|400px|center|thumb|Map&solve algorithm (update?)]] | [[File:Emc03 wayfindingCP1.png|400px|center|thumb|Map&solve algorithm (update?)]] | ||
= Structure = | |||
The maze will consist of nodes and edges. A node is either a dead end, or any place in the maze where the robot can go in more than one direction. An edge is the connection between one node and another. An edge may also lead to the same node. In the latter case, this edge is a loop. The algorithm is called by the general decision maker whenever the robot encounters a node (junction or a dead end). The input of the algorithm is the possible routes the robot can go (left, straight ahead, right, turn around) and the output is the direction that is advised, based on the Tremaux algorithm. | The maze will consist of nodes and edges. A node is either a dead end, or any place in the maze where the robot can go in more than one direction. An edge is the connection between one node and another. An edge may also lead to the same node. In the latter case, this edge is a loop. The algorithm is called by the general decision maker whenever the robot encounters a node (junction or a dead end). The input of the algorithm is the possible routes the robot can go (left, straight ahead, right, turn around) and the output is the direction that is advised, based on the Tremaux algorithm. | ||
| Line 19: | Line 19: | ||
* Travel time for a corridor. This can be used to give priorities in case multiple options are present. | * Travel time for a corridor. This can be used to give priorities in case multiple options are present. | ||
= Schedule = | |||
The schedule looks like this: | The schedule looks like this: | ||
* Updating the map: | * Updating the map: | ||
** Robot tries to find where he is located in global | ** Robot tries to find where he is located in global coordinates. Now it can decide if it is on a new node or on an old node. | ||
** The robot figures out from which node it came from. Now it can define what edge it has been traversing. It marks the edge as 'visited once more'. | ** The robot figures out from which node it came from. Now it can define what edge it has been traversing. It marks the edge as 'visited once more'. | ||
** All sorts of other properties may be associated with the edge. Energy consumption, traveling time, shape of the edge... This is not necessary for the algorithm, but it may help formulating more advanced weighting functions for optimizations. | ** All sorts of other properties may be associated with the edge. Energy consumption, traveling time, shape of the edge... This is not necessary for the algorithm, but it may help formulating more advanced weighting functions for optimizations. | ||
| Line 37: | Line 37: | ||
** e.g., the current node is saved as a 'nodeWhereICameFrom', so the next time the algorithm is called, it knows where it came from and start figuring out the next step. | ** e.g., the current node is saved as a 'nodeWhereICameFrom', so the next time the algorithm is called, it knows where it came from and start figuring out the next step. | ||
= Tremaux Algorithm = | |||
Revision as of 14:07, 9 June 2015
Mapping
This page is part of the EMC03 CST-wiki.
Mapping block
The mapping block contains a very high-level model of the world. The mapping has been created in such a way that only essential information is stored, in order to create a very flexible and modular world model.
For solving the maze, a variant of the Tremaux algorithm is used: [1]. The Tremaux algorithm is an implementation of DFS (Depth First Search), which proves to be an efficient way of solving a maze with minimum backtracking.
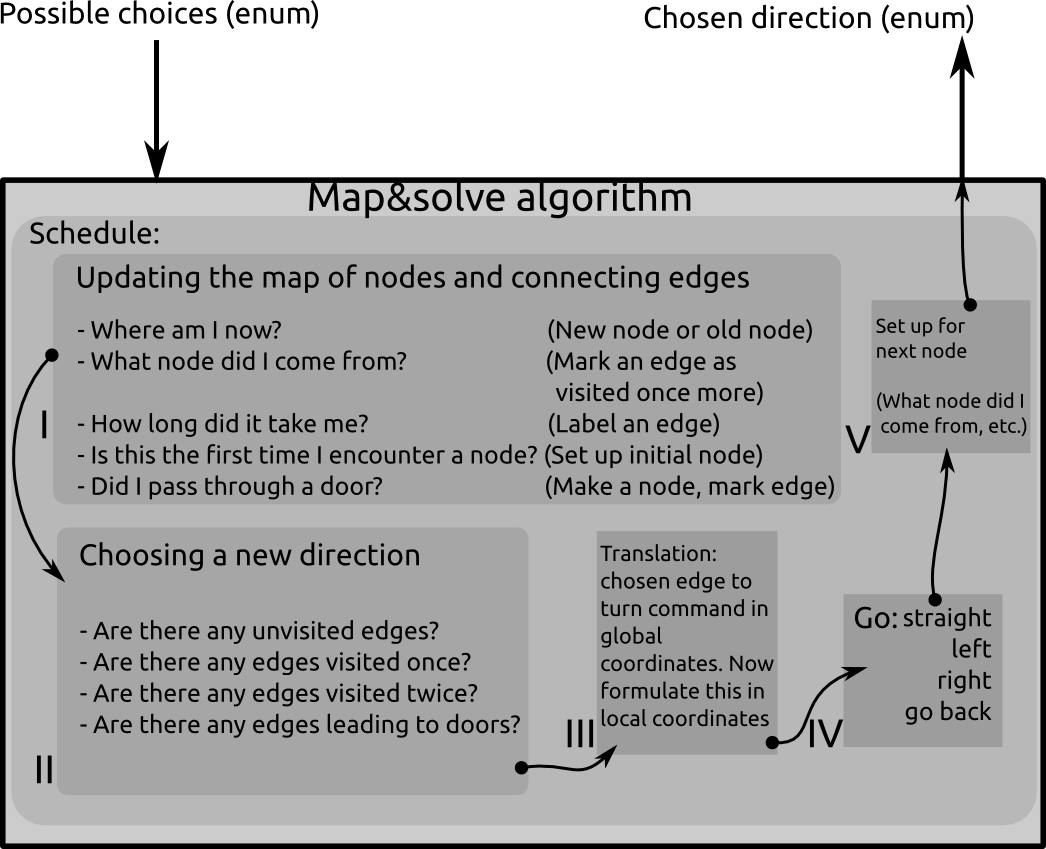
Structure
The maze will consist of nodes and edges. A node is either a dead end, or any place in the maze where the robot can go in more than one direction. An edge is the connection between one node and another. An edge may also lead to the same node. In the latter case, this edge is a loop. The algorithm is called by the general decision maker whenever the robot encounters a node (junction or a dead end). The input of the algorithm is the possible routes the robot can go (left, straight ahead, right, turn around) and the output is the direction that is advised, based on the Tremaux algorithm.
For each node, the following information is stored:
- Position. The position is used to identify and close loops within the maze, by matching a new node with a previous node.
- Adjacent corridors. Since the maze is axis-aligned, there can be anything between one (dead end) and four (cross-intersection) corridors/edges leading to a node. Because of this, the corridors are stored in an array with each element corresponding to a (global) direction.
For each corridor/edge, the following information is stored:
- Number of times Pico has traversed a corridor. This is important for Tremaux algorithm, which will be explained later.
- Travel time for a corridor. This can be used to give priorities in case multiple options are present.
Schedule
The schedule looks like this:
- Updating the map:
- Robot tries to find where he is located in global coordinates. Now it can decide if it is on a new node or on an old node.
- The robot figures out from which node it came from. Now it can define what edge it has been traversing. It marks the edge as 'visited once more'.
- All sorts of other properties may be associated with the edge. Energy consumption, traveling time, shape of the edge... This is not necessary for the algorithm, but it may help formulating more advanced weighting functions for optimizations.
- The robot will also have to realize if the current node is connected to a dead end. In that case, it will request the possible door to open.
- Choosing a new direction:
- Check if the door opened for me. In that case: Go straight ahead and mark the edge that lead up to the door as Visited 2 times. If not, choose the edge where you came from
- Are there any unvisited edges connected to the current node? In that case, follow the edge straight in front of you if that one is unvisited. Otherwise, follow the unvisited edge that is on your left. Otherwise, follow the unvisited edge on your right.
- Are there any edges visited once? Do not go there if there are any unvisited edges. If there are only edges that are visited once, follow the one straight ahead. Otherwise left, otherwise right.
- Are there any edges visited twice? Do not go there. According to the Tremaux algorithm, there must be an edge left to explore (visited once or not yet), or you are back at the starting point and the maze has no solution.
- Translation from chosen edge to turn command:
- The nodes are stored in a global coordinate system. The edges have a vector pointing from the node to the direction of the edge in global coordinates. The robot must receive a command that will guide it through the maze in local coordinates.
- The actual command is formulated
- A set-up is made for the next node
- e.g., the current node is saved as a 'nodeWhereICameFrom', so the next time the algorithm is called, it knows where it came from and start figuring out the next step.