Mobile Robot Control 2024 Optimus Prime

Introduction

We are Optimus Prime, a team of six members applying various control techniques and coding skills to optimize a robot for restaurant environments. Our goal is to enable the robot to efficiently deliver orders from the kitchen to the tables, even when faced with various obstacles. This project focuses on ensuring precise and reliable performance, ultimately improving service efficiency and the overall dining experience.

Group Members

Caption

Name	student ID
Yuvan Dwaraga	1563793
Wiktor Bocian	1628798
Ramakrishnan Rajasekar	1979027
Ariyanayag Ramesh Skandan	2012618
Abhir Adiverekar	1984136
Suryakumar Hariharan	1974076

Exercise 1 - The art of not crashing

This exercise aims to enhance our understanding of control techniques and obstacle avoidance algorithms.

Solution 1

The odometry and laser data were obtained based on the instructions from the manual, enabling the robot to be aware of its surroundings. Although this sensor data does not provide instructions for the robot to stop or go when an obstacle is on its way, a discussion was held to include a constant safe distance value, which ensures that the robot maintains a safe distance from obstacles and avoids collisions. Loops were also introduced as the robot operates to check whether the obstacles are close to the robot or not. Specifically, if an obstacle is detected within a certain range less than the predefined safe distance (0.5 meters) the robot will come to a halt. This algorithm ensures that the robot can navigate in its surroundings safely.

Solution 2

Advancements to the previous solution were made by introducing rotation values and forward motion values to enhance the robot's performance. These values were effective when the obstacle was too close to the robot. The stoppage of the robot comes into play and the rotation values allow it to rotate with movement restriction and later it allows the robot to move in the forward direction with constant units. This approach ensures that the robot not only stops to avoid immediate collisions but also actively seeks a safe route forward. Overall, the combination of a constant safe distance, rotation and forward actions allows the robot to perform more efficiently.

Learnings from solution

The robot's performance in this case was evidenced in both simulation and practical sessions. Alterations in the code were made so that, in case of obstacle detection, the robot was made to move in the x direction in adherence to the safe distance.

Visual representation of sim

https://youtu.be/Q3MBRWl5mNM

The robot detects the obstacles based on the LIDAR data and maintains a safe distance of 0.5m away from the obstacle.

Practical session

The live testing of the don't crash test can be evidenced by accessing the link https://youtu.be/QnT6EBChmf4

The robot follows the expected behavior as demonstrated in the videos.

Exercise 2 - Local navigation

Moving a robot from an initial position to a goal position is done with two components: Global and Local planning. Global planning takes care of the overarching route that the robot must take to reach the final destination. Using the path planned by the global planner as a reference, the local planner ensure that the robot avoids collisions with obstacles (static or dynamic). The two types of local planners chosen to explore in this project are Artificial Potential Field (APF), and Dynamic Window Approach (DWA).

Artificial potential fields

An Artificial Potential Field (APF), also known as Artificial Potential Field Navigation, is a technique used in robotics for local path planning and obstacle avoidance. It's inspired by the concept of potential energy in physics, where objects move from regions of higher potential energy to regions of lower potential energy.

Basic Concept:

1. Potential Field: In APF, the environment is represented as a virtual field where each point has an associated "potential" value. The robot's objective is to move from its current position to the goal while avoiding obstacles. The goal has the lowest potential, while obstacles have high potentials.
2. Attractive and Repulsive Forces: The potential field consists of two types of forces:
   • Attractive Force: Pulls the robot towards the goal. It's strongest when the robot is far from the goal and diminishes as it gets closer.
   • Repulsive Force: Pushes the robot away from obstacles. It's stronger when the robot is closer to obstacles.
3. Navigation: The robot navigates by moving in the direction of the resultant force, which is the sum of the attractive and repulsive forces.

Motivation

Choosing the artificial potential field (APF) method for the local navigation of a robot comes with several compelling motivations:

1. Simplicity and intuitiveness: The APF approach is reasonably easy to grasp and apply. It mimics the environment using attractive and repulsive forces that naturally direct the robot to its destination while avoiding obstacles.
2. Continuous and smooth path generation: This approach creates smooth and continuous tracks for the robot without any jerks. Because the forces are computed as gradients of potential fields, the resulting motion is smooth, avoiding the possibility of sudden changes in direction that would be difficult for the robot to perform.
3. Scalability: APF is easily adaptable to many types and sizes of settings (environment). The approach may be adjusted to a variety of circumstances by modifying the potential field parameters, ranging from basic inside navigation to more difficult outdoor settings.
4. Combination with Other Methods: APF may be utilized effectively with other navigation systems. For example, it may be used for local navigation inside a larger framework that handles global path planning, integrating the benefits of several frameworks.
5. Computation time: This method is much less computationally intensive than other ones.

Implementation

1. Converting the body fixed frame into global coordinates To implement this the transformedOdometry() function was created which was used to convert the odometry data of the robot into the global coordinate system.
2. Normalizing the angle The normalize_angle() function ensures that any given angle is mapped to an equivalent angle within the standard range of −π to π radians. This is useful because angles can be represented in multiple ways (e.g., 3π is the same as π), and having a consistent representation simplifies many calculations and comparisons.
3. Calculating attractive forces The attraction_force() function calculates a linear attractive force towards a target position. This force is proportional to the distance between the current position and the target position, scaled by an attraction coefficient. The formula used for calculating attractive forces - [math]\displaystyle{ F_{\text{att}}(\mathbf{q}) = k_a (\mathbf{q}_{\text{goal}} - \mathbf{q}_{\text{current}}) }[/math] where, [math]\displaystyle{ k_a }[/math] is the attraction gain. [math]\displaystyle{ \mathbf{q}_{\text{goal}} }[/math] is the goal position. [math]\displaystyle{ \mathbf{q}_{\text{current}} }[/math] is the current postion of the robot
4. Calculating repulsive forces The repulsion_force() function calculates a repulsive force that acts to push a point (or robot) away from an obstacle when it gets too close. The force is designed to be strong when the point is very close to the obstacle and diminishes as the point moves away, ensuring safe navigation around obstacles. The formula used for calulating the repulsive forces - [math]\displaystyle{ F_{\text{rep}}(\mathbf{q}) = \begin{cases} k_{\text{rep}} \left( \frac{1}{\|\mathbf{q}\|} - \frac{1}{d_{\text{safe}} + m_{\text{safety}}} \right) \left( \frac{1}{\|\mathbf{q}\|^2} \right) & \text{if } \|\mathbf{q}\| \lt d_{\text{safe}} + m_{\text{safety}} \\ 0 & \text{if } \|\mathbf{q}\| \geq d_{\text{safe}} + m_{\text{safety}} \end{cases} }[/math] where, q is the distance. [math]\displaystyle{ d_{\text{safe}} }[/math] is the safe distance [math]\displaystyle{ m_{\text{safety}} }[/math] is the extra margin. [math]\displaystyle{ k_{\text{rep}} }[/math] is the repulsion gain
5. Calculating the resultant forces the resultant force was calculated by adding the attraction forces and repulsion forces in (x, y) directions which gave the linear velocity component. And resulting θ was calculated by arctan(y/x) which gave the angular velocity component.

Learnings from each solution

While the artificial potential field (APF) approach has significant benefits for robot navigation, it also has certain drawbacks, such as the possibility of being caught in local minima or oscillations. To address these concerns, many fixes and improvements to the APF approach have been proposed:

Gradient Descent with Escape Strategies: One typical problem with APF is getting stuck in local minima when the attractive and repulsive forces cancel out.

Solution: Random Walks or Perturbations - By introducing small random movements or perturbations, the robot can escape local minima. To come out of the local minima random perturbations were added in the APF algorithm and it was successful at the end.

Combination with Global Path Planning: Integrating APF with a global path planning algorithm can provide a more comprehensive navigation solution.

Solution: Hybrid Approaches - Finding a rough path with a global planner such as A* or Dijkstra's algorithm, and then using APF for local navigation to fine-tune the path and avoid obstacles.

Testing and tuning

Initially, the robot was not given a maximum velocity that it can achieve while moving using using artificial potential fields algorithm. This approach worked in simulation well with the robot getting to the end position with a smooth trajectory. However, when testing in practice this proved to be insufficient, since the robot always just drove into obstacles, because it couldn't rotate fast enough. To avoid that behavior and make sure the robot has enough time to avoid the obstacle extra guard for the maximum linear velocity of the robot was added. This method led to comparatively less smooth trajectories however it ensured that both in simulation and in practice robot does not hit obstacles.

Furthermore, when testing different gains for the APF (attraction gain and repulsion gain), it was found that for some maps it was stuck in the local minima. This is typical for this method, however, to check if by further tuning, the goal can be reached on all the given maps parameters were tuned (attractive gains and repulsive gains) for each map and after implementing this strategy the robot was able to complete the task in every scenario.

Visual representation of sim

1. Map 1 - https://www.youtube.com/watch?v=PWZg0-T9-U8
2. Map 2 - https://www.youtube.com/watch?v=E6Xz24zsPdE
3. Map 3 - https://www.youtube.com/watch?v=ZnRjnttkkrE
4. Map 4 - https://www.youtube.com/watch?v=ERdRPLcliLk

For the first three simulations, the parameters were the same, but for the fourth simulation, the parameters were a bit different.

Practical video

1. Map 1-https://youtube.com/shorts/2iPmLHOHZgY?feature=share
2. Map 2-https://youtube.com/shorts/V9yEWU9jpt0?feature=share
3. Map 3-https://youtube.com/shorts/jpvrOMJoCuI?feature=share
4. Map 4-https://youtu.be/s8pXRdhEtTc
5. Map 3 with a dynamic moving obstacle - https://www.youtube.com/shorts/jFs7r0aP9Ws

Assignment Questions and Answers

1. What are the advantages and disadvantages of your solutions?
   • Advantages
     1. Simplicity: The APF approach is straightforward to implement and understand. It uses simple mathematical functions to represent attractive forces towards the goal and repulsive forces away from obstacles.
     2. Real-time Computation: APF algorithms are computationally efficient, making them suitable for real-time applications. The computations involved are minimal and can be handled by most modern processors with ease.
     3. Scalability: APF methods can be scaled to handle different sizes and types of robots without significant modifications to the algorithm.
   • Disadvantages
     1. Local Minima Problem: One of the significant drawbacks of APF methods is the local minima problem, where the robot can get stuck in a position that is not the goal due to equal attractive and repulsive forces cancelling each other out.
     2. Inability to Handle Complex Environments: APF methods may struggle with complex environments with narrow passages or multiple closely spaced obstacles, leading to suboptimal or infeasible paths.
     3. Parameter Tuning: The performance of APF methods heavily depends on the tuning of parameters such as the strength of attractive and repulsive forces. Improper tuning can lead to inefficient navigation or failure to reach the goal
2. What are possible scenarios which can result in failures (crashes, movements in the wrong direction, ...) for each implementation?
   • Crash
     1. If the target position is set inside an obstacle - The robot collides with the obstacle repeatedly as it tries to get as close as possible to the goal.
     2. Not initializing the maximum velocity - The robot follows the path and once it detects the obstacles, it drives into the obstacle and crashes.
     3. Less repulsive force - The robot is confused with the less repulsive force and safe distance ultimately crashing into obstacles
   • Movement in the wrong direction
     1. Poor tuning of the values - The robot makes an oscillatory behaviour by moving back and forth between obstacles and is unable to make a decision.
   • Repeated movement
     1. Local minima - The robot gets trapped in a local minima where the attractive and repulsive forces balance out to zero. It makes a constant circular movement wasting energy.
3. How would you prevent these scenarios from happening?
   • Crash
     1. Target position and obstacle - Use a map of the environment to ensure the target is in a free space and not inside an obstacle.
     2. Maximum velocity - Always initialize and cap the robot's maximum velocity based on the environment's characteristics and the robot's specifications. Implement obstacle detection and dynamic re-planning to slow down or stop when obstacles are detected.
     3. Repulsive force - Adjust the repulsive force parameters through careful calibration so that the robot maintains a safe distance from obstacles without causing instability.
   • Movement in the wrong direction
     1. Tuning the values - Use a systematic approach to tune the attractive and repulsive parameters. Implement adaptive parameter tuning algorithms that adjust parameters in real time based on the robot's performance and the environment.
   • Repeated movement
     1. Local minima - By introducing small random movements or perturbations, the robot can escape local minima.
4. For the final challenge, you will have to link local and global navigation. The global planner will provide a list of (x, y) (or (x, y, θ)) positions to visit. How could these two algorithms be combined? (Implementing this will be part of next week's assignment.)
   • Global navigation - The global planner is in charge of creating a high-level path from the start to that goal position. The path is often expressed as a succession of waypoints ( 𝑥 , 𝑦 ) or ( 𝑥 , 𝑦 , 𝜃 ) for the robot to follow. These waypoints can be termed as nodes, algorithms like as A* and Dijkstra's are commonly used for the purpose of finding the optimal nodes through which robot can navigate, taking into account the robot's environment map.
   • Local navigation - The local planner uses the waypoints from the global planner to create a collision-free path in the robot's near surrounding area. It detects obstacles using sensor data (such as LiDAR) and dynamically adjusts the robot's route.
   • Integration of Global and Local Planners - The robot receives the whole list of waypoints from the global planner. The local planner focuses on getting to the next near waypoint while avoiding collisions. The local planner constantly adjusts the robot's path to the next waypoint. When the robot reaches a waypoint (within a certain threshold), it chooses the next waypoint from the global path. This process continues till the robot reaches the final goal destination.

Dynamic window approach

Dynamic Window Approach (DWA) is a dynamic velocity-based approach wherein the best combination of linear and angular velocity is sent to the robot every iteration. In this application, an iteration is initiated every time the LIDAR sensor logs new data. This section details the DWA algorithm as well as its implementation.

Working principle and motivation

Given that DWA is a velocity based approach, it is important to define the range of velocities that is possible for the robot to achieve for both the linear and angular cases. Realistically, not all the possible velocities might be reachable due to acceleration constraints, so it is required to define the maximum linear and angular deceleration of the robot. For all the velocities that are admissible, and reachable, the algorithm choses the best combination from a reward function which accounts for the orientation of the robot with respect to the goal, the distance to obstacles. Another term is included in the reward function which prioritizes high velocities. Once the best combination is sent to the robot at the end of the first iteration, it is important to note that the reachable velocities (from the current) will change. Hence, the search space of velocities  will dynamically evolve each iteration. The algorithm will remain active until the desired position is reached. While the algorithm might be computationally heavy, it is relatively easy to comprehend, implement. And since it can also be easily expanded to a global planner, DWA algorithm is chosen to implement as the second local path planner.

Implementation

As mentioned above, the velocity and acceleration constraints for both the linear and angular cases must be defined first. The set of all possible velocities is generated according to:

[math]\displaystyle{ V_S = \{v, \omega \mid v \in [v_{\text{min}}, v_{\text{max}}] \wedge \omega \in [\omega_{\text{min}}, \omega_{\text{max}}]\} }[/math]

Implementation wise, the all_possible_velocities() function is used which takes as inputs the maximum velocity, and the number of samples. The velocities are discretized based on (Max_vel/samples) and stored as floats in a vector. This function is called twice, once for the linear case and also for the angular case. The implementation ensures that linear velocities are always non-negative, while angular velocities can be either positive or negative. All possible combinations of velocities from the two sets are checked for reachability based on the current velocity of the robot and the acceleration constraints within a predefined timestep. The following formula is used to check reachability.

[math]\displaystyle{ V_d = \{v, \omega \mid v \in [v_a - \dot{v}t, v_a + \dot{v}t] \wedge \omega \in [\omega_a - \dot{\omega}t, \omega_a + \dot{\omega}t]\} }[/math]

Here, va and wa correspond to the pair of velocities for which the reachability is tested for. Only if a pair is reachable, it is checked if the pair is also admissible such that it avoids running onto obstacles if sent to the robot within the next timestep. A modification of one of the SUVAT equations is used to check admissibility. This is shown below:

[math]\displaystyle{ V_a = \{v, \omega \mid v \leq \sqrt{2d(v, \omega) \dot{v}_b}} \wedge \omega \leq \sqrt{2d(v, \omega) \dot{\omega}_b\} }[/math]

Here, d(v,w) is the distance to the obstacles measured by the LIDAR sensor, vbd and wbd are the maximum linear and angular accelerations. The guard imposed checks if each of the reachable velocities will travel more than the distance to the closest obstacle if a certain pair is assigned to the robot. To compute the admissible velocities, it is important to calculate the distance to the closest obstacle. This is done using the min_dist_to_obj()function which takes in as input the coordinates of all measurements by the LIDAR sensor in the map frame, the current pose, and each of the reachablevelocity pair. This function iterates over N time steps calculating its future pose using the input velocity pair, and calculates the distance to each obstacle in each of these discretised time steps. Over these time steps, if the distance to any of the obstacle is less than a limit, it calculates the minimum distance it must travel(from current pose) before it gets too close to the limit. This function gives the minimum distance the robot has to travel before it is very close to the obstacle. In fact, this limit is set such that the robot’s dimensions are also accounted for. The reachable pairs that satisfy the kinematic constraint imposed will proceed for reward calculations which is used to identify the best pair. The reward function considers the heading direction of the robot, its distance to the closest obstacle that prioritizes high linear velocities. The expression below shows the reward function design for this application:

[math]\displaystyle{ G(v, \omega) = \sigma(k_h h(v, \omega) + k_d d(v, \omega) + k_s s(v, \omega)) }[/math]

Kh, Kd, and Ks are gains that balance the three components relative to one another. H(v, w) calculates the heading direction, d(v, w) measures the distance the robot can travel before approaching too close to the nearest obstacle, and s(v, w) is the function that favors high velocities. The Next_Pose()function is used to compute the pose of the robot one time step into the future which takes the current pose, the time step, and a velocity pair as inputs. This future pose, the final goal pose, and the current yaw orientation are used in the Header_Error()function which computes the relative difference in orientation to the final goal when a pair is chosen. When computing the reward function, the heading angle is normalized between -pi and pi degrees. The high velocity prioritization term normalizes the velocity with respect to the maximum linear velocity.

The pair with highest linear velocity which is best oriented towards the goal pose and maximizes the distance it must travel before it gets too close to an obstacle is preferred over others. Given the structure of the main() function, all the reachable velocities are tested for, and the best one is sent to the robot. Updating all relevant variables, the loop carries on until the final goal is reached. The first four videos attached below shows the performance of DWA in simulation, whilst the latter demonstrate real-life performance.

Visual representation of simulations

1. Map 1- https://youtu.be/fWEViUxkSyA
2. Map 2- https://youtu.be/TZJ3P-D1R30
3. Map 3- https://youtu.be/T5NK8HIP7wA
4. Map 4- https://youtu.be/QHgEemnbkn0

The four links above demonstrate the performance of the robot in simulations. The robot easily navigates itself through the first three maps. It must be noted that the robot does travel a little on the slower side. Given that the algorithm looks at 12 time steps in the future for every iteration of velocity pairs, it is computationally demanding. On top this, the rate at which new data is logged from both the LIDAR and odometry sensors is once every quarter of a second. Expanding the velocity search space further always took more time than the rate at which new data is logged. And if the discretization is made more coarse, the robot was found to be stuck in situations where it just stops as the algorithm didnt allow for lower velocities (due to lack of access). Such limitations caused the robot to operate at low velocities and perform well when the map is less crowded. With the fourth map, the tuning is the issue for it to recorrect its orientation by going in circles twice. The three gains can be further tuned for a better response. However, it most of the cases, when the robot is past all obstacles and is heading towards the goal, it is clear that it corrects itself (moves in zig-zag form) a lot of times.

Visual representation of real life demonstrations

1. Map 1-https://youtube.com/shorts/-xgMeAtbdBQ?feature=share
2. Map 2-https://youtube.com/shorts/nsv2eGVvw7o?feature=share
3. Map 3-https://youtube.com/shorts/1eL7xdEf0vs?feature=share
4. DWA with human obstacles- https://youtube.com/shorts/djTUpc08Cjw?feature=share

As far as testing the robot's response in the real world, it is quite similar to the simulations. However, an important factor that the simulation dis-regards is the drift present which introduces noise to the odometry data. This causes the robot to not exactly stop after 6 meters. Sometimes it stops before it could reach the target, but there have been cases where it has travelled a little more as well. In the testing sessions, it was found that the rotations are quite slow as well. However, when increasing them further, the robot completely comes to a halt near an obstacle. This is because it cannot find an optimal decision to continue further. Therefore, it is tuning intensive. In the case of more obstacles, the algorithm isnt as robust as the simulator behaves. In testing with the fourth map, the robot did pass the first set of obstacles, but then came to a halt completely shortly after.

Assignment questions

1. What are the advantages and disadvantages of your solutions?

• Advantages
  1. DWA takes into account the velocity and acceleration constraints in a dynamic manner which allows for a smooth motion of the robot to its goal destination. (It is not jerky) Since it is dynamic, it does not allow the robot to jump to velocities that it cant reach in the next timestep.
  2. DWA involves real time computations which make it viable for static as well as dynamic obstacles which are map independent. In fact, the test involving a human actively walking around the map along with the robot clearly shows that the algorithm does function well. But it must be noted that it only works with slowly moving obstacles. This is due to the magnitude of velocities the code itself is built around.
  3. The algorithm simulates future poses and effectively works out the distance to the closest obstacle. Additionally, the robot also accounts for the size of the robot which is necessary to avoid running into obstacles. So it takes preemptive actions to avoid them.
  4. The algorithm allows for efficient tuning which will ensure that for scenarios where the map is known, it can be optimized for that particular setting. This would allow one to get optimal performance in using the robot along with global navigation.
• Disadvantages
  1. While DWA does do a good job with low number of velocities, as the number of samples is increased further, it gets very computationally heavy. This is evident from the fact that for each velocity pair, the algorithm has to simulate future poses and evaluate the reward function. Given that the rate of logging data is also a variable that can be altered, the computational power rises drastically. During testing this was noted as well, hence the rate is set to an optimal value of 4 Hz.
  2. When the algorithm is made very stringent to reach the goal position, it can get stuck in circles due to lack of velocities to choose from.
  3. As mentioned before, the algorithm also struggles with extremely crowded environments which is constrained by the computational power as well as tuning. One can weigh the reward functions differently and tune for the application. But even then, due to discretization, it will not account for all possible velocities.
  4. The drift with the sensors will not guarantee accuracy of the position of the robot.

2. What are possible scenarios which can result in failures (crashes, movements in the wrong direction, ...) for each implementation?

• The robot might end up crashing or leaving the map in trying to reach the goal position:
  1. If the target position is set inside an obstacle, the robot could end up running into the obstacle as it tries to reach the goal. But, this is heavily dependent on the way the components of the reward function are weighed. It could also just keep rotating left and right as it will try to find the best angle that will orient itself with the target.
  2. As mentioned before, the robot will also start running in circles if it is asked to reach the goal position with high accuracy. This is caused due to the fact that the robot moves in arcs (unless the angular velocity component is 0) as it tries to reach the goal position. But due to the way the velocities are discretized, if a velocity pair (which is required to reach the goal) is not reachable it can never converge to the desired position.
  3. The robot fails to avoid fast-moving dynamic obstacles effectively, especially if the other entities are moving unpredictably, leading to a crash.
• The robot could be stuck in a single position:
  1. When the robot encounters a narrow passage that is difficult to navigate due to its velocity and acceleration constraints. The DWA may fail to find a feasible velocity that fits through the narrow opening, causing the robot to get stuck. In fact this was a very frequently encountered with map 4 of the simulation linked above. This also highlights the fact that DWA is (to an extent) map specific and may require tuning in different environments.

3. How would you prevent these scenarios from happening?

• The following could be used to solve issues to avoid the robot from crashing into an obstacle when reaching the goal position:
  1. Ensuring that the goal is positioned inside well inside the boundary of the map and does not have any obstacles just in front or behind it. If this isnt the case, the robot can wait for few seconds to see if this changes. If it doesnt, it can ask for human intervention.
  2. The guard on reaching the goal position (singular) can be relaxed by allowing the robot to stop if it reaches an area just around the goal. This could be accounted for by asking it to stop if it is anywhere between 10 to 20 cm away from the goal. This has been incorporated in the algorithm already.
  3. As far as avoiding crashes due to fast moving obstacles is concerned, it can only be solved by sampling for a wider range of velocities that are sufficiently high and allowing the robot to move at faster velocities. In order to minimize computation time, it is necessary to follow coding abstraction.
• In case the robot is stuck in a position:
  1. Improve the DWA by incorporating global path planning algorithms that can recognize dead ends and provide alternative routes. Additionally, enhances the local planning aspect of DWA to better handle narrow passages by fine-tuning velocity and acceleration constraints and implementing more sophisticated search techniques within the dynamic window. Or this can also be done together with the global planner that requests for a new route if the current one is not feasible.

4. For the final challenge, you will have to link local and global navigation. The global planner will provide a list of (x, y) (or (x, y, θ)) positions to visit. How could these two algorithms be combined?

The DWA algorithm in itself only helps in finding the route between two points that avoids obstacles. However, since the global planner provides a sequence of nodes which helps in reaching the goal, it can be incorporated along with the local planner. The local planner can be active between nodes provided by the global planner. It is analogous to treating each node output by the global planner as goal nodes for the robot to reach from its current node. This will allow for the robot to reach to the goal in a smooth manner.

Exercise 3 - Global Path Planning

A* algorithm

A* algorithm is used to determine the shortest path from the start node to the goal node through the known network of nodes and their connections. It initializes the _nodelist() which contains all the nodes and the connection data generated by the PRM algorithm. During each iteration, the next node in the connection of the current node is chosen based on the minimum cost (f) to reach the goal. (i.e.) the sum of cost-to-come and cost-to-go (heuristic cost). This cost represents the absolute distance between the node being evaluated and the goal node. The algorithm iterates until the goal node is reached and all open nodes have been evaluated.

• Node with minimum f

The node with a minimum f value from the list of open nodes is selected. The variable 'nodeID minimum f' is initialized to signify that no node has been identified yet. The 'minimum_f' variable is initialized to infinity assuming that the actual 'f' value will be from the nodes will be finite and lower when iteration starts. Subsequently, a for-loop iterates over all node IDs in the 'open nodes' container. For each node, it retrieves the 'f' value from the '_nodelist' vector storing nodes. If the 'f' value of the current node is less than the recorded minimum, 'minimum f' is updated with the new lower value and 'nodeID minimum f' will be set to the current node's ID.

• Exploring the node connections

Exploration of node connections is iterating over nodes connected to the current node, verifying if they have already been evaluated (in the 'closed nodes' list). For each unprocessed adjacent node, it computes a new cost-to-come ('g') as the sum of the current node's 'g'(value) and the distance between both nodes. If this new 'g' is lower than the adjacent node's existing 'g', the node's 'g', heuristic estimate ('h'), and total cost ('f') are updated, and its parent is set to the current node. If the adjacent node isn't in the 'open nodes' list, it is added for subsequent evaluation. After processing all connections, the current node is moved to the 'closed nodes' list, marking it as evaluated. This ensures that the search focuses on the path with the optimal cost, efficiently guiding the search towards the goal.

• Trace back the optimal path

The final step involves tracing back the optimal path, As soon as the goal node is reached the algorithm starts tracing the optimal path. It begins at the goal node and works backwards using the 'parent node ID' of each node, which points to the preceding node on the optimal path. In the loop, the current node ID is appended at the beginning of the 'path node IDs' list within a loop, constructing the path from start to goal. This backtracking persists until it reaches the start node, which is then added to the list. Once the path is fully identified, the list of node IDs is stored and the algorithm marks the path as successfully found. This ensures that the shortest path is clearly outlined and can be utilized by the respective local planner to navigate towards the goal while avoiding obstacles.

Inflated walls with dilation size equal to 1

Probabilistic Road Map (PRM)

To implement the path planning algorithm, a preliminary step involves generating a set of potential paths on the map that will be used to find an optimal path. The Probabilistic Roadmap Method (PRM) serves this purpose by generating connections between randomly positioned points on the map.

• Wall inflation

In the process of wall inflation, the walls on the map are expanded to mitigate the risk of collision for the robot, which occupies more space than a point. This inflation is achieved through dilation on the map image. To do that, the map colours are first inverted since dilation works on white parts of the binary image. It is done by specifying the type and size of the Kernel that is used to check if there is a white point inside it and if there is such a point it changes the other ones inside the kernel to this color. For the desired implementation the square kernel is being used since all of the maps mostly consist of straight lines and the size of this kernel can be adjusted by changing the dilation size variable.

Inflated walls with dilation size equal to 2

After the dilation, the map is reverted to its original color scheme and examples with different kernel sizes can be seen on the Figures.

• Distance from other points

To ensure a more even distribution of points across the map, the distance between newly generated vertices and previously existing ones is checked. This is done by verifying the difference between the x and y coordinates of each vertex exceeds a predefined threshold which is no smaller than 0.3 meters. Thus, each vertex occupies a distinct 0.3x0.3 meter area without overlapping with neighboring vertices.

• Check for valid edge

To verify if the vertex is valid, two checks are done. First verification is to ensure only the vertices that are relatively close to each other are connected and the distance between them is being checked. This is done by computing the absolute value of a difference between the x and y variables of 2 vertices and then taking a square root of a sum of those values squared, which allows us to compute the distance between them in a straight line.

Another crucial validation step involves checking for the presence of walls between two nodes. This is done by using Bresenham's algorithm to create a line between the two points of interest. By generating all points along this straight line, the algorithm detects any instances of a black point, indicating the presence of a wall obstructing the path. In such cases, the line is deemed invalid and consequently, the edge connecting the two nodes is not established. This algorithm works by calculating the difference between the x and y positions along the line and its final destination. Subsequently, the difference in y is subtracted from the difference in x and doubled to ensure integer operations. This algorithm provides insights into the deviation of the generated line from the ideal straight line connecting the two points. If this error exceeds the difference in the y coordinate, adjustments are made to render the lines less horizontal. A similar process is applied to the x coordinate.

This approach ensures the identification of obstacles between nodes, thereby guaranteeing a path between the generated network of nodes. By systematically validating edge connections, the algorithm effectively constructs a representation of traversable paths on the map, essential for efficient path planning and avoiding collisions with obstacles.

Example

Example of the map created using the probabilistic roadmap

Efficient node placement in maze

To test the algorithm the example map was used with several vertices equal to 70, and a dilation size equal to 2 which means that (5,5) square kernel was used for dilation and a maximum distance between two edges of 1 m was created and can be seen on the Figure.

Assignment questions

1. How could finding the shortest path through the maze using the A* algorithm be made more efficient by placing the nodes differently? Sketch the small maze with the proposed nodes and the connections between them. Why would this be more efficient?
   • The A* algorithm functions by systematically searching through nodes within a graph to identify those offering the shortest path from the start node to the end goal. Firstly, By reducing the number of nodes, both storage space utilization within the node_lists() and computational demands can be minimized as the algorithm will have fewer nodes to evaluate. This can be done by placing the nodes strategically at places where there are junctions, ends or where paths diverge in the maze (see orange blocks places at strategic points in the maze). Focusing on these critical junctures ensures that the algorithm concentrates its evaluation efforts on nodes to path determination. As a result, the algorithm's efficiency is enhanced, enabling more streamlined pathfinding through the maze.
2. Would implementing PRM in a map like the maze be efficient?
   • Yes, Utilizing Probabilistic Roadmap (PRM) in a maze-like environment can indeed offer efficiency, particularly in scenarios where the maze and has many obstacles to tackle. PRM uses a approach of sampling nodes which are more useful to find possible paths around the obstacles. However, it is worth noting that while PRM excels in such environments, the reliance on numerous sampling nodes can lead to increased storage requirements and computational demands. In instances where the maze features relatively straightforward passages or corridors, the abundance of nodes generated by PRM may not be necessary. In these cases, it is more efficient and practical to position nodes strategically at pivotal points within the maze. This ensures that computational resources are allocated where needed the most and focusing efforts on evaluating nodes at key decision points. Thus, while PRM offers valuable capabilities in negotiating complex mazes, careful consideration must be given to balancing its benefits with the associated storage and computational costs.
3. What would change if the map suddenly changes (e.g. the map gets updated)?
   • In case the map changes, the robot has certain time to try to reach the next node. In case if the time exceeds before reaching the node the robot will hold onto its current position and initiate a function 'Node_unreachable()' which sets the parent_node_ID of the unreachable node as a new _start_nodeID and discards all the connections to the unreachable node ensuring that this node is not used in anymore in path planning. Further, initiating pathplan() again to plan a new path with a new start node and a same end goal. Once a new path is generated the local planner is initiated again to follow new path until it reaches the goal. This will help whenever there is an unexpected obstacle in the path or the way is blocked and also to escape when the robot gets stuck in a local minima while using AFP local planner.
4. How did you connect the local and global planner?
   • When seen conceptually, the local planner uses the global planner as an input or guide to reach a given goal from its starting point. Global planner uses PRM or the grid map algorithm to explore and plot the feasible nodes with connections between them throughout the map forming networks and potential paths and stores it. These are used by the A* algorithm to find the most optimal path by evaluating each node connection and the result is stored in a structured path_node_ID() list. Whereas the local planner retrieves this list from "planner.h". Then planner algorithm sets the initial node in the list as the target node and continuously updates its target node coordinates (Target_x, Target_y) to the next node in the list. This is updated when the robot reaches within a predefined safe distance of the current target node, as soon as the robot reaches the goal node (last item in the list) the target node updating loop is terminated.
   • Conceptually, the connection between the local and global planners is implemented in a manner where the local planner utilizes the global planner as a reference or guide to navigate from its initial position to a designated goal. the global planner implements techniques like Probabilistic Roadmap (PRM) or grid map algorithms to explore the map, identifying feasible nodes and establishing connections between them to form networks and potential paths. These paths are then stored for retrieval. Subsequently, the A* algorithm is utilized by the global planner to determine the most optimal path by evaluating each node connection. The resulting optimal path is structured and stored in a list known as "path_node_ID()". In the implementation of the local planner, this list is retrieved from "planner.h". The local planner algorithm sets the initial node in the list as the target node. Continuously, it updates the coordinates of the target node (Target_x, Target_y) to the next node in the list. This updating occurs when the robot approaches within a predefined safe distance of the current target node. Upon reaching the goal node (the last item in the list), the loop for updating the target node is terminated. This synchronization between the local and global planners ensures that the robot effectively follows the optimal path generated by the global planner while navigating towards the goal, thereby facilitating efficient and safe navigation within the environment.
5. Test the combination of your local and global planner for a longer period on the real robot. What do you see that happens in terms of the calculated position of the robot? What is a way to solve this?
   • It was observed that the actual position of the robot was not exactly equal to what the odometry data shown. This could be due to the slip of wheels while turning and was observed more when angular velocity was high. For now, this slip can be avoided by lowering the angular velocity and avoiding jerks. Also, Localization will help to solve this issue by identifying the exact location of the robot in the environment.
6. Run the A* algorithm using the grid map (with the provided node list) and using the PRM. What do you observe? Comment on the advantage of using PRM in an open space.
   • Simulation video for A* with grid map: https://youtu.be/UN-J4saDtEw
   • The main advantage of having PRM over grid map is the route/path in grid map has sharp and sudden turns which makes robot to rotate with sudden jerk which is not suitable for the application, on the other side in PRM the the path has much smoother turns.

Simulation

1. Global + Local (Artificial potential fields): https://youtu.be/7N9LWmMrCGY
2. Global + Local (Dynamic window approach): https://youtu.be/GyHqKcMxtDw
3. Simulation video for A* with PRM: https://youtu.be/f1PKLg8FLyA

The behavior when combining local with global is very similar to exactly following the reference created with only the global implemented. Since the obstacle distance when repulsive forces start to act is smaller than the distance to the walls inside the initial corridor, the robots sways left and right. This could be fixed by tuning APF parameters further.

Physical setup

1. Global + Local (Artificial potential fields): https://www.youtube.com/watch?v=__dvgxrpebI
2. Global + Local (Artificial potential fields) with the dynamic obstacle: https://www.youtube.com/watch?v=6UgUIg0o0kk

With the real-life experiments, the robot reaches the goal with either of the local planners. But with APF, it completes an extra circle in the top right corner. It could be because of the inaccurate scaling in the map which cant be compensated for since localization is not implemented yet. This did not happen when testing with human obstacles on Hero. In this case, the robot did avoid the moving human, and reached the goal without the extra circle.

Exercise 4 - Localization

Localization in robot navigation is the process by which a robot determines its position and orientation within a known environment. This involves estimating the robot's coordinates and direction, typically using data from sensors (such as LiDAR, odometery). Accurate localization is essential for tasks like path planning, navigation, and avoiding obstacles, allowing the robot to move and operate autonomously.

Assignment 0.1

1. How is the code structured?

Tests passed for assignment 0.2

The code for the Localization is split into several different files and classes and they are combined in the main.cpp file. The differences between those files are explained below.

2. What is the difference between the ParticleFilter and ParticleFilterBase classes, and how are they related to each other?

Particle filter inherits from the ParticlefilterBase class which gives it access to the members of PatricleFilterBase. In the ParticleFilterBase, the particles are initialized, and has all the information about the group of all particles. While the particleFilter is responsible for defining the sampling algorithm and determines when the resampling happens.

3. How are the ParticleFilter and Particle class related to each other?

The ParticleFilter class consists of the information about all the particles that are created by the particle filter and this data can be used to estimate the state of the system. Particle class, however, consists of information about a singular particle and has several information about it like the position and its weight.

4. Both the ParticleFilterBase and Particle classes implement a propagation method. What is the difference between the methods?

The Particle class propagates the particle position of a singular node using the odometry and noise data for each particle individually. While the ParticleFilterBase propagates all particles by iterating over each of the particles.

Assignment 0.2

The figure to the right depicts that all test cases are passed when running the Localization code after including code form the other assignments.

Ass. 1.1 Initialization of the particle filter

Assignment 1.1- Initialization

What are the advantages/disadvantages of using the first constructor, what are the advantages/disadvantages of the second one?

The first constructor uses a uniform distribution to initialize the particle by creating the particles around the initial guess area, while the second one uses Gaussian distributions to do the same.

Uniform constructor

Advantages:

• The spread of particles over the entire map allows the robot to find its position even when there is no initial estimate and the robots previous position was unknown. Since the particles would be everywhere around the map.

Disadvantages:

• Computationally inefficient- many particles may be placed in unrealistic positions that have a low likelihood of being the robot's actual position. It may also need more particles to find the position of the robot.
• Slow convergence since many particles are not close to the real position the guess will converge to the real position much slower.

Gaussian constructor

Advantages:

• The particles are more concentrated around the initial guess area, which in the case of a good initial estimate gives more particles around the real position of the robot.
• Computationally efficient- fewer particles are needed to find the robot position if the previous position had a good guess.

Disadvantages:

• If the initial guess is wrong the Gaussian constructor may lead too the robot not being able to find its actual position this is due to the fact that there will be no particles around actual robot position.
  

In which cases should either of them be used?

Ass. 1.2 Pose estimate

If there is a good initial guess the Guassian particle should be used this is due to the fact that hen most of the particles would be around the robots actual position which would allow the robot position from the particle filter to converge much faster. However, the uniform constructor still has its use, if the initial position on the map is unknown it spreads particles around the entire map which allows the particle filter to converge to the certain position which would be impossible when using the Gaussian constructor.

Assignment 1.2- Pose estimate

Interpret the resulting filter average. What does it resemble? Is the estimated robot pose correct? Why?

The resulting filter average is shown by the green arrow on the Figure to the right. It shows the position computed using the weighted average of the particles created using the Gaussian constructor and gives the psosition and rotation of the robot. It is close to the initial guess of the particle filter and because of that it is shifted relative to the actual position of the robot, since position of the initial guess was not exactly the same as robots position on the map. Imagine a case in which the filter average is inadequate for determining the robot's position.

If there are similar environmental features in a map that are present at different ends or far away from each other, then the particles will be distributed near both these positions. In this scenario the average will be in between the two features which completely does not resemble the true robot position. The computed average robot position would be placed in between those two areas where the particles are concentrated and not in one of those two positions.

Assignment 1.3- Propagation of particles

Why do we need to inject noise into the propagation when the received odometry information already has an unknown noise component?

Without addition of the noise variance of the particles is very low, because of that the particles would be at similar position to each other and can converge with time to one point. When this happens the particle filter behaves like it only has less particles than desired value which drastically decreases its accuracy. What happens when we stop here and do not incorporate a correction step?

If the correction step is not done, then the initially created particles propagate continuously which leads to multiple particles indicating positions that have a low likelihood that do not help with localization. This is computationally demanding even though it does not give reasonable approximations.

Video- https://www.youtube.com/watch?v=oThxcGkbwPg

Assignment 2.1- LiDAR correction

In the measurement model all the components of measurement model are guarded by the max range, in reality, in both simulation and practical test it became apparent that lidar can give the value as infinity for the range and because of that the likelihood of the particle would be zero since we multiply with the likelihood with another particle, if one particle is out of range it will get the likelihood to out of range or as infinity. because of this, an if statement was added which checks the range value of each laser data, if it were higher than the max range this value was overwritten to the max range.

What does each of the components of the measurement model represent, and why is each necessary.

Measurement model consists of 4 different components:

• Gaussian Distribution - From the map the expected range that the LiDAR would read is known this value is represented with the Gaussian distribution. Thanks to the bell shape of this distribution it also accounts for potential noises and inaccuracies of the reading since it also assigns higher likelihood to the particles that are close to the expected distance, but are not exactly the same.

• Exponential component - There is a chance that an unexpected obstacle that is not present on the map can be seen by the LiDAR. This may be a new static object or a person passing by. In this scenario a lower reading than expected from the map is given by the LiDAR. The exponential guess is used to compute likelihood of the particle in these scenario. Thanks to it the readings that are lower than the ones expected from the map are also considered when computing the likelihood of the particle.

• Uniform component - LiDAR can have some noise which leads to unexpected readings. Those are accounted for in the uniform distribution that assigns the probability to the reading over the entire range of the LiDAR without it even one inaccurate reading could lead to the likelihood of the particle being 0.

• Uniform component for max range - This components is used to account for the readings that are returned when the LiDAR doesn't hit an obstacle inside its range. Furthermore, during testing on physical setup and in the simulator LiDAR returned the range values equal to inf those values where also accounted for in this component. This was done by changing readings that are higher than max range to the max range value.

With each particle having N >> 1 rays, and each likelihood being ∈ [0, 1], where could you see an issue given our current implementation of the likelihood computation.

Likelihood of the particle with this implementation can be a really small number and when multiplying them with each other several time the accuracy of the final result can be compromised. Even though measurement likelihood in the implementation is of a type float that has accuracy of up to 15 decimal points.

Assignment 2.2- Resampling

What are the benefits and disadvantages of both the multinomial resampling and the stratified resampling?

Multinomial resampling

Multinomial resampling is a technique used in particle filtering, where a set of weighted particles represents the probability distribution of a system's state. During resampling, new particles are drawn from this set with replacement, where each particle's probability of being selected is proportional to its weight. This means particles with higher weights are more likely to be chosen multiple times, while particles with lower weights may not be selected at all. The result is a new set of particles, called the resampled set, that reflects the system's state distribution more accurately.

Advantages:

• Simplicity: Multinomial resampling is simple to implement and comprehend, making it useful in practice.
• It is computationally efficient, particularly for small to medium-sized particle collections, because it involves sampling particles and replacing them depending on their weights.

Disadvantages:

• Multinomial resampling can suffer from sample degeneracy, which occurs when a small number of particles dominate the posterior distribution, resulting in poor estimate performance.
• High Variance: It has higher variance than other resampling approaches, which might result in poor estimate accuracy.

Stratified resampling

Stratified resampling is a technique used in particle filtering, where a set of weighted particles represents the probability distribution of a system's state. During resampling, the state space is divided into subsets, and within each subset, particles are drawn with replacement using a uniform distribution. This ensures that each subset contributes particles to the resampled set, leading to improved diversity compared to simple random resampling methods.

Advantages:

• Improved Variety: Stratified resampling draws particles from various parts of the state space, resulting in a more varied resampled set than basic random resampling approaches. This variety reduces particle degeneracy and improves estimate accuracy.
• Reduced risk of Degeneracy: By guaranteeing that each subgroup contributes particles to the resampled set, stratified resampling minimizes the possibility of particle degeneracy, which occurs when just a few particles have considerable weight.
• Enhanced Estimation Accuracy: The increased variety and lower likelihood of degeneracy associated with stratified resampling often result in more accurate state estimation,

Disadvantages:

• Additional Computational complexity: Stratified resampling requires splitting the state space into subsets, which adds computational complexity to the resampling procedure.
• Implementation Complexity: Stratified resampling may be more hard to implement than basic random resampling approaches. It involves additional stages for splitting the state space and drawing particles from each subset, which might complicate the algorithm and require close attention to detail.

Videos

1. Multinomial Resampling Algorithm tested on simulator - https://www.youtube.com/watch?v=OfiZdNQ-8fg
2. Stratified Resampling Algorithm tested on simulator - https://www.youtube.com/watch?v=wNeE1HUUhO0

Assignment 2.3- Physical setup test

How you tuned the parameters.

With initial parameters that were given the particle filter had a negative impact on the robots performance the localization was updating quite fast on the visualization but sending commands via teleop was much slower and there was a big delay between the command and actual movement. Because of the limited amount of time that the group had available only the particle number was decreased to 1500. This change increased the performance of the robot drastically. However, more tuning may still be needed before the final assignment to see how accurate the initial guess needs to be especially since this will have an impact on how well the robot can do any of the tasks. How accurate and fast your localization is, and whether this will be sufficient for the final challenge.

The accuracy of localization is quite high as can be seen in the video below. However the exact value was not quantified. But as shown on the video the robot position correlates the position on the map and it is also updated in the real time. However via further testing other sampling schemes can be tested if it becomes even faster.

How your algorithm responds to unmodeled obstacles.

As mentioned before only a limited time for testing the localization was available so no tests with unmodeled obstacles were conducted. However if there are unmodeled obstacles the exponential component of the measurement model should handle them if this will not be the case the weight of this component will need to be adjusted.

Video- https://www.youtube.com/watch?v=pfD3A7Y9ox8

Report

State Flow Diagram

State Flow Diagram

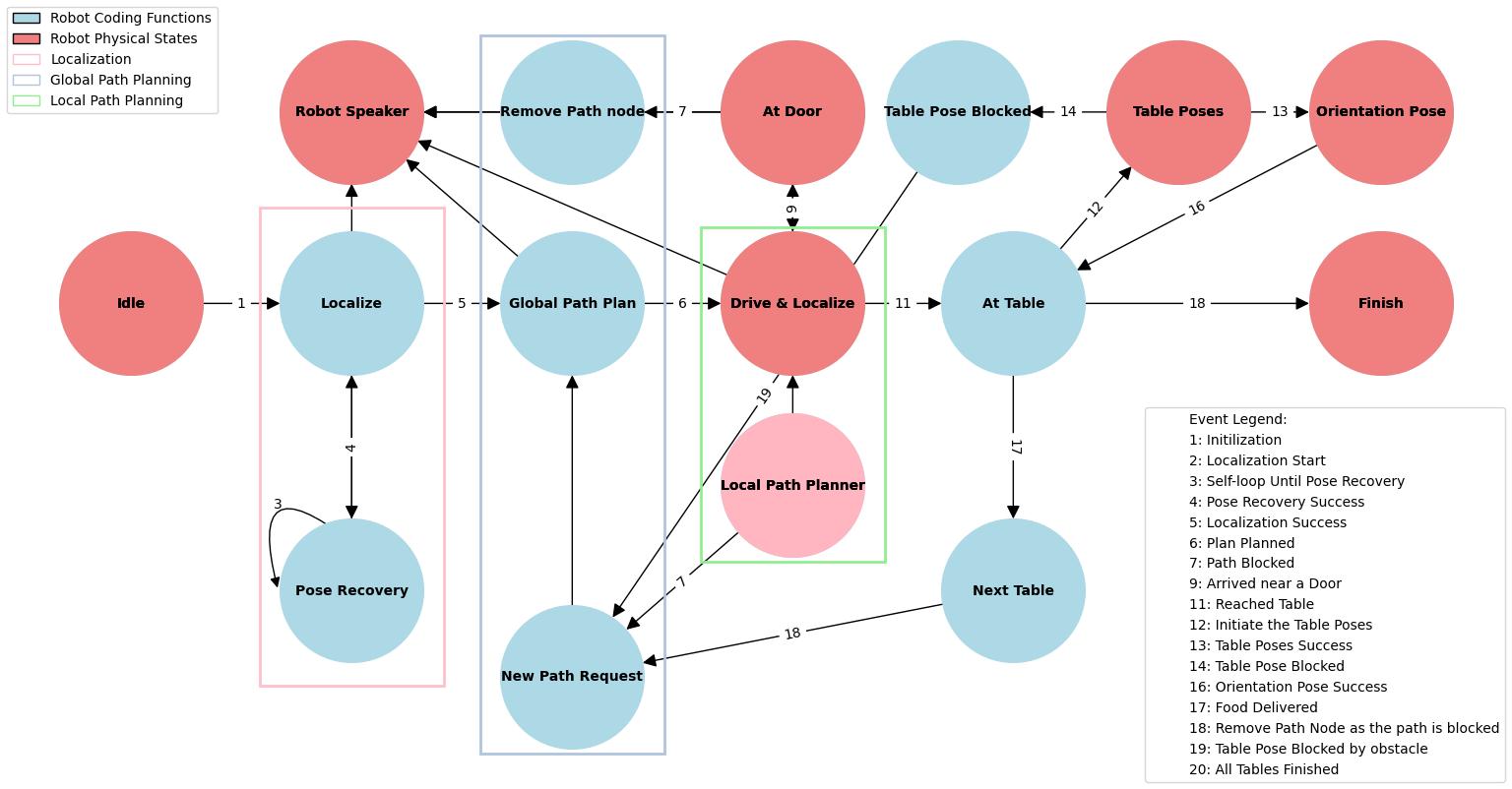
The state flow diagram for the Hero robot begins in the "Idle" state, where the robot remains inactive until it receives a command to start the localization process. Initialization triggers the localization process and transitions the robot to the "Localize" state, where it attempts to determine its initial position on the provided map. If the robot fails to localize accurately, it enters the "Pose Recovery using uniform spacing technique" state, which includes a self-loop to repeatedly attempt pose recovery until successful. Once localized, the robot proceeds to the "Global Path Plan" state to calculate a valid path to its destination table. The robot follows this path, avoiding static and dynamic obstacles in real-time. If the path is completely blocked, it creates a "New Path Request" to the global path planner, which generates a new route until the destination is reached.

Next, the robot enters the "Drive & Localize" state, moving while continuously updating its position on the map. Upon encountering doors, it transitions to the "At Door" state, waiting up to 10 seconds for the door to open. If the door remains closed, the robot requests a new path from the global path planner, which excludes the blocked path from future consideration. This process continues until a viable path bypassing the doorway is found. If the Door is opened and robot Successfully passes the door, the robot continues with the path until it is closer to the destination table. Once closer, the robot will try to reach the "Table Pose 1" state, aligning itself for the first position near the table. If this table pose is blocked, it will try to find a docking position on the other side of the table by requesting a new path from the global path planner. Once a pose is reached without obstacles, the robot adjusts its orientation to face the table correctly, preparing to deliver food.

Once the food is delivered, the robot transitions to the "Next Table" state if there are additional tables to visit. This process repeats until all tables are served, after which the robot transitions to the "Finish" state, marking the end of its tasks. Throughout this process, The robot will utilise the speaker as a medium to express the current states and the actions performed. The robot continuously monitors its path and surroundings, dynamically adjusting its actions to ensure successful task completion and efficiently navigation through obstacles. This state flow ensures the robot operates effectively within its restaurant environment.

Local navigation

As elaborated previously, localization provides an estimate of the robot’s current pose, and global planner lists the order of nodes to be visited before reaching the final goal. However, a local planner is necessary to travel between these nodes and additionally, an obstacle avoidance feature is also implemented. Through the course of this project, two such planners in Dynamic Window Approach (DWA) and Artificial Potential Field (APF) were explored.

DWA is a velocity-based algorithm that simulates the future positions for a range of considered speeds. Based on their final positions and a reward function, the better pair (one that maximizes the reward) of linear and angular velocities are assigned to the robot. The implementation is detailed further in section 4.2. Upon testing, it was realized that DWA leads to smooth motion of the robot as it predicts future pose and accounts for the position of obstacles beforehand. However, its computational complexity of pose estimation, DWA is only warranted for a small range of velocities and time-frame for future estimation. This was evident especially when the simulation output warning messages regarding time per iteration exceeding the sample-frequency for new data. In addition to this limitation, it was also realized that DWA was not robust enough in cluttered environments as it struggled to find its way in the fourth map when tested in real-life.

Inspired by repulsive and attractive forces, APF is an artificial potential energy based algorithm that attracts the robot towards the final goal but repels it from obstacles. The force terms are inversely proportional to the current pose wherein the attractive component is more dominant farther from the goal whilst the repulsive counterpart is more apparent closer to obstacles. The vector sum of these forces are used in navigating the robot. As detailed in section 4.1.6, APF performed well in simulations. However, there was a need for tuning the parameters to replicate it in real life as depicted in 4.1.7. APF proved to have difficulties in reaching the goal as there were situations when repulsive forces cancelled with the attractive ones. This was overcome by applying random perturbations of small magnitudes  to push it out of the local minima. With these additions, APF managed to avoid obstacles and reach the final goal.

In comparing the two techniques, APF out-performed DWA even in cluttered environments with ease. However, in narrow paths (corridors) the repulsion and attraction caused jerky behavior while DWA did handle them better. It was also found that APF reacted faster to dynamic obstacles as this technique was not constrained with the magnitude of velocities. Upon widening the range of velocities for DWA, to account for the computational complexity, the time interval for pose estimation had to be reduced. This hindered DWA’s performance even in front of static obstacles. Given these drawbacks associated with tuning DWA, APF was more preferred for its simplicity and scalability. So, APF was the chosen one.

The APF function integrated for the final challenge takes the average pose estimate from localization as input. This allowed the robot to locate itself in its environment efficiently and take feasible decisions to reach the next node as proposed by the global A* planner. The local planner performed sufficiently well in the final demonstration avoiding static obstacles (chair), and dynamic obstacles (people). Even when localization was lost during testing, the APF algorithm successfully avoided collisions. As far as the integration between local and global planners is concerned, APF treats each node from the A* node list as a temporary goal node. Once a node is reached, the goal node is updated iteratively until the food is served to all tables in the table-sequence.

(VIDEO LINK FOR OBSTACLE AVOIDANCE)

(VIDEO LINK FOR TRAVELLING BETWEEN NODES)

It must be noted that the parameters of APF can be tuned further to avoid jerky behavior when cruising through narrow corridors. In the context of the stake-holders, it will avoid accidental food spillage due to the sudden jerks. Weights can be added to attractive and repulsive forces that evolve dynamically which could lead smoother motions.

Global navigation

Path Replanning

When the robot encounters a local minima, an unexpected obstacle, or a change in the map that prevents it from reaching the next node using the local planner, or if it becomes disoriented due to the number of obstacles, it activates a re-routing algorithm. This re-routing process is triggered if the robot fails to reach the next path node within a specified timeframe (15 seconds). This timestamp is reset whenever a new target node is established.

If the specified timeframe is exceeded before reaching the node, the robot halts its current position and activates the 'Node_unreachable()' function. This function designates the parent node ID of the unreachable node as the new start node ID and eliminates all connections to the unreachable node, ensuring that it is excluded from future path planning. Subsequently, the pathplan() function is invoked again to generate a new path with the updated start node while maintaining the same end goal. Once a new path is formulated, the local planner is reinitiated to follow the new path until the robot successfully reaches its destination. During the final challenge, the robot was tasked with traveling from table 4 to table 3. However, the direct path between these tables was obstructed, causing the robot to repeatedly attempt to reach the next node located on the opposite side of the blockage. Despite its efforts, the robot was unable to proceed due to the obstruction. The robot continued its attempts until the allotted time expired, at which point it initiated a re-routing algorithm with a new start node.

Unfortunately, the robot encountered the same blockage, causing it to run out of time again. The re-routing algorithm persisted in trying to find a path through the obstructed passage until all nodes in that passage were marked as unusable. Only then did the planner search for an alternative route, eventually discovering a path through a door and continuing toward its goal. This behavior was consistently observed during testing.

In the final challenge, the robot replanned twice through the same blocked passage. However, by utilizing the local planner, it eventually reached the door in the effort to reach the node. Upon opening the door, it was noted that the robot was still attempting to reach the same node, which was in the opposite direction to table 3. It is assumed that this node was likely situated within the obstacle itself.

As a result, before the robot could replan and reach table 3, the time for trial 1 expired. Given more time, the robot would have successfully replanned a new path towards its goal. To enhance the efficiency and speed of the replanning process, an alternative approach was implemented during testing before the final challenge. Instead of setting the parent node of the unreachable node as the new start node, the robot's current position coordinates ('Current_x' and 'Current_y') were retrieved from the localization system. These coordinates were then provided to the construct planner with PRM function.

The construct planner function was initiated, updating the x_start and y_start coordinates with the robot's current position coordinates. The planner then establishes new connections between the updated start node and existing surrounding nodes. Once the start node is set planPath() function is initiated with the timer being reset. This method proved to be faster and more efficient, as it enabled the robot to replan its path from its current position, eliminating the necessity to move towards the new start node to resume path following. Consequently, even if the robot became disoriented or deviated from its path, the new path planning commenced directly from its current location enabling the robot proceed directly towards its goal table.

Localization

Localization is a crucial component of any robotic system because without it being robust the robot will not be able to achieve any task. This is due to the factg that to complete the task robot needs to be where it is inside the room. In the case of the restaurant the exact initial position is not fully known and especially due to uncertainities of the angle of the robot odometry is not sufficient to knwo robots position. That is why particle filter is being used which uses LiDar data paired with odmetry to predict the robots position. There are several components that need to be considered regarding the localization that are discussed below.

Map of the final challenge

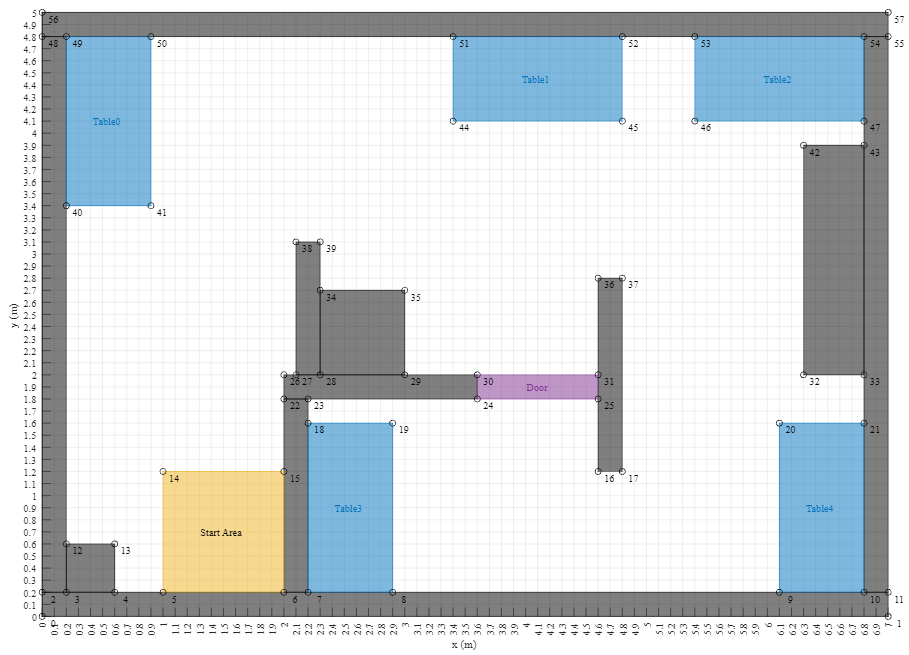
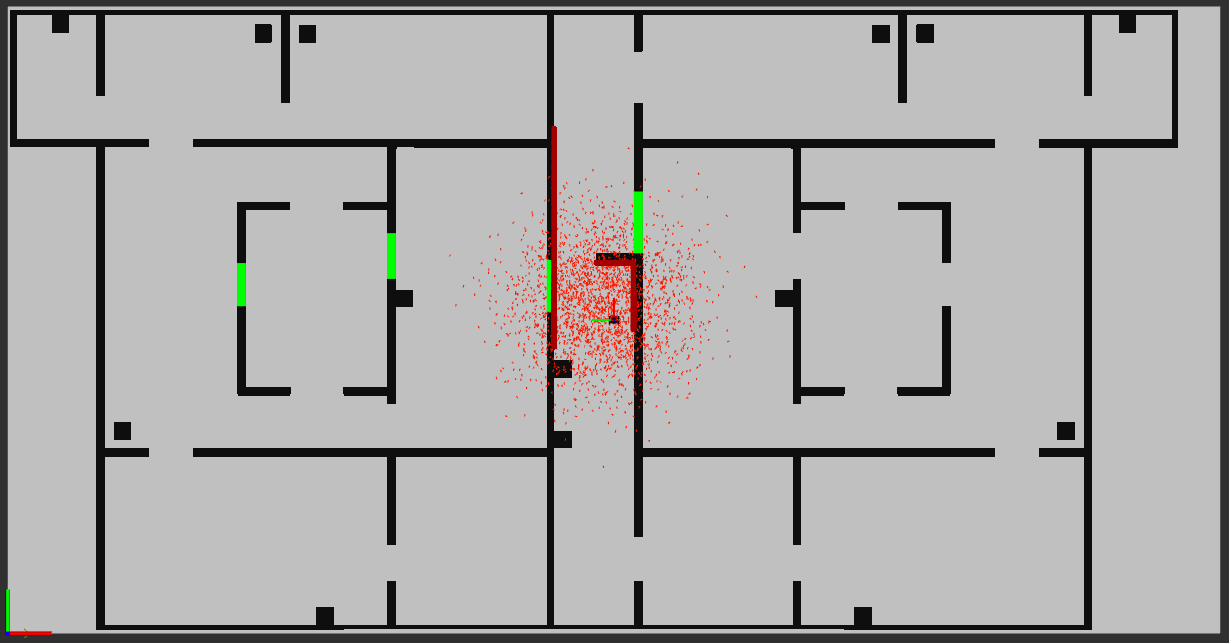
Initial guess

During the final challenge, the area where the robot starts is known and can be seen in the figure. Due to this, initializng particle filter using gaussian distribution seems to be a better method to initialize. The reason behind this is that there are many more particles around the actual position of the robot in comparison to uniform distribution, which should allow the position obtained from the particle filter to converge much faster. However, after initial testing, this method showed to have one major drawback, it was very sensitive to uncertainties in the intial angle of the robot, and often, if the actual angle of the robot deviated too much from the initial guess, the robot position would converge in a wrong spot. It often happened that the robot would think that it is on the other side of the wall in the area next to table three. After that unaccurate initial guess almost no amount of driving to try recover the robot position was sufficient because the difference was too big.

To fix this problem, a different method to initialize the particle filter was chosen. A uniform distribution was used, which leads to the creation of particles randomly spread around certain area. This method does not need an accurate initial guess but comes with other downsides: it is much more computationally demanding (a higher number of particles may be needed), it takes much longer for the robot to converge to an accurate position, and the method may struggle with retrieving the robot's actual position if certain map components are similiar to one another. Due to these issues, this approach also needed adjustments before being implemented on the robot.

Since the initial position is still known, it can be used to improve the initial particle distribution and minimize reliance on the angle. To do this, the particles are initialized uniformly only in the area of the initial guess in the final design of the system. This approach proved to be robust and did not require extra movement before the robot's position converged, as this happened almost instantly after starting the robot. To ensure that the problem of localizing in the area around table three was resolved, tests were conducted with the robot placed in different orientations in the initial guess area. After checking all the corner scenarios with different rotation this method was proven to be robust, the robot was always able to find its position in regards to the map cocrdinate frame.

Doors

Map used for localization- without doors

Another difficulty encountered during testing was the loss of localization accuracy around the door area when using the challenge map as an input. When going through the doors or driving close to them when they were open, the robot's position on the map started to diverge more and more from its actual position and was never able to recover. The reason for this is that the robot expected input from the LiDAR to be the same as when driving next to a wall. According to the measurement model, these distances are the most probable. When the doors were open, this obstacle was not present, and thus the accuracy of the particle filter decreased drastically in this spot.

The initial idea to fix this problem was to try increasing the probability of a random component of the particle filter, but this led to other undesired problems. Increasing the probability of this component caused the robot to expect more readings that did not correlate with the map, resulting in decreased accuracy across the entire map.

However, since the measurement model already compensates for objects closer to the robot than walls with the exponential component, instead of trying to localize based on a map with doors that may not always be visible, a new map was created that does not include doors. Testing proved that this approach is effective and robust, as the new map fixed the problem of the robot losing its position when moving through the door. The expectation of a wall being at the door position was no longer used to compute robots position and when the doors were closed they were treated in the same way as any other obstacle, thus maintaining accuracy of the particle filter.

Tunable parameters

There are several parameters of the particle filter that can be adjusted to increase its accuracy, such as the number of particles or the weights of certain components of the measurement model. With more particles, there is a bigger spread, and averaging the robot's position should lead to more accurate results. However, there is a significant downside to increasing this value. Generating more particles takes more computing power, which can lead to drastic delays and a decrease in the accuracy of the particle filter.

To compensate for this, the number of particles was changed to 1,000. This value still proved to be sufficient during testing, and the computer was able to update the filter fast enough. Furthermore, the probability of the exponential hit was increased. During testing, when several people were standing around the robot, it sometimes started to localize itself further and further away from its actual position. A similar behavior occurred next to the doors. To compensate for this, the probability of the exponential component was increased.

Extra functionality

Door opening

With the doors being no different than walls for the laser range finder, the only way to detect that the robot is approaching the door is to use the map and the robot's relative position to the door. Using this information, a specific behavior can be implemented when the robot approaches the door.

Since there is only one door on the map, a new boolean variable indicates whether the door has been opened, with its initial value set to false. When the robot approaches the door's position at a certain angle, it will stop and make a reference LiDAR scan, which will be used for comparison with scans taken over the next 20 seconds. The average value of the range from this initial scan is computed, and the robot asks for the door to be opened. Then, over the next 20 seconds, the robot will continue making scans until it detects that the average distance has increased by at least 20 cm. Whenever this happens, the robot updates the boolean to true and continues along its path. If the door cannot be opened within the given 20 seconds, the robot will resume its movement and, if the path through the door is still blocked, it will replan the path until it finds a route that does not go through the door.

Since it is assumed that the door is always closed at the start, an extra function was added. The robot always waits for 20 seconds the first time it reaches the door. If the door is open, it will also stop. In this case, the reference scan and subsequent scans will have the same value, and the robot will not resume its movement until the timer runs out. After this happens, the robot will display the same behavior as when the doors are opened and resume its movement along the path.

This functionality could be improved even more in the future. The behavior of the robot stopping near the door should be kept, but it should occur every time the robot approaches the door, as the door may get closed after the robot moved through it. This could be implemented by updating the boolean after the robot passes the door. Furthermore, the reference scan could be used to determine whether the door is open by using predefined thresholds for the average range readings to compare the readings. If the door is open, the robot would not need to wait for the predefined 20 seconds as it does currently and continue moving along the path just after the reference scan is completed.