Mobile Robot Control 2024 Optimus Prime

Introduction

We are Optimus Prime, a team of six members applying various control techniques and coding skills to optimize a robot for restaurant environments. Our goal is to enable the robot to efficiently deliver orders from the kitchen to the tables, even when faced with various obstacles. This project focuses on ensuring precise and reliable performance, ultimately improving service efficiency and the overall dining experience.

Group Members

Caption

Name	student ID
Yuvan Dwaraga	1563793
Wiktor Bocian	1628798
Ramakrishnan Rajasekar	1979027
Ariyanayag Ramesh Skandan	2012618
Abhir Adiverekar	1984136
Suryakumar Hariharan	1974076

Exercise 1 - The art of not crashing

This exercise aims to enhance our understanding of control techniques and obstacle avoidance algorithms.

Simulation of the robot moving

Solution 1

The odometry and laser data were obtained based on the instructions from the manual, enabling the robot to be aware of its surroundings. Although this sensor data does not provide instructions for the robot to stop or go when an obstacle is on its way, a discussion was held to include a constant safe distance value, which ensures that the robot maintains a safe distance from obstacles and avoids collisions. Loops were also introduced as the robot operates to check whether the obstacles are close to the robot or not. Specifically, if an obstacle is detected within a certain range less than the predefined safe distance (0.5 meters) the robot will come to a halt. This algorithm ensures that the robot can navigate in its surroundings safely.

Solution 2

Advancements to the previous solution were made by introducing rotation values and forward motion value to enhance the robot's performance. These values were effective when the obstacle is too close to the robot. The stoppage of the robot comes into play and the rotation values allow it to rotate with movement restriction and later it allows the robot to move in the forward direction with constant units. This approach ensures that the robot not only stops to avoid immediate collisions but also actively seeks a safe route forward. Overall, the combination of a constant safe distance, rotation and forward actions allows the robot to perform more efficiently.

Simulation of the robot movement in x direction

Learnings from solution

The robot's performance in this case was evidenced in both simulation and in practical sessions. Alterations in the code were made so that, in case of the obstacle detection, the robot was made to move in the x direction in adherence to the safe distance.

Practical session

The live testing of don't crash test can be evidenced by accessing the link [1]

Exercise 2 - Local navigation

Artificial potential fields

Motivation

Choosing the artificial potential field (APF) method for local navigation of a robot comes with several compelling motivations:

1. Simplicity and intuitiveness: The APF approach is reasonably easy to grasp and apply. It mimics the environment using attractive and repulsive forces that naturally direct the robot to its destination while avoiding obstacles.
2. Continuous and smooth path generation: This approach creates smooth and continuous tracks for the robot without any jerks. Because the forces are computed as gradients of potential fields, the resulting motion is smooth, avoiding the possibility of sudden changes in direction that would be difficult for the robot to perform.
3. Scalability: APF is easily adaptable to many types and sizes of settings (environment). The approach may be adjusted to a variety of circumstances by modifying the potential field parameters, ranging from basic inside navigation to more difficult outdoor settings.
4. Combination with Other Methods: APF may be utilized effectively with other navigation systems. For example, it may be used for local navigation inside a larger framework that handles global path planning, integrating the benefits of several frameworks.

Solutions

1. Converting the body fixed frame into global coordinate To implement this the transformedOdometry() function was created which was used to convert the odometry data of the robot into global coordinate system.
2. Normalizing the angle The normalize_angle() function ensures that any given angle is mapped to an equivalent angle within the standard range of −π to π radians. This is useful because angles can be represented in multiple ways (e.g., 3π is the same as π), and having a consistent representation simplifies many calculations and comparisons.
3. Calculating attractive forces The attraction_force() function calculates a linear attractive force towards a target position. This force is proportional to the distance between the current position and the target position, scaled by an attraction coefficient.
4. Calculating repulsive forces The repulsion_force() function calculates a repulsive force that acts to push a point (or robot) away from an obstacle when it gets too close. The force is designed to be strong when the point is very close to the obstacle and diminishes as the point moves away, ensuring safe navigation around obstacles.

Learnings from each solution

While the artificial potential field (APF) approach has significant benefits for robot navigation, it also has certain drawbacks, such as the possibility of being caught in local minima or oscillations. To address these concerns, many fixes and improvements to the APF approach have been proposed:

Gradient Descent with Escape Strategies: One typical problem with APF is getting stuck in local minima when the attractive and repulsive forces cancel out.

Solution: Random Walks or Perturbations - By introducing small random movements or perturbations, the robot can escape local minima. To come out of the local minima random perturbations were added in the APF algorithm and it was successful at the end.

Combination with Global Path Planning: Integrating APF with a global path planning algorithm can provide a more comprehensive navigation solution.

Solution: Hybrid Approaches - Finding a rough path with a global planner such as A* or Dijkstra's algorithm, and then using APF for local navigation to fine-tune the path and avoid obstacles.

When tested out with the common settings for the APF it was found that for some maps it was stuck in the local minima, for this different parameters were designed (attractive gains and repulsive gains) for each map and after implementing this strategy the robot was able to function properly for each map efficiently.

Visual representation of sim

1. Map 1 - https://www.youtube.com/watch?v=PWZg0-T9-U8
2. Map 2 - https://www.youtube.com/watch?v=E6Xz24zsPdE
3. Map 3 - https://www.youtube.com/watch?v=ZnRjnttkkrE
4. Map 4 - https://www.youtube.com/watch?v=ERdRPLcliLk

For first three simulation the parameters were the same, but for the fourth simulation the parameters were a bit different.

Pros and cons

Pros

1. Simplicity: The APF approach is straightforward to implement and understand. It uses simple mathematical functions to represent attractive forces towards the goal and repulsive forces away from obstacles.
2. Real-time Computation: APF algorithms are computationally efficient, making them suitable for real-time applications. The computations involved are minimal and can be handled by most modern processors with ease.
3. Scalability: APF methods can be scaled to handle different sizes and types of robots without significant modifications to the algorithm.

Cons

1. Local Minima Problem: One of the significant drawbacks of APF methods is the local minima problem, where the robot can get stuck in a position that is not the goal due to equal attractive and repulsive forces cancelling each other out.
2. Inability to Handle Complex Environments: APF methods may struggle with complex environments with narrow passages or multiple closely spaced obstacles, leading to suboptimal or infeasible paths.
3. Parameter Tuning: The performance of APF methods heavily depends on the tuning of parameters such as the strength of attractive and repulsive forces. Improper tuning can lead to inefficient navigation or failure to reach the goal.

Dynamic window approach

Motivation

Our motivation for choosing the Dynamic Window Approach (DWA) algorithm is that it is one of the most ideal algorithms for local navigation of Mobile Robot Controllers (MRC). DWA strikes a balance between robust obstacle avoidance and efficient navigation. It generates control commands in real-time, which is crucial for dynamic environments. Additionally, it considers the robot's kinematic and dynamic constraints, ensuring that the paths are feasible. The algorithm effectively navigates around obstacles while moving towards its goal, maintaining both precise and responsive movement.

Solutions

1. To converts the robot odometry data from the body-fixed frame to the global coordinate system transformOdometry() function helps in maintaining the robot's current position and orientation in the global frame, which is essential for planning and executing paths.
2. normalize_angle() Normalizes any given angle to the range of -pi to pi radians.

the distance between two points in the 2D space, length() function calculates Measures distances for obstacle avoidance and goal-reaching computations.

1. generateAllPossibleVels() Generates a list of possible velocities within specified minimum and maximum bounds. Provides a range of velocity options to evaluate for the best possible path.
2. SaveXYCoordinatesObstacle() Converts laser scan data to global coordinates of obstacles and helps in identifying the position of obstacles relative to the robot for collision avoidance.
3. the robot future position based on its current state and a given time step, we also use this function to predicts future positions and evaluate possible trajectories and their feasibility using NextPose() function.
4. CalcClosestDistObstacle() Computes the distance to the closest obstacle for a given trajectory and the safety of each potential path by measuring how close the robot will come to obstacles.
5. the angular error between the robot future position (next iteration) and the target goal is done in calcAngleError().

How These Functions Help DWA Coding

• Localization and Coordination: Functions like transformOdometry and normalize_angle ensure the robot accurately knows its position and orientation.
• Path Planning: Functions such as NextPose and CalcClosestDistObstacle are crucial for evaluating possible trajectories and avoiding collisions.
• Trajectory Evaluation: The generateAllPossibleVels and BestVels functions generate and select the best possible velocities, ensuring safe and efficient navigation.
• Obstacle Avoidance: SaveXYCoordinatesObstacle and CalcClosestDistObstacle help in mapping obstacles and ensuring that the robot does not collide with them.
• Goal Alignment: The calcAngleError function ensures that the robot's trajectory is aligned with its goal, improving navigation efficiency.

Learnings from each solution

1. While the Dynamic Window Approach (DWA) is effective for robot navigation, it also faces certain challenges. Here are three common problems that was faced during Implementation:
2. Local Minima : DWA can get stuck in local minima, particularly in complex environments where optimal paths are not available we introduced recovery behaviors such as random perturbations or backtracking. Combine DWA with global path planning algorithms to guide the robot out of local minima.
3. Handling Dynamic Obstacles : DWA may struggle with many obstacles within a small space, recalculations that can be computationally demanding we tried implementing predictive modeling for dynamic obstacles, allowing the algorithm to anticipate and react to future positions of obstacles.
4. Parameter Tunig: DWA performance heavily depends on parameter tuning, such as velocity bounds and acceleration limits we tried implementing adaptive tuning techniques that adjust parameters dynamically based on the robot positin.

Visual representation of sim

To be Updated.

Practical video

To be updated.

Pros and cons

Pros

1. Dynamic Feasibility: DWA accounts for the robot dynamic constraints (like velocity and acceleration) ensuring that the generated paths are feasible and safe for the robot to follow.
2. Collision Avoidance: The algorithm effectively avoids collisions by evaluating possible trajectories within a feasible velocity window.
3. Real-time Feedback : DWA computes in real-time, making it suitable for applications where the robot needs to react quickly to changing environments.
4. Smooth Path Generation: It generates smooth and continuous paths, which are essential for the stable and efficient movement of robots.

Cons

1. Computational Load: DWA evaluates numerous possible trajectories within each window, which can become computationally intensive, especially in environments with many obstacles.
2. Local Minima Problem: Like APF, DWA can get stuck in local minima, particularly in complex environments where optimal paths are hard to find.
3. Handling Dynamic Obstacles: DWA adapts to dynamic environments but may struggle with fast-moving obstacles, requiring frequent recalculations that can be computationally expensive.

Exercise 3 - Global path planning

A* algorithm

A* algorithm finds the shortest path from the start node to the goal node through the known network of nodes and their connections. It initializes the _nodelist() which contains all the nodes and the connection data generated in by PRM algorithm. While finding the shortest path in each iteration the next node in the connection of current node is chosen on the basis of minimum cost (f) to reach goal i.e. the sum of cost-to-come and cost-to-go (heuristic cost). This cost is basically the absolute distance between in the node being analyzed and the goal node. In the algorithm a while node is initialized with a condition until the the goal node isn't reached and all the open nodes are not evaluated.

Node with minimum f

Here the node with minimum f value from the list of open nodes is selected. The variable 'nodeID minimum f' is initialized with a value indicating that no node has been identified yet. The 'minimum_f' variable is initialized to to infinity assuming that the actual 'f' value will be from the nodes will be finite and lower when iteration starts. The for-loop will iterate over all node IDs in the 'open nodes' container. For each node, it will retrieve the 'f' value from '_nodelist', vector storing nodes. If the 'f' value of the current node is less than the recorded minimum, 'minimum f' is updated with the new lower value and 'nodeID minimum f' will be set to the current node's ID.

Exploring the node connections

The loop iterates over nodes connected to this node, checking if they are already evaluated (in the 'closed nodes' list). For each unprocessed adjacent node, it computes a new cost-to-come ('g') as the sum of the current node's 'g' and the distance between both nodes. If this new 'g' is lower than the adjacent node's existing 'g', the node's 'g', heuristic estimate ('h'), and total cost ('f') are updated, and its parent is set to the current node. If the adjacent node isn't in the 'open nodes' list, it's added for future evaluation. After processing all connections, the current node is moved to the 'closed nodes' list, marking it as evaluated. This ensures that the path with the optimal cost is pursued, efficiently guiding the search towards the goal.

Trace back the optimal path

As soon as the goal node is reached the algorithm starts tracing the optimal path. It begins at the goal node, and works backwards using the 'parent node ID' of each node, which points to the preceding node on the optimal path. In the loop, the current node ID is added at the beginning of the 'path node IDs' list, to construct the path from start to goal. This backtracking is done until it reaches the start node which is then added to the list. Once the path is fully identified, the list of node IDs is stored and the algorithm marks the path as successfully found. This ensures the shortest path is clearly outlined and can be further used by respective local planner to reach the goal by avoiding obstacles.

Inflated walls with dilation size equal to 1

Probabilistic Road Map (PRM)

To implement the path planning algorithm a set of the possible paths needs to be created on the map that will be used to find an optimal one needs to be created. To do that the probabilistic roadmap method is used that generates the paths between randomly generated points on the map.

• Wall inflation

Inflated walls with dilation size equal to 2

Because of the size of the robot if the walls on the map are the same size as in reality the chance of the robot clipping the wall or crashing it becomes high since it is not just a point in reality. To avoid that the walls on the map need to be enlarged. To do that dilation on the map image is used. To do that, the map colors are first inverted since dilation works on white parts of the binary image. It is done by specifying the type and size of the Kernel that is used to check if there is a white point inside it and if there is such a point it changes the other ones inside the kernel to this color. For the desired implementation the square kernel is being used since all of the maps mostly consist of straight lines and the size of this kernel can be adjusted by changing the dilation size variable.

After the dilation the map is transformed back to its initial color scheme and examples with different kernel sizes of such operation can be seen to the right.

• Distance from other points

To ensure that points are distributed more evenly around the map the distance between the new vertex and all the previously created ones is being checked. This is done by checking the difference between the x and y coordinates is no smaller than 0.3 m. This ensures that each vertex has a square 0.3x0.3 m area around it of 0.3x0.3 m where there are no other vertices.

• Check for valid edge

To see if the vertex is valid two checks are being done. First to ensure that only the vertices that are relatively close to each other are connected the distance between them is being checked. This is done by computing the absolute value of a difference between the x and y variables of 2 vertices and then taking a square root of a sum of those values squared, which allows us to compute the distance between them in a straight line.

The other check that is being performed is seeing if there is a wall between the two nodes. To do that a line between two points is created using Bresenham's algorithm. It creates all the points along the straight line between two vertices and is used to check if there is a black point along the path. If the line encounters the black point it is marked as invalid and the edge between the two points is not created. This algorithm works by first computing the difference between the x and y position on the line and its final destination. The difference in y is subtracted from the difference in x and doubled to always work on integers, this gives information on how far the generated line is from the ideal straight line between two points. Knowing that if this error is higher than the difference in the y coordinate means that the lines should be less horizontal and the y value needs to be adjusted and the same is done for the x coordinate.

Example

Example of the map created using probabilistic roadmap

To test the algorithm the example map was being used with number of vertices equal to 70, dilation size equal to 2 which means that (5,5) square kernel was used for dilation and maximum distance between two edges of 1 m was created and can be seen on the Figure.

Assignment questions

How could finding the shortest path through the maze using the A* algorithm be made more efficient by placing the nodes differently? Sketch the small maze with the proposed nodes and the connections between them. Why would this be more efficient?

The way A* star works is it searches for the nodes in the graphs and checks for the nodes that can give the shortest path from the start node to the end goal. Firstly, reducing the number of nodes will help in using less storage space in node lists() and as well as reducing the required computational power as the algorithm will have fewer nodes to evaluate. This can be done by placing the nodes strategically at places where there are junctions, ends or where path diverge in the maze. This will surely enhance the efficiency of the A* algorithm by focusing on the nodes on key points.

Would implementing PRM in a map like the maze be efficient?

Yes using PRM can be more effective in the case where the maze is complex and have many obstacles to tackle. PRM uses sampling nodes which is more useful to to find possible path around the obstacles. On contrary, it can be a disadvantage since it uses more storage and computational power to compute and find the minimal cost, when its actually not necessary to have number of nodes in straight paths/passage in fact its more effective logical to have nodes at key points.

What would change if the map suddenly changes (e.g. the map gets updated)?

In the case if map suddenly changes,

How did you connect the local and global planner?

If seen conceptually, local planner uses the global planner as an input or guide to reach given goal from its start point. Global planner uses PRM or the grid map algorithm to explore and plots feasible nodes with connections between them throughout the map forming network and potential paths and stores it. These are used by A* algorithm to find the most optimal path by evaluating each node connection and the result is stored in a structured path node ID() list. Whereas the local planner retrieves this list from "planner.h". Then planner algorithm sets the initial node in the list as target node and continuously update its target node coordinates (Target x, Target y) to the next node in the list. This is updated when the robot reaches within a predefined safe distance of the current target node, as soon as the robot reaches the goal node (last item in the list) the target node updating loop is terminated.

Test the combination of your local and global planner for a longer period of time on the real robot. What do you see that happens in terms of the calculated position of the robot? What is a way to solve this?

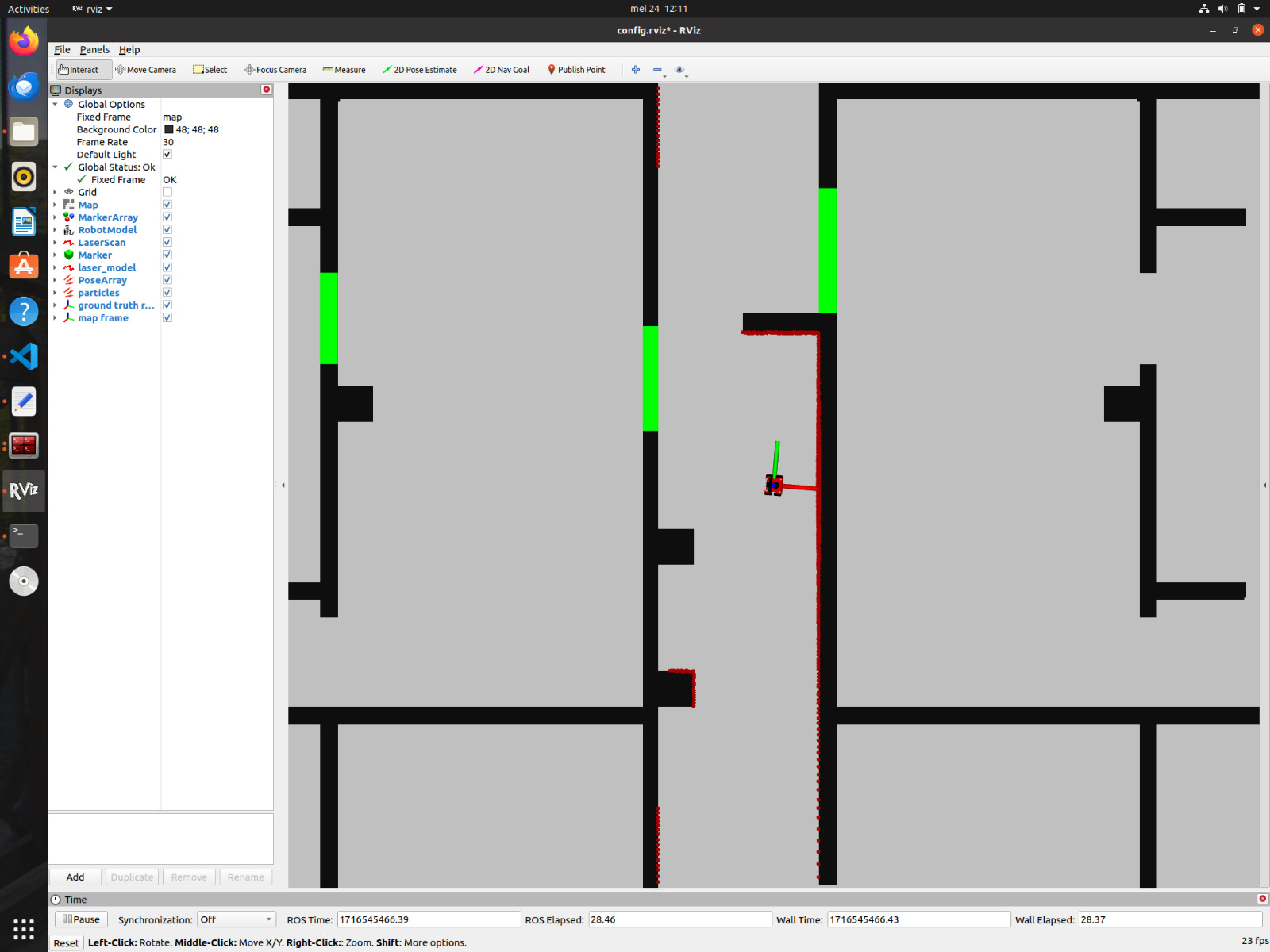
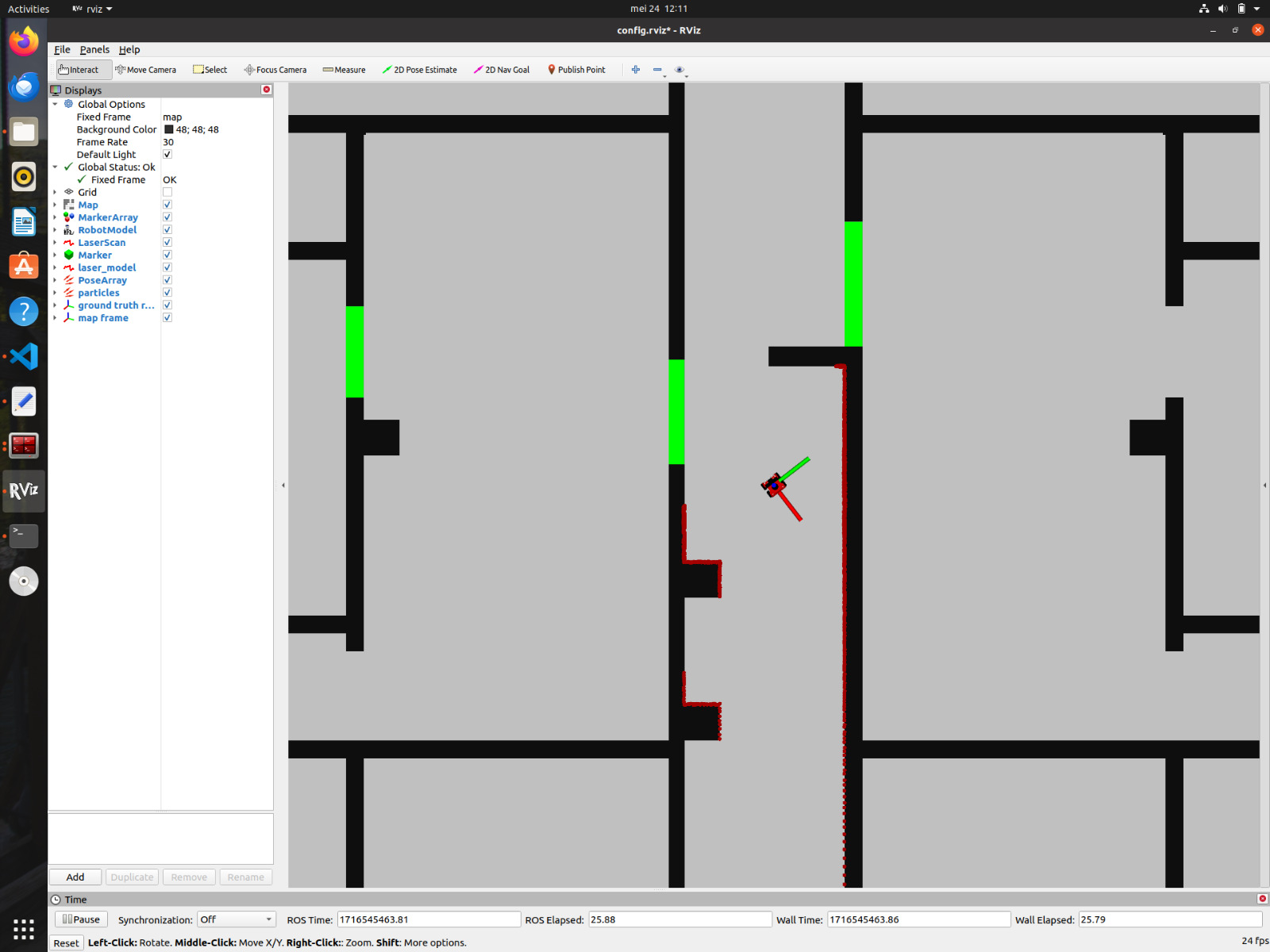
It was observed that the actual position of the robot was not exactly equal to what the odometry data shown. This could be due to the slip of wheels while turning and was observed more when angular velocity was high. For now this slip can be avoided by lowering the angular velocity and avoiding jerks. Also Localization will help to solve this issue by identifying the exact location of the robot in the environment.

Run the A* algorithm using the grid map (with the provided node list) and using the PRM. What do you observe? Comment on the advantage of using PRM in an open space.