Mobile Robot Control 2023 Rosey: Difference between revisions
Added introduction and local navigation text |
added figure to local nav |
||
| Line 37: | Line 37: | ||
<br /> | <br /> | ||
== Introduction == | ==Introduction== | ||
The Mobile Robot Control 2023 course is centered around a project known as the Restaurant challenge. It required a combination of technical skills, teamwork, and effective communication to design and implement a robotic system capable of autonomously navigating a restaurant environment and serving customers. During the build up to the challenge, the team gained valuable experience in various areas related to robotics and computer science. | The Mobile Robot Control 2023 course is centered around a project known as the Restaurant challenge. It required a combination of technical skills, teamwork, and effective communication to design and implement a robotic system capable of autonomously navigating a restaurant environment and serving customers. During the build up to the challenge, the team gained valuable experience in various areas related to robotics and computer science. | ||
| Line 212: | Line 212: | ||
==Local Navigation== | ==Local Navigation== | ||
The local navigation is implemented based on the state diagram provided in | The local navigation is implemented based on the state diagram provided in the figure on the right, following the same structure as the main code. It acts like a finite state machine, within a finite state machine. Each state in the state diagram corresponds to a case in a switch function. After the one pass through switch-case function, the algorithm goes back to the main code to do localization and to get new scan data. When a global path is determined in the main model, this path, represented as a list of nodes called ''pathNodeList'', serves as an input for the sub state diagram. Other important inputs are the current pose that comes from the localization algorithm, and the scan data, that comes from the main code. | ||
[[File:Local nav state diagram.png|thumb|593x593px|State diagram of the local navigation algorithm.]] | |||
<br /> | <br /> | ||
==== INIT_LOCAL_NAV ==== | ====INIT_LOCAL_NAV==== | ||
In the INIT_LOCAL_NAV state, the goal point is initialized. The goal point comprises the x-coordinate, y-coordinate, and a semantic label that indicates its type, such as table, door, or path node. The initialization process relies on two key components: the ''nodeIndex'' and the ''pathNodeList''. The ''nodeIndex'' keeps track of the current node in the list that the robot should navigate towards. Initially, the nodeIndex is set to zero to begin the navigation process at the first node of ''pathNodeList''. Upon reaching a goal point, the robot incrementally increases the ''nodeIndex''. This allows the system to retrieve the next node from the ''pathNodeList'', consequently guiding the robot towards the subsequent location. This iterative process continues until the final node of the path is reached, signifying the completion of the navigation task. When the goal is defined, the robot proceeds to transition into the subsequent state “TURN_TO_GOAL”. | In the INIT_LOCAL_NAV state, the goal point is initialized. The goal point comprises the x-coordinate, y-coordinate, and a semantic label that indicates its type, such as table, door, or path node. The initialization process relies on two key components: the ''nodeIndex'' and the ''pathNodeList''. The ''nodeIndex'' keeps track of the current node in the list that the robot should navigate towards. Initially, the nodeIndex is set to zero to begin the navigation process at the first node of ''pathNodeList''. Upon reaching a goal point, the robot incrementally increases the ''nodeIndex''. This allows the system to retrieve the next node from the ''pathNodeList'', consequently guiding the robot towards the subsequent location. This iterative process continues until the final node of the path is reached, signifying the completion of the navigation task. When the goal is defined, the robot proceeds to transition into the subsequent state “TURN_TO_GOAL”. | ||
<br /> | <br /> | ||
==== TURN_TO_GOAL ==== | ====TURN_TO_GOAL==== | ||
In the TURN_TO_GOAL state, the robot undertakes a turning action towards the designated goal before transitioning to the DRIVE_TO_GOAL state. First the angle to new goal is calculated. If this angle is bigger than one radian, the robot will stop its forward movement and only turn. If it is smaller than one radian, the robot will keep a small forward velocity while it is turning towards its goal. Once the angleToGoal is smaller than the TINY_ANGLE threshold, the state machine will go to next state. In the absence of any obstructions, the robot can drive a straight-line trajectory towards the goal point. | In the TURN_TO_GOAL state, the robot undertakes a turning action towards the designated goal before transitioning to the DRIVE_TO_GOAL state. First the angle to new goal is calculated. If this angle is bigger than one radian, the robot will stop its forward movement and only turn. If it is smaller than one radian, the robot will keep a small forward velocity while it is turning towards its goal. Once the angleToGoal is smaller than the TINY_ANGLE threshold, the state machine will go to next state. In the absence of any obstructions, the robot can drive a straight-line trajectory towards the goal point. | ||
<br /> | <br /> | ||
==== DRIVE_TO_GOAL ==== | ====DRIVE_TO_GOAL==== | ||
In the DRIVE_TO_GOAL state, the robot's driving behavior is determined based on several conditions. Initially, the presence of an object within a 50-centimeter range in front of the robot is detected. If no object is detected, the robot proceeds to drive directly towards the goal node, guided by the angle to the goal. Specifically, if the angle to the goal falls within a certain range[ -TINY_ANGLE, TINY_ANGLE], the robot moves straight ahead. However, if the angle exceeds this range, the robot adjusts its motion by simultaneously turning towards the goal and driving at a slightly reduced speed. | In the DRIVE_TO_GOAL state, the robot's driving behavior is determined based on several conditions. Initially, the presence of an object within a 50-centimeter range in front of the robot is detected. If no object is detected, the robot proceeds to drive directly towards the goal node, guided by the angle to the goal. Specifically, if the angle to the goal falls within a certain range[ -TINY_ANGLE, TINY_ANGLE], the robot moves straight ahead. However, if the angle exceeds this range, the robot adjusts its motion by simultaneously turning towards the goal and driving at a slightly reduced speed. | ||
In the event that an object is detected within the specified range, the robot employs an artificial potential field approach for navigation. This method involves calculating an attractive force towards the goal, with the direction of the force aligned towards the goal node, while the magnitude is determined by the distance to the goal node. The attractive force is given by the following formulas: | In the event that an object is detected within the specified range, the robot employs an artificial potential field approach for navigation. This method involves calculating an attractive force towards the goal, with the direction of the force aligned towards the goal node, while the magnitude is determined by the distance to the goal node. The attractive force is given by the following formulas: | ||
# F<sub>attractive_y</sub> = k<sub>attractive</sub> · d<sub>goal</sub><sup>2</sup> · sin(angle<sub>goal</sub>) | #F<sub>attractive_y</sub> = k<sub>attractive</sub> · d<sub>goal</sub><sup>2</sup> · sin(angle<sub>goal</sub>) | ||
# F<sub>attractive_x</sub> = k<sub>attractive</sub> · d<sub>goal</sub><sup>2</sup> · cos(angle<sub>goal</sub>) | #F<sub>attractive_x</sub> = k<sub>attractive</sub> · d<sub>goal</sub><sup>2</sup> · cos(angle<sub>goal</sub>) | ||
Additionally, the objects detected by the robot's laser scanner exert repulsive forces, which magnitude and direction again depend on the direction and distance of the detected object. This force is given by the following formula: | Additionally, the objects detected by the robot's laser scanner exert repulsive forces, which magnitude and direction again depend on the direction and distance of the detected object. This force is given by the following formula: | ||
# F<sub>repulsive_y</sub>= Σ(k<sub>repulsive</sub> · 1/d<sub>scan</sub><sup>2</sup> · sin(angle<sub>scan</sub>)) | #F<sub>repulsive_y</sub>= Σ(k<sub>repulsive</sub> · 1/d<sub>scan</sub><sup>2</sup> · sin(angle<sub>scan</sub>)) | ||
# F<sub>repulsive_x</sub>= Σ(k<sub>repulsive</sub> · 1/d<sub>scan</sub><sup>2</sup> · cos(angle<sub>scan</sub>)) | #F<sub>repulsive_x</sub>= Σ(k<sub>repulsive</sub> · 1/d<sub>scan</sub><sup>2</sup> · cos(angle<sub>scan</sub>)) | ||
In the case of the respulsive force, there are two different force gains depending on the distance to the obstacle. If an obstacle is within the HORIZON_MIN range, the repulsive gain k<sub>repulsive</sub> is almost 3 times higher than when the obstacle is between HORIZON_MIN and HORIZON_MAX. | In the case of the respulsive force, there are two different force gains depending on the distance to the obstacle. If an obstacle is within the HORIZON_MIN range, the repulsive gain k<sub>repulsive</sub> is almost 3 times higher than when the obstacle is between HORIZON_MIN and HORIZON_MAX. | ||
| Line 243: | Line 243: | ||
In the DRIVE_TO_GOAL state, assuming a successful navigation process, the robot reaches the goal node. In each cycle within this state, it is checked whether the distanceToGoal is within a certain threshold. If this is the case, the state machine will go to the next state based on the semantic of the node. There exist three distinct types of goal nodes: door nodes, path nodes, and table nodes. Each type of goal node needs specific subsequent actions in the navigation procedure. Consequently, based on the type of goal node reached, the robot can progress into three different states: AT_DOOR_NODE, AT_PATH_NODE, or AT_TABLE_NODE. | In the DRIVE_TO_GOAL state, assuming a successful navigation process, the robot reaches the goal node. In each cycle within this state, it is checked whether the distanceToGoal is within a certain threshold. If this is the case, the state machine will go to the next state based on the semantic of the node. There exist three distinct types of goal nodes: door nodes, path nodes, and table nodes. Each type of goal node needs specific subsequent actions in the navigation procedure. Consequently, based on the type of goal node reached, the robot can progress into three different states: AT_DOOR_NODE, AT_PATH_NODE, or AT_TABLE_NODE. | ||
==== AT_DOOR_NODE ==== | ====AT_DOOR_NODE==== | ||
In the “AT_DOOR_NODE” state, the robot has arrived at a door node and the robot is stopped. The objective of this state is to navigate the robot through the door. Regrettably, we encountered challenges during the implementation of this functionality which will be explained further below. Nevertheless, the underlying idea was as follows: Firstly, the subsequent goal node for the robot is determined based on the ''pathNodeLis''t. If the next goal node is also a door node, the robot will orient itself towards this node and check the laserdata to see whether the door is open or closed. | In the “AT_DOOR_NODE” state, the robot has arrived at a door node and the robot is stopped. The objective of this state is to navigate the robot through the door. Regrettably, we encountered challenges during the implementation of this functionality which will be explained further below. Nevertheless, the underlying idea was as follows: Firstly, the subsequent goal node for the robot is determined based on the ''pathNodeLis''t. If the next goal node is also a door node, the robot will orient itself towards this node and check the laserdata to see whether the door is open or closed. | ||
| Line 250: | Line 250: | ||
Conversely, if the subsequent goal node is not a door node, the model will transition to the TURN_TO_GOAL state and continue following the predefined path. | Conversely, if the subsequent goal node is not a door node, the model will transition to the TURN_TO_GOAL state and continue following the predefined path. | ||
==== AT_PATH_NODE ==== | ====AT_PATH_NODE==== | ||
In the AT_PATH_NODE state, which represents reaching a node situated between the start node and the table node where an order is to be delivered, the robots velocity first is reduced. The ''nodeIndex'' is then incremented by one. After updating the ''nodeIndex'', the navigation system proceeds to the state INIT_LOCAL_NAV, where the new goal node will be initialized. | In the AT_PATH_NODE state, which represents reaching a node situated between the start node and the table node where an order is to be delivered, the robots velocity first is reduced. The ''nodeIndex'' is then incremented by one. After updating the ''nodeIndex'', the navigation system proceeds to the state INIT_LOCAL_NAV, where the new goal node will be initialized. | ||
==== AT_TABLE_NODE ==== | ====AT_TABLE_NODE==== | ||
In the AT_TABLE_NODE state, a similar process as with a table node would happen, where it first checks if the node is the final node in the ''pathNodeList, indicating it is at the table''. Upon confirmation of arriving at the correct table node, the robot proceeds with orienting itself towards the table. This orientation is done by adding an extra semantic to each table node, which states the position of the middle of the relevant table. The robot uses this to turn towards the table, similar to the TURN_TO_GOAL state. Furthermore, the ''nodeIndex'' is reset to zero since the current path, as indicated in the ''pathNodeList'', has been successfully completed. In the event that this is the final order, the robot's tasks are concluded; however, if there are additional orders, a new order needs to be specified, and thus the code initializes the global path planner again. | In the AT_TABLE_NODE state, a similar process as with a table node would happen, where it first checks if the node is the final node in the ''pathNodeList, indicating it is at the table''. Upon confirmation of arriving at the correct table node, the robot proceeds with orienting itself towards the table. This orientation is done by adding an extra semantic to each table node, which states the position of the middle of the relevant table. The robot uses this to turn towards the table, similar to the TURN_TO_GOAL state. Furthermore, the ''nodeIndex'' is reset to zero since the current path, as indicated in the ''pathNodeList'', has been successfully completed. In the event that this is the final order, the robot's tasks are concluded; however, if there are additional orders, a new order needs to be specified, and thus the code initializes the global path planner again. | ||
==== STOPPED ==== | ====STOPPED==== | ||
The robot enters the STOPPED state whenever it detects an object within its close distance range, referred to as ''closeByDistance''. In such situations, the robot is instructed to remain stationary until no object is detected within this range. Currently, the implemented behavior involves the robot remaining stationary for a few seconds and then politely requesting the removal of the object. If, however, the object cannot be or isn't removed, such as in the case of a wall, the robot initiates a turning motion. The direction of rotation depends on the angle towards its current goal. Once the robot has a clear view, it will resume driving. However, there may be instances where the robot encounters the same object again, such as when it needs to pass through it. In such cases, the robot will consider the next goal point as the new target and attempt to reach it. This approach is taken because there might be an object obstructing the original node the robot was trying to reach. If the robot encounters further obstacles and needs to stop again, the robot will go into the OBSTRUCTED_PATH state, which is explained below. | The robot enters the STOPPED state whenever it detects an object within its close distance range, referred to as ''closeByDistance''. In such situations, the robot is instructed to remain stationary until no object is detected within this range. Currently, the implemented behavior involves the robot remaining stationary for a few seconds and then politely requesting the removal of the object. If, however, the object cannot be or isn't removed, such as in the case of a wall, the robot initiates a turning motion. The direction of rotation depends on the angle towards its current goal. Once the robot has a clear view, it will resume driving. However, there may be instances where the robot encounters the same object again, such as when it needs to pass through it. In such cases, the robot will consider the next goal point as the new target and attempt to reach it. This approach is taken because there might be an object obstructing the original node the robot was trying to reach. If the robot encounters further obstacles and needs to stop again, the robot will go into the OBSTRUCTED_PATH state, which is explained below. | ||
<br /> | <br /> | ||
==== OBSTRUCTED_PATH ==== | ====OBSTRUCTED_PATH==== | ||
''Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.'' | ''Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.'' | ||
| Line 266: | Line 266: | ||
<br /> | <br /> | ||
==== LOCAL_MINIMUM ==== | ====LOCAL_MINIMUM==== | ||
''Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.'' | ''Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.'' | ||
During navigation using an artificial potential field, it is possible for the robot to become stuck due to the repulsive forces and the attractive forces canceling each other out. One example would be an straight object right before or on top of the goal node. In this scenario, the robot could never get to its goal node. This behavoir is detected by a function that calculates the average traveled amount over a period of about 10 samples. If this average travelled distance is smaller then a certain threshold, a ''localMinimum'' Boolean would be set to true and the robot would cut the node link like in the OBSTRUCTED_PATH state. | During navigation using an artificial potential field, it is possible for the robot to become stuck due to the repulsive forces and the attractive forces canceling each other out. One example would be an straight object right before or on top of the goal node. In this scenario, the robot could never get to its goal node. This behavoir is detected by a function that calculates the average traveled amount over a period of about 10 samples. If this average travelled distance is smaller then a certain threshold, a ''localMinimum'' Boolean would be set to true and the robot would cut the node link like in the OBSTRUCTED_PATH state. | ||
==== STOPPED_BUMPER ==== | ====STOPPED_BUMPER==== | ||
''Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.'' | ''Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.'' | ||
| Line 277: | Line 277: | ||
<br /> | <br /> | ||
===== Improvements ===== | =====Improvements===== | ||
It is important to note that each time the local navigation is executed by the main function, the first step is to check the laser's view angle of 90 degrees in front of the robot for any objects detected within a range of 0.2 meters, known as ''closeByDistance''. Additionally, the function verifies if the robot's bumper has been pressed. | It is important to note that each time the local navigation is executed by the main function, the first step is to check the laser's view angle of 90 degrees in front of the robot for any objects detected within a range of 0.2 meters, known as ''closeByDistance''. Additionally, the function verifies if the robot's bumper has been pressed. | ||
Revision as of 20:10, 4 July 2023
Welcome to the group page of team Rosey! This page is currently under construction.
Project organisation
| Name | Student ID |
|---|---|
| Eline Wisse | 1335162 |
| Lotte Rassaerts | 1330004 |
| Marijn Minkenberg | 1357751 |
| Rainier Heijne | 1227575 |
| Tom Minten | 1372300 |
| Lowe Blom | 1266020 |
Midterm presentation
During the midterm presentation, team Rosey presented their plan of action to make the robot deliver orders in a restaurant. The slides are available below for comparison to the final product.File:Midterm presentation Rosey.pdf
Work division
The group identified three 'major parts' of the assignment. These are the localisation, the global and local navigation of the robot. The group additionally saw use for an overseeing role, which should ensure that the interfaces between the functions are clear. The work is divided as follows:
- Marijn : System architecture and overview
- Tom : Global navigation
- Eline & Rainier : Local navigation
- Lowe & Lotte : Localisation
Introduction
The Mobile Robot Control 2023 course is centered around a project known as the Restaurant challenge. It required a combination of technical skills, teamwork, and effective communication to design and implement a robotic system capable of autonomously navigating a restaurant environment and serving customers. During the build up to the challenge, the team gained valuable experience in various areas related to robotics and computer science.
Throughout the course, different algorithms and techniques for robot control were explored, such as localization, mapping, path planning, and object detection. Hands-on experience was obtained by working with the Toyota HSR robot, known as Hero, which was equipped with sensors and actuators for perception and driving tasks. This practical engagement enhanced the understanding of the fundamental principles and challenges associated with robotic systems and nearly as importantly, enabled the team to test developed algorithms for the restaurant challenge.
One of the significant obstacles encountered was the presence of dynamic obstacles. Developing a robust and efficient system to detect and avoid these obstacles while successfully delivering orders to the correct tables posed a significant challenge. Additionally, making sure all the parameters were tuned correctly within the limited amount of experiment time became quite the challenge.
On this wiki page, group Rosey's final restaurant challenge algorithm will be explained in detail, including shortcomings of the algorithm, and possible solutions to these problems.
System architecture and overview
...
Current state diagram
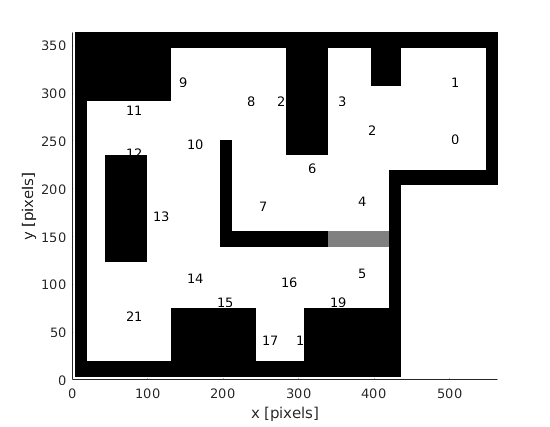
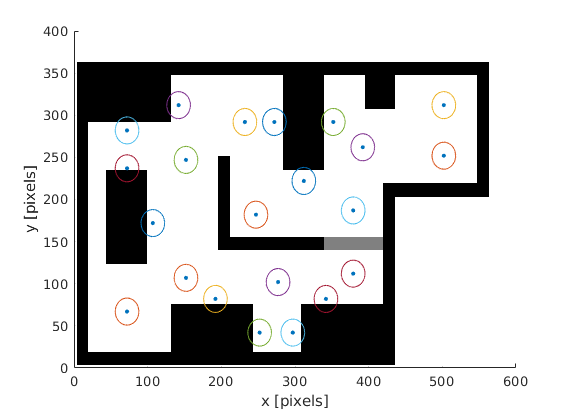
The global navigation uses the A* algorithm to find the shortest path to from a starting node to a goal node. The A* algorithm uses a predefined grid of nodes. This grid is applied by a JSON file, generated with Matlab. With Matlab, the grid nodes with their connections are manually chooses in the known map. On top of that, we were inspired by the lecture about Safe navigation in a hospital environment to introduce some context-aware navigation into our model, by means of semantics. Each node contains some semantic information about its environment, described by a integer. The following semantic integers are included: 0 = table 0, 1= table 1, ..., 49 = table 49, 50 = door, 99 = empty (meaning no semantic information present). This information is also included in the JSON file. The global path finder can find a table by looking for the node with the corect semantic integer.
Preparation phase
Create a JSON containing the grid information with the Matlab script below. The script has a visualization tool for plotting the position of all nodes. In the next graphs, the locations of the grid points in the final challenge are visualised. The circle has a radius of 20 centimeters. The local navigation assumed that the robot has reached the node when it is 20 centimeters from the node.
The corresponding Matlab script to generate the graphs and the JSON grid file: (click 'Expand'):
%% Data
clear all;
% Points in pixels, personally used pinta for that
x = [500,500,390,350,377,377,310,245,230,140,150,70,70,105,150,190,275,250,295,340,270,70];
y = [110,50,100,70,175,250,140,180,70,50,115,80,125,190,255,280,260,320,320,280,70,295];
% move zero point for matching worldmodel
x = x+2;
y = (y*-1+362);
% scale to meter
res= 1/80; % 80 pixels per meter
x_m = x*res;
y_m = y*res;
%% semantics
% add semantics to certain nodes
% 0: table 0, 1: table 1, ... 49: table 49, 50: door, 99: empty
% also add coordinates of the semantic objects when necessary
sem(1:length(x)) = 99; % fill array with 99 (empties)
semx(1:length(x)) = 0; % fill array with 99 (empties)
semy(1:length(x)) = 0; % fill array with 99 (empties)
sem(10) = 0;
semx(10) = 0.9375;
semy(10) = 4.0625;
sem(12) = 0;
semx(12) = 0.9375;
semy(12) = 4.0625;
sem(4) = 1;
semx(4) = 3.8750;
semy(4) = 3.7500;
sem(7) = 1;
semx(7) = 3.8750;
semy(7) = 3.7500;
sem(21) = 1;
semx(21) = 3.8750;
semy(21) = 3.7500;
sem(13) = 2;
semx(13) = 0.8750;
semy(13) = 2.2500;
sem(14) = 2;
semx(14) = 0.8750;
semy(14) = 2.2500;
sem(16) = 3;
semx(16) = 2.3750;
semy(16) = 0.5625;
sem(18) = 3;
semx(18) = 2.3750;
semy(18) = 0.5625;
sem(20) = 4;
semx(20) = 4.6250;
semy(20) = 0.5625;
sem(19) = 4;
semx(19) = 4.6250;
semy(19) = 0.5625;
doorNodes = [5,6] % door nodes
for i =1:length(doorNodes)
sem(doorNodes(i)) = 50;
end
%% connections
% define connections for each node, using input mode of matlab
conn_challenge_restaurant = zeros(length(x),10);
for i = 1:length(x)
i
prompt="type Connections, in form [a,b] when more connections exists: "
output = input(prompt)
for j = 1:length(output)
conn_challenge_restaurant(i,j) = output(j)
end
end
%% Plot
close all;
figure()
text(x, y, string((1:numel(x))-1)); % python numbering (index 0:..)
%text(x, y, string((1:numel(x))-0)); % matlab numbering (index 1:...)
axis([0, 564, 0, 364])
hold on
% visualise bitmap with points
I = imread('RestaurantChallengeMapRotatedFlipH.png');
h = image(2,2,I);
uistack(h,'bottom')
% size of points, which forms the circle around node
sm = 10;
% radius of circle about node
R = 16; % 0.2*80, 20 centimeter radius
th = linspace(0,2*pi) ;
figure()
scatter(x,y,sm,"filled")
hold on
for i = 1:length(x)
x_c = R*cos(th)+x(i) ;
y_c = R*sin(th)+y(i) ;
scatter(x_c,y_c,1,"filled")
end
I = imread('RestaurantChallengeMapRotatedFlipH.png');
h = image(2,2,I);
uistack(h,'bottom')
%% generate JSON
S.nodes = struct("x", num2cell(x_m), "y", num2cell(y_m), "semantic",num2cell(sem),"semanticX",num2cell(semx),"semanticY",num2cell(semy))
S.connections = conn_challenge_restaurant
s = jsonencode(S,PrettyPrint=true)
if exist('grid.json', 'file')==2
prompt="do you want to remove old grid.json file? (y=1/n=0) "
output = input(prompt);
if output == 1
delete('grid.json');
disp("Caution, old grid.json file is deleted...")
end
end
fid=fopen('grid.json','w');
fprintf(fid, s);
disp("new grid.json is succesfully saved")
Initiation phase (run once)
The json file is imported with the loadConfigFile()and the grid is constructed withconstructGrid(). The grid information is placed in the global variable *grid.
Global path finder phase
In globalNavigation(), there are a few steps which has to be taken for determining the best path as node sequence.
- First, the robot determines its own position in its map and the closest node is found. One assumed that there is no complete blocking object as a wall in between the robot and the closest node, i.e. sufficient nodes has to be properly placed.
- The goal node is found by finding the corresponding semantic number of the destination table
- The
aStar()is executed to find the best path - In case the output is [-1], there is no path available with the provided information. Possibly causes: connections are not correctly defined or essential connections are removed. On the end, the output with the sequence of nodes to (and including) the goal node is written to the global*pathNodeIDsvariable. - The main function returns whether a path is found.
Cutting connections in case of blocking objects or close doors (updating the grid)
Note that the code for updating the grid is present, but not implemented in local navigation due to time constraints. So, it is not used. However, the plan for updating the grid will be explained below:
In case a node cannot be reached according to a certain trajectory, the grid information has to be revised by removing the connection between the last node and the not reachable node. Then, a new trajectory has to be determined while taking into account the removed connection. This should result in another trajectory to the goal, providing that the removed connection is not crucial. When defining the grid, one should take into account that a connection can be removed and that another trajectory still has to be possible. To remove a connection, the function cutConnections() can be used.
Note that a connection can be unavailable for a limited time. To handle that, the connections list has to be reset when a goal (e.g. table) is reached or when there are no other trajectories possible, due to all removed connections. In the grid, there are two connections list: one will be updated, while the other saves the initial connections list. To reset the connections list, the updated list is overwritten with the initial connections list. This can be done by using the resetConnections() function.
Known bug while selecting the table node
On the day before the demo day, we found out that the goal node selection is not perfect. Now, the node list is looped to find a node with the corresponding semantic integer for a certain table. So, the first node with this semantic integer is chosen directly. There are multiple nodes around the table which has the semantic integer for the specific table, but the lowest node number is always taken. Then, this node is used as finish node for the A* algorithm. For the demo, it was decided to only assign one node to each table. However during the demo, the specific node for the first table was giving problems. In case the selection of the goal node is able to take the closest table node, this issue was avoided by going to the closest table node on the side of the table.
The way to solve this bug is to generate different paths to all table nodes, check the cost to come for all available table nodes, and select the path with the lowest cost to come. Due to lack of time, this bug fix could not be implemented. In addition, when the cutConnections()is used, the robot can cut the connection when the table node is not reachable, which was the case during the demo. Then, another table node can be used to reach the table.
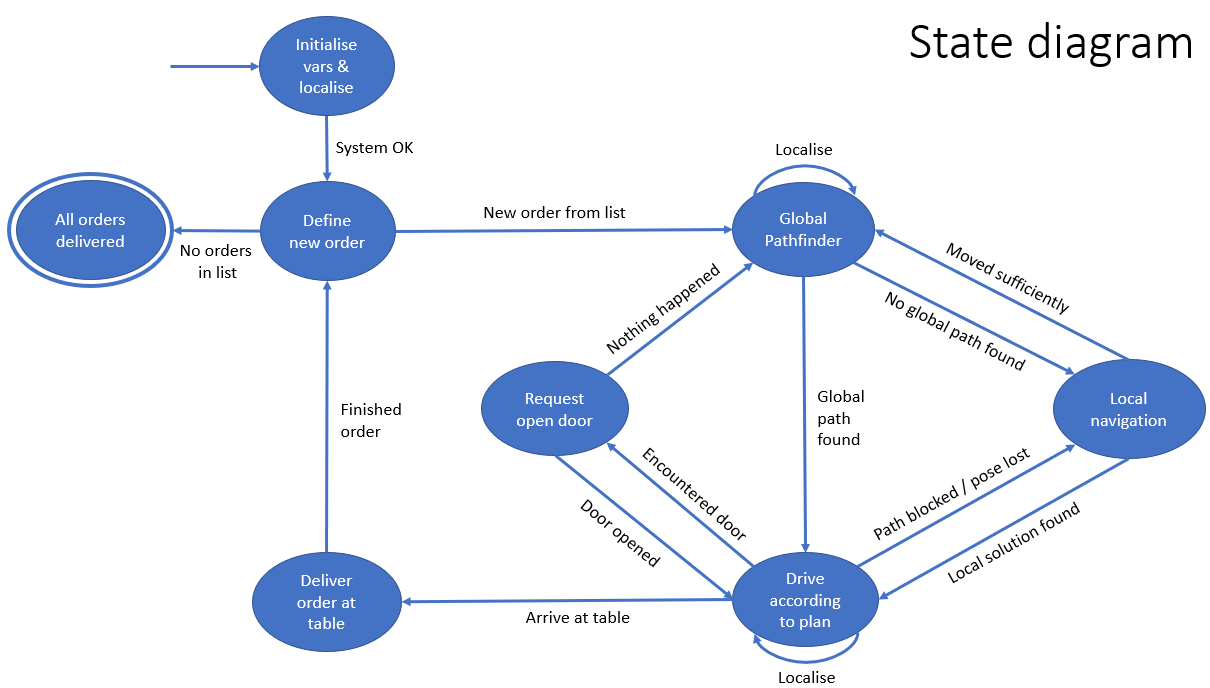
The local navigation is implemented based on the state diagram provided in the figure on the right, following the same structure as the main code. It acts like a finite state machine, within a finite state machine. Each state in the state diagram corresponds to a case in a switch function. After the one pass through switch-case function, the algorithm goes back to the main code to do localization and to get new scan data. When a global path is determined in the main model, this path, represented as a list of nodes called pathNodeList, serves as an input for the sub state diagram. Other important inputs are the current pose that comes from the localization algorithm, and the scan data, that comes from the main code.

INIT_LOCAL_NAV
In the INIT_LOCAL_NAV state, the goal point is initialized. The goal point comprises the x-coordinate, y-coordinate, and a semantic label that indicates its type, such as table, door, or path node. The initialization process relies on two key components: the nodeIndex and the pathNodeList. The nodeIndex keeps track of the current node in the list that the robot should navigate towards. Initially, the nodeIndex is set to zero to begin the navigation process at the first node of pathNodeList. Upon reaching a goal point, the robot incrementally increases the nodeIndex. This allows the system to retrieve the next node from the pathNodeList, consequently guiding the robot towards the subsequent location. This iterative process continues until the final node of the path is reached, signifying the completion of the navigation task. When the goal is defined, the robot proceeds to transition into the subsequent state “TURN_TO_GOAL”.
TURN_TO_GOAL
In the TURN_TO_GOAL state, the robot undertakes a turning action towards the designated goal before transitioning to the DRIVE_TO_GOAL state. First the angle to new goal is calculated. If this angle is bigger than one radian, the robot will stop its forward movement and only turn. If it is smaller than one radian, the robot will keep a small forward velocity while it is turning towards its goal. Once the angleToGoal is smaller than the TINY_ANGLE threshold, the state machine will go to next state. In the absence of any obstructions, the robot can drive a straight-line trajectory towards the goal point.
DRIVE_TO_GOAL
In the DRIVE_TO_GOAL state, the robot's driving behavior is determined based on several conditions. Initially, the presence of an object within a 50-centimeter range in front of the robot is detected. If no object is detected, the robot proceeds to drive directly towards the goal node, guided by the angle to the goal. Specifically, if the angle to the goal falls within a certain range[ -TINY_ANGLE, TINY_ANGLE], the robot moves straight ahead. However, if the angle exceeds this range, the robot adjusts its motion by simultaneously turning towards the goal and driving at a slightly reduced speed.
In the event that an object is detected within the specified range, the robot employs an artificial potential field approach for navigation. This method involves calculating an attractive force towards the goal, with the direction of the force aligned towards the goal node, while the magnitude is determined by the distance to the goal node. The attractive force is given by the following formulas:
- Fattractive_y = kattractive · dgoal2 · sin(anglegoal)
- Fattractive_x = kattractive · dgoal2 · cos(anglegoal)
Additionally, the objects detected by the robot's laser scanner exert repulsive forces, which magnitude and direction again depend on the direction and distance of the detected object. This force is given by the following formula:
- Frepulsive_y= Σ(krepulsive · 1/dscan2 · sin(anglescan))
- Frepulsive_x= Σ(krepulsive · 1/dscan2 · cos(anglescan))
In the case of the respulsive force, there are two different force gains depending on the distance to the obstacle. If an obstacle is within the HORIZON_MIN range, the repulsive gain krepulsive is almost 3 times higher than when the obstacle is between HORIZON_MIN and HORIZON_MAX.
By adding up the attractive and repulsive forces, the robot derives the total force, which in turn determines the translational and rotational velocities. The rotational velocity depends on the direction of the total force vector, while the translational velocity is influenced by the magnitude of the total force. This artificial potential field enables the robot to maneuver around obstacles that may partially obstruct its path.
In the DRIVE_TO_GOAL state, assuming a successful navigation process, the robot reaches the goal node. In each cycle within this state, it is checked whether the distanceToGoal is within a certain threshold. If this is the case, the state machine will go to the next state based on the semantic of the node. There exist three distinct types of goal nodes: door nodes, path nodes, and table nodes. Each type of goal node needs specific subsequent actions in the navigation procedure. Consequently, based on the type of goal node reached, the robot can progress into three different states: AT_DOOR_NODE, AT_PATH_NODE, or AT_TABLE_NODE.
AT_DOOR_NODE
In the “AT_DOOR_NODE” state, the robot has arrived at a door node and the robot is stopped. The objective of this state is to navigate the robot through the door. Regrettably, we encountered challenges during the implementation of this functionality which will be explained further below. Nevertheless, the underlying idea was as follows: Firstly, the subsequent goal node for the robot is determined based on the pathNodeList. If the next goal node is also a door node, the robot will orient itself towards this node and check the laserdata to see whether the door is open or closed.
In the event that the door is open, the robot will proceed directly to the subsequent node. However, if the door is closed, the robot will request if the door could be opened and then patiently wait for a period of about 10 seconds. If the door is successfully opened within this timeframe, the robot will pass through it. For this, the localization algorithm would switch to a map with an open door and relocalize. This did not work however, as the robot would misinterpret the corner and the heading would be off by about 90 degrees. If The door would not open, the algorithm would go into the OBSTRUCTED_PATH state, where it would cut the link between the two door nodes and go back to the global path planner to find a new path.
Conversely, if the subsequent goal node is not a door node, the model will transition to the TURN_TO_GOAL state and continue following the predefined path.
AT_PATH_NODE
In the AT_PATH_NODE state, which represents reaching a node situated between the start node and the table node where an order is to be delivered, the robots velocity first is reduced. The nodeIndex is then incremented by one. After updating the nodeIndex, the navigation system proceeds to the state INIT_LOCAL_NAV, where the new goal node will be initialized.
AT_TABLE_NODE
In the AT_TABLE_NODE state, a similar process as with a table node would happen, where it first checks if the node is the final node in the pathNodeList, indicating it is at the table. Upon confirmation of arriving at the correct table node, the robot proceeds with orienting itself towards the table. This orientation is done by adding an extra semantic to each table node, which states the position of the middle of the relevant table. The robot uses this to turn towards the table, similar to the TURN_TO_GOAL state. Furthermore, the nodeIndex is reset to zero since the current path, as indicated in the pathNodeList, has been successfully completed. In the event that this is the final order, the robot's tasks are concluded; however, if there are additional orders, a new order needs to be specified, and thus the code initializes the global path planner again.
STOPPED
The robot enters the STOPPED state whenever it detects an object within its close distance range, referred to as closeByDistance. In such situations, the robot is instructed to remain stationary until no object is detected within this range. Currently, the implemented behavior involves the robot remaining stationary for a few seconds and then politely requesting the removal of the object. If, however, the object cannot be or isn't removed, such as in the case of a wall, the robot initiates a turning motion. The direction of rotation depends on the angle towards its current goal. Once the robot has a clear view, it will resume driving. However, there may be instances where the robot encounters the same object again, such as when it needs to pass through it. In such cases, the robot will consider the next goal point as the new target and attempt to reach it. This approach is taken because there might be an object obstructing the original node the robot was trying to reach. If the robot encounters further obstacles and needs to stop again, the robot will go into the OBSTRUCTED_PATH state, which is explained below.
OBSTRUCTED_PATH
Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.
The robot gets into this state if the robot entered the STOPPED state for the second time after trying to move away from the obstacle. Subsequently, the link between the current node from which the robot is moving and the destination node should be removed. If such a scenario occurs, it would necessary to find a new global path, accounting for the deletion of the node link caused by the presence of an object or an obstructed path. Thus, a transition to the main code, or more specifically, the “GLOBAL_PATH” state, needs to be executed. The deleted node link would be reset once the robot does get to the table.
LOCAL_MINIMUM
Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.
During navigation using an artificial potential field, it is possible for the robot to become stuck due to the repulsive forces and the attractive forces canceling each other out. One example would be an straight object right before or on top of the goal node. In this scenario, the robot could never get to its goal node. This behavoir is detected by a function that calculates the average traveled amount over a period of about 10 samples. If this average travelled distance is smaller then a certain threshold, a localMinimum Boolean would be set to true and the robot would cut the node link like in the OBSTRUCTED_PATH state.
STOPPED_BUMPER
Unfortunately, we were unable to successfully test this functionality in our code, mainly due to time concerns.
This is a distinct intermediate state that occurs when the robot's bumper is pressed. In this state, the robot initially moves backward for a duration of half a second before transitioning to the “STOPPED” state.
Improvements
It is important to note that each time the local navigation is executed by the main function, the first step is to check the laser's view angle of 90 degrees in front of the robot for any objects detected within a range of 0.2 meters, known as closeByDistance. Additionally, the function verifies if the robot's bumper has been pressed.
In hindsight, it may have been wiser to exclude the stop and bumper detection processes when the robot reaches a table node. Since the robot is programmed to turn towards the designated table upon reaching the corresponding node, it is conceivable that the table itself falls within the closeByDistance range, causing the robot to stop rotating and enter the STOPPED state. Ideally, the robot should not stop for a table but rather proceed to deliver the order as intended.
This behavior did come up in simulation and more crucially during the final challenge. A solution that was not implemented is to change the closeByDistance based on the semantic of the next node. This closeByDistance can be decreased once the robot is near a table node. Also, the robot should only go into the STOPPED state from TURN_TO_GOAL or DRIVE_TO_GOAL states, and not from any state other.
Since the robot did drive relatively well during testing, but failed straight away during the final challenge, it is hard to say what other changes to the current code would be made.
Localisation
...
Testing the software
Practical sessions
...
Final challenge day
...