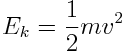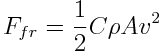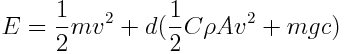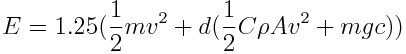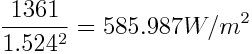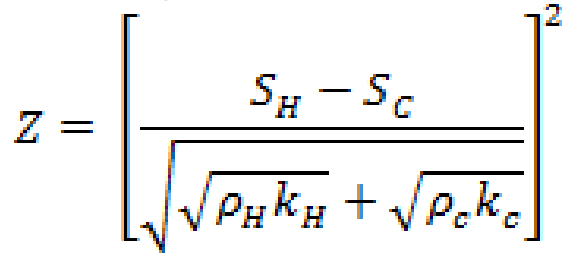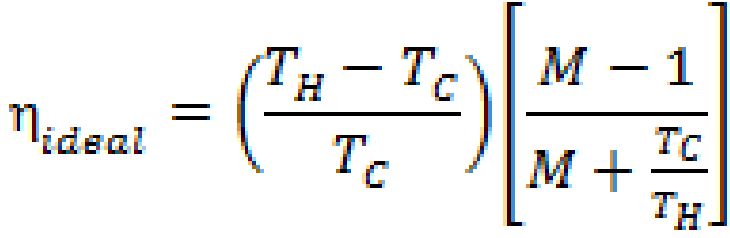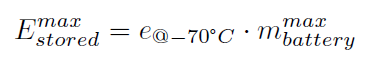PRE2019 3 Group3: Difference between revisions
TUe\20181902 (talk | contribs) |
TUe\20181902 (talk | contribs) |
||
| (171 intermediate revisions by 3 users not shown) | |||
| Line 11: | Line 11: | ||
In order to build a colony, different factors to choose a certain spot for a colony have to be examined. To look at the different factors that determine what a good place to build a colony is, two different situations will be looked at. Firstly, there should be a good landing spot for the crew to arrive on Mars. Secondly, there should be a good location to actually start the colony. Ideally, these two locations should be on the same sport or really close to each other. For now, let’s assume the colony will be build on or around the landing spot, since too great a distance between them will create problems for travel. For a good landing spot, the landing area should be as flat as possible. According to [https://www.popsci.com/if-humans-go-to-mars-wheres-best-place-to-land/] It also needs to be clear of rocks and boulders, since this would make landing dangerous and the landing area should not be too soft. It states that Mars has areas where the dust is several meters high, which is unfitted for landing. For building a colony, this also seems important. Building will be hard on areas that are too soft, since this would require better foundations. Non-flat and rocky areas can be not ideal for building, but can be worked around. [https://mars.nasa.gov/insight/timeline/prelaunch/landing-site-selection/] States that a good landing spot should be as close as possible to the equator, because this ensures that the solar arrays of the lander can deliver enough power at all times of the year and the temperature is high enough for the lander to stay warm. This factor is situational but can be really helpful when the colony will rely on solar power for generating energy. This will also decrease the power needs for warming the colony. Both previously mentioned articles say that the altitude of the area is also an important aspect. According to these articles, a lower altitude is better for landing. This means that there is more atmosphere above the land to slow down and steer for a good landing. [https://www.sciencedaily.com/releases/2018/02/180227094728.htm] talks about food production which is another important aspect. At first the colonizers can live from provisions sent with them, but in order for them to live on mars indefinitely they have to grow crops. In order to grow crops there needs to be usable soil at the landing site and there needs to be enough water. Water is not only important for food production, but also for drinking or even as a fuel by turning it into hydrogen. Currently, the best way to get water on Mars is by gathering ice that is located underneath the surface on Mars. Ideally, this ice will be located as close to the surface as possible, since this makes it as easy as possible to mine. The image [https://www.nasaspaceflight.com/2019/12/mars-colonization-new-water-map-hold-key-land/] below shows the depth of the ice on the surface of Mars. | In order to build a colony, different factors to choose a certain spot for a colony have to be examined. To look at the different factors that determine what a good place to build a colony is, two different situations will be looked at. Firstly, there should be a good landing spot for the crew to arrive on Mars. Secondly, there should be a good location to actually start the colony. Ideally, these two locations should be on the same sport or really close to each other. For now, let’s assume the colony will be build on or around the landing spot, since too great a distance between them will create problems for travel. For a good landing spot, the landing area should be as flat as possible. According to [https://www.popsci.com/if-humans-go-to-mars-wheres-best-place-to-land/] It also needs to be clear of rocks and boulders, since this would make landing dangerous and the landing area should not be too soft. It states that Mars has areas where the dust is several meters high, which is unfitted for landing. For building a colony, this also seems important. Building will be hard on areas that are too soft, since this would require better foundations. Non-flat and rocky areas can be not ideal for building, but can be worked around. [https://mars.nasa.gov/insight/timeline/prelaunch/landing-site-selection/] States that a good landing spot should be as close as possible to the equator, because this ensures that the solar arrays of the lander can deliver enough power at all times of the year and the temperature is high enough for the lander to stay warm. This factor is situational but can be really helpful when the colony will rely on solar power for generating energy. This will also decrease the power needs for warming the colony. Both previously mentioned articles say that the altitude of the area is also an important aspect. According to these articles, a lower altitude is better for landing. This means that there is more atmosphere above the land to slow down and steer for a good landing. [https://www.sciencedaily.com/releases/2018/02/180227094728.htm] talks about food production which is another important aspect. At first the colonizers can live from provisions sent with them, but in order for them to live on mars indefinitely they have to grow crops. In order to grow crops there needs to be usable soil at the landing site and there needs to be enough water. Water is not only important for food production, but also for drinking or even as a fuel by turning it into hydrogen. Currently, the best way to get water on Mars is by gathering ice that is located underneath the surface on Mars. Ideally, this ice will be located as close to the surface as possible, since this makes it as easy as possible to mine. The image [https://www.nasaspaceflight.com/2019/12/mars-colonization-new-water-map-hold-key-land/] below shows the depth of the ice on the surface of Mars. | ||
[[File:Mars-water-ice-map (1).jpg]] | [[File:Mars-water-ice-map (1).jpg|700px|Depth of the ice on the surface of Mars]] | ||
As shown on the map, the ideal location for digging up ice according to NASA is noted with the white box. This is fairly close to the north pole however, which contradicts with the earlier mentioned preference of building the colony as close as possible to the equator. This already shows that there is not one ideal location to build a colony. Different countries/companies might choose a different location for their colony. Now, let’s assume some choose to build their colony close to the north pole, in the white boxed area, because they think water is more important than other factors. Now, other countries or companies choose to build their colony close to the equator, because they know other colonies can already easily mine water. They now value the better temperatures and sunlight more because they know they can buy and/or trade with the other colonies for water. This means that the citizens of the colony need a way of transporting water from colony to colony. Another possible option could be that a company chooses to build a colony close to the equator and a separate mining site for water. This way, they have the better temperatures and sunlight for solar power at their living area, the colony, and have a way to gather water on Mars. However, this again, brings the need for a transportation system between the colony and the mining site. | As shown on the map, the ideal location for digging up ice according to NASA is noted with the white box. This is fairly close to the north pole however, which contradicts with the earlier mentioned preference of building the colony as close as possible to the equator. This already shows that there is not one ideal location to build a colony. Different countries/companies might choose a different location for their colony. Now, let’s assume some choose to build their colony close to the north pole, in the white boxed area, because they think water is more important than other factors. Now, other countries or companies choose to build their colony close to the equator, because they know other colonies can already easily mine water. They now value the better temperatures and sunlight more because they know they can buy and/or trade with the other colonies for water. This means that the citizens of the colony need a way of transporting water from colony to colony. Another possible option could be that a company chooses to build a colony close to the equator and a separate mining site for water. This way, they have the better temperatures and sunlight for solar power at their living area, the colony, and have a way to gather water on Mars. However, this again, brings the need for a transportation system between the colony and the mining site. | ||
| Line 19: | Line 19: | ||
== Solutions == | == Solutions == | ||
There are | There are several possible solutions for this: | ||
Option 1: Building a transportation conveyor tube. | * Option 1: Building a transportation conveyor tube. | ||
Option 2: Building a protected manned transportation vehicle. This vehicle must be protecting the people inside from radiation and temperatures. | * Option 2: Building a protected manned transportation vehicle. This vehicle must be protecting the people inside from radiation and temperatures. | ||
Option 3: Building a remote-controlled unmanned transport vehicle with cameras attached which will be controlled by someone in the colony. There must be someone controlling the vehicle. | * Option 3: Building a remote-controlled unmanned transport vehicle with cameras attached which will be controlled by someone in the colony. There must be someone controlling the vehicle. | ||
Option 4: Building a transport robot that would be able to autonomously deliver water from the one colony to the other. | * Option 4: Building a transport robot that would be able to autonomously deliver water from the one colony to the other. | ||
===Comparing solutions=== | ===Comparing solutions=== | ||
| Line 49: | Line 49: | ||
Using both techniques a colony would be able to sustain humans, but would not have enough water to also sustain water for growing crops and industrial use. Industrial use includes creating rocket fuel and usage for fabricating, processing, washing, diluting, cooling, or transporting a product. Large amounts of water are used mostly to produce food, paper, and chemicals.[https://www.cdc.gov/healthywater/other/industrial/index.html] | Using both techniques a colony would be able to sustain humans, but would not have enough water to also sustain water for growing crops and industrial use. Industrial use includes creating rocket fuel and usage for fabricating, processing, washing, diluting, cooling, or transporting a product. Large amounts of water are used mostly to produce food, paper, and chemicals.[https://www.cdc.gov/healthywater/other/industrial/index.html] | ||
== | = Users = | ||
=== | == Technological Difficulties == | ||
- | Aside from the financial aspect, there are some other difficulties in conducting a journey to Mars. The most prominent ones will be elaborated here. | ||
==== Distance ==== | |||
Mars is the planet that is closest to earth in our solar system. However, the distance that would have to be covered if we launch a manned vessel to Mars is still significantly large. On average Mars is around 225 million km from earth, with 55 million km at its closest, occurring every 26 months. This journey would take around 150-300 days, according to [https://interestingengineering.com/what-would-a-martian-colony-look-like]. This is a reasonable amount of time, but the trouble lies in fuel consumption, as a manned vessel would be larger than a unmanned vessel, due to supplies that a manned mission needs. This would lead to a large fuel consumption. However, technologies are present to cover this distance in space with a manned vessel [https://interestingengineering.com/what-would-a-martian-colony-look-like]. | |||
==== Housing ==== | |||
Three other factors to take in consideration are the atmosphere, the temperatures and the storms on Mars. As for the atmosphere, oxygen could be produced using the carbon-dioxide that is present in the Martian atmosphere [https://www.space.com/16903-mars-atmosphere-climate-weather.html]. For example, greenhouses could be built with plants that convert CO2 into O2 or a device for converting carbon-dioxide into oxygen could be developed. The temperatures range anywhere from -125°C to +20°C [https://www.space.com/16903-mars-atmosphere-climate-weather.html]. These kinds of temperatures are acceptable in the building of a space colony, with good isolation and air-conditioning systems. There are also severe dust storms on Mars from time to time. This means that a rigid structure needs to be built to withstand such storms, building underground or in caves. | |||
==== Supplies ==== | |||
Once a group of people is settled on Mars, a huge challenge will be to supply them in their needs. First of all, food is needed to keep the population alive. This could be realized by both transportation of food from earth and, ultimately, growing food on Mars. Also building materials must be transported through space. This requires new rockets that can carry heavy loads. NASA is developing these spacecrafts [https://interestingengineering.com/what-would-a-martian-colony-look-like]. This means that this issue, although very cost-intensive, can be technologically overcome. | |||
In conclusion, we can say that a colony on Mars is possible in the future, because all the technologies to realize it is there. It is only a matter of further development and major investments to make this happen. This means that there will be a need for Mars-exploring robot technologies in the future. | |||
The main users of the robots will be a Martian space colony. This colony is non-existent today. However, the idea of a Mars-colony is widely researched right now. NASA, for example, has launched several Mars-exploration-robots in the past [https://mars.nasa.gov/] and still does extensive research on the planet today. There is also an organization that focuses solely on the development of a human colony on Mars. This organization is called Mars One and it focuses on the selection of astronauts and the raise of funding [http://www.mars-one.com/about-mars-one/current-mission-status]. Mars One claims that all technologies to get to Mars and to begin a colony there, are already present. Only a return mission is impossible right now, but that will not be needed if the crew of the mission will settle on Mars. This means that, in theory, a Mars colony is feasible within the coming 50 years [http://www.mars-one.com/mission/technical-feasibility]. This means that the navigation technology, that we will design, is certainly of use for this yet to be founded colony. | |||
Other parties of interest for this technology would be organizations like NASA, ESA, Space-X, Mars One, and other space-oriented companies, as they will be the organizations that will put people on Mars. | |||
== Stakeholders == | |||
The users of a device that can navigate itself across a planet, in this case Mars, are the people that live on Mars. At the moment, there are no people living on Mars yet. This means we should look at the probability for a Mars-colony to be formed in the near future. | |||
===People on Mars=== | |||
The people that live on Mars are certainly the most obvious users of a transportation robot that transports water on Mars. If Martian colonies are realized, the people that live on Mars will have to get enough water to survive. When this colony is not built on a water source, there will be a need for a robot that transports the water from mining site to the colony that needs the water. | |||
The requirements that these people will have for a water transporting technology are listed below. | |||
* Transport as much water as possible in one journey | |||
* Travel as fast as possible | |||
* Easy to empty the tank | |||
* Fast charging of the battery | |||
* Device should have a lifespan of at least a few years | |||
Besides the people that live on Mars, there are other stakeholders that play a part in the implementation of a transport robot, for example the companies that put the people on Mars. | |||
===Organizations=== | |||
There are several organizations that have plans to establish colonies on Mars. The most prominent ones are elaborated below. | |||
====Mars One==== | |||
People have always dreamed about relocating the human race to another planet, in case something would happen to planet earth. This idea generates even more interest nowadays, than it did, say, 50 years ago, with the current problem of climate change affecting the earth. Now, more than ever, people are looking for another place to live in the galaxy. One of the most prominent candidates for this migration would be Mars, because it is ‘close’ to earth in comparison to other planets. Furthermore, it is believed to have water, which is a major life source, in its soil. But are we ready to move there in the near future? | |||
Mars One is an organization, that certainly believes that a Mars colony is possible. Mars One handles the selection procedure for astronauts that want to settle on Mars in the yet to be formed space colony. It is also responsible for raising funds in order to make the mission happen. In [http://www.mars-one.com/mission/technical-feasibility] they state that the formation of a space colony, instead of a visiting mission that has to return to earth, excludes most technological and cost-intensive problems. Namely, if people want to settle on mars, no return vehicle, return propellant or the systems to produce the propellant locally are required. This decreases technological challenges and reduces costs dramatically. Furthermore, they mention that all the technologies to send people to Mars and make them survive there are already present. This means that a Mars colony is certainly feasible within the next 50 years. | |||
However, in [http://www.mars-one.com/about-mars-one/current-mission-status] they mention that the funds to actually develop a Mars settlement mission are not present right now (1 million USD of the 1 billion USD required). On the other hand, donations and investments might rapidly increase when more research is conducted in this field, and people would get convinced that a Mars colony is feasible. Also, if the situation on earth gets worse, people might have no choice but to invest in these kinds of missions. | |||
This means that, if Mars One succeeds in its’ mission, they will have an interest in a transporting technology on Mars. | |||
====Space-X==== | |||
Space-X is another (privately owned) organization that has made concrete plans for a Mars mission and a Mars settlement [https://www.spacex.com/mars]. Their goal is to send a cargo flight to Mars as early as 2022 and they have set the target for a manned vessel in the year 2024. Although optimistic, these plans are very concrete and ambitious. This means that Space-X is an organization that could certainly have an interest in the technology that we are researching for our project. | |||
====NASA==== | |||
NASA is a governmental organization that also has the ambition to put humans on Mars [https://www.nasa.gov/topics/moon-to-mars/overview]. Their goal is to put humans on Mars within the next decade. NASA is the organization that is most likely to succeed in completing this mission, because they have put men on the moon before, so they have the technologies in store to conduct such a mission. Furthermore, this is the organization that has gathered most of the data of Mars that is present today, as they have sent multiple satellites and exploration vessels to the planet [https://www.nasa.gov/mission_pages/mars/missions/index-past.html]. Therefore, NASA is a major player that could have an interest in the technology we are investigating. | |||
====Other organizations==== | |||
There are other privately-owned companies that have also conducted research in the field of establishing a Mars colony, like Lockheed Martin and Boeing [https://en.wikipedia.org/wiki/Colonization_of_Mars#Possible_locations_for_settlements]. Furthermore, there are other governmental organizations, like ESA, Roscosmos, ISRO and the CNSA [https://en.wikipedia.org/wiki/Colonization_of_Mars#Possible_locations_for_settlements], that could also have an interest in the technology. However, the plans of these organizations are not as advanced as the plans of the organizations mentioned before. Therefore, they are less likely to have an interest in a transport technology in the near future. | |||
The requirements that these organizations will have for a water transporting technology are largely the same as the requirements that the people on Mars have. However, there are some additional requirements that the organizations may have: | |||
* Production process should be as cheap as possible | |||
* The usage of the device should be energy efficient, and therefore cost efficient | |||
* The device should be easy to transport from earth to Mars, as it will most likely be produced on earth. | |||
However these needs are considered to be subordinate to the people’s need in this project, so they will be added as preferences. | |||
===Governments=== | |||
Other major players in the Mars colonization field, are the governments of the different countries involved in the previously mentioned governmental organizations. In the case of NASA this will be the American governments, in the case of ESA the European union, and so on. These governments sometimes have different needs and interests than the organizations which they govern. For example, NASA cares greatly for the scientific knowledge that is gained through new space missions, while the government might care more if they are world leader in the field of space engineering. This sometimes leads to conflicting interests. | |||
Moreover, a competition between countries can occur in the building of the first Mars colony. In the past, for example, we have seen a so-called ‘space race’ between the Russians and the Americans [https://en.wikipedia.org/wiki/Space_Race]. It could be that the colonization of Mars will follow a similar scenario. However, it could also be the case that governments will establish multinational Mars colonies, as they did in the past with the ISS (International Space Station [https://www.nasa.gov/mission_pages/station/overview/index.html]). | |||
Some additional requirements, besides the requirements of the people and the organizations, that governments will have for a water transportation device are: | |||
* Easy to reproduce the manufacturing techniques (cooperation) | |||
* Difficult to copy technology (competition) | |||
The requirements for cooperation are implemented, as this is the most likely scenario. This requirement is also treated as a preference. | |||
===Other stakeholders=== | |||
There are some other stakeholders that would have an interest in the technology. One could, for example, think of mechanics that have to work on the device, possible organizations that are formed on Mars among the colonists, environmental organizations, manufacturers (although the manufactures probably have to answer to the organizations), suppliers of manufacturers and so on. The interests of these groups are largely in line with the interests that are previously mentioned. Moreover, the interests of these groups are much smaller than the groups that are mentioned before. Therefore, the interests of these groups are not accounted for in this project. | |||
===User requirements=== | |||
A full list of user requirements is given below: | |||
{| border=1 style="border-collapse: collapse;" cellpadding = 2 | |||
! User Group | |||
{| border=1 style="border-collapse: collapse;" cellpadding = | ! Requirement | ||
|-style="text-align: left" | |||
! | |People in colony || | ||
! | * Transport as much water as possible in one journey | ||
|- style="text-align: | * Travel as fast as possible | ||
| | * Easy to empty the tank | ||
|-style="text-align: | * Fast charging of the battery | ||
| | * Device should have a lifespan of at least a few years | ||
|-style="text-align: left" | |||
|Organizations || | |||
|- style="text-align: | * Production process should be as cheap as possible | ||
| | * The usage of the device should be energy efficient, and therefore cost efficient | ||
* The device should be easy to transport from earth to Mars | |||
|-style="text-align: left" | |||
|Governments || | |||
* Easy to reproduce the manufacturing techniques | |||
|} | |} | ||
=== | =Scenarios= | ||
==Research question== | |||
This research will mostly focus on the energy system used in the water transport robot, this will include research on different energy sources which will be compared, power storage on Mars is also researched. The goal of this research is to find out if it is doable to provide such a water transport robot on Mars with enough energy for long distances. The main research question chosen is: Is it doable to provide a water transport robot with enough energy? To answer this question for the scenario described below a model is made. | |||
== | ==Assumptions== | ||
To research different possibilities for power storage and power supply, it is first needed to know how much power the robot needs. For this a quantitative description of the situation is needed. Since this situation is still an idea and not the reality, this will consist mostly of assumptions. All the time related units will be based on the situation on Earth. In other words, one day means one day on Earth. Most of the assumptions are based on values experienced on Earth, so it makes sense to use this time scheme as well. Not that it matters that much, since a day on Mars is equivalent to 1.02749125 days on Earth [https://en.wikipedia.org/wiki/Sol_(day_on_Mars)], which is not that big of a difference. To start, it is assumed that there are 50 people living in the colony around the equator that needs water. When looking at the water map displayed in the setting section at the beginning of the wiki, it can be said the equator is about ⅛ of the Martian circumference away from the white boxed section which is about 2500 kilometers. So, the colonies are 2500 kilometers apart. The goal is to let the robot drive at a speed of at least 10 kilometer per hour, which will result at a travel time of 500 hours or about 21 days to drive from colony to colony and back. We also assume the transport robot gets the maintenance and cleaning it should need, like for example cleaning the solar panels of dust, at each colony. | To research different possibilities for power storage and power supply, it is first needed to know how much power the robot needs. For this a quantitative description of the situation is needed. Since this situation is still an idea and not the reality, this will consist mostly of assumptions. All the time related units will be based on the situation on Earth. In other words, one day means one day on Earth. Most of the assumptions are based on values experienced on Earth, so it makes sense to use this time scheme as well. Not that it matters that much, since a day on Mars is equivalent to 1.02749125 days on Earth [https://en.wikipedia.org/wiki/Sol_(day_on_Mars)], which is not that big of a difference. To start, it is assumed that there are 50 people living in the colony around the equator that needs water. When looking at the water map displayed in the setting section at the beginning of the wiki, it can be said the equator is about ⅛ of the Martian circumference away from the white boxed section which is about 2500 kilometers. So, the colonies are 2500 kilometers apart. The relative height difference between the two colonies is assumed to be 0. The goal is to let the robot drive at a speed of at least 10 kilometer per hour, which will result at a travel time of 500 hours or about 21 days to drive from colony to colony and back. We also assume the transport robot gets the maintenance and cleaning it should need, like for example cleaning the solar panels of dust, at each colony. | ||
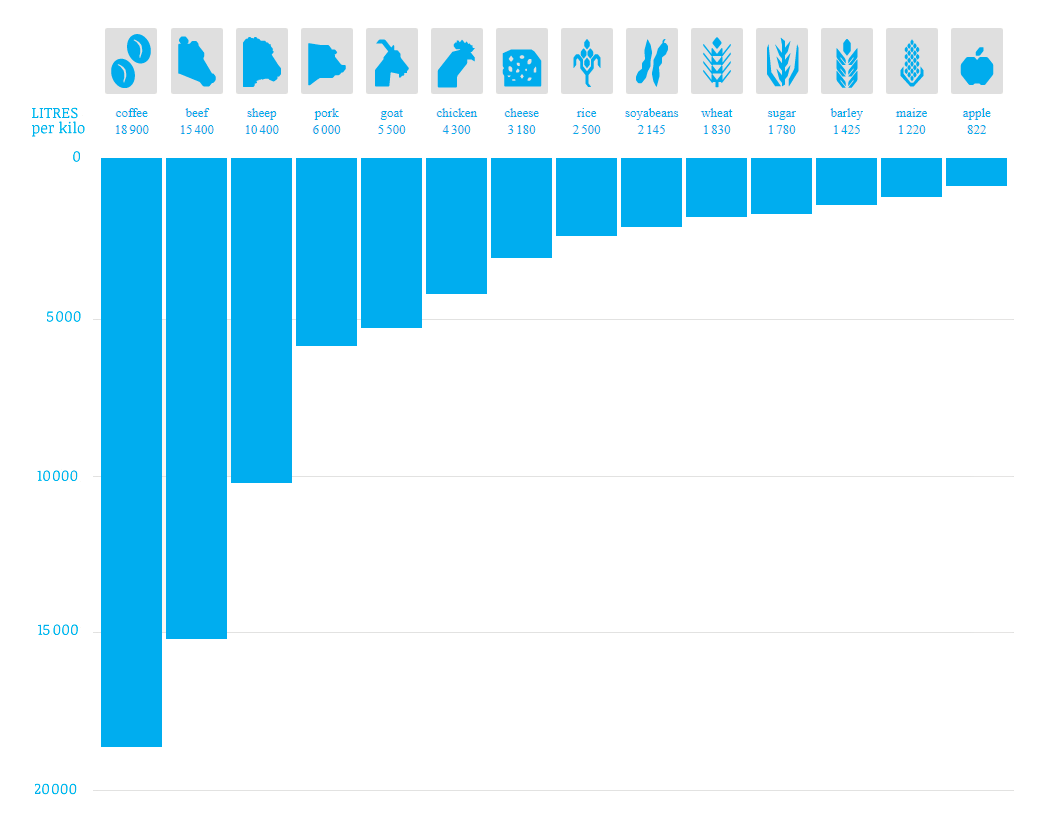
In order to know how much water the robot needs to transport, the water usage of the colony needs to be established. Every person in the colony will use about 50 liters of water per day [https://www.mars-one.com/faq/health-and-ethics/will-the-astronauts-have-enough-water-food-and-oxygen] for drinking, washing etc. From these 50 liters, it is assumed that 80% can be recycled at the colony [https://www.esa.int/Science_Exploration/Human_and_Robotic_Exploration/International_Space_Station/Water_in_space]. However, water is also needed for other things. If the colony is growing its own food, water is needed to grow crops. A human eats around 2.5 - 4.6 kilograms of food per day [http://www.ibiblio.org/lunar/school/InterStellar/Explorer_Class/Food_Mass_numbers.html]. For simplicity, it assumed that humans eat 3.5 kilograms of food per day. The water cost for food production of different types of food can be found in the graph below [https://thewaterweeat.com/]. Since it will be likely that in this stage of the colony no animals will be on Mars, it is assumed that the only food produced on Mars is in the form of growing crops. Because of this, the average amount of water needed for 1 kilogram of food is about 1675 liters which is obtained by taking the average of the production cost of apples, maize, barley, wheat, soyabeans and rice. Here on earth, a part of the water used for hydrating the crops disappears in the earth, but on Mars, a greenhouse could extract all extra water from the soil and reuse it. Also, a part of the water inside the crops that is consumed will be turned into urine which is recycled at the colony. While based on nothing, it is assumed that 30% of the water needed for growing crops can eventually be recycled. This brings the total water cost to 1182.5 liters per day per person, which is 59125 liters for the whole colony per day. This is a lot, but it is just an assumption. It could be that a lot more of the water needed for crops could be recycled, which will bring the number down by a lot. But for now, this number is what will be worked with. Another option is that all the food is produced at the colony where the water is coming from, which will result in the need for another transport infrastructure for the food, or could be combined with the water transport. This will bring the water consumption down to 500 liters per day for the colony at the equator. This seems like a way better option, so it is assumed that food is supplied by another transport robot. This means the total amount of water that the water transport robot needs to supply is '''500 liters per day'''. | In order to know how much water the robot needs to transport, the water usage of the colony needs to be established. Every person in the colony will use about 50 liters of water per day [https://www.mars-one.com/faq/health-and-ethics/will-the-astronauts-have-enough-water-food-and-oxygen] for drinking, washing etc. From these 50 liters, it is assumed that 80% can be recycled at the colony [https://www.esa.int/Science_Exploration/Human_and_Robotic_Exploration/International_Space_Station/Water_in_space]. However, water is also needed for other things. If the colony is growing its own food, water is needed to grow crops. A human eats around 2.5 - 4.6 kilograms of food per day [http://www.ibiblio.org/lunar/school/InterStellar/Explorer_Class/Food_Mass_numbers.html]. For simplicity, it assumed that humans eat 3.5 kilograms of food per day. The water cost for food production of different types of food can be found in the graph below [https://thewaterweeat.com/]. Since it will be likely that in this stage of the colony no animals will be on Mars, it is assumed that the only food produced on Mars is in the form of growing crops. Because of this, the average amount of water needed for 1 kilogram of food is about 1675 liters which is obtained by taking the average of the production cost of apples, maize, barley, wheat, soyabeans and rice. Here on earth, a part of the water used for hydrating the crops disappears in the earth, but on Mars, a greenhouse could extract all extra water from the soil and reuse it. Also, a part of the water inside the crops that is consumed will be turned into urine which is recycled at the colony. While based on nothing, it is assumed that 30% of the water needed for growing crops can eventually be recycled. This brings the total water cost to 1182.5 liters per day per person, which is 59125 liters for the whole colony per day. This is a lot, but it is just an assumption. It could be that a lot more of the water needed for crops could be recycled, which will bring the number down by a lot. But for now, this number is what will be worked with. Another option is that all the food is produced at the colony where the water is coming from, which will result in the need for another transport infrastructure for the food, or could be combined with the water transport. This will bring the water consumption down to 500 liters per day for the colony at the equator. This seems like a way better option, so it is assumed that food is supplied by another transport robot. This means the total amount of water that the water transport robot needs to supply is '''500 liters per day'''. | ||
[[File:GraphWater.png]] | [[File:GraphWater.png|700px|Water cost for food production of different types of food]] | ||
Since 1 transport robot can be back at the colony every 21 days, and the colony needs 500 liters of water per day, it can be concluded that 1 transport robot should be able to carry at least 10.500 liters of water. While, for this project, it is assumed that this transport robot will always reach its destination, in reality, it could always go wrong. The transport robot could get stuck, lost in a dust storm or just get a malfunction. For this reason, it is assumed that 4 of these robots will drive from and to the colony. 1 Robot will dispatch every 5¼ day and is assumed to have a capacity of 5000 liters. This means that, assuming the colony itself has storage capacity enough for more water than consumed, even if 1 robot will fail to come back, the colony always has water enough to survive. For comparison, the Mercedes Atego 1317-A 4x4 Lindner-Fischer 2017, which can be seen in the picture below [https://www.pktrucks.com/product/mercedes-atego-1317-a-4x4-water-tank-me4154], has a capacity of 6000 liters. This means that the transport robot needs to be around this size. This model weights about 11900 kilograms. With a full tank of water, this means it will weight about 12400 kilograms. This means that it can be assumed that the transport robot will weigh approximately the same on earth. Since the gravity on Mars is about 38% of the gravity on Earth [http://coolcosmos.ipac.caltech.edu/ask/73-How-strong-is-the-gravity-on-Mars-] this will result in a weight of about 4712 kilograms on Mars. For calculations however, mass is used, which will not change with gravity so it still has a mass of '''12400 kilograms''' on Mars. | Since 1 transport robot can be back at the colony every 21 days, and the colony needs 500 liters of water per day, it can be concluded that 1 transport robot should be able to carry at least 10.500 liters of water. While, for this project, it is assumed that this transport robot will always reach its destination, in reality, it could always go wrong. The transport robot could get stuck, lost in a dust storm or just get a malfunction. For this reason, it is assumed that 4 of these robots will drive from and to the colony. 1 Robot will dispatch every 5¼ day and is assumed to have a capacity of 5000 liters. This means that, assuming the colony itself has storage capacity enough for more water than consumed, even if 1 robot will fail to come back, the colony always has water enough to survive. For comparison, the Mercedes Atego 1317-A 4x4 Lindner-Fischer 2017, which can be seen in the picture below [https://www.pktrucks.com/product/mercedes-atego-1317-a-4x4-water-tank-me4154], has a capacity of 6000 liters. This means that the transport robot needs to be around this size. This model weights about 11900 kilograms. With a full tank of water, this means it will weight about 12400 kilograms. This means that it can be assumed that the transport robot will weigh approximately the same on earth. Since the gravity on Mars is about 38% of the gravity on Earth [http://coolcosmos.ipac.caltech.edu/ask/73-How-strong-is-the-gravity-on-Mars-] this will result in a weight of about 4712 kilograms on Mars. For calculations however, mass is used, which will not change with gravity so it still has a mass of '''12400 kilograms''' on Mars. | ||
[[File:Mercedes.jpg]] | Another important aspect to consider is that Mars has the occasion dust storm. During these storms the robot will not be able to function correctly, having almost no sunlight and the possibility of dust to damage the robot. It would therefore be best to not have the robots drive during such storms. Since the colonies won’t have a delivery of water, they need enough storage to last during such storms. If we assume that the colonies have such storage, the is also the need to refill those storages for the next dust storm. We assume that a dust storm last for about a month. [https://www.nasa.gov/feature/goddard/the-fact-and-fiction-of-martian-dust-storms] The size of such a storage will then need to be 500 * 30.42 = 15.210 L. The amount of days it will take to refill this storage will depend on the final design and will be further discussed in the discussion. | ||
[[File:Mercedes.jpg|300px|Mercedes Atego 1317-A 4x4 Lindner-Fischer 2017]] | |||
Now, the last thing to do is calculate how much energy the transport robot will approximately need. The energy needed to bring the transport robot from standing still to a certain speed can be calculated with the formula stated below. | Now, the last thing to do is calculate how much energy the transport robot will approximately need. The energy needed to bring the transport robot from standing still to a certain speed can be calculated with the formula stated below. | ||
[[File:EnergyEquation.png]] | [[File:EnergyEquation.png|Kinetic energy]] | ||
In this formula, Ek represents the kinetic energy put into the robot when it reached this speed, m represents the mass and v represents the speed. As any car on Earth, the transport robot will experience friction while moving across the surface. This friction consists of the friction created by the ground on the wheels and the air friction. The friction created by the ground on the wheels can be calculated with the formula stated below. | In this formula, Ek represents the kinetic energy put into the robot when it reached this speed, m represents the mass and v represents the speed. As any car on Earth, the transport robot will experience friction while moving across the surface. This friction consists of the friction created by the ground on the wheels and the air friction. The friction created by the ground on the wheels can be calculated with the formula stated below. | ||
[[File:Friction1.png]] | [[File:Friction1.png|Air friction]] | ||
In this formula, Ffr represents the friction force, m represents the mass, g represents the gravitational acceleration and c represents the rolling resistance coefficient. The friction caused by the air while moving can be calculated with the formula stated below. | In this formula, Ffr represents the friction force, m represents the mass, g represents the gravitational acceleration and c represents the rolling resistance coefficient. The friction caused by the air while moving can be calculated with the formula stated below. | ||
[[File:Friction2.png]] | [[File:Friction2.png|Rolling resistance friction]] | ||
In this formula, Ffr represents the friction force, C represents the drag coefficient, ρ represents the air density, A represents the cross-sectional area and v represents the speed of the transport robot. Both these friction forces will bring the transport robot to a stop when the engine of the robot stops putting kinetic energy in the robot. During the trip, these forces will put work on the robot which will require the engine to put new kinetic energy in the transport robot. This work is equal to the total friction force times the distance travelled. This means, that the total energy needed to move the transport robot from one colony to another at a certain speed can approximately be calculated with the formula below. | In this formula, Ffr represents the friction force, C represents the drag coefficient, ρ represents the air density, A represents the cross-sectional area and v represents the speed of the transport robot. Both these friction forces will bring the transport robot to a stop when the engine of the robot stops putting kinetic energy in the robot. During the trip, these forces will put work on the robot which will require the engine to put new kinetic energy in the transport robot. This work is equal to the total friction force times the distance travelled. This means, that the total energy needed to move the transport robot from one colony to another at a certain speed can approximately be calculated with the formula below. | ||
[[File:EnergyEquation2.png]] | [[File:EnergyEquation2.png|Total energy needed]] | ||
In this formula, E represents the total energy needed and d represents the distance. Some of these variables/coefficients are unknown, assumptions are made as presented in the table below. | In this formula, E represents the total energy needed and d represents the distance. Some of these variables/coefficients are unknown, assumptions are made as presented in the table below. | ||
| Line 143: | Line 231: | ||
Electric engines offer an efficiency of about 80% from grid to wheels [https://www.fueleconomy.gov/feg/atv-ev.shtml], meaning that the energy that should be produced by the transport robot can be calculated with the formula stated below. | Electric engines offer an efficiency of about 80% from grid to wheels [https://www.fueleconomy.gov/feg/atv-ev.shtml], meaning that the energy that should be produced by the transport robot can be calculated with the formula stated below. | ||
[[File:EnergyEquation3.png]] | [[File:EnergyEquation3.png|Total energy prodcution needed]] | ||
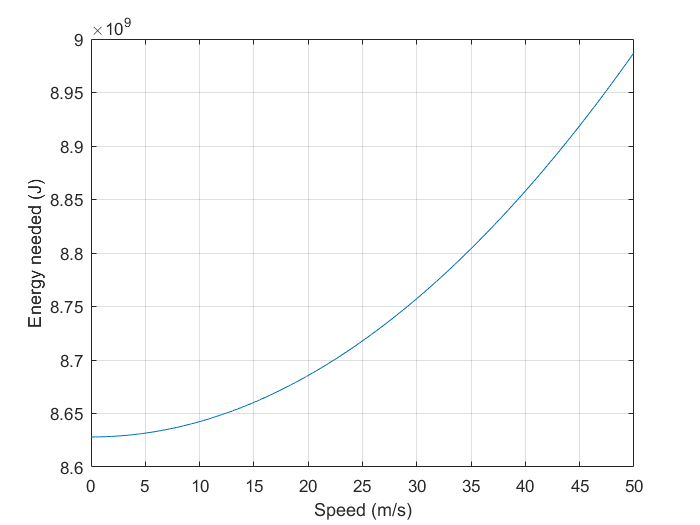
It is important to note that this formula does not account for everything and is just an approximation of the energy needed. A plot of the speed and the total energy needed can be found in the graph below. The noted point represents the wanted speed of 10 kilometers per hour, which is equal to 2.7778 meters per second. This speed results in a total needed energy of 8.63*10^9 Joule for driving. | It is important to note that this formula does not account for everything and is just an approximation of the energy needed. A plot of the speed and the total energy needed can be found in the graph below. The noted point represents the wanted speed of 10 kilometers per hour, which is equal to 2.7778 meters per second. This speed results in a total needed energy of 8.63*10^9 Joule for driving. | ||
[[File:USEPLOT2.png]] | [[File:USEPLOT2.png|500px|Total energy production needed as a function of velocity]] | ||
Other energy needs could include keeping the water at a certain temperature. Temperatures on Mars range from -125 degrees Celsius on a cold winter day to 20 degrees Celsius on a summer day [https://www.space.com/16907-what-is-the-temperature-of-mars.html]. This means that for the most part, the temperature is under 0 degrees Celsius and the water will be ice. While energy could be used to keep the water under 0 always, it seems best to let the water alternate between these two states of matter, solid and liquid. If the tank is big enough to keep 5000 liters liquid water in ice state, it should not be a problem. This will cut the need to put energy in keeping the water in a certain state. Since the density of ice is 0.92 times the density of liquid water [http://chemistry.elmhurst.edu/vchembook/122Adensityice.html], the tank should be able to carry 5435 liters of ice. For simplicity, we assume the tank has to have a capacity of 5500 liters. | Other energy needs could include keeping the water at a certain temperature. Temperatures on Mars range from -125 degrees Celsius on a cold winter day to 20 degrees Celsius on a summer day [https://www.space.com/16907-what-is-the-temperature-of-mars.html]. This means that for the most part, the temperature is under 0 degrees Celsius and the water will be ice. While energy could be used to keep the water under 0 always, it seems best to let the water alternate between these two states of matter, solid and liquid. If the tank is big enough to keep 5000 liters liquid water in ice state, it should not be a problem. This will cut the need to put energy in keeping the water in a certain state. Since the density of ice is 0.92 times the density of liquid water [http://chemistry.elmhurst.edu/vchembook/122Adensityice.html], the tank should be able to carry 5435 liters of ice. For simplicity, we assume the tank has to have a capacity of 5500 liters. | ||
| Line 153: | Line 241: | ||
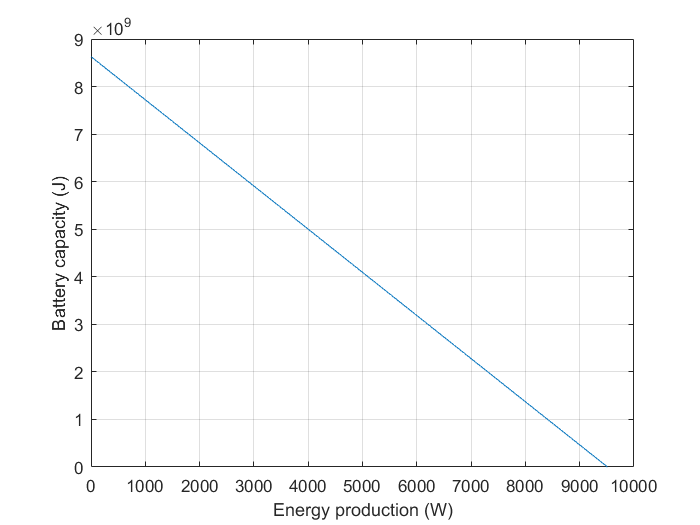
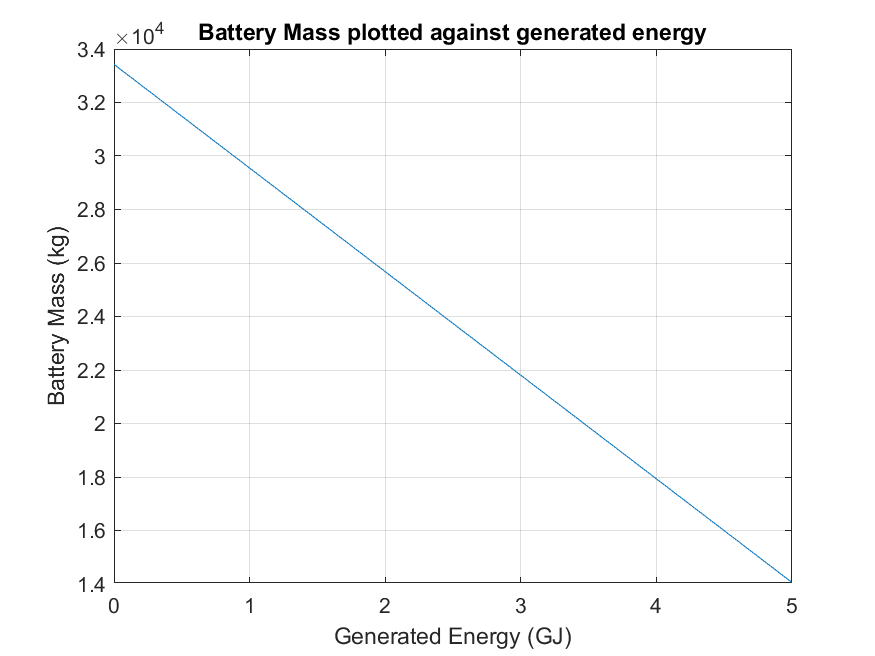
All in all, this means that if the transport robot moves with a speed of 10 kilometers per hour, it needs to be able to either storage at least 8.63 GJ of energy or needs to be able to, assuming it travels for 10.5 days one way, generate at least 9511.89 Joule of energy per second (9511.89 Watt). A combination of a power storage that is charged at the colony and a power supply during the trip could also be an option. The amount of battery capacity and the amount of energy production needed can be found plotted against each other in the graph below. | All in all, this means that if the transport robot moves with a speed of 10 kilometers per hour, it needs to be able to either storage at least 8.63 GJ of energy or needs to be able to, assuming it travels for 10.5 days one way, generate at least 9511.89 Joule of energy per second (9511.89 Watt). A combination of a power storage that is charged at the colony and a power supply during the trip could also be an option. The amount of battery capacity and the amount of energy production needed can be found plotted against each other in the graph below. | ||
[[File:BatteryPlot2.png]] | [[File:BatteryPlot2.png|500px|Battery capacity needed as a function of total energy prodcution]] | ||
== RPC list == | |||
{| border=1 style="border-collapse: collapse;" cellpadding = 4 | |||
! Requirements | |||
! Preferences | |||
! Constraints | |||
|- style="text-align: center" | |||
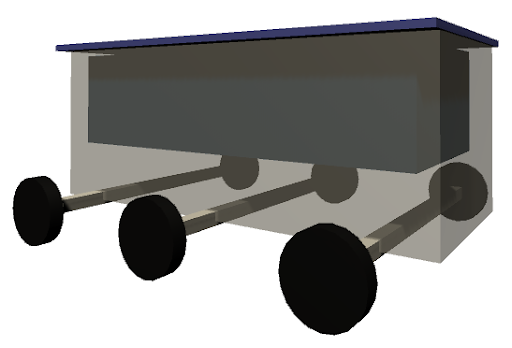
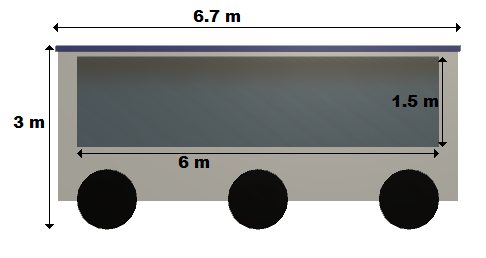
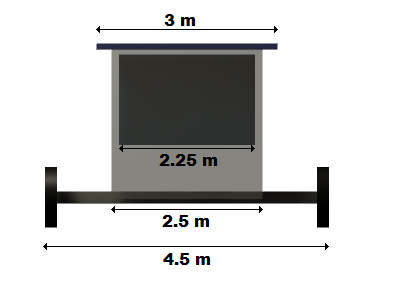
| Needs to travel 2500 Kilometers from colony to colony || There should not be the need for too many robots (around 4) || Dimensions of robot (662x250x300cm) | |||
|-style="text-align: center" | |||
| Needs to supply 500 Liters of water per day || The robot should have a speed of 10 km/h || | |||
|} | |||
== What does the robot already know? == | |||
The robot already knows the location of the colonies and already knows the terrain of Mars in between. Unexpected obstacles such as boulders, duststorms or cave-ins are not known however. | |||
=Plan= | =Plan= | ||
| Line 252: | Line 354: | ||
* Is only a battery enough? How much energy production is needed if we use the battery only as a buffer? | * Is only a battery enough? How much energy production is needed if we use the battery only as a buffer? | ||
* | * Should we drive slower than 10 km / h | ||
===Making the presentation=== | ===Making the presentation=== | ||
| Line 275: | Line 377: | ||
* Conclusion | * Conclusion | ||
* Discussion | |||
* Presentation | * Presentation | ||
| Line 368: | Line 472: | ||
- Wiki (Before Thursday 02-04-2020) | - Wiki (Before Thursday 02-04-2020) | ||
|| Everyone | || Everyone | ||
|} | |} | ||
| Line 515: | Line 503: | ||
The Curiosity rover uses a Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) in order to generate energy. This is a device that relies on radioactive material to generate energy. It is a preferable energy source for Mars rovers, because the energy generation method does not require oxygen. Furthermore, Curiosity also has solar panels to generate energy. | The Curiosity rover uses a Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) in order to generate energy. This is a device that relies on radioactive material to generate energy. It is a preferable energy source for Mars rovers, because the energy generation method does not require oxygen. Furthermore, Curiosity also has solar panels to generate energy. | ||
For the storage of this energy, two lithium ion batteries are present on board of the rover. These batteries have the highest known storage capacity, and are reliable in Martian conditions. For example, discharging is possible at the low temperatures that are present on Mars. These batteries are used for backup for the energy generators in times of peak demands. [https://mars.nasa.gov/mars2020/spacecraft/rover/electrical-power/] | For the storage of this energy, two lithium ion batteries are present on board of the rover. These batteries have the highest known storage capacity, and are reliable in Martian conditions. For example, discharging is possible at the low temperatures that are present on Mars. These batteries are used for backup for the energy generators in times of peak demands. [https://mars.nasa.gov/mars2020/spacecraft/rover/electrical-power/] | ||
==Literature== | |||
=== General === | |||
[https://www.nasa.gov/centers/hq/library/find/bibliographies/space_colonization] NASA page including all kinds of information sources about space colonies. | |||
[https://space.nss.org/settlement/nasa/75SummerStudy/Table_of_Contents1.html] Space Settlements: A Design Study. Includes information about all aspects of a space settlement including resources needed to maintain and expand. | |||
===Mars Terrain=== | |||
[https://authors.library.caltech.edu/36642/1/aharonson98_grl.pdf] This paper investigates the slope distribution in the northern hemisphere of Mars from topographic profiles collected | |||
by the Mars Orbiter Laser Altimeter. | |||
[https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/1999JE001051] This paper describes the calculation of slopes and the characterization of surface roughness using profiles | |||
obtained by the Mars Orbiter Laser Altimete. | |||
=== Transporting materials === | |||
[https://patents.google.com/patent/US2558648A/en] June 26, 1951 R. w. GAUSMANN APPARATUS FOR TRANSPORTING MATERIALS 5 Sheets-Sheet 1. Is about a technique for for transporting materials without changing the compounds temperature which may be necessary to prevent chemical changes in the material being transported, or to prevent it from solidifying within the car whereupon it would have to be heated to be removed therefrom. | |||
[https://www.sciencedirect.com/science/article/pii/S0079642519300593] Extraterrestrial construction materials by M.Z.Naser. This review explores the suitability of construction materials derived from lunar and Martian regolith along with concrete derivatives, space-native metals and composites, as well as advanced and non-traditional materials for interplanetary construction. | |||
[https://www.sciencedirect.com/science/article/abs/pii/S0094576518307033] Space-native construction materials for earth-independent and sustainable infrastructure. This review covers feasibility of exploiting in-situ lunar and Martian resources as well as harvesting of elements and compounds, from near Earth objects (NEOs), to produce extraterrestrial materials suitable for construction of space-based infrastructure. | |||
[https://www.sciencedirect.com/science/article/abs/pii/S0376042118300150] Materials and design concepts for space-resilient structures. This paper presents a state-of-the-art literature review on recent developments of “space-native” construction materials, and highlights evolutionary design concepts for “space-resilient” structures. | |||
= Research = | = Research = | ||
| Line 521: | Line 535: | ||
[[File:SolarPanel.png]][https://www.powerfromsunlight.com/solar-panel-frame-important/] | [[File:SolarPanel.png|400px|Parts of a solarpanel]] | ||
[https://www.powerfromsunlight.com/solar-panel-frame-important/] | |||
=== Performance === | === Performance === | ||
The performance of a solar panel depends on many different aspects. The most important aspects are the sunlight that hits the surface of the solar panel, the efficiency of the conducting material in the cells of the solar panel and the size of the surface of the solar panel. There are also many other aspects that determine how many energy is created like whether there is something blocking the sunlight, like an object or dust particles, and the temperature of the photovoltaic cells. The global formula to estimate the energy generated by a photovoltaic system is stated as presented below [https://photovoltaic-software.com/principle-ressources/how-calculate-solar-energy-power-pv-systems] . | The performance of a solar panel depends on many different aspects. The most important aspects are the sunlight that hits the surface of the solar panel, the efficiency of the conducting material in the cells of the solar panel and the size of the surface of the solar panel. There are also many other aspects that determine how many energy is created like whether there is something blocking the sunlight, like an object or dust particles, and the temperature of the photovoltaic cells. The global formula to estimate the energy generated by a photovoltaic system is stated as presented below [https://photovoltaic-software.com/principle-ressources/how-calculate-solar-energy-power-pv-systems] . | ||
[[File:OneOneOne.png]] | [[File:OneOneOne.png|Energy generated by a photovoltaic system]] | ||
In this formula, the following variables are used; | In this formula, the following variables are used; | ||
| Line 543: | Line 558: | ||
To determine the average solar radiation on the panels, the sunlight intensity on mars can give a good estimate. Power received from the sun is often measured in solar irradiance, which is the power per unit area of electromagnetic radiation. To be precise, irradiance in general is defined as “the amount of light energy from one thing hitting a square meter of another each second” [https://www.nasa.gov/mission_pages/sdo/science/Solar%20Irradiance.html]. Solar irradiance is measured in watt per square meter (W/m^2). The solar irradiance on Mars can be calculated using the solar constant [https://en.wikipedia.org/wiki/Solar_constant]. At a distance from the sun of 1 UA, which is approximately the distance between the Sun and Earth, the solar irradiance is equal to 1361 W/m^2. Since the average distance from the Sun to Mars is equal to 1.524 UA [https://www.universetoday.com/14822/how-far-is-mars-from-the-sun/], the solar irradiance on Mars can be calculated as stated below. | To determine the average solar radiation on the panels, the sunlight intensity on mars can give a good estimate. Power received from the sun is often measured in solar irradiance, which is the power per unit area of electromagnetic radiation. To be precise, irradiance in general is defined as “the amount of light energy from one thing hitting a square meter of another each second” [https://www.nasa.gov/mission_pages/sdo/science/Solar%20Irradiance.html]. Solar irradiance is measured in watt per square meter (W/m^2). The solar irradiance on Mars can be calculated using the solar constant [https://en.wikipedia.org/wiki/Solar_constant]. At a distance from the sun of 1 UA, which is approximately the distance between the Sun and Earth, the solar irradiance is equal to 1361 W/m^2. Since the average distance from the Sun to Mars is equal to 1.524 UA [https://www.universetoday.com/14822/how-far-is-mars-from-the-sun/], the solar irradiance on Mars can be calculated as stated below. | ||
[[File:TwoTwoTwo.png]] | [[File:TwoTwoTwo.png|Solar irradiance on Mars]] | ||
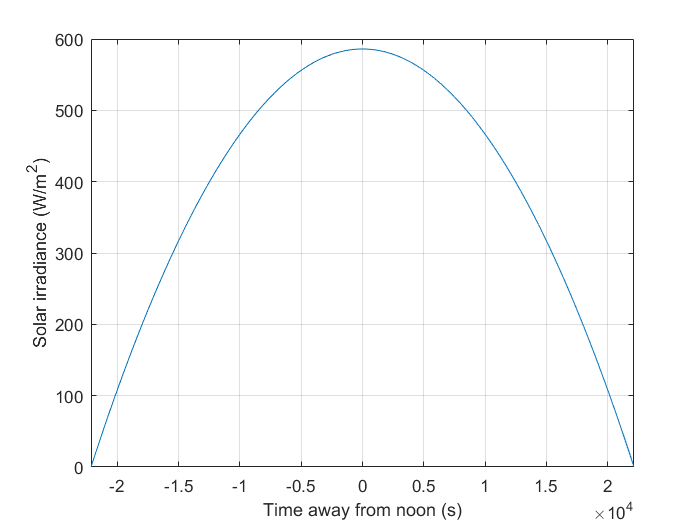
To check this calculation, the average solar irradiance on Mars according to NASA is 586.2 W/m^2 [https://nssdc.gsfc.nasa.gov/planetary/factsheet/marsfact.html]. Since one day on Mars takes 24.62 hours [http://coolcosmos.ipac.caltech.edu/ask/74-How-long-is-a-day-on-Mars-] it can be assumed that there will be approximately 12.31 hours of sun and 12.31 hours of darkness each day. Of course, the sunlight intensity will be at its peak at noon, which is when it will produce the 585.987W/m^2 calculated before. The sunlight irradiance during the rest of the day could be approximated using a parabola, which can be used to calculate the total energy production during one day [http://ecgllp.com/files/3514/0200/1304/2-Solar-Radiation.pdf]. This parabola will have its peak at 585.987 and will go through the x-axis at -22158 and at 22158, which is equal to the amount of seconds in 6.155 hours. This can be achieved with the equation stated below. | To check this calculation, the average solar irradiance on Mars according to NASA is 586.2 W/m^2 [https://nssdc.gsfc.nasa.gov/planetary/factsheet/marsfact.html]. Since one day on Mars takes 24.62 hours [http://coolcosmos.ipac.caltech.edu/ask/74-How-long-is-a-day-on-Mars-] it can be assumed that there will be approximately 12.31 hours of sun and 12.31 hours of darkness each day. Of course, the sunlight intensity will be at its peak at noon, which is when it will produce the 585.987W/m^2 calculated before. The sunlight irradiance during the rest of the day could be approximated using a parabola, which can be used to calculate the total energy production during one day [http://ecgllp.com/files/3514/0200/1304/2-Solar-Radiation.pdf]. This parabola will have its peak at 585.987 and will go through the x-axis at -22158 and at 22158, which is equal to the amount of seconds in 6.155 hours. This can be achieved with the equation stated below. | ||
[[File:FourFourFour.png]] | [[File:FourFourFour.png|Formula sunlight irradiance throughout the day]] | ||
This parabola also has negative y-values, but these can be ignored. A plot of this equation can be found in the image below. | This parabola also has negative y-values, but these can be ignored. A plot of this equation can be found in the image below. | ||
[[File:ThreeThreeThree.png]] | [[File:ThreeThreeThree.png|500px|Graph sunlight irradiance throughout the day]] | ||
In order to calculate the total energy produced during one day, the area underneath the graph should be obtained. For this, the antiderivative of the function is needed, which can be found in the equation below. | In order to calculate the total energy produced during one day, the area underneath the graph should be obtained. For this, the antiderivative of the function is needed, which can be found in the equation below. | ||
[[File:FiveFiveFive.png]] | [[File:FiveFiveFive.png|Total energy produced during one day]] | ||
Since the function is symmetrical, the total area under the graph can be calculated by taking the integral from x = 0 to x = 22158 twice, which results in 17312399.93 Joule per square meter per day. The robot is driving for 10.5 Earth days (252 hours), which is equal to approximately 10.219 days on Mars. Thus, there will be, approximately, 176915414.9 Joule of sunlight per square meter over the course of the 10.219 days on Mars. | Since the function is symmetrical, the total area under the graph can be calculated by taking the integral from x = 0 to x = 22158 twice, which results in 17312399.93 Joule per square meter per day. The robot is driving for 10.5 Earth days (252 hours), which is equal to approximately 10.219 days on Mars. Thus, there will be, approximately, 176915414.9 Joule of sunlight per square meter over the course of the 10.219 days on Mars. | ||
To get the most out of this energy, the solar panels should be positioned correctly. The solar panels will generate the most amount of electricity when the sunlight is perpendicular to the surface of the solar panel [https://www.mpptsolar.com/en/best-angle-for-solar-panels.html]. This means that, ideally, the solar panel will always be directed directly towards the sun using a tilting mechanism. An example on earth where a system tilts the solar panels so that they always face the sun at a 90-degree angle is in a operation in Piteå [https://www.nordicenergy.org/article/solar-power-at-the-arctic-circle/]. The helianthus smart solar panel is a solar panel that is able to track the sun using a microcontroller based embedded system [https://www.researchgate.net/publication/323226176_HELIANTHUS-SMART_SOLAR_PANEL]. This will ensure that the angle of the sunlight hitting the solar panel is always 90 degrees. Some form of this mechanism should be implemented in the robot, should it use solar energy. | To get the most out of this energy, the solar panels should be positioned correctly. The solar panels will generate the most amount of electricity when the sunlight is perpendicular to the surface of the solar panel [https://www.mpptsolar.com/en/best-angle-for-solar-panels.html]. This means that, ideally, the solar panel will always be directed directly towards the sun using a tilting mechanism. An example on earth where a system tilts the solar panels so that they always face the sun at a 90-degree angle is in a operation in Piteå [https://www.nordicenergy.org/article/solar-power-at-the-arctic-circle/]. The helianthus smart solar panel is a solar panel that is able to track the sun using a microcontroller based embedded system [https://www.researchgate.net/publication/323226176_HELIANTHUS-SMART_SOLAR_PANEL]. This will ensure that the angle of the sunlight hitting the solar panel is always 90 degrees. Some form of this mechanism should be implemented in the robot, should it use solar energy. | ||
==== Efficiency (r) ==== | ==== Efficiency (r) ==== | ||
| Line 579: | Line 593: | ||
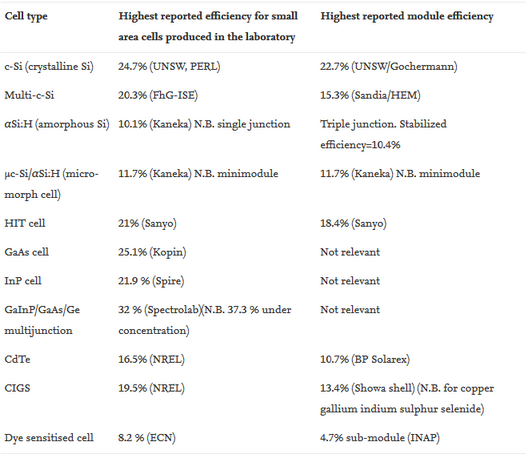
Table containing efficienty of materials [https://www.sciencedirect.com/science/article/pii/S0042207X06000182] | Table containing efficienty of materials [https://www.sciencedirect.com/science/article/pii/S0042207X06000182] | ||
[[File:Efficientytable.png]] | [[File:Efficientytable.png|500px|Efficienty of materials]] | ||
====Total solar panel area (A)==== | ====Total solar panel area (A)==== | ||
| Line 594: | Line 608: | ||
Having one large solar panel with a length and width of 6.50 m will give a huge surface of 42.25 m^2. However, it will most likely not be possible to have a height of 6.5 m and therefore not be able to tilt and turn fully. Also it is questionable whether the giant solar panel will be able to catch wind and make the robot tilt at high wind force. Moreover having a solar panel stick about 1,3 m of the front and back when they turn, since the diameter is around 9.2 m and 3,3 m of the sides which can be problamatic as well. Therfore this option will not be viable. | Having one large solar panel with a length and width of 6.50 m will give a huge surface of 42.25 m^2. However, it will most likely not be possible to have a height of 6.5 m and therefore not be able to tilt and turn fully. Also it is questionable whether the giant solar panel will be able to catch wind and make the robot tilt at high wind force. Moreover having a solar panel stick about 1,3 m of the front and back when they turn, since the diameter is around 9.2 m and 3,3 m of the sides which can be problamatic as well. Therfore this option will not be viable. | ||
Having multiple solar panels with a lenght and width equal to the width of the robot (200 cm) we will be able to put 3 solar panels on the robot and have a total solar panel surface of 12 m^2. The height should be around 1 m in order for the solar panels to turn which is quite doable. However, the solar panel sticks 15 cm off the side when they turn, since the diameter of each solar panel is around 2.8 m and 1 m off the front and back. This could be problamatic as well when driving up or down a slope. However by sacficing some area and making the middle solar panel a bit higher, about 0,5 m and putting the first and last solar panel closer to the middle the solar panels will not stick too much over the front and back. This will however cost some effective area since the large solar panel will shade the 2 smaller ones. So if we lose 50 cm of the front and back, the the area will decrease by 0.5 m * 2 m * 2 solar panels * 0.8 ( | Having multiple solar panels with a lenght and width equal to the width of the robot (200 cm) we will be able to put 3 solar panels on the robot and have a total solar panel surface of 12 m^2. The height should be around 1 m in order for the solar panels to turn which is quite doable. However, the solar panel sticks 15 cm off the side when they turn, since the diameter of each solar panel is around 2.8 m and 1 m off the front and back. This could be problamatic as well when driving up or down a slope. However by sacficing some area and making the middle solar panel a bit higher, about 0,5 m and putting the first and last solar panel closer to the middle the solar panels will not stick too much over the front and back. This will however cost some effective area since the large solar panel will shade the 2 smaller ones. So if we lose 50 cm of the front and back, the the area will decrease by 0.5 m * 2 m * 2 solar panels * 0.8 (20% loss due to shade) = 1.6 m^2. So we will have a remaining solar panel area of 10.4 m^2. | ||
Another solution for the solar panel width / length is to have many small solar panels with length and width 1 m. We can put them in pair on the robot, such that they only stick about 10 cm of the side, since it will have a diameter of 140 cm, and have height 0.5 m. This will enable us to put around 5 pair of solar panels and the robot, having the solar panels only stick 25 cm of the front and back. This gives us a total solar panel area of around 1 m2 area per panel * 2 solar panels per pair * 5 pairs = 10 m^2. | Another solution for the solar panel width / length is to have many small solar panels with length and width 1 m. We can put them in pair on the robot, such that they only stick about 10 cm of the side, since it will have a diameter of 140 cm, and have height 0.5 m. This will enable us to put around 5 pair of solar panels and the robot, having the solar panels only stick 25 cm of the front and back. This gives us a total solar panel area of around 1 m2 area per panel * 2 solar panels per pair * 5 pairs = 10 m^2. | ||
| Line 661: | Line 675: | ||
====Total energy==== | ====Total energy==== | ||
[[File:OneOneOne.png]] | [[File:OneOneOne.png|Total energy produced by solar panels durin one trip]] | ||
H = 176915414.9 J/m^2 | H = 176915414.9 J/m^2 | ||
| Line 699: | Line 713: | ||
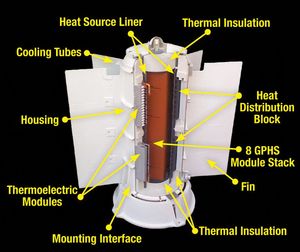
A typical design of a radioisotope thermoelectric generator (RTG) consists of 2 main ingredients: fuel that will decay radioactively and a large set of thermocouples to convert heat into electricity.[http://large.stanford.edu/courses/2013/ph241/jiang1/] A thermocouple is a set of 2 wires made of 2 different metals that are placed in electric contact at each end.[https://www.britannica.com/technology/thermocouple] When two metals are placed in electric contact, electrons flow out of the one in which the electrons have a higher Fermi level. The Fermi level of the metal represents the thermodynamic work required to add one electron to the metal. The energy of an electron in the metal at the Fermi level is −W relative to a free electron outside the metal. The flow of electrons between the two conductors in contact continues until the change in electric potential brings the Fermi levels of the two metals (W1 and W2) to the same value. This electric potential is called the contact potential ϕ12 and is given by eϕ12 = W1 − W2, where e is the electrical charge of one electron (1.6 × 10−19 coulomb.) [https://www.britannica.com/science/electricity/Electric-properties-of-matter#ref71578] If a closed circuit is made of two different metals at the same temperature, there will be no net electromotive force in the circuit because the two contact potentials oppose each other and no current will flow, however if the temperature of one of the junctions is raised relatively to the other there will be a current. Since the Fermi levels of the two metals have a different temperature dependance there will be a net electromotive force generated in the circuit. To maintain the temperature difference, heat must enter the hot junction and leave the cold junction, in a RTG this heat is produced by the fuel that will decay radioactively. The generation of a thermal electromotive force at a junction is called the Seebeck effect. The electromotive force is approximately linear with the temperature difference between two junctions of the different metals, these two different metals are the thermocouple mentioned before. The picture shown below [https://mars.nasa.gov/mars2020/files/mep/MMRTG_FactSheet_update_10-2-13.pdf] shows a Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) which is a typical modern RTG. | A typical design of a radioisotope thermoelectric generator (RTG) consists of 2 main ingredients: fuel that will decay radioactively and a large set of thermocouples to convert heat into electricity.[http://large.stanford.edu/courses/2013/ph241/jiang1/] A thermocouple is a set of 2 wires made of 2 different metals that are placed in electric contact at each end.[https://www.britannica.com/technology/thermocouple] When two metals are placed in electric contact, electrons flow out of the one in which the electrons have a higher Fermi level. The Fermi level of the metal represents the thermodynamic work required to add one electron to the metal. The energy of an electron in the metal at the Fermi level is −W relative to a free electron outside the metal. The flow of electrons between the two conductors in contact continues until the change in electric potential brings the Fermi levels of the two metals (W1 and W2) to the same value. This electric potential is called the contact potential ϕ12 and is given by eϕ12 = W1 − W2, where e is the electrical charge of one electron (1.6 × 10−19 coulomb.) [https://www.britannica.com/science/electricity/Electric-properties-of-matter#ref71578] If a closed circuit is made of two different metals at the same temperature, there will be no net electromotive force in the circuit because the two contact potentials oppose each other and no current will flow, however if the temperature of one of the junctions is raised relatively to the other there will be a current. Since the Fermi levels of the two metals have a different temperature dependance there will be a net electromotive force generated in the circuit. To maintain the temperature difference, heat must enter the hot junction and leave the cold junction, in a RTG this heat is produced by the fuel that will decay radioactively. The generation of a thermal electromotive force at a junction is called the Seebeck effect. The electromotive force is approximately linear with the temperature difference between two junctions of the different metals, these two different metals are the thermocouple mentioned before. The picture shown below [https://mars.nasa.gov/mars2020/files/mep/MMRTG_FactSheet_update_10-2-13.pdf] shows a Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) which is a typical modern RTG. | ||
[[File:f1.jpg]] | [[File:f1.jpg|300px|Multi-Mission Radioisotope Thermoelectric Generator]] | ||
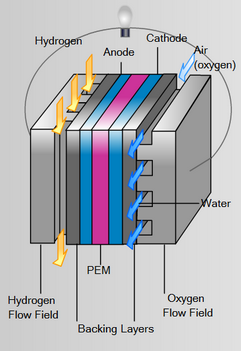
The fuel is located behind the thermal insulation layer and the thermocouples are lined in modules throughout the sides of the RTG. | The fuel is located behind the thermal insulation layer and the thermocouples are lined in modules throughout the sides of the RTG. | ||
| Line 723: | Line 737: | ||
* Strontium-90 (Sr-90) | * Strontium-90 (Sr-90) | ||
Of these Plutonium-238 is the most cited fuel in resources about RTGs. [http://large.stanford.edu/courses/2013/ph241/jiang1/] In fact because of the frequent use of Plutonium-238 for the use in RTGs, including its use in more than 20 space missions, there is a current shortage of this isotope. Since Plutonium-238 is a byproduct of creating nuclear weapons most of what NASA uses is left over from the cold war. [https://www.syfy.com/syfywire/nasa-can-only-make-three-more-batteries-one-powers-mars-rover] However this does not mean it can’t be produced anymore: In 2012, the Obama administration got Congress to go along with a plutonium-238 restart, under the condition that NASA pay to repair aging DOE infrastructure. When these repairs are complete, the Energy Department of Energy will start producing 1.5 kilograms of plutonium-238 a year. [https://spacenews.com/u-s-plutonium-stockpile-good-for-two-more-nuclear-batteries-after-mars-2020/] Pu-238 satisfies all of the RTG fuel characteristic needed with high radiation output, mainly alpha decay channels and is thus safer to use for any Martian colonist, a very long half-life of 88 years, and a small fuel pellet packaged into the size of a marshmallow as seen in the picture shown below [https://spacenews.com/u-s-plutonium-stockpile-good-for-two-more-nuclear-batteries-after-mars-2020/] | Of these Plutonium-238 is the most cited fuel in resources about RTGs. [http://large.stanford.edu/courses/2013/ph241/jiang1/] In fact because of the frequent use of Plutonium-238 for the use in RTGs, including its use in more than 20 space missions, there is a current shortage of this isotope. Since Plutonium-238 is a byproduct of creating nuclear weapons most of what NASA uses is left over from the cold war. [https://www.syfy.com/syfywire/nasa-can-only-make-three-more-batteries-one-powers-mars-rover] However this does not mean it can’t be produced anymore: In 2012, the Obama administration got Congress to go along with a plutonium-238 restart, under the condition that NASA pay to repair aging DOE infrastructure. When these repairs are complete, the Energy Department of Energy will start producing 1.5 kilograms of plutonium-238 a year. [https://spacenews.com/u-s-plutonium-stockpile-good-for-two-more-nuclear-batteries-after-mars-2020/] Pu-238 satisfies all of the RTG fuel characteristic needed with high radiation output, mainly alpha decay channels and is thus safer to use for any Martian colonist, a very long half-life of 88 years, and a small fuel pellet packaged into the size of a marshmallow as seen in the picture shown below. [https://spacenews.com/u-s-plutonium-stockpile-good-for-two-more-nuclear-batteries-after-mars-2020/] All these factors make Plutonium-238 the best isotope to use for RTGs on Mars. | ||
[[File:Plutonium238_pellet02-316x253.jpg]] | [[File:Plutonium238_pellet02-316x253.jpg|200px|Small fuel pellet of plutonium]] | ||
Production of Plutonium-238 will not be possible on Mars in the early stages of colonization since the production process is really complicated, thus all the Plutonium-238 would have to be transported to Mars from Earth. | Production of Plutonium-238 will not be possible on Mars in the early stages of colonization since the production process is really complicated, thus all the Plutonium-238 would have to be transported to Mars from Earth. | ||
| Line 733: | Line 747: | ||
To determine how much energy can be produced by using a RTG, we need to know the heat energy generated and the efficiency of the energy conversion. The latter depends on the materials used and the temperature on the cold and hot side. The following material properties influence the efficiency: Electrical conductivity, Thermal Conductivity and the Seebeck Coefficient. [https://pdfs.semanticscholar.org/8fc7/f7c5c7a5ba0d15f911b9469e97be8078edd2.pdf] If these are known then the efficiency by which a material is capable of generating power can be determined. | To determine how much energy can be produced by using a RTG, we need to know the heat energy generated and the efficiency of the energy conversion. The latter depends on the materials used and the temperature on the cold and hot side. The following material properties influence the efficiency: Electrical conductivity, Thermal Conductivity and the Seebeck Coefficient. [https://pdfs.semanticscholar.org/8fc7/f7c5c7a5ba0d15f911b9469e97be8078edd2.pdf] If these are known then the efficiency by which a material is capable of generating power can be determined. | ||
[[File:Pasted_image_0.png]] | [[File:Pasted_image_0.png|200px|Efficiency by which a material is capable of generating power]] | ||
Then, by using the temperature on the hot and cold side, the conversion unit can be calculated. | Then, by using the temperature on the hot and cold side, the conversion unit can be calculated. | ||
[[File:Pasted_image_0_(1).png]] | [[File:Pasted_image_0_(1).png|200px|Conversion unit]] | ||
Once M and Z are known the ideal efficiency can be calculated. | Once M and Z are known the ideal efficiency can be calculated. | ||
[[File:Pasted_image_0_(2).png]] | [[File:Pasted_image_0_(2).png|200px|Ideal efficiency]] | ||
These formulas could be used to determine the efficiency of a custom setup, but for existing setups such as the MMRTG the power output is already known. | These formulas could be used to determine the efficiency of a custom setup, but for existing setups such as the MMRTG the power output is already known. | ||
| Line 748: | Line 762: | ||
In the Multi-mission radioisotope thermoelectric generator (MMRTG) developed by NASA for multiple space missions, PbTe (Lead Telluride) and TAGS is used, where TAGS material is a material incorporating Tellurium, Silver Germanium and Antimony. This material and the temperature inside the generator result in a thermal power generation of 1975 W and an efficiency of 5,6%. Concluding in a netto electrical output of 110 W at the start of the mission, falling to about 100 W after 14 years. The MMRTG weights 43.6 kg which means the netto energy density is 2,52 W/kg. [https://www.nasa.gov/sites/default/files/files/4_Mars_2020_MMRTG.pdf] For every one kg added to the Transport robot would require an extra 695.8 kJ of energy, calculated with the formula shown below, or 0.767 W if the Transport robot would travel at 10 km/h. This means the net energy gain of a MMRTG would be 1.753 W/kg if the Transport robot would travel at 10 km/h. | In the Multi-mission radioisotope thermoelectric generator (MMRTG) developed by NASA for multiple space missions, PbTe (Lead Telluride) and TAGS is used, where TAGS material is a material incorporating Tellurium, Silver Germanium and Antimony. This material and the temperature inside the generator result in a thermal power generation of 1975 W and an efficiency of 5,6%. Concluding in a netto electrical output of 110 W at the start of the mission, falling to about 100 W after 14 years. The MMRTG weights 43.6 kg which means the netto energy density is 2,52 W/kg. [https://www.nasa.gov/sites/default/files/files/4_Mars_2020_MMRTG.pdf] For every one kg added to the Transport robot would require an extra 695.8 kJ of energy, calculated with the formula shown below, or 0.767 W if the Transport robot would travel at 10 km/h. This means the net energy gain of a MMRTG would be 1.753 W/kg if the Transport robot would travel at 10 km/h. | ||
[[File:EnergyEquation3.png]] | [[File:EnergyEquation3.png|Total energy prodcution needed]] | ||
===Safety of a Radioisotope Thermoelectric generator=== | ===Safety of a Radioisotope Thermoelectric generator=== | ||
| Line 768: | Line 782: | ||
==Hydrogen Energy== | ==Hydrogen Energy== | ||
Hydrogen energy is a rather new and experimental energy source and has many different applications like energy production, storage, and distribution; electricity, heat, and cooling for buildings and households; the industry; transportation; and the fabrication of feedstock. [https://www.sciencedirect.com/book/9780128142516/science-and-engineering-of-hydrogen-based-energy-technologies]. There are many benefits to using hydrogen as a fuel, namely it | Hydrogen energy is a rather new and experimental energy source and has many different applications like energy production, storage, and distribution; electricity, heat, and cooling for buildings and households; the industry; transportation; and the fabrication of feedstock. [https://www.sciencedirect.com/book/9780128142516/science-and-engineering-of-hydrogen-based-energy-technologies]. There are many benefits to using hydrogen as a fuel, namely it has a lower mass density than fossil fuels, has 3 times as much energy than fossil fuels per kg and hydrogen does not produce harmful emissions. However, hydrogen takes up a lot of space, cannot be found in nature, is difficult to store and is highly flammable. [https://books.google.nl/books?id=jMWCDsJesbcC&pg=PA11&lpg=PA11&dq=pound+for+pound,+hydrogen+contains+almost+three+times+as+much+energy+as+natural+gas&source=bl&ots=iVsINEVzpj&sig=ACfU3U07KsJpL85MGf_qNKhY_b1ePA6i0g&hl=en&sa=X&ved=2ahUKEwjHv_bEpr3oAhXF0qQKHQyNC6UQ6AEwC3oECA4QAQ#v=onepage&q=pound%20for%20pound%2C%20hydrogen%20contains%20almost%20three%20times%20as%20much%20energy%20as%20natural%20gas&f=false ] | ||
Hydrogen energy needs a fuel cell in order to work. A fuel cell uses chemical energy of a fuel (often hydrogen) and an oxidizing agent to create energy. Installation will depend on the size available for the fuel cell. A fuel cell ignites the fuel with agent which creates a vapor of water and a lot of energy. | Hydrogen energy needs a fuel cell in order to work. A fuel cell uses chemical energy of a fuel (often hydrogen) and an oxidizing agent to create energy. Installation will depend on the size available for the fuel cell. A fuel cell ignites the fuel with agent which creates a vapor of water and a lot of energy. | ||
Figure of a fuel cell: [https://www.hydrogenics.com/technology-resources/hydrogen-technology/fuel-cells/] | Figure of a fuel cell: [https://www.hydrogenics.com/technology-resources/hydrogen-technology/fuel-cells/] | ||
[[File:FuelCell1.png]] | [[File:FuelCell1.png|Hydrogen fuel cell]] | ||
===Assumptions=== | ===Assumptions=== | ||
| Line 797: | Line 811: | ||
Electrolysis: | Electrolysis: | ||
* Pros: Only water and an electrolysis device is needed. | |||
* Cons: Needs to use energy from the colonies. | |||
High-Temperature Water Splitting: | High-Temperature Water Splitting: | ||
* Pros: Only solar concentrators and water is needed. | |||
* Cons: Nuclear reactor most likely not feasible. | |||
Photobiological Water Splitting: | Photobiological Water Splitting: | ||
* Pros: Only needs water, green algae, sunlight. | |||
* Cons: Needs green algae. | |||
Photoelectrochemical Water Splitting: | Photoelectrochemical Water Splitting: | ||
* Pros: Needs water and sunlight as resources | |||
* Cons: A special semiconductors is needed. | |||
Each of these are valid options for generating hydrogen on Mars. We think electrolysis is the best choice since the energy needed can be produced at the colony at easy using solar panels. | Each of these are valid options for generating hydrogen on Mars. We think electrolysis is the best choice since the energy needed can be produced at the colony at easy using solar panels. | ||
| Line 826: | Line 840: | ||
Figure of different fuel cell types: [https://www.californiahydrogen.org/wp-content/uploads/files/doe_fuelcell_factsheet.pdf] | Figure of different fuel cell types: [https://www.californiahydrogen.org/wp-content/uploads/files/doe_fuelcell_factsheet.pdf] | ||
[[File:ComparingFuelCells.png]] | [[File:ComparingFuelCells.png|700px|Different fuel cell types]] | ||
Since our robot most likely does not need more than 250 kW, the best choice for the electrolyte is PEM. Also because it has a lower operating temperature then the others, it is more likely to perform near its upper efficiency. PEM fuel cells have an output range from 50 to 250 kW. | Since our robot most likely does not need more than 250 kW, the best choice for the electrolyte is PEM. Also because it has a lower operating temperature then the others, it is more likely to perform near its upper efficiency. PEM fuel cells have an output range from 50 to 250 kW. | ||
| Line 833: | Line 847: | ||
The combustion in the fuel cell work [https://personal.utdallas.edu/~metin/Merit/MyNotes/energyScience2.pdf] | The combustion in the fuel cell work [https://personal.utdallas.edu/~metin/Merit/MyNotes/energyScience2.pdf] | ||
[[File:FuelCell2.png]] | [[File:FuelCell2.png|500px|Workings combustion in the fuel cell]] | ||
The formula for hydrogen reaction: [https://www.u-cursos.cl/usuario/c1f33623c53cd7f58fd77ef459693d6c/mi_blog/r/Fuel_Cell_Systems_Explained.pdf] | The formula for hydrogen reaction: [https://www.u-cursos.cl/usuario/c1f33623c53cd7f58fd77ef459693d6c/mi_blog/r/Fuel_Cell_Systems_Explained.pdf] | ||
[[File:HydrogenFormula.png]] | [[File:HydrogenFormula.png|200px|Chemical reaction combustion hydrogen]] | ||
In order to calculate what the total energy is that a fuel cell can produce depends on the available moles of hydrogen and oxygen. For both the hydrogen and oxygen the uncompressed forms take too much space. Therefore each compound must be compressed to a certain degree. We will assume the hydrogen is pressed at 700 bar at a temperature of -60 degrees and the oxygen is pressed at 200 bar at a temperature of -60 degrees. Taking all together the total kg of hydrogen is calculated as: | In order to calculate what the total energy is that a fuel cell can produce depends on the available moles of hydrogen and oxygen. For both the hydrogen and oxygen the uncompressed forms take too much space. Therefore each compound must be compressed to a certain degree. We will assume the hydrogen is pressed at 700 bar at a temperature of -60 degrees and the oxygen is pressed at 200 bar at a temperature of -60 degrees. Taking all together the total kg of hydrogen is calculated as: | ||
| Line 876: | Line 890: | ||
The simplest biofuel is ethanol. There has to be oxygen present to burn ethanol and as result of the reaction water and co2 will be made. | The simplest biofuel is ethanol. There has to be oxygen present to burn ethanol and as result of the reaction water and co2 will be made. | ||
[[File:ethanol.png]] | [[File:ethanol.png|Chemical reaction combustion ethanol]] | ||
The above chemical equation is the idealised relationship. This reaction can be executed in a generator. In space or a low atmospheric environment this brings some issues with it. The engine must be specially made to work with these circumstances. The assumption has been made such an engine can be produced in the future. | The above chemical equation is the idealised relationship. This reaction can be executed in a generator. In space or a low atmospheric environment this brings some issues with it. The engine must be specially made to work with these circumstances. The assumption has been made such an engine can be produced in the future. | ||
| Line 886: | Line 900: | ||
===Calculations to determine use=== | ===Calculations to determine use=== | ||
Let’s assume to have 1L ethanol as fuel. The density of ethanol is around 850 kg/m3 in Mars temperatures | Let’s assume to have 1L ethanol as fuel. The density of ethanol is around 850 kg/m3 in Mars temperatures. | ||
We can do calculations to see the volume ratios between oxygen and ethanol required. | We can do calculations to see the volume ratios between oxygen and ethanol required. | ||
1L ethanol equals 0.85kg ethanol. (850kg/m3 @-60C, 1bar) | 1L ethanol equals 0.85kg ethanol.[http://ddbonline.ddbst.de/DIPPR105DensityCalculation/DIPPR105CalculationCGI.exe] (850kg/m3 @-60C, 1bar) | ||
0.85kg ethanol equals 18.45 mole ethanol (46.07g/mole) | 0.85kg ethanol equals 18.45 mole ethanol (46.07g/mole) | ||
| Line 901: | Line 912: | ||
55.35 mole oxygen equals 1.77kg oxygen (32g/mole) | 55.35 mole oxygen equals 1.77kg oxygen (32g/mole) | ||
1.77kg oxygen equals 978.4L oxygen (1.803kg/m3 @-60C, 1bar) | 1.77kg oxygen equals 978.4L oxygen[https://www.engineeringtoolbox.com/oxygen-O2-density-specific-weight-temperature-pressure-d_2082.html] (1.803kg/m3 @-60C, 1bar) | ||
1.77kg oxygen equals 6.6L oxygen (267kg/m3 @20C, 200bar) | 1.77kg oxygen equals 6.6L oxygen[https://www.engineeringtoolbox.com/oxygen-O2-density-specific-weight-temperature-pressure-d_2082.html] (267kg/m3 @20C, 200bar) | ||
| Line 940: | Line 951: | ||
There are some requirements that the battery needs to meet in order to perform on Mars: | There are some requirements that the battery needs to meet in order to perform on Mars: | ||
* Able to operate at low temperatures (temperatures range from -140°C to 20°C with an average of -53°C during the day). [https://hypertextbook.com/facts/2001/AlbertEydelman.shtml] | |||
* Able to fit inside the device (dimensions: 6.62x2.5x3 m = 49.65 m3) | |||
* Able to store 1923 kWh of energy | |||
The latest mars rover ‘Mars 2020’ uses a ‘Multi-Mission Radioisotope Thermoelectric Generator’ or MMRTG to generate power (''Note: This method of generating electricity also gives the highest and most reliable power output in our calculations''). For the power storage, two lithium-ion batteries are used.[https://mars.nasa.gov/mars2020/spacecraft/rover/electrical-power/] This suggests that this method should be sufficient for Martian conditions, as NASA uses it. However, the capacity drops significantly with temperature. This factor will be accounted for later. | The latest mars rover ‘Mars 2020’ uses a ‘Multi-Mission Radioisotope Thermoelectric Generator’ or MMRTG to generate power (''Note: This method of generating electricity also gives the highest and most reliable power output in our calculations''). For the power storage, two lithium-ion batteries are used.[https://mars.nasa.gov/mars2020/spacecraft/rover/electrical-power/] This suggests that this method should be sufficient for Martian conditions, as NASA uses it. However, the capacity drops significantly with temperature. This factor will be accounted for later. | ||
| Line 955: | Line 966: | ||
When we take the highest energy density (670 Wh/L), the battery should be at least 2870 L of volume to store the required 1923 kWh. This is a volume of 2.87 m3. This is a small volume in comparison to the total volume of the device; it takes up about 5.8% of the total volume. | When we take the highest energy density (670 Wh/L), the battery should be at least 2870 L of volume to store the required 1923 kWh. This is a volume of 2.87 m3. This is a small volume in comparison to the total volume of the device; it takes up about 5.8% of the total volume. | ||
However, if we look at the required weight of the battery, we encounter a problem. The minimum weight of such a battery, using a specific energy of '''265 Wh/kg''' would be an additional 7256 kg, which is 59% of the total weight of the truck without batteries. To transport this additional weight, more energy is needed, and therefore more batteries, which increases the weight again. | However, if we look at the required weight of the battery, we encounter a problem. The minimum weight of such a battery, using a specific energy of '''265 Wh/kg''' would be an additional 7256 kg, which is 59% of the total weight of the truck without batteries. To transport this additional weight, more energy is needed, and therefore more batteries, which increases the weight again. | ||
====Battery mass==== | ====Battery mass==== | ||
For this constraint, a balance in power need and weight must be found. Assuming that the generator generates the same power output of 474 kWh, the following energy balance can be used to calculate the ideal mass: | For this constraint, a balance in power need and weight must be found. Assuming that the generator generates the same power output of 474 kWh, the following energy balance can be used to calculate the ideal mass: | ||
[[File:E_vergelijking.png]] | [[File:E_vergelijking.png|900px|Energy balance]] | ||
In which mt is the mass of the truck, mb is the mass of the battery and e is the specific energy for a lithium ion battery. The rest of the constants are given in the table in the scenario section. | In which mt is the mass of the truck, mb is the mass of the battery and e is the specific energy for a lithium ion battery. The rest of the constants are given in the table in the scenario section. | ||
| Line 966: | Line 977: | ||
For a speed of 10 km/h or 2.778 m/s, the energy balance gives a mass of 26837 kg for the battery. This is way too much and needs to be reduced in some way. There are three parameters that we can change in order to achieve this: | For a speed of 10 km/h or 2.778 m/s, the energy balance gives a mass of 26837 kg for the battery. This is way too much and needs to be reduced in some way. There are three parameters that we can change in order to achieve this: | ||
* The velocity v (assumed to have a value of 10 km/h) | |||
* The distance from colony to colony d (2500 km) | |||
* The energy produced by the generator Egen (1.706 GJ) | |||
To determine the influence of these parameters on the equilibrium battery mass, a Matlab script was made to create the following plots: | To determine the influence of these parameters on the equilibrium battery mass, a Matlab script was made to create the following plots: | ||
[[File:velocity.png]] | [[File:velocity.png|500px|Battery mass required as a function of velocity]] | ||
[[File:distance.png]] | [[File:distance.png|500px|Battery mass required as a function of travel distance]] | ||
[[File:Egen.png]] | [[File:Egen.png|500px|Battery mass required as a funtion of the poer generated during the trip]] | ||
As shown in the plots above, the velocity has almost no influence on the battery mass, because it only shows small deviations from the calculated 26387 kg. However, the distance has a very big influence on the battery mass. For example if we reduce the assumed distance from 2500 to 1500 km, we only need a battery that is 7000 kg instead of 26000 kg. Furthermore, also the energy generated on board has a big influence on the battery weight. The best way to save battery weight will therefore be a combination of ''reducing distance'' and ''increasing the generated energy''. However, reducing the distance would require a change in assumptions, which is not realistic. That means that we will have to do further research into energy generation methods. | As shown in the plots above, the velocity has almost no influence on the battery mass, because it only shows small deviations from the calculated 26387 kg. However, the distance has a very big influence on the battery mass. For example if we reduce the assumed distance from 2500 to 1500 km, we only need a battery that is 7000 kg instead of 26000 kg. Furthermore, also the energy generated on board has a big influence on the battery weight. The best way to save battery weight will therefore be a combination of ''reducing distance'' and ''increasing the generated energy''. However, reducing the distance would require a change in assumptions, which is not realistic. That means that we will have to do further research into energy generation methods. | ||
| Line 986: | Line 997: | ||
The average temperature on Mars is -53 °C and the minimum and maximum temperatures are -140 °C and 20 °C. [https://hypertextbook.com/facts/2001/AlbertEydelman.shtml] Any form of energy storage for the water transport robot would have to be capable of charging and recharging energy with this vast range of external temperatures, specifically the lower end of the range could cause problems for energy storage. | The average temperature on Mars is -53 °C and the minimum and maximum temperatures are -140 °C and 20 °C. [https://hypertextbook.com/facts/2001/AlbertEydelman.shtml] Any form of energy storage for the water transport robot would have to be capable of charging and recharging energy with this vast range of external temperatures, specifically the lower end of the range could cause problems for energy storage. | ||
Currently the battery with the lowest operational temperature only functions well for temperatures as low as -70 °C. | Currently the battery with the lowest operational temperature only functions well for temperatures as low as -70 °C. [https://www.sciencedaily.com/releases/2018/02/180228131132.htm] This battery was developed by researchers in China in 2018 and utilises electrodes based on two organic compounds. Unlike the electrodes in used lithium-ion batteries, these organic compounds don’t rely on intercalation, which is the reversible inclusion or insertion of ions into their molecular structure. | ||
Typical lithium ion batteries can store and release energy in cold temperatures. However, their capacity will be significantly reduced. For example, a normal lithium ion battery, that has 100% capacity at room temperature, will typically have 50% of that capacity at -20°C. If we follow this trend for -70°C we find a capacity of about 20% of its original capacity. This means that the specific energy for this battery type will go from 265 Wh/kg to '''53 Wh/kg'''. This is a factor that should be taken into account when determining the maximum battery capacity. | Typical lithium ion batteries can store and release energy in cold temperatures. However, their capacity will be significantly reduced. For example, a normal lithium ion battery, that has 100% capacity at room temperature, will typically have 50% of that capacity at -20°C. If we follow this trend for -70°C we find a capacity of about 20% of its original capacity. This means that the specific energy for this battery type will go from 265 Wh/kg to '''53 Wh/kg'''. This is a factor that should be taken into account when determining the maximum battery capacity. | ||
| Line 993: | Line 1,004: | ||
In order to determine the amount of storage capacity that the battery can provide, a few assumptions have to be made: | In order to determine the amount of storage capacity that the battery can provide, a few assumptions have to be made: | ||
* The on-board power supplies (whether it is solar panels, radioisotope or any other source) provide the rest of the energy needed to run the robot at some constant velocity from colony to colony. Therefore, the battery is fully emptied, when travelling from colony to colony. | |||
* The battery should only weigh a maximum of 20% of the mass of the truck when fully loaded. This results in a maximum mass of 2480 kg. This should be enough to provide the truck with extra energy. | |||
* The capacity drops to 20% of the capacity at room temperature, which results in a capacity of 134 Wh/L or 53 Wh/kg. | |||
Using these assumptions, we determine the maximum storage using the following formula: | Using these assumptions, we determine the maximum storage using the following formula: | ||
[[File:Emaxbattery.png]] | [[File:Emaxbattery.png|Maximum storage of the battery]] | ||
In which E is the maximum stored energy in the battery, e is the capacity of the battery at -70°C and m is the maximum mass of the battery. | In which E is the maximum stored energy in the battery, e is the capacity of the battery at -70°C and m is the maximum mass of the battery. | ||
| Line 1,042: | Line 1,053: | ||
| Performance ratio || % || 0 - 100 || Solar Energy | | Performance ratio || % || 0 - 100 || Solar Energy | ||
|-style="text-align: center" | |-style="text-align: center" | ||
| | | Conductor material || / || / || Solar Energy | ||
|-style="text-align: center" | |-style="text-align: center" | ||
| Generator size || Kilogram || 0 - infinite || Radioisotope Energy | | Generator size || Kilogram || 0 - infinite || Radioisotope Energy | ||
| Line 1,061: | Line 1,072: | ||
The goal of the model is to calculate the maximum velocity the transport robot can move with the design choices given by the user. In order to achieve this, when the user presses the calculate button, the algorithm will first calculate the total weight of the transport robot with the given variables for both a full water tank and an empty water tank. It will also calculate the battery storage capacity and total energy production per Martian day using the input variables. For further calculations, the algorithm constructs an array with velocity values from 0 to 100 meter per second in steps of 0.001 meter per second. This array will be used to calculate values for multiple velocities to compare them in order to see what the maximum possible velocity is for the situation. With this velocity, it will calculate the total energy that needs to be produced during a one way trip for both a full and an empty water tank for every velocity in the array. For this it will first calculate the total energy needed for such a trip and subtract the battery storage from this value. In order to calculate this needed energy it will use the formula established earlier, which is also presented again below. | The goal of the model is to calculate the maximum velocity the transport robot can move with the design choices given by the user. In order to achieve this, when the user presses the calculate button, the algorithm will first calculate the total weight of the transport robot with the given variables for both a full water tank and an empty water tank. It will also calculate the battery storage capacity and total energy production per Martian day using the input variables. For further calculations, the algorithm constructs an array with velocity values from 0 to 100 meter per second in steps of 0.001 meter per second. This array will be used to calculate values for multiple velocities to compare them in order to see what the maximum possible velocity is for the situation. With this velocity, it will calculate the total energy that needs to be produced during a one way trip for both a full and an empty water tank for every velocity in the array. For this it will first calculate the total energy needed for such a trip and subtract the battery storage from this value. In order to calculate this needed energy it will use the formula established earlier, which is also presented again below. | ||
[[File:EnergyEquation3.png]] | [[File:EnergyEquation3.png|Total energy prodcution needed]] | ||
As stated before, while in our situation we assumed the relative height difference between the two colonies to be zero, this is a factor that could be different for another situation. In order to implement this in the model, there should be a way to calculate the energy needed to overcome this height difference. For this, the formula stated below is used. | As stated before, while in our situation we assumed the relative height difference between the two colonies to be zero, this is a factor that could be different for another situation. In order to implement this in the model, there should be a way to calculate the energy needed to overcome this height difference. For this, the formula stated below is used. | ||
[[File:PotentialEnergy.gif]] | [[File:PotentialEnergy.gif|150px|Difference in potential energy]] | ||
With this formula, the potential energy due to gravity is calculated using the mass m, height h and gravitational acceleration g. If the end goal is higher than the start point, this acts as extra energy that needs to be produced. Furthermore, the algorithm will calculate the duration of a one-way trip for every velocity in the array. This will be used to calculate the total energy produced during a one-way trip for every velocity. Now both the total energy production and the energy production need for every velocity are known, the algorithm will compare these two using a for loop. Starting from the lowest velocity, it will check for every velocity if the total energy production is equal or greater than the energy needed. If so, it will store this velocity in a separate variable. This means that at the end of the for loop, this variable will contain the highest velocity for which the energy production is high enough to supply the robot. The algorithm will execute this for loop for both a full and an empty water tank. Now, it knowns the maximum velocity the robot can move with for both a full and an empty water tank. It will use this knowledge to calculate the minimal duration for the two-way trip, which is then used to calculate the amount of transport robots that are needed to supply the users in the colony. At the end, it will present its results in the GUI of the model. The full flow of the algorithm can be found in the flowchart below. | With this formula, the potential energy due to gravity is calculated using the mass m, height h and gravitational acceleration g. If the end goal is higher than the start point, this acts as extra energy that needs to be produced. Furthermore, the algorithm will calculate the duration of a one-way trip for every velocity in the array. This will be used to calculate the total energy produced during a one-way trip for every velocity. Now both the total energy production and the energy production need for every velocity are known, the algorithm will compare these two using a for loop. Starting from the lowest velocity, it will check for every velocity if the total energy production is equal or greater than the energy needed. If so, it will store this velocity in a separate variable. This means that at the end of the for loop, this variable will contain the highest velocity for which the energy production is high enough to supply the robot. The algorithm will execute this for loop for both a full and an empty water tank. Now, it knowns the maximum velocity the robot can move with for both a full and an empty water tank. It will use this knowledge to calculate the minimal duration for the two-way trip, which is then used to calculate the amount of transport robots that are needed to supply the users in the colony. At the end, it will present its results in the GUI of the model. The full flow of the algorithm can be found in the flowchart below. | ||
[[File:modelflowchart.png]] | [[File:modelflowchart.png|1000px|Flowchart of the model]] | ||
[[https://www.mediafire.com/file/o7v64ltu0d81ewc/USEMODELV3.rar/file|The model can be downloaded via this link]] | [[https://www.mediafire.com/file/o7v64ltu0d81ewc/USEMODELV3.rar/file|The model can be downloaded via this link]] | ||
= | =Our design= | ||
Since there is now enough information to see whether the robot can be supplied enough energy to drive from colony to colony it is time to look back at the RPC list established prior to the research. The robot has the requirement to drive 2500 kilometers from colony to colony, which it has to drive twice to deliver water once. The robot also needs to deliver 500 liter of water per day, using either a large enough tank or multiple robots. The robot should preferably drive 10 km/h, if this is possible, and there should not be too many robots needed for the colony, since this would skyrocket the cost of the total project. As a limit around 4 robots were chosen. One preference that has been added to this list when researching different power supply solutions is that it would be best to only used solar energy. To see if this is possible, the model can be used. As a first test, the values established during the research and assumptions will be used. These are the standard values configured when first opening the model, which are the values presented in the table below. | |||
== | {| border=1 style="border-collapse: collapse;" cellpadding = 4 | ||
|-style="text-align: center" | |||
| '''Distance between colonies''' || 2500 km | |||
|-style="text-align: center" | |||
| '''Amount of people''' || 50 | |||
|-style="text-align: center" | |||
| '''New water per person''' || 10 L | |||
|-style="text-align: center" | |||
| '''Robot tank capacity''' || 5000 L | |||
|-style="text-align: center" | |||
| '''Height difference''' || 0 m | |||
|-style="text-align: center" | |||
| '''Battery size''' || 2480 kg | |||
|-style="text-align: center" | |||
| '''Solar panel size''' || 10.4 m^2 | |||
|-style="text-align: center" | |||
= | | '''Solar panel performance ratio''' || 63.92 % | ||
|-style="text-align: center" | |||
| '''Conductor material''' || Multi-junction GalnP/GaAs/Ge | |||
|-style="text-align: center" | |||
| '''Radioisotope energy generator size''' || 0 kg | |||
|} | |||
When supplying these values to the model, it seems that it is possible to use the transport robot using this design. However, it would take a robot 635 Martian days to return with water, resulting in the need for 64 robots to supply enough water. The robot also won’t reach it’s preferable speed of 10 km/h, having a maximum speed of 0.378 km/h without a full water tank instead. One way to increase the performance of the robot would be to find a way to increase the solar panel size. The total area on top of the robot would be 16.55 m^2. If the top of the robot would be totally filled with solar panel, this would mean there would already be about a 50% increase in solar panel size. Placing a solar panel with a size of 6.7 by 3 meters on top of the robot, will result in just a little bit of solar panel hanging over the sides of the robot. 4 cm at the front and back and 25 cm at both sides. If this solar panel is attached on a rail with an extendable arm that can extend 3 meters, it would be able to rotate a full 90°, reaching a maximum extra height of about 3 meters. If this construction would be placed on a panel or frame that can rotate 360°, it would be able to point at any direction in order to get the most sunlight. This will mean however, that when the panel or frame is rotated it would be hanging 2.1 meters over the side of the robot on both sides. This will, using the values established in the solar panel section, equal to about 94.5 kg of solar panel on each side. Since this is not that much in comparison to the weight of the full robot and the weight is present on both sides, it will not be likely to cause the issue of tipping the robot over. When going up a steep hill or another difficult situation, it could always rotate the solar panel back. Another way to solve this problem is to extend the wheels more to the side, giving it more stability. If the wheels are placed 4.5 meters apart from each other, the solar panels will only extend a maximum of 1.1 meter over the side of the robot which equals 49.5 kilogram on both sides. The configuration that would be placed on top of the robot can be seen in the drawing below. This will already result in a larger solar panel area of 20.1 m^2. | |||
[[File:topofrobot.png|Solar panel on top of the transport robot]] | |||
Another way to improve the situation is to increase the tank capacity of the robot. The original tank capacity was based on the truck used for the dimensions, however, there will not be the need for a driving seat on this robot, increasing the space that could be used for water storage. Considering the dimensions of the robot, a water storage tank of 600x225x150 could be possible. This will result in a capacity of 20250 liters. Considering the fact that ice is larger than water, this will be able to contain 18630 or about 18500 liters of water. Using these new values for both solar panel size and tank capacity already gives way better results. The maximum speed with a full water tank is now about 0.31 km/h and without a full water tank about 0.73 km/h. In this way, there are 13 robots required to deliver enough water, which is a huge improvement over the 64 obtained before. To visualize the size of the different components, simple drawings of both the side and front view can be found below. On top is the solar panel and inside the water tank is visible. | |||
[[File:schuinview.png|300px|The transport robot]] | |||
[[File:sideview.png|350px|Side view of the transport robot]] | |||
[[File:frontview2.png|350px|Front view of the transport robot]] | |||
One quite large component that also needs to be present is the battery, which has a volume of 6.27 m^3 in this situation. This still easily fits in the remaining space inside the robot. In worst case, the robot could be made a little bit bigger to the sides, since the wheels are extended anyway. While it is unknown how big other components like the motor will be exactly, there should be enough space for it. Assuming the robot will float 0.5 meter above the ground because of the wheels, there will be a total volume of 41.375 m^3 (662x250x250) available for components. Subtracting the volume of the water tank and battery results in a volume of 14.855 m^3 left for the motor and other components. Using this configuration, the solar panels will produce on average 8207.61W. This means, assuming it will use half of the energy during the day and half of the energy during night, it has to store 363679215.6 J of energy in its battery during the night. Since the battery of 2480 kilogram will be able to carry 131 kWh, which is equal to 471600000 J of energy, this will not cause a problem. | |||
=Conclusion= | |||
The colonization of Mars is still some time away and presents many new challenges in order to be successful. We have tried to create an accurate scenario of Mars when there are multiple small colonies, where not every colony has access to water. Since water is such a vital resource, we have created and modeled a robot that can solve this problem. Since the robot is an autonomous vehicle it requires the capability to provide enough power for itself. Therefore the goal of this research is to find out if it is doable to provide such a water transport robot on Mars with enough energy for long distances. This meant finding all possible methods and compare them. A huge challenge herein lies with the fact that Mars is still unknown terrain to some degree and assumption where needed for each method. This makes it difficult to determine the exact consequences for each decision and makes testing difficult. By using a model we have tried to bridge this gap and support our final choice of energy. Three important aspects that determine the total energy the robot needs travel between colonies are weight of the robot, distance between colonies and average speed of the robot. Using assumptions we can now now answer the research question: Is it doable to provide a water transport robot with enough energy? Yes, it is possible, but the robot can’t drive very fast. Using the design we currently consider, the duration of a two-way trip is 463.9 Martian days. With a capacity of 18500 liters of water, this results in the need of at least 13 robots. While this solves the requirements presented earlier, the preferences are not achievable using this design. The power supply used for this design are solar panels, since these are easy in use, requiring no fuel or extra supplies from Earth. They are also the safest option. | |||
=Discussion= | |||
Dust storms on Mars can last for a couple of weeks. Incase such a dust storm occurs we have already made the assumption that each colony has enough extra storage capacity for water reserves to last a couple of week, In our scenario this would be 15.210 L, based on a dust storm that would last a month. However, after a dust storm this extra reserve storage would need to be refilled, for this atleast one extra robot would be needed on top of the amount calculated using the model, in our scenario with our design this means we would need at least 14 transport robots instead of the previously mentioned 13. It would take this robot with a water capacity of 18500 liter one trip or 463.9 Martian days to fill this reserve back up. | |||
The velocity chosen as a preference was 10 km /h, however our design has according to the model a maximum speed with a full water tank of 0.31 km/h and without a full water tank a maximum speed of 0.73 km/h. This comes nowhere close to our preference velocity. To improve the maximum speed of our design more solar panels could be added for example on the sides of the robot, radioisotope generator could also be implemented into the design, however this would make it way more complicated since all the radioisotope fuel would have to be transported from Earth. We also had a preferences of a around 4 robots driving at onc. In the end it become a much larger number. To bring down the number of robots driving up and down, the speed for each robot has to be larger, or the amount of water per robot has to be larger. | |||
Several assumptions were made during our research. Each of these assumptions could be wrong or vary hugely. We will now discuss the impact of having incorrect assumptions: | |||
* In creating our scenario we made the a big assumption for the location of both colonies which determines the distance the robot would have to travel. This may be much smaller, since the disctance assumed was already huge. This might take the number of required robots down from 14 to 6-7. | |||
* We also made the assumption that a separate robot will bring food and / or no water is needed for food of the colony. Likewise, we assumed that no water is needed for industrial purposes in the colony. We also made some assumption on how much what people need per day, how much people life in the kolonies and how much water can be recycled. These can all be combined with misassuming how much water is needed per day. This will affect the number of robots that are needed which is already quite large. Needing an even bigger number of robots may make the robot other solutions to this problem much more attractive. | |||
* Assumption made for the variables in the energy cost formulas, the assumptions for the performance ratio of the solar panels and the assumptions for the battery will affect the energy consumption and total energy that the robot can use. If this drops a certain degree the robot will take much longer to travel or may be unable to travel at all. | |||
Latest revision as of 11:18, 7 April 2020
General information
Information about the groupmembers and the logbooks each week can be found here.
Problem statement
Setting
For years now, new initiatives to colonize Mars kept popping up all over the world. Examples include Mars One [1] and SpaceX [2]. It still seems far away, but when these plans eventually become reality, Mars will likely be covered with multiple colonies within the near future. While some companies and/or countries might try to work together to build one colony, others might end up establishing their own. This behaviour can also be seen in the construction of space stations right now. While the ISS is a collaboration between multiple space agencies, China is building their own space station in the form of the Tiangong program [3]. Because of political distrust, China is not allowed to collaborate on the ISS [4]. This distrust will probably continue when the time of Mars colonies is here. Some companies also might choose to build their own colony, like Bigelow Aerospace is doing with the Genesis program [5] when looking at space stations.
When these colonies are established, they will need resources to continue and expand. Delivering these resources from earth through rockets is time consuming and very expensive, so gathering as much of these materials as possible on Mars would be a better option. Ideally, these colonies would be build on locations that offer one or more of these resources, like water, building materials or minerals like copper and iron, at their site. However, these resources will eventually run out at the colony site and there is a possibility that not every resource is available at one location. This also could be a reason for having multiple colonies or a separate mining site. In this situation, trading or transporting resources between other colonies or mining sites becomes a solution. Just like countries here on earth trade with other countries to get their hands on things they can’t get in their own country, like for example oil, colonies on Mars could trade with each other to get easy access to the resources they need.
In order to build a colony, different factors to choose a certain spot for a colony have to be examined. To look at the different factors that determine what a good place to build a colony is, two different situations will be looked at. Firstly, there should be a good landing spot for the crew to arrive on Mars. Secondly, there should be a good location to actually start the colony. Ideally, these two locations should be on the same sport or really close to each other. For now, let’s assume the colony will be build on or around the landing spot, since too great a distance between them will create problems for travel. For a good landing spot, the landing area should be as flat as possible. According to [6] It also needs to be clear of rocks and boulders, since this would make landing dangerous and the landing area should not be too soft. It states that Mars has areas where the dust is several meters high, which is unfitted for landing. For building a colony, this also seems important. Building will be hard on areas that are too soft, since this would require better foundations. Non-flat and rocky areas can be not ideal for building, but can be worked around. [7] States that a good landing spot should be as close as possible to the equator, because this ensures that the solar arrays of the lander can deliver enough power at all times of the year and the temperature is high enough for the lander to stay warm. This factor is situational but can be really helpful when the colony will rely on solar power for generating energy. This will also decrease the power needs for warming the colony. Both previously mentioned articles say that the altitude of the area is also an important aspect. According to these articles, a lower altitude is better for landing. This means that there is more atmosphere above the land to slow down and steer for a good landing. [8] talks about food production which is another important aspect. At first the colonizers can live from provisions sent with them, but in order for them to live on mars indefinitely they have to grow crops. In order to grow crops there needs to be usable soil at the landing site and there needs to be enough water. Water is not only important for food production, but also for drinking or even as a fuel by turning it into hydrogen. Currently, the best way to get water on Mars is by gathering ice that is located underneath the surface on Mars. Ideally, this ice will be located as close to the surface as possible, since this makes it as easy as possible to mine. The image [9] below shows the depth of the ice on the surface of Mars.
As shown on the map, the ideal location for digging up ice according to NASA is noted with the white box. This is fairly close to the north pole however, which contradicts with the earlier mentioned preference of building the colony as close as possible to the equator. This already shows that there is not one ideal location to build a colony. Different countries/companies might choose a different location for their colony. Now, let’s assume some choose to build their colony close to the north pole, in the white boxed area, because they think water is more important than other factors. Now, other countries or companies choose to build their colony close to the equator, because they know other colonies can already easily mine water. They now value the better temperatures and sunlight more because they know they can buy and/or trade with the other colonies for water. This means that the citizens of the colony need a way of transporting water from colony to colony. Another possible option could be that a company chooses to build a colony close to the equator and a separate mining site for water. This way, they have the better temperatures and sunlight for solar power at their living area, the colony, and have a way to gather water on Mars. However, this again, brings the need for a transportation system between the colony and the mining site.
Problem
In order to trade or transport water from colony to and from another colony/mining site a way of transportation between the colonies is needed. Going out themselves is dangerous for the colony citizens. Radiation, low temperatures, dust storms and a toxic atmosphere [10] [11] [12] are all reasons to search for another solution than letting humans drive from colony to colony in person. Because of this, the colonies are in need of a transport system that does not require the citizens to go out themselves.
Solutions
There are several possible solutions for this:
- Option 1: Building a transportation conveyor tube.
- Option 2: Building a protected manned transportation vehicle. This vehicle must be protecting the people inside from radiation and temperatures.
- Option 3: Building a remote-controlled unmanned transport vehicle with cameras attached which will be controlled by someone in the colony. There must be someone controlling the vehicle.
- Option 4: Building a transport robot that would be able to autonomously deliver water from the one colony to the other.
Comparing solutions
We are going to dismiss options by comparing the most important properties needed to solve the problem:
Option 1 can only transport from two static locations, while option 2, 3 & 4 are more dynamic in this aspect. Because of uncertainty of the location of the colonies in the current development it might be best to leave this one out. Also, with the big distance between colonies this could be an extremely big project that is way too expensive and would still need human help in the dangerous environment to build.
The difference between option 2 versus 3 & 4 is that if we are sending a human on the transportation vehicle or not. As stated before sending a human on the vehicle would be dangerous and would require the vehicle to be of much higher quality to ensure safety of the human inside, which is most likely much more expensive solution than option 3 & 4. Also the added weight of the drivers and extra materials in order to protect the drivers will increase energy consumption of the vehicle.
Now we are left with a remote-controlled transportation vehicle versus an autonomous transportation vehicle. The remote-controlled vehicle will be controlled by a human. This means that the human is always aware of its position and situation allowing to help with overcoming obstacles. This means that decision making will be in human hands which the users might prefer over handing the driving over to an AI. However, the remote-controlled vehicle requires a driver. Since distances could be pretty far in between the colonies/mining sites it would be a better option for the users since they don’t have to spend that much time driving and/or routing.
Because the user will most likely prefer a transportation system that does not require a driver, we have decided to go for solution option 4: Building a transport robot that would be able to autonomously deliver water from the one colony to the other. This robot will autonomously drive to a colony or mining site and will bring back water for the colony.
Alternative
There is one simple alternative namely, using no transport at all. This is the case if every colony can obtain enough water, such that no transport is needed. The 2 most likely ways any colonies will have enough water will be whether it is near a water source or not. There are 2 methods that do not rely on location based water obtaining techniques namely recycling and obtaining water from the air.
Water can almost perfectly be recycled. However, this is only possible when recycling human waste water, like urine and washing water, not when the water is used for growing crops or industrial usage.[13]
Water can also be obtained from the air using humidifiers. One example is the Water Vapor Adsorption Reactor(WAVAR), an industrial-level dehumidifier, that could extract water from the atmosphere. This should be able to obtain some amount of water a day but this would not be enough when also water is needed for crops and such. This is also the reason it is not the first choice between getting water from the glaciers or soil. However, the WAVAR is a very energy efficient method, so it might still be useful under certain conditions.[14]
Using both techniques a colony would be able to sustain humans, but would not have enough water to also sustain water for growing crops and industrial use. Industrial use includes creating rocket fuel and usage for fabricating, processing, washing, diluting, cooling, or transporting a product. Large amounts of water are used mostly to produce food, paper, and chemicals.[15]
Users
Technological Difficulties
Aside from the financial aspect, there are some other difficulties in conducting a journey to Mars. The most prominent ones will be elaborated here.
Distance
Mars is the planet that is closest to earth in our solar system. However, the distance that would have to be covered if we launch a manned vessel to Mars is still significantly large. On average Mars is around 225 million km from earth, with 55 million km at its closest, occurring every 26 months. This journey would take around 150-300 days, according to [16]. This is a reasonable amount of time, but the trouble lies in fuel consumption, as a manned vessel would be larger than a unmanned vessel, due to supplies that a manned mission needs. This would lead to a large fuel consumption. However, technologies are present to cover this distance in space with a manned vessel [17].
Housing
Three other factors to take in consideration are the atmosphere, the temperatures and the storms on Mars. As for the atmosphere, oxygen could be produced using the carbon-dioxide that is present in the Martian atmosphere [18]. For example, greenhouses could be built with plants that convert CO2 into O2 or a device for converting carbon-dioxide into oxygen could be developed. The temperatures range anywhere from -125°C to +20°C [19]. These kinds of temperatures are acceptable in the building of a space colony, with good isolation and air-conditioning systems. There are also severe dust storms on Mars from time to time. This means that a rigid structure needs to be built to withstand such storms, building underground or in caves.
Supplies
Once a group of people is settled on Mars, a huge challenge will be to supply them in their needs. First of all, food is needed to keep the population alive. This could be realized by both transportation of food from earth and, ultimately, growing food on Mars. Also building materials must be transported through space. This requires new rockets that can carry heavy loads. NASA is developing these spacecrafts [20]. This means that this issue, although very cost-intensive, can be technologically overcome.
In conclusion, we can say that a colony on Mars is possible in the future, because all the technologies to realize it is there. It is only a matter of further development and major investments to make this happen. This means that there will be a need for Mars-exploring robot technologies in the future.
The main users of the robots will be a Martian space colony. This colony is non-existent today. However, the idea of a Mars-colony is widely researched right now. NASA, for example, has launched several Mars-exploration-robots in the past [21] and still does extensive research on the planet today. There is also an organization that focuses solely on the development of a human colony on Mars. This organization is called Mars One and it focuses on the selection of astronauts and the raise of funding [22]. Mars One claims that all technologies to get to Mars and to begin a colony there, are already present. Only a return mission is impossible right now, but that will not be needed if the crew of the mission will settle on Mars. This means that, in theory, a Mars colony is feasible within the coming 50 years [23]. This means that the navigation technology, that we will design, is certainly of use for this yet to be founded colony.
Other parties of interest for this technology would be organizations like NASA, ESA, Space-X, Mars One, and other space-oriented companies, as they will be the organizations that will put people on Mars.
Stakeholders
The users of a device that can navigate itself across a planet, in this case Mars, are the people that live on Mars. At the moment, there are no people living on Mars yet. This means we should look at the probability for a Mars-colony to be formed in the near future.
People on Mars
The people that live on Mars are certainly the most obvious users of a transportation robot that transports water on Mars. If Martian colonies are realized, the people that live on Mars will have to get enough water to survive. When this colony is not built on a water source, there will be a need for a robot that transports the water from mining site to the colony that needs the water.
The requirements that these people will have for a water transporting technology are listed below.
- Transport as much water as possible in one journey
- Travel as fast as possible
- Easy to empty the tank
- Fast charging of the battery
- Device should have a lifespan of at least a few years
Besides the people that live on Mars, there are other stakeholders that play a part in the implementation of a transport robot, for example the companies that put the people on Mars.
Organizations
There are several organizations that have plans to establish colonies on Mars. The most prominent ones are elaborated below.
Mars One
People have always dreamed about relocating the human race to another planet, in case something would happen to planet earth. This idea generates even more interest nowadays, than it did, say, 50 years ago, with the current problem of climate change affecting the earth. Now, more than ever, people are looking for another place to live in the galaxy. One of the most prominent candidates for this migration would be Mars, because it is ‘close’ to earth in comparison to other planets. Furthermore, it is believed to have water, which is a major life source, in its soil. But are we ready to move there in the near future?
Mars One is an organization, that certainly believes that a Mars colony is possible. Mars One handles the selection procedure for astronauts that want to settle on Mars in the yet to be formed space colony. It is also responsible for raising funds in order to make the mission happen. In [24] they state that the formation of a space colony, instead of a visiting mission that has to return to earth, excludes most technological and cost-intensive problems. Namely, if people want to settle on mars, no return vehicle, return propellant or the systems to produce the propellant locally are required. This decreases technological challenges and reduces costs dramatically. Furthermore, they mention that all the technologies to send people to Mars and make them survive there are already present. This means that a Mars colony is certainly feasible within the next 50 years.
However, in [25] they mention that the funds to actually develop a Mars settlement mission are not present right now (1 million USD of the 1 billion USD required). On the other hand, donations and investments might rapidly increase when more research is conducted in this field, and people would get convinced that a Mars colony is feasible. Also, if the situation on earth gets worse, people might have no choice but to invest in these kinds of missions. This means that, if Mars One succeeds in its’ mission, they will have an interest in a transporting technology on Mars.
Space-X
Space-X is another (privately owned) organization that has made concrete plans for a Mars mission and a Mars settlement [26]. Their goal is to send a cargo flight to Mars as early as 2022 and they have set the target for a manned vessel in the year 2024. Although optimistic, these plans are very concrete and ambitious. This means that Space-X is an organization that could certainly have an interest in the technology that we are researching for our project.
NASA
NASA is a governmental organization that also has the ambition to put humans on Mars [27]. Their goal is to put humans on Mars within the next decade. NASA is the organization that is most likely to succeed in completing this mission, because they have put men on the moon before, so they have the technologies in store to conduct such a mission. Furthermore, this is the organization that has gathered most of the data of Mars that is present today, as they have sent multiple satellites and exploration vessels to the planet [28]. Therefore, NASA is a major player that could have an interest in the technology we are investigating.
Other organizations
There are other privately-owned companies that have also conducted research in the field of establishing a Mars colony, like Lockheed Martin and Boeing [29]. Furthermore, there are other governmental organizations, like ESA, Roscosmos, ISRO and the CNSA [30], that could also have an interest in the technology. However, the plans of these organizations are not as advanced as the plans of the organizations mentioned before. Therefore, they are less likely to have an interest in a transport technology in the near future.
The requirements that these organizations will have for a water transporting technology are largely the same as the requirements that the people on Mars have. However, there are some additional requirements that the organizations may have:
- Production process should be as cheap as possible
- The usage of the device should be energy efficient, and therefore cost efficient
- The device should be easy to transport from earth to Mars, as it will most likely be produced on earth.
However these needs are considered to be subordinate to the people’s need in this project, so they will be added as preferences.
Governments
Other major players in the Mars colonization field, are the governments of the different countries involved in the previously mentioned governmental organizations. In the case of NASA this will be the American governments, in the case of ESA the European union, and so on. These governments sometimes have different needs and interests than the organizations which they govern. For example, NASA cares greatly for the scientific knowledge that is gained through new space missions, while the government might care more if they are world leader in the field of space engineering. This sometimes leads to conflicting interests.
Moreover, a competition between countries can occur in the building of the first Mars colony. In the past, for example, we have seen a so-called ‘space race’ between the Russians and the Americans [31]. It could be that the colonization of Mars will follow a similar scenario. However, it could also be the case that governments will establish multinational Mars colonies, as they did in the past with the ISS (International Space Station [32]).
Some additional requirements, besides the requirements of the people and the organizations, that governments will have for a water transportation device are:
- Easy to reproduce the manufacturing techniques (cooperation)
- Difficult to copy technology (competition)
The requirements for cooperation are implemented, as this is the most likely scenario. This requirement is also treated as a preference.
Other stakeholders
There are some other stakeholders that would have an interest in the technology. One could, for example, think of mechanics that have to work on the device, possible organizations that are formed on Mars among the colonists, environmental organizations, manufacturers (although the manufactures probably have to answer to the organizations), suppliers of manufacturers and so on. The interests of these groups are largely in line with the interests that are previously mentioned. Moreover, the interests of these groups are much smaller than the groups that are mentioned before. Therefore, the interests of these groups are not accounted for in this project.
User requirements
A full list of user requirements is given below:
| User Group | Requirement |
|---|---|
| People in colony |
|
| Organizations |
|
| Governments |
|
Scenarios
Research question
This research will mostly focus on the energy system used in the water transport robot, this will include research on different energy sources which will be compared, power storage on Mars is also researched. The goal of this research is to find out if it is doable to provide such a water transport robot on Mars with enough energy for long distances. The main research question chosen is: Is it doable to provide a water transport robot with enough energy? To answer this question for the scenario described below a model is made.
Assumptions
To research different possibilities for power storage and power supply, it is first needed to know how much power the robot needs. For this a quantitative description of the situation is needed. Since this situation is still an idea and not the reality, this will consist mostly of assumptions. All the time related units will be based on the situation on Earth. In other words, one day means one day on Earth. Most of the assumptions are based on values experienced on Earth, so it makes sense to use this time scheme as well. Not that it matters that much, since a day on Mars is equivalent to 1.02749125 days on Earth [33], which is not that big of a difference. To start, it is assumed that there are 50 people living in the colony around the equator that needs water. When looking at the water map displayed in the setting section at the beginning of the wiki, it can be said the equator is about ⅛ of the Martian circumference away from the white boxed section which is about 2500 kilometers. So, the colonies are 2500 kilometers apart. The relative height difference between the two colonies is assumed to be 0. The goal is to let the robot drive at a speed of at least 10 kilometer per hour, which will result at a travel time of 500 hours or about 21 days to drive from colony to colony and back. We also assume the transport robot gets the maintenance and cleaning it should need, like for example cleaning the solar panels of dust, at each colony.
In order to know how much water the robot needs to transport, the water usage of the colony needs to be established. Every person in the colony will use about 50 liters of water per day [34] for drinking, washing etc. From these 50 liters, it is assumed that 80% can be recycled at the colony [35]. However, water is also needed for other things. If the colony is growing its own food, water is needed to grow crops. A human eats around 2.5 - 4.6 kilograms of food per day [36]. For simplicity, it assumed that humans eat 3.5 kilograms of food per day. The water cost for food production of different types of food can be found in the graph below [37]. Since it will be likely that in this stage of the colony no animals will be on Mars, it is assumed that the only food produced on Mars is in the form of growing crops. Because of this, the average amount of water needed for 1 kilogram of food is about 1675 liters which is obtained by taking the average of the production cost of apples, maize, barley, wheat, soyabeans and rice. Here on earth, a part of the water used for hydrating the crops disappears in the earth, but on Mars, a greenhouse could extract all extra water from the soil and reuse it. Also, a part of the water inside the crops that is consumed will be turned into urine which is recycled at the colony. While based on nothing, it is assumed that 30% of the water needed for growing crops can eventually be recycled. This brings the total water cost to 1182.5 liters per day per person, which is 59125 liters for the whole colony per day. This is a lot, but it is just an assumption. It could be that a lot more of the water needed for crops could be recycled, which will bring the number down by a lot. But for now, this number is what will be worked with. Another option is that all the food is produced at the colony where the water is coming from, which will result in the need for another transport infrastructure for the food, or could be combined with the water transport. This will bring the water consumption down to 500 liters per day for the colony at the equator. This seems like a way better option, so it is assumed that food is supplied by another transport robot. This means the total amount of water that the water transport robot needs to supply is 500 liters per day.
Since 1 transport robot can be back at the colony every 21 days, and the colony needs 500 liters of water per day, it can be concluded that 1 transport robot should be able to carry at least 10.500 liters of water. While, for this project, it is assumed that this transport robot will always reach its destination, in reality, it could always go wrong. The transport robot could get stuck, lost in a dust storm or just get a malfunction. For this reason, it is assumed that 4 of these robots will drive from and to the colony. 1 Robot will dispatch every 5¼ day and is assumed to have a capacity of 5000 liters. This means that, assuming the colony itself has storage capacity enough for more water than consumed, even if 1 robot will fail to come back, the colony always has water enough to survive. For comparison, the Mercedes Atego 1317-A 4x4 Lindner-Fischer 2017, which can be seen in the picture below [38], has a capacity of 6000 liters. This means that the transport robot needs to be around this size. This model weights about 11900 kilograms. With a full tank of water, this means it will weight about 12400 kilograms. This means that it can be assumed that the transport robot will weigh approximately the same on earth. Since the gravity on Mars is about 38% of the gravity on Earth [39] this will result in a weight of about 4712 kilograms on Mars. For calculations however, mass is used, which will not change with gravity so it still has a mass of 12400 kilograms on Mars.
Another important aspect to consider is that Mars has the occasion dust storm. During these storms the robot will not be able to function correctly, having almost no sunlight and the possibility of dust to damage the robot. It would therefore be best to not have the robots drive during such storms. Since the colonies won’t have a delivery of water, they need enough storage to last during such storms. If we assume that the colonies have such storage, the is also the need to refill those storages for the next dust storm. We assume that a dust storm last for about a month. [40] The size of such a storage will then need to be 500 * 30.42 = 15.210 L. The amount of days it will take to refill this storage will depend on the final design and will be further discussed in the discussion.
Now, the last thing to do is calculate how much energy the transport robot will approximately need. The energy needed to bring the transport robot from standing still to a certain speed can be calculated with the formula stated below.
In this formula, Ek represents the kinetic energy put into the robot when it reached this speed, m represents the mass and v represents the speed. As any car on Earth, the transport robot will experience friction while moving across the surface. This friction consists of the friction created by the ground on the wheels and the air friction. The friction created by the ground on the wheels can be calculated with the formula stated below.
In this formula, Ffr represents the friction force, m represents the mass, g represents the gravitational acceleration and c represents the rolling resistance coefficient. The friction caused by the air while moving can be calculated with the formula stated below.
In this formula, Ffr represents the friction force, C represents the drag coefficient, ρ represents the air density, A represents the cross-sectional area and v represents the speed of the transport robot. Both these friction forces will bring the transport robot to a stop when the engine of the robot stops putting kinetic energy in the robot. During the trip, these forces will put work on the robot which will require the engine to put new kinetic energy in the transport robot. This work is equal to the total friction force times the distance travelled. This means, that the total energy needed to move the transport robot from one colony to another at a certain speed can approximately be calculated with the formula below.
In this formula, E represents the total energy needed and d represents the distance. Some of these variables/coefficients are unknown, assumptions are made as presented in the table below.
| Variable/coefficient | Assumed value | Based on |
|---|---|---|
| C | 0.58 | Drag coefficient of a Jeep Wrangler TJ [41] |
| A | 7.5 m^2 | Dimensions of Mercedes truck |
| c | 0.06 | Value also assumed by NASA [42] |
| m | 12400 kg | Mercedes truck |
| d | 2500 km | Distance colony to colony |
| Variable/coefficient | Known value | Based on |
|---|---|---|
| ρ | 0.020 kg/m^3 | Air density on surface of Mars [43] |
| g | 3.711 m/s^2 | Gravitational acceleration on Mars |
Electric engines offer an efficiency of about 80% from grid to wheels [44], meaning that the energy that should be produced by the transport robot can be calculated with the formula stated below.
It is important to note that this formula does not account for everything and is just an approximation of the energy needed. A plot of the speed and the total energy needed can be found in the graph below. The noted point represents the wanted speed of 10 kilometers per hour, which is equal to 2.7778 meters per second. This speed results in a total needed energy of 8.63*10^9 Joule for driving.
Other energy needs could include keeping the water at a certain temperature. Temperatures on Mars range from -125 degrees Celsius on a cold winter day to 20 degrees Celsius on a summer day [45]. This means that for the most part, the temperature is under 0 degrees Celsius and the water will be ice. While energy could be used to keep the water under 0 always, it seems best to let the water alternate between these two states of matter, solid and liquid. If the tank is big enough to keep 5000 liters liquid water in ice state, it should not be a problem. This will cut the need to put energy in keeping the water in a certain state. Since the density of ice is 0.92 times the density of liquid water [46], the tank should be able to carry 5435 liters of ice. For simplicity, we assume the tank has to have a capacity of 5500 liters.
All in all, this means that if the transport robot moves with a speed of 10 kilometers per hour, it needs to be able to either storage at least 8.63 GJ of energy or needs to be able to, assuming it travels for 10.5 days one way, generate at least 9511.89 Joule of energy per second (9511.89 Watt). A combination of a power storage that is charged at the colony and a power supply during the trip could also be an option. The amount of battery capacity and the amount of energy production needed can be found plotted against each other in the graph below.
RPC list
| Requirements | Preferences | Constraints |
|---|---|---|
| Needs to travel 2500 Kilometers from colony to colony | There should not be the need for too many robots (around 4) | Dimensions of robot (662x250x300cm) |
| Needs to supply 500 Liters of water per day | The robot should have a speed of 10 km/h |
What does the robot already know?
The robot already knows the location of the colonies and already knows the terrain of Mars in between. Unexpected obstacles such as boulders, duststorms or cave-ins are not known however.
Plan
Research question
Main question
Is it doable to provide a water transport robot with enough energy?
The goal of our project is to research different possibilities for producing energy to see if it is doable to store/produce enough energy on the robot in order to be able to drive such long distances on it's own. In order to be able to answer this question, different sub-questions need to be answered. Also a model is created to calculate the maximum velocity the robot can drive given a certain design. This can be used to see what kind of design would work the best and could also be used by the manufacturers during the design process to see if certain designs would work at all nor not.
Sub-questions
Which possibilities are available to generate power on Mars?
First, the possibilities of different kinds of energy production methods are looked into; in our situation to see how much energy can be produced by each of them and to see if they are applicable to our robot.
- Solar Energy
- Radioisotope Energy
- Hydrogen Energy
- Biomass Energy
- Fossil Fuels
How much power can the transport robot store?
Then, research will be done on the amount of power that the robot can store. This will be done to reduce the amount of energy that has to be generated on board.
- Needed battery capacity
- Maximum battery capacity that is possible
Given the generated and stored energy, is there an optimal velocity at which the robot can travel?
A model will be created in order to find the velocity at which the robot will travel. Furthermore, the ideal methods of power generation and power storage can be extracted from this model.
- Inputs
- Calculations
Which options are the best for our scenario?
Lastly, the optimal combination of power generation and power storage will be found.
- Which power generation design could be used best?
- Are we dependent on energy storage?
Milestones
Research on power storage
- How much capacity does the battery need?
- How much capacity can the battery have?
- Can a battery be used at these temperatures?
Research different possibilities for power supply
Solar energy
- How does it work?
- What is the solar intensity on Mars?
- What is the best angle for the solar panels?
- How much solar panels can we put on the transport robot?
- How much energy can we produce using solar energy?
Radioisotope Thermoelectric
- How does it work?
- Is fuel for this obtainable on Mars?
- How safe is this?
- How much energy can we produce using Radioisotope Thermoelectric energy?
Alternative Fuels
- Are fossil fuels, biomass or hydrogen energy feasible options for power generation?
Comparing different energy supply methods
- Which produces the most energy?
- Which is the safest form of energy production?
- Which is the easiest to produce locally on Mars?
Think about final design
- Is only a battery enough? How much energy production is needed if we use the battery only as a buffer?
- Should we drive slower than 10 km / h
Making the presentation
Deliverables
- Research on users of the product
- Research on the state of the art in this field
- Making problem statement and scenario
- In-depth research of the power storage
- In-depth research of energy generation methods
- Proper plan for power supply of the transport robot
- Proper plan for power storage of the transport robot
- Model
- Conclusion
- Discussion
- Presentation
Task Division
| Task | People working on it |
|---|---|
| Research on users and state of the art | - Rik, Zeph, Nick (Week 3 & 4) |
| Writing problem statement and scenario | - Zeph, Finn, Nick (Week 3 & 4) |
| Research on power storage | - Thomas (Week 5)
- Rik (Week 5) |
| Research different possibilities for power supply (Solar Energy) | - Zeph (Week 5)
- Stefan (Week 5) |
| Research different possibilities for power supply (Radioisotope Thermoelectric) | - Nick (Week 5)
- Finn (Week 5) |
| Compare different power supply methods | - Zeph (Week 6)
- Stefan (Week 6) - Finn (Week 6) |
| Think about final design
(includes creating model and writing conclusion) |
- Nick (Week 6 & 7)
- Rik (Week 6) - Thomas (Week 6) - Zeph (Week 7) - Finn (Week 7) |
| Start on presentation | - Thomas (Week 7)
- Stefan (Week 7) - Rik (Week 7) |
| Finishing Presentation | - Everyone (Week 8) |
| Finishing Wiki | - Everyone (Week 8) |
Planning
| Week | Working on | Deliverable finished at end of week | Mainly responsible for finished deliverable |
|---|---|---|---|
| Week 3 & 4 | - Users and state of the art
- Problem statement and scenario |
- Research on users and state of the art (1)
- Writing problem statement and scenario (2) |
- (1) Rik, Zeph, Nick
- (2) Zeph, Finn, Nick |
| Week 5 | - Research on power storage
- Research different possibilities for power supply |
- In-depth research of both energy sources (1) Solar Energy (2) Radioisotope Thermoelectric
- In-depth research of the power storage (3) |
- (1) Zeph & Stefan
- (2) Finn & Nick - (3) Thomas & Rik |
| Week 6 | - Extra time for research on power supplies if needed
- Comparing different power supply methods - Starting on model |
\ | \ |
| Week 7 | - Creating model and draw conclusions from it
- Start on presentation |
- Proper plan for power supply of the transport robot (1)
- Proper plan for power storage of the transport robot (2) - Model (3) - Conclusion (4) |
- (1 & 2) Rik, Stefan
- (3 & 4) Zeph, Finn & Nick |
| Week 8 | - Finishing Wiki
- Finishing Presentation |
- Presentation (Before Thursday 02-04-2020)
- Wiki (Before Thursday 02-04-2020) |
Everyone |
State of the art
In the area of navigation on mars, there are several things that have already been tried. In order to understand what has already been done in the field of navigation on Mars, we need to have a look at the most recent, still working devices that have landed on Mars. In the past there have been a lot of rovers and other devices that have landed on Mars in order to explore the planet and its surface. However, the only two landers that are still active and in contact with earth are Insight (2018) and Curiosity (2012)[47]. All the other spacecrafts that have ever been on Mars are either broken, or have lost contact with earth in another way. There is also a future rover, scheduled to launch in 2020, which is called Mars 2020. Next, Insight, Curiosity and Mars 2020 will be elaborated.
Insight
The Insight Mars lander was launched in 2018 and landed successfully on Mars. Its primary goal is to investigate the ‘inside’ of the planet. More specifically its "pulse" (seismology), "temperature" (heat flow), and "reflexes" (precision tracking) [48]. It is a stationary device, as it does not navigate itself across the surface of the planet. Instead, it measures the key characteristics of Mars from one place on the surface, with the goal to determine how small, rocky planets in our solar system have been formed. Therefore, this mars lander does not contribute to the state of the art of our project, as we will focus on the energy generation of an autonomous vehicle on Mars. Insight is a stationary device and therefore not of much interest for the project.
Curiosity
The Curiosity Mars lander was launched in 2011 and reached Mars in 2012. It is a car-sized Mars rover that will explore the Gale crater on Mars. The rover navigates itself across the surface of Mars by itself, which makes it an interesting device to look at for our project. Furthermore, its primary goal is to investigate whether or not life was ever possible. This means that it also looks for essential life conditions like water, oxygen, sulfur, phosphor and other minerals [49]. It uses very sophisticated techniques in order to collect samples from the Mars surface and to analyze them. To navigate itself across the surface, Curiosity uses so called ‘Hazcams’ and ‘Navcams’. These are hazard avoidance cameras and navigation cameras. These will be further elaborated.
Hazcams
The four hazard avoidance cameras are located on the lower front and back of the vehicle. They operate in black and white, using visible light to create a 3D-image of its surrounding environment [50]. It also works in tandem with software that allows the rover make its own safety choices and to "think on its own", which makes it autonomous. The cameras each have a wide field of view of about 120 degrees. The rover uses pairs of Hazcam images to map out the shape of the terrain as far as 3 meters in front of it, in a "wedge" shape that is over 4 meters wide at the farthest distance. The cameras need to see far to either side because unlike human eyes, the Hazcam cameras cannot move independently; they are mounted directly to the rover body.
Navcams
Mounted on the mast (the rover "neck and head"), these black-and-white cameras use visible light to gather panoramic, three-dimensional imagery. The navigation camera unit is a stereo pair of cameras, each with a 45-degree field of view that supports ground navigation planning by scientists and engineers. They work in cooperation with the hazard avoidance cameras by providing a complementary view of the terrain. [51]
Mars 2020
The Mars 2020 rover is basically a more advanced version of the Curiosity rover. It has as a goal to not only investigate if life was ever possible on Mars, but also to look for signs of microbiological life in the past. It will collect promising rock samples and store them for future investigation with equipment that is too large to take to Mars. Furthermore it will also look for ways to produce oxygen from the Mars atmosphere and for ways to collect water from the Martian soil [52]. It will use the same navigation instruments as the Curiosity rover, only a bit more advanced.
Power
The Curiosity rover uses a Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) in order to generate energy. This is a device that relies on radioactive material to generate energy. It is a preferable energy source for Mars rovers, because the energy generation method does not require oxygen. Furthermore, Curiosity also has solar panels to generate energy. For the storage of this energy, two lithium ion batteries are present on board of the rover. These batteries have the highest known storage capacity, and are reliable in Martian conditions. For example, discharging is possible at the low temperatures that are present on Mars. These batteries are used for backup for the energy generators in times of peak demands. [53]
Literature
General
[54] NASA page including all kinds of information sources about space colonies.
[55] Space Settlements: A Design Study. Includes information about all aspects of a space settlement including resources needed to maintain and expand.
Mars Terrain
[56] This paper investigates the slope distribution in the northern hemisphere of Mars from topographic profiles collected by the Mars Orbiter Laser Altimeter.
[57] This paper describes the calculation of slopes and the characterization of surface roughness using profiles obtained by the Mars Orbiter Laser Altimete.
Transporting materials
[58] June 26, 1951 R. w. GAUSMANN APPARATUS FOR TRANSPORTING MATERIALS 5 Sheets-Sheet 1. Is about a technique for for transporting materials without changing the compounds temperature which may be necessary to prevent chemical changes in the material being transported, or to prevent it from solidifying within the car whereupon it would have to be heated to be removed therefrom.
[59] Extraterrestrial construction materials by M.Z.Naser. This review explores the suitability of construction materials derived from lunar and Martian regolith along with concrete derivatives, space-native metals and composites, as well as advanced and non-traditional materials for interplanetary construction.
[60] Space-native construction materials for earth-independent and sustainable infrastructure. This review covers feasibility of exploiting in-situ lunar and Martian resources as well as harvesting of elements and compounds, from near Earth objects (NEOs), to produce extraterrestrial materials suitable for construction of space-based infrastructure.
[61] Materials and design concepts for space-resilient structures. This paper presents a state-of-the-art literature review on recent developments of “space-native” construction materials, and highlights evolutionary design concepts for “space-resilient” structures.
Research
Solar energy
Solar panels or also called photovoltaic modules are a collection of photovoltaic cells. These cells use sunlight as source to generate electricity.[62]
Performance
The performance of a solar panel depends on many different aspects. The most important aspects are the sunlight that hits the surface of the solar panel, the efficiency of the conducting material in the cells of the solar panel and the size of the surface of the solar panel. There are also many other aspects that determine how many energy is created like whether there is something blocking the sunlight, like an object or dust particles, and the temperature of the photovoltaic cells. The global formula to estimate the energy generated by a photovoltaic system is stated as presented below [64] .
In this formula, the following variables are used;
- E = Energy (kWh)
- H = Average solar radiation on tilted panels (kWh/m^2)
- r = solar panel efficiency (%)
- A = Total solar panel Area (m^2)
- PR = Performance ratio, coefficient for losses (range between 0.5 and 0.9, default value = 0.75).
Average solar radiation on tilted panels (H)
To determine the average solar radiation on the panels, the sunlight intensity on mars can give a good estimate. Power received from the sun is often measured in solar irradiance, which is the power per unit area of electromagnetic radiation. To be precise, irradiance in general is defined as “the amount of light energy from one thing hitting a square meter of another each second” [65]. Solar irradiance is measured in watt per square meter (W/m^2). The solar irradiance on Mars can be calculated using the solar constant [66]. At a distance from the sun of 1 UA, which is approximately the distance between the Sun and Earth, the solar irradiance is equal to 1361 W/m^2. Since the average distance from the Sun to Mars is equal to 1.524 UA [67], the solar irradiance on Mars can be calculated as stated below.
To check this calculation, the average solar irradiance on Mars according to NASA is 586.2 W/m^2 [68]. Since one day on Mars takes 24.62 hours [69] it can be assumed that there will be approximately 12.31 hours of sun and 12.31 hours of darkness each day. Of course, the sunlight intensity will be at its peak at noon, which is when it will produce the 585.987W/m^2 calculated before. The sunlight irradiance during the rest of the day could be approximated using a parabola, which can be used to calculate the total energy production during one day [70]. This parabola will have its peak at 585.987 and will go through the x-axis at -22158 and at 22158, which is equal to the amount of seconds in 6.155 hours. This can be achieved with the equation stated below.
This parabola also has negative y-values, but these can be ignored. A plot of this equation can be found in the image below.
In order to calculate the total energy produced during one day, the area underneath the graph should be obtained. For this, the antiderivative of the function is needed, which can be found in the equation below.
Since the function is symmetrical, the total area under the graph can be calculated by taking the integral from x = 0 to x = 22158 twice, which results in 17312399.93 Joule per square meter per day. The robot is driving for 10.5 Earth days (252 hours), which is equal to approximately 10.219 days on Mars. Thus, there will be, approximately, 176915414.9 Joule of sunlight per square meter over the course of the 10.219 days on Mars.
To get the most out of this energy, the solar panels should be positioned correctly. The solar panels will generate the most amount of electricity when the sunlight is perpendicular to the surface of the solar panel [71]. This means that, ideally, the solar panel will always be directed directly towards the sun using a tilting mechanism. An example on earth where a system tilts the solar panels so that they always face the sun at a 90-degree angle is in a operation in Piteå [72]. The helianthus smart solar panel is a solar panel that is able to track the sun using a microcontroller based embedded system [73]. This will ensure that the angle of the sunlight hitting the solar panel is always 90 degrees. Some form of this mechanism should be implemented in the robot, should it use solar energy.
Efficiency (r)
The most important aspect that will determine the efficiency of the solar panels is the material that is used as the conductor. A better conductor will cause less loss of energy when converting sunlight to energy. The most common materials used in mass production at the moment are; Crystalline silicon (c-Si), amorphous silicon (a-Si), gallium arsenide (GaAs) and organometallics (soluble platinum). Each type of material has its own advantages and disadvantages, mostly being efficiency against the production cost.
- Crystalline silicon is most common at the moment for mass production. It has a conversion rate of about 20 - 25%. It is not the cheapest material but has a low enough cost to be considered the best material for solar panels in home installations.
- Gallium arsenide is a better conductor than silicone. However, it is very rare, expensive and manufacturing gallium arsenide is dangerous since arsenide is poisonous. This could be a reason maintenance is less ideal for the users on Mars that will be tasked with fixing the robot when needed.
- Organometallics (soluble platinum) is a metal conjugated polymer and an even better conductor than gallium arsenide. It is lightweight and relatively cheap to produce. [74]
- Multi-junction solar cell is GaInP/GaAs/Ge multijunction solar panels with a high efficiency of over 30%. However it is more complex and more expensive than any other. [75]
While having the most efficiency seems like the best idea, money is probably a big deal for certain users. Think about the companies manufacturing and funding these robots, like for example NASA. for now, calculations will be done using the material with the highest efficiency, but the manufacturer could decide to pick another conducting material.
Table containing efficienty of materials [76]
Total solar panel area (A)
To calculate how many solar panels can be put on the robot, an estimation is needed of how much space is needed for a solar panel with length L, width W and height H. Since every solar panel needs the ability to turn 360 degrees and tilt about 90 degrees, each solar panel will have surface of L * W m2 and should have a height such that H >= 0.5 * L AND H >= 0.5 * W. Now it is important to determine what the best setup is e.g. what is the optimal placement of the solar panels on the robot such that no solar panel will overlap and we have maximum utilized surface of solar panels:
- One large solar panel.
- Couple of mid range solar panels
- Many small solar panels.
The robot will have similair dimensions as the Mercedes Atego 1317-A 4x4 Lindner-Fischer. [77] with length: 6.62 m, width: 2.50 m and height: 3.00 m.
Having one large solar panel with a length and width of 6.50 m will give a huge surface of 42.25 m^2. However, it will most likely not be possible to have a height of 6.5 m and therefore not be able to tilt and turn fully. Also it is questionable whether the giant solar panel will be able to catch wind and make the robot tilt at high wind force. Moreover having a solar panel stick about 1,3 m of the front and back when they turn, since the diameter is around 9.2 m and 3,3 m of the sides which can be problamatic as well. Therfore this option will not be viable.
Having multiple solar panels with a lenght and width equal to the width of the robot (200 cm) we will be able to put 3 solar panels on the robot and have a total solar panel surface of 12 m^2. The height should be around 1 m in order for the solar panels to turn which is quite doable. However, the solar panel sticks 15 cm off the side when they turn, since the diameter of each solar panel is around 2.8 m and 1 m off the front and back. This could be problamatic as well when driving up or down a slope. However by sacficing some area and making the middle solar panel a bit higher, about 0,5 m and putting the first and last solar panel closer to the middle the solar panels will not stick too much over the front and back. This will however cost some effective area since the large solar panel will shade the 2 smaller ones. So if we lose 50 cm of the front and back, the the area will decrease by 0.5 m * 2 m * 2 solar panels * 0.8 (20% loss due to shade) = 1.6 m^2. So we will have a remaining solar panel area of 10.4 m^2.
Another solution for the solar panel width / length is to have many small solar panels with length and width 1 m. We can put them in pair on the robot, such that they only stick about 10 cm of the side, since it will have a diameter of 140 cm, and have height 0.5 m. This will enable us to put around 5 pair of solar panels and the robot, having the solar panels only stick 25 cm of the front and back. This gives us a total solar panel area of around 1 m2 area per panel * 2 solar panels per pair * 5 pairs = 10 m^2.
Therefore the best option is to use 3 middle size solar panels.
Performance ratio (PR)
The performance ratio is most difficult to determine and will require many assumptions. The losses for certain temperature, shade and dust can be determined with some precision, while others will depend on the implementation, wiring and manufacturing of the solar panels. Example of detailed losses that gives the PR value are: [78]
- Inverter losses
- Temperature losses
- DC cables losses
- AC cables losses
- Shadings
- Losses at weak radiation
- Losses due to dust, snow...
Temperature losses
A higher temperature reduces the efficiency of the solar panels. [79] In contrast a lower temperature will increase the efficiency of the solar panel. The formula for calculating the loss of temperature is:
TL = TC * (TT - MT) [80] with:
- TL = temperature losses
- TC = temperature coefficient
- TT = tested temperature
- MT = modular temperature
The temperature coefficient depends on the type of conductor that is used for the solar panel. The temperature coefficient of GaInP/GaAs/Ge multijunction is -0.09%.[81] The efficiency is tested at a standard of 25 °C, therefore the tested temperature is also 25 °C. The modular temperature is the temperature of the area where the solar panel is placed. For now, we wil use the average temperature on Mars of -63 °C .Therefore the total temperature loss (or gain in this case) = -0.09% (25 - (-63)) = -7.92%.
Do solar panels work at -70 degrees? [82]
Shadings
Most clouds on mars exist of ice water and clouds are also formed during dust storms. These clouds can decrease the brightness of the sun up to 40%. [83] As such we will assume the average of performance decrease to be around 20%.
Dust
Dust can be a large problem for the energy output of the solar panels. We can assume that at the start of every trip the solar panels are cleaned and the loss due to dust is 0%. However, since Mars has a lot of dust on its surface and can have a lot of dust in the air after dust storm/ dust devils it can stick to the surface of the solar panel and dramatically decrease the energy generator to 30%. [84]
To increase the performance of the solar panel during or after sandstorms, an Arduino Uno microcontroller can be used to track the power generation and cleans the photovoltaic surface when it drops to 50% from its rate value. It then uses a wiping tool to clean the surface of the solar panels. This method was proposed for solar panels in Iraq since dust storms are quite normal there. [85] For the water transport robot it could be wise to set the bound for cleaning the solar panel lower such that it cleans the panels at a lower drop. We will assume that it is possible to have the module clean the solar panels when its rate value drops to 15%. This would of course mean that more wiping fluid is needed.
Another method is to implement MPPT for each module individually which can measure performance and fault detection at module level. This ensures that if a part of the solar panel becomes shaded or too dusty, the power output doesn’t drop to zero. [86]
If both methods described above are implemented, dust will most likely not exceed a loss of 15% and have an average loss of about 8%.
Other losses
Since it is difficult to determine what the other losses will be we will assume the average for each of he remaining losses [87]:
- Inverter losses (7%),
- DC cables losses (2%),
- AC cables losses (2%)
- losses at weak radiation (5%)
These combined give a loss of 16%.
Total energy
H = 176915414.9 J/m^2
r = 32.00%
A = 10.40 m^2
PR = 100% - ((-7.92%) + 20% + 8% + 16%) = 63.92%
E = 176915414.9 J/m^2 * 0.3200 * 10.40 m^2 * 0.6392 = 376344660.9 J
Thus, the total energy produced by the solar panels is 376344660.9 J during the 10.5 Earth days, which equals, on average, an energy production of 414.8419984 W (414.84 W).
Other important aspect for solar panels
Maintenance
We will assume that at the start of each trip the robot will be fully functional. This includes the robot having no dust on the solar panels, which means that the occupants should wipe the solar panels each time a robot leaves for transport. Ofcourse regular maintance should be neccessary, but most solar panels have a life of 25 years [89]. Moreover, the solar panels when unrepairable can be recycled. Circa 95% of the a solar panel can be recycled, depending on the materials used to create them. [90] [91]
Weight
It is important for efficienty purposes to add the weight of the solar panel to the total weight of the robot and thus increase the total energy the robot needs. Since there will be 3 solar panels with length / width 2m and height of 1m.
We will assume that the solar panel will weight 15 kg per square meter. [92] This makes each solar panel weight around 80 kg and the total weight around 240 kg.
Since the solar panels need to turn, there is also the need of the pilar that of 1m that will lift the solar panels. This will most likely be a pole with the same material as the frame for solar panels being aluminum. [93] Aluminum is a “lightweight, non-ferrous metals with good corrosion resistance, ductility, and strength.” [94] The thickness of the round bar of aluminium will be around 10 cm. Therefore the total weight of all 3 pipes will be around 65-70 kg in total, depending on the type of aluminium used. [95]
Thus the total weight of all solar panels will be around 310 kg.
Degration
Slowly a solar panel will lose efficiency and produce less energy. After 25 solar panels can produce only up to 80% of their original efficiency. [96] We will assume that the solar panels will be replaced after 25 years.
Radioisotope Thermoelectric energy
Workings of a Radioisotope Thermoelectric generator
A typical design of a radioisotope thermoelectric generator (RTG) consists of 2 main ingredients: fuel that will decay radioactively and a large set of thermocouples to convert heat into electricity.[97] A thermocouple is a set of 2 wires made of 2 different metals that are placed in electric contact at each end.[98] When two metals are placed in electric contact, electrons flow out of the one in which the electrons have a higher Fermi level. The Fermi level of the metal represents the thermodynamic work required to add one electron to the metal. The energy of an electron in the metal at the Fermi level is −W relative to a free electron outside the metal. The flow of electrons between the two conductors in contact continues until the change in electric potential brings the Fermi levels of the two metals (W1 and W2) to the same value. This electric potential is called the contact potential ϕ12 and is given by eϕ12 = W1 − W2, where e is the electrical charge of one electron (1.6 × 10−19 coulomb.) [99] If a closed circuit is made of two different metals at the same temperature, there will be no net electromotive force in the circuit because the two contact potentials oppose each other and no current will flow, however if the temperature of one of the junctions is raised relatively to the other there will be a current. Since the Fermi levels of the two metals have a different temperature dependance there will be a net electromotive force generated in the circuit. To maintain the temperature difference, heat must enter the hot junction and leave the cold junction, in a RTG this heat is produced by the fuel that will decay radioactively. The generation of a thermal electromotive force at a junction is called the Seebeck effect. The electromotive force is approximately linear with the temperature difference between two junctions of the different metals, these two different metals are the thermocouple mentioned before. The picture shown below [100] shows a Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) which is a typical modern RTG.
The fuel is located behind the thermal insulation layer and the thermocouples are lined in modules throughout the sides of the RTG.
Fuel in a Radioisotope Thermoelectric generator
There are several possible isotopes that can be used as a fuel for RTGs, there are a couple of criteria that these isotopes have pass in order to be candidates. Dr. Bertram Blanke research on the development of RTGs evaluated over 1300 radioactive isotopes for the project, but only found that 47 of them had the suitable characteristics needed to be a possible fuel for RTGs. [101] These characteristics include:
- Possession of long half-life for continuous energy production.
- Ability to produce high energy radiation.
- Large heat power-density.
- Tendency to produce radiation decay heat.
Based on these characteristics, the most frequently used isotopes for RTG fuels include:
- Plutonium-238 (Pu-238)
- Curium-244 (Cm-244)
- Strontium-90 (Sr-90)
Of these Plutonium-238 is the most cited fuel in resources about RTGs. [102] In fact because of the frequent use of Plutonium-238 for the use in RTGs, including its use in more than 20 space missions, there is a current shortage of this isotope. Since Plutonium-238 is a byproduct of creating nuclear weapons most of what NASA uses is left over from the cold war. [103] However this does not mean it can’t be produced anymore: In 2012, the Obama administration got Congress to go along with a plutonium-238 restart, under the condition that NASA pay to repair aging DOE infrastructure. When these repairs are complete, the Energy Department of Energy will start producing 1.5 kilograms of plutonium-238 a year. [104] Pu-238 satisfies all of the RTG fuel characteristic needed with high radiation output, mainly alpha decay channels and is thus safer to use for any Martian colonist, a very long half-life of 88 years, and a small fuel pellet packaged into the size of a marshmallow as seen in the picture shown below. [105] All these factors make Plutonium-238 the best isotope to use for RTGs on Mars.
Production of Plutonium-238 will not be possible on Mars in the early stages of colonization since the production process is really complicated, thus all the Plutonium-238 would have to be transported to Mars from Earth.
Amount of energy produced using a Radioisotope Thermoelectric generator
To determine how much energy can be produced by using a RTG, we need to know the heat energy generated and the efficiency of the energy conversion. The latter depends on the materials used and the temperature on the cold and hot side. The following material properties influence the efficiency: Electrical conductivity, Thermal Conductivity and the Seebeck Coefficient. [106] If these are known then the efficiency by which a material is capable of generating power can be determined.
Then, by using the temperature on the hot and cold side, the conversion unit can be calculated.
Once M and Z are known the ideal efficiency can be calculated.
These formulas could be used to determine the efficiency of a custom setup, but for existing setups such as the MMRTG the power output is already known.
In the Multi-mission radioisotope thermoelectric generator (MMRTG) developed by NASA for multiple space missions, PbTe (Lead Telluride) and TAGS is used, where TAGS material is a material incorporating Tellurium, Silver Germanium and Antimony. This material and the temperature inside the generator result in a thermal power generation of 1975 W and an efficiency of 5,6%. Concluding in a netto electrical output of 110 W at the start of the mission, falling to about 100 W after 14 years. The MMRTG weights 43.6 kg which means the netto energy density is 2,52 W/kg. [107] For every one kg added to the Transport robot would require an extra 695.8 kJ of energy, calculated with the formula shown below, or 0.767 W if the Transport robot would travel at 10 km/h. This means the net energy gain of a MMRTG would be 1.753 W/kg if the Transport robot would travel at 10 km/h.
Safety of a Radioisotope Thermoelectric generator
There is a risk of radioactive contamination with the use of RTGs. Any fuel leaks could result in the radioactive material contaminating the environment. To reduce the risk of this, the fuel is stored in individual modular units with their own heat shielding in current space-exploration RTGs. In NASA’s RTGs each marshmallow-sized pellet of plutonium fuel used in an RTG is encased in iridium, this iridium cladding is designed to deform and contain the nuclear fuel incase of an impact. A pair of these iridium-clad fuel pellets are encased inside a cylindrical casing l made of a hard carbon-carbon fiber, this cylinder is then covered in an insulating sleeve made of graphite. Two of these carbon-carbon cylinders are then enclosed inside a casing of even more carbon-carbon fiber to form the basic ‘building block’ of an RTG. A typical RTG contains two to eight of these ‘building blocks’. [108] The main isotope used in RTG is plutonium-238. The alpha radiation emitted by the isotope will not penetrate the skin, but it can irradiate internal organs if the plutonium is inhaled or ingested. In the past there have been several accidents involving RTGs: [109]
- On 21 April 1964 a the U.S. navigation satellite, the Transit-5BN-3, failed to achieve orbit and burned up on reentry somewhere north of Madagascar. The 630 TBq plutonium metal fuel in its RTG was injected into the atmosphere over the Southern Hemisphere where it burned up, and traces of plutonium-238 were detected in the area a few months later.
- The Nimbus B-1 weather satellite whose launch vehicle was deliberately destroyed shortly after launch on 21 May 1968 because of erratic trajectory. Its RTG containing relatively inert plutonium dioxide was recovered intact from a seabed five months later and no environmental contamination was detected.
- In 1969, the first Lunokhod rovers of the USSR were launched with another isotope polonium-210 on board. However, the rocket exploded and radioactivity was spread over a large area of Russia.
- In April 1970 the failure of the Apollo 13 mission meant that the lunar module reentered the atmosphere ant burned up. the RTG it was carrying, which survived reentry, and its 3.9 kilograms of plutonium dioxide plunged into the Tonga Trench in the Pacific Ocean, where it will remain radioactive for the next 2,000 years. Subsequent water testing has shown the RTG is not leaking radioactivity into the ocean.
- In 1996 Russia launched Mars 96, but it failed to leave Earth orbit, and re-entered the atmosphere a few hours later. The two RTGs onboard carried in total 200 g of plutonium and are assumed to have survived reentry as they were designed to do. They are thought to now lie somewhere 32 km east of Iquique, Chile. [110]
All of these accidents were not caused by the RTG, but the RTG made the environmental impact way more severe. The only possibility for such an accident with the Martian transport robot would be when transporting the radioisotope fuel from Earth to Mars.
Hydrogen Energy
Hydrogen energy is a rather new and experimental energy source and has many different applications like energy production, storage, and distribution; electricity, heat, and cooling for buildings and households; the industry; transportation; and the fabrication of feedstock. [111]. There are many benefits to using hydrogen as a fuel, namely it has a lower mass density than fossil fuels, has 3 times as much energy than fossil fuels per kg and hydrogen does not produce harmful emissions. However, hydrogen takes up a lot of space, cannot be found in nature, is difficult to store and is highly flammable. [112] Hydrogen energy needs a fuel cell in order to work. A fuel cell uses chemical energy of a fuel (often hydrogen) and an oxidizing agent to create energy. Installation will depend on the size available for the fuel cell. A fuel cell ignites the fuel with agent which creates a vapor of water and a lot of energy. Figure of a fuel cell: [113]
Assumptions
We will assume that there is a maximum of m^3 that can be made available for the tank and there is enough space for the rest of the fuel cell. The amount of available space for the tank will be set to 2 m^3.
We will assume that the fuel used will only be available at the colony with a surplus of water. This means that the robot will have to travel twice as far. This would also mean that the robot is restricted to always have to return to the starting colony, but for our scenario this does not matter.
Obtaining the fuel
The fuel cell needs a chemical energy in order to work. The most commonly used is hydrogen with the molecular formula H2. The problem with hydrogen is that it cannot be found in nature, or Mars in this case, but almost always found as part of another compound. However, it is possible to separate these substances such that hydrogen can be extracted. The most obvious compound is water (H2O). Our scenario already provides the water needed, since we know that the colony where the robot starts has an abundance of water. There are many different methods hydrogen can be extracted from water (H2O), splitting it into hydrogen and oxide: [114] Natural Gas Reforming/Gasification: Synthesis gas, a mixture of hydrogen, carbon monoxide, and a small amount of carbon dioxide, is created by reacting natural gas with high-temperature steam. The carbon monoxide is reacted with water to produce additional hydrogen. This method is the cheapest, most efficient, and most common. Natural gas reforming using steam accounts for the majority of hydrogen produced in the United States annually. Electrolysis: An electric current splits water into hydrogen and oxygen. High-Temperature Water Splitting: High temperatures generated by solar concentrators or nuclear reactors drive chemical reactions that split water to produce hydrogen. Photobiological Water Splitting: Microbes consume water in the presence of sunlight, producing hydrogen as a byproduct. Photoelectrochemical Water Splitting: Photoelectrochemical systems produce hydrogen from water using special semiconductors and energy from sunlight.
There are also some alternative methods of obtaining hydrogen that do not use water: Renewable Liquid Reforming: Renewable liquid fuels, such as ethanol, are reacted with high-temperature steam to produce hydrogen near the point of end use. Fermentation: Biomass is converted into sugar-rich feedstocks that can be fermented to produce hydrogen. Ammonia: Liquid ammonia contains more hydrogen by volume than compressed hydrogen or liquid hydrogen. It is not a greenhouse gas and has a high hydrogen density, which leads to NH3 being a favorable alternative to hydrogen.
Comparing methods
Since Mars, and our scenario of Mars, have different properties then the processes on Earth, a comparison of the methods is needed to determine what method is best for our situation. The alternative methods and the natural gas reforming/gasification all need some resources as fuel that are not found on Mars and are therefore unfit to use as method. There could be a material among these that could be found on mars on further research or created on Mars, but will for now not be considered a valid method. The prime reason therefore is that these resources would have to be shipped to Mars each time. The remaining methods are:
Electrolysis:
- Pros: Only water and an electrolysis device is needed.
- Cons: Needs to use energy from the colonies.
High-Temperature Water Splitting:
- Pros: Only solar concentrators and water is needed.
- Cons: Nuclear reactor most likely not feasible.
Photobiological Water Splitting:
- Pros: Only needs water, green algae, sunlight.
- Cons: Needs green algae.
Photoelectrochemical Water Splitting:
- Pros: Needs water and sunlight as resources
- Cons: A special semiconductors is needed.
Each of these are valid options for generating hydrogen on Mars. We think electrolysis is the best choice since the energy needed can be produced at the colony at easy using solar panels.
Comparison of Fuel Cell Technologies
All fuel cells operate using the same methods. The difference between each fuel cell is determined by what kind of electrolyte is used. The electrolyte is responsible the kind of chemical reactions that take place in the fuel cell, the temperature range of operation, and other factors that determine its most suitable applications.
Figure of different fuel cell types: [115]
Since our robot most likely does not need more than 250 kW, the best choice for the electrolyte is PEM. Also because it has a lower operating temperature then the others, it is more likely to perform near its upper efficiency. PEM fuel cells have an output range from 50 to 250 kW.
Performance
The combustion in the fuel cell work [116]
The formula for hydrogen reaction: [117]
In order to calculate what the total energy is that a fuel cell can produce depends on the available moles of hydrogen and oxygen. For both the hydrogen and oxygen the uncompressed forms take too much space. Therefore each compound must be compressed to a certain degree. We will assume the hydrogen is pressed at 700 bar at a temperature of -60 degrees and the oxygen is pressed at 200 bar at a temperature of -60 degrees. Taking all together the total kg of hydrogen is calculated as: 1L hydrogen equals 0.062 kg hydrogen (61,98 kg/m3 @-60 C, 700 bar) 0.062 kg hydrogen equals 61,51 mole hydrogen (1.00794 g/mole) 61,51 mole hydrogen reacts with 30,76 mole oxygen. (1:0.5) 30,76 mole oxygen equals 0,961 kg oxygen (32 g/mole) 0,961 kg oxygen equals 2,66 L oxygen (360,6 kg/m3 @-60 C, 200 bar)
So in order to have 0.062 kg of hydrogen, 3.66 liter is needed. Having 2 m3 of available space, there is a total of 33,88 kg of hydrogen available. Hydrogen has total energy of 33.6 kWh per kg, so the total energy that the fuel cell has is 1138,4 kWh. If we assume the performance ratio to be 56.7% since the fuel cell will have a PEM electrolyte, the fuel cell will have an effective total energy of 645,45 kWh.
Other important aspects
The danger of hydrogen. Working at low temperature: A fuel cell works best at a high temperature. Since Mars has a very low average temperature this may impact the fuel cells efficiency by giving the combustion a slower reaction, creating less energy per combustion. The three main ways of dealing with the slow reaction rates are: [118]
- The use of catalysts
- Raising the temperature
- Increasing the electrode area
Depending on the implementation and resulting efficiency of the fuel cell, these variables can be adjusted such that the resulting system has the correct efficiency.
Finalizing results
Total energy production in kW: 645,45 kWh.
Pros of this energy: Only needs fuel cell in order to operate.
Cons of this energy: The tank takes up 2 m3 space and the fuel cell will need space as well, depending on the implementation. Hydrogen needs to be produced Storing it may be problematic, since high pressure storage is needed. Hydrogen is also quite dangerous since it is highly flammable.
Biofuel energy
General
Biofuel energy is energy that is produced by using biomass as fuel. Examples of these are Biodiesel, ethanol, vegetable oil and biogas. Currently ethanol fuels blends are already used in many transport vehicles around the globe, however mostly these do not use more than 15% ethanol in the fuel mixture because else it will damage the engine because they are not made for higher biofuel-mixtures.
Ethanol
The simplest biofuel is ethanol. There has to be oxygen present to burn ethanol and as result of the reaction water and co2 will be made.
The above chemical equation is the idealised relationship. This reaction can be executed in a generator. In space or a low atmospheric environment this brings some issues with it. The engine must be specially made to work with these circumstances. The assumption has been made such an engine can be produced in the future.
To use this biofuel engine it can be stored in two separate tanks, one with oxygen and one with the biofuel. These can be injected in the engine with the correct mass ratios. In current internal combustion engines air is injected instead of pure oxygen which is a lot less flammable and less prone to accidents assuming it is even possible to burn ethanol with pure oxygen successfully.
Obtaining the fuel
There are various ways to obtain fuels like ethanol, but the most common one is via fermentation. This can be done by treating crops. When producing crops just for the sake of making biofuel it seems like a waste of good resources. That's one reason why this fuel might not be the best as a main fuel in a Mars colony. It requires a lot of resources to grow the crops. However, there will be biomass remains which could be transformed into biofuel but this is likely to be a very tiny amount of the necessary energy for the robot to function. The biomass energy is better off being used in the colony or converted to electrical energy.
Calculations to determine use
Let’s assume to have 1L ethanol as fuel. The density of ethanol is around 850 kg/m3 in Mars temperatures.
We can do calculations to see the volume ratios between oxygen and ethanol required.
1L ethanol equals 0.85kg ethanol.[119] (850kg/m3 @-60C, 1bar)
0.85kg ethanol equals 18.45 mole ethanol (46.07g/mole)
18.45 mole ethanol reacts with 55.35 mole oxygen. (1:3)
55.35 mole oxygen equals 1.77kg oxygen (32g/mole)
1.77kg oxygen equals 978.4L oxygen[120] (1.803kg/m3 @-60C, 1bar)
1.77kg oxygen equals 6.6L oxygen[121] (267kg/m3 @20C, 200bar)
So the tank of oxygen needs to be a factor 6.6 bigger than the biofuel tank if on the oxygen is compressed with a pressure of 200 bar. Let’s see how much energy we would get from burning 1L ethanol. This can done by checking how much energy in heat-form gets released by doing the reaction. Then the transfer efficiency of turning this heat into work must be applied to obtain the netto energy that can be obtained from the reaction. According to sources 1.368 kJ/mole ethanol burnt gets released in heat-energy. [122]
This means that by burning 1L ethanol using 6.6L oxygen corresponds 25 kJ heat energy released. By transferring this heat energy into electric energy there will be a lot of energy lost. How much exactly is hard to tell without knowing the exact specifications of the generator used. So let’s assume the efficiency to be 50%.
Assumptions
There is a combustion engine that works in low-pressure atmospheres and is capable of combusting ethanol or another similar biofuel with pure oxygen injection from another tank with the correct ratios.
The efficiency of this process is 50%
Results
This concludes to 12.5 kJ electrical energy is produced by burning 1L of ethanol and 6.6L pressurised oxygen in an oxygen tank. This is the same amount of oxygen that is present in the 6500L dry air at sea level to put things to perspective.
Including a 900L liquid ethanol & 6000L pressurised 200bar oxygen tank to the water transporting robot would result in obtaining 11.25MJ energy before the fuel tanks are empty and it would create 1461 kg CO2 and 900kg water.
Gasoline energy
The same problem occurs if trying to use combustion engines with gasoline, except there is even more oxygen needed with a pure gasoline combustion engine. So it is not necessary to look more into this as this technology is not viable for the water transporting robot.
Comparing different energy generation methods
Hydrogen, biomass and gasoline all need an enormous oxygen tank, even when the robot carries pure compressed oxygen. These technologies are developed with the idea of oxygen being available everywhere through air here on Earth and would require massive amounts of oxygen production on Mars itself. Since the people in the colony also need oxygen to breath, this seems like a way better goal for the oxygen that is available. On top of this, carrying pure oxygen can form a big danger risk. Because of these reasons only Solar energy and Radioisotope thermoelectric energy are considered viable options for energy production of the water transport robot. When choosing which of these two source of energy the robot should mainly use there are different aspects that should be considered. These consist of; energy production capabilities, safety, ease of use and self-sustainability. First, let’s look at the energy production capabilities of all energy sources. According to the calculations, solar energy will generate approximately 414.84W when used on the robot in our situation, while radioisotope thermoelectric power will generate about 2.52W/kg. This means about 164.62 kilograms of engines and radioactive fuel is needed to generate as much power when using solar energy. Secondly, let’s look at the safety. While solar panels have no safety hazards at all, radioisotope thermoelectric power has the potential of contaminating the environment in the event of a crash, although the risk of this happening is very low for a land vehicle on Mars. Radioisotope energy also has the potential to harm the Martian colonists handling the fuel, this will only happen if the plutonium dust is inhaled or ingested, since the alpha radiation emitted by the isotope cannot penetrate the skin. Overall Solar energy is the safer option. Then let us look at the ease of use and self-sustainability of the energy sources. Solar energy can only generate power during the day and can’t generate power during dust storms, which can last for weeks at a time [123], while radioisotope thermoelectric energy can be generated at all times, even during dust storms. However, RTG needs to be fueled with materials that need to be transported from Earth, while solar panels can operate on their own. Both methods need maintenance and repair. Even though solar panels are useless during a dust storm, they seem like the better option overall. If a colony has a big water storage capacity and the robots deliver more than used, they could build up a buffer in case a dust storm happens. The use of solar energy is obviously way more self-sustainable compared to Radioisotope energy because, as stated before, solar energy doesn’t require any fuel to be transported to Mars from Earth, while radioisotope energy requires Plutonium-238 which can’t be produced on Mars in an early stage of colonization and would have to be transported from Earth. All in all, it would be preferable to rely only on solar energy if possible.
Power storage
Amount of storage needed
In order for the robot to work, the most important thing is storing energy that it can use for driving. Whether the electricity is generated by solar panels or by a radioisotope generator, the generated energy must be stored. For example, when solar panels are used, the solar intensity will not always remain the same, due to weather conditions such as dust storms, or general cloudiness. This would means that the amount of electricity that is generated will not always remain the same. This means that power storage is important. A radioisotopic generator will produce a more consistent power output, because it is less dependent on outside conditions. However, there is another important factor that makes power storage necessary.
Both the energy production methods will not provide enough energy to complete a full journey from colony to colony (assuming that they are 2500 km apart as stated in the scenario). The amount of storage needed is therefore dependent on the amount of energy that can be produced along the way. The total amount of energy needed to travel the distance from colony to colony is equal to 8.63 GJ. The amount of energy that can be generated by solar panels and radioisotope thermal generation at a velocity of 10 km/h is listed below:
- Solar panels: 105 kWh or 0.376 GJ [124]
- Radioisotope thermal generation: 474 kWh or 1.706 GJ [125]
Both of these generation methods are far from sufficient to generate the required 8.63 GJ (even when ideal conditions are assumed). This means that there should be a possibility to store 1923 kWh or 6.924 GJ of energy on board of the device, if we want to run on a velocity of 10 km/h.
Battery used
There are some requirements that the battery needs to meet in order to perform on Mars:
- Able to operate at low temperatures (temperatures range from -140°C to 20°C with an average of -53°C during the day). [126]
- Able to fit inside the device (dimensions: 6.62x2.5x3 m = 49.65 m3)
- Able to store 1923 kWh of energy
The latest mars rover ‘Mars 2020’ uses a ‘Multi-Mission Radioisotope Thermoelectric Generator’ or MMRTG to generate power (Note: This method of generating electricity also gives the highest and most reliable power output in our calculations). For the power storage, two lithium-ion batteries are used.[127] This suggests that this method should be sufficient for Martian conditions, as NASA uses it. However, the capacity drops significantly with temperature. This factor will be accounted for later.
Lithium-ion battery
A lithium ion battery is based on a principle of energy production using movement of ions inside an electrolyte. In this specific battery, positively charged Lithium-ions will move from the negative electrode to the positive electrode. Energy is released in the process. When charging the battery, the lithium-ions will move back, storing the energy in the process.
The reason that lithium-ion batteries are used is because there is no battery known with a higher maximum theoretical capacity (3860 mAh/g [128]) and a higher practical energy density (100-265 Wh/kg or 250-670 Wh/L [129]).
When we take the highest energy density (670 Wh/L), the battery should be at least 2870 L of volume to store the required 1923 kWh. This is a volume of 2.87 m3. This is a small volume in comparison to the total volume of the device; it takes up about 5.8% of the total volume.
However, if we look at the required weight of the battery, we encounter a problem. The minimum weight of such a battery, using a specific energy of 265 Wh/kg would be an additional 7256 kg, which is 59% of the total weight of the truck without batteries. To transport this additional weight, more energy is needed, and therefore more batteries, which increases the weight again.
Battery mass
For this constraint, a balance in power need and weight must be found. Assuming that the generator generates the same power output of 474 kWh, the following energy balance can be used to calculate the ideal mass:
In which mt is the mass of the truck, mb is the mass of the battery and e is the specific energy for a lithium ion battery. The rest of the constants are given in the table in the scenario section.
For a speed of 10 km/h or 2.778 m/s, the energy balance gives a mass of 26837 kg for the battery. This is way too much and needs to be reduced in some way. There are three parameters that we can change in order to achieve this:
- The velocity v (assumed to have a value of 10 km/h)
- The distance from colony to colony d (2500 km)
- The energy produced by the generator Egen (1.706 GJ)
To determine the influence of these parameters on the equilibrium battery mass, a Matlab script was made to create the following plots:
As shown in the plots above, the velocity has almost no influence on the battery mass, because it only shows small deviations from the calculated 26387 kg. However, the distance has a very big influence on the battery mass. For example if we reduce the assumed distance from 2500 to 1500 km, we only need a battery that is 7000 kg instead of 26000 kg. Furthermore, also the energy generated on board has a big influence on the battery weight. The best way to save battery weight will therefore be a combination of reducing distance and increasing the generated energy. However, reducing the distance would require a change in assumptions, which is not realistic. That means that we will have to do further research into energy generation methods.
Temperature influence
The average temperature on Mars is -53 °C and the minimum and maximum temperatures are -140 °C and 20 °C. [130] Any form of energy storage for the water transport robot would have to be capable of charging and recharging energy with this vast range of external temperatures, specifically the lower end of the range could cause problems for energy storage.
Currently the battery with the lowest operational temperature only functions well for temperatures as low as -70 °C. [131] This battery was developed by researchers in China in 2018 and utilises electrodes based on two organic compounds. Unlike the electrodes in used lithium-ion batteries, these organic compounds don’t rely on intercalation, which is the reversible inclusion or insertion of ions into their molecular structure.
Typical lithium ion batteries can store and release energy in cold temperatures. However, their capacity will be significantly reduced. For example, a normal lithium ion battery, that has 100% capacity at room temperature, will typically have 50% of that capacity at -20°C. If we follow this trend for -70°C we find a capacity of about 20% of its original capacity. This means that the specific energy for this battery type will go from 265 Wh/kg to 53 Wh/kg. This is a factor that should be taken into account when determining the maximum battery capacity.
Amount of storage the battery can have
In order to determine the amount of storage capacity that the battery can provide, a few assumptions have to be made:
- The on-board power supplies (whether it is solar panels, radioisotope or any other source) provide the rest of the energy needed to run the robot at some constant velocity from colony to colony. Therefore, the battery is fully emptied, when travelling from colony to colony.
- The battery should only weigh a maximum of 20% of the mass of the truck when fully loaded. This results in a maximum mass of 2480 kg. This should be enough to provide the truck with extra energy.
- The capacity drops to 20% of the capacity at room temperature, which results in a capacity of 134 Wh/L or 53 Wh/kg.
Using these assumptions, we determine the maximum storage using the following formula:
In which E is the maximum stored energy in the battery, e is the capacity of the battery at -70°C and m is the maximum mass of the battery.
If we fill in the values that are mentioned previously, we find a maximum stored energy of 131 kWh, which would be a good value to work with from now on.
Model
Inputs
The goal of the model is to calculate the maximum velocity the robot can drive given a certain design. This can be used to see what kind of design would work the best and could also be used by the manufacturers during the design process to see if certain designs would work at all nor not. The model will take multiple different inputs, which are variables that can be decided on when designing this robot and variables decided by the situation on Mars. Some of these variable inputs already have been given a value in our assumptions, but can be changed in the model for the situation in which our assumptions turn out to be wrong. All these inputs can be found in the tables below. Their variable name correspond to the names presented in the model.
Situation variables
| Viarable | Unit | Range | Section in model |
|---|---|---|---|
| Distance between colonies | Kilometer | 0 - 10648.45 | General |
| Amount of people | / | 0 - 10648.45 | General |
| New water per person | Liter | 0 - infinite | General |
| Height difference | Meter | 0 - infinite | General |
Design variables
| Viarable | Unit | Range | Section in model |
|---|---|---|---|
| Robot tank capacity | Liter | 0 - infinite | General |
| Battery size | Kilogram | 0 - 10648.45 | Power Storage |
| Solar panel size | m^2 | 0 - infinite | Solar Energy |
| Performance ratio | % | 0 - 100 | Solar Energy |
| Conductor material | / | / | Solar Energy |
| Generator size | Kilogram | 0 - infinite | Radioisotope Energy |
Distance between colonies. The range is based on half the perimeter of Mars, since this is the max distance colonies could be apart. In our situation, this distance is 2500 kilometer.
Amount of people. These are the amount of people living in the colony that needs water. In our situation, this is 50 people.
New water per person. This is the new amount of water that needs to be supplied by the transport robot per person per day. This is not the same as water usage per person per day, since some of the water will be recycled. This recycled water is not included in this variable. In our situation, this is 10 liter.
Height difference. This is the relative difference in height between the two colonies. While in our situation this is 0, this should be a variable that can be inputted in the model.
Robot tank capacity. This is the amount of water the robot will transport, because of the reasons mentioned in the assumptions section, the eventual capacity of the tank will be higher, to compensate for the lower density of ice. However, this is purely the amount of water the robot should transport, which in our situation was determined to be 5000 liter.
Calculations
The goal of the model is to calculate the maximum velocity the transport robot can move with the design choices given by the user. In order to achieve this, when the user presses the calculate button, the algorithm will first calculate the total weight of the transport robot with the given variables for both a full water tank and an empty water tank. It will also calculate the battery storage capacity and total energy production per Martian day using the input variables. For further calculations, the algorithm constructs an array with velocity values from 0 to 100 meter per second in steps of 0.001 meter per second. This array will be used to calculate values for multiple velocities to compare them in order to see what the maximum possible velocity is for the situation. With this velocity, it will calculate the total energy that needs to be produced during a one way trip for both a full and an empty water tank for every velocity in the array. For this it will first calculate the total energy needed for such a trip and subtract the battery storage from this value. In order to calculate this needed energy it will use the formula established earlier, which is also presented again below.
As stated before, while in our situation we assumed the relative height difference between the two colonies to be zero, this is a factor that could be different for another situation. In order to implement this in the model, there should be a way to calculate the energy needed to overcome this height difference. For this, the formula stated below is used.
With this formula, the potential energy due to gravity is calculated using the mass m, height h and gravitational acceleration g. If the end goal is higher than the start point, this acts as extra energy that needs to be produced. Furthermore, the algorithm will calculate the duration of a one-way trip for every velocity in the array. This will be used to calculate the total energy produced during a one-way trip for every velocity. Now both the total energy production and the energy production need for every velocity are known, the algorithm will compare these two using a for loop. Starting from the lowest velocity, it will check for every velocity if the total energy production is equal or greater than the energy needed. If so, it will store this velocity in a separate variable. This means that at the end of the for loop, this variable will contain the highest velocity for which the energy production is high enough to supply the robot. The algorithm will execute this for loop for both a full and an empty water tank. Now, it knowns the maximum velocity the robot can move with for both a full and an empty water tank. It will use this knowledge to calculate the minimal duration for the two-way trip, which is then used to calculate the amount of transport robots that are needed to supply the users in the colony. At the end, it will present its results in the GUI of the model. The full flow of the algorithm can be found in the flowchart below.
[model can be downloaded via this link]
Our design
Since there is now enough information to see whether the robot can be supplied enough energy to drive from colony to colony it is time to look back at the RPC list established prior to the research. The robot has the requirement to drive 2500 kilometers from colony to colony, which it has to drive twice to deliver water once. The robot also needs to deliver 500 liter of water per day, using either a large enough tank or multiple robots. The robot should preferably drive 10 km/h, if this is possible, and there should not be too many robots needed for the colony, since this would skyrocket the cost of the total project. As a limit around 4 robots were chosen. One preference that has been added to this list when researching different power supply solutions is that it would be best to only used solar energy. To see if this is possible, the model can be used. As a first test, the values established during the research and assumptions will be used. These are the standard values configured when first opening the model, which are the values presented in the table below.
| Distance between colonies | 2500 km |
| Amount of people | 50 |
| New water per person | 10 L |
| Robot tank capacity | 5000 L |
| Height difference | 0 m |
| Battery size | 2480 kg |
| Solar panel size | 10.4 m^2 |
| Solar panel performance ratio | 63.92 % |
| Conductor material | Multi-junction GalnP/GaAs/Ge |
| Radioisotope energy generator size | 0 kg |
When supplying these values to the model, it seems that it is possible to use the transport robot using this design. However, it would take a robot 635 Martian days to return with water, resulting in the need for 64 robots to supply enough water. The robot also won’t reach it’s preferable speed of 10 km/h, having a maximum speed of 0.378 km/h without a full water tank instead. One way to increase the performance of the robot would be to find a way to increase the solar panel size. The total area on top of the robot would be 16.55 m^2. If the top of the robot would be totally filled with solar panel, this would mean there would already be about a 50% increase in solar panel size. Placing a solar panel with a size of 6.7 by 3 meters on top of the robot, will result in just a little bit of solar panel hanging over the sides of the robot. 4 cm at the front and back and 25 cm at both sides. If this solar panel is attached on a rail with an extendable arm that can extend 3 meters, it would be able to rotate a full 90°, reaching a maximum extra height of about 3 meters. If this construction would be placed on a panel or frame that can rotate 360°, it would be able to point at any direction in order to get the most sunlight. This will mean however, that when the panel or frame is rotated it would be hanging 2.1 meters over the side of the robot on both sides. This will, using the values established in the solar panel section, equal to about 94.5 kg of solar panel on each side. Since this is not that much in comparison to the weight of the full robot and the weight is present on both sides, it will not be likely to cause the issue of tipping the robot over. When going up a steep hill or another difficult situation, it could always rotate the solar panel back. Another way to solve this problem is to extend the wheels more to the side, giving it more stability. If the wheels are placed 4.5 meters apart from each other, the solar panels will only extend a maximum of 1.1 meter over the side of the robot which equals 49.5 kilogram on both sides. The configuration that would be placed on top of the robot can be seen in the drawing below. This will already result in a larger solar panel area of 20.1 m^2.
Another way to improve the situation is to increase the tank capacity of the robot. The original tank capacity was based on the truck used for the dimensions, however, there will not be the need for a driving seat on this robot, increasing the space that could be used for water storage. Considering the dimensions of the robot, a water storage tank of 600x225x150 could be possible. This will result in a capacity of 20250 liters. Considering the fact that ice is larger than water, this will be able to contain 18630 or about 18500 liters of water. Using these new values for both solar panel size and tank capacity already gives way better results. The maximum speed with a full water tank is now about 0.31 km/h and without a full water tank about 0.73 km/h. In this way, there are 13 robots required to deliver enough water, which is a huge improvement over the 64 obtained before. To visualize the size of the different components, simple drawings of both the side and front view can be found below. On top is the solar panel and inside the water tank is visible.
One quite large component that also needs to be present is the battery, which has a volume of 6.27 m^3 in this situation. This still easily fits in the remaining space inside the robot. In worst case, the robot could be made a little bit bigger to the sides, since the wheels are extended anyway. While it is unknown how big other components like the motor will be exactly, there should be enough space for it. Assuming the robot will float 0.5 meter above the ground because of the wheels, there will be a total volume of 41.375 m^3 (662x250x250) available for components. Subtracting the volume of the water tank and battery results in a volume of 14.855 m^3 left for the motor and other components. Using this configuration, the solar panels will produce on average 8207.61W. This means, assuming it will use half of the energy during the day and half of the energy during night, it has to store 363679215.6 J of energy in its battery during the night. Since the battery of 2480 kilogram will be able to carry 131 kWh, which is equal to 471600000 J of energy, this will not cause a problem.
Conclusion
The colonization of Mars is still some time away and presents many new challenges in order to be successful. We have tried to create an accurate scenario of Mars when there are multiple small colonies, where not every colony has access to water. Since water is such a vital resource, we have created and modeled a robot that can solve this problem. Since the robot is an autonomous vehicle it requires the capability to provide enough power for itself. Therefore the goal of this research is to find out if it is doable to provide such a water transport robot on Mars with enough energy for long distances. This meant finding all possible methods and compare them. A huge challenge herein lies with the fact that Mars is still unknown terrain to some degree and assumption where needed for each method. This makes it difficult to determine the exact consequences for each decision and makes testing difficult. By using a model we have tried to bridge this gap and support our final choice of energy. Three important aspects that determine the total energy the robot needs travel between colonies are weight of the robot, distance between colonies and average speed of the robot. Using assumptions we can now now answer the research question: Is it doable to provide a water transport robot with enough energy? Yes, it is possible, but the robot can’t drive very fast. Using the design we currently consider, the duration of a two-way trip is 463.9 Martian days. With a capacity of 18500 liters of water, this results in the need of at least 13 robots. While this solves the requirements presented earlier, the preferences are not achievable using this design. The power supply used for this design are solar panels, since these are easy in use, requiring no fuel or extra supplies from Earth. They are also the safest option.
Discussion
Dust storms on Mars can last for a couple of weeks. Incase such a dust storm occurs we have already made the assumption that each colony has enough extra storage capacity for water reserves to last a couple of week, In our scenario this would be 15.210 L, based on a dust storm that would last a month. However, after a dust storm this extra reserve storage would need to be refilled, for this atleast one extra robot would be needed on top of the amount calculated using the model, in our scenario with our design this means we would need at least 14 transport robots instead of the previously mentioned 13. It would take this robot with a water capacity of 18500 liter one trip or 463.9 Martian days to fill this reserve back up.
The velocity chosen as a preference was 10 km /h, however our design has according to the model a maximum speed with a full water tank of 0.31 km/h and without a full water tank a maximum speed of 0.73 km/h. This comes nowhere close to our preference velocity. To improve the maximum speed of our design more solar panels could be added for example on the sides of the robot, radioisotope generator could also be implemented into the design, however this would make it way more complicated since all the radioisotope fuel would have to be transported from Earth. We also had a preferences of a around 4 robots driving at onc. In the end it become a much larger number. To bring down the number of robots driving up and down, the speed for each robot has to be larger, or the amount of water per robot has to be larger.
Several assumptions were made during our research. Each of these assumptions could be wrong or vary hugely. We will now discuss the impact of having incorrect assumptions:
- In creating our scenario we made the a big assumption for the location of both colonies which determines the distance the robot would have to travel. This may be much smaller, since the disctance assumed was already huge. This might take the number of required robots down from 14 to 6-7.
- We also made the assumption that a separate robot will bring food and / or no water is needed for food of the colony. Likewise, we assumed that no water is needed for industrial purposes in the colony. We also made some assumption on how much what people need per day, how much people life in the kolonies and how much water can be recycled. These can all be combined with misassuming how much water is needed per day. This will affect the number of robots that are needed which is already quite large. Needing an even bigger number of robots may make the robot other solutions to this problem much more attractive.
- Assumption made for the variables in the energy cost formulas, the assumptions for the performance ratio of the solar panels and the assumptions for the battery will affect the energy consumption and total energy that the robot can use. If this drops a certain degree the robot will take much longer to travel or may be unable to travel at all.