PRE2018 1 Group3 1024503: Difference between revisions
No edit summary |
|||
| (21 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=Introduction= | =Introduction= | ||
Automation through robots is becoming more and more commonplace, so it is only a matter of time until it makes its way into supermarkets by replacing tasks for, for example, store clerks. One part that is crucial for robots, is still being able to navigate from point A to B efficiently despite the store being crowded. The supermarket's security cameras can help with this, in combination with a model that keeps track of where customers might be now and in the future. | |||
=Problem Statement= | |||
The goal of this project will be to find an effective and ''good'' way of guiding a robot through a crowded supermarket. | |||
=Requirements= | =Requirements= | ||
To determine what exactly makes a navigation method 'good', we will have a look at the users that are involved. There are three classes of users: human store clerks, customers, and the supermarket management. Each of these will have requirements that need to be taken into account when designing a navigation system: | |||
1. <u>Be safe</u>: Robots should not bump into people or objects | 1. <u>Be safe</u>: Robots should not bump into people or objects | ||
| Line 28: | Line 32: | ||
To model the possibility distribution of customers in invisible areas, we will make a grid based on the map. The advantage of this is that we will now be able to assign a probability to each grid square and use that for an A* navigation algorithm. | To model the possibility distribution of customers in invisible areas, we will make a grid based on the map. The advantage of this is that we will now be able to assign a probability to each grid square and use that for an A* navigation algorithm. | ||
The distribution of customers in areas without camera coverage will be modelled as a so-called cellular automaton. | The distribution of customers in areas without camera coverage will be modelled as a so-called cellular automaton. Each cell gets two variables: probability of it being occupied (a number between 0 and 1) and the direction a person in that cell would most likely be moving in (a vector of two numbers between -1 and 1, of at most length 1). After each time step, the cell's probability is distributed over its neighbours, most of which to those closest to the direction of movement. | ||
[[File:1024503-CA_transition1.png]] In the general situation, the largest fraction will go in the direction of movement. Smaller fractions go off to the sides, and the smallest fraction stays put. | [[File:1024503-CA_transition1.png]] In the general situation, the largest fraction will go in the direction of movement. Smaller fractions go off to the sides, and the smallest fraction stays put. | ||
[[File:1024503-CA_transition2.png]] | [[File:1024503-CA_transition4.png]] When a cell that would have been spread to is occupied, the spread to the rest of the cells is scaled so it still sums up to the original chance. | ||
[[File:1024503-CA_transition2.png]] When a cell's direction is (0,0), the chance for spreading to any neighbouring cell is equal, but the chance to stay stationary is the highest. | |||
[[File:1024503-CA_transition3.png]] When two cells spread to the same cell, the chance is added and the cell's direction is calculated as the weighted component-wise mean of the directions each cell would give it, scaled by the chance that comes from each of the cells. | |||
==Navigation Algorithm== | |||
Using this model, we can both estimate how busy the unseen areas of the store are and as a bonus it can also be used to try to predict what the customer distribution will be after a number of time steps. The one key difference between these to uses is that for estimating the current distribution we can let cells we know to be visible function as walls, as we know exactly if a customer moved towards it or if it is empty. When we attempt to make a prediction we cannot use this. To make a navigation algorithm that uses this knowledge, we can modify the basic A* algorithm to add a cost to each grid cell dependent on the probability of it being occupied when the robot reaches it. We will use 1 plus some constant times the cell's probability after running a model step for each preceding cell in the path. The optimal value of this constant very much depends on the situation and as such stays a parameter. Since the minimal cost per grid cell is one and we only let the robot move to cells that are directly adjacent, the Manhattan distance makes for a good heuristic. | |||
=Simulation= | =Simulation= | ||
| Line 42: | Line 52: | ||
Based on the ceiling cameras and the robot's own position and orientation, certain areas will be declared visible. Only while a customer is in such a visible area will its position and walking direction will be reported to the model; outside these areas it will only know the position of the objects on the given map, such as walls and shelves. | Based on the ceiling cameras and the robot's own position and orientation, certain areas will be declared visible. Only while a customer is in such a visible area will its position and walking direction will be reported to the model; outside these areas it will only know the position of the objects on the given map, such as walls and shelves. | ||
[[Media: | |||
==Optimising Parameters== | |||
Now that the simulation gives us a concrete situation, we can figure out the accompanying optimal value for the parameter that determines how heavily the probability of a cell being occupied is taken into account. For this, we will run a couple of tests with many different parameter values and compare the results. Each test will consist of the robot having to move to 50 different positions, while reporting the amount of times it landed in an occupied cell and the amount of time steps the total procedure took. | |||
First, a test with the constant ranging from 0 to 200 is done. Here, it appears that low values for the collisions and time are more often taken in the interval from 0 to 50. | |||
Using this, we run four tests on all constants between 0 and 50. From these we conclude that values between 18 and 30 give the best outcomes. | |||
Finally, we run ten tests on all constants between 18 and 30. The conclusion we draw from this is that 28 is the best value for the weight parameter in this situation. | |||
[[Media:1024503-parameter_tests.zip | The test results are given here.]] | |||
=Results= | =Results= | ||
| Line 48: | Line 66: | ||
[[File:1024503-BoxplotT.png|512 px|thumb|Time taken (robot's camera only, without model, with model)]] | [[File:1024503-BoxplotT.png|512 px|thumb|Time taken (robot's camera only, without model, with model)]] | ||
To compare the | To get an idea of the effectiveness of the ideas presented before this, we will want to compare the performance of the robot using only its own camera, using all available cameras, and the robot using the complete model. To compare these well, we need to choose a metric to compare them by. For this, we can bring back the user requirements once again. 1 (safety) and 4 (time) can easily be quantified, so these will be compared directly. Since no cameras are added, the cost (5) is the same (although the computations to be done get slightly heavier). The privacy of customers (6) is respected equally by all three methods, as all that is done is extracting the position and velocity of people from already existing camera images. | ||
After running the same 100 tests of the robot moving to 50 positions on | After running the same 100 tests of the robot moving to 50 positions on the three methods, these are the results: | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! Method | ! Method | ||
! Collisions | ! Mean Collisions | ||
! Time | ! Median Collisions | ||
! Mean Time | |||
! Median Time | |||
|- | |- | ||
| Robot's camera only | | Robot's camera only | ||
| 11.7 | | 11.7 | ||
| 10 | |||
| 967 | | 967 | ||
| 991 | |||
|- | |- | ||
| Without model | | Without model | ||
| 10.9 | | 10.9 | ||
| 9 | |||
| 922 | | 922 | ||
| 924 | |||
|- | |- | ||
| With model | | With model | ||
| 10.6 | | 10.6 | ||
| 8 | |||
| 915 | | 915 | ||
| 912 | |||
|} | |} | ||
From this can be concluded that both using the security cameras and using the model help fulfil the requirements. | |||
[[Media:1024503-tests.zip | A ZIP file with the results of all tests can be found here]] | |||
=Conclusion= | =Conclusion= | ||
As seen in the results, the security cameras at supermarkets can definitely help robots navigate when it is crowded. Furthermore, combining this with a with a model based on cellular automata can make this even more effective. | |||
The used simulation can be [[Media:StoreSim.zip | found here]] and was compiled from [[Media:1024503-source.zip | these source files]]. | |||
=Discussion= | =Discussion= | ||
Something that might still be interesting to look into is the optimal placement of security cameras. It can be expected that having many small or simple blind spots will make it easier to predict where customers are, as we know exactly which blind spot they entered. It would thereby make sense that the model-based navigation will be even better if the security cameras were placed to cover entire intersections. | |||
Using a fine grid for the model<ref>https://arxiv.org/ftp/arxiv/papers/1406/1406.3567.pdf</ref> and/or switching to a finer or continuous time scale will allow the model to be more realistic by e.g. allowing for different walking speeds and making it possible to make a better judgement of the comfort of customers. | |||
=Planning= | =Planning= | ||
| Line 110: | Line 145: | ||
|} | |} | ||
=References= | =References= | ||
<references/> | <references/> | ||
Latest revision as of 23:54, 29 October 2018
Introduction
Automation through robots is becoming more and more commonplace, so it is only a matter of time until it makes its way into supermarkets by replacing tasks for, for example, store clerks. One part that is crucial for robots, is still being able to navigate from point A to B efficiently despite the store being crowded. The supermarket's security cameras can help with this, in combination with a model that keeps track of where customers might be now and in the future.
Problem Statement
The goal of this project will be to find an effective and good way of guiding a robot through a crowded supermarket.
Requirements
To determine what exactly makes a navigation method 'good', we will have a look at the users that are involved. There are three classes of users: human store clerks, customers, and the supermarket management. Each of these will have requirements that need to be taken into account when designing a navigation system:
1. Be safe: Robots should not bump into people or objects
2. Feel safe: People should feel comfortable around the robot(s)
3. Not get in the way: People should have to change their behaviour as little as possible to accommodate for the robot(s)
4. Not take too much time: Robots should not get stuck or take unreasonably long
5. Be economically viable: New equipment and maintenance should not cost more than they save and take at most a few years to pay for itself
6. Respect privacy: Keeping profiles of customers is ethically dubious and will upset them
Supermarkets
There are a couple of things that make navigation and behaviour in a supermarket stand out. First of all, the environment itself is completely known; a map of the supermarket should not be hard to acquire. Another interesting factor is that most (if not all) supermarkets have a few security cameras installed on the ceiling. These can be used to keep track of people in some of the areas the robots can't directly see. We can then use image recognition and our knowledge of the environment to place all clearly visible customers on the map[1]. We can add more cameras, but we also have to keep the cost (requirement 5) in mind. This means there will inevitably be blind spots. We can, however, use a model that keeps track of the probability distribution of customers in those blind spots. This can be used to improve navigation by staying away from potentially crowded spaces and avoiding collisions in a timely manner.
The behaviour of people in a supermarket is also very different from people on the street: people will often stop in front of a shelf or change direction. It would be possible to base the probabilities of a customer stopping in front of a shelf on their age, outwardly appearance or even their customer card, but this would very much be against requirement 6.
Model
To model the possibility distribution of customers in invisible areas, we will make a grid based on the map. The advantage of this is that we will now be able to assign a probability to each grid square and use that for an A* navigation algorithm.
The distribution of customers in areas without camera coverage will be modelled as a so-called cellular automaton. Each cell gets two variables: probability of it being occupied (a number between 0 and 1) and the direction a person in that cell would most likely be moving in (a vector of two numbers between -1 and 1, of at most length 1). After each time step, the cell's probability is distributed over its neighbours, most of which to those closest to the direction of movement.
In the general situation, the largest fraction will go in the direction of movement. Smaller fractions go off to the sides, and the smallest fraction stays put.
When a cell that would have been spread to is occupied, the spread to the rest of the cells is scaled so it still sums up to the original chance.
When a cell's direction is (0,0), the chance for spreading to any neighbouring cell is equal, but the chance to stay stationary is the highest.
When two cells spread to the same cell, the chance is added and the cell's direction is calculated as the weighted component-wise mean of the directions each cell would give it, scaled by the chance that comes from each of the cells.
Using this model, we can both estimate how busy the unseen areas of the store are and as a bonus it can also be used to try to predict what the customer distribution will be after a number of time steps. The one key difference between these to uses is that for estimating the current distribution we can let cells we know to be visible function as walls, as we know exactly if a customer moved towards it or if it is empty. When we attempt to make a prediction we cannot use this. To make a navigation algorithm that uses this knowledge, we can modify the basic A* algorithm to add a cost to each grid cell dependent on the probability of it being occupied when the robot reaches it. We will use 1 plus some constant times the cell's probability after running a model step for each preceding cell in the path. The optimal value of this constant very much depends on the situation and as such stays a parameter. Since the minimal cost per grid cell is one and we only let the robot move to cells that are directly adjacent, the Manhattan distance makes for a good heuristic.
Simulation
Since getting enough actual data of the movement of customers in supermarkets is somewhere between difficult and impossible, customer walking behaviour will be simulated instead. Customers enter the simulation through one of the entrance gates with geometrically distributed inter-arrival times. This makes it a Bernoulli process, which is often used to describe similar situations. They will then proceed to pick up a (Poisson distributed) random amount of products. Finally, they will exit at one of the checkout areas. Requirement 3 states that customers should be able to ignore the robot and always assume right of way, so in the simulation they will completely ignore the robot. Any collision that occurs because of that will be blamed on the robot breaking said requirement.
Based on the ceiling cameras and the robot's own position and orientation, certain areas will be declared visible. Only while a customer is in such a visible area will its position and walking direction will be reported to the model; outside these areas it will only know the position of the objects on the given map, such as walls and shelves.
Optimising Parameters
Now that the simulation gives us a concrete situation, we can figure out the accompanying optimal value for the parameter that determines how heavily the probability of a cell being occupied is taken into account. For this, we will run a couple of tests with many different parameter values and compare the results. Each test will consist of the robot having to move to 50 different positions, while reporting the amount of times it landed in an occupied cell and the amount of time steps the total procedure took.
First, a test with the constant ranging from 0 to 200 is done. Here, it appears that low values for the collisions and time are more often taken in the interval from 0 to 50. Using this, we run four tests on all constants between 0 and 50. From these we conclude that values between 18 and 30 give the best outcomes. Finally, we run ten tests on all constants between 18 and 30. The conclusion we draw from this is that 28 is the best value for the weight parameter in this situation.
The test results are given here.
Results
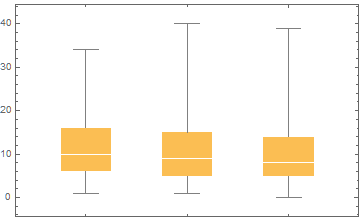
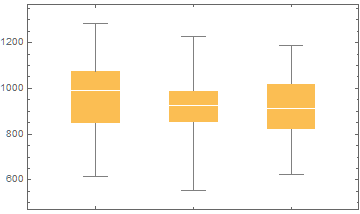
To get an idea of the effectiveness of the ideas presented before this, we will want to compare the performance of the robot using only its own camera, using all available cameras, and the robot using the complete model. To compare these well, we need to choose a metric to compare them by. For this, we can bring back the user requirements once again. 1 (safety) and 4 (time) can easily be quantified, so these will be compared directly. Since no cameras are added, the cost (5) is the same (although the computations to be done get slightly heavier). The privacy of customers (6) is respected equally by all three methods, as all that is done is extracting the position and velocity of people from already existing camera images.
After running the same 100 tests of the robot moving to 50 positions on the three methods, these are the results:
| Method | Mean Collisions | Median Collisions | Mean Time | Median Time |
|---|---|---|---|---|
| Robot's camera only | 11.7 | 10 | 967 | 991 |
| Without model | 10.9 | 9 | 922 | 924 |
| With model | 10.6 | 8 | 915 | 912 |
From this can be concluded that both using the security cameras and using the model help fulfil the requirements.
A ZIP file with the results of all tests can be found here
Conclusion
As seen in the results, the security cameras at supermarkets can definitely help robots navigate when it is crowded. Furthermore, combining this with a with a model based on cellular automata can make this even more effective.
The used simulation can be found here and was compiled from these source files.
Discussion
Something that might still be interesting to look into is the optimal placement of security cameras. It can be expected that having many small or simple blind spots will make it easier to predict where customers are, as we know exactly which blind spot they entered. It would thereby make sense that the model-based navigation will be even better if the security cameras were placed to cover entire intersections.
Using a fine grid for the model[2] and/or switching to a finer or continuous time scale will allow the model to be more realistic by e.g. allowing for different walking speeds and making it possible to make a better judgement of the comfort of customers.
Planning
| Week | Milestones | |
|---|---|---|
| 5 |
|
|
| 6 | ||
| 7 |
|
|
| 8 |
|
References
- ↑ http://pedestrian.msstate.edu/docs/IERC%202008%20Lee.pdf
- ↑ https://arxiv.org/ftp/arxiv/papers/1406/1406.3567.pdf
- ↑ http://pedestrian.msstate.edu/docs/IERC%202007.pdf
- ↑ https://pdfs.semanticscholar.org/8e62/a5275c198eb8f6f15d1e2777f64c066d8997.pdf
- ↑ https://arxiv.org/ftp/arxiv/papers/1406/1406.3567.pdf
- ↑ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3873946/