Movements: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
The first important movement is turning around its axle, with both of the tracks turning in opposite directions. This is the fastest way to turn, but not allways possible due to the edges of the window.<br> | The first important movement is turning around its axle, with both of the tracks turning in opposite directions. This is the fastest way to turn, but not allways possible due to the edges of the window.<br> | ||
[[File:Axle_turn.gif]]<br> | [[File:Axle_turn.gif]]<br> | ||
There are two main values that determine the time it takes to rotate a certain angle. The first is of course the speed of the tracks <math>v</math>, the second is the distance between the tracks and the center of the robot <math>r</math>. The rotation speed is simply <math>v/r</math>, and the time it takes to rotate a certain amount is that angle <math>\alpha</math> divided by the rotation speed, <math>t=\alpha*r/v</math>. | There are two main values that determine the time it takes to rotate a certain angle. The first is of course the speed of the tracks <math>v</math>, the second is the distance between the tracks and the center of the robot <math>r</math>. The rotation speed is simply <math>v/r</math>, and the time it takes to rotate a certain amount is that angle <math>\alpha</math> divided by the rotation speed, <math>t=\alpha*r/v</math>. | ||
When taking acceleration into account, it is easiest to look at the distance the tracks actually travel, which is the rotation angle times the distance from the tracks to the center of the robot, <math>x = α * r</math>. When assuming constant acceleration <math>a</math>, the travelled distance is given by the following equation: <math>x=1/2*a*t^2</math>. The time it takes the robot to reach <math>Vmax</math> is <math>Vmax/a</math>. In that time, the robot travels <math>1/2*Vmax^2/a</math>. Because the robot also needs to decelerate, the total distance spent decelerating is <math>Vmax^2/a</math>. For distances less than <math>Vmax^2/a</math>, the travel time is <math>2*sqrt(x/av)</math>. For distances larger than <math>Vmax^2/a</math>, the travel time is <math>2*sqrt(x/av)+(x-(Vmax^2)/a)/Vmax.</math> | |||
== edge turn == | == edge turn == | ||
| Line 15: | Line 16: | ||
<br> | <br> | ||
[[File:Edge_turn.png]]<br> | [[File:Edge_turn.png]]<br> | ||
The results are as follows: | |||
For a square robot with a size of 25 centimeters placed half a centimeter from the edge of a window with a speed <math>v</math>, it takes <math>0.33 * v</math> seconds to get far enough away from the edge to be able to make a full stationary turn. In that time, the robot rotates 45 degrees, moves 0.256 meters to the right and 0.047 meters down. | |||
When taking a constant acceleration into account, the distance travelled is equal to 0.33 m and the corresponding travel time can be calculated using the formula above. | |||
Latest revision as of 13:30, 20 March 2018
stationary turn
The first important movement is turning around its axle, with both of the tracks turning in opposite directions. This is the fastest way to turn, but not allways possible due to the edges of the window.

There are two main values that determine the time it takes to rotate a certain angle. The first is of course the speed of the tracks [math]\displaystyle{ v }[/math], the second is the distance between the tracks and the center of the robot [math]\displaystyle{ r }[/math]. The rotation speed is simply [math]\displaystyle{ v/r }[/math], and the time it takes to rotate a certain amount is that angle [math]\displaystyle{ \alpha }[/math] divided by the rotation speed, [math]\displaystyle{ t=\alpha*r/v }[/math].
When taking acceleration into account, it is easiest to look at the distance the tracks actually travel, which is the rotation angle times the distance from the tracks to the center of the robot, [math]\displaystyle{ x = α * r }[/math]. When assuming constant acceleration [math]\displaystyle{ a }[/math], the travelled distance is given by the following equation: [math]\displaystyle{ x=1/2*a*t^2 }[/math]. The time it takes the robot to reach [math]\displaystyle{ Vmax }[/math] is [math]\displaystyle{ Vmax/a }[/math]. In that time, the robot travels [math]\displaystyle{ 1/2*Vmax^2/a }[/math]. Because the robot also needs to decelerate, the total distance spent decelerating is [math]\displaystyle{ Vmax^2/a }[/math]. For distances less than [math]\displaystyle{ Vmax^2/a }[/math], the travel time is [math]\displaystyle{ 2*sqrt(x/av) }[/math]. For distances larger than [math]\displaystyle{ Vmax^2/a }[/math], the travel time is [math]\displaystyle{ 2*sqrt(x/av)+(x-(Vmax^2)/a)/Vmax. }[/math]
edge turn
The second movement is the edge turn, it is the movement the robot needs to make in order to get away from an edge it is parallel to. It should be noted that there will allways be some room between the side of the robot and the edge of the window because alse the robot is unable to turn.

During the movement one of the corners of the robot will almost touch the edge of the window. The further the robot moves away from the edge, the more it can turn and the faster it can get away from the edge.
This movement has been simulated in matlab, using the code below:
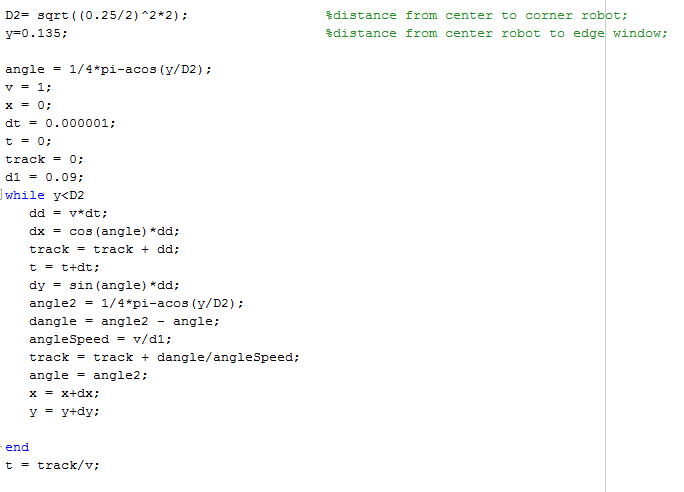
The results are as follows:
For a square robot with a size of 25 centimeters placed half a centimeter from the edge of a window with a speed [math]\displaystyle{ v }[/math], it takes [math]\displaystyle{ 0.33 * v }[/math] seconds to get far enough away from the edge to be able to make a full stationary turn. In that time, the robot rotates 45 degrees, moves 0.256 meters to the right and 0.047 meters down.
When taking a constant acceleration into account, the distance travelled is equal to 0.33 m and the corresponding travel time can be calculated using the formula above.