Ultra Wide Band System - Trilateration: Difference between revisions
No edit summary |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
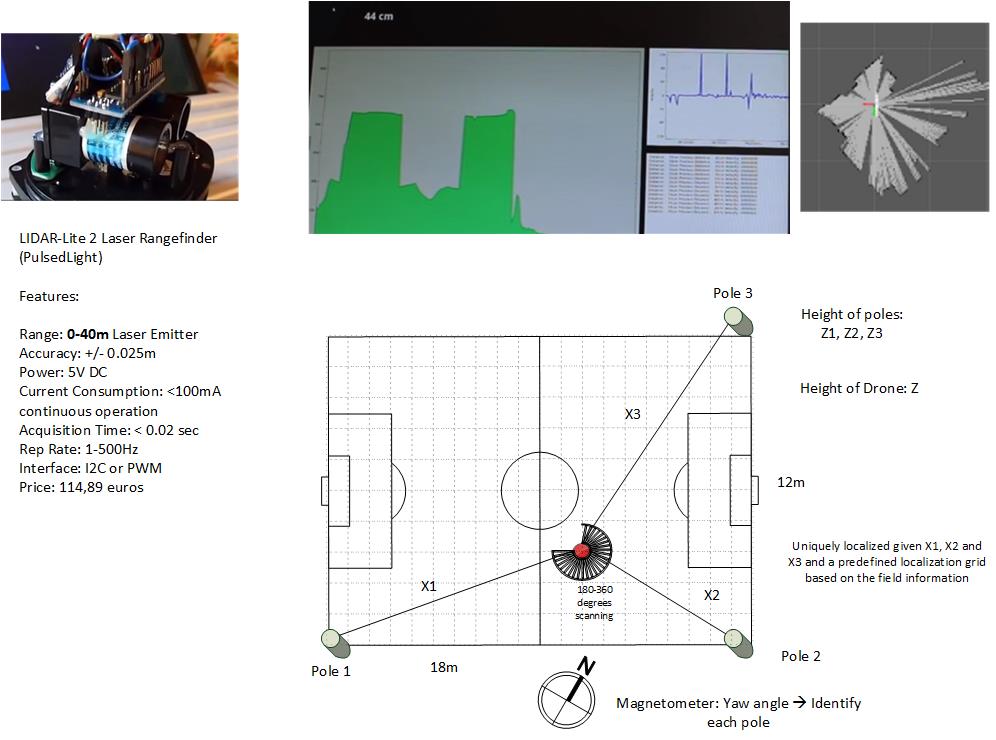
A laser range extender can be used to determine the distance between the laser itself and an object reflecting the beam. A company was found that produces, small lightweight laser range extenders that can rotate. By placing three poles at known positions around the field, and measuring the distance to those poles, the drone can be positioned using trilateration. Trilateration is a type of positioning algorithm, an easy way of understanding is that if a circle with the distance between each pole and the drone were to be drawn around every pole, only one intersection point would remain. If the height is also known, the drone state is thus known. Unfortunately, the sensor was out of stock for the duration of the project, and no alternative was found at it is an emerging technology. As such this concept was abandoned. | A laser range extender can be used to determine the distance between the laser itself and an object reflecting the beam. A company was found that produces, small lightweight laser range extenders that can rotate. By placing three poles at known positions around the field, and measuring the distance to those poles, the drone can be positioned using trilateration. Trilateration is a type of positioning algorithm, an easy way of understanding is that if a circle with the distance between each pole and the drone were to be drawn around every pole, only one intersection point would remain. If the height is also known, the drone state is thus known. Unfortunately, the sensor was out of stock for the duration of the project, and no alternative was found at it is an emerging technology. As such this concept was abandoned. | ||
[[File:LaserSolution.jpg|600px|thumb|middle|Overview Laser Range Extender Concept]] | [[File:LaserSolution.jpg|600px|thumb|middle|Figure 1: Overview Laser Range Extender Concept]] | ||
=== Trilateration using Ultra-Wideband Beacons === | === Trilateration using Ultra-Wideband Beacons === | ||
| Line 28: | Line 28: | ||
The different concepts were compared based on a number of categories as shown below. Each specification was given a certain weight and concepts received points based on their score. By summing up all category scores, a final score is obtained. Based on this score, as well as a prediction of the usability and ease of implementation and development for the different solutions, the Ultra-Wideband System was chosen. The table with categories is shown below. | The different concepts were compared based on a number of categories as shown below. Each specification was given a certain weight and concepts received points based on their score. By summing up all category scores, a final score is obtained. Based on this score, as well as a prediction of the usability and ease of implementation and development for the different solutions, the Ultra-Wideband System was chosen. The table with categories is shown below. | ||
[[File:PositioningConceptComparison. | [[File:PositioningConceptComparison.JPG|600px|thumb|center|Table 1: Concept Comparison]] | ||
== Implementation == | |||
=== Introduction === | |||
From DecaWave, the TREK1000 evaluation kit was acquired. This kit and its content are described in detail on the [http://www.decawave.com/products/trek1000 company page]. This kit contains four beacons, of which three are intended to be used as anchors and the fourth as a tag. If required, additional beacons are available to extend the system to four anchors and up to eight tags. Most importantly, the beacons have already been programmed. The most essential part is the DWM1000 chip, which facilitates the UWB communication. In this evaluation kit, this chip has been incorporated into a PCB, which means that the time intensive process of creating our own beacons and programming them to communicate and give the distances between anchors and between the anchors and the tag can be skipped. This also means that the system is bound to limitations of the programming, which means there is a maximum of four anchors. However, the ARM processors on the PCBs are reprogrammable with the right tool and the source code is available from DecaWave on request. In the future, a system can be made especially for the drone. In this project, the existing programming was used. | |||
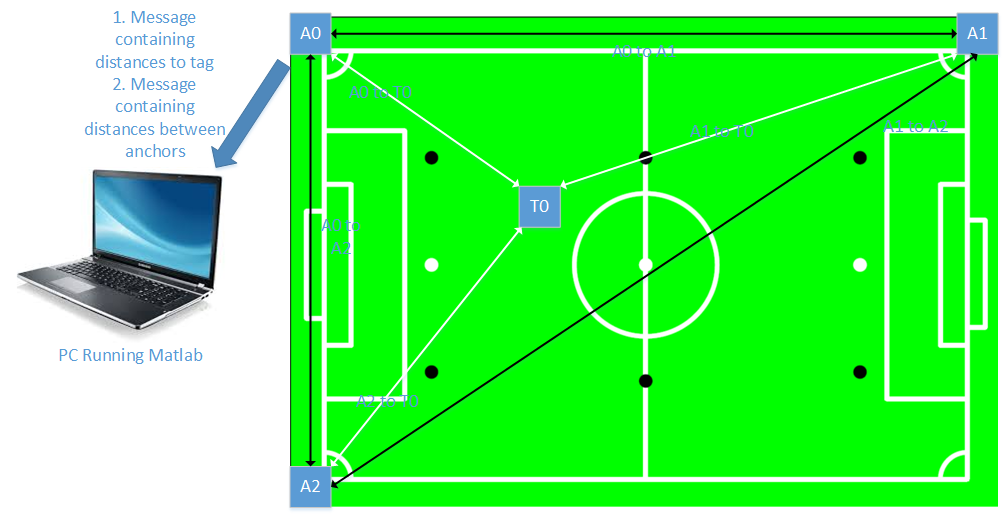
The implemented system has three anchors, A0, A1 and A2 and one tag, T1. If all are powered, the distances between the anchors of the tag are measured and known to each anchor. By connecting an anchor to a computer and using either the DecaWave application or reading out the serial connection, the measurement can be obtained. Furthermore, A0 also gives a measurement report containing the distance between the anchors. Using this measurement report, a coordinate system for the anchors can be set up. If the anchors are placed in a predetermined coordinate system, the positions can be confirmed. Figure 2 shows the different names and definitions as well as the working principle of the system. All distances are measured and compiled in two messages, one containing distances to the tag and the other containing distances between anchors. By connecting anchor A0 to a computer and establishing a serial connection in Matlab, the messages can be received. | |||
[[File:UWB Drawing.png|800px|thumb|center|Figure 2: Definitions and names in the UWB system]] | |||
=== Coordinate Systems === | |||
The UWB system should provide a way to position the drone in the field within 0.5 meters, but it should also be easy to set up and easy to use. In order to apply trilateration, the positions of the anchors must be known. This can be done by manual measurements, but this is time consuming and not very flexible. Instead the message containing the distances between the anchors is used in the following algorithm. | |||
# Anchor A0 forms the origin in point (0,0) | |||
# Anchor A1 is placed on the X-axis in point (A0 to A1,0), A0 to A1 is the distance as defined in Figure 2 | |||
# The Y-axis is perpendicular to the X-axis and is set to positive on the side where A2 is placed | |||
# Using the distances A0 to A2 and A1 to A2, A2 is positioned in this coordinate system | |||
Any placement of the anchors will in this way lead to a coordinate system without manual measurements. This coordinate system is henceforth referred to as ACS (Anchor Coordinate System). The tag can then be positioned in ACS. However, the real question is how ACS relates to the global coordinate system. For this purpose, the GCS (Global Coordinate System) is defined in Figure 3. | |||
[[File:GlobalCoordinateSystem.png|200px|thumb|right|Figure 3: Coordinate System GCS]] | |||
If the anchor positions are known in GCS, the drone is also directly positioned in GCS. In order to transform the anchor positions from ACS to GCS, distance between the origins of ACS and GCS as well as the rotation between ACS and GCS are required. Furthermore, due to the way it is set up, it is not known whether ACS is a right or left-handed system while GCS is right-handed. In order to transform between the systems, they must both be of the same orientation. | |||
The solution is to use the tag to measure the four corners of the field in ACS as a calibration step. This calibration takes only a few minutes, in order to improve accuracy, multiple measurements can be taken of each corner. With these coordinates, the transformation can be computed. | |||
# By taking the average of the corners, the center of the field and the origin of GCS is found. | |||
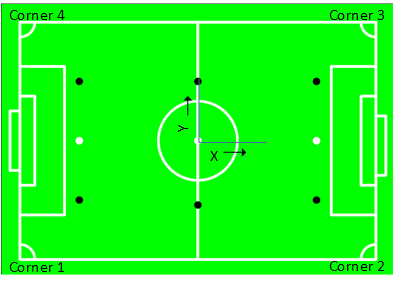
# By taking the cross product of the vectors formed by Corner 1-Corner 2 and Corner 1-Corner 4, the orientation of ACS is found. If necessary, by flipping the Y-axis is it can be made right-handed. The corner numbers are shown in Figure 3. | |||
# By computing the angle between the vectors Corner 1-Corner 2 and 1-0, the rotation matrix to rotate points in ACS to GCS can be found. | |||
Subsequently, the anchor points and measured corners can be transformed to GCS by subtracting the origin of ACS, multiplying y-values by -1 if required, and applying the rotation matrix. The added value of this approach is that by knowing the corner positions, information such as the field size is measured. In the future, this can be extended to measure other important field marks such as the goal posts. For a detailed implementation of the described functionality the reader is referred to the repository. | |||
=== Trilateration === | |||
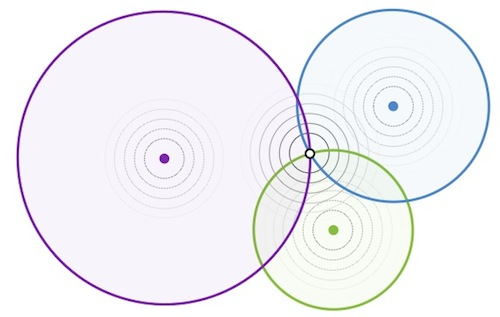
Now that the anchor positions are known in GCS, and the sensors are giving the distances between the anchors and the tag, all required inputs for the trilateration algorithm are known. The principle behind trilateration is shown in 2D in Figure 4. | |||
[[File:PrincipleOfTrilateration.png|300px|thumb|right|Figure 4: Principle of Trilateration]] | |||
In the Figure the 2D case is shown, but the drone moves in 3D. This means that instead of one point, there are two remaining candidates and a fourth measurement is needed to eliminate the second point. However, if the anchors are placed in the same plane, having the same value for Z in XYZ, the two points will have the same XY. Furthermore, if it is known whether the tag will always be below or above the anchors, this already narrows down the options to one. As such, a fourth anchor is not required, especially since the drone already measures its own height. | |||
While in the perfect case the measurement always intersect in one point, due to errors and inaccuracy this is not always the case. A good trilateration algorithm must be able to deal with this. In the case of more than four anchors, the problem is named the multilateration problem. More than four anchors leads to redundant measurements, but are a good tool to improve accuracy and reduce the effects of errors. | |||
The implemented algorithm was found already implemented in Matlab. The algorithm is explained in the paper [https://www.researchgate.net/publication/275027725_An_Algebraic_Solution_to_the_Multilateration_Problem ‘An Algebraic Solution to the Multilateration Problem’] by A. Norrdine. The Matlab implementation was found on [https://www.researchgate.net/publication/288825016_Trilateration_Matlab_Code this Research Gate page]. It uses an algebraic approach and is computationally very cheap. If there is no single intersection point or no intersection at all, the algorithm approximates can yield complex numbers, in order to deal with this only the real part is considered. If the number of anchors is expanded in the future, this algorithm also has an already implemented least-squares approach to the multilateration problem. | |||
=== Operation and Specifications === | |||
While it is difficult to accurately assess the systems precision, some measurements could be performed. Especially while stationary, the anchor system is accurate and meats the 20 centimeters advertised and gives measurements at a rate of 3-4 Hz. However, while moving the precision drops because of the Doppler Effect. Additionally, while moving it becomes clear that there is a delay on the measurement, most likely because of the way it is set up. The anchors gather all measurements of a certain timestamp in one message before sending it. The delay appears to be in the order of a few hundred milliseconds. If this turns out to be a problem for control, a Kalman predictor filter can be used to reduce the delay and create a higher sample rate. These problems probably arise because this is an evaluation kit, not intended for high performance. The beacons could be reprogrammed for higher speeds, or when the technology develops further a new set designed for this type of control can be acquired. | |||
Latest revision as of 15:34, 31 March 2016
One of the most important building blocks for the drone referee is a method for positioning. At all times, the drone state, namely the set {X,Y,Z,Yaw}, should be known in order to perform the refereeing duties. Of the drone state, Z and the Yaw are measured by either the drone sensor suite or other programs as they are required for the low-level control of the drone. However, in order to localize w.r.t. the field and to find X and Y, a solution has to be found. To this end, several concepts were composed. Of those concepts, trilateration using Ultra Wide Band Anchors (UWB) was realized. First, the rejected concepts are shortly listed, followed by a detailed explanation of the UWB system.
Concepts
The positioning system must provide an accurate enough signal at a high enough sample rate for position control. As ball out of pitch detection is to be detected using image processing, an accuracy of 0.5 meters was chosen as minimum accuracy for the positioning system. This means that a circle with a radius of half a meter designate the position of the drone. For the sample rate a minimum of 10 measurements per second was chosen. However, as most of the technologies listed here are very new or still in development, this information could not be obtained for all of them. The following concepts will be discussed:
- Trilateration using a Laser Range Extender
- Trilateration using ultra-wideband beacons
- Positioning using Bluetooth beacons
- Positioning using image processing
Trilateration using a Laser Range Extender
A laser range extender can be used to determine the distance between the laser itself and an object reflecting the beam. A company was found that produces, small lightweight laser range extenders that can rotate. By placing three poles at known positions around the field, and measuring the distance to those poles, the drone can be positioned using trilateration. Trilateration is a type of positioning algorithm, an easy way of understanding is that if a circle with the distance between each pole and the drone were to be drawn around every pole, only one intersection point would remain. If the height is also known, the drone state is thus known. Unfortunately, the sensor was out of stock for the duration of the project, and no alternative was found at it is an emerging technology. As such this concept was abandoned.
Trilateration using Ultra-Wideband Beacons
Similar to the previous concept are Ultra-Wideband Beacons. These are small sensors communicating with one another over the ultra-wide band radio spectrum. Given the time between sending and receiving, the distance can be estimated with a promised accuracy of around 10 centimeters. By placing at least three beacons at known positions and placing one beacon on the drone, trilateration can again be applied to find the drone position w.r.t. to the stationary beacons. The beacons around the field are referred to as anchors and the beacon on the drone is referred to as the tag. Multiple tags can be in the system as well as more than three anchors providing more accuracy through redundancy, making it a very extendable concept. This method is very new, and only a few manufacturers are available. Ready-to-use systems are still rare. There is a company, DecaWave, offering evaluation kits that are instantly usable without additional development, but these are expensive and maybe too fragile for use on a drone.
Positioning using Bluetooth Beacons
This concept is based on creating a grid of uniquely identifiable Bluetooth beacons around the edges of the field. By evaluating the signal strength of the different Bluetooth beacons and their ID numbers, a normally distributed position estimate can be obtained. There are some start-ups that are developing this approach, but not much is known about range and accuracy. However, individual beacons are quite cheap at around 10 euros. Worst case scenario it would be a good method to support or supplement another concept using sensor fusion.
Positioning using Image Processing
A more traditional method also applied by the soccer robots of TechUnited is to use visual methods and position the drone based on recognized field points and line segments. The algorithm used by TechUnited draws a number of line from the middle of the frame to the edges of the field of vision. Along these lines, field line points are detected based on the transition from dark to light to dark. This generates a point cloud that can be matched on the known layout of the field. If this algorithm can be used, it will have no additional material costs and it can be based on the existing code from TechUnited. In order to apply such a method on the drone, it should be adjusted to have a variable height. However, perturbations in the roll and pitch of the drone as well as the narrower field of vision might make this algorithm difficult to apply. Finally, it is questionable how scalable this solution is with growing field sizes, as lines become sparser.
Concept Choice
The different concepts were compared based on a number of categories as shown below. Each specification was given a certain weight and concepts received points based on their score. By summing up all category scores, a final score is obtained. Based on this score, as well as a prediction of the usability and ease of implementation and development for the different solutions, the Ultra-Wideband System was chosen. The table with categories is shown below.

Implementation
Introduction
From DecaWave, the TREK1000 evaluation kit was acquired. This kit and its content are described in detail on the company page. This kit contains four beacons, of which three are intended to be used as anchors and the fourth as a tag. If required, additional beacons are available to extend the system to four anchors and up to eight tags. Most importantly, the beacons have already been programmed. The most essential part is the DWM1000 chip, which facilitates the UWB communication. In this evaluation kit, this chip has been incorporated into a PCB, which means that the time intensive process of creating our own beacons and programming them to communicate and give the distances between anchors and between the anchors and the tag can be skipped. This also means that the system is bound to limitations of the programming, which means there is a maximum of four anchors. However, the ARM processors on the PCBs are reprogrammable with the right tool and the source code is available from DecaWave on request. In the future, a system can be made especially for the drone. In this project, the existing programming was used. The implemented system has three anchors, A0, A1 and A2 and one tag, T1. If all are powered, the distances between the anchors of the tag are measured and known to each anchor. By connecting an anchor to a computer and using either the DecaWave application or reading out the serial connection, the measurement can be obtained. Furthermore, A0 also gives a measurement report containing the distance between the anchors. Using this measurement report, a coordinate system for the anchors can be set up. If the anchors are placed in a predetermined coordinate system, the positions can be confirmed. Figure 2 shows the different names and definitions as well as the working principle of the system. All distances are measured and compiled in two messages, one containing distances to the tag and the other containing distances between anchors. By connecting anchor A0 to a computer and establishing a serial connection in Matlab, the messages can be received.
Coordinate Systems
The UWB system should provide a way to position the drone in the field within 0.5 meters, but it should also be easy to set up and easy to use. In order to apply trilateration, the positions of the anchors must be known. This can be done by manual measurements, but this is time consuming and not very flexible. Instead the message containing the distances between the anchors is used in the following algorithm.
- Anchor A0 forms the origin in point (0,0)
- Anchor A1 is placed on the X-axis in point (A0 to A1,0), A0 to A1 is the distance as defined in Figure 2
- The Y-axis is perpendicular to the X-axis and is set to positive on the side where A2 is placed
- Using the distances A0 to A2 and A1 to A2, A2 is positioned in this coordinate system
Any placement of the anchors will in this way lead to a coordinate system without manual measurements. This coordinate system is henceforth referred to as ACS (Anchor Coordinate System). The tag can then be positioned in ACS. However, the real question is how ACS relates to the global coordinate system. For this purpose, the GCS (Global Coordinate System) is defined in Figure 3.
If the anchor positions are known in GCS, the drone is also directly positioned in GCS. In order to transform the anchor positions from ACS to GCS, distance between the origins of ACS and GCS as well as the rotation between ACS and GCS are required. Furthermore, due to the way it is set up, it is not known whether ACS is a right or left-handed system while GCS is right-handed. In order to transform between the systems, they must both be of the same orientation. The solution is to use the tag to measure the four corners of the field in ACS as a calibration step. This calibration takes only a few minutes, in order to improve accuracy, multiple measurements can be taken of each corner. With these coordinates, the transformation can be computed.
- By taking the average of the corners, the center of the field and the origin of GCS is found.
- By taking the cross product of the vectors formed by Corner 1-Corner 2 and Corner 1-Corner 4, the orientation of ACS is found. If necessary, by flipping the Y-axis is it can be made right-handed. The corner numbers are shown in Figure 3.
- By computing the angle between the vectors Corner 1-Corner 2 and 1-0, the rotation matrix to rotate points in ACS to GCS can be found.
Subsequently, the anchor points and measured corners can be transformed to GCS by subtracting the origin of ACS, multiplying y-values by -1 if required, and applying the rotation matrix. The added value of this approach is that by knowing the corner positions, information such as the field size is measured. In the future, this can be extended to measure other important field marks such as the goal posts. For a detailed implementation of the described functionality the reader is referred to the repository.
Trilateration
Now that the anchor positions are known in GCS, and the sensors are giving the distances between the anchors and the tag, all required inputs for the trilateration algorithm are known. The principle behind trilateration is shown in 2D in Figure 4.
In the Figure the 2D case is shown, but the drone moves in 3D. This means that instead of one point, there are two remaining candidates and a fourth measurement is needed to eliminate the second point. However, if the anchors are placed in the same plane, having the same value for Z in XYZ, the two points will have the same XY. Furthermore, if it is known whether the tag will always be below or above the anchors, this already narrows down the options to one. As such, a fourth anchor is not required, especially since the drone already measures its own height. While in the perfect case the measurement always intersect in one point, due to errors and inaccuracy this is not always the case. A good trilateration algorithm must be able to deal with this. In the case of more than four anchors, the problem is named the multilateration problem. More than four anchors leads to redundant measurements, but are a good tool to improve accuracy and reduce the effects of errors.
The implemented algorithm was found already implemented in Matlab. The algorithm is explained in the paper ‘An Algebraic Solution to the Multilateration Problem’ by A. Norrdine. The Matlab implementation was found on this Research Gate page. It uses an algebraic approach and is computationally very cheap. If there is no single intersection point or no intersection at all, the algorithm approximates can yield complex numbers, in order to deal with this only the real part is considered. If the number of anchors is expanded in the future, this algorithm also has an already implemented least-squares approach to the multilateration problem.
Operation and Specifications
While it is difficult to accurately assess the systems precision, some measurements could be performed. Especially while stationary, the anchor system is accurate and meats the 20 centimeters advertised and gives measurements at a rate of 3-4 Hz. However, while moving the precision drops because of the Doppler Effect. Additionally, while moving it becomes clear that there is a delay on the measurement, most likely because of the way it is set up. The anchors gather all measurements of a certain timestamp in one message before sending it. The delay appears to be in the order of a few hundred milliseconds. If this turns out to be a problem for control, a Kalman predictor filter can be used to reduce the delay and create a higher sample rate. These problems probably arise because this is an evaluation kit, not intended for high performance. The beacons could be reprogrammed for higher speeds, or when the technology develops further a new set designed for this type of control can be acquired.