Embedded Motion Control 2015 Group 4: Difference between revisions
| (5 intermediate revisions by the same user not shown) | |||
| Line 370: | Line 370: | ||
=Final maze challenge= | =Final maze challenge= | ||
The final maze challenge was held at the 17th of July. During this challenge the hard work of 10 groups was put to the test to see which groups were able to finish the maze. Each group was allowed to make two attempts at solving the maze. The maze consisted of relatively standard part containing a loop, with a branch that | The final maze challenge was held at the 17th of July. During this challenge the hard work of 10 groups was put to the test to see which groups were able to finish the maze. Each group was allowed to make two attempts at solving the maze. The maze consisted of a relatively standard part containing a loop, with a branch that led to a door. Behind this door was a short corridor followed by an open space with a wall in the middle. at the other end of the open space the exit was situated. Unfortunately we were unable to finish the world model and the Kalman filter in time before the challenge. Therefore we relied and a backup in the form of a righthand rule with loop detection. | ||
==Strategy== | ==Strategy== | ||
For the final maze challenge we had two versions of the code: | For the final maze challenge we had two versions of the code: | ||
Latest revision as of 22:15, 26 June 2015
Authors: T. Cornelissen, T van Bommel, M. Oligschläger, B. Hendrikx, P. Rooijakkers, T. Albers
Requirements and function specifications
Problem statement
The software design process starts with a statement of the problem. Although all the details of the assignment are not yet known at this point, we can best summarize the statement with the following sentence:
- Design the software in C/C++ for the (existing) Pico/Jazz robot that enables to find the exit of an unknown and dynamically changing maze in minimal time.
Requirements
A (draft) list of the requirements contains the following points:
- Exiting the maze in minimal time.
- Avoiding damage of the robot and the environment.
- Robustness of pathfinding algorithm with respect to maze layout.
- Design software using modular approach.
- Implement algorithm using only available hardware and software API's.
- Manage code development with multiple developers.
Existing hardware interfaces
- The Pico/Jazz robot with customized inner workings and a robot operating system with C++ API's.
- A (still unknown) wheelbase layout of which the possible DoF/turning radius is a design constraint.
- A lasersensor and acoustic sensor of which the range-of-visibility is a design constraint.
Unknown design constraints
- Simulation environment for code testing?
- Location of sensors and wheels relative to robot fixed frame?
- What data can we extract form the sensors?
- What does the maze look like? How do the doors operate?
Main focus point in the first two weeks
- Learn basics of C/C++ and software development.
- Determine the layout of the robot and the possibilities of the sensors and wheel structure.
- Become familiar with the integrated development environment.
- Explore the possibilities of th API's (how much postprocessing of the aquired sensor data is necessary and what techniques must be learned?).
Software design strategy
The figure below shows the overview of a posible software layout. The skill functions can be assigned to different programmers that are also responsible for exploring the API's and gathering details about the hardware. The maze solving strategy can be handled separately and the supervisory controller is the brain of the robot combining all the information. File:Maze example.pdf
Composition pattern
The task of the robot is to solve a maze autonomously. In order to do this a piece of intelligent software has to be developed. The software must be able to give valid instructions to the hardware on the base of stimuli and knowledge. In order to obtain a reliable system behavior it is wise to use a structured system architecture. Our solution for solving a maze can be seen as constructing a subsystem that is connected to other systems. An approach to defining our system is to divide the system in structure, behavior and action in an appropriate way. The structure describes the interaction between behaviors and activities; this is the composition or the system architecture. The behavior is the reaction to stimuli, a possible model for this is the Task-Skill-Motion model. The activity is responsible for how the behavior is realized (the execution of code).
In the scheme below the Task-Skill-Motion model of our solution is shown, this model has functioned as a base for our design.

- The User Interface Context provides the communication with the user, this is a bilateral exchange of instructions/information between user and software/robot.
- The Task Context functions in our case acts as a kind of supervisor. It feeds and monitors the separate skills.
- In our Skill context a distinction is made between skills that are dedicated to: solving the maze, motion skills and service skills.
- The Maze solving skills produce optimal decisions for solving the maze, it also translates and maintains the data in the semantic world model.
- The motion skills produce instructions for the hardware, it moves the robot in corridors and corners and open spaces.
- The so called service skills deliver a service to the other skills. For example the laser vision skills are responsible for detecting junctions, calculating alignment errors and producing a current state local mini map of the world. For global localization and mapping of the global world a SLAM implementation is used.
- The environmental context contains a model of the world. This model can be provided by the user or build, expand and maintained by the skills. The semantic model for solving the maze contains nodes with additional information at junctions in the form of a graph. On the other hand we have a 2d model of the world in the form of a list of lines and corners used for the global localization (this is for localization also very semantic).
- The Robot Abstraction performs the communication between our software and the hardware. This shell is in our case provided, however we added a very thin layer on top (between our software and the Robot Hardware Abstraction). This layer passes the parameters that have to do with the difference between the dynamics in the real robot and the kinematic model in the simulation (this is mainly about motion control gains).
Implementation of software
Our software design is based on a principle that is also used in a programmable logic controller (plc). The software does not run on an industrial plc but on the embedded Linux pc in the robot. Our program consists of a main loop that is executed with a frequency of 10Hz. Within the loop the following process sequence is followed as much as possible:
- Communicate
- Coordinate
- Configure
- Schedule-acts
- Act
- Communicate
- Schedule-prepares
- Tasks’ prepare
- Coordinate
- Communicate
- Log
such that the whole process can be executed in a serial fashion.
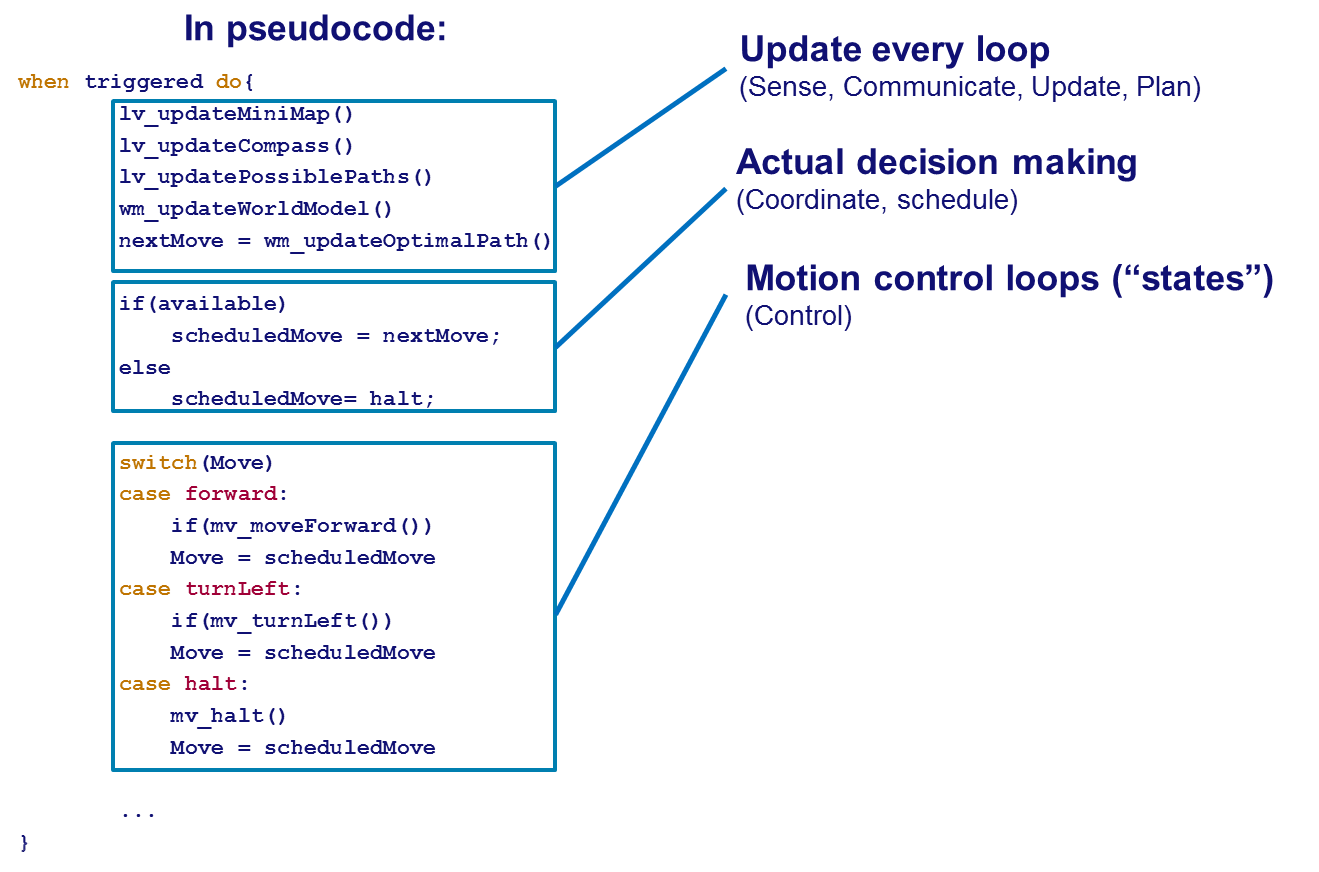
In the figure above some pseudo code of our approach is shown. The advantages of this setup are:
- No multithreading overhead
- Maintainability
- Predictable behavior
On the other hand the disadvantages are:
- No prioritizing
- Calculations made every loop
- No configurability
Actual code
The code snippet below contains the code of the supervisor/coordinator loop used in the actual maze challenge.
Code snippet: https://gist.github.com/anonymous/5bdc865a5d10a7a7c312
Motion Skills
The motion skills are contained in the motionwrapper.cpp file and handle all basic motion tasks as well as the door handling task. The motion skills get initiated by the supervisor and are mutually exclusive. If a skill is initiated it communicates to the supervisor when it is done (for example a door has opened or a turn is finished). Another scenario is that the skill is aborted because for example laservision has thrown an event.
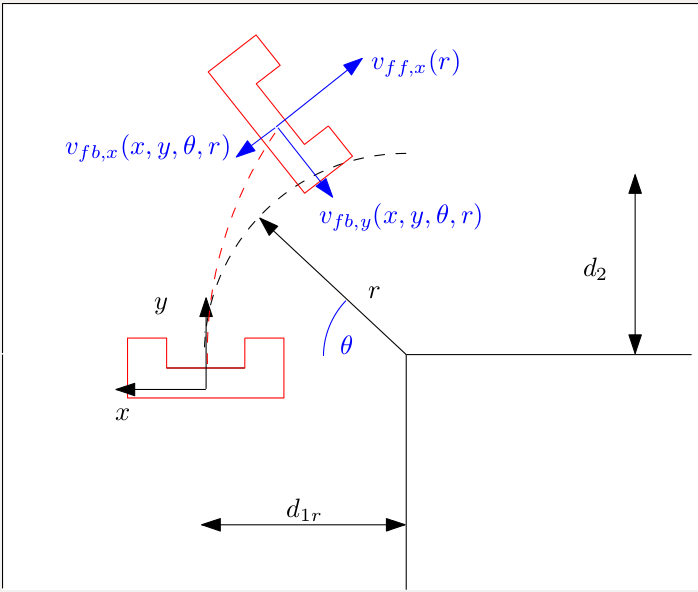
The motion skills use basic feedback loops in which the alignment and position error obtained through the laservision code is used for correcting the robot trajectory. One particular skill of interest is taking a turn. If the laservision code detects a turn, the coordinator reacts on this event and initiates a turn based on the policy of the pathsolver. The steps taken just before and during a turn are:
- Acquire the junction measurements [math]\displaystyle{ {d1,d2,d3,dx,dy} }[/math].
- Calculate the turn radius.
- Append an ad-hoc coordinate frame at the beginning of the turn.
- Calculate x- and y-positions as a function of rotation in the fixed frame.
- Calculate error based on odometry in fixed frame.
- Use a feedforward law based on path length and a feedback law for both x- and y-error in robot-fixed frame, calculated with a coordinate transformation matrix. The robot is forced to it's "ideal" (x,y) coordinates corresponding to rotation and turn-radius.
The code snippet below contains the code of motion skills used in the actual maze challenge.
Code snippet: https://gist.github.com/anonymous/577e6d9f20390c74963a
Motion skills in action
- Video 1: righthand rule with doors:
 |
- Video 2: testing
 |
Laser vision
Compass function
This function measures the angular misalignment of the robot with it's environment. The compass function gives a valid estimate of the angular misalignment under the following assumptions.
Assumptions:
- The world consists of mainly straight lines.
- All the lines cross each-other approximately with an angle which is a multiple of the world angle (when for example all the angles are perpendicular then the world angle is 90 degrees)
- The current misalignment of the robot with it's environment is small: [math]\displaystyle{ \theta_{robot}\lt \lt 0.5\cdot\theta_{world\,angle} }[/math]. This implies that the compass function is unreliable during large rotations.
- There are enough sample points (preferably in front of the robot) to ensure that lines can be detected in the so called trust area.
- The trust area is defined as a bounded square around the robot which is aligned with the robot frame. Only the samples in this square are used for the compass function calculations. As is shown in the figure below.
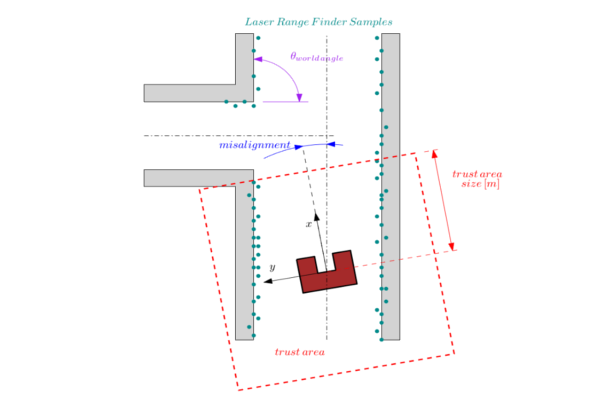
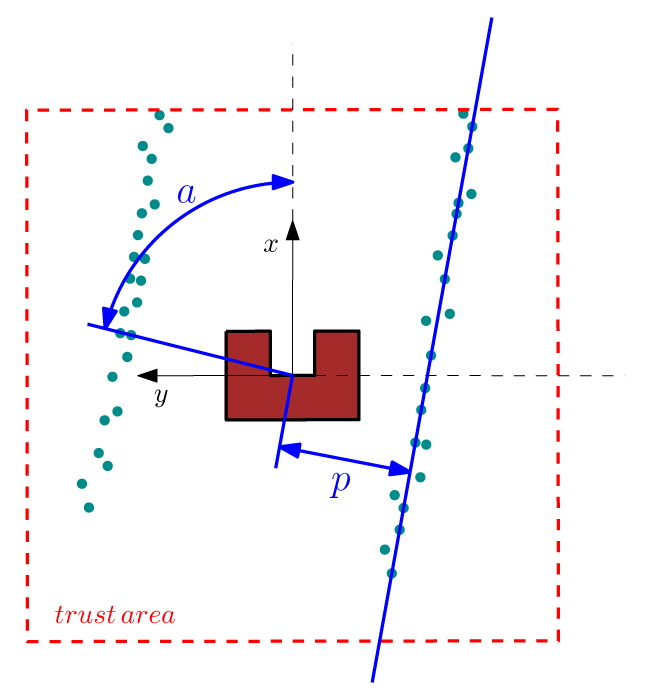
Approach:
We are searching for a reference line from which we can calculate the angular misalignment of the robot. This calculation proceeds in the following sequence: First the laser data is expressed in a orthogonal frame (fixed to the robot). A line through point [math]\displaystyle{ [x_i,y_i] }[/math] can be described in polar coordinates as [math]\displaystyle{ p(\alpha)=x_i \cos(\alpha)+y_i \sin(\alpha) }[/math] where [math]\displaystyle{ p }[/math] and [math]\displaystyle{ \alpha }[/math] are unknown parameters. We want to find a [math]\displaystyle{ \alpha\in[0,\pi] }[/math] and a [math]\displaystyle{ p\in [-p_{max},p_{max}] }[/math] where [math]\displaystyle{ p_{max}=\sqrt{(2\cdot trust\,area\,size)^2} }[/math] is half the trust area diagonal. The Hough transform [1] gives a procedure to find [math]\displaystyle{ p }[/math] and [math]\displaystyle{ \alpha }[/math]. The procedure is as follows: for each [math]\displaystyle{ [x_i,y_i] }[/math] in the trust area and [math]\displaystyle{ \alpha\in[0,\pi] }[/math] the value of [math]\displaystyle{ p(\alpha) }[/math] is calculated.
The calculated [math]\displaystyle{ p }[/math] values are round to the closest value in a discrete set. The Hough parameter space can in this case be interpreted as a 2 dimensional grid where the first axis represents the value of [math]\displaystyle{ \alpha }[/math] and the second axis the [math]\displaystyle{ p }[/math] value, where for each solution of [math]\displaystyle{ p }[/math] a value of one is added to the corresponding cell in the grid. The parameters of our reference line are the parameters that corresponds to the highest value in the Hough parameter grid.
The Hough transformation is shown in the following figure. The x and y values of the laser measurements are shown on the left. On the right the Hough space is shown, where the red line represents the current [math]\displaystyle{ \alpha }[/math] value of our reference line.
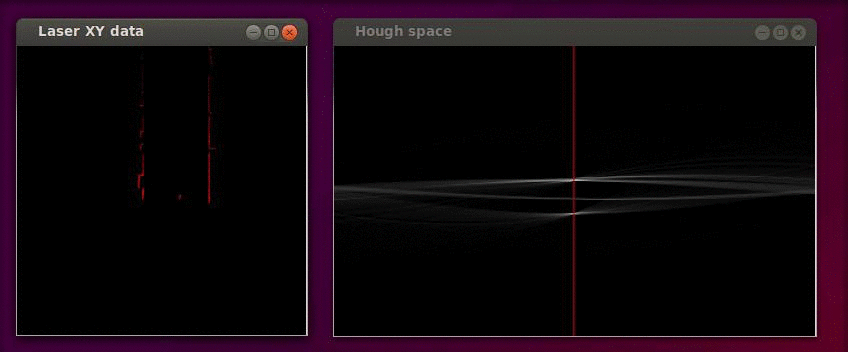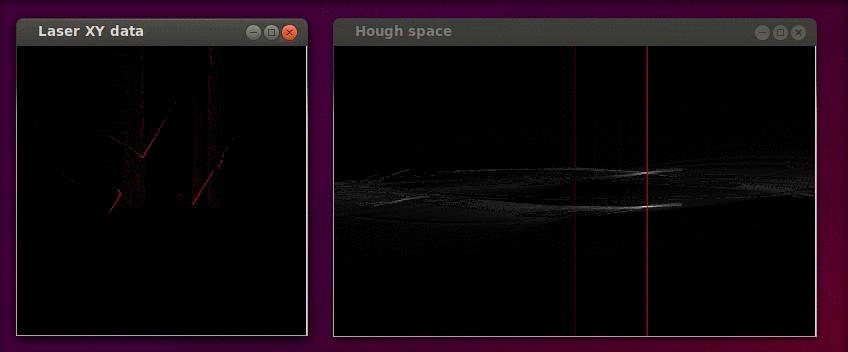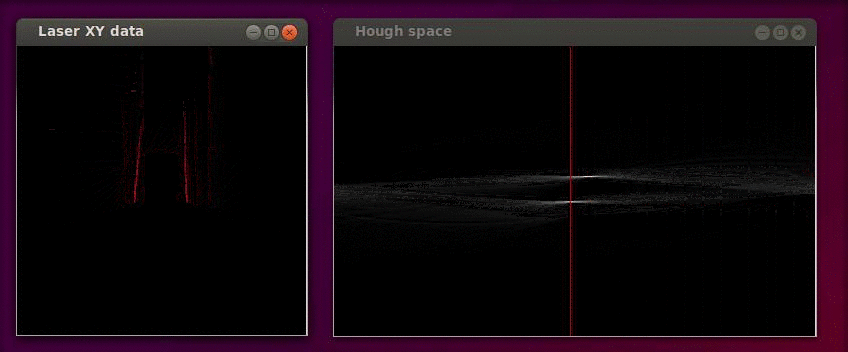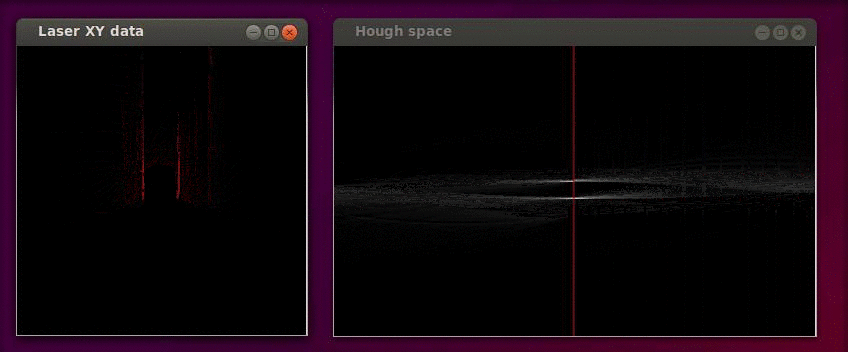
Only the [math]\displaystyle{ \alpha }[/math] parameter is in this case of interest. Since we assumed that the angular error of the robot with its environment is small we calculate the misalignment as the smallest difference between the parameter [math]\displaystyle{ \alpha }[/math] and a multiple of the world angle (in other words it does not matter for the result when we find a reference line parallel to the robot y axis instead of a line parallel to the y axis).
Applications:
The result of the compass function can be directly used to reduce the angular misalignment of the robot with its environment. This is accomplished in the form of a simple gain feedback control rule: [math]\displaystyle{ \omega_z=K_ze_z }[/math] where [math]\displaystyle{ \omega_z }[/math] is the rotation velocity, [math]\displaystyle{ K_z }[/math] is a control gain and [math]\displaystyle{ e_z }[/math] is the angular misalignment found by this function. The other application of the compass function is to align the mini map with the robot’s environment.
Minimap
This function creates from the sample data a small map around the robot. The map indicates areas where obstacles are and where not. The purpose of the mini map is to make it possible for sub functions to simply and flexibly detect maze futures such as side paths, maze exits and position errors it forms also an important input for the world model.
The following points are of interest in this function:
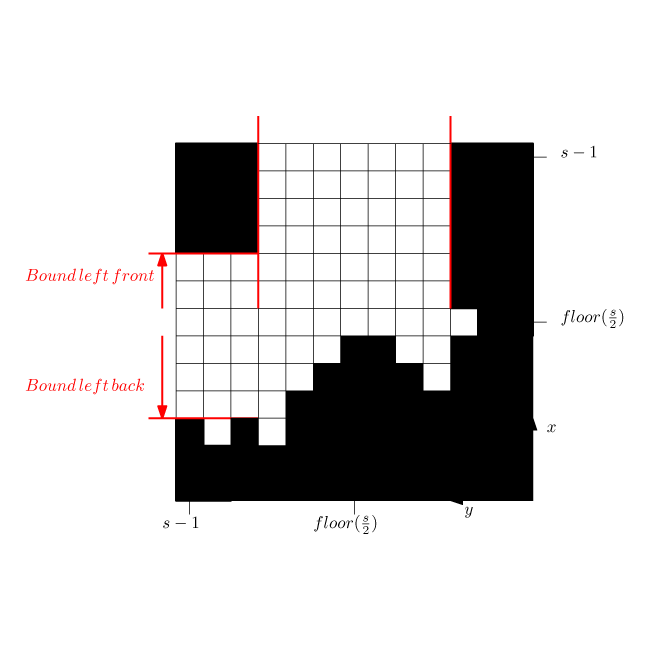
Assumed in the compass function was that the angular misalignment is small and will converge to zero since it will be compensated by a controller. Therefore we align the mini map not with the robot frame but with the world. A second trust area is created, which forms the bounds of the mini map (with different dimensions as in the compass function). The map is discretized in blocks of a specified size (x-y accuracy in [m]).
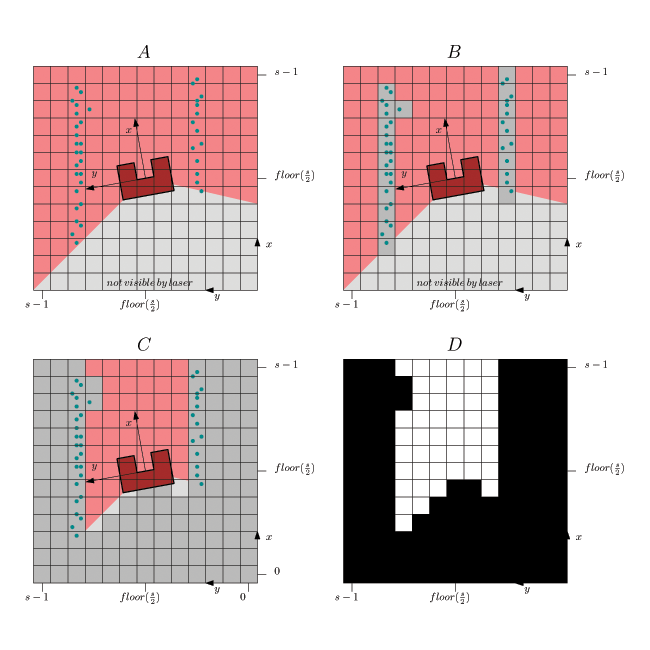
In the figure above is shown:
- In A. the laser range finder data is transformed to a orthogonal frame:[math]\displaystyle{ x_i=r_i\cos(\theta_i) }[/math] and [math]\displaystyle{ y_i=r_i\sin(\theta_i) }[/math]
where [math]\displaystyle{ \theta_i=\theta_{increment}i+\theta_{min}-e_z }[/math]. - In B each sample i is fit in a block and when there is a sample in the block then the block/pixel value is changed to 1. The remaining blocks are left 0.
- In C a collision detection is applied to detect areas where there are no obstacles. This is a simple line search for each angle from the middle (robot position) up to a block or the trust area border. This is done for all the angles in the range of laser range finder. The maximum allowed angular step is the angle that a rib of a block on the thrust area border makes.
- In D the final binary mini map is shown (the center cell represents the robot position).
In the figure below is shown that the minimap is aligned with the world rather than with the robot, this simplifies the calculations in the feature detection functions. A simple gain feedback is used to align the robot with the world.
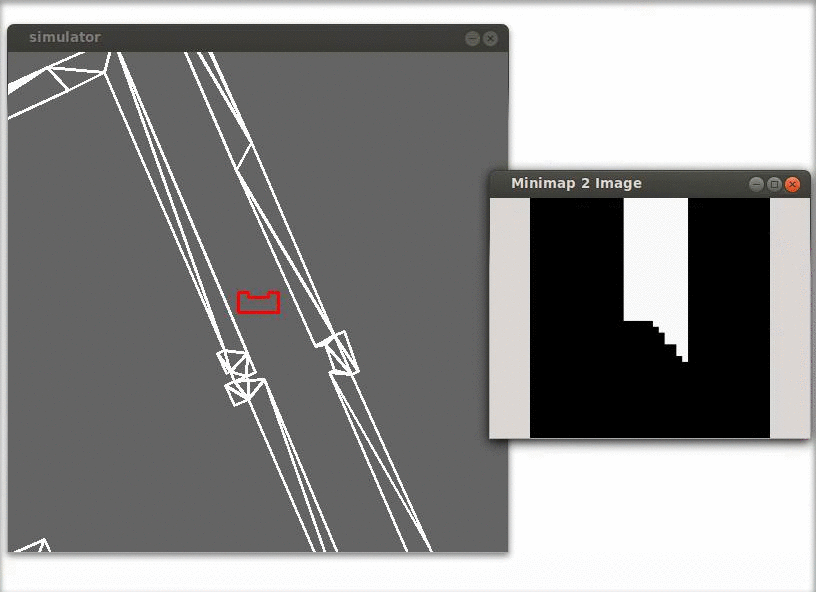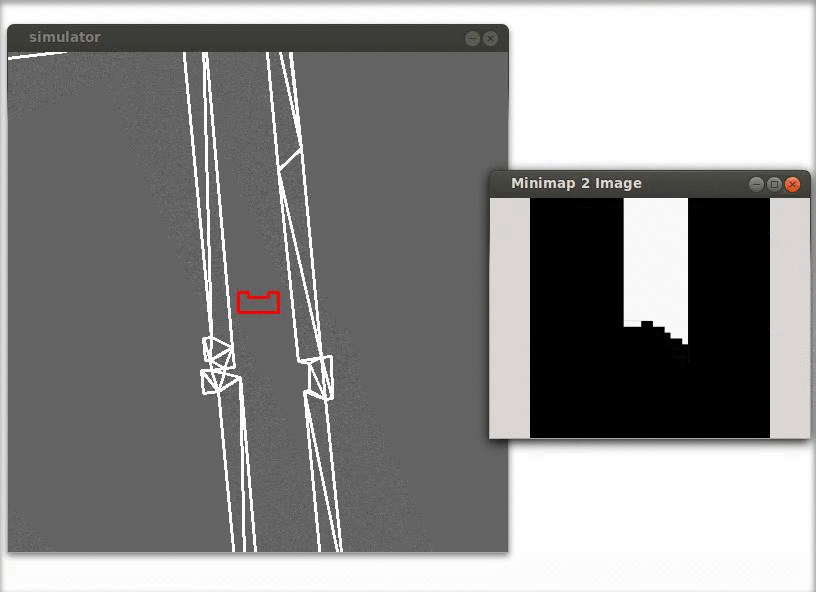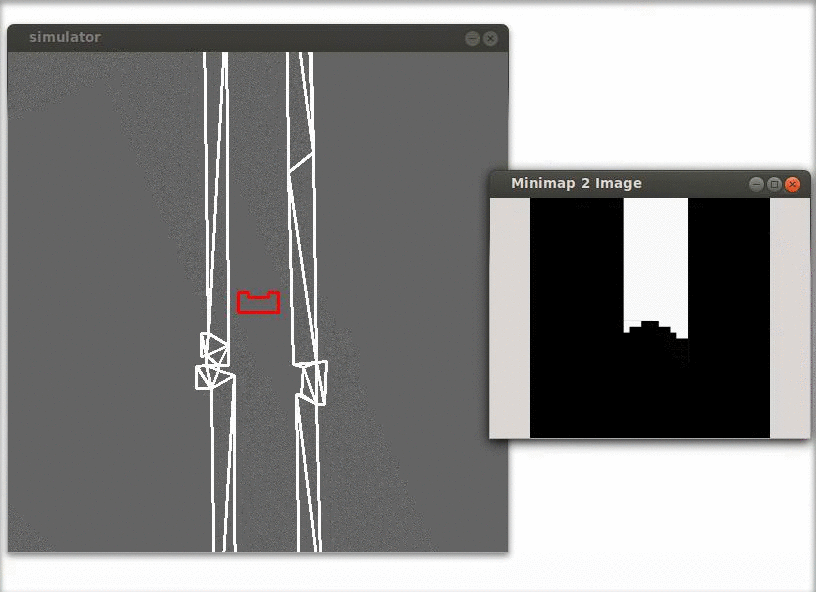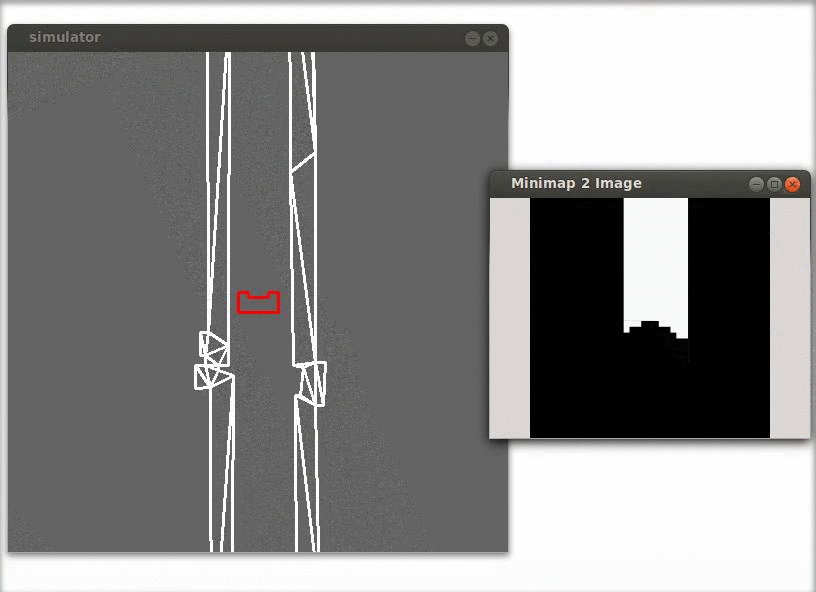
Some code of the laser vision functions: Implementation of the Hough space, calculation of the misalignment, creation of the minimap and calculation of the y-position error.
Code snippet: https://gist.github.com/anonymous/7723917455961e2a2313
Junction detection
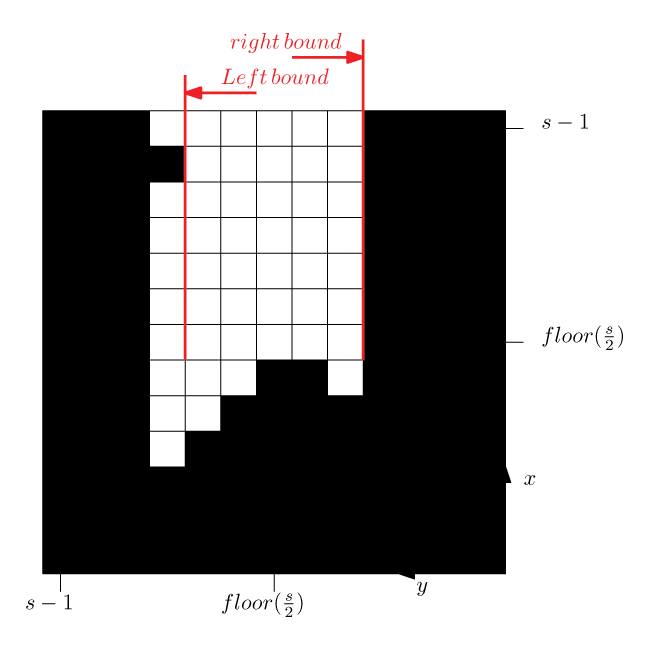
Junctions can be detected by applying a simple analysis of the Minimap. The basic principle that we are using is to try to fit a box of an appropriate size in the side-paths. If the box fits in the side-path then also the robot fits in the side-path. We detect side-paths on the right, on the left and in front. In addition we check if the side-paths are probably doors by scanning the depth of the junction. If there are no side-paths detected a distinction between corridor or dead end is made. Approach:
- The analysis starts with measuring the size of the corridor [math]\displaystyle{ a_1 }[/math] and [math]\displaystyle{ a_2 }[/math] in the figure below.
- The second step is checking whether there is a horizontal boundary on the lefthandside or the righthandside. If this is the case, the minimal height of the empty space, with a certain depth of 20 cm, is calculated and stored in [math]\displaystyle{ a_3 }[/math] and [math]\displaystyle{ a_5 }[/math].
- A corridor on the right or on the left is detected when a box that has the minimal measurements of a corridor fits into the calculated empty space. This box is shown in the figure below as a green box.
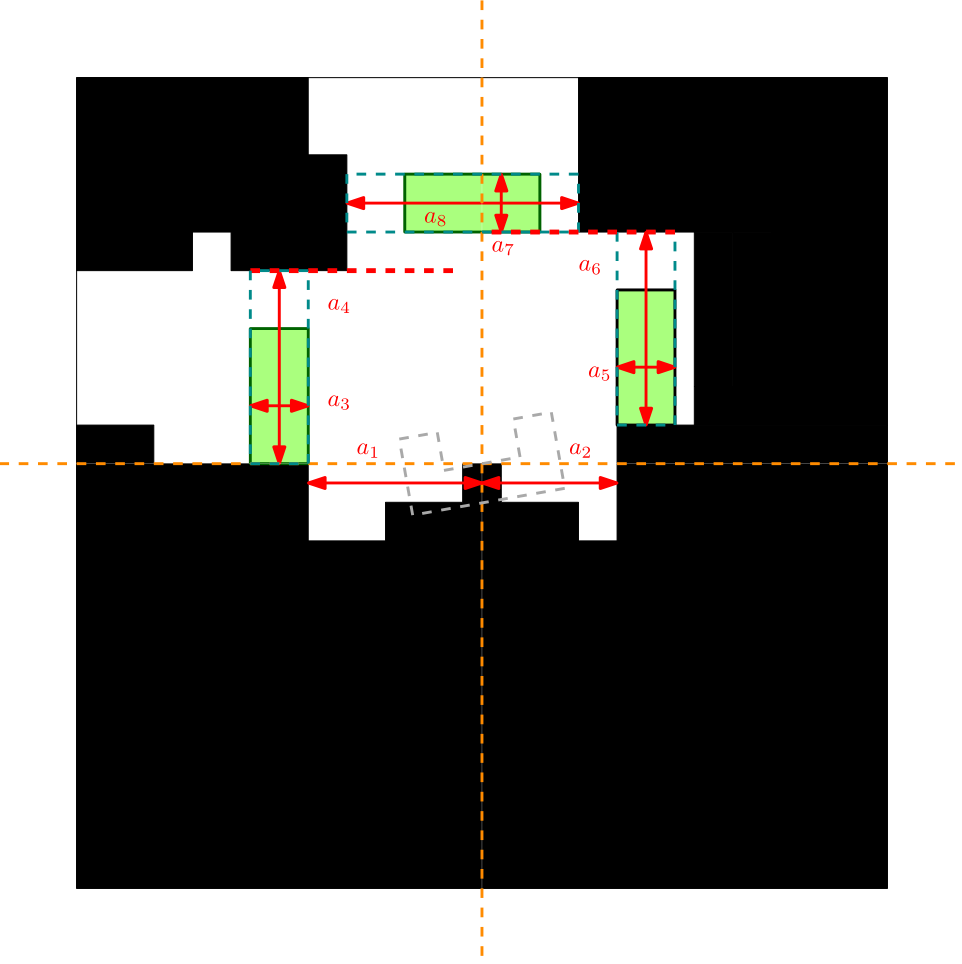
- At this moment, PICO detects a corridor on the left or on the right when there is an alcove with a depth of 20 cm. However, it is possible that this is a door or a dead end. Therefore, the upper boundary is analyzed to check whether the boundary of the trust area is empty or a wall, which results respectively in a corridor or a dead end (with the possibility of a door).
- A corridor in the front is detected when there is a complete empty space with the correct width. The same strategy is used as the detection of the corridor on the left- or righthandside. The two smallest boundaries are detected after which the width of the empty space is calculated. When the space is wide enough, corridorCenter is set as true. However, it is unknown whether it is a corridor or a dead end/door. The distance to the end of the corridor/wall is compared to the maximum value of the upper boundary of the left or the right corridor. This results in a dead end (or a possible door) or a corridor.
- Finally, the data of the corridors is combined to create possible junction types:
- corridorRight == true && corridorLeft == true && corridorCenter == false → T-junction
- corridorRight == true && corridorLeft == false && corridorCenter == true → T-junction (Right)
- corridorRight == true && corridorLeft == true && corridorCenter == true → Crossing
- etc.
- The junction type is sent to the supervisor. Besides that, the possibility of a dead end or a door in that junction is also sent. In this way, the supervisor is able to give a certain direction a higher priority.
The laservision function ensures that the motion skills get the correct distances to create a trajectory. The figure below gives an overview of the map with the distances [math]\displaystyle{ d_{1L},d_{1R},d_2,d_3,d_4 }[/math].
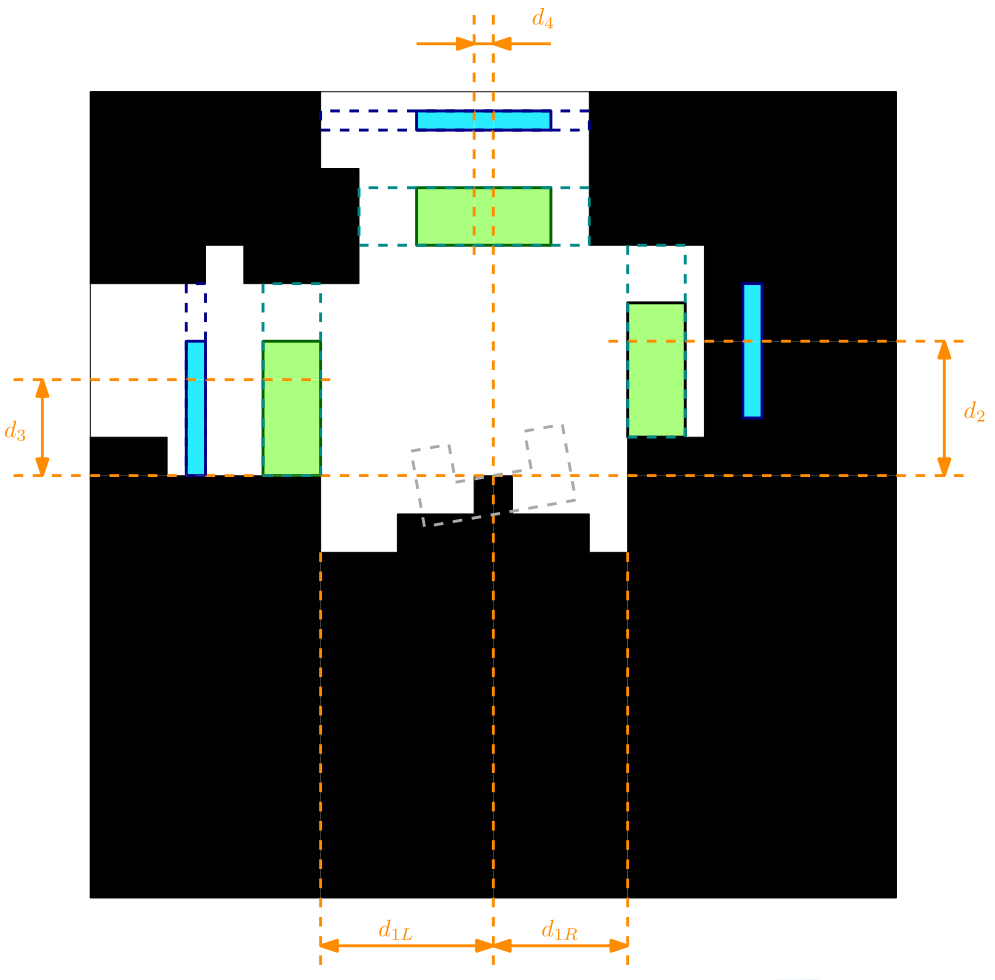
Y position error (center error in corridor)
The Y position error is the distance of the robot to the middle of the corridor. The approach is to calculate a left and a right bound in front of the robot (we don’t look sideward but in front of the robot). From these bounds the following center error is calculated:
[math]\displaystyle{ e_y=\frac{k_{left}+k_{right}}{2} }[/math]
This center error is used to control the robot to the middle of the corridor with control rule: [math]\displaystyle{ v_y=K_ye_y }[/math]
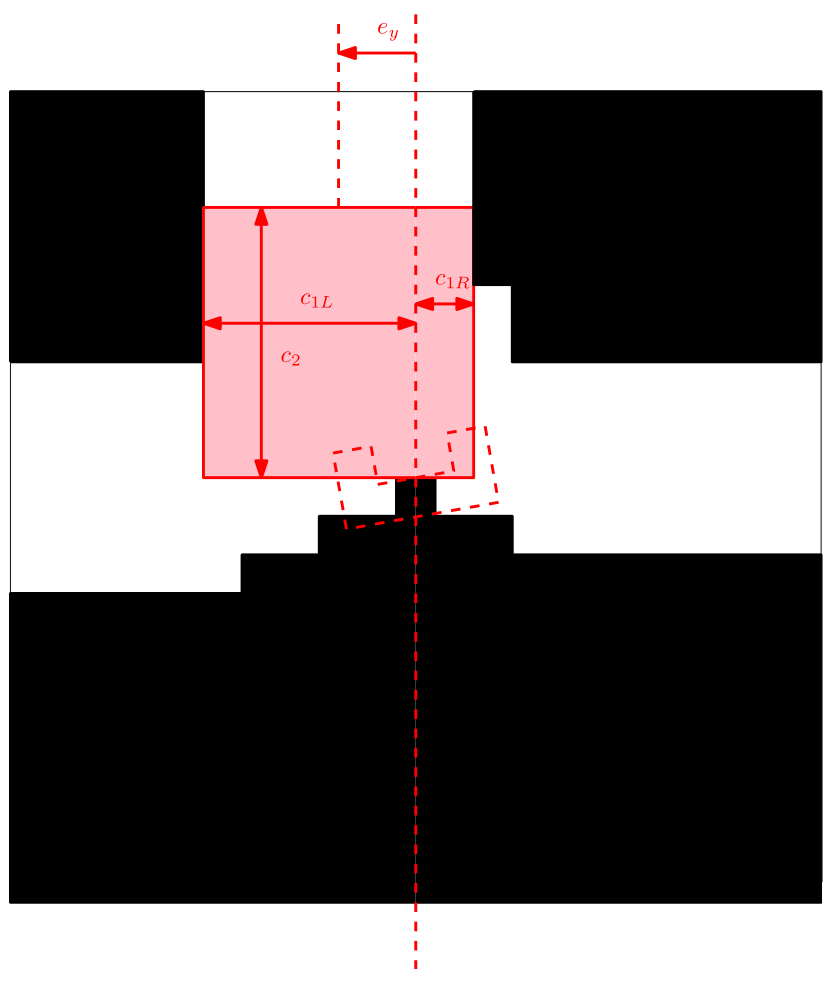
In the figure below an example is shown of the correction of the robot alignment with only a simple gain feedback in y-direction. Note that the robot already aligns before it enters the corridor.
Side path detection (as was used in the corridor challenge)
This function triggers when there is a side path found. The function calculates a front and a back bound. During the corridor challenge this function triggered the rotation function (which was tuned way to slow) under the conditions:
[math]\displaystyle{ |k_{front}|+|k_{back}|\gt minimal\,door\,size }[/math]
and
[math]\displaystyle{ |k_{back}|\gt |k_{front}| }[/math]
Exit detection (as was used in the corridor challenge)
If there is nothing in front of the robot then it is an exit.

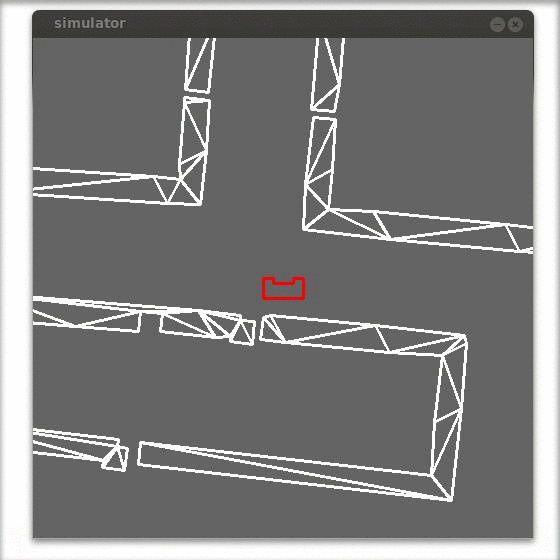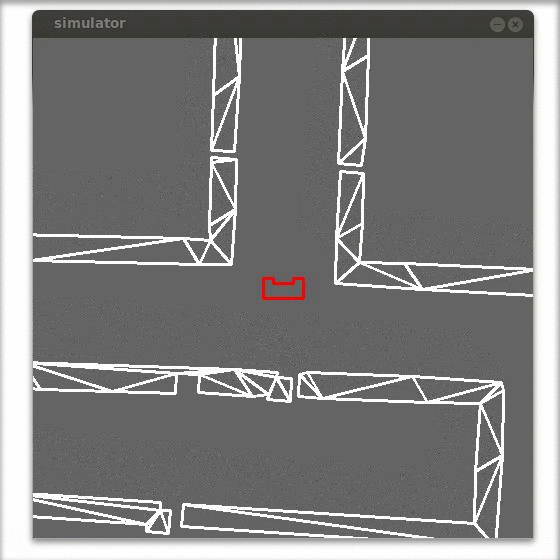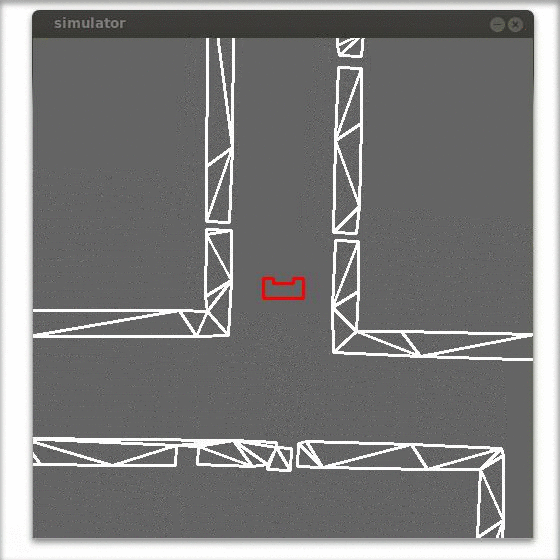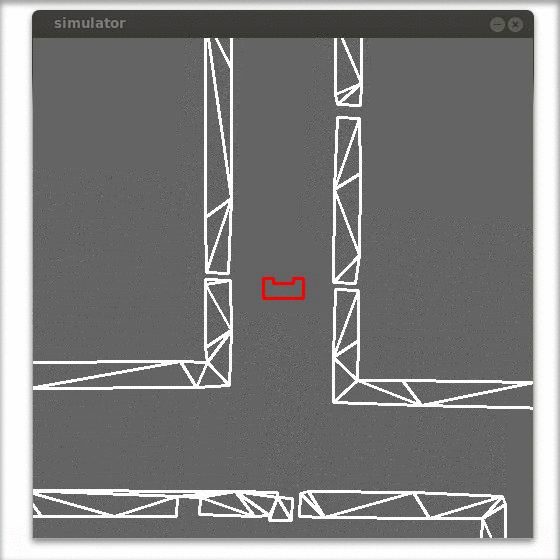
Laser vision in action
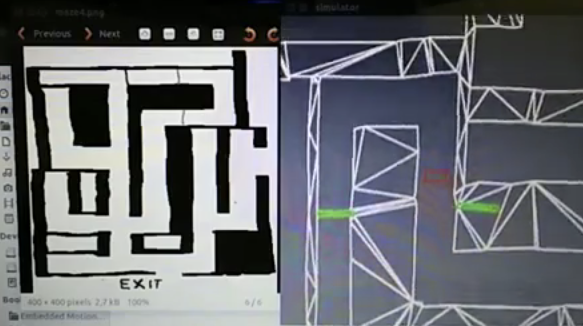
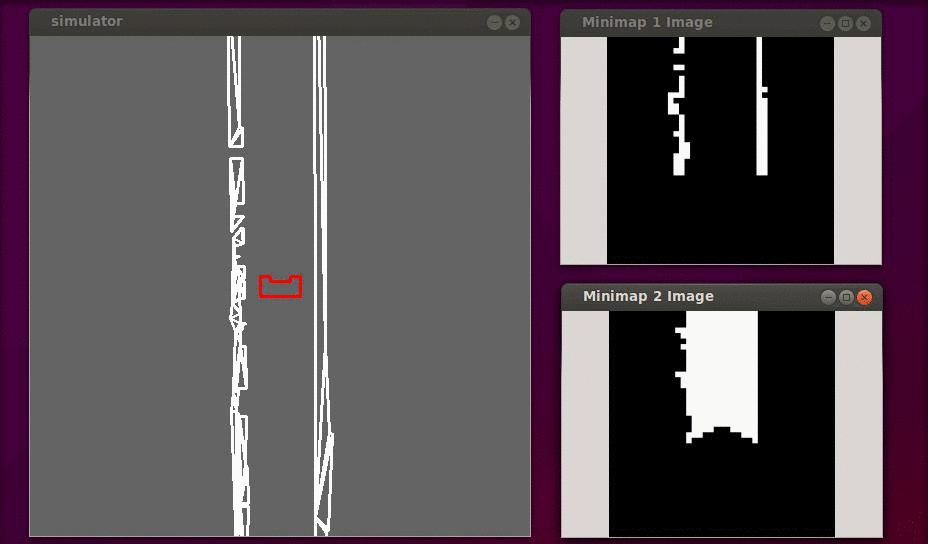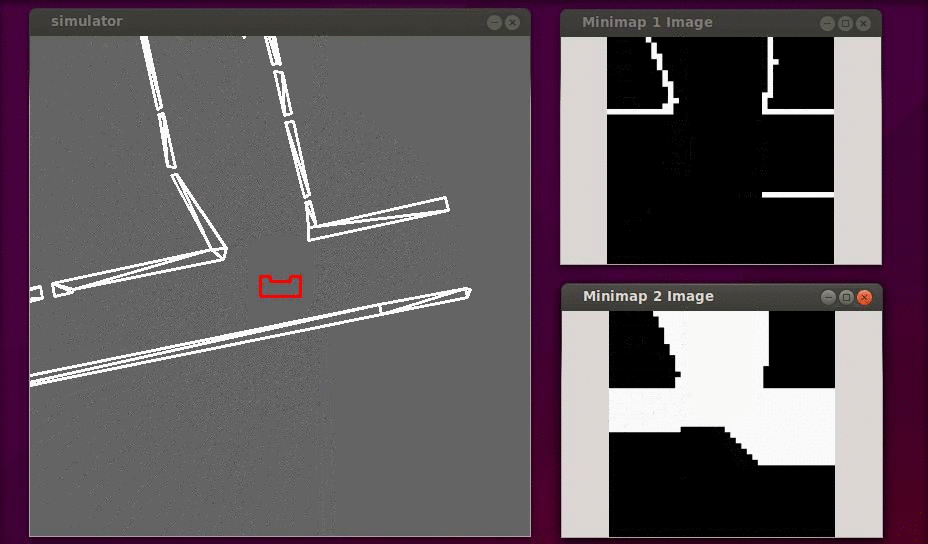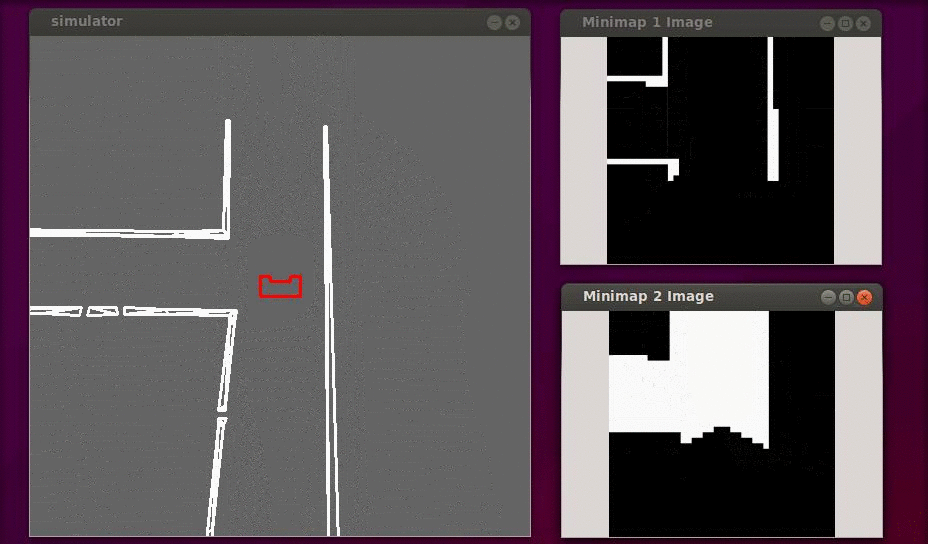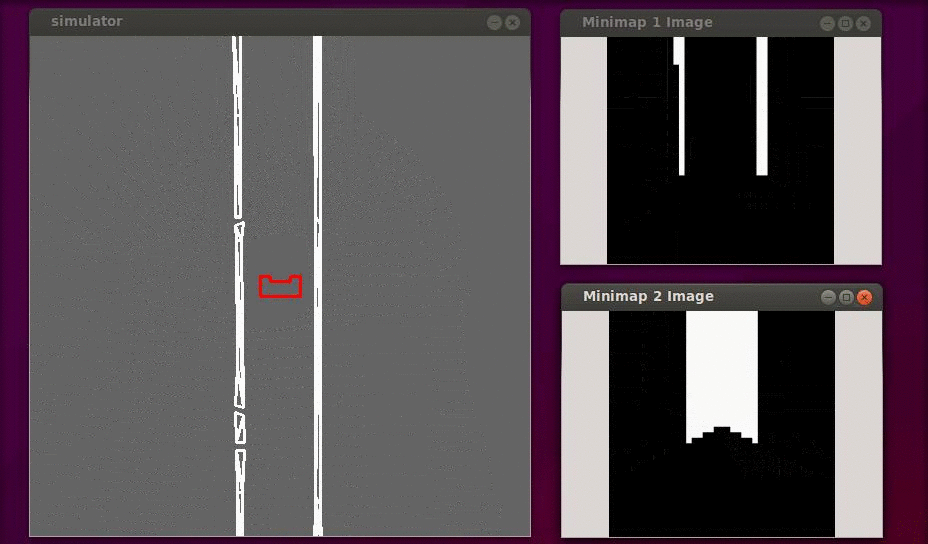
In the figure below a simulation of a corridor challenge is shown, it illustrates the robustness and simplicity of object detection in action. On the left the simulation of the robot trough the corridor is shown and on the right the mini map is shown.
World Model
In this project, slam is implemented. Slam itself stands for Simultaneously Localisation And Mapping. It means that while pico is driving through the maze, it builds a map from the maze, and tracks where it has been. The main reason why this should be implemented, is in order to solve the maze, it should know what corridors it has already been. In case of a wall follower, it is possible to get stuck in a maze if pico starts at a position, where it can drive in circles, and drives through the same corridors every time, a so called loop. Slam should detect such features and let pico know that the loop should be exited.
Slam is mainly build in two pieces of code. The first part is landmark extraction and the second part is filtering and keeping track of picos position.
Landmark Extraction
Landmark extraction is based on a Hough Transform. Since the maze is defined as a set of walls, which are 90 degrees orientated, the Hough Transform can deliver a function for the wall. The main goal is to describe the walls with as few information as possible. In other words, landmark extraction is providing a solution, which does not give the walls as a set of 1000 measurements, but instead as values and function parameters.
In an ideal situation, the wall is defined as a line function in the form defined in Hough Space section, and 2 coordinates which are the corners of the wall. The hardest part of SLAM is landmark association. If the software would define a wall as a start and an end point, chances are that no landmark will be associated, and all landmarks are new landmarks. In order to prevent this situation, the wall function parameters are also delivered. In this case a comparison of the measured function parameters and the saved parameters can be made, and reveals if a new wall is found, or an already discovered one is seen. In case of an already discovered wall, the software can detect if the new measurement contains the entire wall, or only parts, and even old part and new parts of the wall. This entire philosophy is not possible if only start and end points were used. The noise and disturbances would get to much influence on the final result.
Finding the maximum in the Hough space
The maximum is found in the hough space, by iterating every solution and determining which P combinations have the most hits. This combination is the wall with the most measurements. Since the maze exists of walls of 90 degrees, all other wall segments are [math]\displaystyle{ \frac{\pi}{2} }[/math] away from the maximum. The hough space is a space, which has a domain of [math]\displaystyle{ \left[0, \pi\right] }[/math], so in most cases, the maximum has one other line where walls can be found. Only in the case if the maximum is at [math]\displaystyle{ 0 }[/math], [math]\displaystyle{ \frac{\pi}{2} }[/math] of [math]\displaystyle{ \pi }[/math], there are three solutions for possible walls. This is due to the fact that [math]\displaystyle{ 0 }[/math] and [math]\displaystyle{ \pi }[/math] are the same set of walls, but 180 degrees rotated.
After the wall angles are detected, the wall parameters are searched. As told earlier, the walls are described as P = X cos(a) + Y sin(a). The wall angles are found, so a is known. Finding P is more like a filtering process. Every wall angle, has its maximum. After the maximum is found, a second maximum is searched for. The second wall maximum should meet certain conditions;
- It needs a certain amount of measurements.
- The distance of previous maximum should be far enough away.
- Contains a minimum amount of measurements.
These conditions can be changed in order to configure the landmark extraction.
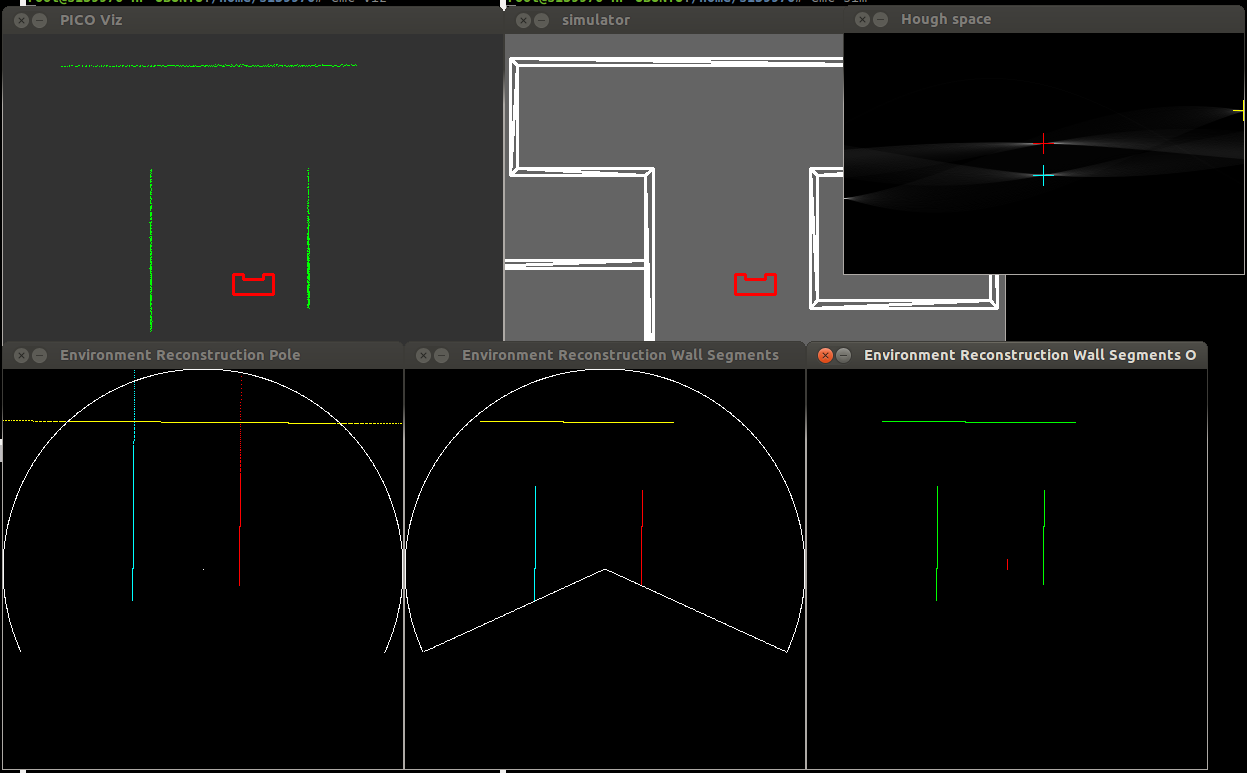
In the right figure, the process is visualised.
- Top left visualizes what pico sees.
- Top center is the position in the maze of pico.
- Top right is the Hough Space. In the Hough space, coloured crosses represents the landmarks which meet the conditions.
- Bottom left are the landmark functions plotted (P = X cos(a) + Y sin(a)), the white circle is the vision circle of pico.
- Bottom center are the landmarks, but cut off at the start and end coordinate.
- Bottom right shows the entire output of the landmarks, the red line is pico.
Calculate start points and end points of wall
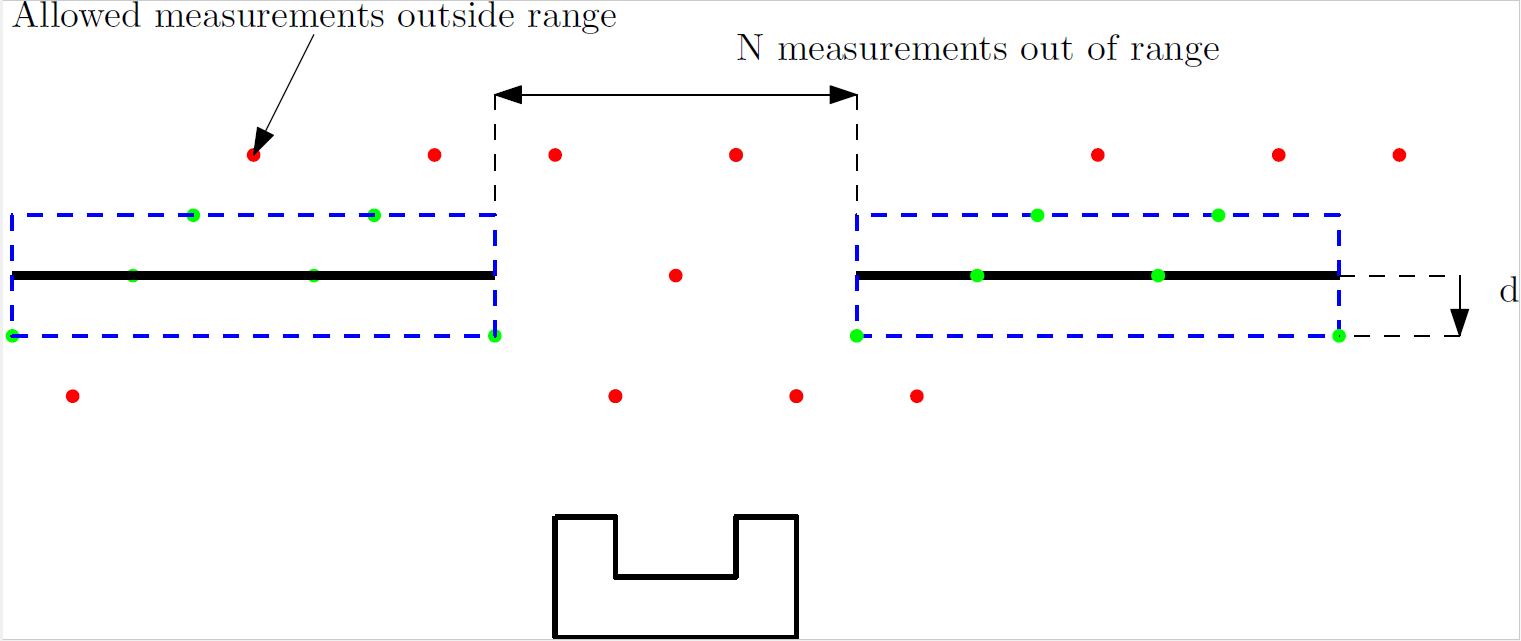
After the parameters p and a are found, the startpoint and endpoint of the walls are calculated. First the distance from the measurement to the walls are calculated by taking the root square of the measurement and the closest point to the measured wall.
[math]\displaystyle{ X_1=sin(\alpha)\times\left(X_isin(\alpha)-Y_icos(\alpha)\right)+pcos(\alpha) }[/math]
[math]\displaystyle{ Y_1=cos(\alpha)\times\left(Y_icos(\alpha)-X_isin(\alpha)\right)+psin(\alpha) }[/math]
[math]\displaystyle{ d=\sqrt{(X_i-X_1)^2+(Y_i-Y_1)^2} }[/math]
If the distance is smaller than a treshold distance, the measurement is taken into account. This comparison results in a matrix with zeros and ones, for measurements which are close enough and those who are not close enough. By finding the first hit, a start point is found. If the wall contains more than 100 measurements in range of the wall, then the start point is taken as a start point of a wall. This should make sure that each detected wall, contains at least hundred matched measurements.
Finding an end point is almost the same method. As long as we have measurements within distance of the wall, no end point is found. As soon as a measurement is not in range of the wall, the end point is found. Since small disturbances can occur in the measurement, at least 50 measurements need to be out of range, before the software assumes it is the end point of the wall.
In order to send out the wall functions, all the coordinates need to be transformed from the local frame to the global frame. This is done by rotating the frame with picos angle and then adding up picos position.
The output is an array which contains 10 landmarks with each 6 specific properties. The landmarks looks like the table blow, for each landmark and X,Y position for the start point is given, an X,Y position for the end point and a function description in the from of P a, which are explained in the Hough space section.
| Start point | Function parameters for wall | End point | |||
|---|---|---|---|---|---|
| X1 | Y1 | a1 | p1 | X1 | Y1 |
| ... | ... | ... | ... | ... | ... |
| X10 | Y10 | a10 | p10 | X10 | Y10 |
Results
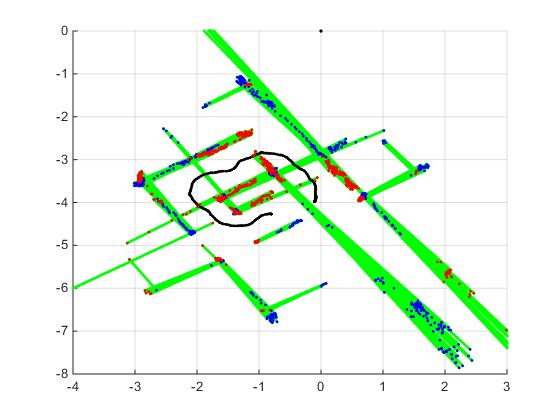
During the maze challenge, data from the landmark extraction algorithm is logged. The results are visible in the figure on the right. The black dots are the position measurements of pico. The red dots are start points of landmarks, and the blue dots are the end points of the landmarks. So far, landmark extraction looks promising, a few changes are needed in order to improve the results:
- A solution for improving blind spots. Means 2 things:
- Gaps/corridors further away from pico are not detected.
- Solution is to make the trust area of the measurements smaller.
- Or to make the number of allowed number of measurements outside range smaller.
- After junction, one of the walls is a blind spot. Is a result of pico turning away from the wall.
- Possible solution is to let pico rotate in opposite direction. During the turn, pico gets a glimpse of the walls in corridors where pico doesn't go to.
- Gaps/corridors further away from pico are not detected.
Extended Kalman Filter
The Kalman Filter can be used in the SLAM algorithm to predict the location of Pico in the maze and predict the location of the landmarks.
The position of Pico can can be described by an x and y position with an angle for orientation. Both the odometry and laser data can be used to measure the Pico's positon. Especially the odometry has significant measurement noise. The figure below shows the position parameters for Pico.
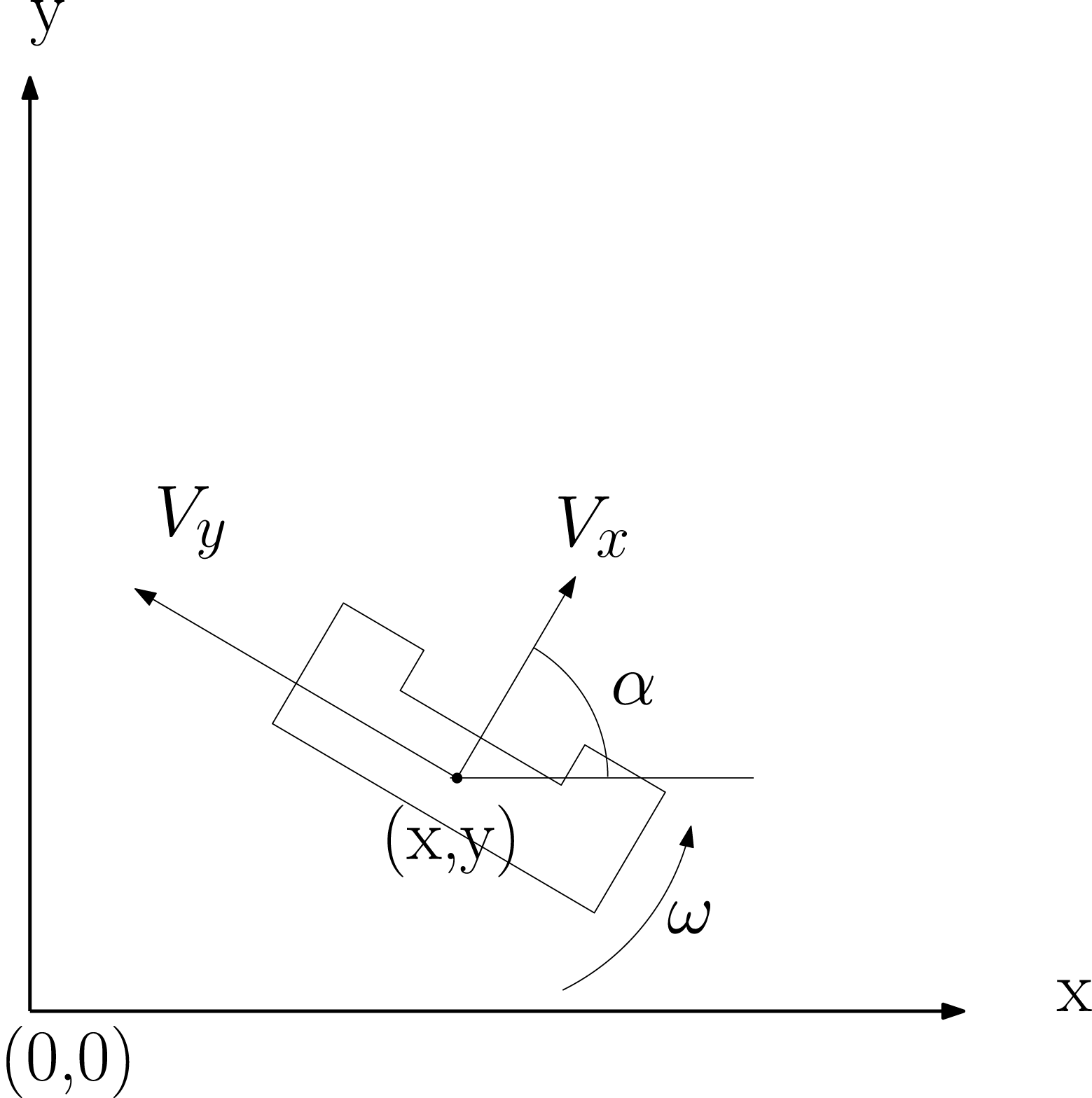
Here the x, y and [math]\displaystyle{ \alpha }[/math] are the position states. And [math]\displaystyle{ V_{x} }[/math], [math]\displaystyle{ V_{y} }[/math] and [math]\displaystyle{ \omega }[/math] are control inputs to the base. So the control and state vector becomes:
[math]\displaystyle{ x_{k} = \begin{bmatrix} x_{pos,k}\\ y_{pos,k}\\ \alpha_{k} \end{bmatrix}, u = \begin{bmatrix} V_{x}\\ V_{y}\\ \omega \end{bmatrix}, (\omega = \dot{\alpha}) }[/math]
To update the position state based on a motion model of the Pico the following equations are used: [math]\displaystyle{ x_{k+1}=f(x_{k},u_{k})= \begin{bmatrix} x_{k} + \Delta t(V_{x}cos(\alpha_{k}) - V_{y}sin(\alpha_{k})) \\ y_{k} + \Delta t(V_{x}sin(\alpha_{k}) - V_{y}cos(\alpha_{k})) \\ \alpha_{k} + \omega\Delta t \end{bmatrix} }[/math]
These equations are non-linear and that is the main reason why it is necessary to use the Extended Kalman Filter. The Jacobian used to update the covariance is the derivative of the above model:
[math]\displaystyle{ J = \frac{\partial f }{\partial x} = \begin{bmatrix} 1 & 0 & -\Delta t(V_{y}cos(\alpha_{k}) + V_{x}sin(\alpha_{k}))\\ 0 & 1 & \Delta t(V_{x}cos(\alpha_{k}) - V_{y}sin(\alpha_{k})\\ 0 & 0 & 1 \end{bmatrix} }[/math]
At first a MatLab implementation has been created to test the model. The animation below shows the location data from a Pico-sim run with noise added to the odometry data. Based on the model and measurement the filter makes a state estimation
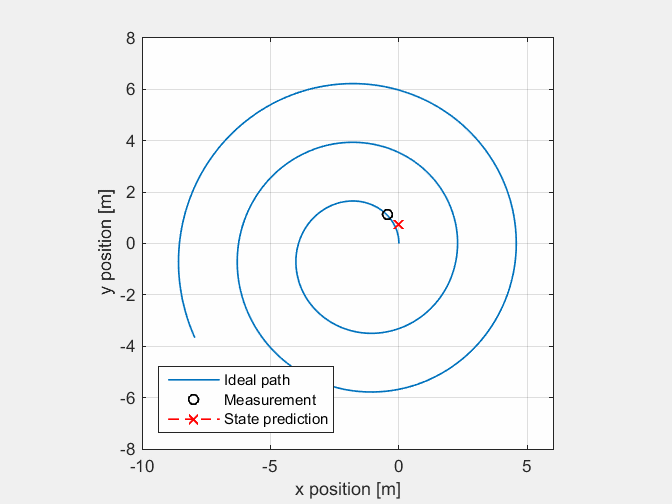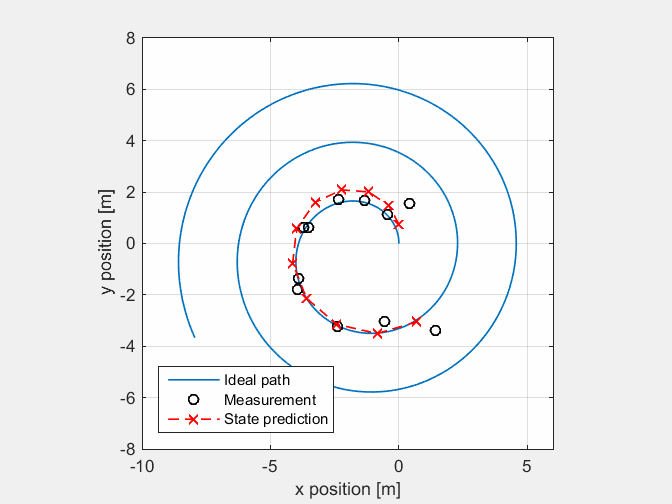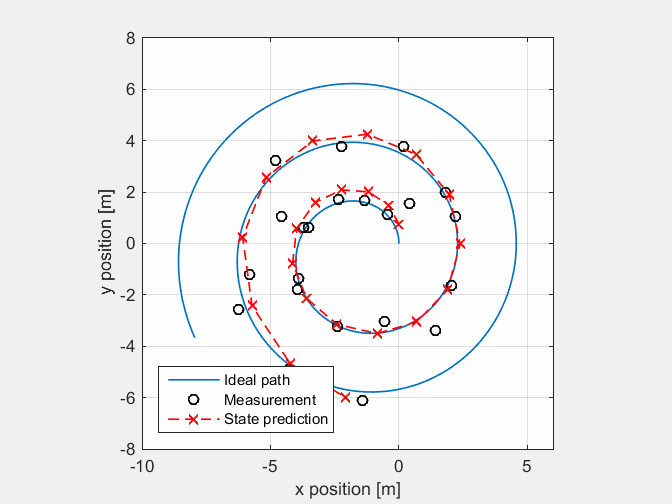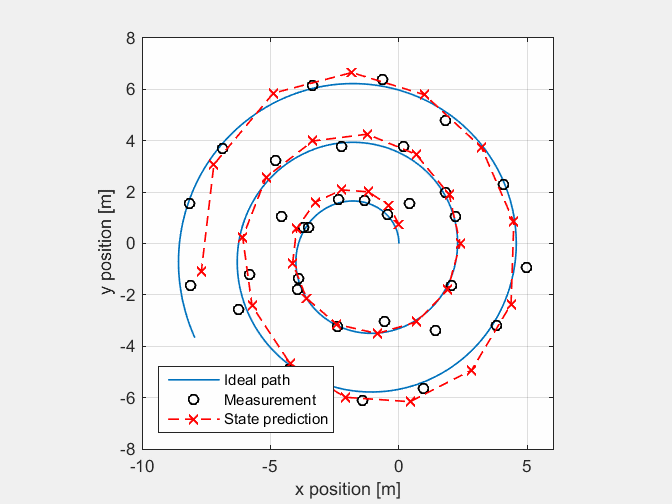
Homogeneous transformation
A small but effective function is the placement of local frames in the global world of the robot. These frames are for example created just before entering a corner, the robot can then navigate in a simple way on the odometry in the corner.
The implementation is nothing more then defining the elements of the homogeneous transformation matrix. From then on the robot odometry can be linearly mapped to the new defined frame.
[math]\displaystyle{ T=\begin{bmatrix}
cos(\alpha) & sin(\alpha) & -cos(\alpha)x_0 - sin(\alpha)y_0 \\
-sin(\alpha) & cos(\alpha) & sin(\alpha)x_0 - cos(\alpha)y_0)\\
0 & 0 & 1\\
\end{bmatrix} }[/math]
where [math]\displaystyle{ \alpha,x_0,y_0 }[/math] are the values of the global odometry at the time of creating the frame.
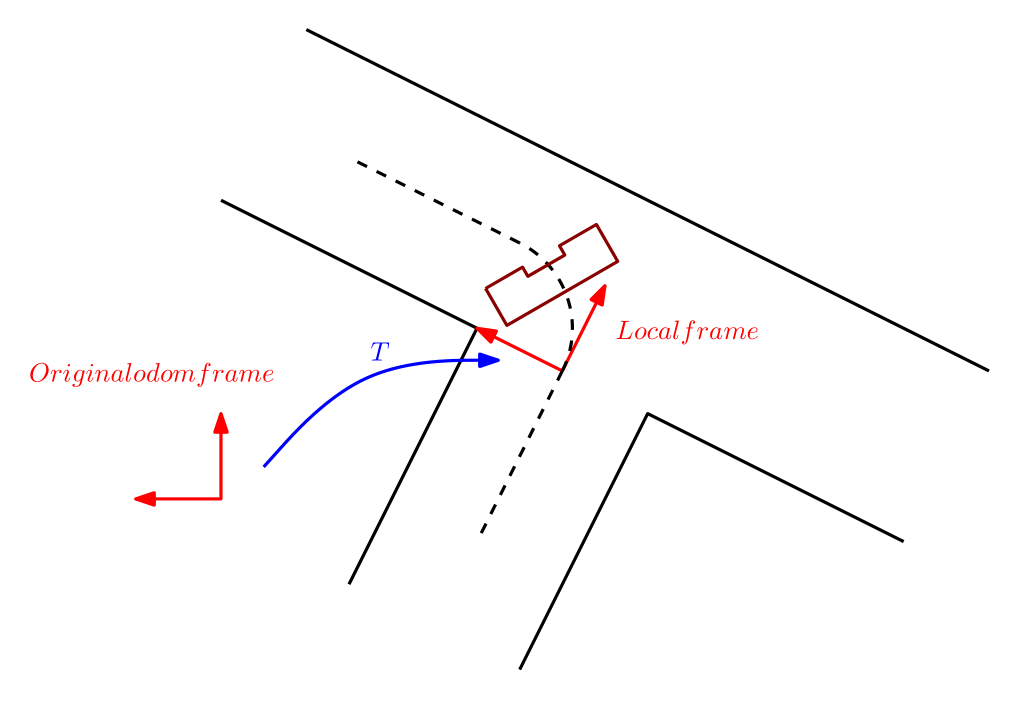
Code snippet: https://gist.github.com/anonymous/543170ac203c99a15405
Corridor Challenge
The image below links to a youtube video of the Corridor Challenge, in which we obtained a 3rd (19 seconds) place.
 |
Final maze challenge
The final maze challenge was held at the 17th of July. During this challenge the hard work of 10 groups was put to the test to see which groups were able to finish the maze. Each group was allowed to make two attempts at solving the maze. The maze consisted of a relatively standard part containing a loop, with a branch that led to a door. Behind this door was a short corridor followed by an open space with a wall in the middle. at the other end of the open space the exit was situated. Unfortunately we were unable to finish the world model and the Kalman filter in time before the challenge. Therefore we relied and a backup in the form of a righthand rule with loop detection.
Strategy
For the final maze challenge we had two versions of the code:
- Version 1: A version that partly relied on code that was tested before. However some changes were made after the last testing session, consisting of an updated motion skill section that chose a different alignment error when an open space was detected. This would result in wall-following in open spaces. Furthermore a basic solving strategy was implemented using the right-hand rule with an added loop detection feature. This way the robot would be able to break a loop in the maze by not choosing the rightmost branch if it detected a loop based on odometry data.
- Version 2: A safer version that originated form the last testing session. No loop detection was present and handling open spaces was not ideal.
What went wrong?
The video below shows the two trials. Clearly we did not finish the maze and did not even make it to the door. Both versions of the software detected a possibility to go right where there was none. After diving into the code we encountered the source of the bug. The laservision code had multiple ways of communicating the junction semantics to the supervisor. One was through junction type integers and the other was through booleans for {left, right,front}. The latter functionality was however not updated in later versions since the laservision department assumed that the type codes would be used. This was a miscommunication that unfortunately led to the bug we see in the video. The reason that we did not catch this bug during testing sessions is because it only surfaces for particular junction configurations. The junction in the final challenge with the parallel wall offset where the faulty behavior occurred was unfortunately not a scenario we built during testing sessions.
Video of the maze challenge
 |
Learning experiences
- Structure
- Original design
- Maintainable, scalable software
- Applicable to future designs
- Communication
- Unambiguous communication between developers
- Using “standards”
- Prioritizing requirements
- Essential vs. nice-to-have
- Limited test time -> use cases
- C++ programming in Linux
- Hands-on introduction in software development, GIT
- Software development costs time
- Reliable software is just as essential as hardware
- Well-documented, well designed software is important
 |