Mobile Robot Control 2024 Rosey: Difference between revisions
made all code references consistent |
|||
| (23 intermediate revisions by 6 users not shown) | |||
| Line 38: | Line 38: | ||
''Riccardo Dalferro Nucci & Ruben Dragt'' | ''Riccardo Dalferro Nucci & Ruben Dragt'' | ||
In this implementation the instruction to the robot is the most simple. The robot is instructed to keep moving forward using the io.sendBaseReference function and when the laser returns a distance within 0.3 meters, the robot is commanded to stop by setting the forward velocity in io.sendBaseReference back to 0. Using this method means the robot will not continue moving as long as the obstacle is within the 0.3 meters. If the robot is in front of a wall it will stay there forever, but with a moving obstacle such as a human walking by, the robot will eventually move forward again until the next obstacle. Video of the simulation can be found [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/EbWIje2GvzRInrJRvwxO44cBloUo262_6LwdQOqhViCpLA?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=GVbDab here]. | In this implementation the instruction to the robot is the most simple. The robot is instructed to keep moving forward using the <code>''io''.''sendBaseReference''()</code> function and when the laser returns a distance within 0.3 meters, the robot is commanded to stop by setting the forward velocity in <code>''io''.''sendBaseReference''()</code> back to 0. Using this method means the robot will not continue moving as long as the obstacle is within the 0.3 meters. If the robot is in front of a wall it will stay there forever, but with a moving obstacle such as a human walking by, the robot will eventually move forward again until the next obstacle. Video of the simulation can be found [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/EbWIje2GvzRInrJRvwxO44cBloUo262_6LwdQOqhViCpLA?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=GVbDab here]. | ||
'''<big>Implementation 2'':'' Turning away</big>''' | '''<big>Implementation 2'':'' Turning away</big>''' | ||
| Line 44: | Line 44: | ||
Using this method, the robot is not instructed to just stop but to also turn away from the obstacle. The added benefit of this approach is that the robot will be able to start moving forward again, as the laser will eventually stop returning obstacles in the set distance. | Using this method, the robot is not instructed to just stop but to also turn away from the obstacle. The added benefit of this approach is that the robot will be able to start moving forward again, as the laser will eventually stop returning obstacles in the set distance. | ||
* '''Method 1''' ''Tessa Janssen -'' In this code, the robot loops over part of the data by setting the for loop from <code>scan.ranges.size()/2 - range</code> to <code>scan.ranges.size/2 + range</code> (setting variable range at 150 means a view of approximately 1.2 rad). Then, when an obstacle is detected in within a set distance e.g. 0.5 m, the forward velocity is set to 0, but the angular velocity is given a positive value. This results in the robot turning left when it has reached an obstacle. When there are no longer any obstacles the angular velocity is set back to 0 and the forward velocity is given a positive value. The downside of always turning left is that the robot can get easily get stuck in corners and will not take into account efficiency. Video of the simulation can be found [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/EbYqk0Ff0CFAjBtN-R8STfcB8drJKfsxID3TAu6xb4ybGw?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=0QKdF1 here]. | * '''Method 1''' ''Tessa Janssen -'' In this code, the robot loops over part of the data by setting the for loop from <code>''scan''.''ranges''.''size''()/2 - ''range''</code> to <code>''scan''.''ranges''.''size''/2 + ''range''</code> (setting variable range at 150 means a view of approximately 1.2 rad). Then, when an obstacle is detected in within a set distance e.g. 0.5 m, the forward velocity is set to 0, but the angular velocity is given a positive value. This results in the robot turning left when it has reached an obstacle. When there are no longer any obstacles the angular velocity is set back to 0 and the forward velocity is given a positive value. The downside of always turning left is that the robot can get easily get stuck in corners and will not take into account efficiency. Video of the simulation can be found [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/EbYqk0Ff0CFAjBtN-R8STfcB8drJKfsxID3TAu6xb4ybGw?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=0QKdF1 here]. | ||
[[File:Thijs Rosey dontCrash.gif|thumb|Figure 1: Coco driving around with the don't crash code (Thijs).]] | [[File:Thijs Rosey dontCrash.gif|thumb|Figure 1: Coco driving around with the don't crash code (Thijs).]] | ||
| Line 51: | Line 51: | ||
* '''Method 3''' ''Thijs Beurskens -'' Here, the cone of vision of the robot is determined by setting the minimum and maximum angle, which is then translated to the amount of points the for loop should cover. The turning direction of the robot is determined by checking on which side of the robot the obstacles are closer and thus turning where there is more space. The code also keeps track of which direction it is turning, which prevents the robot from getting stuck in a corner. This approach has again the benefit of being able to keep moving around a map/obstacle course while also being more clever on where it can go. This approach makes the robot less likely to get stuck in certain areas and makes it more robust to changing environments. | * '''Method 3''' ''Thijs Beurskens -'' Here, the cone of vision of the robot is determined by setting the minimum and maximum angle, which is then translated to the amount of points the for loop should cover. The turning direction of the robot is determined by checking on which side of the robot the obstacles are closer and thus turning where there is more space. The code also keeps track of which direction it is turning, which prevents the robot from getting stuck in a corner. This approach has again the benefit of being able to keep moving around a map/obstacle course while also being more clever on where it can go. This approach makes the robot less likely to get stuck in certain areas and makes it more robust to changing environments. | ||
* '''Method 4''' ''Jose Puig Talavera -'' My implementation for the ''dont_crash() | * '''Method 4''' ''Jose Puig Talavera -'' My implementation for the <code>''dont_crash''()</code> code initially checks whether the robot is receiving laser and odometry data. If yes, command a forward motion of 0.5 meters per second. Then, read laser data through a cone of vision. If one of the laser range values is within or at 0.3 meters, stop the vehicle. Check distance to the right (''i'' = 200), then check distance to the left (''i'' =800). If left > right, turn +0.3 radians per second (counter-clockwise). Inversely, if right > left, turn -0.3 radians per second (clockwise). A video of the simulation can be found [https://tuenl-my.sharepoint.com/personal/t_h_janssen_student_tue_nl/_layouts/15/stream.aspx?id=%2Fpersonal%2Ft%5Fh%5Fjanssen%5Fstudent%5Ftue%5Fnl%2FDocuments%2FMobile%20Robot%20Control%20%20%2D%20Team%20Rosey%2FExercise%201%20%2D%20%20Don%27t%20crash%2FDont%5FCrash%5FJose%5FPuig%2Emp4&referrer=StreamWebApp%2EWeb&referrerScenario=AddressBarCopied%2Eview%2E4cd20d86%2D0bb0%2D4231%2Da19b%2Dd2088de315e0 here]. I personally like the part where it gets stuck at a point where the distance to the left and right are really similar && has an obstacle within 0.3 meters. | ||
* '''Method 5''' ''Riccardo Dalferro Nucci'' - After successfully implementing a ''dont_crash() | * '''Method 5''' ''Riccardo Dalferro Nucci'' - After successfully implementing a <code>''dont_crash''()</code> that would only stop once the robot encountered any obstacles, a new updated version was created. As the first version, this code initially checks if the <code>LaserData</code> is received correctly, if so, a velocity of 0.5 meters per second in the x direction is given. While the robots moves a for loop checks if there is any obstacle in the cone of vision of the robot, which is of plus and minus one radiant from the x axis. When this loop detects an object it stops the forward motion. If the closest object is on the right it will turn left and viceversa. This code still showed some problem, like for example when the right and left obstacles are at the same distance the robot just start to oscillate in between and it is unlikely to get out of that. It also showed some problem when going towards a wall from a very skewed angle, some times it was turning to slow and slightly bumping into the obstacle. A video of the simulation can be found [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/EQpCQWMlcdlHmN6mW5SR5gEBh6PMa_8TEn7WFX1xflmBlw?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=4BBmsE here]. | ||
=== Exercise 2 - Testing your don't crash === | === Exercise 2 - Testing your don't crash === | ||
During the first testing session it became clear that the parameters that were used in simulation needed to be adjusted to the robot in real life. Especially the velocity needed to be tuned down when using Coco/Bobo as they do not have the speed limiter built in. Moving too fast towards an obstacle meant that when it saw an obstacle within the safety range, it did not have enough time to stop before hitting the obstacle. Though tuning the velocities and obstacle distances was a doable fix and the code from method 3 (Thijs) ended up working very nicely in an environment with multiple different obstacles. The full video showing this approach can be seen [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/EfOj6xPD00tFkXR1Ucylq2QBkDdMrKnozQXRP-P926NqbQ?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=fG8zYF here] and a brief clip is shown in figure 1. | During the first testing session it became clear that the parameters that were used in simulation needed to be adjusted to the robot in real life. Especially the velocity needed to be tuned down when using Coco/Bobo as they do not have the speed limiter built in. Moving too fast towards an obstacle meant that when it saw an obstacle within the safety range, it did not have enough time to stop before hitting the obstacle. Though tuning the velocities and obstacle distances was a doable fix and the code from method 3 (Thijs) ended up working very nicely in an environment with multiple different obstacles. The full video showing this approach can be seen [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/EfOj6xPD00tFkXR1Ucylq2QBkDdMrKnozQXRP-P926NqbQ?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=fG8zYF here] and a brief clip is shown in figure 1. | ||
| Line 63: | Line 63: | ||
==== <big>Concept</big> ==== | ==== <big>Concept</big> ==== | ||
The main idea behin the Vector Field Histogram (VFH) method is to treat objects as vectors in a 2D cartesian histogram grid and create a polar histogram to determine possible "open spaces" to get to the goal. A polar histogram is created, centered in the robot's current position, using the LaserData and a number of sectors that can be given as an input. Every Laser Data from ''min_angle'' to ''max_angle'' (the data behind the robot are considered as not visible, even though defined in the polar histogram) is then treated as a vector, where its magnitude and direction are computed based on the following formula. | The main idea behin the Vector Field Histogram (VFH) method is to treat objects as vectors in a 2D cartesian histogram grid and create a polar histogram to determine possible "open spaces" to get to the goal. A polar histogram is created, centered in the robot's current position, using the <code>LaserData</code> and a number of sectors that can be given as an input. Every Laser Data from ''<code>min_angle</code>'' to ''<code>max_angle</code>'' (the data behind the robot are considered as not visible, even though defined in the polar histogram) is then treated as a vector, where its magnitude and direction are computed based on the following formula. | ||
<math> \beta = \arctan(y - y_{current}, x - x_{current}) </math>, | <math> \beta = \arctan(y - y_{current}, x - x_{current}) </math>, | ||
| Line 69: | Line 69: | ||
<math> m = a - b * distance </math>, | <math> m = a - b * distance </math>, | ||
where ''a'' is the product of b and the maximum distance, which needs to be given as input along with ''b''. Moreover, ''distance'' is the magnitude of the vector expressing the current position. Using a ''sendPath'' command, a visual representation of the sectors was given. Once the histogram is completly defined the program finds every ''valley,'' which means every sector with a value below ''threshold'' (also given as input) and chooses the best one, that is the one closest to the target direction. Every value of the histogram is normalized. A control input is then given to the robot to make it go in that direction. To note that a PID has been added to control the rotational speed, in order to best align the robot to the goal direction. | where ''a'' is the product of b and the maximum distance, which needs to be given as input along with ''b''. Moreover, ''<code>distance</code>'' is the magnitude of the vector expressing the current position. Using a ''sendPath'' command, a visual representation of the sectors was given. Once the histogram is completly defined the program finds every ''valley,'' which means every sector with a value below ''<code>threshold</code>'' (also given as input) and chooses the best one, that is the one closest to the target direction. Every value of the histogram is normalized. A control input is then given to the robot to make it go in that direction. To note that a <code>PID</code> has been added to control the rotational speed, in order to best align the robot to the goal direction. | ||
====<big>Simulation and Implementation</big>==== | ====<big>Simulation and Implementation</big>==== | ||
| Line 79: | Line 79: | ||
'''Advantages of the approach''' | '''Advantages of the approach''' | ||
The first advantage of this approach is the computational efficiency. Moreover, the implementation on the real robot showed a good robustness to noisy sensor data. Furthermore, the mathematical tools used, such as the polar histogram and the vectors, were quite familiar object, which allowed to implement the code without too many difficulties. Since the object density is computed on real-time LaserData the program is quite robust for what concerns moving objects or changing environments. Finally, since the code looks for closest free valley to the goal direction, the VFH method does not usually suffer from local minima. | The first advantage of this approach is the computational efficiency. Moreover, the implementation on the real robot showed a good robustness to noisy sensor data. Furthermore, the mathematical tools used, such as the polar histogram and the vectors, were quite familiar object, which allowed to implement the code without too many difficulties. Since the object density is computed on real-time <code>LaserData</code> the program is quite robust for what concerns moving objects or changing environments. Finally, since the code looks for closest free valley to the goal direction, the VFH method does not usually suffer from local minima. | ||
'''Disadvantages of the approach''' | '''Disadvantages of the approach''' | ||
The first disadvantage is that this method might struggle with narrow passages and sharp corners. Moreover, since this code uses real time LaserData the robot needs to have a relatively low speed, to be able to compute the new direction before bumping into an obstacle. | The first disadvantage is that this method might struggle with narrow passages and sharp corners. Moreover, since this code uses real time <code>LaserData</code> the robot needs to have a relatively low speed, to be able to compute the new direction before bumping into an obstacle. | ||
'''What could result in failure?/How would you prevent these scenarios from happening?''' | '''What could result in failure?/How would you prevent these scenarios from happening?''' | ||
| Line 130: | Line 130: | ||
'''Initialization''' | '''Initialization''' | ||
The code starts with an open set called open_nodes containing the initial node <code>_start_nodeID</code>, and another set <code>closed_nodes</code> where the visited nodes will be stored, to make sure that they are only visited once. The next step is to initialize a cost map to keep track of the cost from the start node to each node "h-cost", using the function <code>calculate_distance()</code>. Then a heuristic map is initialized estimating the cost from each node to the goal called "g-cost", these are initialized at the start as infinity and will be recalculated for each visited node to the surrounding nodes. This way the nodes with no edge connecting them from the <code>current_node</code> will have a cost that is | The code starts with an open set called open_nodes containing the initial node <code>''_start_nodeID''</code>, and another set <code>''closed_nodes''</code> where the visited nodes will be stored, to make sure that they are only visited once. The next step is to initialize a cost map to keep track of the cost from the start node to each node "h-cost", using the function <code>''calculate_distance''()</code>. Then a heuristic map is initialized estimating the cost from each node to the goal called "g-cost", these are initialized at the start as infinity and will be recalculated for each visited node to the surrounding nodes. This way the nodes with no edge connecting them from the <code>''current_node''</code> will have a cost that is infinitely large. The f-cost is the summation of the g-cost and h-cost is calculated for the initial node and the nodes connected to the initial node by edges. | ||
'''Processing''' | '''Processing''' | ||
While the open set is not empty, select the node with the lowest f-cost from the open nodes set. If this node is the goal, the path is found. Otherwise, the current node is moved from the open set to the closed set. While moving to different nodes the parent node of the node is also stored in a list <code>path_node_IDs</code>, the eventual parent node list will have the nodes stored that are part of the shortest path from the starting node to the goal. | While the open set is not empty, select the node with the lowest f-cost from the open nodes set. If this node is the goal, the path is found. Otherwise, the current node is moved from the open set to the closed set. While moving to different nodes the parent node of the node is also stored in a list <code>''path_node_IDs''</code>, the eventual parent node list will have the nodes stored that are part of the shortest path from the starting node to the goal. | ||
'''Expansion and repeat''' | '''Expansion and repeat''' | ||
For each neighbor of the current node, calculate the tentative g-cost. If this tentative g-cost is lower than the previously recorded g-cost for that neighbor, update it and change the parent node to the current node. This will also result in a new f-cost namely the f-cost for the neighbor is f = new g + h. Finally if the neighbor is not in the open set, add it. This process is then continued untill the goal is reached or the open set is empty, indicating no path exists. To store the optimum path from the initial node to the goal <code>path_node_IDs</code>, we start at the goal node and move to its parent node, because of this every node will have a list of a certain length with its parent nodes. If the current node is the goal node the robot just has to follow the parent nodes of the goal node to reach the goal. | For each neighbor of the current node, calculate the tentative g-cost. If this tentative g-cost is lower than the previously recorded g-cost for that neighbor, update it and change the parent node to the current node. This will also result in a new f-cost namely the f-cost for the neighbor is f = new g + h. Finally if the neighbor is not in the open set, add it. This process is then continued untill the goal is reached or the open set is empty, indicating no path exists. To store the optimum path from the initial node to the goal <code>''path_node_IDs''</code>, we start at the goal node and move to its parent node, because of this every node will have a list of a certain length with its parent nodes. If the current node is the goal node the robot just has to follow the parent nodes of the goal node to reach the goal. | ||
===<big>Probabilistic Road Map implementation:</big>=== | ===<big>Probabilistic Road Map implementation:</big>=== | ||
| Line 149: | Line 149: | ||
'''Inflate the map''' | '''Inflate the map''' | ||
The first exercise was to inflate the occupied spaces in a map to adjust for the size of the robot: <code>inflatedMap()</code>. This was done by looping over the pixels of the image by column and row and checking if the pixel has a value below the threshold that was previously defined in the assignment (<code>thresh_occ = 130</code>). If this is the case, the pixel is deemed occupied and a matrix of size <code>radius | The first exercise was to inflate the occupied spaces in a map to adjust for the size of the robot: <code>''inflatedMap''()</code>. This was done by looping over the pixels of the image by column and row and checking if the pixel has a value below the threshold that was previously defined in the assignment (<code>''thresh_occ'' = 130</code>). If this is the case, the pixel is deemed occupied and a matrix of size <code>''radius'' * ''radius''</code> is looped through, centered around that pixel. Then every pixel in that square is given value 0. The variable <code>''radius''</code> can be set depending on the size of the robot that is used. | ||
'''Check vertices''' | '''Check vertices''' | ||
The second exercise was writing a function that checked if the vertices generated into the map were at least a certain distance away from each other: <code>checkIfVertexIsValid()</code>. Our function loops through the existing vertices in the Graph, and for every vertex calculates the distance between this one and <code>new_vertex</code> that is given as an argument. The distance between the new vertex and the existing ones is calculated by applying the Pythagorean theorem on the distances between the first and second coordinates of the vertices. If the distance is smaller than some allowed distance (here we chose 0.25 meters), the function returns false, meaning the vertex is not added to the Graph. | The second exercise was writing a function that checked if the vertices generated into the map were at least a certain distance away from each other: <code>''checkIfVertexIsValid''()</code>. Our function loops through the existing vertices in the Graph, and for every vertex calculates the distance between this one and <code>''new_vertex''</code> that is given as an argument. The distance between the new vertex and the existing ones is calculated by applying the Pythagorean theorem on the distances between the first and second coordinates of the vertices. If the distance is smaller than some allowed distance (here we chose 0.25 meters), the function returns false, meaning the vertex is not added to the Graph. | ||
[[File:Local Global combined vector field histogram.gif|thumb|Figure 5: Coco driving through real-life map_compare.png using global and local planning.]] | [[File:Local Global combined vector field histogram.gif|thumb|Figure 5: Coco driving through real-life map_compare.png using global and local planning.]] | ||
'''Check edges''' | '''Check edges''' | ||
The final exercise is about checking if an edge between two vertices is valid: <code>checkIfEdgeIsValid()</code>. | The final exercise is about checking if an edge between two vertices is valid: <code>''checkIfEdgeIsValid''()</code>. | ||
First this means checking if the two vertices an not too far away from each other (<code>checkIfVerticesAreTooClose()</code>). This function was filled with pretty much the exact same code used in<code>checkIfVertexIsValid()</code>, only now the function checks if the distance between two vertices is bigger than some allowed distance (here we chose 1 meter). If this is the case the function returns false and no edge is created between these two vertices. | First this means checking if the two vertices an not too far away from each other (<code>''checkIfVerticesAreTooClose''()</code>). This function was filled with pretty much the exact same code used in<code>''checkIfVertexIsValid''()</code>, only now the function checks if the distance between two vertices is bigger than some allowed distance (here we chose 1 meter). If this is the case the function returns false and no edge is created between these two vertices. | ||
A second requirement is that the edge between two vertices cannot cross an obstacle:<code>checkIfEdgeCrossedObstacle()</code>. This function converts the coordinates (first and second) of two vertices into their pixel equivalent and arranges them to make sure that pixel 1 is always to the left of pixel 2. The function loops over all pixels that lie in the square you can draw with the two pixels as opposite corners. Then for each pixel in this square it is checked if it is occupied, using the same threshold as before. If it is indeed occupied, the distance from this pixel to the line connecting the corner pixels is calculated. If this distance is within a 2 pixel range, it is said to be in the 'edge' territory and the function will return true: the edge crosses an obstacle. This method was chosen because it only considers obstacles a problem when they are actually on the edge between two vertices. This makes efficient use of the map as will not remove edges only because they are too close to obstacles. | A second requirement is that the edge between two vertices cannot cross an obstacle:<code>''checkIfEdgeCrossedObstacle''()</code>. This function converts the coordinates (first and second) of two vertices into their pixel equivalent and arranges them to make sure that pixel 1 is always to the left of pixel 2. The function loops over all pixels that lie in the square you can draw with the two pixels as opposite corners. Then for each pixel in this square it is checked if it is occupied, using the same threshold as before. If it is indeed occupied, the distance from this pixel to the line connecting the corner pixels is calculated. If this distance is within a 2 pixel range, it is said to be in the 'edge' territory and the function will return true: the edge crosses an obstacle. This method was chosen because it only considers obstacles a problem when they are actually on the edge between two vertices. This makes efficient use of the map as will not remove edges only because they are too close to obstacles. | ||
===<big>Combining A* and PRM</big>=== | ===<big>Combining A* and PRM</big>=== | ||
| Line 199: | Line 199: | ||
'''How is the code is structured?''' | '''How is the code is structured?''' | ||
The workable code is split into two folders called FilterComponents and Filter. The | The workable code is split into two folders called FilterComponents and Filter. The <code>Particle</code> and <code>Resampler</code> classes live in the Filter components folder whereas the <code>ParticleFilter</code> and <code>ParticleFilterBase</code> classes live in Filter folder. The <code>Particle</code> class holds all the meaningful information and methods regarding each particle. This class will be called by methods in the other classes. Depending on the arguments passed to the constructor, a particle with uniform distribution or Gaussian distribution can be constructed. The other classes are in charge of predicting, updating and resampling the particles. The code is nested with ''Particle'' being the lowest level and <code>ParticleFilter</code> being highest level. | ||
'''What is the difference between the ParticleFilter and ParticleFilterBase classes, and how are they related to each other?''' | '''What is the difference between the ParticleFilter and ParticleFilterBase classes, and how are they related to each other?''' | ||
The difference between the | The difference between the <code>ParticleFilter</code> and <code>ParticleFilterBase</code> classes is that <code>ParticleFilterBase</code> implements the estimation and propagation of the particles whereas the <code>ParticleFilter</code> class determines when and how particles should update and propagate. <code>ParticleFilter</code> is a public subclass of <code>ParticleFilterBase</code>, meaning all the methods and members from <code>ParticleFilterBase</code> are also available in <code>ParticleFilter</code>. | ||
'''How are the ParticleFilter and Particle class related to eachother?''' | '''How are the ParticleFilter and Particle class related to eachother?''' | ||
The | The <code>ParticleFilterBase</code> class (and thus also the <code>ParticleFilter</code> class) contains a <code>ParticleList</code>, which is a vector of <code>Particles</code>. The <code>Particle</code> class contains methods for updating individual particles, and <code>ParticleFilterBase</code> contains methods for evaluating the complete <code>ParticleList</code>''.'' | ||
'''Both the ParticleFilterBase and Particle classes implement a propagation method. What is the difference between the methods?''' | '''Both the ParticleFilterBase and Particle classes implement a propagation method. What is the difference between the methods?''' | ||
The | The <code>ParticleFilterBase</code> and <code>Particle</code> propagation methods do two different things. The <code>''propagateSample''()</code> method of the <code>Particle</code> class ensures a detailed pose update of one particle, incorporating the motion model and noise. On the other hand, the <code>''propagateSamples''()</code> method of the <code>ParticleFilterBase</code> class calls the <code>''propagateSample''()</code> method for every particle by looping through each one. | ||
===1. Week 5=== | ===1. Week 5=== | ||
| Line 218: | Line 218: | ||
As explained above, the particle filter estimates the pose of the robot through a set of weighted particles, each of them representing a hypothesis of the current robot pose. The set of all the particles approximates the probability distribution over all possible robot poses. In this part of the assignment the methods which construct the set of particles is implemented. The implementation can either be done using uniform or gaussian distribution. | As explained above, the particle filter estimates the pose of the robot through a set of weighted particles, each of them representing a hypothesis of the current robot pose. The set of all the particles approximates the probability distribution over all possible robot poses. In this part of the assignment the methods which construct the set of particles is implemented. The implementation can either be done using uniform or gaussian distribution. | ||
Inside the Particle class, precisely in the Particle method, a random pose is generated. A pose is composed of x and y coordinates, and an orientation theta. Depending on the input given to the function, the pose can either be generated with a uniform distribution ( | Inside the Particle class, precisely in the Particle method, a random pose is generated. A pose is composed of x and y coordinates, and an orientation theta. Depending on the input given to the function, the pose can either be generated with a uniform distribution (<code>Particle::''Particle''(&''world'', &''weight'', *''generatorPtr'');</code>) or with a gaussian one (<code>Particle::''Particle''(&''world'', ''mean''[3], ''sigma''[3], &''weight'', *''generatorPtr'');</code>) . | ||
Finally, the uniform distribution is easier to implement and it does not require any a priori knowledge of the initial position of the robot, but is obviously less precise and it will take more iteration to find the actual position of the robot. The gaussian distribution, on the other hand, it requires a good estimate of the initial position, but it will be more likely for most of the particles to be close to the real pose, allowing to find it faster. | Finally, the uniform distribution is easier to implement and it does not require any a priori knowledge of the initial position of the robot, but is obviously less precise and it will take more iteration to find the actual position of the robot. The gaussian distribution, on the other hand, it requires a good estimate of the initial position, but it will be more likely for most of the particles to be close to the real pose, allowing to find it faster. | ||
| Line 264: | Line 264: | ||
=== <big>'''The State flow'''</big> === | === <big>'''The State flow'''</big> === | ||
[[File:Image stateflow.png|thumb|519x519px|Figure 10: Stateflow used for final integration.]] | [[File:Image stateflow.png|thumb|519x519px|Figure 10: Stateflow used for final integration.]] | ||
In figure 10 the state flow as shown during the presentation is shown. This framework was used as a guide to integrate the separate components into a state machine. Below, the different states from this diagram are explained in greater detail. The relevant functions and variables are explained as well as the boundaries that are set for moving on to the next state. | In figure 10 the state flow as shown during the presentation is shown. This framework was used as a guide to integrate the separate components into a state machine. Below, the different states from this diagram are explained in greater detail. The relevant functions and variables are explained as well as the boundaries that are set for moving on to the next state. This whole state process is managed by the <code>Navigator</code> class that performs the actions described in the state flow diagram. This class contains a function corresponding to each state, except off, all the variables and classes that are persistent for each loop cycle, a constructor to initialize every variable and class, and finally a <code>''run''()</code> function, which implements the main loop of the program. | ||
To keep track of the current state, the <code>Navigator</code> class contains the ''<code>current_state</code>'' variable, which is of type <code>state</code>. <code>state</code> is an enum, with an entry for each possible state. The <code>''run''()</code> function consists of a while loop, with a single switch statement. This switch statement checks ''<code>current_state</code>'' and runs the corresponding state function. The loop also contains <code>''r.sleep''()</code>, which is used to keep a consistent time for each loop step. The system is designed such that each state function represents a single loop iteration, and as such the states do not contain large loops. The idea is that a state function will be called in a loop, as long as ''<code>current_state</code>'' remains unchanged. To change the state, the state function has to modify the value of ''<code>current_state</code>'', and when the state function returns, the switch statement will run the new state function on the next loop iteration. It may be desirable to return immediately after changing the ''<code>current_state</code>'' variable, but this is not required, and the state will continue to execute as normal until it returns normally. As mentioned previously, there is one state without a state function, namely <code>state::''off''</code>. When ''<code>current_state</code>'' is set to <code>state::''off''</code>, the switch statement will instead terminate the main loop, and as such the program ends. | |||
==== <big>State ~ | ====<big>State ~ Off</big>==== | ||
The off state is not a proper state. It does not have a function. Instead, it is used to indicate the program should terminate. | |||
==== <big>State ~ | ====<big>State ~ Initialize</big>==== | ||
The Initialize state is the first state reached by the robot right after being turned on. Although having a map of the layout of its environment, the robot has no clue on its initial position. For this reason, this first phase is designed to let the robot localize itself. As a first step the odometry data are updated, then laser data are defined and localization, as explained in "Week 5 + Week 6: Localization" section, starts. To be able to understand when the robot is localized, thus the next state can be reached, a ''spread'' variable is defined as the root mean square of the weighted error of the localization. The state is structured such that the robot enters an ''if'' statement: if the spread is greater than an acceptable value (or the loop has been completed less than 50 times) a rotation is commanded (<code>''io''.''sendBaseReference''(0,0,1)</code>) while the robot still performs the localization. When the if statement becomes false the robot enters the ''else'' condition: it stops spinning and the ''<code>current_state</code>'' is set to <code>state::''planning_global''</code>. Localization has been performed. The extra constraint of at most 50 rounds was added to avoid the robot getting stuck in localizing: we decided it would be better to start with a bit of a bigger spread than spin in circles too long. | |||
When testing this program one problem arose: the spread was never lower than the acceptable constant, and the state change would only happen after 50 loops, even though the simulation did show the spread decreasing significantly. This is probably due to an error in the error rms computation. This state would have been faster if the code worked as intended, but this problem did not affect the whole system, since the robot was always localized after 50 loops. | |||
==== <big>State ~ | ====<big>State ~ Global path planner</big>==== | ||
As mentioned before, once the initial localization is completed the state is switched to the global path planner. In this state, the global planning is executed to get higher level optimal path from the desired waypoint. First, the start is set to the current location, which makes the robot more efficient as it does not have to use local navigation to get to the starting position. The goal coordinates are read from the config file one by one, this means that the paths are individually calculated every time a goal is reached. Both start and goal are <code>pose2D</code> types and do not necessarily coincide with a specific node, in fact, they most likely don’t. To solve this, <code>''plan_path''()</code> runs through all the nodes in the graph to find the closest nodes to both the start and goal. Once found, we execute the A* algorithm to find the optimal route as explained in “Week 4 -Global navigation”. In case this task is unsuccessful, the robot is set to communicate it that and the specific table (goal) that was not able to plan a path to, and the table is skipped for the next one. If the path is planned successful, the robot is commanded to communicate that it did it and the table goal, <code>''current_state''</code> is set to <code>state::''following_path''</code>. | |||
One situation that arose during the implementation of opening door functionality was that the vertices that would serve as waiting node that had to be reached to enter the <code>''state_open_door''()</code> could land on the door or very close to it such that local navigation would not allow to reach the point. This was solved in the prm by declaring as invalid the vertices that randomly landed in the near door area that was tuned. | |||
==== <big>State ~ | ====<big>State ~ Following path</big>==== | ||
This state is entered when the global planner has drawn out a path to the next table. It uses the local navigation class (explained in more detail below). In this state the required variables are set for the local navigation to be executed. This included the target coordinates that were computed in the global planner and the current position of the robot. The local navigation is executed unless one of two thing happens before it reaches this statement. | |||
First the robot can be near the door. In the if-statement it is first checked that the door is indeed currently on the path of the robot. This is done by a separate function <code>''door_on_path''()</code> that checks if the door is on the planned path, if so which node is placed in front of the door, and if the robot is currently on that node. It is also verified that the door has not been checked before to see if it is open. If it were, it would be redundant to check again, when it can already pass through. If both statements hold, the robot is brought to a stop, in order to move on to the next state: <code>state::''open_door''</code>. Before changing the state, the bool <code>''requested_open_door''</code> is set to false. A variable that is used later on to make sure the door is only requested to be opened once. | |||
A second way the robot does not go through with the local navigation, is when the robot is close enough to the table it is approaching. This if-statement is entered if the distance of the robot is within a set threshold of the table. This threshold was set to 0.2 m. reaching this statement means the state is switched to <code>state::''approach_table''</code> where the final positioning of the robot with respect to the table is determined. The value of 0.2 m was found through trial and error in both simulations and in the lab. This value allowed for the path following to be able to properly do its work before the aligning to the table takes over. It is also far enough away that the robot does not have to bump into the table before taking its final position. | |||
==== | ====<big>State ~ Open door</big>==== | ||
The state open door is reached when in the following path state a node is reached with an edge that will go through the door. If the door has not been checked yet the new state will become “Open door” and the speed will be set to zero in x y and theta. Also the variable <code>''requested_open_door''</code> will be set to false, this variable exists to be able to open the door every time in the case that the door is closed again after opening it. When the robot is in the open door state it will set the target angle and the current pose and use this to run the <code>''align_to_angle''()</code> boolean function which will align the robot with the angle the user inputs if this is not the case already and returns 'true' when this action is finished. | |||
If 'true' is returned the robot is aligned to the door, at this point the laser data is stored and transformed to points using a <code>''laser_to_points''()</code> function which transforms the laser data to a vector of <code>coord2D</code> points, which includes <code>''x''</code> and <code>''y''</code> , using the scan data the current pose and the position of the laser scanner on the robot. It then uses a process similar to the vector field histogram method to check for the door being open or not. To be more precise a field of view for the door is defined <code>''door_field_of_view''</code> which was set at 0.25 because we wanted a narrow enough angle such that the robot would not see the edges of the doorway . The direction of every point was then calculated by the predefined <code>angle</code> class to get the angle to every point. If this angle minus the rotation of the robot was within the 0.25 radians bound the distance to that point was added to the sector and the <code>''sum_of_weights''</code> variable is increased by 1. This process was performed for every point. If the sector divided by the weights was less than the distance to the node behind the door the robot knew the door was open, in this case the new state will become following path and <code>''checked_door''</code> will be set to true. If not the door was closed and the robot will ask for the door to be opened and the <code>''requested_open_door''</code> will be set to true. In the new loop true this state the robot should find the door to be opened if it was not the case before and such the robot will move to the following path state. | |||
==== <big> | ==== <big>State ~ Approach table</big>==== | ||
The approach table state is set as the current state when the robot is close enough to a table. This is measured by calculating the distance between the current pose of the robot and the table which is the target of the robot and checking if it is smaller than a predefined threshold in our case 0.2. We found during testing that 0.2 was sufficiently close, taking robot size into account, to perform the alignment actions of the approach table state and not to close such that table edges could be hit. | |||
In the approach table state a timeout is started if this has not been done yet, also <code>''timeout_started''</code> is set to true, this is done to make sure the timeout is not restarted in a new iteration. The timeout is actually a counter that adds 1 to <code>''cycle_counter''</code> for every cycle and therefore the cycles devided by the frequency are used as a measurement of time. If the approach timeout is reached, which was set at 15 seconds, is not reached and the robot is not close enough to the predefined approach pose it is currently trying to reach (same threshold as before applies) the approach pose is assigned to <code>''local_navigator''.''target''</code> and the local navigator is used to move to that goal. Two things can happen then either the timeout is reached in which case the approach posed is changed to the next one in the list until there is no new approach pose anymore. In this case the robot will say that it could not reach the table and the state is changed to table reached. The other thing that can happen is that the robot is actually within the predefined threshold of the approach pose. In this case the robot will align with the table using the same align function as mentioned in open door. If the correct angle is reached the robot will greet the table by table number and go to the table reached state. | |||
==== | ====<big>State ~ Table reached</big>==== | ||
If the robot has alligned to the target table and the order has been delivered the <code>''current_state''</code> will be set to <code>state::''table_reached''</code>. In table reached the motors are all set to zero and a timeout is started if this is not done already, the timeout exists because we wanted the robot to wait at the table for 10 seconds, if the timeout is reached the robot will go to the next state. As long as this timeout is not reached <code>''i_next''</code> is increased such that the robot can go to the next table. If this value is higher than the size of the table list the robot will go to the off state else the robot will go to <code>state::''planning_global''</code> and calculate the path to the new table. | |||
==== What should we do a next time? ==== | === <big>'''Classes'''</big>=== | ||
*Data handler: The <code>DataHandler</code> class is designed to interface with an IO system to retrieve odometry and laser data for use in navigation and localization. The class holds two methods: <code>''getOdomData''()</code> and <code>''getLaserData''()</code>. The first method, <code>''getOdomData''()</code>, is in charge of checking whether there is odometry data and returns the latest data as a <code>pose2D</code> type if it exists. Similarly, <code>''getLaserData''()</code> checks for laser data and returns an <code>emc::LaserData</code> type if the data exists. | |||
*Local Navigation: The <code>LocalNav</code> class is designed to provide flexibility in the local navigation approach. The constructor, among other arguments, takes a JSON file object from which parameters are read. In this configuration file, the approach can be changed from a Vector Field Histogram to Artificial Potential Field method by simply changing the "approach" parameter to either "histogram" or "potential_field." | |||
*Global Navigation: The <code>PathFollower</code> class is designed to design a path made up of a sequence of 2D coordinates. The methods in the class do the tasks of loading settings, setting the path, updating the current position, and checking whether the target has been reached. The <code>PRM</code> class deals with the loading of the map and creation of the roadmap. The methods generate random vertices that are evaluated to make sure that vertices are not in the walls nor too close to each other, to fully populate the map. The edges are also verified not to cross any wall. | |||
*Localisation: The <code>PoseTracker</code> class deals with localization. The class takes in odometry data and keeps track of the odometry since the last update. It is also possible to provide it with LRF data, which will allow it to run a particle filter and update the location. There are two public functions that can be used to localise: <code>''perform_localisation''()</code> and <code>''perform_async_localisation''()</code>. perform_localisation runs the <code>''localise''()</code> function and resets the odometry data. <code>''localise''()</code> is a private function that deals with the particle filter and returns the new location. Using this method, the localisation runs in the middle of the program, and because localisation can take a lot of time, this can block other parts of the code from running immediately. This method is used in the initialisation, because in this state, the only thing we want to do is get our localisation to a reasonable accuracy. The second function, <code>''perform_async_localisation''()</code> is a bit more involved. Instead of running the <code>''localise''()</code> function directly, this function runs <code>''async_localise''()</code> in a new thread. It also sets the ''<code>awaiting_pose</code>'' flag indicating that localisation is running, and it sets an estimate for ''<code>last_localised_pose</code>'' and resets ''<code>odom_since_last_update</code>'', because we don't know when localisation will be finished, and when the result is in, the ''<code>odom_since_last_update</code>'' has to correspond to the situation when localisation was called. Meanwhile, the <code>''async_localise''()</code> function calls <code>''localise''()</code>, and when this function returns, it sets ''<code>last_localised_pose</code>'' to the result. It also resets the ''<code>awaiting_pose</code>'' flag, since localisation is no longer running and a new localisation can now be performed. Because we are now accessing the same data from different threads, we may run into an issue known as a race condition. This happens when two parts of the code attempt to read or write the same data at the same time, and in c++, this results in undefined behavior, which is bad. To prevent race conditions, we use something called a mutex. A mutex allows the code to indicate it is working on a particular part of the data, and that nothing else is allowed to work on it until it is finished. Our code uses mutex locks whenever we read or write the ''<code>localised_pose</code>'' or the ''<code>awaiting_pose</code>'' flag. | |||
====Types==== | |||
To help with the project, a handful of custom types were created. These custom types are meant to make it easier to manipulate and move the data, as well as ensuring consistency and compatibility between each part of our code. The types created are <code>coord2D</code>, <code>pose2D</code> and <code>angle</code>. | |||
<code>coord2D</code> is a class consisting of two <code>doubles</code>, ''<code>x</code>'' and ''<code>y</code>''. This class is used to represent points in 2D space. It also implements a number of arithmetic operators, namely addition, subtraction, multiplication and division. Addition and division is supported between two <code>coord2D</code> objects, while multiplication and division are supported between a <code>coord2D</code> and a <code>double</code>. There is also a <code>''length''()</code> function, which is used to calculate the distance from the coordinate to the origin. In combination with the subtraction operator, this can be used to determine the distance between two points, which is a common calculation in this project. It also contains a <code>''transform''()</code> function, which takes in a <code>pose2D</code> as a transformation and transforms the point accordingly. | |||
<code>pose2D</code> is a subclass of <code>coord2D</code>, which means it has access to every function and variable defined for <code>coord2D</code>, but with some changes. Most notably, in addition to an ''<code>x</code>'' and ''<code>y</code>'' value, <code>pose2D</code> contains an <code>angle</code> ''<code>theta</code>''. This allows it to represent any position and rotation in 2D space. Being a subclass of <code>coord2D</code>, <code>pose2D</code> can be used in any situation where <code>coord2D</code> can be used, which makes it quite flexible. The class redefines most of the arithmetic operators to work properly with <code>pose2D</code>, and also has support for adding or subtracting two poses. This can be very useful when calculating an average pose. | |||
<code>angle</code> is a class meant to represent angles using a private ''<code>x</code>'' and ''<code>y</code>'' value. This means that any angle is automatically wrapped between -pi and pi. The class is designed to work seamlessly as a replacement for a <code>double</code>, and as such it supports automatic casting to and from a <code>double</code>. When casting to an <code>angle</code>, we use the <code>''sin''()</code> and <code>''cos''()</code> functions to convert the angle to ''<code>x</code>'' and ''<code>y</code>'', and when casting back into a <code>double</code>, the <code>''atan2''()</code> function is used to recover the angle. To save a small amount of performance when casting, there is a simple caching system that stores the last calculated angle as long as there are no changes. In addition to the standard arithmetic operators, which simply cast to and from a double to calculate the result, there are also the <code>''add''()</code> and <code>''multiply_weight''()</code> functions. These functions acknowledge the fact that the angle is represented by an ''<code>x</code>'' and ''<code>y</code>'' value, and allow you to manipulate those values in a different way. The <code>''add''()</code> function adds up the raw ''<code>x</code>'' and ''<code>y</code>'' values of two angles, which is very useful when calculating average angles. The <code>''multiply_weight''()</code> function multiplies the ''<code>x</code>'' and ''<code>y</code>'' values with a scalar. This is also used in average calculations, to assign different weights to specific angles. These functions are also used in the arithmetic operators for <code>pose2D</code>. | |||
===<big>'''Final Results'''</big>=== | |||
====<big>Final challenge day</big>==== | |||
On the final challenge day two problems arose from this code implementation. The first one regards the fact that the robot cannot avoid chairs when only detecting its legs. As it was seen during the challenge, this problem was solved by inserting a box underneath the chairs. When this measure was taken, the robot could smoothly avoid the obstacles. Secondly, the program did not have a replanning function. This caused troubles with the monkey that was placed to block the path in between table 3 and 4. While the local navigator was avoiding the obstacle, the global planner was not looking for an alternative path, hence pushing the robot against the obstacle. This caused the robot to stay in front of the unexpected obstacle, without replanning for a new way to reach its target. In the Reflection and Conclusions section we will discuss how this problems could have been solved. Our two attempts can be find [https://tuenl-my.sharepoint.com/:v:/r/personal/k_d_vos_tue_nl/Documents/MRC2024/DSCF9767.MOV?csf=1&web=1&nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=obVJUI here] and [https://tuenl-my.sharepoint.com/:v:/r/personal/k_d_vos_tue_nl/Documents/MRC2024/DSCF9768.MOV?csf=1&web=1&nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=izNTuE here]. | |||
==== <big>Simulation</big>==== | |||
Before implementing the code on the real setup the ''mrc-sim'' tool was used, this allowed to solve some initial bugs. Videos of the simulation can be found [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/EaEZxI1a73BKm8kraOGH9PwBg_MkOtiidXQIV4toOLu65Q?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=1345rm here] and [https://tuenl-my.sharepoint.com/:v:/g/personal/t_h_janssen_student_tue_nl/ESdbYNHVxqlNnuuaAFjhizcB1k3-USdHXrQFj-7DLr6byw?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=M5kDRE here]. The first video uses the table order [3,1,3,2], in order to show that the ''open_door'' state works well, on both sides of the door. The second video uses the order [0,2,4,3], which was the final challenge day order. | |||
N.B: Different orders were tried in the simulation, including one where the robot had to open the door from the side close to table 3. This revealed a problem in the simulation tool, which does not let the robot open the door from that side. The same was tried by ''mrc-teleop'' the robot on that side and then manually inserting the command ''mrc-open-door'', the result was the same. | |||
==='''<big>Reflection and Conclusions</big>'''=== | |||
====What went well? ==== | |||
At the end of the 10 weeks we had for this course, we managed to get a robot navigating through a dynamic environment to different tables and ask for a door to be opened. Starting from building the different components in the exercises, we had some well working implementations of the local navigation, localization and global planning. These buildings blocks were used for an overall integration that can now be executed with only a few lines of code. Some things in particular that works really well is the asynchronous localization. This means that the code is more efficient and robust while the robot is navigating through an environment. In addition to this, our local navigation used in the final testing (Vector Field Histogram) is very consistent at smoothly avoiding obstacles once detected. | |||
====What could have gone better?==== | |||
Of course there are also some things that leave room for improvement. An important lesson we learned, is that it is very important to leave enough time for testing. Our approach for integrating everything left little room for testing in the lab. This was due to the structure that was chosen for the code. Because all of the different components are commanded through one file, it was hard to test the individual parts of the code when adjustments were made. Though it is nice when you actually have all components in place, this made it difficult to test any of our code in real life until the final week of testing. This meant that we had to test and adjust our code to real life conditions in just a few hours. This far from perfect time management is also what ended up causing the chair incidents during the final challenge day. As there are no chairs in simulation, we did not have enough time to work out a way to detect the legs properly. | |||
In the end, the code worked the way we intended it to and we were able to test all functions, but it would have definitely helped if we would have had testing in some of the lab sessions before. If we had, we would have seen the chair issue in time to fix it and we would have had proper video footage of what our code can actually achieve. | |||
====What should we do a next time?==== | |||
Though the course is now finished, there are still some improvements that should be made/some ideas that would make the robot more efficient in navigating a restaurant. | |||
*Tune parameters. There are a lot of parameters in this code ranging from distances to tables to numbers of nodes in PRMs. Not all were tested to the same extend due to the time limit and room for improvement is still there. | |||
*Fix the spread calculation. Initializing localization is now dependent on a timer rather than a measure of when the localization is good enough. Fixing this would increase the efficiency and accuracy of the robot as it can already move as soon as it is localized properly. Of course, the definition of properly here should also be tested with different values. | |||
*Add a replanner. Now, our code only calculates one path from the robots position to the target (next table on the list), but is doesn’t update when the path seems unfeasible. This is an important addition to make the robot suitable for dynamic environments. This also means that there should be a measure of what an unfeasible path is. This will likely be a timeout. | |||
*Add unexpected objects to the world model. This would mean recognizing that an obstacle is ‘permanent’ and as such needs to be placed into the map that is used for path planning. | |||
Latest revision as of 19:50, 28 June 2024
This wiki page describes the work undertaken by Team Rosey during the Mobile Robot Control course. The objective was to develop functional code for a robot to navigate a map, handling both known and unknown, static and dynamic obstacles, to reach specific waypoints efficiently and in a controlled manner.
The work is organized by weeks, showcasing the team's progress in solving the given assignments and advancing toward the Final Challenge. Design decisions are justified by evaluating potential advantages and disadvantages, providing a clear explanation of our approach.
Group members:
| Name | student ID |
|---|---|
| Tessa Janssen | 1503782 |
| Jose Puig Talavera | 2011174 |
| Ruben Dragt | 1511386 |
| Thijs Beurskens | 1310909 |
| Pablo Ruiz Beltri | 2005611 |
| Riccardo Dalferro Nucci | 2030039 |
Week 1 - Don't crash code
Exercise 1 - The art of not crashing.
Overall approach
Every member of the group worked on this exercise separately, after which we combined and discussed the different approaches. Though each implementation the members of our group came up with is slightly different, they all have the same starting approach. The robot is constantly looping through the laser data and when the returned laser range of one of the laser points is within a predefined distance, the robot is commanded to act on this. Additionally, most approaches only loop through the front/middle part of the laser data to make sure only obstacles that are actually in the robots path are taken into account. The different methods of going about this are explained below.
Implementation 1: Stopping
Riccardo Dalferro Nucci & Ruben Dragt
In this implementation the instruction to the robot is the most simple. The robot is instructed to keep moving forward using the io.sendBaseReference() function and when the laser returns a distance within 0.3 meters, the robot is commanded to stop by setting the forward velocity in io.sendBaseReference() back to 0. Using this method means the robot will not continue moving as long as the obstacle is within the 0.3 meters. If the robot is in front of a wall it will stay there forever, but with a moving obstacle such as a human walking by, the robot will eventually move forward again until the next obstacle. Video of the simulation can be found here.
Implementation 2: Turning away
Using this method, the robot is not instructed to just stop but to also turn away from the obstacle. The added benefit of this approach is that the robot will be able to start moving forward again, as the laser will eventually stop returning obstacles in the set distance.
- Method 1 Tessa Janssen - In this code, the robot loops over part of the data by setting the for loop from
scan.ranges.size()/2 - rangetoscan.ranges.size/2 + range(setting variable range at 150 means a view of approximately 1.2 rad). Then, when an obstacle is detected in within a set distance e.g. 0.5 m, the forward velocity is set to 0, but the angular velocity is given a positive value. This results in the robot turning left when it has reached an obstacle. When there are no longer any obstacles the angular velocity is set back to 0 and the forward velocity is given a positive value. The downside of always turning left is that the robot can get easily get stuck in corners and will not take into account efficiency. Video of the simulation can be found here.

- Method 2 Pablo Ruiz Beltri - In this approach, a safety distance and a cone size (in number of laser points) are set. The cone is centered in front of the robot. While we are properly connected, the laser data in this cone is verified to be greater than the safety distance. If it is, the robot moves forward, if not the robot rotates. To keep a forward path, the direction of rotation is determined by assessing if the safety distance violation was in the left or the right of the cone. After testing this approach, it is concluded that it is vulnerable to corners, where safety distance violations come equally from left and right, leaving the robot in a blocked position.
- Method 3 Thijs Beurskens - Here, the cone of vision of the robot is determined by setting the minimum and maximum angle, which is then translated to the amount of points the for loop should cover. The turning direction of the robot is determined by checking on which side of the robot the obstacles are closer and thus turning where there is more space. The code also keeps track of which direction it is turning, which prevents the robot from getting stuck in a corner. This approach has again the benefit of being able to keep moving around a map/obstacle course while also being more clever on where it can go. This approach makes the robot less likely to get stuck in certain areas and makes it more robust to changing environments.
- Method 4 Jose Puig Talavera - My implementation for the
dont_crash()code initially checks whether the robot is receiving laser and odometry data. If yes, command a forward motion of 0.5 meters per second. Then, read laser data through a cone of vision. If one of the laser range values is within or at 0.3 meters, stop the vehicle. Check distance to the right (i = 200), then check distance to the left (i =800). If left > right, turn +0.3 radians per second (counter-clockwise). Inversely, if right > left, turn -0.3 radians per second (clockwise). A video of the simulation can be found here. I personally like the part where it gets stuck at a point where the distance to the left and right are really similar && has an obstacle within 0.3 meters. - Method 5 Riccardo Dalferro Nucci - After successfully implementing a
dont_crash()that would only stop once the robot encountered any obstacles, a new updated version was created. As the first version, this code initially checks if theLaserDatais received correctly, if so, a velocity of 0.5 meters per second in the x direction is given. While the robots moves a for loop checks if there is any obstacle in the cone of vision of the robot, which is of plus and minus one radiant from the x axis. When this loop detects an object it stops the forward motion. If the closest object is on the right it will turn left and viceversa. This code still showed some problem, like for example when the right and left obstacles are at the same distance the robot just start to oscillate in between and it is unlikely to get out of that. It also showed some problem when going towards a wall from a very skewed angle, some times it was turning to slow and slightly bumping into the obstacle. A video of the simulation can be found here.
Exercise 2 - Testing your don't crash
During the first testing session it became clear that the parameters that were used in simulation needed to be adjusted to the robot in real life. Especially the velocity needed to be tuned down when using Coco/Bobo as they do not have the speed limiter built in. Moving too fast towards an obstacle meant that when it saw an obstacle within the safety range, it did not have enough time to stop before hitting the obstacle. Though tuning the velocities and obstacle distances was a doable fix and the code from method 3 (Thijs) ended up working very nicely in an environment with multiple different obstacles. The full video showing this approach can be seen here and a brief clip is shown in figure 1.
Vector field histogram:

Thijs Beurskens, Pablo Ruiz Beltri & Riccardo Dalferro Nucci
Concept
The main idea behin the Vector Field Histogram (VFH) method is to treat objects as vectors in a 2D cartesian histogram grid and create a polar histogram to determine possible "open spaces" to get to the goal. A polar histogram is created, centered in the robot's current position, using the LaserData and a number of sectors that can be given as an input. Every Laser Data from min_angle to max_angle (the data behind the robot are considered as not visible, even though defined in the polar histogram) is then treated as a vector, where its magnitude and direction are computed based on the following formula.
[math]\displaystyle{ \beta = \arctan(y - y_{current}, x - x_{current}) }[/math],
[math]\displaystyle{ m = a - b * distance }[/math],
where a is the product of b and the maximum distance, which needs to be given as input along with b. Moreover, distance is the magnitude of the vector expressing the current position. Using a sendPath command, a visual representation of the sectors was given. Once the histogram is completly defined the program finds every valley, which means every sector with a value below threshold (also given as input) and chooses the best one, that is the one closest to the target direction. Every value of the histogram is normalized. A control input is then given to the robot to make it go in that direction. To note that a PID has been added to control the rotational speed, in order to best align the robot to the goal direction.
Simulation and Implementation
When simulating the code, the visual representation of the polar histogram was very useful, allowing to debug eventual errors in the code. The code was tested in the given maps file, with increasing difficulty. The simulations showed that with an increasing number of obstacles the robot was prone to cutting corners, up to the point where in map 4, due to a very narrow point of the map, the robot slightly bumped into a wall, which was caused by the fact that the robot has no knowledge of its dimensions. This problem was then solved by increasing the threshold. Screen recording of the simulation can be find in map1 and map4
Once the program was working well in the simulation it was tested in the lab. At first, the Hero robot was moving very erratically, and was very aggressively cutting corners. Upon closer inspection, it was clear that the code assumed the laser range finder is at the center of the robot, but this is not the case for Hero. The problem was resolved by translating all the laser points to compensate for the offset. As it can be seen from Fig. 2, the code showed good results also on the real robot.
Reflection
Advantages of the approach
The first advantage of this approach is the computational efficiency. Moreover, the implementation on the real robot showed a good robustness to noisy sensor data. Furthermore, the mathematical tools used, such as the polar histogram and the vectors, were quite familiar object, which allowed to implement the code without too many difficulties. Since the object density is computed on real-time LaserData the program is quite robust for what concerns moving objects or changing environments. Finally, since the code looks for closest free valley to the goal direction, the VFH method does not usually suffer from local minima.
Disadvantages of the approach
The first disadvantage is that this method might struggle with narrow passages and sharp corners. Moreover, since this code uses real time LaserData the robot needs to have a relatively low speed, to be able to compute the new direction before bumping into an obstacle.
What could result in failure?/How would you prevent these scenarios from happening?
As said above, a narrow passage or a sharp corner could result in failure. This could be fixed by properly tuning the threshold. This problem was clear when testing on the real set-up, when the robot would hit some corner or struggling when trying to pass in a narrow passage. This could also be caused by the fact that the robot has no knowledge of its dimensions at all, and it could therefore be solved by implementing this.
After the test in the lab, when this problems arised, some modifications were made to the original code in order to try to solve them. First of all, the actual movement direction is now weighted based on the histogram values in the valley, which resulted in a smoother control input. Moreover, the eligibility of the valley, which was initially based on the angle, was made dependent on the actual width of the valley. By checking the distance to the object and the angle in fact, it is possible to compute the actual width of the free valley, which partially solved the narrow passages problem. A video of this new version implemented in the lab can be found here.
Artificial potential fields:
Tessa Janssen, Jose Puig Talavera & Ruben Dragt
Concept
The main idea behind an artificial potential field is calculating both an attractive potential towards a target and a repulsive potential away from obstacles, which are summed together to form the potential field. The resulting force vector is calculated by taking the negative of the gradient of the potential field.

The attractive potential is determined by the equation 2 and is dependent on the difference between the current position of the robot and the target position. The target position was set as a point 6 meters further in the y direction than the starting position, the current pose was calculated by using odometry data from the robot (with starting coordinate (1.5, 0, 0)). Because the odometry is not perfect, this introduced a small error to the final position of the robot, which was not corrected for in this exercise. The repulsive force is given by equation 3 and it uses laser data to determine the distance from the robot to an obstacle. For this specific implementation, each laser point in the for-loop returning a distance that fell within the predefined space buffer ρo was registered as a separate obstacle, with the corresponding repulsive potential being added to the total potential field. The constants katt and krep were used to adjust the relative importance of attracting and repulsing.
The forces are broken down into [math]\displaystyle{ F_x }[/math] and [math]\displaystyle{ F_y }[/math] components after calculating the analytical partials derivatives of the attractive and repulsive potential energies. The partial derivatives of the attractive potential energy are shown in equations 4 and 5. The partial derivatives of the repulsive potential energy are in equations 6 and 7. The resulting force vector at the current location of the robot was used as input to the robot by calculating the angle corresponding to the vector. These are in equations 8 and 9. The commanded angle is the arctangent of the x and y components of the force (shown in equation 10). This was used as reference angular velocity for the robot, while y-velocity (world frame) was kept mostly constant. Mostly constant here means that in the original implementation the velocity of the robot was kept low to allow the robot to have enough time to respond to all obstacles, but after testing, code was added that made sure the robot picked up its speed when there were no obstacles in sight.
Simulation and Implementation

Testing the code in simulation revealed that tuning katt, krep, ρo, and the forward and angular velocity were very important. Map 1 compared to map 4, for example, showed that when there are not a lot of obstacles, the robot can get away with higher attraction to the target, making the path more efficient. With more obstacles, however, the robot would get too close to the walls and the krep had to be retuned as well as increasing ρo. In the first few iterations of the code, the robots movements were very jittery. This was due to the calculation of the angle of the force vector. When moving up in difficulty through the different maps, the forward velocity and angular velocity had to be reduced in order to get a smooth trajectory. Screen recordings of the simulation were made for both map 1 and map 4.
One of the first test sessions after the code was working well in simulations, already showed a smooth trajectory as can be seen in the full video here or in the snippet in figure 3. The robot moves around the objects to the target approximately 6 meters away, but at a pace that is quite boring and seems inefficient from a users point of view. Code was then added to make the robot increase its speed when it no longer saw any objects within the buffer ρo. This helps slightly with efficiency, but only once it was already outside of the maze we set up. Another video including this speed increase can be found here.
Reflection
Advantages of the approach
One advantage about the potential fields is that it makes sense intuitively: walk away from obstacles and walk towards your goal. The mathematical components that are required to calculate the potentials, gradients and corresponding vectors are also familiar methods, making it a very doable method to implement from scratch. Another advantage is that the repulsion to obstacles is calculated on real-time laser data. This makes the robot quite robust to changing environments as new obstacles (walls around the corner or people standing in the way) are incorporated into the navigation immediately.
Disadvantages of the approach
A disadvantage that is clear from both the simulation and the test sessions is that in order for the robot to be able to recognize all obstacles in time, its velocity needs to be quite low. This speed-accuracy trade-off is especially evident in more complex environments with many obstacles. And although it is an advantages that the robot updates the obstacles around it constantly, the computational speed is not always sufficient to recognize moving obstacles such as people. In addition, in case of local minima in the gradient, the robot will get stuck while not having reached its target. Another disadvantage that was best seen in the simulation was that the robot most from left to right a lot when passing through a narrow street as the resulting force vector keeps shifting from left to right.
What could result in failure?/How would you prevent these scenarios from happening?
One situation that could lead to failure is a local minimum as explained above. In case the robot is faced with a wall directly between itself and the target and the repulsive potential is equal and exactly opposite to the attraction potential, the result will be net zero and the robot will not move. This might be prevented by including some code that makes sure that if the input to the robot is zero, but it has not yet reached it target it will go in a certain direction. This correction should of course be careful of nearby obstacles. Another potential failure is not recognizing a living obstacle passing by and crashing into it. Completely eliminating this is hard, but it can be mitigated by having a low speed and increasing the range in which it classifies obstacles. Both of these give the algorithm more time to process the obstacle.
A* algorithm implementation:
Pablo Ruiz Beltri, Riccardo Dalferro Nucci & Ruben Dragt
Concept and Implementation
The A* algorithm is a widely used path finding and graph traversal algorithm. It combines the benefits of Dijkstra's Algorithm and Greedy Best-First Search to find the shortest path between nodes in a weighted graph. The calculation efforts are a bit higher than the previous mentioned algorithms but an advantages of the A* algorithm over the other two algorithms is that it will always find the shorters route if there exists one. To do this it uses a value of the cost to reach a target and a value for the distance from that new node to the target. The code that calculates the shortest path between the nodes to the end goal by follows the next structure
Initialization
The code starts with an open set called open_nodes containing the initial node _start_nodeID, and another set closed_nodes where the visited nodes will be stored, to make sure that they are only visited once. The next step is to initialize a cost map to keep track of the cost from the start node to each node "h-cost", using the function calculate_distance(). Then a heuristic map is initialized estimating the cost from each node to the goal called "g-cost", these are initialized at the start as infinity and will be recalculated for each visited node to the surrounding nodes. This way the nodes with no edge connecting them from the current_node will have a cost that is infinitely large. The f-cost is the summation of the g-cost and h-cost is calculated for the initial node and the nodes connected to the initial node by edges.
Processing
While the open set is not empty, select the node with the lowest f-cost from the open nodes set. If this node is the goal, the path is found. Otherwise, the current node is moved from the open set to the closed set. While moving to different nodes the parent node of the node is also stored in a list path_node_IDs, the eventual parent node list will have the nodes stored that are part of the shortest path from the starting node to the goal.
Expansion and repeat
For each neighbor of the current node, calculate the tentative g-cost. If this tentative g-cost is lower than the previously recorded g-cost for that neighbor, update it and change the parent node to the current node. This will also result in a new f-cost namely the f-cost for the neighbor is f = new g + h. Finally if the neighbor is not in the open set, add it. This process is then continued untill the goal is reached or the open set is empty, indicating no path exists. To store the optimum path from the initial node to the goal path_node_IDs, we start at the goal node and move to its parent node, because of this every node will have a list of a certain length with its parent nodes. If the current node is the goal node the robot just has to follow the parent nodes of the goal node to reach the goal.
Probabilistic Road Map implementation:
Tessa Janssen, Jose Puig Talavera & Thijs Beurskens

Overall approach
For this exercise a framework of code to create a Probabilistic Road Map (PRM) was already given. We worked through the given exercises one by one to obtain the final result as is shown in figure 4. More detailed explanations of each sub-exercise are given below.
Inflate the map
The first exercise was to inflate the occupied spaces in a map to adjust for the size of the robot: inflatedMap(). This was done by looping over the pixels of the image by column and row and checking if the pixel has a value below the threshold that was previously defined in the assignment (thresh_occ = 130). If this is the case, the pixel is deemed occupied and a matrix of size radius * radius is looped through, centered around that pixel. Then every pixel in that square is given value 0. The variable radius can be set depending on the size of the robot that is used.
Check vertices
The second exercise was writing a function that checked if the vertices generated into the map were at least a certain distance away from each other: checkIfVertexIsValid(). Our function loops through the existing vertices in the Graph, and for every vertex calculates the distance between this one and new_vertex that is given as an argument. The distance between the new vertex and the existing ones is calculated by applying the Pythagorean theorem on the distances between the first and second coordinates of the vertices. If the distance is smaller than some allowed distance (here we chose 0.25 meters), the function returns false, meaning the vertex is not added to the Graph.

Check edges
The final exercise is about checking if an edge between two vertices is valid: checkIfEdgeIsValid().
First this means checking if the two vertices an not too far away from each other (checkIfVerticesAreTooClose()). This function was filled with pretty much the exact same code used incheckIfVertexIsValid(), only now the function checks if the distance between two vertices is bigger than some allowed distance (here we chose 1 meter). If this is the case the function returns false and no edge is created between these two vertices.
A second requirement is that the edge between two vertices cannot cross an obstacle:checkIfEdgeCrossedObstacle(). This function converts the coordinates (first and second) of two vertices into their pixel equivalent and arranges them to make sure that pixel 1 is always to the left of pixel 2. The function loops over all pixels that lie in the square you can draw with the two pixels as opposite corners. Then for each pixel in this square it is checked if it is occupied, using the same threshold as before. If it is indeed occupied, the distance from this pixel to the line connecting the corner pixels is calculated. If this distance is within a 2 pixel range, it is said to be in the 'edge' territory and the function will return true: the edge crosses an obstacle. This method was chosen because it only considers obstacles a problem when they are actually on the edge between two vertices. This makes efficient use of the map as will not remove edges only because they are too close to obstacles.
Combining A* and PRM
Combining the two frameworks described above results in a path planned such as in figure **. The A* algorithm uses the PRM graph as input vertices to find the optimal path to the starting position to the target.
Combining Local and Global planning
For a first iteration of combining the local and global planning, the code from the local planners in week 2 - Local Navigation was used to replace the path planner in this assignments framework. This meant that the global planner would provide the local navigation with its next target as defined by the A* algorithm. In this version the Vector Field Histogram method was used. From the simulation it became clear that parameters such as when a 'target' was reached needed to be tuned. Due to the local navigation avoiding obstacles along the way, the robot would sometimes 'miss' a vertex in the planned path. To mitigate this and keep the robot from needlessly searching for this one vertex, the radius in which a target was marked as reached was increased to xx. This meant that the robot only had to pass nearby in order to continue to the next one. This first version of global+local planning was tested in the lab by building the map_compare to scale. The full video can be seen here and a brief snippet is show in figure 5.
How could finding the shortest path through the maze using the A* algorithm be made more efficient by placing the nodes differently? Sketch the small maze with the proposed nodes and the connections between them. Why would this be more efficient?

Removing the nodes that are on a straight line would make the algorithm more efficient. We would still need nodes on all junctions as it is a potential location where the robot could turn. The sketch in figure 6 shows an example of how the nodes can be placed more efficiently. This method only needs 20 nodes compares to the 42 you would need for each block of the grid.
Would implementing PRM in a map like the maze be efficient?
No it would not be more efficient because there is no guarantee that all the nodes would connect and if a corner is missed then algorithm would not find the turn.
What would change if the map suddenly changes (e.g. the map gets updated)?
If the map gets updated and the global navigation (A* and PRM) is not configured again on the new map it could occur that a node that the robot tries to go to because it was chosen by the A* algorithm is no longer reachable. For example a person or object could cover the node, in this case the local navigation will make sure that the robot does not crash but the node will not be reached and therefore the robot will be stuck in a never ending loop. A way to overcome this is to build in a timer where after a certain amount of time the robot moves on to the new node or the laser data is used to update the map and the global navigation function is configured again on the new map with the obstacle in it.
How did you connect the local and global planner?
Connecting the local and global planner requires three main steps. First of all, a library for the local planner was made. Then this library was connected to the global planner via CMakeLists.txt. Finally an instance of the local planner and the pose tracker was made and the points created by the global planner were passed to it.
Test the combination of your local and global planner for a longer period of time on the real robot. What do you see that happens in terms of the calculated position of the robot? What is a way to solve this?
Implementing local and global planner together for a long time period showed some problems in the robot position. Particularly, this was drifting more and more with time. The only solutions to this problem is to add localization usign LRF data.
Run the A* algorithm using the gridmap (with the provided nodelist) and using the PRM. What do you observe? Comment on the advantage of using PRM in an open space.
The advantage of PRM in open space is that it can create diagonals which are more efficient than simply orthogonal directions.
Week 5 + Week 6 - Localization
Particle filters are a type of probabilistic algorithm used for estimating the state of a system that evolves over time. The main idea behind this concept is to approximate a probability density function representing a continuous random variable by a set of "particles", where each particle represents a possible value of the state. Particles are moved based on the robot's odometry and the weight of each particle can be adjusted based on the LRF data. Finally, particles are resampled based on their weights to focus on the more likely poses. Some advantages of this method are that the particles can be distributed over the map in any form and that the predictions and measurements models have minimal restriction (i.e. the noise can be non-gaussian and the model can be non linear). The main disadvantages are the fact that the computational load is obviously proportional to the number of particles and that the number of required particles scales poorly with the state dimension.
0. Exploring the code framework
How is the code is structured?
The workable code is split into two folders called FilterComponents and Filter. The Particle and Resampler classes live in the Filter components folder whereas the ParticleFilter and ParticleFilterBase classes live in Filter folder. The Particle class holds all the meaningful information and methods regarding each particle. This class will be called by methods in the other classes. Depending on the arguments passed to the constructor, a particle with uniform distribution or Gaussian distribution can be constructed. The other classes are in charge of predicting, updating and resampling the particles. The code is nested with Particle being the lowest level and ParticleFilter being highest level.
What is the difference between the ParticleFilter and ParticleFilterBase classes, and how are they related to each other?
The difference between the ParticleFilter and ParticleFilterBase classes is that ParticleFilterBase implements the estimation and propagation of the particles whereas the ParticleFilter class determines when and how particles should update and propagate. ParticleFilter is a public subclass of ParticleFilterBase, meaning all the methods and members from ParticleFilterBase are also available in ParticleFilter.
How are the ParticleFilter and Particle class related to eachother?
The ParticleFilterBase class (and thus also the ParticleFilter class) contains a ParticleList, which is a vector of Particles. The Particle class contains methods for updating individual particles, and ParticleFilterBase contains methods for evaluating the complete ParticleList.
Both the ParticleFilterBase and Particle classes implement a propagation method. What is the difference between the methods?
The ParticleFilterBase and Particle propagation methods do two different things. The propagateSample() method of the Particle class ensures a detailed pose update of one particle, incorporating the motion model and noise. On the other hand, the propagateSamples() method of the ParticleFilterBase class calls the propagateSample() method for every particle by looping through each one.
1. Week 5
1.1 Initializing the particle filter
As explained above, the particle filter estimates the pose of the robot through a set of weighted particles, each of them representing a hypothesis of the current robot pose. The set of all the particles approximates the probability distribution over all possible robot poses. In this part of the assignment the methods which construct the set of particles is implemented. The implementation can either be done using uniform or gaussian distribution.
Inside the Particle class, precisely in the Particle method, a random pose is generated. A pose is composed of x and y coordinates, and an orientation theta. Depending on the input given to the function, the pose can either be generated with a uniform distribution (Particle::Particle(&world, &weight, *generatorPtr);) or with a gaussian one (Particle::Particle(&world, mean[3], sigma[3], &weight, *generatorPtr);) .
Finally, the uniform distribution is easier to implement and it does not require any a priori knowledge of the initial position of the robot, but is obviously less precise and it will take more iteration to find the actual position of the robot. The gaussian distribution, on the other hand, it requires a good estimate of the initial position, but it will be more likely for most of the particles to be close to the real pose, allowing to find it faster.
1.2 Calculating the pose estimate
Interpret the resulting filter average. What does it resemble? Is the estimated robot pose correct? Why?
The filter average resembles the center of mass of a particle cloud. The denser the weight, the more influence it will have on the robot pose. Right now, the estimated robot pose is not correct since no laser data is being applied and solely relying on odometry.
Imagine a case in which the filter average is inadequate for determining the robot position
The filter average is inadequate for determining the robot position when there is wheel slip or uneven terrain (loss of odometry data). If the odometry data is noisy then this will also cause issues in estimating the robot pose.
1.3 Propagate the particles with odometry

Why do we need to inject noise into the propagation when the received odometry information already has an unknown noise component?
Injecting noise would be unnecessary if the odometry information didn't have any noise component. The unknown noise has to be compensated for using the laser data, and to do that we need to check multiple locations. Explicitly injecting noise distributes the particles across a wider area, which increases the chance that at least one of the particles is in the correct location. Moreover, noise maintains particle diversity, which ensures that particles do not converge to quickly to a narrow area, potentially missing the true robot pose. Thanks to this, the filter remains adaptable to new sensor data.
What happens when we stop here, and do not incorporate a correction step?
Without incorporating the correction step, the particle filter will be no better than simply following the odometry data. By simply injecting noise, without checking the likelihood of the particles, there is no additional information gained, and the error is likely bigger than using just the odometry data.
2. Week 6
2.1 Correcting particle with LiDAR
What does each of the component of the measurement model represent, and why is each necessary.
In the implemented measurement model method, each component helps to have an accurate representation of the likelihood of a measurement given a predicted particle pose. The gaussian component models the probability of the actual measurement being close to the predicted one (the normalization of the gaussian integral makes sure that the likelihood is properly scaled over the range of possible measurement. Furthermore, the exponential component accounts for when the actual measurement is shorter than the predicted one, while the discrete component models the probability of a maximum range reading, which usually indicates that no obstacles were detected within the sensors range. Finally, the uniform component accounts for random measurements that do not fit the other models, basically providing the same probability for any measurement.

With each particle having N >> 1 rays, and each likelihood being ∈ [0, 1], where could you see an issue given our current implementation of the likelihood computation.
The first issue comes from the number of rays for particle, being this way bigger than 1 it increases the computational complexity. This could jeopardize the real-time performance of the program. It is also important to correctly normalize each likelihood, in order to avoid having inaccurate weight updates after the resampling.
2.2 Re-sampling the particles
What are the benefits and disadvantages of both the multinomial resampling and the stratified resampling?
Multinomial sampling is a simple method to implement since it involves drawing samples based on particle weight and requires little to no preprocessing of data. On the other hand, this sampling method is known for yielding higher variance since there are scenarios where only high weight particles will be chosen from a set. For stratified sampling however, the set has to be divided into strata therefore making it a slightly more complex problem. On the positive side however, stratified sampling results in reduced variance and higher sample diversity due to its nature of breaking down the set into strata.
Week 7 + 8 + 9: Final Challenge
The State flow
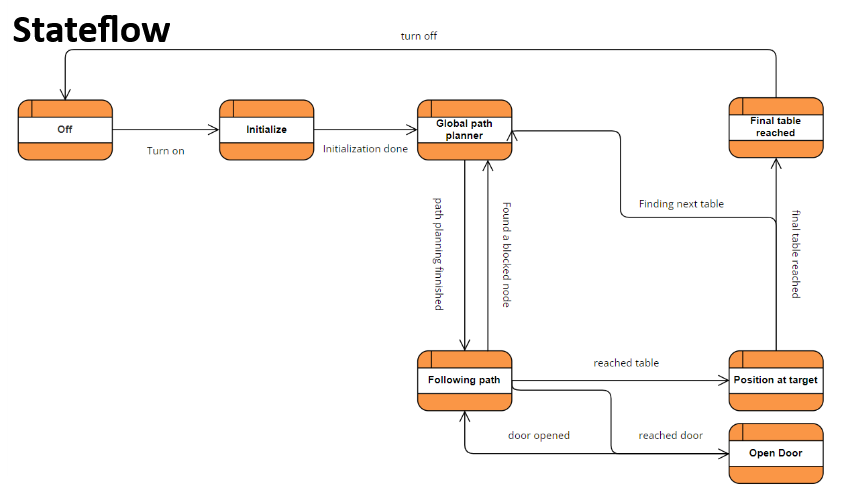
In figure 10 the state flow as shown during the presentation is shown. This framework was used as a guide to integrate the separate components into a state machine. Below, the different states from this diagram are explained in greater detail. The relevant functions and variables are explained as well as the boundaries that are set for moving on to the next state. This whole state process is managed by the Navigator class that performs the actions described in the state flow diagram. This class contains a function corresponding to each state, except off, all the variables and classes that are persistent for each loop cycle, a constructor to initialize every variable and class, and finally a run() function, which implements the main loop of the program.
To keep track of the current state, the Navigator class contains the current_state variable, which is of type state. state is an enum, with an entry for each possible state. The run() function consists of a while loop, with a single switch statement. This switch statement checks current_state and runs the corresponding state function. The loop also contains r.sleep(), which is used to keep a consistent time for each loop step. The system is designed such that each state function represents a single loop iteration, and as such the states do not contain large loops. The idea is that a state function will be called in a loop, as long as current_state remains unchanged. To change the state, the state function has to modify the value of current_state, and when the state function returns, the switch statement will run the new state function on the next loop iteration. It may be desirable to return immediately after changing the current_state variable, but this is not required, and the state will continue to execute as normal until it returns normally. As mentioned previously, there is one state without a state function, namely state::off. When current_state is set to state::off, the switch statement will instead terminate the main loop, and as such the program ends.
State ~ Off
The off state is not a proper state. It does not have a function. Instead, it is used to indicate the program should terminate.
State ~ Initialize
The Initialize state is the first state reached by the robot right after being turned on. Although having a map of the layout of its environment, the robot has no clue on its initial position. For this reason, this first phase is designed to let the robot localize itself. As a first step the odometry data are updated, then laser data are defined and localization, as explained in "Week 5 + Week 6: Localization" section, starts. To be able to understand when the robot is localized, thus the next state can be reached, a spread variable is defined as the root mean square of the weighted error of the localization. The state is structured such that the robot enters an if statement: if the spread is greater than an acceptable value (or the loop has been completed less than 50 times) a rotation is commanded (io.sendBaseReference(0,0,1)) while the robot still performs the localization. When the if statement becomes false the robot enters the else condition: it stops spinning and the current_state is set to state::planning_global. Localization has been performed. The extra constraint of at most 50 rounds was added to avoid the robot getting stuck in localizing: we decided it would be better to start with a bit of a bigger spread than spin in circles too long.
When testing this program one problem arose: the spread was never lower than the acceptable constant, and the state change would only happen after 50 loops, even though the simulation did show the spread decreasing significantly. This is probably due to an error in the error rms computation. This state would have been faster if the code worked as intended, but this problem did not affect the whole system, since the robot was always localized after 50 loops.
State ~ Global path planner
As mentioned before, once the initial localization is completed the state is switched to the global path planner. In this state, the global planning is executed to get higher level optimal path from the desired waypoint. First, the start is set to the current location, which makes the robot more efficient as it does not have to use local navigation to get to the starting position. The goal coordinates are read from the config file one by one, this means that the paths are individually calculated every time a goal is reached. Both start and goal are pose2D types and do not necessarily coincide with a specific node, in fact, they most likely don’t. To solve this, plan_path() runs through all the nodes in the graph to find the closest nodes to both the start and goal. Once found, we execute the A* algorithm to find the optimal route as explained in “Week 4 -Global navigation”. In case this task is unsuccessful, the robot is set to communicate it that and the specific table (goal) that was not able to plan a path to, and the table is skipped for the next one. If the path is planned successful, the robot is commanded to communicate that it did it and the table goal, current_state is set to state::following_path.
One situation that arose during the implementation of opening door functionality was that the vertices that would serve as waiting node that had to be reached to enter the state_open_door() could land on the door or very close to it such that local navigation would not allow to reach the point. This was solved in the prm by declaring as invalid the vertices that randomly landed in the near door area that was tuned.
State ~ Following path
This state is entered when the global planner has drawn out a path to the next table. It uses the local navigation class (explained in more detail below). In this state the required variables are set for the local navigation to be executed. This included the target coordinates that were computed in the global planner and the current position of the robot. The local navigation is executed unless one of two thing happens before it reaches this statement.
First the robot can be near the door. In the if-statement it is first checked that the door is indeed currently on the path of the robot. This is done by a separate function door_on_path() that checks if the door is on the planned path, if so which node is placed in front of the door, and if the robot is currently on that node. It is also verified that the door has not been checked before to see if it is open. If it were, it would be redundant to check again, when it can already pass through. If both statements hold, the robot is brought to a stop, in order to move on to the next state: state::open_door. Before changing the state, the bool requested_open_door is set to false. A variable that is used later on to make sure the door is only requested to be opened once.
A second way the robot does not go through with the local navigation, is when the robot is close enough to the table it is approaching. This if-statement is entered if the distance of the robot is within a set threshold of the table. This threshold was set to 0.2 m. reaching this statement means the state is switched to state::approach_table where the final positioning of the robot with respect to the table is determined. The value of 0.2 m was found through trial and error in both simulations and in the lab. This value allowed for the path following to be able to properly do its work before the aligning to the table takes over. It is also far enough away that the robot does not have to bump into the table before taking its final position.
State ~ Open door
The state open door is reached when in the following path state a node is reached with an edge that will go through the door. If the door has not been checked yet the new state will become “Open door” and the speed will be set to zero in x y and theta. Also the variable requested_open_door will be set to false, this variable exists to be able to open the door every time in the case that the door is closed again after opening it. When the robot is in the open door state it will set the target angle and the current pose and use this to run the align_to_angle() boolean function which will align the robot with the angle the user inputs if this is not the case already and returns 'true' when this action is finished.
If 'true' is returned the robot is aligned to the door, at this point the laser data is stored and transformed to points using a laser_to_points() function which transforms the laser data to a vector of coord2D points, which includes x and y , using the scan data the current pose and the position of the laser scanner on the robot. It then uses a process similar to the vector field histogram method to check for the door being open or not. To be more precise a field of view for the door is defined door_field_of_view which was set at 0.25 because we wanted a narrow enough angle such that the robot would not see the edges of the doorway . The direction of every point was then calculated by the predefined angle class to get the angle to every point. If this angle minus the rotation of the robot was within the 0.25 radians bound the distance to that point was added to the sector and the sum_of_weights variable is increased by 1. This process was performed for every point. If the sector divided by the weights was less than the distance to the node behind the door the robot knew the door was open, in this case the new state will become following path and checked_door will be set to true. If not the door was closed and the robot will ask for the door to be opened and the requested_open_door will be set to true. In the new loop true this state the robot should find the door to be opened if it was not the case before and such the robot will move to the following path state.
State ~ Approach table
The approach table state is set as the current state when the robot is close enough to a table. This is measured by calculating the distance between the current pose of the robot and the table which is the target of the robot and checking if it is smaller than a predefined threshold in our case 0.2. We found during testing that 0.2 was sufficiently close, taking robot size into account, to perform the alignment actions of the approach table state and not to close such that table edges could be hit.
In the approach table state a timeout is started if this has not been done yet, also timeout_started is set to true, this is done to make sure the timeout is not restarted in a new iteration. The timeout is actually a counter that adds 1 to cycle_counter for every cycle and therefore the cycles devided by the frequency are used as a measurement of time. If the approach timeout is reached, which was set at 15 seconds, is not reached and the robot is not close enough to the predefined approach pose it is currently trying to reach (same threshold as before applies) the approach pose is assigned to local_navigator.target and the local navigator is used to move to that goal. Two things can happen then either the timeout is reached in which case the approach posed is changed to the next one in the list until there is no new approach pose anymore. In this case the robot will say that it could not reach the table and the state is changed to table reached. The other thing that can happen is that the robot is actually within the predefined threshold of the approach pose. In this case the robot will align with the table using the same align function as mentioned in open door. If the correct angle is reached the robot will greet the table by table number and go to the table reached state.
State ~ Table reached
If the robot has alligned to the target table and the order has been delivered the current_state will be set to state::table_reached. In table reached the motors are all set to zero and a timeout is started if this is not done already, the timeout exists because we wanted the robot to wait at the table for 10 seconds, if the timeout is reached the robot will go to the next state. As long as this timeout is not reached i_next is increased such that the robot can go to the next table. If this value is higher than the size of the table list the robot will go to the off state else the robot will go to state::planning_global and calculate the path to the new table.
Classes
- Data handler: The
DataHandlerclass is designed to interface with an IO system to retrieve odometry and laser data for use in navigation and localization. The class holds two methods:getOdomData()andgetLaserData(). The first method,getOdomData(), is in charge of checking whether there is odometry data and returns the latest data as apose2Dtype if it exists. Similarly,getLaserData()checks for laser data and returns anemc::LaserDatatype if the data exists. - Local Navigation: The
LocalNavclass is designed to provide flexibility in the local navigation approach. The constructor, among other arguments, takes a JSON file object from which parameters are read. In this configuration file, the approach can be changed from a Vector Field Histogram to Artificial Potential Field method by simply changing the "approach" parameter to either "histogram" or "potential_field." - Global Navigation: The
PathFollowerclass is designed to design a path made up of a sequence of 2D coordinates. The methods in the class do the tasks of loading settings, setting the path, updating the current position, and checking whether the target has been reached. ThePRMclass deals with the loading of the map and creation of the roadmap. The methods generate random vertices that are evaluated to make sure that vertices are not in the walls nor too close to each other, to fully populate the map. The edges are also verified not to cross any wall. - Localisation: The
PoseTrackerclass deals with localization. The class takes in odometry data and keeps track of the odometry since the last update. It is also possible to provide it with LRF data, which will allow it to run a particle filter and update the location. There are two public functions that can be used to localise:perform_localisation()andperform_async_localisation(). perform_localisation runs thelocalise()function and resets the odometry data.localise()is a private function that deals with the particle filter and returns the new location. Using this method, the localisation runs in the middle of the program, and because localisation can take a lot of time, this can block other parts of the code from running immediately. This method is used in the initialisation, because in this state, the only thing we want to do is get our localisation to a reasonable accuracy. The second function,perform_async_localisation()is a bit more involved. Instead of running thelocalise()function directly, this function runsasync_localise()in a new thread. It also sets theawaiting_poseflag indicating that localisation is running, and it sets an estimate forlast_localised_poseand resetsodom_since_last_update, because we don't know when localisation will be finished, and when the result is in, theodom_since_last_updatehas to correspond to the situation when localisation was called. Meanwhile, theasync_localise()function callslocalise(), and when this function returns, it setslast_localised_poseto the result. It also resets theawaiting_poseflag, since localisation is no longer running and a new localisation can now be performed. Because we are now accessing the same data from different threads, we may run into an issue known as a race condition. This happens when two parts of the code attempt to read or write the same data at the same time, and in c++, this results in undefined behavior, which is bad. To prevent race conditions, we use something called a mutex. A mutex allows the code to indicate it is working on a particular part of the data, and that nothing else is allowed to work on it until it is finished. Our code uses mutex locks whenever we read or write thelocalised_poseor theawaiting_poseflag.
Types
To help with the project, a handful of custom types were created. These custom types are meant to make it easier to manipulate and move the data, as well as ensuring consistency and compatibility between each part of our code. The types created are coord2D, pose2D and angle.
coord2D is a class consisting of two doubles, x and y. This class is used to represent points in 2D space. It also implements a number of arithmetic operators, namely addition, subtraction, multiplication and division. Addition and division is supported between two coord2D objects, while multiplication and division are supported between a coord2D and a double. There is also a length() function, which is used to calculate the distance from the coordinate to the origin. In combination with the subtraction operator, this can be used to determine the distance between two points, which is a common calculation in this project. It also contains a transform() function, which takes in a pose2D as a transformation and transforms the point accordingly.
pose2D is a subclass of coord2D, which means it has access to every function and variable defined for coord2D, but with some changes. Most notably, in addition to an x and y value, pose2D contains an angle theta. This allows it to represent any position and rotation in 2D space. Being a subclass of coord2D, pose2D can be used in any situation where coord2D can be used, which makes it quite flexible. The class redefines most of the arithmetic operators to work properly with pose2D, and also has support for adding or subtracting two poses. This can be very useful when calculating an average pose.
angle is a class meant to represent angles using a private x and y value. This means that any angle is automatically wrapped between -pi and pi. The class is designed to work seamlessly as a replacement for a double, and as such it supports automatic casting to and from a double. When casting to an angle, we use the sin() and cos() functions to convert the angle to x and y, and when casting back into a double, the atan2() function is used to recover the angle. To save a small amount of performance when casting, there is a simple caching system that stores the last calculated angle as long as there are no changes. In addition to the standard arithmetic operators, which simply cast to and from a double to calculate the result, there are also the add() and multiply_weight() functions. These functions acknowledge the fact that the angle is represented by an x and y value, and allow you to manipulate those values in a different way. The add() function adds up the raw x and y values of two angles, which is very useful when calculating average angles. The multiply_weight() function multiplies the x and y values with a scalar. This is also used in average calculations, to assign different weights to specific angles. These functions are also used in the arithmetic operators for pose2D.
Final Results
Final challenge day
On the final challenge day two problems arose from this code implementation. The first one regards the fact that the robot cannot avoid chairs when only detecting its legs. As it was seen during the challenge, this problem was solved by inserting a box underneath the chairs. When this measure was taken, the robot could smoothly avoid the obstacles. Secondly, the program did not have a replanning function. This caused troubles with the monkey that was placed to block the path in between table 3 and 4. While the local navigator was avoiding the obstacle, the global planner was not looking for an alternative path, hence pushing the robot against the obstacle. This caused the robot to stay in front of the unexpected obstacle, without replanning for a new way to reach its target. In the Reflection and Conclusions section we will discuss how this problems could have been solved. Our two attempts can be find here and here.
Simulation
Before implementing the code on the real setup the mrc-sim tool was used, this allowed to solve some initial bugs. Videos of the simulation can be found here and here. The first video uses the table order [3,1,3,2], in order to show that the open_door state works well, on both sides of the door. The second video uses the order [0,2,4,3], which was the final challenge day order.
N.B: Different orders were tried in the simulation, including one where the robot had to open the door from the side close to table 3. This revealed a problem in the simulation tool, which does not let the robot open the door from that side. The same was tried by mrc-teleop the robot on that side and then manually inserting the command mrc-open-door, the result was the same.
Reflection and Conclusions
What went well?
At the end of the 10 weeks we had for this course, we managed to get a robot navigating through a dynamic environment to different tables and ask for a door to be opened. Starting from building the different components in the exercises, we had some well working implementations of the local navigation, localization and global planning. These buildings blocks were used for an overall integration that can now be executed with only a few lines of code. Some things in particular that works really well is the asynchronous localization. This means that the code is more efficient and robust while the robot is navigating through an environment. In addition to this, our local navigation used in the final testing (Vector Field Histogram) is very consistent at smoothly avoiding obstacles once detected.
What could have gone better?
Of course there are also some things that leave room for improvement. An important lesson we learned, is that it is very important to leave enough time for testing. Our approach for integrating everything left little room for testing in the lab. This was due to the structure that was chosen for the code. Because all of the different components are commanded through one file, it was hard to test the individual parts of the code when adjustments were made. Though it is nice when you actually have all components in place, this made it difficult to test any of our code in real life until the final week of testing. This meant that we had to test and adjust our code to real life conditions in just a few hours. This far from perfect time management is also what ended up causing the chair incidents during the final challenge day. As there are no chairs in simulation, we did not have enough time to work out a way to detect the legs properly.
In the end, the code worked the way we intended it to and we were able to test all functions, but it would have definitely helped if we would have had testing in some of the lab sessions before. If we had, we would have seen the chair issue in time to fix it and we would have had proper video footage of what our code can actually achieve.
What should we do a next time?
Though the course is now finished, there are still some improvements that should be made/some ideas that would make the robot more efficient in navigating a restaurant.
- Tune parameters. There are a lot of parameters in this code ranging from distances to tables to numbers of nodes in PRMs. Not all were tested to the same extend due to the time limit and room for improvement is still there.
- Fix the spread calculation. Initializing localization is now dependent on a timer rather than a measure of when the localization is good enough. Fixing this would increase the efficiency and accuracy of the robot as it can already move as soon as it is localized properly. Of course, the definition of properly here should also be tested with different values.
- Add a replanner. Now, our code only calculates one path from the robots position to the target (next table on the list), but is doesn’t update when the path seems unfeasible. This is an important addition to make the robot suitable for dynamic environments. This also means that there should be a measure of what an unfeasible path is. This will likely be a timeout.
- Add unexpected objects to the world model. This would mean recognizing that an obstacle is ‘permanent’ and as such needs to be placed into the map that is used for path planning.