Mobile Robot Control 2020 Group 1: Difference between revisions
| (222 intermediate revisions by 6 users not shown) | |||
| Line 22: | Line 22: | ||
| B. Godschalk || 1265172 | | B. Godschalk || 1265172 | ||
|} | |} | ||
= Introduction = | = Introduction = | ||
This Wiki-page reports the progress made by Group 1 towards completion of the Escape Room Challenge and Hospital Challenge. The goal of the Escape Room Challenge is to escape a rectangular room as fast as possible without bumping into walls. The goal of the Hospital Challenge is to deliver medicines from one cabinet to another as fast as possible and without bumping into static and dynamic objects. | This Wiki-page reports the progress made by Group 1 towards completion of the Escape Room Challenge and the Hospital Challenge. The goal of the Escape Room Challenge is to escape a rectangular room as fast as possible without bumping into walls. The goal of the Hospital Challenge is to deliver medicines from one cabinet to another as fast as possible and without bumping into static and dynamic objects. | ||
This year, due to COVID-19, all meetings and tests are done from home. The meeting schedule is shown at the end of the wiki. The software for the autonomous robot (PICO) is written in C++ and applied to a simulation environment since there has been no interaction with PICO. The simulation environment should represent the real test as closely as possible and therefore the information on this page should be applicable to the real test. | |||
= Design document = | = Design document = | ||
In order to get a good overview of the assignment a design document was composed which can be found [[:File:4SC020___Design_Document-v1.pdf|here]]. This document describes the requirements, the software architecture which consists of the functions, components and interfaces and at last the system specifications. This document provides a guideline to succesfully complete the | In order to get a good overview of the assignment a design document was composed which can be found [[:File:4SC020___Design_Document-v1.pdf|here]]. This document describes the requirements, the software architecture which consists of the functions, components and interfaces and at last the system specifications. This document provides a guideline to succesfully complete the Escape Room Challenge. | ||
= Escape Room Challenge = | = Escape Room Challenge = | ||
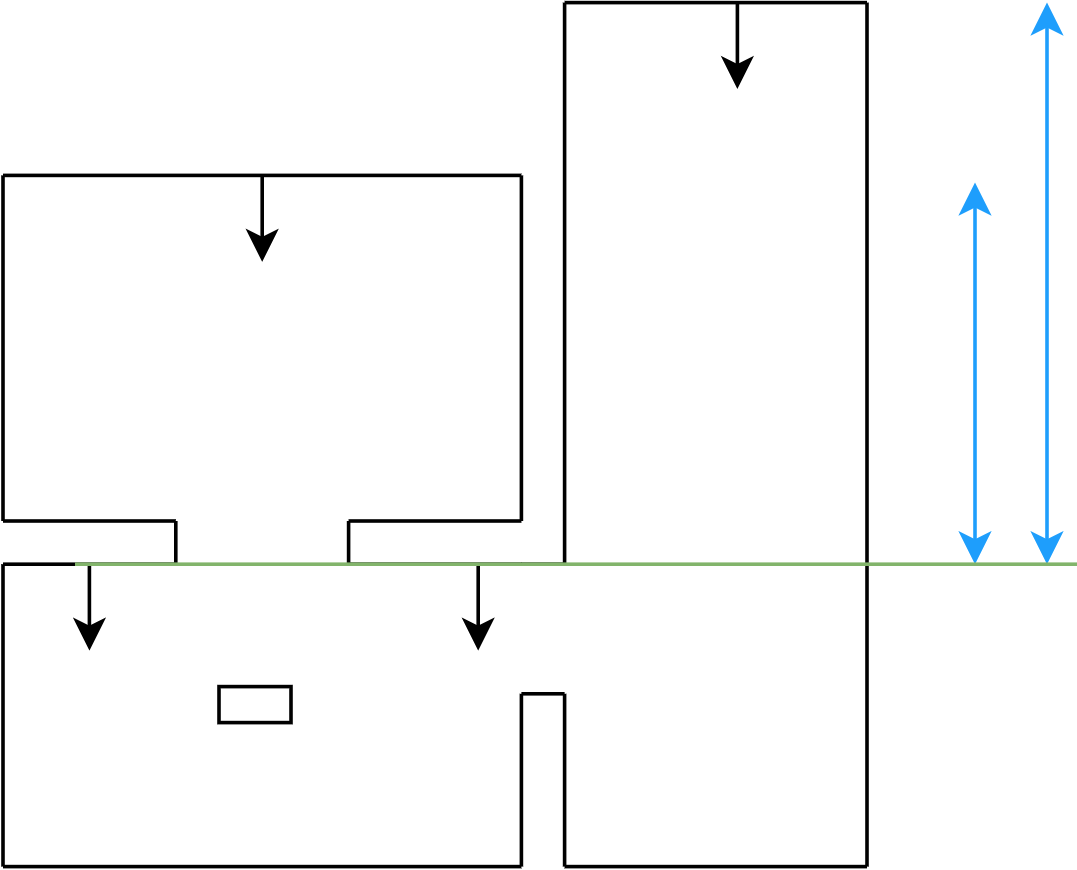
The Escape Room Challenge consists of a rectangular room with one way out. PICO will be placed on a random position on a map which is unknown to the challengers before taking the challenge. PICO should be able to detect the way out by itself and drive out of the room without hitting a wall | The Escape Room Challenge consists of a rectangular room with one way out. PICO will be placed on a random position on a map which is unknown to the challengers before taking the challenge. PICO should be able to detect the way out by itself using the Laser Range Finder (LRF) data and drive out of the room without hitting a wall using its three omni wheels. | ||
To create a solid strategy a number of options have been outlined. Two solid versions were considered; wall following and a gap scan version. After confirming that the gap scan version can, if correctly implemented, be a lot faster than following the wall, this option was chosen. Wall following does not require much understanding of the perception of PICO. By constantly looking at the wall and turning if a corner is reached, PICO will move forward as soon as no wall is visible in front of it indicating that the corridor is found. One other reason to use gap detection over wall following as a strategy is that the gap detection and moving to certain targets can later on be used in the Hospital Challenge. In the Hospital Challenge multiple rooms are present, objects are placed in the rooms and cabinets have to be reached which make wall following unapplicable. | |||
The | The code is divided in multiple parts, or functions, which work together to complete the task. These functions are separated code-wise in order to maintain a clear, understandable code. Next, the state machine of PICO is elaborated. Finally, the simulations will be discussed together with the result of the Escape Room Challenge. | ||
== Functions == | == Functions == | ||
=== Finding walls and gaps === | === Finding walls and gaps === | ||
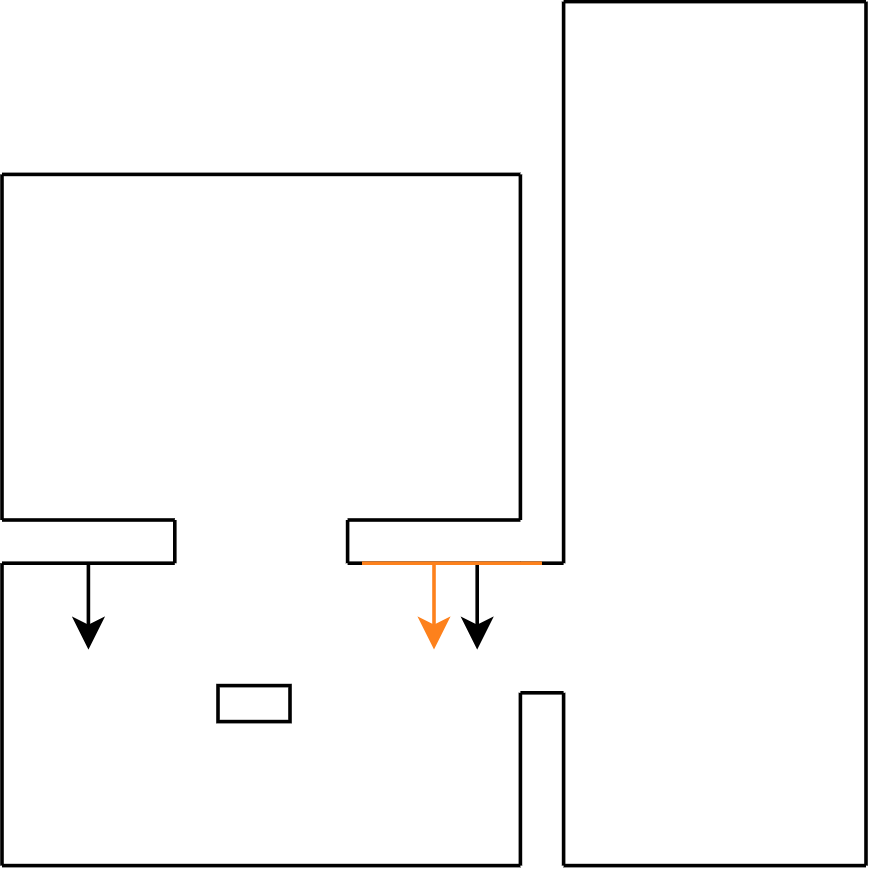
To differentiate between the walls and the exit a least squares regression line algorithm has been written. | Using the LRF, data points are obtained. To differentiate between the walls and the exit a least squares regression line algorithm has been written. This algorithm fits a line over all found data points in order to find a wall in the field of view (FOV) of the LRF. By connecting the walls together it can be possible that a gap occurs, which will be saved into the global reference frame. To collect the data, PICO starts with a 360 degree FOV rotation, while doing so collecting all gaps. When the scan stops, all the collected gaps are checked based on some criteria to see if it is an exit and if it is the best exit possible and, if needed, fixed (straightened based on the adjacent walls). This function is also used in the Hospital Challenge and elaborated in the section Perception. | ||
=== Path planning === | === Path planning === | ||
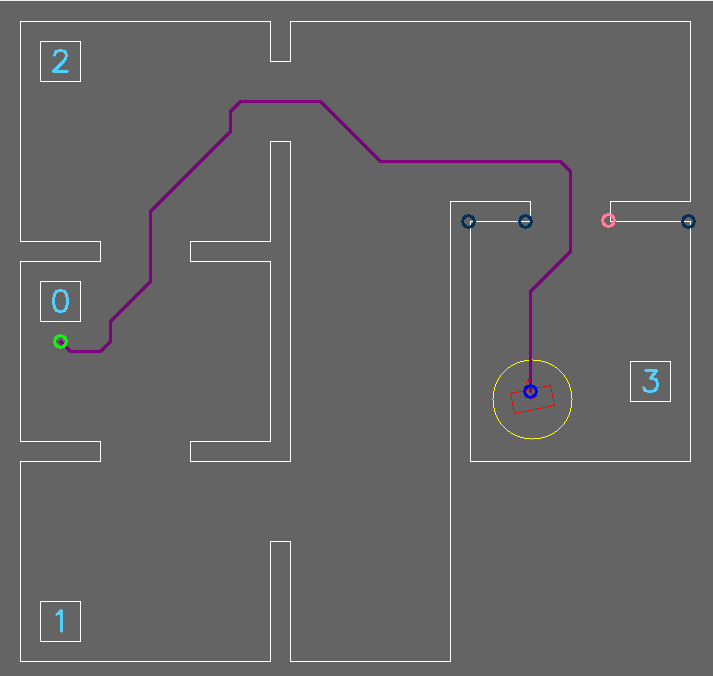
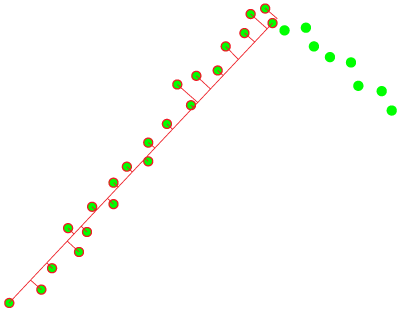
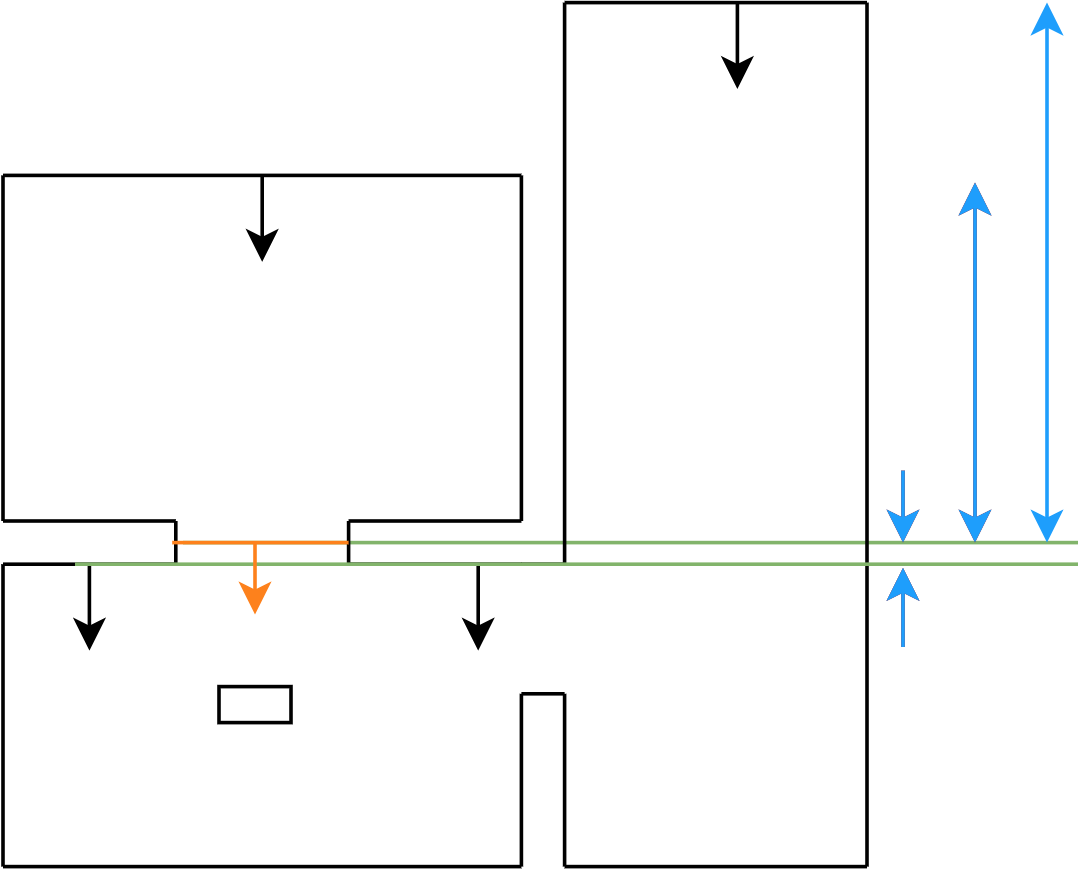
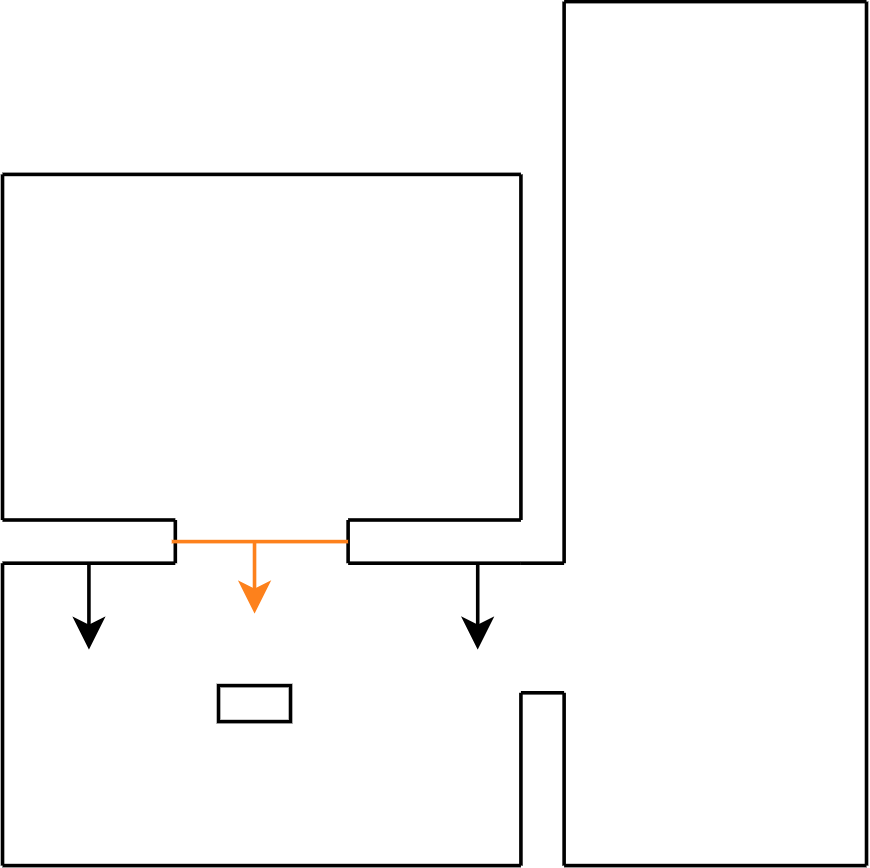
To let PICO move from | To let PICO move from the start location to the exit, a path was generated for PICO to follow. This path consisted out of two points, a pre target (denoted as target B) before the exit gap and a target in the center of the gap (denoted as target A). See Figure 1. This section describes how these points were computed. | ||
[[Image:Pathplan2.PNG | thumb | | [[Image:Pathplan2.PNG | thumb | 400px | center | Figure 1: Path planning]] | ||
If a gap has been found by PICO, the corners of this gap are obtained. From this, target A can easily be computed by taking the average in both x and y direction. Target B is then placed perpendicular to the gap on a distance of 0.4 meters, which is the width of PICO. This is done to prevent PICO from attempting to drive to his target through a wall. | |||
Target B was computed as follows. First, the gap and the line between points A and B were denoted as a vector representation | |||
[[Image: vectorBgroup12020.png | frameless | 200px | center ]] | [[Image: vectorBgroup12020.png | frameless | 200px | center ]] | ||
Then, a and b were computed. Since it is known that the vectors are orthogonal, the inner product should be zero, resulting in | |||
[[Image: innerproductBgroup12020.png | frameless | 200px | center ]] | [[Image: innerproductBgroup12020.png | frameless | 200px | center ]] | ||
Depending on the values of the x and y coordinates of the corners of the gap, either a or b was set to | Depending on the values of the x and y coordinates of the corners of the gap, either a or b was set to the value 1 in order to compute the other value. With a and b known, the direction of the vector AB is known. The length of this vector is also known, hence equating the two norm of the vector to the length of the vector results in | ||
[[Image: normBgroup12020.png| frameless | 200px | center ]] | [[Image: normBgroup12020.png| frameless | 200px | center ]] | ||
After these computations are completed, two possible locations for point B can be obtained. One before and after the gap. To determine the correct point, the distance from PICO to both points was computed. The point with the smallest distance will always be the point before the gap and thus the correct point B. Note that this will hold only when the room from which PICO needs to escape is a rectangle or when the corners of the gap are obtuse angles. | After these computations are completed, two possible locations for point B can be obtained. One before and after the gap. To determine the correct point, the distance from PICO to both points was computed. The point with the smallest distance will always be the point before the gap and thus the correct point B. Note that this will hold only when the room from which PICO needs to escape is a rectangle or when the corners of the gap are obtuse angles. | ||
=== Potential field corridor === | === Potential field corridor === | ||
When PICO drives in the corridor, PICO starts to monitor the left and right wall to center itself between the walls of the corridor while moving towards the finish line. | When PICO drives in the corridor, PICO starts to monitor the left and right wall to center itself between the walls of the corridor while moving towards the finish line. This is done using proportional control. | ||
== State machine == | |||
In Figure 2, the flow chart is depicted which starts at 'Inactive' and ends at 'Move forwards' until PICO stops. | |||
The first step that will be executed is the 'Initialize' step. This step will be used to clear and set all variable values (the odometry data from the wheels as well as the LRF data) to the default state from which it will continue to the '360° scan', where using the LRF data all walls and possible gaps are detected. In this scan all LRF measurements will be mapped into wall objects if obtained data points connect. When data points do not connect, a gap occurs which can be a possible exit or a faulty measurement. When the scan can not find any gaps in the walls, PICO will move 1 meter to the furthest point measured in the scan and performs a new scan. If, for any reason, PICO tends to walk into a wall, the robot will move backwards and starts a new scan. | |||
The next step 'Gap?' is checking if the gaps found can be considered as an exit. If no gaps meet the specifications of a gap, the next step will be 'Move to better scan position' and PICO will redo the previous steps. If a gap meets the requirements of the exit, then PICO will move on to ‘Path Planning, which will be executed to calculate the best possible way to the exit. When the path is set the following step will be 'Move to gap'. | |||
The final step will be 'Center?' which will center the robot in the corridor of the exit to prevent that incorrect alignment with the exit will result in a crash with the walls. | |||
Parallel to this flow PICO will continuously keep track of objects with the laser range finder. Whenever a object is detected in a specific range of the robot a flag will be thrown. This flag can be used to update the path planning, which will prevent crashes when the robot is heading in the wrong direction. | |||
[[Image:Group1_ER_Strategy_update_1.jpg | thumb | 750px | center | Figure 2: Strategy for Escape Room Challenge ]] | |||
== Simulation == | == Simulation == | ||
The result of the strategy and the implemented functions is shown in Figure 3 where one can see that a gap is detected. PICO moves to a point in front of the opening and rotates towards the opening. While driving through the corridor, PICO keeps its distance to the walls. | |||
[[File:Group1_ER_Simulation_1.gif| frame | 100px | center | Figure 3: Simulation in emc-sim for Escape Room]] | |||
File:Group1_ER_Simulation_1.gif| Simulation in emc-sim for Escape Room | In Figure 4 one can see how PICO behaves if no gaps are detected. PICO keeps on moving 1 meter from its scan location to scan again. | ||
File:Group1_NoGapRoutine.gif| Escape Room no gap simulation in emc-sim | |||
[[File:Group1_NoGapRoutine.gif| frame | 100px | center | Figure 4: Escape Room no gap simulation in emc-sim]] | |||
== Escape Room Challenge results == | == Escape Room Challenge results == | ||
The challenge attempt can be seen in Figure 5. As can be seen in the scanning, the robot rotates in a smooth counterclockwise rotation in which the gap detection algorithm detects the exit. After validation of the gap, a pre-target and target are placed in relation to the detected gap location. However, the movement towards it went wrong. Normally, the motion component of the software calculates the smallest rotation between the angle of PICO and the pre-target & target of the gap. During the development and validation of the written software in the simulator, this component worked as expected. However, during the challenge it emerged that the calculation did not work when comparing positive and negative angles. As a result, the calculation showed that a positive angle had to turn into the negative direction in order to reach its target. Because of this problem PICO started to rotate 270 degrees to the right instead of 90 degrees to the left. This problem came up 2 times, both after the 360 degrees scan and after reaching the pretarget. | |||
Immediately in the first attempt PICO moved out of the room in 55 seconds. However, PICO decided to align itself with the reference angle using the largest rotation which costed a lot of time. In the end group 1 is proud of the result. | |||
After the challenge we looked at this problem and applied a possible solution. If the simulation would be performed again with the right rotations the simulation time could be reduced to 25 seconds which would have resulted in a 2nd place during the challenge, instead of our 4th place that we were placed this time. | After the challenge we looked at this problem and applied a possible solution. If the simulation would be performed again with the right rotations the simulation time could be reduced to 25 seconds which would have resulted in a 2nd place during the challenge, instead of our 4th place that we were placed this time. | ||
In summary, every software component worked fine without failing completely. However, after a bug fix in the motion component, everything works optimally without any known errors. | In summary, every software component worked fine without failing completely. However, after a bug fix in the motion component, everything works optimally without any known errors. The wall detection and motion software can be used for the hospital challenge and made usable with some additions without starting from scratch again. | ||
[[ | |||
[[file:Group1_ERC_result.gif | frame | 800px | center | Figure 5: Escape Room Challenge live stream result]] | |||
= Hospital Challenge = | = Hospital Challenge = | ||
The shortage of care services is increasing over time due to the ageing population and is expected to increase for the coming years as well [https://www.cbs.nl/nl-nl/dossier/arbeidsmarkt-zorg-en-welzijn]. Without an increase in the amount of care providers, the chances of burnouts and other health issues for these people will increase significantly. Knowing that a spontaneous increase in healthcare personnel is unlikely, other solutions for work relieve need to be found. One of these solutions can be found in the way of automated robots. These robots can perform relatively simple tasks and thereby assist the care providers. A simple, yet time consuming, task of these care providers is fetching medicines from certain cabinets to give to the patients. The Hospital challenge is based on this task. | |||
In this challenge, a robot (PICO in this case) should be programmed in such a way that it can ‘fetch’ and ‘deliver’ items from one place to another. The fetching and delivering is for this challenge not physically possible, therefore a specific procedure needs to be followed which is specified in the problem description [http://cstwiki.wtb.tue.nl/index.php?title=Mobile_Robot_Control#Hospital_Competition]. Logically, this robot should be able to move without bumping into either static (i.e. walls or doors) or dynamic (i.e. people) objects and it should work as fast as possible. Also, this robot should be able to perform these tasks with only the order of cabinets to visit as input. | |||
== Design architecture == | == Design architecture == | ||
Like for the Escape room challenge, the first step of the Hospital challenge was to | Like for the Escape room challenge, the first step of the Hospital challenge was to determine the internal information exchange in a clear way. This meant only specifying the main components with its main functions. The goal for the Escape room challenge was to define an architecture which could be used for the Hospital challenge as well. When discussing the structure of the previous architecture it became clear that it would not hold for the Hospital challenge. Reasons for altering the architecture were ambiguities in the goals of certain components and the underestimation of the size of the Perception component. Ambiguities mainly occurred in de information transfer in the strategy component and into the movement control component. Previously, it was assumed that Movement Control needed the current state from the Final State Machine (FSM). Later it was decided that only the target would suffice. Also, by splitting Monitoring from Perception as a separate component it was ensured that the code would remain clear. The Perception component was relatively small during the Escape room challenge, therefore it was assumed Monitoring could be a main function of Perception in the Hospital challenge as well. However, during the discussions for the design architecture for the Hospital challenge it became clear this assumption was wrong. Perception was expected to contain a considerable amount of functions more. By setting Monitoring as a separate component, Perception would become smaller, thus clearer to read. This also maps with the paradigms explained in this course. Namely, once a code starts becoming more complex, it should remain explainable [3]. | ||
[[Image:designarchitecture.png | thumb | 750px | center | Design architecture ]] | [[Image:designarchitecture.png | thumb | 750px | center | Figure 6: Design architecture ]] | ||
The software architecture for the Hospital challenge thus has one more component compared to the Escape room challenge, in the form of monitoring. | The software architecture for the Hospital challenge thus has one more component compared to the Escape room challenge, in the form of monitoring. Additionally, the transfer of data from the output of Strategy/Planning to the World Model and the transfer of data from World Model to Movement Control is changed. These changes made it clear that if a component is expected to grow significantly in size, it is wise to look for functions inside that component that can be separated from that component. Discussing the internal data transfer between components more thoroughly also became a learning point, since it needed to be changed after the Escape room challenge. | ||
The final Design architecture is thus formed by the components Perception, Monitoring, World Model, Visualization, Movement Control and Strategy/Planning. These components, combined with their main functionalities and their inputs and outputs, can be found in Figure 6. For instance, one of the main functions of the Strategy/Planning component is the FSM, which determines the state PICO is in and what it should do next. As input it needs, among other things, the current position of PICO. As output it sends the state to the World Model and a goal to the Path planning function of Strategy/Planning. Whether it is input or output can be determined by the direction of the arrow. | |||
All the components and their functionalities, mentioned in the Design architecture, are explained more elaborately in the following sections. | |||
== Components == | == Components == | ||
In the following sections, the different components and its main functions are explained elaborately. Furthermore, the testing phase and final challenge results are discussed. | In the following sections, the different components and its main functions are explained elaborately. Furthermore, the testing phase and final challenge results are discussed. | ||
=== Finite state machine === | |||
To be able to navigate and do necessary actions during the hospital challenge, a finite state machine has been composed. The FSM combines all the functions written in all the different components in a predefined sequence to be able to go to different cabinets in the order provided at startup. The FSM will be written in a switch case structure which will do specific actions in each state, and depending on the transition conditions move through it. In Figure 7, the FSM is visualized in a flow state graph which shows the connection between the different state. The description and transition conditions are explained below. | |||
[[Image:Group_1_State_flow.PNG | thumb | 800px | center | Figure 7: FSM state structure and connection ]] | |||
'''States''' | |||
* '''INIT''': During the init state all variables used within the FSM are set to their default values. This state is used to be able to recover from crashes within the program, more specific, from a unknown state or an exception within the FSM. By resetting all the variables withing the FSM, the program can continue its operation like nothing happened. | |||
* '''IDLE''': The Idle state is used to set PICO into Idle mode when the program has finished the cabinet sequence. If this state is executed from startup, the state will do nothing else then moving to the next state. | |||
* '''LOCALIZE''': Before PICO can be moved within the environment the location of PICO needs to be estimated. By rotating and translating PICO it would generate enough data for the perception module to localize PICO. | |||
* '''GETTARGET''': This state is used to get the next cabinet ID from the provided sequence and setting the goal position where PICO should be to pickup or deliver the medicines. | |||
* '''CALCULATEPATH''': The A* pathfinding algorithm is executed which will produce a path based on the current position of PICO and the goal received from the ‘gettarget’ state. | |||
* '''MOVE''': Move will walk over the generated path by the ‘calculatepath’ state which contains a set of positions to move to to get at the goal. | |||
* '''FOCUS''': When PICO arrives at the cabinet the orientation of PICO should be facing towards the closest cabinet side. | |||
* '''ARRIVED''': Remove reached cabinet from sequence and trigger the export event for the LRF data. | |||
* '''FINISHED''': All the cabinets from the provided sequence are visited when this state is executed. This state is used to notify the user and allows to exit the program. | |||
* '''RESETGRID''': When no path can be produced between PICO and the current goal the grid will be reset to the static layout of the map. By doing this possible false positives can be removed from the known data which will enable PICO to create a new path. | |||
* '''RAGDOL''': Fail-safe to prevent deadlocks when a dynamic object is preventing path generation. This can occure when an dynamic object is standing in a doorway or when the object pushes PICO into a corner and restrict the movement of PICO completely. | |||
* '''ROTATEANDSCAN''': This state will be executed when PICO can’t move towards the direction it is facing due to a door or static object or when the localization has not been updated enough. It can be that the LRF data on that position is not good enough to meet the requirements for object recognition, by rotating PICO the LRF data can give more information about the surroundings. Another effect of this is that the localization algorithm uses this data to update the position of PICO. | |||
'''Transition conditions''' | |||
* '''A''': Finished flag is false. | |||
* '''B''': Localization algorithm returns true when location is known. | |||
* '''C''': Cabinets left in the commited sequence. | |||
* '''D''': Path exist to selected cabinet. | |||
* '''E''': Arrived at the end of the path. | |||
* '''F''': Alligned with cabinet side. | |||
* '''G''': No cabinets left from the commited sequence. | |||
* '''H''': Finished flag is true. | |||
* '''I''': PICO is already on the goal position. | |||
* '''J''': Could not create an existing path to the goal position. | |||
* '''K''': Grid resetted attempt is under 10 times. | |||
* '''L''': Grid resetted for the 10th time. | |||
* '''M''': Ragdol has been active for 5 seconds. | |||
* '''N''': Monitoring component detects less then 0.25 meter of movement in 7 seconds. | |||
* '''O''': Scan modus has been active for 3 seconds. | |||
* '''P''': Monitoring component flags that path to goal is obstructed. | |||
=== World model === | === World model === | ||
The worldmodel component of the project lays down the foundation of the coding structure which is used since the beginning of the course. Information that had to be shared between the different components was written to and read from this class. This structure allowd that the components could be constructed without dependencies of other components. A summery of the data that is stored within the worldmodel: | |||
*'''World model data''': static layout of the map divided into walls, cabinet sides and corners where convex and concave types are saved seperated. | |||
*'''Localization data''': current position and odom travel from last known position. | |||
*'''Perception data''': LRF data, the detected walls, the detected corners which are divided in convex and concave lists, the detected static objects, resulting potentialfield vector and the closest point from PICO. | |||
*'''Strategy data''': 2D grid, path nodes and string pulled path nodes. | |||
*'''Monitoring data''': Error flags for path obstruction and movement check. | |||
[[Image:Group1_wm_json_format.PNG | thumb | 200px | left | Figure 8: JSON data structure]] | |||
In addition to sharing and storing data of all the other components, the worldmodel was also responsible for loading and parsing the | In addition to sharing and storing data of all the other components, the worldmodel was also responsible for loading and parsing the JSON map to a usable format. Loading the map from the JSON file was done by using the opensource JSON for Modern C++ library written by Niels Lohmann [https://github.com/nlohmann/json|[4]]. Based on the available information from the file structure of the map from 2019 a format has been constructed to be used in the project. Seen from Figure 8, the JSON file consisted of three datatypes which would be delivered one week before the challenge; a list of corner points in world space location, a list of connected corner points seen as walls, and a list of objects representing the cabinets which consisted a list of connected corner points that made up the four sides for each cabinet. The left bottom corner of the map was considered as the world frame origin with position (0,0). Besides that, the ID of the corners started at the origin with an index of 0 and persistently increased by one when moving to the next one. By building on this logic it was possible to define closed polygon shapes by setting end points for each one based on specified corner indexes. This functionality is used to determine for each corner if it had a convex or concave property, which is used within the perception module to stabilize the localization algorithm. The loading sequence of the walls and cabinets are used to distinguish the inner walls and cabinet sides from the external walls. This was done by defining a normal vector direction based on the loading order of the corners that made up the wall or cabin side. The usage of these functionalities will be explained in more detail in the perception section. | ||
[[Image:Group1_Reference_frames.jpeg | thumb | 400px | right | Figure 9: Reference frame visualization]] | |||
Storing the corners from the JSON file was done in a Vector3D object. This object was created to store three double values, namely the x and y position in the world frame and the third one was used to store the corner type; convex (pi/2) or cancave (3pi/2). The walls and cabinets are stored seperatly into a vector in the worldmodel as Line2D objects. The Line2D object is a class that stored two Vector3D objects which represented the begin and end point of a wall of cabin side. Next to storing the two positions it was possible to get the length of the line and getting the normal of it. | |||
By now, the project contained three coordinate frames, where one was independent of the other two, namely: PICO’s own and global reference frame (seen from PICO and its initial starting position within the world) and the world frame (loaded from the JSON file). To get everything working together in the same frame, the world frame was used as a global reference frame to make it straightforward when doing calculations. By doing this in the same frame for all components the amount of coordinate transformations is reduced to a bare minimum which reduces the complexity of the calculations and is easilier to explain. As said before, the global coordinate frame started at (0, 0) at the left bottom of the map, which was chosen such that their x- and y-axis were positive defined to the right and upwards. Next to that was PICO’s own frame where the x-axis was positive upwards and their y-axis was positive defined to the left of PICO. Both are shown in Figure 9 which also explains the relationship between them, here the world reference frame position is given in orange, the PICO’s global reference frame is given in red and PICO’s frame is expressed in green. | |||
One week before the hospital challenge the map of this year was released (the heightmap is shown in Figure 10), unfortunately the data [http://cstwiki.wtb.tue.nl/images/Mrc2020_finalmap_corrected.zip|[5]] was not in the same format as last year [http://cstwiki.wtb.tue.nl/images/Finalmap2019.zip|[6]], negative coordinates were provided, which were not taken into account when writing the loading sequence. So, before the file could be used, small modification had to be executed in such a way that the data had the same format as the map from previous year. One of the modifications was shifting all world coordinates up until everything had a positive value. Another modification that has been done is renumbering the indexing of the corner ID’s in such a way that the first corner started at 0 and was sequentially increased by one when going to the next corner. And the last was again reversing the corner index numbering of the internal walls and cabin sides. | |||
[[Image:Group1_wm_maplayout.PNG| thumb | | right |Figure 10: Visualization of heightmap used]] | |||
The next | In order to create a bridge between the loaded JSON map and the collected data from the perception module towards the strategy component a 2D grid has been constructed. The grid is used to combine all the different collected pieces of data such that the strategy component can calculate the next steps that needed to be taken to get to the next goal. The choise for a 2D grid instead of a node based architecture was to be more flexible in path creation and the tuning of it. It allowed to specify various zones around objects and walls to create a safety zone without having to place them manually in the JSON map file and specify the connections between the nodes. An additional advantage of the grid was the navigation around dynamic objects, when an (dynamic) object was obstructing the current path a new path could be constructed which seamlessly transitioned with the old path, resulting in smooth movement behavious. This was harder to accomplish with a node based structure, since it could be that a node closeby would interrupt the movement which would slow PICO down. How the data from the 2D grid is handled will be explained in more detail in the strategy section. The content of the grid started with integer values corresponding to the type of data which was stored in the cell belonging on the world position, such as: walls, corners and sensed objects. Further on in the project it became clear that the only thing needed within the strategy component was if the world position belonging to that specific cell was reachable or unreachable by PICO. To reduce the complexity of the grid the datatype was changed to a Boolean value. This meant that cells who store a 1 (true) that its world location was accessible and a 0 (false) that the world position was unreachable. Changing the datatype of the grid had no effect on the workings of the A* pathfinding, the grid was used to see where PICO could go and where it should stay away from, which is in fact just a Boolean value. | ||
The first step made to build the 2D grid was to break up the world space which was occupied by the hospital environment in equally large pieces. To achieve this, the maximum horizontal and vertical position are saved while loading the corner data from the map file. Then, the grid dimensions were set to the length divided by the grid resolution. In order to get the best grid result, the resolution is determined based on the given data in the JSON file. Since all corner positions are rounded to one decimal place, except for 6 corner positions with more decimals, the courser resolution could be set to 0.1 meters without loss of accuracy. This resolution would result in a grid of 67x130 nodes for the provided map which has 6.7x13 meter as surface dimension. Lowering the resolution results in a higher grid density but will increase the processing time required by the pathfinding algorithm. In Figure 11a the initial grid is shown where all the grid data is set to accessible. | |||
The next step was filling the grid with the loaded data stored in the Line2D objects from before. Since these objects stored the beginning and ending of all the walls and side cabinets it was possible to loop over each object, dividing the line between it into smaller segments who could be matched to the grid and setting the corresponding grid cell at the belonging world position to unreachable (false) in the grid. This eventually led to a grid as seen in Figure 11b. By giving different offsets to specified Line2D objects it was possible to create some space for error within the movement and path planning, such that PICO will not move directly next to obstructions such as the walls and cabinets. This effect can be seen in Figure 11c. | |||
To let PICO react to sensed obstacles within the hospital environment the grid was considered as a living object, which meant that when an object got pushed to the worldmodel that the grid cells corresponding to the pushed object location got put into the grid as unreachable. Just like for the walls and cabinets an offset could be specified which would be filled in the grid around the locations where obstacles were detected. The combined result can be seen in Figure 11d. | |||
<gallery widths=150px heights=250px perrow=5> | |||
Image:Group1_wm_empty_map.PNG|Figure 11a: Empty 2D grid | |||
Image:Group1_mw_load_map.PNG|Figure 11b: Loaded JSON data parsed | |||
Image:Group1_wm_offset_map.PNG|Figure 11c: Added offset | |||
Image:Group1_wm_obstacle_map.PNG|Figure 11d: Sensed object parsed | |||
</gallery> | |||
=== Strategy === | === Strategy === | ||
The purpose of the strategy class is to compute and return the path that PICO needs to take in order to complete its tasks. This path should be a vector of 2D points in the global reference frame. These waypoints are determined in two steps | The purpose of the strategy class is to compute and return the path that PICO needs to take in order to complete its tasks. This path should be a vector of 2D points in the global reference frame. These waypoints are determined in two steps. | ||
First, the shortest path from PICO to its destination is computed using an A* shortest path algorithm. This algorithm is used on the grid nodes of the world map | First, the shortest path from PICO to its destination is computed using an A* shortest path algorithm [https://en.wikipedia.org/wiki/A*_search_algorithm| [7]]. This algorithm is used on the grid nodes of the world map which is shown in Figure 12. A* is a similar algorithm compared to Dijkstra’s shortest path algorithm. However, due to the implemented heuristic A* is much faster [https://www.youtube.com/watch?v=g024lzsknDo|[8]]. Figure 13 shows a path found by the A* algorithm. | ||
After the A* algorithm has found a shortest path, a large vector is obtained with all grid nodes that need to be visited. There is however no need to reach all these points one by one, in fact, using this as a reference trajectory will only slow PICO down due to it correcting for overshoot. For this reason, a string pulling algorithm was used to only keep the waypoints that are strictly necessary in order | After the A* algorithm has found a shortest path, a large vector is obtained with all grid nodes that need to be visited. There is however no need to reach all these points one by one, in fact, using this as a reference trajectory will only slow PICO down due to it correcting for overshoot. For this reason, a string pulling algorithm was used to only keep the waypoints that are strictly necessary in order to not hit any obstacles or walls. This string pulling algorithm works as follows. | ||
It starts evaluating if it can reach the second node from the first node in a straight line without crossing an unreachable space. If so, then it continues evaluating if the third node can be reached and so on. If it stumbles on a node that cannot be reached in a straight line, in other words, it would cross an unreachable grid node on the straight line between the first node and the node that it is being evaluated, then it will save one node prior to the unreachable node and stores this node as a waypoint. The algorithm is then repeated with the saved waypoint as the new node from which the path is evaluated. This process continues until the final waypoint is reached. This results in a vector only containing the waypoints that are strictly necessary for it to reach the target without hitting an obstacle or wall, see | It starts evaluating if it can reach the second node from the first node in a straight line without crossing an unreachable space. If so, then it continues evaluating if the third node can be reached and so on. If it stumbles on a node that cannot be reached in a straight line, in other words, it would cross an unreachable grid node on the straight line between the first node and the node that it is being evaluated, then it will save one node prior to the unreachable node and stores this node as a waypoint. The algorithm is then repeated with the saved waypoint as the new node from which the path is evaluated. This process continues until the final waypoint is reached. This results in a vector only containing the waypoints that are strictly necessary for it to reach the target without hitting an obstacle or wall, see Figure 14. | ||
<center> | <center> | ||
<gallery mode=packed heights=300px widths= | <gallery mode=packed heights=300px widths=290px> | ||
File:gridgroup12020.png| Visualization of the grid | File:gridgroup12020.png| Figure 12: Visualization of the grid | ||
File:waypointsgroup12020.png| | File:waypointsgroup12020.png| Figure 13: Path generated using A* algorithm | ||
File:waypointsnewgroup12020.png| Waypoints with string pulling algorithm | File:waypointsnewgroup12020.png| Figure 14: Waypoints with string pulling algorithm | ||
</gallery> | </gallery> | ||
</center> | </center> | ||
=== Perception === | |||
The main goal of the perception component is to translate the real world data into data which can be used for the simulation. The real world data consists of the LRF-data and the odometry data. Perception uses this data to localize PICO, detect obstacles and to measure the distance to objects around PICO. | |||
A mathematical tool which is used a lot in this class is the vector projection, depicted in Figure 15. | |||
[[Image: vectorprojectiongroup12020.png| thumb | 400px | center | Figure 15: Vector projection [9]]] | |||
This tool is used to get the orthogonal of the vector projection of a point onto another vector and to get the point of intersection between this orthogonal and vector. | |||
==== Line fitting ==== | |||
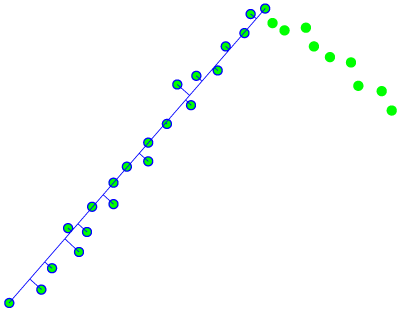
In order to extract features from the LRF data it is necessary to transform this data into lines. In essence this is done by the method of least squares. In general this goes by two steps; the first step is to make an estimation of which points belong to the same line and the second step is to find a line which fits the best between these points. The LRF sensor returns a collection of data points which is ordered counter clockwise. The line fitting algorithm loops through this data. In each iteration of this loop a subset from the first to the j-th element of the sensor data is taken. For each of these subsets a line is drawn from the first to last element of the subset and the squared norm of the vector projection of each of the intermediate elements onto this line is calculated. The sum of squared norms is used as an error variable. | |||
There are two condition which can break this loop. The first condition is met when the error variable exceeds a certain error threshold. The second condition is met when the distance between two consecutive points is bigger than a certain distance threshold. The figures below represents the first condition visually. Figure 16 shows one subset for which this condition is not violated and thus the error is smaller than the threshold. Figure 17 shows the next iteration which does violate the first condition as you can clearly see that the red line will drift away from the data points as the iteration continues. | |||
=== | <center> | ||
<gallery mode=packed heights=300px widths=400px> | |||
File:linefitting_fig1.png| Figure 16: Fitting error shown visually, iteration i | |||
File:linefitting_fig2.png| Figure 17: Fitting error shown visually, iteration i+1 | |||
</gallery> | |||
</center> | |||
When a subset violates one of these conditions, the previous subset is taken again. In the example of Figure 16 above, this would result in the subset of the left part depicted by the blue encircled dots. From this subset the best line fit is calculated using the sum of least squares. This method uses the relative error in y-coordinates to find the best line fit. One disadvantage of this method is that it is not particularly good at fitting ‘vertical’ lines. To solve this the calculation is performed twice, one time where the relative error in y-coordinates is used and a second time where the relative error in x-coordinates is used. This means that a line is fitted in both directions. This results in two possible fits for each subset. From these two lines the longest of the two is used since this is the one which results in the best fit. A small cleaning procedure is done to make sure the best fit starts and ends at the first and last element of the subset respectively. This is done by extending/trimming the best fit to coincide with the vector projection of the first and last element of the subset onto the best fit. Figure 18 shows for three different data collections the fitted line by using the relative error in y-coordinates (red line) and by using the relative error in x-coordinates (blue line). The detailed part of set 1 shows the extending/trimming procedure where the grey part depicts the part of the best fit which is being trimmed. | |||
[[Image: linefitting_fig3.png| thumb | 400px | center | Figure 18: The best in line fit calculate in both directions. The red lines represent best fit calculated with relative error in y-coordinates and the blue lines represent best fit calculated with relative error in x-coordinates. The detailed view shows the trimming/extending procedure.]] | |||
When the best fit is found its corresponding subset it is then removed from the original set and the iteration continues until the original set is empty. | |||
The error threshold which bounds the fitting error is determined by trial and error until it yielded a satisfactory result. Taking this value too small results in the sensor data being divided into a large number of lines. Taking this value too big results in a bad representation of the sensor data, the corners will be rounded for example. A point of improvement is to make the error threshold a function of the distance measured by the LRF sensor since the error of the sensor also increases with a larger distance. The distance threshold is chosen to be sufficiently less than 200 mm. This prevents that cabinets, walls and other objects are being connected to each other. This value is chosen because the distance between a wall and a cabinet is 200 mm. This also prevents that datapoints which are far away and thus have a big spacing are being used to make lines, since this could lead to unreliable results. | |||
The main objective of this function is to extract lines from the sensor data. There are a lot of different solutions to this problem but we chose specifically for this solution because it resulted in an easy and lightweight implementation which yielded satisfactory results. A possible motive to use another method is that this method is not particularly good at handling outliers but this did not affect the performance of our algorithm since the number of outliers is apparently small compared to the number of datapoints. | |||
==== Localization ==== | ==== Localization ==== | ||
| Line 214: | Line 249: | ||
1. Calculating the detected corners from the fitted lines | 1. Calculating the detected corners from the fitted lines | ||
2. Determining the set of map corners which could | 2. Determining the set of map corners which could possibly match the observed ones | ||
3. Determining which combination of possible corners fit the observed corners | 3. Determining which combination of possible corners fit the observed corners | ||
From the lines which are the result of the line fitting algorithm the observed corners are determined. Since the LRF sensor data is ordered clockwise, so is the set of fitted lines. The angle between each pair of consecutive lines is calculated. If the angle is (within a certain variance) 90 degrees it is denoted as an acute corner and if it is 270 degrees it is an obtuse | From the lines which are the result of the line fitting algorithm the observed corners are determined. Since the LRF sensor data is ordered clockwise, so is the set of fitted lines. The angle between each pair of consecutive lines is calculated. If the angle is (within a certain variance) 90 degrees it is denoted as an acute corner and if it is 270 degrees it is an obtuse corner, both seen from PICOs perspective. This has as additional condition that the end point of the first line and starting point of the second line are within a certain distance of each other. This results in a set of observed corners. From this set the three corners which are the closest to PICO and no further than 5 meters are used for localization. This is because these are determined by LRF data which is close to PICO and thus is more reliable. This threshold of 5 meters is determined via trial and error and led to a good result. The used localization procedure requires three angles to localize. This is why it is important not to have walls connected to cabinets since this would make a false corner. The observed corners are depicted in Figure 19 by the green dots. | ||
Next the set of corners which could possibly form a match with the three observed corners is calculated. The known map has walls and cabinets which all have corners. The first step is to determine which corners are connected to a wall which faces PICO. This is done by checking if the normal vector of each wall/cabinet intersects the x or y axis of PICO with a positive scalar value | Next the set of corners which could possibly form a match with the three observed corners is calculated. The known map has walls and cabinets which all have corners. The first step is to determine which corners are connected to a wall which faces PICO. This is done by checking if the normal vector of each wall/cabinet intersects the x or y axis of PICO with a positive scalar value multiplying the direction vector. The start/endpoints of the walls/cabinets which face PICO are added to the set of possible corner matches. The normal vectors for all the walls and cabinets are defined such that the all point into the walkable area. The red lines in Figure 19 depict the walls which face PICO, the blue lines do not face PICO. | ||
The second step in determining the possible corner match set is to only add map corners that are within the observed radius of PICO. The observed radius is the circle around PICO which encloses the three observed corners, as shown by the dashed green circle in | The second step in determining the possible corner match set is to only add map corners that are within the observed radius of PICO. The observed radius is the circle around PICO which encloses the three observed corners, as shown by the dashed green circle in Figure 19. This results in the possible corner matches which are depicted by the orange circles with green border and the observed corners itself. It is important that this set is as small as possible since this influences the computation time a lot. | ||
[[Image: loc_fig4.png| frame | 400px | center | Visual representation of the possible corner matches set]] | [[Image: loc_fig4.png| frame | 400px | center | Figure 19: Visual representation of the possible corner matches set]] | ||
When both sets of observed corners and possible corner matches are determined the actual localization procedure can begin. In essence this is reverse of the trilateration method used by for example GPS. We have three observed corners A_O, B_O and C_O. We want to find a combination of three corners A_M, B_M and C_M which match with the observed ones. In order to do this we define a new set which holds all the possible combinations of triplets from the set with possible corner matches. From this set we want to find a subset which satisfy the following conditions: | When both sets of observed corners and possible corner matches are determined the actual localization procedure can begin. In essence this is reverse of the trilateration method used by for example GPS. We have three observed corners A_O, B_O and C_O. We want to find a combination of three corners A_M, B_M and C_M which match with the observed ones. In order to do this we define a new set which holds all the possible combinations of triplets from the set with possible corner matches. From this set we want to find a subset which satisfy the following conditions: | ||
| Line 234: | Line 269: | ||
For each element of this subset a possible location can be determined. | For each element of this subset a possible location can be determined. | ||
[[Image: loc_fig5.png| frame | 400px | center | Representation of the corners A, B and C and its corresponding radius and intersection point]] | [[Image: loc_fig5.png| frame | 400px | center | Figure 20: Representation of the corners A, B and C and its corresponding radius and intersection point]] | ||
For each point in the observed triplet the distance to PICO is exactly known. This distance defines the radius of the circle around each counterpart in the possible triplet. So the distance from PICO to | For each point in the observed triplet the distance to PICO is exactly known. This distance defines the radius of the circle around each counterpart in the possible triplet. So the distance from PICO to | ||
A_O equals the radius of the circle around A_M. For each possible triplet we thus have a set of three circles. The intersection point of these three circles is a possible new location for PICO, which are shown in | A_O equals the radius of the circle around A_M. For each possible triplet we thus have a set of three circles. The intersection point of these three circles is a possible new location for PICO, which are shown in Figure 20. | ||
Since there is measurement noise and estimation errors this will most likely not be a single point but rather a region. This region is determined by calculating the radical line of each pair of circles in the possible triplet. The radical is the line which intersects both circles, both end points of the radical are the intersection points of the circle. This results in three radicals and thus six intersection points. Each possible combination of three of these intersection points define the region in which the new location of PICO lies. But since the LRF data is measured in a specific order and the calculation of the radical proceeds in a specific (predetermined) order it suffices take only one combination of three intersection points. To make this invariant to a specific order one should do the next steps for all possible regions. The possible new location of PICO is taken to be the centre of the circumcircle described by the three intersection points. This possible location is said to be the new location of PICO if the following conditions hold: | Since there is measurement noise and estimation errors this will most likely not be a single point but rather a region. This region is determined by calculating the radical line of each pair of circles in the possible triplet. The radical is the line which intersects both circles, both end points of the radical are the intersection points of the circle. This results in three radicals and thus six intersection points. Each possible combination of three of these intersection points define the region in which the new location of PICO lies. But since the LRF data is measured in a specific order and the calculation of the radical proceeds in a specific (predetermined) order it suffices take only one combination of three intersection points. To make this invariant to a specific order one should do the next steps for all possible regions. The possible new location of PICO is taken to be the centre of the circumcircle described by the three intersection points. This possible location is said to be the new location of PICO if the following conditions hold: | ||
| Line 251: | Line 286: | ||
The disadvantage of this method is that the conditions for localization are very strict. When PICO senses a corner of an unknown object it can not localize and it has to observe at least three corners. But when the conditions are met, the localization deemed to be very reliable. | The disadvantage of this method is that the conditions for localization are very strict. When PICO senses a corner of an unknown object it can not localize and it has to observe at least three corners. But when the conditions are met, the localization deemed to be very reliable. | ||
The reason why we chose for this approach is that we did not succeed in implementing a particle filter. | The reason why we chose for this approach is that we did not succeed in implementing a particle filter due to time constraints. This would results in a much better performance in the 'real' situation since it is more robust, but the approach we now used worked suffienctly good in the simulation. | ||
==== Filtering algrorithm ==== | ==== Filtering algrorithm ==== | ||
As explained earlier, perception is able to translate raw LRF data into lines which do or do not correspond with known obstacles from the given simulation map. What this filtering algorithm does is simply checking if the fitted lines are in fact known obstacles, i.e. walls or cabinets, or unknown obstacles. The method of filtering the known from the unknown obstacles is done over multiple procedures which are explained next. | As explained earlier, perception is able to translate raw LRF data into lines which do or do not correspond with known obstacles from the given simulation map. What this filtering algorithm does is simply checking if the fitted lines are in fact known obstacles, i.e. walls or cabinets, or unknown obstacles. The method of filtering the known from the unknown obstacles is done over multiple procedures which are explained next. | ||
Once the fitted line data is retrieved from the | Once the fitted line data is retrieved from the World Model, it is converted into a vector containing the coordinates of the first point of the line and the coordinates of the last point of the line. Since these coordinates are local, they first have to be converted to global coordinates. After converting the coordinate system, the actual filtering will take place. This filtering will be done in two steps, namely first filtering out the walls from the fitted lines and last is to filter out the cabinets from the fitted lines. What remains are the fitted lines corresponding to unknown objects, i.e. static or dynamic objects. | ||
The filtering takes place in a specific function. The input for this function consists of one of the fitted lines, to be called F, the data where this fitted line has to be compared with, to be called C, being walls or cabinets, and some thresholds which will be dealt with later on. The output is either a true or a false, since a fitted line does or does not coincide with a certain wall or cabinet. | The filtering takes place in a specific function. The input for this function consists of one of the fitted lines, to be called F, the data where this fitted line has to be compared with, to be called C, being walls or cabinets, and some thresholds which will be dealt with later on. The output is either a true or a false, since a fitted line does or does not coincide with a certain wall or cabinet. | ||
The first step in comparing a line | The first step in comparing a line F to a set of line C’s, is to check whether the normals of the lines have the same direction. This already filters out a large part of the data with a relatively simple, thus saving computation time for later procedures. One of the input margins for this function is the ‘angle threshold’ determining the margin on the difference in the angles of the normal lines. This threshold has been set to a relatively low value, since there cannot be large differences in normal lines for them to be comparable, this procedure can be seen in Figure 21: step 1 until step 3. Comparing normals alone does not suffice. After that step, the distance from the fitted line F to the comparable line C is calculated. This is done by means of a vector projection. This coincides with the z in Figure 11. | ||
Specifically the distance from the center of F to C is measured. The reason for this is because in some situations the fitted line data is heavily influenced by noise of the LRF. This mainly occurs when fitting the lines of long hallways. By measuring from the center of F, this problem was solved. Another input threshold for this function is the ‘distance threshold’. This threshold ensures that lines from other parts of the map cannot be compared with the measured line. For instance, the normals from C in room 1 and C in room 2 can coincide with F, but the distance from C in room 1 to F is way smaller than that of C in room 2. Thus, the C from room 2 is filtered out. This is visualized in Figure 21: step 4 and step 5. | |||
The final step in comparing line C to a fitted line F is to check whether line F falls within the boundaries of C. This final step is mainly to check if the fitted line F is not a door. In this project it was assumed doors would be somewhat in the center of 2 walls, since in previous years that was the case as well. This however would mean that both the normals would have the same direction and the vector projection would be short, since the distance would be equal to the depth of the door in the wall. This final step filters out these possibilities. The last step checks if the distances from the first and the last point of F to the first and the last point of C are shorter than or equal to the length of C. If so, it means that both points lie in between or on line C. There is a last threshold for this procedure called ‘overshoot threshold’, which ensures that slight differences in distances cannot influence the process. If after all these steps, a line C from the set of comparable lines is left, then line F equals line C and the filtering process for this data set is complete. These final steps can be seen in Figure 21: step 6 until step 8. Figure 22 visualizes the same procedure according to the same steps, only now an unknown object is filtered. | |||
<gallery widths=200 perrow=4> | |||
Image:Group1_Filtering_wall_Step2.PNG|Figure 21a: step 1 | |||
Image:Group1_Filtering_wall_Step3.PNG|Figure 21b: step 2 | |||
Image:Group1_Filtering_wall_Step4.PNG|Figure 21c: step 3 | |||
Image:Group1_Filtering_wall_Step5.PNG|Figure 21d: step 4 | |||
Image:Group1_Filtering_wall_Step6.PNG|Figure 21e: step 5 | |||
Image:Group1_Filtering_wall_Step7.PNG|Figure 21f: step 6 | |||
Image:Group1_Filtering_wall_Step8.PNG|Figure 21g: step 7 | |||
Image:Group1_Filtering_wall_Step9.PNG|Figure 21h: step 8 | |||
</gallery> | |||
This process first compares all fitted lines to all the known walls. The lines that were not comparable to a wall are then compared to cabinets with the same procedure. If there are still fitted lines left after this process, the remaining fitted lines are used to check for obstacles. | This process first compares all fitted lines to all the known walls. The lines that were not comparable to a wall are then compared to cabinets with the same procedure. If there are still fitted lines left after this process, the remaining fitted lines are used to check for obstacles. | ||
<gallery widths=150 perrow=5> | |||
Image:Group1_filter_obstacle_Step0.PNG|Figure 22a: step 1 | |||
Image:Group1_filter_obstacle_Step1.PNG|Figure 22b: step 2 | |||
Image:Group1_filter_obstacle_Step2.PNG|Figure 22c: step 3 | |||
Image:Group1_filter_obstacle_Step3.PNG|Figure 22d: step 4 | |||
Image:Group1_filter_obstacle_Step4.PNG|Figure 22e: step 5 | |||
Image:Group1_filter_obstacle_Step5.PNG|Figure 22f: step 6 | |||
Image:Group1_filter_obstacle_Step6.PNG|Figure 22g: step 7 | |||
Image:Group1_filter_obstacle_Step7.PNG|Figure 22h: step 8 | |||
Image:Group1_filter_obstacle_Step8.PNG|Figure 22i: step 9 | |||
Image:Group1_filter_obstacle_Step9.PNG|Figure 22j: step 10 | |||
</gallery> | |||
==== Obstacle detection ==== | ==== Obstacle detection ==== | ||
The obstacle detection process is based on the theory of a histogram filter, but then simplified. The perception of PICO is able to detect obstacles by using the remaining fitted lines after the filtering process. By using a histogram filter it is ensured that not every remaining line is immediately pushed as obstacle. The exact procedure is explained in the following sections. | The obstacle detection process is based on the theory of a histogram filter, but then simplified. The perception of PICO is able to detect obstacles by using the remaining fitted lines after the filtering process. By using a histogram filter it is ensured that not every remaining line is immediately pushed as obstacle. The exact procedure is explained in the following sections. | ||
Once the perception of PICO measures something which is not comparable to either a wall or a cabinet, it is analyzed in the obstacle detection function. The first time something enters this function, the line data, combined with an initial weight of 1, is saved in an array. If the next loop of the main cycle, another line enters the obstacle detection function. This new fitted line is compared to the line which is saved earlier. By means of the filtering algorithm described before, the new fitted line is either similar or not similar to the earlier saved line. Which leads to two different scenarios. If the new fitted line is similar to the earlier saved line, it means the same line is measured twice. In this case, the weight of this line in the array is increased by 1. If the two lines are not similar, the new fitted line will be added to the array of earlier measured lines with a weight of 1 and the earlier measured line will have a weight decrease of 0.5. This procedure repeats itself every new cycle of the main loop. Once a certain line has a weight of 0 or lower, the line is deleted from the array of earlier measured lines meaning it was probably a wrong measurement. If a line has a weight which is bigger or equal to the number specifying the rate of the main loop, that line is pushed to the | Once the perception of PICO measures something which is not comparable to either a wall or a cabinet, it is analyzed in the obstacle detection function. The first time something enters this function, the line data, combined with an initial weight of 1, is saved in an array. If the next loop of the main cycle, another line enters the obstacle detection function. This new fitted line is compared to the line which is saved earlier. By means of the filtering algorithm described before, the new fitted line is either similar or not similar to the earlier saved line. Which leads to two different scenarios. If the new fitted line is similar to the earlier saved line, it means the same line is measured twice. In this case, the weight of this line in the array is increased by 1. If the two lines are not similar, the new fitted line will be added to the array of earlier measured lines with a weight of 1 and the earlier measured line will have a weight decrease of 0.5. This procedure repeats itself every new cycle of the main loop. Once a certain line has a weight of 0 or lower, the line is deleted from the array of earlier measured lines meaning it was probably a wrong measurement. If a line has a weight which is bigger or equal to the number specifying the rate of the main loop, that line is pushed to the World Model as an obstacle. The World Model ensures this data is processed accordingly. | ||
The difference between a regular histogram filter and this version, is that a regular histogram filter usually uses all the available data and this version only a filtered amount. The choice for the altered histogram filter was made because it was considered to be redundant to measure all the data, since the filtering procedure already filters out the expected data. Also, by using the filtered amount of data, it was easier to separate unknown static objects from known objects. This in its turn made it easier to visualize static objects only. In hindsight, it would have been better to use all the available LRF data. This however, is discussed more thoroughly in the Discussion. | |||
==== Potential field ==== | ==== Potential field ==== | ||
The potential field enables PICO to safely move in any direction. It measures distances from itself to objects and finds the direction in which moving can be done safely. The potential field is designed in the following way. | The potential field enables PICO to safely move in any direction. It measures distances from itself to objects and finds the direction in which moving can be done safely. The potential field is designed in the following way. | ||
After obtaining a trajectory from the strategy/planning component, PICO starts moving in the desired direction. This desired direction can be visualized by a vector pointing towards the next waypoint. As mentioned before, the potential field measures the distances from PICO itself to objects around it. The potential field is specified to be around 30 centimeters around PICO itself, ensuring that objects far away will not have any influence on the movement. Thus, as long as objects are out of the range of the potential field, the potential field will not give any direction since the sum of all vectors in the potential field will result in 0. This will on its turn result in a movement in only the direction of the desired direction. This can be seen in the most left | After obtaining a trajectory from the strategy/planning component, PICO starts moving in the desired direction. This desired direction can be visualized by a vector pointing towards the next waypoint. As mentioned before, the potential field measures the distances from PICO itself to objects around it. The potential field is specified to be around 30 centimeters around PICO itself, ensuring that objects far away will not have any influence on the movement. Thus, as long as objects are out of the range of the potential field, the potential field will not give any direction since the sum of all vectors in the potential field will result in 0. This will on its turn result in a movement in only the direction of the desired direction. This can be seen in the most left of Figure 23. | ||
Once an object (or objects) enter(s) the potential field, the vectors in the potential field will have different lengths. This will result in a potential field vector pointing in the direction where the distances to any object are equal. Adding this vector to the desired direction vector results in the right figures of Figure 23. Once the sum of all the potential field vectors equals zero again, the direction will again be decided by the desired direction vector. | |||
[[Image: potentialfieldgroup12020.png| thumb | 750px | center | Figure 23: Examples of the behavior of the potential field vector [10] ]] | |||
To ensure the ‘power’ of the potential field vector will not dominate the ‘power’ of the desired direction vector or the other way around, both vectors are scaled to perform optimally. This is further explained in the section Movement. | |||
[[Image: | |||
=== Movement === | === Movement === | ||
| Line 321: | Line 359: | ||
The monitor class serves as a safety net in case PICO shows undesired behavior. Initially the monitoring checked multiple cases. First of all, if an object was too close to PICO a flag would be given. The object would be in PICO’s safe space which is a circle around PICO with a certain radius. Furthermore, if the potential field vector became too large, also a flag would be given. The idea was that if the potential field vector became too large, PICO should not be able to pass an object. Lastly, if something was placed on the desired location of PICO, also a flag would be given. There was initially thought that in this case the path of PICO could not be continued. However, since the desired locations of PICO is reached by means of waypoints, the waypoints could be changed in order to reach the desired location. | The monitor class serves as a safety net in case PICO shows undesired behavior. Initially the monitoring checked multiple cases. First of all, if an object was too close to PICO a flag would be given. The object would be in PICO’s safe space which is a circle around PICO with a certain radius. Furthermore, if the potential field vector became too large, also a flag would be given. The idea was that if the potential field vector became too large, PICO should not be able to pass an object. Lastly, if something was placed on the desired location of PICO, also a flag would be given. There was initially thought that in this case the path of PICO could not be continued. However, since the desired locations of PICO is reached by means of waypoints, the waypoints could be changed in order to reach the desired location. | ||
Eventually, only the following flag is used in the hospital challenge | Eventually, only the following flag is used in the hospital challenge: the grid that is used consists of nodes which are accessible or not. A node is not accessible if an object is located on it. If a node that is used in the A* path planning coincides with an inaccessible node, a flag will be given. Because all relevant obstacles were acknowledged by the grid, PICO creates a new path when his previous path is blocked by an obstacle. | ||
The first two flags were not used because the parameters of the potential field are chosen in such a way that these flags would not become true. | |||
=== Visualization === | |||
A visualization tool was built from scratch and written with the idea of making debugging easier. Mainly for the algorithms developed within the perception module which were used to show the line fitting from the collected LFR data, the corner detection, the filtering of the obstacles and the potential field of PICO, and for the strategy component to show the output of the path finding algorithm. When the project evolved and more data got shared within the World Model module, the visualization tool also increased in size and the decision was made to transform it to a UI tool with debugging capability. | |||
The visualization module makes use of the OpenCV library [https://opencv.org/|[11]]. OpenCV is an open source library with the focus on real-time computer vision and machine learning in C++. By using the data from the World Model it was possible to display the data in real-time. The visualization is done by drawing all the data on top of three separate canvasses, namely: worldCanvas, gridData and laserData. Eventually the worldCanvas is used in the end visualisation which combines all the canvasses and is shown in Figure 24. | |||
[[Image:Group1_Visualization.gif | thumb | 650px | right | Figure 24: World canvas visualization]] | |||
The first | The first step was to fill the worldCanvas with the physical layout of the map, which was loaded from file. From here it was possible to grab the corner positions, cabinets and the wall objects which made up the static layout of the map and drawn in white color. To show the location were PICO was according to the simulation a red rectangle was placed on the position of the Odom data from the World Model. Here an arrow has been added to show the direction which PICO was facing. To be able to see when the potentialfield of PICO was active or now, a yellow circle was drawn with the same sense range. | ||
On top of the static data the sensed walls and corners were drawn to visualise the output of the linefitting and corner feature algorithmes from the perception module. The walls that were found were drawn as lines in salmon color, and the corners in pink or navy blue depending on the angle; pink for convex corners and navy blue for concave corners. Another output of the perception module was the detection of static objects, which were coming from the histogram filter and were drawn in black. There were no visualizations for dynamical objects, the reason for this was explained in the perception section. | |||
Another piece of information that was shown was coming from the strategy component, which was the path that PICO had to travel to get to the selected cabinet. The path was drawn by connecting the list of target points together by a set of lines. The path was divided into two categories; the path that was left and the path that was been wandered, which was visualized with dark and light purple in that order. PICO moved over all targets on the path, to show the active target point where PICO was heading to a blue circle on top op the path was drawn. The end target of the path, the goal in this case next to the side of the cabin, was shown as a green circle. | |||
The gridData canvas was used to draw all the cells of the 2D grid that were created and maintained by the World Model module. This visualization was used to check whether the map was parsed correctly to the grid and to check if the sensed obstacles were put into the correct cells of the grid. Based on the Boolean data from the grid each cell was colored red for unreachable (false) and green when it was reachable (true) for PICO. The choice for a separate canvas was done be able to alpha blend the grid into the worldCanvas to not lose the overview of the other data when the grid was drawn. | |||
[[Image:Group1_LRF_Snapshot0.png | thumb | 180px | left | Figure 25: Snapshot export of the LRF data]] | |||
Since one part of the visualization was exporting a snapshot of the LRF data when PICO was in front of a cabin a separate canvas was used to be able to export the data on its own, named laserData. When the state machine initialized the export event the visualization class would react to it by exporting the current laserData canvas with a black backgroudn to the ‘dataexport’ folder as a PNG file. To create the visuals, a circle was drawn with radius zero and a line width of one, such that it represented a point on the canvas. To copy the data to the worldCanvas a copy function was written that copy pasted all the data that were not defined as the color black as seen in Figure 25. | |||
Seeing a tremendously amount of information at the same time can be quite hard to process while writing and debugging. To prevent this from happening, a toggle feature has been created in the visualisation tool to be able to turn each part seperatly on and off by pressing a key on the keyboard belonging to that specific feature. Next to the mentioned visualisation a debugging view has beed which will give additional information regarding the objects that are visualized such as the object ID’s, normal vectors of drawn lines and the ID’s of the path. | |||
== Hospital Challenge result == | == Hospital Challenge result == | ||
In general, the Hospital Challenge showed to be a success. The initial localization was completed almost instantly and was maintained for the biggest part of the challenge. The histogram filter detected the static obstacles rather well and the potential field dealt with the dynamic obstacles as intended. It also prevented some crashes when the localization was lost. There were however also some problems which together resulted in a DNF. | In general, the Hospital Challenge showed to be a success. The initial localization was completed almost instantly and was maintained for the biggest part of the challenge. The histogram filter detected the static obstacles rather well and the potential field dealt with the dynamic obstacles as intended. It also prevented some crashes when the localization was lost. There were however also some problems which together resulted in a DNF. | ||
Firstly, during testing, doors were interpreted as a single line within a doorway instead of the doors being completely flush with the walls. This resulted in a rather slow detection of the doors since the detection of the doors (and objects) is mainly based on finding the corners of the objects/doors. Even though not instantly detected, PICO eventually would realize there was a closed door in front of him updating his path to its target. | Firstly, during testing, doors were interpreted as a single line within a doorway instead of the doors being completely flush with the walls. This resulted in a rather slow detection of the doors since the detection of the doors (and objects) is mainly based on finding the corners of the objects/doors. Even though not instantly detected, PICO eventually would realize there was a closed door in front of him updating his path to its target. The behavior of PICO can be seen in Figure 26. | ||
[[file:Group1_Challenge_DoorDetection.gif | frame | 800px | center | Figure 26: Slow door detection]] | |||
The second attempt | The second problem occurring was a due to an error in its localization, see Figure 27. The first attempt resulted in a DNF due to bad localization. This occurred in the room of cabinet 6 and was caused by an offset in PICO’s localization. When PICO reached the cabinet it thought it had to move a bit further due to an offset in his localization. This resulted in PICO’s strategy telling him to drive forward but the potential field telling him to drive backward, this together caused a deadlock and hence the attempt was stopped. | ||
[[file:Group1_results_Deadlock.gif | frame | 800px | center | Figure 27: Deadlock of detection mechanism]] | |||
The second attempt also failed, this time in the room with cabinet 1. PICO’s frame would occasionally rotate and thus give a false positive of an object in the grid, obstructing its path. A monitoring function was implemented to deal with these kind of scenarios. When no path can be found to PICO’s target this means that a false positive has occurred somewhere. This monitoring function would then raise a flag to clear the grid of all detected obstacles which allowed PICO to find another path. However, in the hospital challenge, PICO would keep getting false positives due to bad localization resulting in an infinite loop of resetting the grid and finding no path. This event was not captured on video and unfortunately in testing afterwards this did not occur in the same way as the hospital challenge. However, Figure 27 shows a similar deadlock occurring. | |||
The bad localization had two reasons. Firstly, the localization is based on detecting features in the map (e.g. corners). However in the hospital challenge objects were added that “cluttered” these features. Secondly, since the doors were closed flush with the walls, two additional corners could not be used to localize PICO and together with the objects this seemed too much to handle in the room with cabinet 1. | The bad localization had two reasons. Firstly, the localization is based on detecting features in the map (e.g. corners). However in the hospital challenge objects were added that “cluttered” these features. Secondly, since the doors were closed flush with the walls, two additional corners could not be used to localize PICO and together with the objects this seemed too much to handle in the room with cabinet 1. | ||
| Line 345: | Line 403: | ||
= Discussion = | = Discussion = | ||
The reason why the Hospital Challenge could not be concluded is the fact that doors were not recognized. By choosing to feed the histogram filter with only the filtered amount of data, we complied to the flaws of the filtering algorithm. These flaws were that doors, modelled as straight lines between two walls, were frequently unobservable for this algorithm. The reason for this is because the filtering algorithm was unable to separate a door from its attached walls, causing the data of the door to be filtered out. Meaning that obstacle detection also could not ‘detect’ doors as an obstacle. If we would have used all the LRF data for the histogram filter, we would lose our ability to solely visualize unknown static objects. However, this would provide us with the ability to detect everything, including doors, therefore it would increase the robustness of the code. | |||
In our own simulations, where doors were modelled as obstacles in the middle between walls, our code worked well. One of those simulations is shown in Figure 28. | |||
[[file:Hospitalc12020.gif | frame | 800px | center | Figure 28: Successful Hospital Challenge attempt]] | |||
= Meeting schedule = | |||
Meetings were scheduled twice a week (with some exceptions) on Microsoft Teams. | |||
{| class="TablePager" style="width: 90%; min-width: 240px; margin-left: 2em; color: black;" | |||
|- | |||
! scope="col" | ''' Meeting''' | |||
! scope="col" | '''Date''' | |||
! scope="col" | '''Time''' | |||
! scope="col" | '''Chairman''' | |||
! scope="col" | '''Secretary''' | |||
! scope="col" | '''Summary''' | |||
|- | |||
| 1 || 24-04-2020 || 15.00 || - || - || Introduction | |||
|- | |||
| 2 || 28-04-2020 || 15.00 || - || T.J.M. Snijders || Introduction to tutor, discussed contents of Design Document | |||
|- | |||
| 3 || 01-05-2020 || 14.00 || B. Godschalk || S.C.M. Mennen || Discussed software architecture | |||
|- | |||
| 4 || 03-05-2020 || 14.00 || - || - || Discussed strategy for Escape Room Challenge | |||
|- | |||
| 5 || 05-05-2020 || 14.00 || - || - || Discussed Escape Room Challenge software structure | |||
|- | |||
| 6 || 08-05-2020 || 15.00 || S.C.M. Mennen || B.P.J. Reijnen || - | |||
|- | |||
| 7 || 11-05-2020 || 14.00 || - || - || Decided that the current solution for the escape room challenge is sufficient | |||
|- | |||
| 8 || 12-05-2020 || 14.00 || - || - || Last meeting before Escaperoom Challenge | |||
|- | |||
| 9 || 15-05-2020 || 14.00 || B.P.J. Reijnen || J.H.B. de Zwart || Start architecture and flow chart for Hospital Challenge | |||
|- | |||
| 10 || 19-05-2020 || 14.00 || - || - || Decided upon Hosptial Challenge strategy | |||
|- | |||
| 11 || 22-05-2020 || 14.00 || A.C.C.E. Vissers || J.H.B. de Zwart || Continue in same groups on specific parts | |||
|- | |||
| 12 || 26-05-2020 || 14.00 || - || - || | |||
|- | |||
| 13 || 29-05-2020 || 14.00 || J.H.B. de Zwart || T.J.M. Snijders || Discussion about presentation and Hospital Challenge | |||
|- | |||
| 14 || 02-06-2020 || 14.00 || - || - || | |||
|- | |||
| 15 || 05-06-2020 || 14.00 || T.J.M. Snijders || B. Godschalk || Continue with separate parts, more testing required | |||
|- | |||
| 16 || 09-06-2020 || 14.00 || - || - || Last preparation for Hospital Challenge | |||
|- | |||
| 17 || 12-06-2020 || 13.00 || - || - || Division of tasks for Wiki page | |||
|- | |||
| 18 || 16-06-2020 || 14.00 || - || - || Division of tasks for Wiki page | |||
|- | |||
| 19 || 19-06-2020 || 14.00 || - || - || Feedback on wiki parts | |||
|- | |||
| 20 || 22-06-2020 || 13.30 || - || - || Collect all parts and finish the wiki | |||
|- | |||
| 21 || 22-06-2020 || 13.30 || - || - || Last wiki update progression meeting | |||
|} | |||
= Code snippets = | |||
String pulling: https://gitlab.tue.nl/MRC2020/group1/snippets/655 | |||
Visualization: https://gitlab.tue.nl/MRC2020/group1/snippets/656 | |||
= Sources = | |||
[1] https://www.cbs.nl/nl-nl/dossier/arbeidsmarkt-zorg-en-welzijn | |||
[2] http://cstwiki.wtb.tue.nl/index.php?title=Mobile_Robot_Control#Hospital_Competition | |||
[3] M.J.G. van de Molengraft. MRC Lecture 1.1: ''Introductory Lecture''. 2020. | |||
[4] https://github.com/nlohmann/json (JSON file by Niels Lohmann) | |||
[5] http://cstwiki.wtb.tue.nl/images/Mrc2020_finalmap_corrected.zip (Provided map JSON 2020 by TU/e) | |||
[6] http://cstwiki.wtb.tue.nl/images/Finalmap2019.zip (Provided map JSON 2019 by TU/e) | |||
[7] https://en.wikipedia.org/wiki/A*_search_algorithm | |||
[8] https://www.youtube.com/watch?v=g024lzsknDo | |||
[9] Linear Algebra with Applications 9th ed - Steven J. Leon (Pearson, 2015) | |||
[10] http://cstwiki.wtb.tue.nl/index.php?title=Embedded_Motion_Control_2019_Group_3 | |||
[11] https://opencv.org/ (openCV library) | |||
Latest revision as of 22:51, 24 June 2020
Group Members
| Name | Student Number |
|---|---|
| T.J.M. Snijders | 1017557 |
| B.P.J. Reijnen | 0988918 |
| J.H.B. de Zwart | 1020347 |
| S.C.M. Mennen | 1004332 |
| A.C.C.E. Vissers | 0914776 |
| B. Godschalk | 1265172 |
Introduction
This Wiki-page reports the progress made by Group 1 towards completion of the Escape Room Challenge and the Hospital Challenge. The goal of the Escape Room Challenge is to escape a rectangular room as fast as possible without bumping into walls. The goal of the Hospital Challenge is to deliver medicines from one cabinet to another as fast as possible and without bumping into static and dynamic objects. This year, due to COVID-19, all meetings and tests are done from home. The meeting schedule is shown at the end of the wiki. The software for the autonomous robot (PICO) is written in C++ and applied to a simulation environment since there has been no interaction with PICO. The simulation environment should represent the real test as closely as possible and therefore the information on this page should be applicable to the real test.
Design document
In order to get a good overview of the assignment a design document was composed which can be found here. This document describes the requirements, the software architecture which consists of the functions, components and interfaces and at last the system specifications. This document provides a guideline to succesfully complete the Escape Room Challenge.
Escape Room Challenge
The Escape Room Challenge consists of a rectangular room with one way out. PICO will be placed on a random position on a map which is unknown to the challengers before taking the challenge. PICO should be able to detect the way out by itself using the Laser Range Finder (LRF) data and drive out of the room without hitting a wall using its three omni wheels.
To create a solid strategy a number of options have been outlined. Two solid versions were considered; wall following and a gap scan version. After confirming that the gap scan version can, if correctly implemented, be a lot faster than following the wall, this option was chosen. Wall following does not require much understanding of the perception of PICO. By constantly looking at the wall and turning if a corner is reached, PICO will move forward as soon as no wall is visible in front of it indicating that the corridor is found. One other reason to use gap detection over wall following as a strategy is that the gap detection and moving to certain targets can later on be used in the Hospital Challenge. In the Hospital Challenge multiple rooms are present, objects are placed in the rooms and cabinets have to be reached which make wall following unapplicable.
The code is divided in multiple parts, or functions, which work together to complete the task. These functions are separated code-wise in order to maintain a clear, understandable code. Next, the state machine of PICO is elaborated. Finally, the simulations will be discussed together with the result of the Escape Room Challenge.
Functions
Finding walls and gaps
Using the LRF, data points are obtained. To differentiate between the walls and the exit a least squares regression line algorithm has been written. This algorithm fits a line over all found data points in order to find a wall in the field of view (FOV) of the LRF. By connecting the walls together it can be possible that a gap occurs, which will be saved into the global reference frame. To collect the data, PICO starts with a 360 degree FOV rotation, while doing so collecting all gaps. When the scan stops, all the collected gaps are checked based on some criteria to see if it is an exit and if it is the best exit possible and, if needed, fixed (straightened based on the adjacent walls). This function is also used in the Hospital Challenge and elaborated in the section Perception.
Path planning
To let PICO move from the start location to the exit, a path was generated for PICO to follow. This path consisted out of two points, a pre target (denoted as target B) before the exit gap and a target in the center of the gap (denoted as target A). See Figure 1. This section describes how these points were computed.
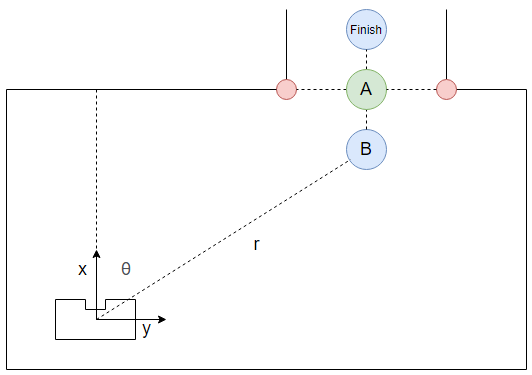
If a gap has been found by PICO, the corners of this gap are obtained. From this, target A can easily be computed by taking the average in both x and y direction. Target B is then placed perpendicular to the gap on a distance of 0.4 meters, which is the width of PICO. This is done to prevent PICO from attempting to drive to his target through a wall. Target B was computed as follows. First, the gap and the line between points A and B were denoted as a vector representation
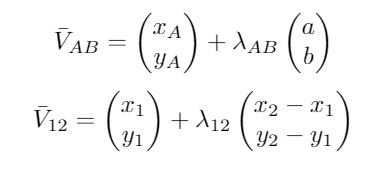
Then, a and b were computed. Since it is known that the vectors are orthogonal, the inner product should be zero, resulting in
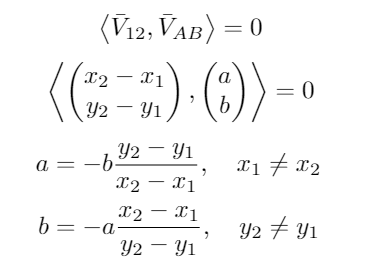
Depending on the values of the x and y coordinates of the corners of the gap, either a or b was set to the value 1 in order to compute the other value. With a and b known, the direction of the vector AB is known. The length of this vector is also known, hence equating the two norm of the vector to the length of the vector results in
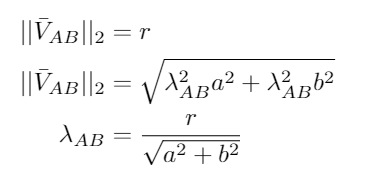
After these computations are completed, two possible locations for point B can be obtained. One before and after the gap. To determine the correct point, the distance from PICO to both points was computed. The point with the smallest distance will always be the point before the gap and thus the correct point B. Note that this will hold only when the room from which PICO needs to escape is a rectangle or when the corners of the gap are obtuse angles.
Potential field corridor
When PICO drives in the corridor, PICO starts to monitor the left and right wall to center itself between the walls of the corridor while moving towards the finish line. This is done using proportional control.
State machine
In Figure 2, the flow chart is depicted which starts at 'Inactive' and ends at 'Move forwards' until PICO stops.
The first step that will be executed is the 'Initialize' step. This step will be used to clear and set all variable values (the odometry data from the wheels as well as the LRF data) to the default state from which it will continue to the '360° scan', where using the LRF data all walls and possible gaps are detected. In this scan all LRF measurements will be mapped into wall objects if obtained data points connect. When data points do not connect, a gap occurs which can be a possible exit or a faulty measurement. When the scan can not find any gaps in the walls, PICO will move 1 meter to the furthest point measured in the scan and performs a new scan. If, for any reason, PICO tends to walk into a wall, the robot will move backwards and starts a new scan.
The next step 'Gap?' is checking if the gaps found can be considered as an exit. If no gaps meet the specifications of a gap, the next step will be 'Move to better scan position' and PICO will redo the previous steps. If a gap meets the requirements of the exit, then PICO will move on to ‘Path Planning, which will be executed to calculate the best possible way to the exit. When the path is set the following step will be 'Move to gap'.
The final step will be 'Center?' which will center the robot in the corridor of the exit to prevent that incorrect alignment with the exit will result in a crash with the walls.
Parallel to this flow PICO will continuously keep track of objects with the laser range finder. Whenever a object is detected in a specific range of the robot a flag will be thrown. This flag can be used to update the path planning, which will prevent crashes when the robot is heading in the wrong direction.
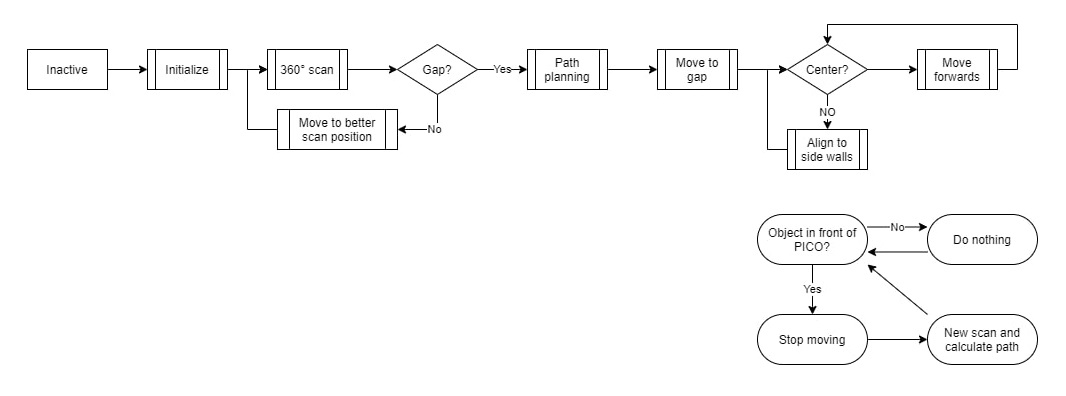
Simulation
The result of the strategy and the implemented functions is shown in Figure 3 where one can see that a gap is detected. PICO moves to a point in front of the opening and rotates towards the opening. While driving through the corridor, PICO keeps its distance to the walls.
In Figure 4 one can see how PICO behaves if no gaps are detected. PICO keeps on moving 1 meter from its scan location to scan again.
Escape Room Challenge results
The challenge attempt can be seen in Figure 5. As can be seen in the scanning, the robot rotates in a smooth counterclockwise rotation in which the gap detection algorithm detects the exit. After validation of the gap, a pre-target and target are placed in relation to the detected gap location. However, the movement towards it went wrong. Normally, the motion component of the software calculates the smallest rotation between the angle of PICO and the pre-target & target of the gap. During the development and validation of the written software in the simulator, this component worked as expected. However, during the challenge it emerged that the calculation did not work when comparing positive and negative angles. As a result, the calculation showed that a positive angle had to turn into the negative direction in order to reach its target. Because of this problem PICO started to rotate 270 degrees to the right instead of 90 degrees to the left. This problem came up 2 times, both after the 360 degrees scan and after reaching the pretarget.
Immediately in the first attempt PICO moved out of the room in 55 seconds. However, PICO decided to align itself with the reference angle using the largest rotation which costed a lot of time. In the end group 1 is proud of the result.
After the challenge we looked at this problem and applied a possible solution. If the simulation would be performed again with the right rotations the simulation time could be reduced to 25 seconds which would have resulted in a 2nd place during the challenge, instead of our 4th place that we were placed this time.
In summary, every software component worked fine without failing completely. However, after a bug fix in the motion component, everything works optimally without any known errors. The wall detection and motion software can be used for the hospital challenge and made usable with some additions without starting from scratch again.
Hospital Challenge
The shortage of care services is increasing over time due to the ageing population and is expected to increase for the coming years as well [1]. Without an increase in the amount of care providers, the chances of burnouts and other health issues for these people will increase significantly. Knowing that a spontaneous increase in healthcare personnel is unlikely, other solutions for work relieve need to be found. One of these solutions can be found in the way of automated robots. These robots can perform relatively simple tasks and thereby assist the care providers. A simple, yet time consuming, task of these care providers is fetching medicines from certain cabinets to give to the patients. The Hospital challenge is based on this task.
In this challenge, a robot (PICO in this case) should be programmed in such a way that it can ‘fetch’ and ‘deliver’ items from one place to another. The fetching and delivering is for this challenge not physically possible, therefore a specific procedure needs to be followed which is specified in the problem description [2]. Logically, this robot should be able to move without bumping into either static (i.e. walls or doors) or dynamic (i.e. people) objects and it should work as fast as possible. Also, this robot should be able to perform these tasks with only the order of cabinets to visit as input.
Design architecture
Like for the Escape room challenge, the first step of the Hospital challenge was to determine the internal information exchange in a clear way. This meant only specifying the main components with its main functions. The goal for the Escape room challenge was to define an architecture which could be used for the Hospital challenge as well. When discussing the structure of the previous architecture it became clear that it would not hold for the Hospital challenge. Reasons for altering the architecture were ambiguities in the goals of certain components and the underestimation of the size of the Perception component. Ambiguities mainly occurred in de information transfer in the strategy component and into the movement control component. Previously, it was assumed that Movement Control needed the current state from the Final State Machine (FSM). Later it was decided that only the target would suffice. Also, by splitting Monitoring from Perception as a separate component it was ensured that the code would remain clear. The Perception component was relatively small during the Escape room challenge, therefore it was assumed Monitoring could be a main function of Perception in the Hospital challenge as well. However, during the discussions for the design architecture for the Hospital challenge it became clear this assumption was wrong. Perception was expected to contain a considerable amount of functions more. By setting Monitoring as a separate component, Perception would become smaller, thus clearer to read. This also maps with the paradigms explained in this course. Namely, once a code starts becoming more complex, it should remain explainable [3].

The software architecture for the Hospital challenge thus has one more component compared to the Escape room challenge, in the form of monitoring. Additionally, the transfer of data from the output of Strategy/Planning to the World Model and the transfer of data from World Model to Movement Control is changed. These changes made it clear that if a component is expected to grow significantly in size, it is wise to look for functions inside that component that can be separated from that component. Discussing the internal data transfer between components more thoroughly also became a learning point, since it needed to be changed after the Escape room challenge.
The final Design architecture is thus formed by the components Perception, Monitoring, World Model, Visualization, Movement Control and Strategy/Planning. These components, combined with their main functionalities and their inputs and outputs, can be found in Figure 6. For instance, one of the main functions of the Strategy/Planning component is the FSM, which determines the state PICO is in and what it should do next. As input it needs, among other things, the current position of PICO. As output it sends the state to the World Model and a goal to the Path planning function of Strategy/Planning. Whether it is input or output can be determined by the direction of the arrow.
All the components and their functionalities, mentioned in the Design architecture, are explained more elaborately in the following sections.
Components
In the following sections, the different components and its main functions are explained elaborately. Furthermore, the testing phase and final challenge results are discussed.
Finite state machine
To be able to navigate and do necessary actions during the hospital challenge, a finite state machine has been composed. The FSM combines all the functions written in all the different components in a predefined sequence to be able to go to different cabinets in the order provided at startup. The FSM will be written in a switch case structure which will do specific actions in each state, and depending on the transition conditions move through it. In Figure 7, the FSM is visualized in a flow state graph which shows the connection between the different state. The description and transition conditions are explained below.
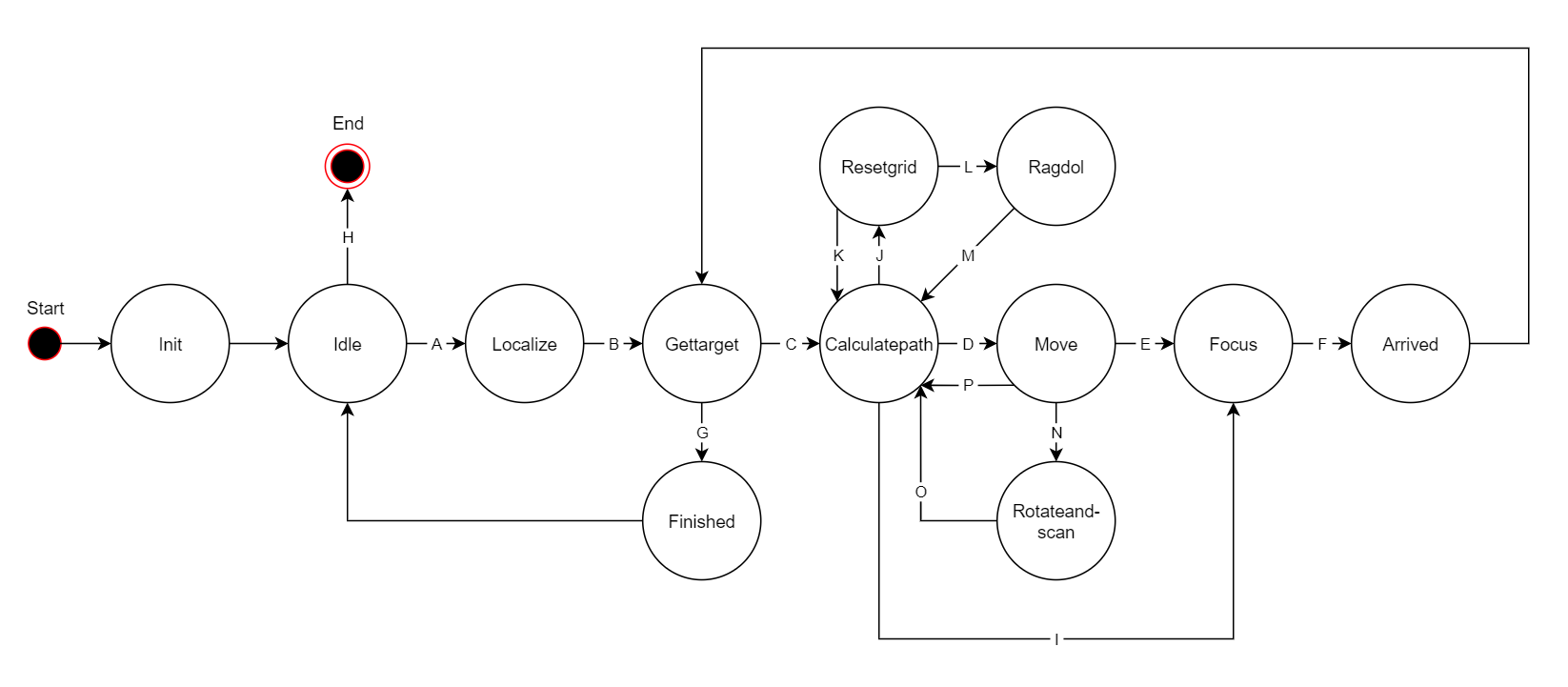
States
- INIT: During the init state all variables used within the FSM are set to their default values. This state is used to be able to recover from crashes within the program, more specific, from a unknown state or an exception within the FSM. By resetting all the variables withing the FSM, the program can continue its operation like nothing happened.
- IDLE: The Idle state is used to set PICO into Idle mode when the program has finished the cabinet sequence. If this state is executed from startup, the state will do nothing else then moving to the next state.
- LOCALIZE: Before PICO can be moved within the environment the location of PICO needs to be estimated. By rotating and translating PICO it would generate enough data for the perception module to localize PICO.
- GETTARGET: This state is used to get the next cabinet ID from the provided sequence and setting the goal position where PICO should be to pickup or deliver the medicines.
- CALCULATEPATH: The A* pathfinding algorithm is executed which will produce a path based on the current position of PICO and the goal received from the ‘gettarget’ state.
- MOVE: Move will walk over the generated path by the ‘calculatepath’ state which contains a set of positions to move to to get at the goal.
- FOCUS: When PICO arrives at the cabinet the orientation of PICO should be facing towards the closest cabinet side.
- ARRIVED: Remove reached cabinet from sequence and trigger the export event for the LRF data.
- FINISHED: All the cabinets from the provided sequence are visited when this state is executed. This state is used to notify the user and allows to exit the program.
- RESETGRID: When no path can be produced between PICO and the current goal the grid will be reset to the static layout of the map. By doing this possible false positives can be removed from the known data which will enable PICO to create a new path.
- RAGDOL: Fail-safe to prevent deadlocks when a dynamic object is preventing path generation. This can occure when an dynamic object is standing in a doorway or when the object pushes PICO into a corner and restrict the movement of PICO completely.
- ROTATEANDSCAN: This state will be executed when PICO can’t move towards the direction it is facing due to a door or static object or when the localization has not been updated enough. It can be that the LRF data on that position is not good enough to meet the requirements for object recognition, by rotating PICO the LRF data can give more information about the surroundings. Another effect of this is that the localization algorithm uses this data to update the position of PICO.
Transition conditions
- A: Finished flag is false.
- B: Localization algorithm returns true when location is known.
- C: Cabinets left in the commited sequence.
- D: Path exist to selected cabinet.
- E: Arrived at the end of the path.
- F: Alligned with cabinet side.
- G: No cabinets left from the commited sequence.
- H: Finished flag is true.
- I: PICO is already on the goal position.
- J: Could not create an existing path to the goal position.
- K: Grid resetted attempt is under 10 times.
- L: Grid resetted for the 10th time.
- M: Ragdol has been active for 5 seconds.
- N: Monitoring component detects less then 0.25 meter of movement in 7 seconds.
- O: Scan modus has been active for 3 seconds.
- P: Monitoring component flags that path to goal is obstructed.
World model
The worldmodel component of the project lays down the foundation of the coding structure which is used since the beginning of the course. Information that had to be shared between the different components was written to and read from this class. This structure allowd that the components could be constructed without dependencies of other components. A summery of the data that is stored within the worldmodel:
- World model data: static layout of the map divided into walls, cabinet sides and corners where convex and concave types are saved seperated.
- Localization data: current position and odom travel from last known position.
- Perception data: LRF data, the detected walls, the detected corners which are divided in convex and concave lists, the detected static objects, resulting potentialfield vector and the closest point from PICO.
- Strategy data: 2D grid, path nodes and string pulled path nodes.
- Monitoring data: Error flags for path obstruction and movement check.

In addition to sharing and storing data of all the other components, the worldmodel was also responsible for loading and parsing the JSON map to a usable format. Loading the map from the JSON file was done by using the opensource JSON for Modern C++ library written by Niels Lohmann [4]. Based on the available information from the file structure of the map from 2019 a format has been constructed to be used in the project. Seen from Figure 8, the JSON file consisted of three datatypes which would be delivered one week before the challenge; a list of corner points in world space location, a list of connected corner points seen as walls, and a list of objects representing the cabinets which consisted a list of connected corner points that made up the four sides for each cabinet. The left bottom corner of the map was considered as the world frame origin with position (0,0). Besides that, the ID of the corners started at the origin with an index of 0 and persistently increased by one when moving to the next one. By building on this logic it was possible to define closed polygon shapes by setting end points for each one based on specified corner indexes. This functionality is used to determine for each corner if it had a convex or concave property, which is used within the perception module to stabilize the localization algorithm. The loading sequence of the walls and cabinets are used to distinguish the inner walls and cabinet sides from the external walls. This was done by defining a normal vector direction based on the loading order of the corners that made up the wall or cabin side. The usage of these functionalities will be explained in more detail in the perception section.
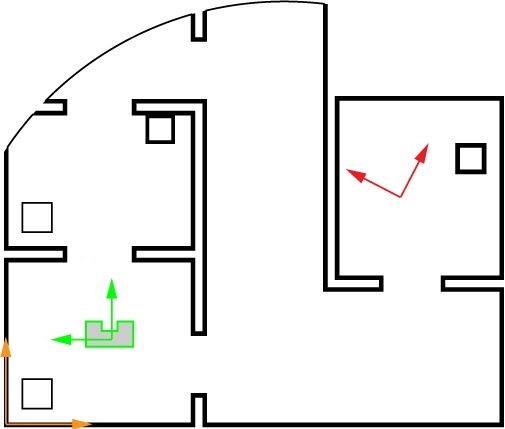
Storing the corners from the JSON file was done in a Vector3D object. This object was created to store three double values, namely the x and y position in the world frame and the third one was used to store the corner type; convex (pi/2) or cancave (3pi/2). The walls and cabinets are stored seperatly into a vector in the worldmodel as Line2D objects. The Line2D object is a class that stored two Vector3D objects which represented the begin and end point of a wall of cabin side. Next to storing the two positions it was possible to get the length of the line and getting the normal of it.
By now, the project contained three coordinate frames, where one was independent of the other two, namely: PICO’s own and global reference frame (seen from PICO and its initial starting position within the world) and the world frame (loaded from the JSON file). To get everything working together in the same frame, the world frame was used as a global reference frame to make it straightforward when doing calculations. By doing this in the same frame for all components the amount of coordinate transformations is reduced to a bare minimum which reduces the complexity of the calculations and is easilier to explain. As said before, the global coordinate frame started at (0, 0) at the left bottom of the map, which was chosen such that their x- and y-axis were positive defined to the right and upwards. Next to that was PICO’s own frame where the x-axis was positive upwards and their y-axis was positive defined to the left of PICO. Both are shown in Figure 9 which also explains the relationship between them, here the world reference frame position is given in orange, the PICO’s global reference frame is given in red and PICO’s frame is expressed in green.
One week before the hospital challenge the map of this year was released (the heightmap is shown in Figure 10), unfortunately the data [5] was not in the same format as last year [6], negative coordinates were provided, which were not taken into account when writing the loading sequence. So, before the file could be used, small modification had to be executed in such a way that the data had the same format as the map from previous year. One of the modifications was shifting all world coordinates up until everything had a positive value. Another modification that has been done is renumbering the indexing of the corner ID’s in such a way that the first corner started at 0 and was sequentially increased by one when going to the next corner. And the last was again reversing the corner index numbering of the internal walls and cabin sides.
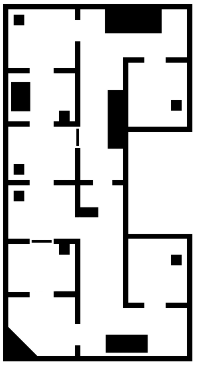
In order to create a bridge between the loaded JSON map and the collected data from the perception module towards the strategy component a 2D grid has been constructed. The grid is used to combine all the different collected pieces of data such that the strategy component can calculate the next steps that needed to be taken to get to the next goal. The choise for a 2D grid instead of a node based architecture was to be more flexible in path creation and the tuning of it. It allowed to specify various zones around objects and walls to create a safety zone without having to place them manually in the JSON map file and specify the connections between the nodes. An additional advantage of the grid was the navigation around dynamic objects, when an (dynamic) object was obstructing the current path a new path could be constructed which seamlessly transitioned with the old path, resulting in smooth movement behavious. This was harder to accomplish with a node based structure, since it could be that a node closeby would interrupt the movement which would slow PICO down. How the data from the 2D grid is handled will be explained in more detail in the strategy section. The content of the grid started with integer values corresponding to the type of data which was stored in the cell belonging on the world position, such as: walls, corners and sensed objects. Further on in the project it became clear that the only thing needed within the strategy component was if the world position belonging to that specific cell was reachable or unreachable by PICO. To reduce the complexity of the grid the datatype was changed to a Boolean value. This meant that cells who store a 1 (true) that its world location was accessible and a 0 (false) that the world position was unreachable. Changing the datatype of the grid had no effect on the workings of the A* pathfinding, the grid was used to see where PICO could go and where it should stay away from, which is in fact just a Boolean value.
The first step made to build the 2D grid was to break up the world space which was occupied by the hospital environment in equally large pieces. To achieve this, the maximum horizontal and vertical position are saved while loading the corner data from the map file. Then, the grid dimensions were set to the length divided by the grid resolution. In order to get the best grid result, the resolution is determined based on the given data in the JSON file. Since all corner positions are rounded to one decimal place, except for 6 corner positions with more decimals, the courser resolution could be set to 0.1 meters without loss of accuracy. This resolution would result in a grid of 67x130 nodes for the provided map which has 6.7x13 meter as surface dimension. Lowering the resolution results in a higher grid density but will increase the processing time required by the pathfinding algorithm. In Figure 11a the initial grid is shown where all the grid data is set to accessible.
The next step was filling the grid with the loaded data stored in the Line2D objects from before. Since these objects stored the beginning and ending of all the walls and side cabinets it was possible to loop over each object, dividing the line between it into smaller segments who could be matched to the grid and setting the corresponding grid cell at the belonging world position to unreachable (false) in the grid. This eventually led to a grid as seen in Figure 11b. By giving different offsets to specified Line2D objects it was possible to create some space for error within the movement and path planning, such that PICO will not move directly next to obstructions such as the walls and cabinets. This effect can be seen in Figure 11c.
To let PICO react to sensed obstacles within the hospital environment the grid was considered as a living object, which meant that when an object got pushed to the worldmodel that the grid cells corresponding to the pushed object location got put into the grid as unreachable. Just like for the walls and cabinets an offset could be specified which would be filled in the grid around the locations where obstacles were detected. The combined result can be seen in Figure 11d.
-
Figure 11a: Empty 2D grid
-
Figure 11b: Loaded JSON data parsed
-
Figure 11c: Added offset
-
Figure 11d: Sensed object parsed
Strategy
The purpose of the strategy class is to compute and return the path that PICO needs to take in order to complete its tasks. This path should be a vector of 2D points in the global reference frame. These waypoints are determined in two steps.
First, the shortest path from PICO to its destination is computed using an A* shortest path algorithm [7]. This algorithm is used on the grid nodes of the world map which is shown in Figure 12. A* is a similar algorithm compared to Dijkstra’s shortest path algorithm. However, due to the implemented heuristic A* is much faster [8]. Figure 13 shows a path found by the A* algorithm.
After the A* algorithm has found a shortest path, a large vector is obtained with all grid nodes that need to be visited. There is however no need to reach all these points one by one, in fact, using this as a reference trajectory will only slow PICO down due to it correcting for overshoot. For this reason, a string pulling algorithm was used to only keep the waypoints that are strictly necessary in order to not hit any obstacles or walls. This string pulling algorithm works as follows.
It starts evaluating if it can reach the second node from the first node in a straight line without crossing an unreachable space. If so, then it continues evaluating if the third node can be reached and so on. If it stumbles on a node that cannot be reached in a straight line, in other words, it would cross an unreachable grid node on the straight line between the first node and the node that it is being evaluated, then it will save one node prior to the unreachable node and stores this node as a waypoint. The algorithm is then repeated with the saved waypoint as the new node from which the path is evaluated. This process continues until the final waypoint is reached. This results in a vector only containing the waypoints that are strictly necessary for it to reach the target without hitting an obstacle or wall, see Figure 14.
-
Figure 12: Visualization of the grid
-
Figure 13: Path generated using A* algorithm
-
Figure 14: Waypoints with string pulling algorithm
Perception
The main goal of the perception component is to translate the real world data into data which can be used for the simulation. The real world data consists of the LRF-data and the odometry data. Perception uses this data to localize PICO, detect obstacles and to measure the distance to objects around PICO.
A mathematical tool which is used a lot in this class is the vector projection, depicted in Figure 15.
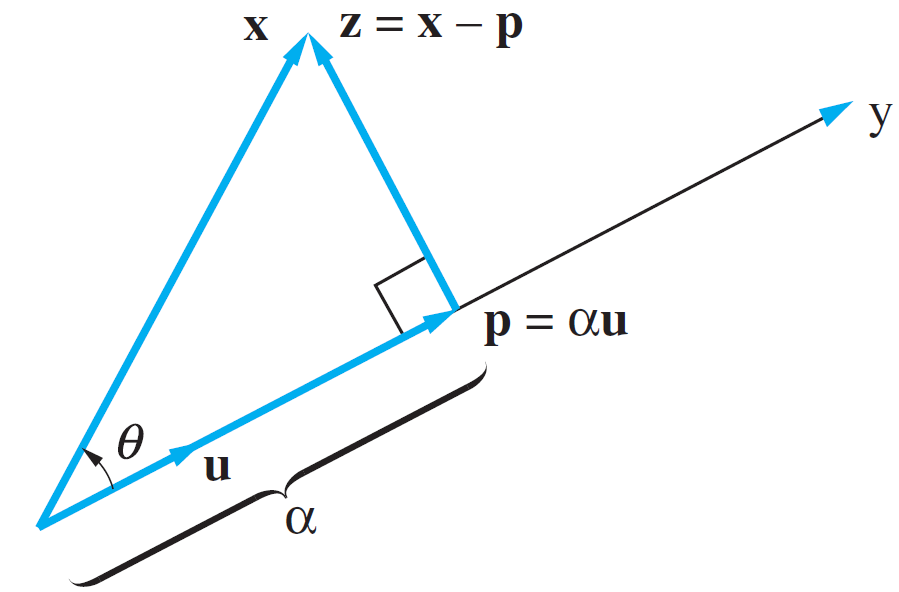
This tool is used to get the orthogonal of the vector projection of a point onto another vector and to get the point of intersection between this orthogonal and vector.
Line fitting
In order to extract features from the LRF data it is necessary to transform this data into lines. In essence this is done by the method of least squares. In general this goes by two steps; the first step is to make an estimation of which points belong to the same line and the second step is to find a line which fits the best between these points. The LRF sensor returns a collection of data points which is ordered counter clockwise. The line fitting algorithm loops through this data. In each iteration of this loop a subset from the first to the j-th element of the sensor data is taken. For each of these subsets a line is drawn from the first to last element of the subset and the squared norm of the vector projection of each of the intermediate elements onto this line is calculated. The sum of squared norms is used as an error variable.
There are two condition which can break this loop. The first condition is met when the error variable exceeds a certain error threshold. The second condition is met when the distance between two consecutive points is bigger than a certain distance threshold. The figures below represents the first condition visually. Figure 16 shows one subset for which this condition is not violated and thus the error is smaller than the threshold. Figure 17 shows the next iteration which does violate the first condition as you can clearly see that the red line will drift away from the data points as the iteration continues.
-
Figure 16: Fitting error shown visually, iteration i
-
Figure 17: Fitting error shown visually, iteration i+1
When a subset violates one of these conditions, the previous subset is taken again. In the example of Figure 16 above, this would result in the subset of the left part depicted by the blue encircled dots. From this subset the best line fit is calculated using the sum of least squares. This method uses the relative error in y-coordinates to find the best line fit. One disadvantage of this method is that it is not particularly good at fitting ‘vertical’ lines. To solve this the calculation is performed twice, one time where the relative error in y-coordinates is used and a second time where the relative error in x-coordinates is used. This means that a line is fitted in both directions. This results in two possible fits for each subset. From these two lines the longest of the two is used since this is the one which results in the best fit. A small cleaning procedure is done to make sure the best fit starts and ends at the first and last element of the subset respectively. This is done by extending/trimming the best fit to coincide with the vector projection of the first and last element of the subset onto the best fit. Figure 18 shows for three different data collections the fitted line by using the relative error in y-coordinates (red line) and by using the relative error in x-coordinates (blue line). The detailed part of set 1 shows the extending/trimming procedure where the grey part depicts the part of the best fit which is being trimmed.
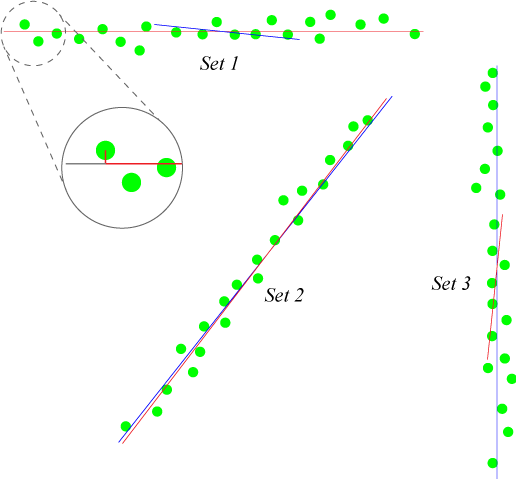
When the best fit is found its corresponding subset it is then removed from the original set and the iteration continues until the original set is empty.
The error threshold which bounds the fitting error is determined by trial and error until it yielded a satisfactory result. Taking this value too small results in the sensor data being divided into a large number of lines. Taking this value too big results in a bad representation of the sensor data, the corners will be rounded for example. A point of improvement is to make the error threshold a function of the distance measured by the LRF sensor since the error of the sensor also increases with a larger distance. The distance threshold is chosen to be sufficiently less than 200 mm. This prevents that cabinets, walls and other objects are being connected to each other. This value is chosen because the distance between a wall and a cabinet is 200 mm. This also prevents that datapoints which are far away and thus have a big spacing are being used to make lines, since this could lead to unreliable results.
The main objective of this function is to extract lines from the sensor data. There are a lot of different solutions to this problem but we chose specifically for this solution because it resulted in an easy and lightweight implementation which yielded satisfactory results. A possible motive to use another method is that this method is not particularly good at handling outliers but this did not affect the performance of our algorithm since the number of outliers is apparently small compared to the number of datapoints.
Localization
Maybe the most important part of the perception class is the localization. Localization is used to find the initial pose of PICO at start-up and to compensate of the uncertainty in odometry data.
PICO observes a portion of the map. The main goal of the localization is to fit this local portion of the map to the global map. In general the localization procedure follows a number of steps
1. Calculating the detected corners from the fitted lines
2. Determining the set of map corners which could possibly match the observed ones
3. Determining which combination of possible corners fit the observed corners
From the lines which are the result of the line fitting algorithm the observed corners are determined. Since the LRF sensor data is ordered clockwise, so is the set of fitted lines. The angle between each pair of consecutive lines is calculated. If the angle is (within a certain variance) 90 degrees it is denoted as an acute corner and if it is 270 degrees it is an obtuse corner, both seen from PICOs perspective. This has as additional condition that the end point of the first line and starting point of the second line are within a certain distance of each other. This results in a set of observed corners. From this set the three corners which are the closest to PICO and no further than 5 meters are used for localization. This is because these are determined by LRF data which is close to PICO and thus is more reliable. This threshold of 5 meters is determined via trial and error and led to a good result. The used localization procedure requires three angles to localize. This is why it is important not to have walls connected to cabinets since this would make a false corner. The observed corners are depicted in Figure 19 by the green dots.
Next the set of corners which could possibly form a match with the three observed corners is calculated. The known map has walls and cabinets which all have corners. The first step is to determine which corners are connected to a wall which faces PICO. This is done by checking if the normal vector of each wall/cabinet intersects the x or y axis of PICO with a positive scalar value multiplying the direction vector. The start/endpoints of the walls/cabinets which face PICO are added to the set of possible corner matches. The normal vectors for all the walls and cabinets are defined such that the all point into the walkable area. The red lines in Figure 19 depict the walls which face PICO, the blue lines do not face PICO.
The second step in determining the possible corner match set is to only add map corners that are within the observed radius of PICO. The observed radius is the circle around PICO which encloses the three observed corners, as shown by the dashed green circle in Figure 19. This results in the possible corner matches which are depicted by the orange circles with green border and the observed corners itself. It is important that this set is as small as possible since this influences the computation time a lot.
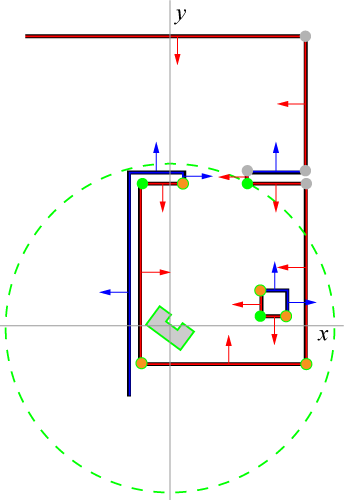
When both sets of observed corners and possible corner matches are determined the actual localization procedure can begin. In essence this is reverse of the trilateration method used by for example GPS. We have three observed corners A_O, B_O and C_O. We want to find a combination of three corners A_M, B_M and C_M which match with the observed ones. In order to do this we define a new set which holds all the possible combinations of triplets from the set with possible corner matches. From this set we want to find a subset which satisfy the following conditions:
- The type of corners (acute/obtuse) in each possible triplet need to be the same as the observed triplet.
- The distance between all the points in each possible triplet need to be the same as between the points of the observed triplet.
For each element of this subset a possible location can be determined.

For each point in the observed triplet the distance to PICO is exactly known. This distance defines the radius of the circle around each counterpart in the possible triplet. So the distance from PICO to A_O equals the radius of the circle around A_M. For each possible triplet we thus have a set of three circles. The intersection point of these three circles is a possible new location for PICO, which are shown in Figure 20.
Since there is measurement noise and estimation errors this will most likely not be a single point but rather a region. This region is determined by calculating the radical line of each pair of circles in the possible triplet. The radical is the line which intersects both circles, both end points of the radical are the intersection points of the circle. This results in three radicals and thus six intersection points. Each possible combination of three of these intersection points define the region in which the new location of PICO lies. But since the LRF data is measured in a specific order and the calculation of the radical proceeds in a specific (predetermined) order it suffices take only one combination of three intersection points. To make this invariant to a specific order one should do the next steps for all possible regions. The possible new location of PICO is taken to be the centre of the circumcircle described by the three intersection points. This possible location is said to be the new location of PICO if the following conditions hold:
- The angle between all the points in each possible triplet is the same as between the points of the observed triplet. Meaning the angle between the vectors A_M and B_M measured from the possible new location need to be the same as the angle between A_O and B_O and so on.
- The new location needs to lie in the vicinity of the old one.
So when a possible triplet passes through all these steps it is a match with the observed triplet and its corresponding possible location is the new location of PICO. The last step that remains is calculating the orientation of PICO. This is done simply by calculating the relative angle between the vectors A_O and A_M.
For all the above calculations an uncertainty radius is taken into account. All the thresholds for the calculations are a function of this radius. Where and what threshold is used is omitted from the explanation of the procedure for clarity. When PICO is in the start area the uncertainty radius is large, when PICO knows its location this radius gets smaller and smaller.
The disadvantage of this method is that the conditions for localization are very strict. When PICO senses a corner of an unknown object it can not localize and it has to observe at least three corners. But when the conditions are met, the localization deemed to be very reliable.
The reason why we chose for this approach is that we did not succeed in implementing a particle filter due to time constraints. This would results in a much better performance in the 'real' situation since it is more robust, but the approach we now used worked suffienctly good in the simulation.
Filtering algrorithm
As explained earlier, perception is able to translate raw LRF data into lines which do or do not correspond with known obstacles from the given simulation map. What this filtering algorithm does is simply checking if the fitted lines are in fact known obstacles, i.e. walls or cabinets, or unknown obstacles. The method of filtering the known from the unknown obstacles is done over multiple procedures which are explained next.
Once the fitted line data is retrieved from the World Model, it is converted into a vector containing the coordinates of the first point of the line and the coordinates of the last point of the line. Since these coordinates are local, they first have to be converted to global coordinates. After converting the coordinate system, the actual filtering will take place. This filtering will be done in two steps, namely first filtering out the walls from the fitted lines and last is to filter out the cabinets from the fitted lines. What remains are the fitted lines corresponding to unknown objects, i.e. static or dynamic objects.
The filtering takes place in a specific function. The input for this function consists of one of the fitted lines, to be called F, the data where this fitted line has to be compared with, to be called C, being walls or cabinets, and some thresholds which will be dealt with later on. The output is either a true or a false, since a fitted line does or does not coincide with a certain wall or cabinet.
The first step in comparing a line F to a set of line C’s, is to check whether the normals of the lines have the same direction. This already filters out a large part of the data with a relatively simple, thus saving computation time for later procedures. One of the input margins for this function is the ‘angle threshold’ determining the margin on the difference in the angles of the normal lines. This threshold has been set to a relatively low value, since there cannot be large differences in normal lines for them to be comparable, this procedure can be seen in Figure 21: step 1 until step 3. Comparing normals alone does not suffice. After that step, the distance from the fitted line F to the comparable line C is calculated. This is done by means of a vector projection. This coincides with the z in Figure 11.
Specifically the distance from the center of F to C is measured. The reason for this is because in some situations the fitted line data is heavily influenced by noise of the LRF. This mainly occurs when fitting the lines of long hallways. By measuring from the center of F, this problem was solved. Another input threshold for this function is the ‘distance threshold’. This threshold ensures that lines from other parts of the map cannot be compared with the measured line. For instance, the normals from C in room 1 and C in room 2 can coincide with F, but the distance from C in room 1 to F is way smaller than that of C in room 2. Thus, the C from room 2 is filtered out. This is visualized in Figure 21: step 4 and step 5.
The final step in comparing line C to a fitted line F is to check whether line F falls within the boundaries of C. This final step is mainly to check if the fitted line F is not a door. In this project it was assumed doors would be somewhat in the center of 2 walls, since in previous years that was the case as well. This however would mean that both the normals would have the same direction and the vector projection would be short, since the distance would be equal to the depth of the door in the wall. This final step filters out these possibilities. The last step checks if the distances from the first and the last point of F to the first and the last point of C are shorter than or equal to the length of C. If so, it means that both points lie in between or on line C. There is a last threshold for this procedure called ‘overshoot threshold’, which ensures that slight differences in distances cannot influence the process. If after all these steps, a line C from the set of comparable lines is left, then line F equals line C and the filtering process for this data set is complete. These final steps can be seen in Figure 21: step 6 until step 8. Figure 22 visualizes the same procedure according to the same steps, only now an unknown object is filtered.
-
Figure 21a: step 1
-
Figure 21b: step 2
-
Figure 21c: step 3
-
Figure 21d: step 4
-
Figure 21e: step 5
-
Figure 21f: step 6
-
Figure 21g: step 7
-
Figure 21h: step 8
This process first compares all fitted lines to all the known walls. The lines that were not comparable to a wall are then compared to cabinets with the same procedure. If there are still fitted lines left after this process, the remaining fitted lines are used to check for obstacles.
-
Figure 22a: step 1
-
Figure 22b: step 2
-
Figure 22c: step 3
-
Figure 22d: step 4
-
Figure 22e: step 5
-
Figure 22f: step 6
-
Figure 22g: step 7
-
Figure 22h: step 8
-
Figure 22i: step 9
-
Figure 22j: step 10
Obstacle detection
The obstacle detection process is based on the theory of a histogram filter, but then simplified. The perception of PICO is able to detect obstacles by using the remaining fitted lines after the filtering process. By using a histogram filter it is ensured that not every remaining line is immediately pushed as obstacle. The exact procedure is explained in the following sections.
Once the perception of PICO measures something which is not comparable to either a wall or a cabinet, it is analyzed in the obstacle detection function. The first time something enters this function, the line data, combined with an initial weight of 1, is saved in an array. If the next loop of the main cycle, another line enters the obstacle detection function. This new fitted line is compared to the line which is saved earlier. By means of the filtering algorithm described before, the new fitted line is either similar or not similar to the earlier saved line. Which leads to two different scenarios. If the new fitted line is similar to the earlier saved line, it means the same line is measured twice. In this case, the weight of this line in the array is increased by 1. If the two lines are not similar, the new fitted line will be added to the array of earlier measured lines with a weight of 1 and the earlier measured line will have a weight decrease of 0.5. This procedure repeats itself every new cycle of the main loop. Once a certain line has a weight of 0 or lower, the line is deleted from the array of earlier measured lines meaning it was probably a wrong measurement. If a line has a weight which is bigger or equal to the number specifying the rate of the main loop, that line is pushed to the World Model as an obstacle. The World Model ensures this data is processed accordingly.
The difference between a regular histogram filter and this version, is that a regular histogram filter usually uses all the available data and this version only a filtered amount. The choice for the altered histogram filter was made because it was considered to be redundant to measure all the data, since the filtering procedure already filters out the expected data. Also, by using the filtered amount of data, it was easier to separate unknown static objects from known objects. This in its turn made it easier to visualize static objects only. In hindsight, it would have been better to use all the available LRF data. This however, is discussed more thoroughly in the Discussion.
Potential field
The potential field enables PICO to safely move in any direction. It measures distances from itself to objects and finds the direction in which moving can be done safely. The potential field is designed in the following way.
After obtaining a trajectory from the strategy/planning component, PICO starts moving in the desired direction. This desired direction can be visualized by a vector pointing towards the next waypoint. As mentioned before, the potential field measures the distances from PICO itself to objects around it. The potential field is specified to be around 30 centimeters around PICO itself, ensuring that objects far away will not have any influence on the movement. Thus, as long as objects are out of the range of the potential field, the potential field will not give any direction since the sum of all vectors in the potential field will result in 0. This will on its turn result in a movement in only the direction of the desired direction. This can be seen in the most left of Figure 23.
Once an object (or objects) enter(s) the potential field, the vectors in the potential field will have different lengths. This will result in a potential field vector pointing in the direction where the distances to any object are equal. Adding this vector to the desired direction vector results in the right figures of Figure 23. Once the sum of all the potential field vectors equals zero again, the direction will again be decided by the desired direction vector.

To ensure the ‘power’ of the potential field vector will not dominate the ‘power’ of the desired direction vector or the other way around, both vectors are scaled to perform optimally. This is further explained in the section Movement.
Movement
The purpose of the movement class is to compute and send reference velocities to PICO’s actuators. It uses both the potential field from the perception class as the next target node coming from the computed path from the strategy class to determine its direction.
First, the potential field and the target are converted to two unit vectors pointing in the desired directions for each. These vectors are then scaled according to the “obstaclePriority” variable. This value determines how much PICO should focus on avoiding obstacles instead of following its target. An obstacle priority of 1 results in PICO purely driving on the potential field whereas an obstacle priority of 0 results in PICO blindly following the target direction. After testing, an obstacle priority of 0.5 gave the best results. After scaling, the target and potential field vector are added up to find the movement vector. This vector determines the direction in which PICO should move
Next, the angle and distance to the target point are computed. Once these computations are done, three proportional controllers are used to compute the three reference velocities. This is done in the following manner.
First, a proportional controller is used to rotate PICO towards its target where the input to the controller is the difference between PICO’s target angle and its own orientation. Once PICO is within a certain margin of its target it uses two more proportional controllers to compute the velocities in its x and y frame. This time, the movement vector is used together with the distance to the target as an input to the controllers. It has to be noted that the computed velocities are saturated to remain within the maximum allowed velocities.
When a path node is reached (with a certain margin) PICO will send a Boolean signaling it has arrived at the target. Note that this margin is larger for the path nodes compared to the last node in the path (cabinet node). This is done since PICO does not need to track the reference perfectly, however, it needs to be at the precise location when arriving at the cabinet. Also, when arrived at the cabinet, the movement class will align PICO to the cabinet using the same proportional controller as for the rotation in the moving algorithm.
Monitoring
The monitor class serves as a safety net in case PICO shows undesired behavior. Initially the monitoring checked multiple cases. First of all, if an object was too close to PICO a flag would be given. The object would be in PICO’s safe space which is a circle around PICO with a certain radius. Furthermore, if the potential field vector became too large, also a flag would be given. The idea was that if the potential field vector became too large, PICO should not be able to pass an object. Lastly, if something was placed on the desired location of PICO, also a flag would be given. There was initially thought that in this case the path of PICO could not be continued. However, since the desired locations of PICO is reached by means of waypoints, the waypoints could be changed in order to reach the desired location.
Eventually, only the following flag is used in the hospital challenge: the grid that is used consists of nodes which are accessible or not. A node is not accessible if an object is located on it. If a node that is used in the A* path planning coincides with an inaccessible node, a flag will be given. Because all relevant obstacles were acknowledged by the grid, PICO creates a new path when his previous path is blocked by an obstacle.
The first two flags were not used because the parameters of the potential field are chosen in such a way that these flags would not become true.
Visualization
A visualization tool was built from scratch and written with the idea of making debugging easier. Mainly for the algorithms developed within the perception module which were used to show the line fitting from the collected LFR data, the corner detection, the filtering of the obstacles and the potential field of PICO, and for the strategy component to show the output of the path finding algorithm. When the project evolved and more data got shared within the World Model module, the visualization tool also increased in size and the decision was made to transform it to a UI tool with debugging capability.
The visualization module makes use of the OpenCV library [11]. OpenCV is an open source library with the focus on real-time computer vision and machine learning in C++. By using the data from the World Model it was possible to display the data in real-time. The visualization is done by drawing all the data on top of three separate canvasses, namely: worldCanvas, gridData and laserData. Eventually the worldCanvas is used in the end visualisation which combines all the canvasses and is shown in Figure 24.

The first step was to fill the worldCanvas with the physical layout of the map, which was loaded from file. From here it was possible to grab the corner positions, cabinets and the wall objects which made up the static layout of the map and drawn in white color. To show the location were PICO was according to the simulation a red rectangle was placed on the position of the Odom data from the World Model. Here an arrow has been added to show the direction which PICO was facing. To be able to see when the potentialfield of PICO was active or now, a yellow circle was drawn with the same sense range.
On top of the static data the sensed walls and corners were drawn to visualise the output of the linefitting and corner feature algorithmes from the perception module. The walls that were found were drawn as lines in salmon color, and the corners in pink or navy blue depending on the angle; pink for convex corners and navy blue for concave corners. Another output of the perception module was the detection of static objects, which were coming from the histogram filter and were drawn in black. There were no visualizations for dynamical objects, the reason for this was explained in the perception section.
Another piece of information that was shown was coming from the strategy component, which was the path that PICO had to travel to get to the selected cabinet. The path was drawn by connecting the list of target points together by a set of lines. The path was divided into two categories; the path that was left and the path that was been wandered, which was visualized with dark and light purple in that order. PICO moved over all targets on the path, to show the active target point where PICO was heading to a blue circle on top op the path was drawn. The end target of the path, the goal in this case next to the side of the cabin, was shown as a green circle.
The gridData canvas was used to draw all the cells of the 2D grid that were created and maintained by the World Model module. This visualization was used to check whether the map was parsed correctly to the grid and to check if the sensed obstacles were put into the correct cells of the grid. Based on the Boolean data from the grid each cell was colored red for unreachable (false) and green when it was reachable (true) for PICO. The choice for a separate canvas was done be able to alpha blend the grid into the worldCanvas to not lose the overview of the other data when the grid was drawn.

Since one part of the visualization was exporting a snapshot of the LRF data when PICO was in front of a cabin a separate canvas was used to be able to export the data on its own, named laserData. When the state machine initialized the export event the visualization class would react to it by exporting the current laserData canvas with a black backgroudn to the ‘dataexport’ folder as a PNG file. To create the visuals, a circle was drawn with radius zero and a line width of one, such that it represented a point on the canvas. To copy the data to the worldCanvas a copy function was written that copy pasted all the data that were not defined as the color black as seen in Figure 25.
Seeing a tremendously amount of information at the same time can be quite hard to process while writing and debugging. To prevent this from happening, a toggle feature has been created in the visualisation tool to be able to turn each part seperatly on and off by pressing a key on the keyboard belonging to that specific feature. Next to the mentioned visualisation a debugging view has beed which will give additional information regarding the objects that are visualized such as the object ID’s, normal vectors of drawn lines and the ID’s of the path.
Hospital Challenge result
In general, the Hospital Challenge showed to be a success. The initial localization was completed almost instantly and was maintained for the biggest part of the challenge. The histogram filter detected the static obstacles rather well and the potential field dealt with the dynamic obstacles as intended. It also prevented some crashes when the localization was lost. There were however also some problems which together resulted in a DNF.
Firstly, during testing, doors were interpreted as a single line within a doorway instead of the doors being completely flush with the walls. This resulted in a rather slow detection of the doors since the detection of the doors (and objects) is mainly based on finding the corners of the objects/doors. Even though not instantly detected, PICO eventually would realize there was a closed door in front of him updating his path to its target. The behavior of PICO can be seen in Figure 26.
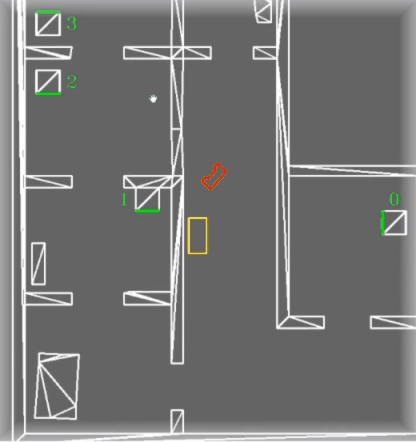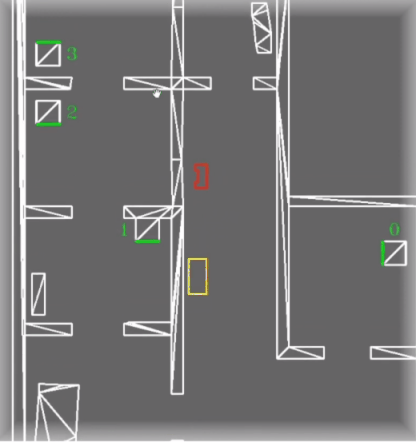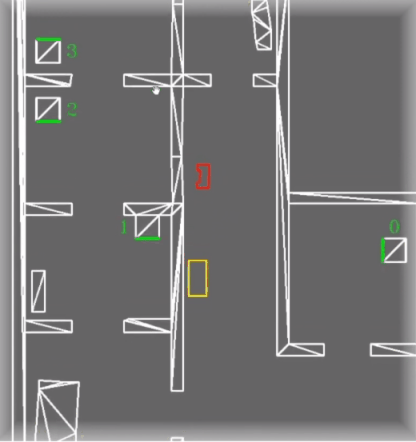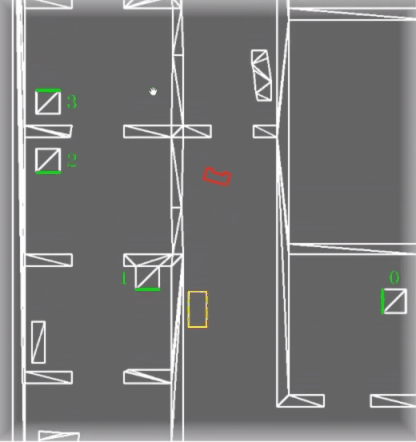
The second problem occurring was a due to an error in its localization, see Figure 27. The first attempt resulted in a DNF due to bad localization. This occurred in the room of cabinet 6 and was caused by an offset in PICO’s localization. When PICO reached the cabinet it thought it had to move a bit further due to an offset in his localization. This resulted in PICO’s strategy telling him to drive forward but the potential field telling him to drive backward, this together caused a deadlock and hence the attempt was stopped.
The second attempt also failed, this time in the room with cabinet 1. PICO’s frame would occasionally rotate and thus give a false positive of an object in the grid, obstructing its path. A monitoring function was implemented to deal with these kind of scenarios. When no path can be found to PICO’s target this means that a false positive has occurred somewhere. This monitoring function would then raise a flag to clear the grid of all detected obstacles which allowed PICO to find another path. However, in the hospital challenge, PICO would keep getting false positives due to bad localization resulting in an infinite loop of resetting the grid and finding no path. This event was not captured on video and unfortunately in testing afterwards this did not occur in the same way as the hospital challenge. However, Figure 27 shows a similar deadlock occurring.
The bad localization had two reasons. Firstly, the localization is based on detecting features in the map (e.g. corners). However in the hospital challenge objects were added that “cluttered” these features. Secondly, since the doors were closed flush with the walls, two additional corners could not be used to localize PICO and together with the objects this seemed too much to handle in the room with cabinet 1.
Even though PICO did not finish its objective, we became second place. This was due to PICO not crashing and driving safely at all times. Also, it was believed that given more time PICO would eventually get a better localization and being able to finish.
To summarize, all functionalities of PICO performed well with the exception of the localization and door detection. These should be improved in the future.
Discussion
The reason why the Hospital Challenge could not be concluded is the fact that doors were not recognized. By choosing to feed the histogram filter with only the filtered amount of data, we complied to the flaws of the filtering algorithm. These flaws were that doors, modelled as straight lines between two walls, were frequently unobservable for this algorithm. The reason for this is because the filtering algorithm was unable to separate a door from its attached walls, causing the data of the door to be filtered out. Meaning that obstacle detection also could not ‘detect’ doors as an obstacle. If we would have used all the LRF data for the histogram filter, we would lose our ability to solely visualize unknown static objects. However, this would provide us with the ability to detect everything, including doors, therefore it would increase the robustness of the code.
In our own simulations, where doors were modelled as obstacles in the middle between walls, our code worked well. One of those simulations is shown in Figure 28.

Meeting schedule
Meetings were scheduled twice a week (with some exceptions) on Microsoft Teams.
| Meeting | Date | Time | Chairman | Secretary | Summary |
|---|---|---|---|---|---|
| 1 | 24-04-2020 | 15.00 | - | - | Introduction |
| 2 | 28-04-2020 | 15.00 | - | T.J.M. Snijders | Introduction to tutor, discussed contents of Design Document |
| 3 | 01-05-2020 | 14.00 | B. Godschalk | S.C.M. Mennen | Discussed software architecture |
| 4 | 03-05-2020 | 14.00 | - | - | Discussed strategy for Escape Room Challenge |
| 5 | 05-05-2020 | 14.00 | - | - | Discussed Escape Room Challenge software structure |
| 6 | 08-05-2020 | 15.00 | S.C.M. Mennen | B.P.J. Reijnen | - |
| 7 | 11-05-2020 | 14.00 | - | - | Decided that the current solution for the escape room challenge is sufficient |
| 8 | 12-05-2020 | 14.00 | - | - | Last meeting before Escaperoom Challenge |
| 9 | 15-05-2020 | 14.00 | B.P.J. Reijnen | J.H.B. de Zwart | Start architecture and flow chart for Hospital Challenge |
| 10 | 19-05-2020 | 14.00 | - | - | Decided upon Hosptial Challenge strategy |
| 11 | 22-05-2020 | 14.00 | A.C.C.E. Vissers | J.H.B. de Zwart | Continue in same groups on specific parts |
| 12 | 26-05-2020 | 14.00 | - | - | |
| 13 | 29-05-2020 | 14.00 | J.H.B. de Zwart | T.J.M. Snijders | Discussion about presentation and Hospital Challenge |
| 14 | 02-06-2020 | 14.00 | - | - | |
| 15 | 05-06-2020 | 14.00 | T.J.M. Snijders | B. Godschalk | Continue with separate parts, more testing required |
| 16 | 09-06-2020 | 14.00 | - | - | Last preparation for Hospital Challenge |
| 17 | 12-06-2020 | 13.00 | - | - | Division of tasks for Wiki page |
| 18 | 16-06-2020 | 14.00 | - | - | Division of tasks for Wiki page |
| 19 | 19-06-2020 | 14.00 | - | - | Feedback on wiki parts |
| 20 | 22-06-2020 | 13.30 | - | - | Collect all parts and finish the wiki |
| 21 | 22-06-2020 | 13.30 | - | - | Last wiki update progression meeting |
Code snippets
String pulling: https://gitlab.tue.nl/MRC2020/group1/snippets/655
Visualization: https://gitlab.tue.nl/MRC2020/group1/snippets/656
Sources
[1] https://www.cbs.nl/nl-nl/dossier/arbeidsmarkt-zorg-en-welzijn
[2] http://cstwiki.wtb.tue.nl/index.php?title=Mobile_Robot_Control#Hospital_Competition
[3] M.J.G. van de Molengraft. MRC Lecture 1.1: Introductory Lecture. 2020.
[4] https://github.com/nlohmann/json (JSON file by Niels Lohmann)
[5] http://cstwiki.wtb.tue.nl/images/Mrc2020_finalmap_corrected.zip (Provided map JSON 2020 by TU/e)
[6] http://cstwiki.wtb.tue.nl/images/Finalmap2019.zip (Provided map JSON 2019 by TU/e)
[7] https://en.wikipedia.org/wiki/A*_search_algorithm
[8] https://www.youtube.com/watch?v=g024lzsknDo
[9] Linear Algebra with Applications 9th ed - Steven J. Leon (Pearson, 2015)
[10] http://cstwiki.wtb.tue.nl/index.php?title=Embedded_Motion_Control_2019_Group_3
[11] https://opencv.org/ (openCV library)