Mobile Robot Control 2020 Group 2: Difference between revisions
No edit summary |
|||
| Line 19: | Line 19: | ||
= Escape Room Challenge= | = Escape Room Challenge= | ||
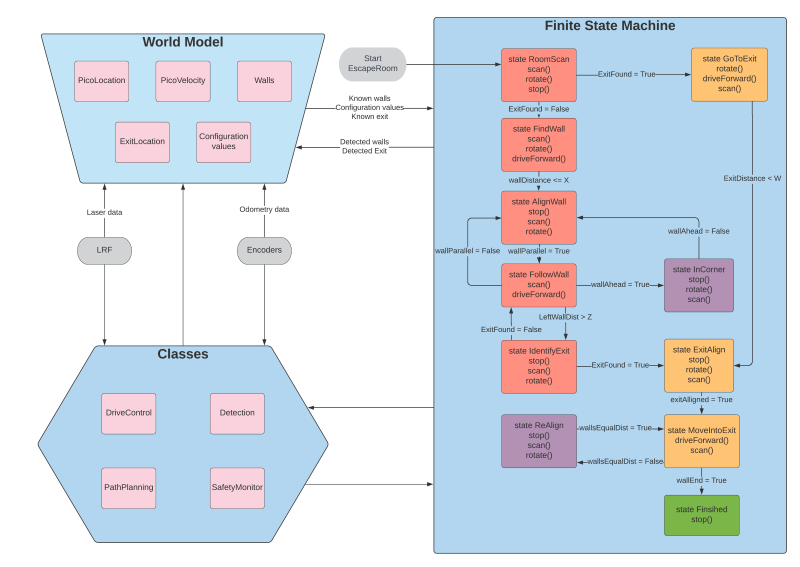
[[File:FlowChart1r.png]] | [[File:FlowChart1r.png]] | ||
[[File:EscapeRoom_Team2.mp4]] | |||
= Hospital Challenge = | = Hospital Challenge = | ||
Revision as of 09:48, 10 June 2020
Group members
Marzhan Baubekova - 1426311
Spyros Chatzizacharias - 1467751
Arjun Menaria - 1419684
Joey Verdonschot - 0893516
Bjorn Walk - 0964797
Bart Wingelaar - 0948655
Design Document
Design document for the escape room challenge can be found here:
File:Mobile Robot Control Design Document Group2.pdf
Escape Room Challenge
Hospital Challenge
Path Planning
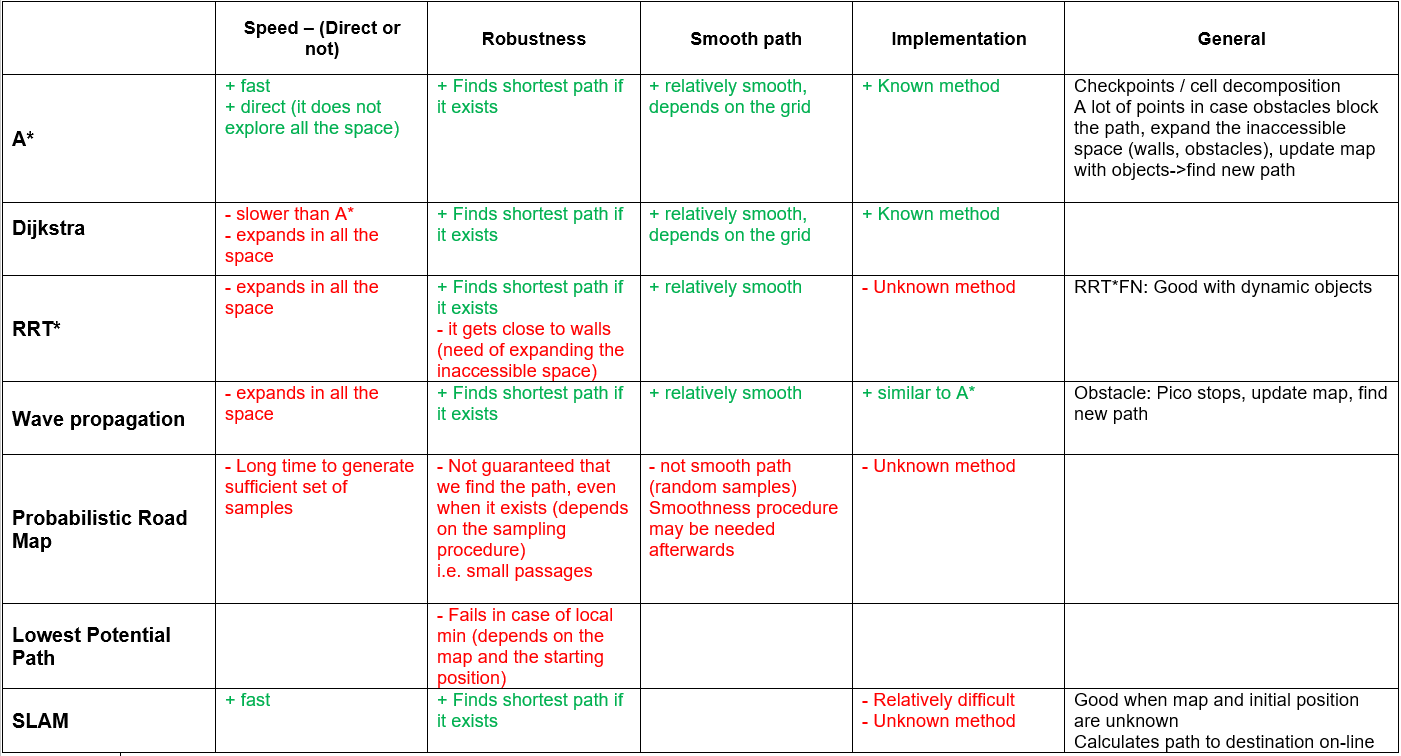
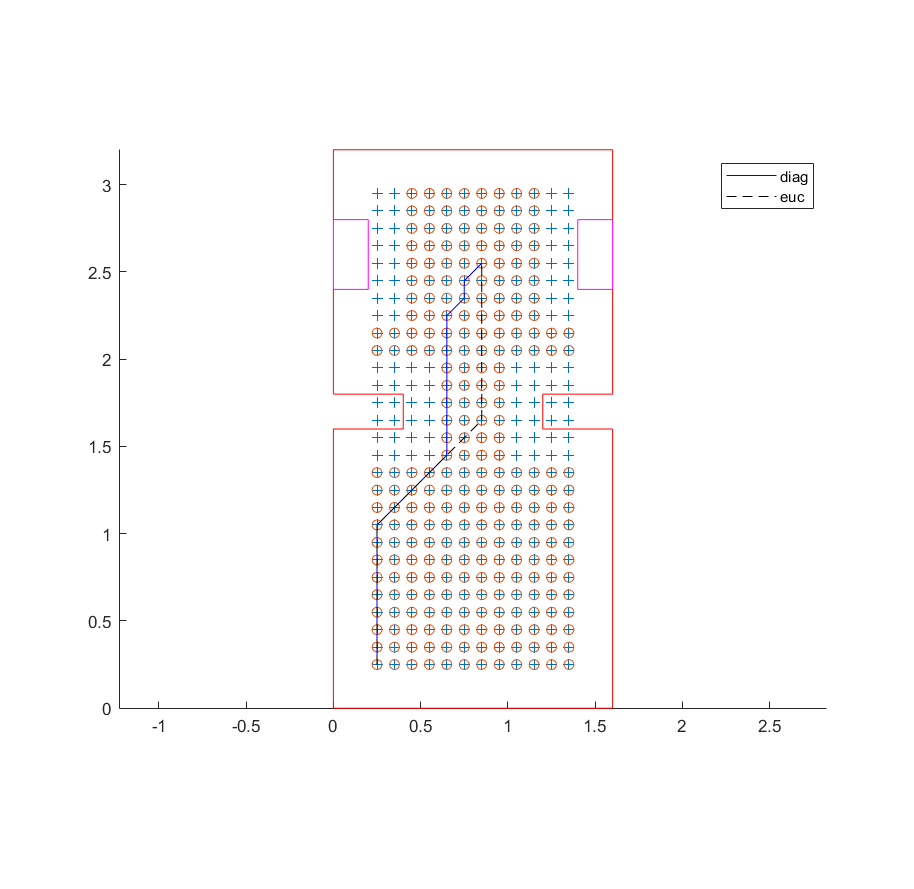
The algorithm that is chosen for the path planning is an A* algorithm. Before proceeding to algorithm, it is essential to transform map to a binary grid map. This step is done in Matlab and later translated to C++. There are two heuristic functions which are tested, namely diagonal and euclidian.
Pathplanning with 2 heuristics.
For the selection of the algorithm used for pathplanning a table of pros and cons has been formulated, which includes the computer performance index. A* is given an index number of 100. The walls and Dijkstra compute indices are an educated guess. The others are based on the amount of nodes used in a study
| Algorithm | Compute index |
|---|---|
| A* | 100 |
| Rapidly-exploring random tree | 100 |
| Potential field algorithm | 40 |
| Dijkstra | 100 or higher |
| Wall following | 100000 |
| Wave propagation | 100 or higher |
In addition, several algorithms are compared with respect to the convergence speed, the robustness of the method, the smoothness of the resulted path, the difficulty of the implementation and the sufficiency for the hospital challenge. The results are demonstrated in the table .........
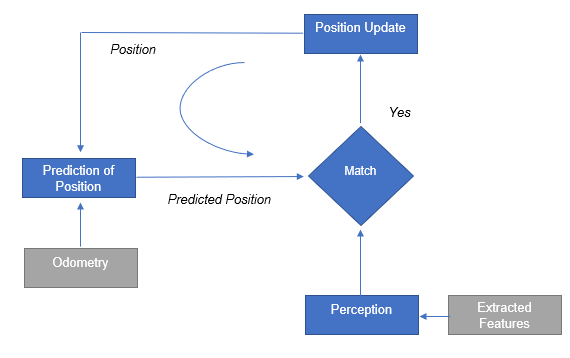
Localization
For the successful navigation it is important that the robot is aware of its current location. After considering known algorithms such as Markov localization, Kalman filter and partilce filters, it has been chosen to implement the line segment based localization. (Why?? restricted in time, experience, identification of landmarkes is problematic and etc.)
First, the algorithm requires features extraction and the most important features in the robot's environment are the straight lines. These features are used to build a local map from laser data. The line detection problem consists of two subproblems, namely segmentation, which deals with the number of lines and correspondence of data points to lines, and line extraction, which answers how to estimate line parameters, given which points belong to which lines. To solve the line extraction problem, we applied least squares solution. For the segmentation, the split and merge algorithm is used, which is a recursive procedure of fitting and splitting.
| Split and Merge Algorithm: |
|---|
| Initialize set S to contain all points. |
| Split |
| * Fit a line to points in current set S. |
| * Find the most distant point to the line. |
| * If distance > threshold, then split and repeat with left and right point sets. |
| Merge |
| * If two consecutive segments are close/collinear enough, obtain the common line and find the most distant point. |
| * If distance <= threshold, merge both segments. |
Logs
| Meeting # | Date and Location | Agenda | Meeting notes |
|---|---|---|---|
| 1 |
Date: 28-04-20 Time: 10:00 Platform: MS Teams |
|
|
| 2 |
Date: 01-05-20 Time: 14:00 Platform: MS Teams |
|
|
| 3 |
Date: 05-05-20 Time: 10:00 Platform: MS Teams |
|
Work division
|
| 4 |
Date: 11-05-20 Time: 11:00 Platform: MS Teams |
|
Work division
|
| 5 |
Date: 18-05-20 Time: 11:00 Platform: MS Teams |
|
Work division
|
| 6 |
Date: 22-05-20 Time: 14:00 Platform: MS Teams |
|
Work division is the same
|
| 7 |
Date: 26-05-20 Time: 11:30 Platform: MS Teams |
|
Work division is the same
|
| 8 | 5 | 10 | 15 |