Embedded Motion Control 2016 Group 7: Difference between revisions
No edit summary |
|||
| Line 232: | Line 232: | ||
== '''Implementation using dlib''' == | == '''Implementation using dlib''' == | ||
= '''Mapping''' = | |||
== '''Local direction recognition''' == | |||
== '''Global mapping''' == | |||
Revision as of 16:29, 12 June 2016
Group Members
| ID-Number | Name | |
| 0816253 | Emile van Halsema | e dot v dot halsema at student dot tue dot nl |
| 0805999 | Nard Strijbosch | n dot w dot a dot strijbosch at student dot tue dot nl |
| 0816608 | Raymond Kerstens | r dot j dot c dot m dot kerstens at student dot tue dot nl |
| 0814199 | Frank Heck | f dot j dot m dot heck at student dot tue dot nl |
| 0816361 | Ids van den Meijdenberg | j dot w dot a dot v dot d dot meijdenberg at student do tue dot nl |
Journal
In the journal the progess of the group will be described
Week 1
In the first week challenges ware specified and concretized. In addition every member installed ubuntu and read up on c++.
Week 2
In the second week we dove into code, a model was written for determining the nodes for corners and intersections, for preventing PICO to hit the wall and for plotting a course trough the corridor. In the simulator this seemed to work, however at the experiments we experienced multiple problems such as 'Ghost nodes' in large gaps, small gaps in the corridor and different values for the minimal angle, maximum angle and number of nodes in the laser data. Also when PICO should be going straight, it is drifting away. During the tutor meeting in week 2, we ware advised to start looking from the top, instead of from the bottom and start looking to the challenges as optimization problems. The lecture on wednesday also reflected this.
Week 3
From the feedback from the tutor meeting we concluded that we got ahead of ourselves and should take a step back to look at the problem from above. With this approach we created the presentation which was held at the end of week 3. For the corridor challenge we devided the model in the sections as thought of in the composition patern. To avoid problems encountered in our previous experiments first préprocessing is done. A function is written that eliminates the 'ghost points', all points beyond a trust region are set to a constant value, and the number of points saved for processing is reduced based on distance between the points. A new optimization function is created which searches for the open space in the obtained laser data using rectangles. The resulting rectangles can then be translated to the possible options in the maze(for example, a left corner, right corner, intersection or T-crossing). For the corridor challenge the only possibility is the T-crossing, in which case it should take the first exit. The resulting rectangle information is then used in the next function which is the setpoint. The setpoint function calculates 4 points in order to take the corner at the crossing. Whenever PICO is near a setpoint, the next point is taken such that it will go trough all points. In addition to the setpoint a potential field pushes PICO away from the wall when it gets to close.
Initial Design Embedded Motion Control Group 7
The project is dived in two parts: the corridor challenge and the maze challenge. The presentation of task-skill-motion system architecture can be found here: File:System architecture Presentation Group 7.pdf
Corridor challenge
For the corridor challenge the goal is to take the first exit.
Requirements
For this corridor challenge a number of requirements have to be met for an arbitrary corridor:
- Reach exit as fast as possible.
- Be able to recognize walls.
- Don't hit the walls.
- Be able to recognize and take the first intersection.
- Be able to rotate and translate.
- Be able to recognize maze exit.
- Stop when exit is reached.
Specifications
These requirements can be rewritten to specifications:
- Reach end within 1 minute.
- Recognition walls and intersection.
- Objects in straight line (with variation under 5 cm) are considered walls.
- Opening of at least 0.5 m is an intersection.
- Don not hit walls.
- Distance to walls at least 10 cm.
- Be able to drive.
- Drive in direction of point (updated 30 times a second).
- Maximal 0.5 m/s during straight line.
- Maximal 1.2 rad/s rotation.
- Recognize exit and stop
- Drive straight for 3 seconds after being 30 cm from intersection, then stop.
Functions
In order to meet these specifications the system is decomposed into multiple functions:
- Intersection recognition: identifying where the intersection is.
- Path planning: calculating the optimal path through the corridor.
- Safety features: Ensuring that PICO does not hit the walls.
Maze challange
For the maze challenge the goal is to find the exit in a maze. The location of the exit is unknown, there might be loops and there is a door in the maze.
Requirements
The requirements of the corridor challenge also hold for the maze challenge but are elaborated with:
- Be able to map the maze.
- Be able to locate itself in map.
- Be able to recognize maze components (doors and walls).
- Be able to open a door.
- Be able to detect the maze exit.
Specification
These additional requirements can be written to specifications:
- Mapping
- Update map 30 times per second.
- Remember path.
- On the driven path map walls, doors, crossings.
- Be able to localize itself in map.
- Localize position with precision of 5 cm.
- Recognition possible doors.
- Recognize dead end of at least 30 cm.
- Open door.
- Beep when in front of detected door.
- Recognize maze exit.
- Stop when no walls are detected in front.
- Mapping
Functions
The functions from the corridor challenge can then be completed to obtain the functions required for the maze challenge:
- Mapping: Save all intersections, doors, and connections.
- Optimal control: determine the best strategy for completing the maze
Interfaces
To keep track of the states in which the robot is, the states will be printed in the screen. Also is the idea to show the mapping for the maze challenge on the screen for debugging.
Mazesolver Corridor Challenge
For the corridor challenge a maze solver is used to determine which setpoints to go to. The maze solver is built using knowledge of the situation that will occur and therefore a more advanced maze solver algorithm will be needed for the maze challenge. The determination of which setpoints to go to is based on a standard test for the corridor. The correct nodes on the path which should be taken for the corridor will be listed as setpoints. If the first setpoint is not listed yet, a setpoint will be created to drive forward. The list will be updated with 10 Hz, as the whole loop used for the corridor challenge is updated with 10 Hz.
Setpoint Check
To determine whether a setpoint is reached, a test based on odomotry will be used. A setpoint will be seen as reached if the robot is within a margin of the actual setpoint. This test is defined as follows:
"The robot should be within the set margin for x and y position and within another set margin for the orientation."
If the robot has not reached the setpoint, the setpoint will be send again. Once the setpoint is reached, a message will be send to the maze solver such that the next setpoint in the list will be sent and the second setpoint gotten from the mazesolver will be send. .
Movement
One of the key elements of this project, is that PICO should be able to drive autonomously. From a higher level, the software receives a setpoint in absolute coordinates with respect to the starting position of the robot. With this information, the robot can move towards this location. However, it should also be avoided to collide into the walls. Therefore, a potential field is implemented which is a relatively easy method. The key elements are the following two forces:
- [math]\displaystyle{ F_{repp} }[/math]: Repelling force to ensure the robot will not collide with the walls
- [math]\displaystyle{ F_{attr} }[/math]: Attracting force responsible for the movement towards the setpoint
The potential field is a method from where the laser data range and angle with respect to the orientation of PICO are used. The wall forces will push PICO away from the walls, while the setpoint will attract PICO, see the Figure below.
For every laser range and angle, the following Equation is executed to calculate the force vector of that data point:
[math]\displaystyle{ F_{repp,i} = \frac{r_{scale}}{1375r_i^3 - 232.5r_i^2 + 12.19r_i} }[/math]
where [math]\displaystyle{ r_{scale} }[/math] is a scaling constant which is used to optimize the repelling force vectors. Afterwards, the contribution in the x- and y-direction can be computed with help of the angle for each laser data. The attracting force is computed by the following Equation:
[math]\displaystyle{ F_{attr} = e_x^2 + e_y^2 }[/math]
in where [math]\displaystyle{ e_x }[/math] and [math]\displaystyle{ e_y }[/math] are the relative error between PICO and the setpoint in meters. Afterwards, this force is normalised to ensure that [math]\displaystyle{ F_{attr} }[/math] will not go to zero when PICO is almost at the desired setpoint. Note that [math]\displaystyle{ F_{attr} }[/math] is with respect to the base coordinate frame. Since [math]\displaystyle{ F_{rep} }[/math] is in the relative coordinate frame, [math]\displaystyle{ F_{attr} }[/math] is rewritten to relative coordinates with a transformation matrix.
The parameters above are scaled in such a way that the following desired behaviour is exacted:
- When PICO is located close to a wall, [math]\displaystyle{ F_{rep} \gt \gt F_{attr} }[/math]
- When PICO is not located at a close distance to a wall, [math]\displaystyle{ F_{rep} \lt \lt F_{attr} }[/math]
Subsequently, the total force [math]\displaystyle{ F_{tot} }[/math] is calculated. From here, an angle [math]\displaystyle{ \phi }[/math] is obtained which can be used to calculate the desired velocities in the x- and y-direction, see the Figure below.
Afterwards, the velocity in x- and y-direction of the PICO is simply calculated by
[math]\displaystyle{ v_{x} = \text{cos}(\phi)v_{max} }[/math]
and
[math]\displaystyle{ v_{y} = \text{sin}(\phi)v_{max} }[/math].
For the rotational velocity, the error between the setpoint orientation and PICO's current rotation is used.
Environment identification
To subtract relevant information from the laser data an environment identification algorithm is used. This algorithm determines the dimensions of the corridor where pico is positioned, and it determines all the position and location of the visible sideroads. Using this information the world model can be updated, and the odometry data can be corrected.
General model
Algorithm
The general algorithm consists out of the following steps
- Preprocess laser data
- Determine the dimensions of current corridor
- Determine location and dimension of side roads
- Determine reliability of the found dimensions
Preprocess laser data
Determine current corridor
Optimization problem formulation
- [math]\displaystyle{ \begin{align} &\underset{x}{\operatorname{maximize}}& & f(x)=(A+B)\cdot(l+m) \\ &\operatorname{subject\;to} & & e_i(x) \leq 0, \quad i = 1,\dots,n \\ &&& x_i \leq x_{max}, \quad i = 1, \dots,5 \\ &&& x_i \geq x_{min}, \quad i = 1, \dots,5 \\ \end{align} }[/math]
where
- the objective function [math]\displaystyle{ f(x) }[/math] is defined by the area of the rectangle,
- [math]\displaystyle{ e_i(x) }[/math]the smallest distance of point [math]\displaystyle{ i }[/math] to the sides of the rectangle, hereby the error is positive if the point is inside the rectangle, and
- [math]\displaystyle{ n }[/math] are the number of points.
Initial conditions
Determine side roads
Optimization problem formulation
- [math]\displaystyle{ \begin{align} &\underset{x}{\operatorname{maximize}}& & f(x)=C\cdot D \\ &\operatorname{subject\;to} & & e_i(x) \leq 0, \quad i = 1,\dots,n \\ &&& x_i \leq x_{max}, \quad i = 1, \dots,3 \\ &&& x_i \geq x_{min}, \quad i = 1, \dots,3 \\ \end{align} }[/math]
where
- the objective function [math]\displaystyle{ f(x) }[/math] is defined by the area of the rectangle,
- [math]\displaystyle{ e_i(x) }[/math]the smallest distance of point [math]\displaystyle{ i }[/math] to the sides of the rectangle, hereby the error is positive if the point is inside the rectangle, and
- [math]\displaystyle{ n }[/math] are the number of points.
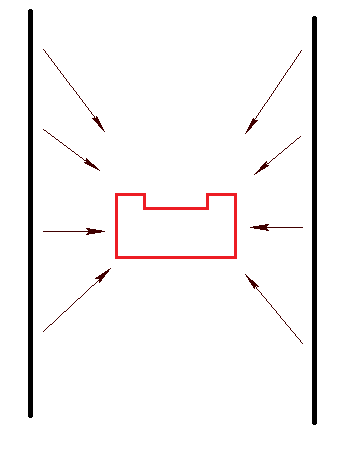
![Schematic representation of total force on PICO together with angle [math]\displaystyle{ \phi }[/math]](/images/Total_force.png)