Simulation: Difference between revisions
No edit summary |
|||
| (42 intermediate revisions by 2 users not shown) | |||
| Line 26: | Line 26: | ||
When a robot is at the clear zone (CZ), it drops whatever it is carrying and decides whether it will go searching or foraging. This choice is made by chance and the probability of it going to Foraging is given by the parameter searchChoice, which is a function of both the size of the blackboard (i.e. the number of coordinates in the blackboard) and the total number of robots. We will elaborate our choice for this parameter in the various simulations later in this article. | When a robot is at the clear zone (CZ), it drops whatever it is carrying and decides whether it will go searching or foraging. This choice is made by chance and the probability of it going to Foraging is given by the parameter searchChoice, which is a function of both the size of the blackboard (i.e. the number of coordinates in the blackboard) and the total number of robots. We will elaborate our choice for this parameter in the various simulations later in this article. | ||
If a robot is send to go foraging (rescuing), it is assigned a pile from the blackboard by chance. The chance of choosing blackboard element x is given by <math>((\text{the pheromones at }x)\cdot(\text{the treshold depending on the size of the blackboard}))^l \cdot (\text{a function of the distance between the robot and }x) \text{divided by the sum of that expression for all x on the blackboard}</math> where the function of the distance the parameter distance2 if the robot is at the CZ, or distance1 otherwise. If the function of the distance is constantly 1, and the treshold is constant in the size of the blackboard, this coincides with the probability in [[Media:Liu,_Chen,_Wang_-_2013_-_A_Model_of_Rescue_Task_in_Swarm_Robots_System.pdf]]. | If a robot is send to go foraging (rescuing), it is assigned a pile from the blackboard by chance. The chance of choosing blackboard element x is given by: | ||
<math>((\text{the pheromones at }x)\cdot(\text{the treshold depending on the size of the blackboard}))^l \cdot (\text{a function of the distance between the robot and }x) \text{divided by the sum of that expression for all x on the blackboard}</math> | |||
where the function of the distance the parameter distance2 if the robot is at the CZ, or distance1 otherwise. If the function of the distance is constantly 1, and the treshold is constant in the size of the blackboard, this coincides with the probability in [[Media:Liu,_Chen,_Wang_-_2013_-_A_Model_of_Rescue_Task_in_Swarm_Robots_System.pdf]]. | |||
The following code makes up the simulation. Runnable versions and settings files can be found in [[media:Total_simulation.zip]]. | The following code makes up the simulation. Runnable versions and settings files can be found in [[media:Total_simulation.zip]]. | ||
Note that the doc-strings aren't entirely accurate. This is because we decided that it would be more useful to write the full documentation on this wiki. | Note that the doc-strings aren't entirely accurate. This is because we decided that it would be more useful to write the full documentation on this wiki. The easiest way of running both the simulation (with and without graphics) and the script for processing the data is to install a package containing both python 2.7.x and matplotlib and then installing pygame to that. The package we used was anaconda (see https://www.continuum.io/downloads), in which I installed pygame by typing "conda install -c https://conda.anaconda.org/krisvanneste pygame" (as described in https://anaconda.org/krisvanneste/pygame) into command prompt. If you don't need to see the graphics, you don't have to install pygame (note that I can't guaranty the safety of using the aforementioned method of installing pygame). The simulation, as shown at our presentation can be viewed at https://goo.gl/photos/xCoAm1C48F3FVqD97 (since this wiki doesn't allow files larger than 10 mb). For running the simulation trough the scripts in .zip file, just run the settings file that contains the settings you want to use (n.b. the settings file should contain quite an elaborate block for the | ||
if __name__=="__main__" | |||
statement for the final version of the simulation, so e.g. settings1.py will work, but settings.py is just the choice of parameters we used for the simulation during the presentation). However, the "simulation 1 final (with USE) - plaatjes.py" file is still in the old format and requires a separate "settings.py" file. It can be run by running "simulation 1 final (with USE) - plaatjes.py". This inconsistency is due to the need for running many simulations with different settings on different computers simultaneously, which made it more practical to move the actual running of things to the settings file. | |||
"""the simulation actually used for running over and over again. | """the simulation actually used for running over and over again. | ||
| Line 874: | Line 880: | ||
runner() | runner() | ||
== Parameters == | == Parameters and USE == | ||
To incorporate ethical decision making in the design of our algorithms and simulation, we have 8 parameters for decision making. In this section we will give an overview of these parameters. We have also run the simulation with different values for the parameters based on underlying ethical choices. We will elaborate on these choices and review the results. <br/> | |||
The parameters for decision making are the following: | |||
*evaporatePile, a function that decides the speed of evaporation of pheromones. Fast evaporation equalizes priorities fast while slow evaporation will fix priorities. | |||
** Input: pheromone level at the end of time step t | |||
** Output: pheromone level at the beginning of time step t+1 | |||
*dropPile, Amount of pheromones dropped by a robot. Dropping large amounts of pheromones will increase the relevance of the pile more than dropping small amounts. An ethical choice to be made here is how the relevance of a pile is determined by the number of victims trapped at it, and by the difficulty of freeing them. | |||
** Input: current pheromone level, pile size (amount of robots needed to clear the pile entirely), number of victims trapped at the pile | |||
** Output: updated pheromone level | |||
* threshold, a function of the blackboard size which plays the role of k in [[Media:Liu,_Chen,_Wang_-_2013_-_A_Model_of_Rescue_Task_in_Swarm_Robots_System.pdf]]. A high treshold will give piles with little pheromones a relatively larger chance of being chosen when a robot goes foraging | |||
** Input: number of blackboard elements | |||
** Output: threshold | |||
* l, the sensitivity of the choice process to differences in pheromones. Large l will make piles with large of amounts of pheromones much more likely to be chosen | |||
** This is a constant | |||
* distance1, a function of the distance between the robot and a pile that influences the chance of the robot choosing that pile as its goal if the robot goes foraging from a position other than the CZ. This can be used to make robots prefer nearby piles over piles that are far away. | |||
** Input: the distance between the robot and a pile | |||
** Output: a factor in the probability of this pile being chosen | |||
* distance2, a function of the distance between the CZ and a pile that influences the chance of a robot choosing that pile as its goal if the robot goes foraging from the CZ. This can be used to give higher priorities to piles that are nearby the CZ (and thus prioritizing easier rescue). | |||
** Input: the distance between the CZ and a pile | |||
** Output: a factor in the probability of this pile being chosen | |||
*goalSwitch, a parameter deciding whether or not a robot may ignore its original goal in order to go to a pile it can immediately reach. This corresponds to the ethical dilemma of whether, if a robot is set out to save person a, it may ignore person b who can be saved by it immediately. | |||
** 0: don't consciously change goals, but if the robot happens to get into another pile, it will start helping out there. | |||
** 1: avoid other piles than the goal, so don't help out at piles that aren't the original goal. | |||
** 2: if another pile is reachable in one time step, go for that pile, no matter what the original goal was. | |||
*searchChoice, a function determining chance of going to foraging mode or going to search mode. This reflects the choice of how important finding unknown victims is compared to saving known victims | |||
** Input: size of blackboard, number of available robots | |||
** Output: the probability of a robot going foraging (n.b. 1-this value is the probability of a robot going searching) | |||
<br/> | |||
As mentioned, varying these parameters based on both ethical decisions and research interests as to their influence, we've created different settings for running the simulation. We will now discuss these settings and the accompanying results. Many graphs we have created but haven't put into this wiki can be found in [[media:results1.zip]] and [[media:results2.zip]]. | |||
===Influence of dropPile and evaporatePile when ignoring presence of victims=== | |||
The first experiment we will describe here is to the influence of the drop size and evaporation speed when ignoring the presence of victims. | |||
The first settings where | |||
name = "dropNoHumans1" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 1 | |||
distance2 = lambda x: 1 | |||
goalSwitch = 0 | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
We don't take distance into account and our searchChoice comes down to saying that if we have less than 10 robots per blackboard element, we want to go foraging for sure since we then can't miss the robots to searching, and otherwise the chance of going foraging should be linear in the number of blackboard elements.<br/> | |||
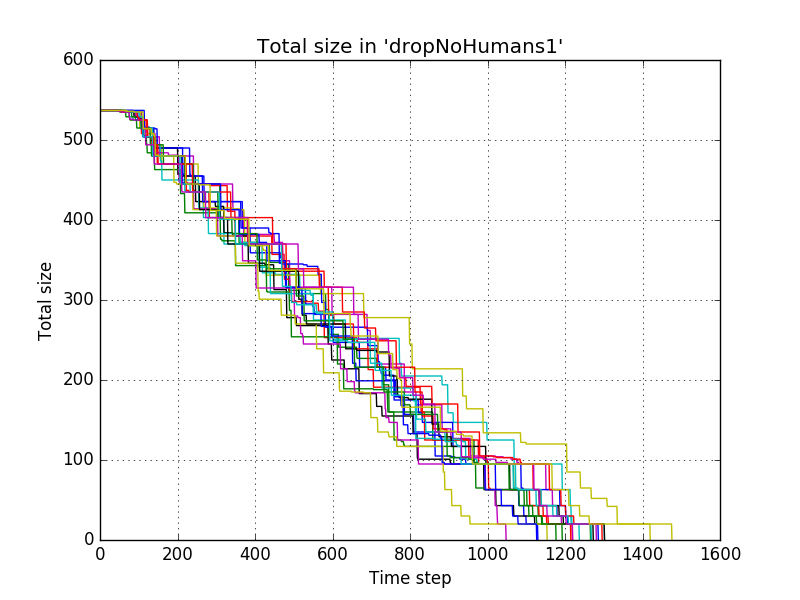
These settings resulted in the following progress of the total size of the piles for 20 simulations<br/> | |||
[[file:dropNoHumans1_-_total_size.png]]<br/> | |||
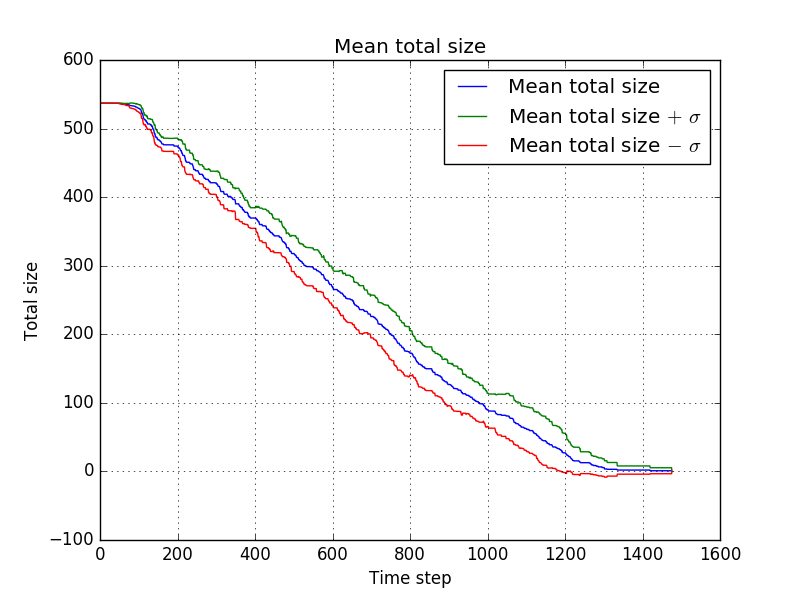
with which comes down to the following average progress<br/> | |||
[[file:dropNoHumans1_-_mean_total_size.png]]<br/> | |||
For the second settings we used a larger drop | |||
name = "dropNoHumans2" | |||
dropPile = lambda x,y,z:x+.07*y | |||
which resulted in<br/> | |||
[[file:dropNoHumans2_-_total_size.png]]<br/> | |||
and with averaging<br/> | |||
[[file:dropNoHumans2_-_mean_total_size.png]]<br/> | |||
For the third a smaller drop | |||
name = "dropNoHumans3" | |||
dropPile = lambda x,y,z:x+.03*y | |||
which resulted in<br/> | |||
[[file:dropNoHumans3_-_total_size.png]]<br/> | |||
and with averaging<br/> | |||
[[file:dropNoHumans3_-_mean_total_size.png]]<br/> | |||
for the fourth settings, the difference with the first settings was in the evaporation speed | |||
name = "evaporateNohumans1" | |||
evaporatePile = lambda x:.80*x | |||
which resulted in<br/> | |||
[[file:evaporateNohumans1_-_total_size.png]]<br/> | |||
and with averaging<br/> | |||
[[file:evaporateNohumans1_-_mean_total_size.png]]<br/> | |||
for the fifth settings, the difference with the first settings was again in the evaporation speed | |||
name = "evaporateNohumans2" | |||
evaporatePile = lambda x:.95*x | |||
which resulted in<br/> | |||
[[file:evaporateNoHumans2_-_total_size.png]]<br/> | |||
and with averaging<br/> | |||
[[file:evaporateNoHumans2_-_mean_total_size.png]]<br/> | |||
Now, to give an overview of the differences, the mean progress for the different settings is shown by <br/> | |||
[[file:Mean_total_size_for_dropNoHumans1-dropNoHumans2-dropNoHumans3-evaporateNohumans1-evaporateNoHumans2.png]]<br/> | |||
and the duration of the simulations (hence the duration before all piles are cleared) is shown by <br/> | |||
[[file:Duration_of_simulations_in_dropNoHumans1-dropNoHumans2-dropNoHumans3-evaporateNohumans1-evaporateNoHumans2.png]]<br/> | |||
This indicates that some settings might be better than others (e.g. settings 1 might be better than settings 3) but we have to little data to draw hard conclusions. It seems that out of these possibilities, the first settings might be the best, but more simulations might be necessary to investigate this further. | |||
=== Influence of dropPile and evaporatePile when taking victims into account === | |||
In the second experiment we do the same, but do take the number of victims into account, as can be seen from our choice of dropPile. For our first settings we took | |||
name = "dropHumans1" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4 | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 1 | |||
distance2 = lambda x: 1 | |||
goalSwitch = 0 | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
Now the number of victims at the pile is taken into account. We take it as <math>.2\cdot \text{number of victims} + .2 </math><br/> | |||
The <math>+.2</math> is necessary to ensure that piles without victims are still cleared (efficiently). We choose this approach because it is somewhat utilitarian in the sense that every human life is worth as much, it being somewhat linear in the number of victims. We will look at sub linear growth later. For compactness we will not show all the graphs for all the settings, but only show the combined results.<br/> | |||
For the second settings: | |||
name = "dropHumans2" | |||
dropPile = lambda x,y,z:x+.07*y*(.2*z + .2) #normal (1) if z == 4 | |||
For the third: | |||
name = "dropHumans3" | |||
dropPile = lambda x,y,z:x+.03*y*(.2*z + .2) #normal (1) if z == 4 | |||
For the fourth: | |||
name = "evaporateHumans1" | |||
evaporatePile = lambda x:.80*x | |||
For the fifth: | |||
name = "evaporateHumans2" | |||
evaporatePile = lambda x:.95*x | |||
All using the first settings as a base. <br/> | |||
The mean progress is shown by <br/> | |||
[[file:Mean_total_size_for_dropHumans1-dropHumans2-dropHumans3-evaporateHumans1-evaporateHumans2.png]]<br/> | |||
and the duration is shown by <br/> | |||
[[file:Duration_of_simulations_in_dropHumans1-dropHumans2-dropHumans3-evaporateHumans1-evaporateHumans2.png]]<br/> | |||
In this case the results are even closer and although settings3 seems to give somewhat better results than the other settings, this might be purely by chance. One thing that does strike the eye is that all of these settings seem to perform better than most of the settings in the previous experiment where humans wheren't taken into account. Note that we're note measuring when all humans are rescued (although that usually coincides with the duration of the simulation for this particular map), so it might be just a quirk of this particular choice of where the piles are. It would be interesting however to look more into this by using larger data sets, taking different maps into account. | |||
=== Influence of distance functions === | |||
For the third experiment we will look into the influence of the distance functions. We will do this from the perspective of ethical decision making, taking stance that we shouldn't ignore humans near us that need help. We will also investigate the influence of taking the same distance functions but without taking the number of victims at a pile into account, and the influence of choosing to search more - from the perspective that known victims should be helped first. The first settings file looks as follows: | |||
name = "ClosestFirst1" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4 | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed | |||
distance2 = lambda x: 1 | |||
goalSwitch = 2 | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
Note that we've put the goalSwitch to 2, so that if a robot comes across a pile it will always go for it. Now distance2 is still constant, so that distance doesn't play a role when starting at the CZ, but distance1 decreases for increasing distance, so that if a robot goes from searching to foraging, or switches goals during foraging due to its original goal being cleared, the robot gives more priority to piles nearby. We'll now show the rest of the settings files, which are basically explained above. | |||
name = "ClosestFirst2" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4 | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed | |||
distance2 = lambda x: 11.*speed/(1+x) #normal for x==10*speed | |||
goalSwitch = 2 | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
The next two will not take the number of victims at a pile into account | |||
name = "ClosestFirst3" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed | |||
distance2 = lambda x: 1 | |||
goalSwitch = 2 | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
name = "ClosestFirst4" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed | |||
distance2 = lambda x: 11.*speed/(1+x) #normal for x==10*speed | |||
goalSwitch = 2 | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
The next two make it less likely for a robot to go searching, so opting for rescuing known victims instead of looking for unknown victims faster | |||
name = "ClosestFirst5" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4 | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed | |||
distance2 = lambda x: 1 | |||
goalSwitch = 2 | |||
searchChoice = lambda bblen, nrob: min((20.*bblen)/(nrob),1) | |||
name = "ClosestFirst6" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4 | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed | |||
distance2 = lambda x: 11.*speed/(1+x) #normal for x==10*speed | |||
goalSwitch = 2 | |||
searchChoice = lambda bblen, nrob: min((20.*bblen)/(nrob),1) | |||
The mean progress is shown in <br/> | |||
[[file:Mean_total_size_for_ClosestFirst1-ClosestFirst2-ClosestFirst3-ClosestFirst4-ClosestFirst5-ClosestFirst6.png]]<br/> | |||
and the duration for the different settings is shown in <br/> | |||
[[file:Duration_of_simulations_in_ClosestFirst1-ClosestFirst2-ClosestFirst3-ClosestFirst4-ClosestFirst5-ClosestFirst6.png]]<br/> | |||
Which shows that going for the closest pile, especially when already in the field, yield much better results than in the previous two experiments. Taking distance into account when starting from the CZ seems however slightly worse than not doing so, although it might be so that this parameter needs some optimisation. | |||
=== Dedication === | |||
Another stance one might take is that when you have committed to saving a certain person, you should stick to that goal, because that person is depending on you. In this experiment, this point of view is explored. The first settings are given by | |||
name = "Dedication1" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4 | |||
treshold = lambda x: max(1,5-x) | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 1 | |||
distance2 = lambda x: 1 | |||
goalSwitch = 1 | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
where the goalSwitch is set to 1, meaning that even when a robot could go to another pile in just one step, it will keep going for its original goal. In the following settings we will experiment with the influence of the searchChoice, since for sticking to a goal to be justified, the goal must be set well informed, and also from the point of view that searching may be a task worth sticking to itself. We also again looked at the influence of taking the number of victims into account. Furthermore, to look into the reliability of an n=20 experiment, we ran another 20 simulations with the same settings as the first settings. We'll now list the divergence in settings from settings1: | |||
name = "Dedication2" | |||
searchChoice = lambda bblen, nrob: min((20.*bblen)/(nrob),1) | |||
making searching less likely | |||
name = "Dedication3" | |||
searchChoice = lambda bblen, nrob: min((5.*bblen)/(nrob),1) | |||
making searching more likely | |||
name = "Dedication4" | |||
dropPile = lambda x,y,z:x+.05*y | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
not taking victims into account | |||
name = "Dedication5" | |||
The last settings are the same as the first.<br/> | |||
The mean progress is shown by <br/> | |||
[[file:Mean_total_size_for_Dedication1-Dedication2-Dedication3-Dedication4-Dedication5.png]]<br/> | |||
and the duration of the simulations by <br/> | |||
[[file:Duration_of_simulations_in_Dedication1-Dedication2-Dedication3-Dedication4-Dedication5.png]]<br/> | |||
Which shows that the role of chance is still very large for such a small experiment. | |||
=== Kant === | |||
In the last experiment, we look at what happens if one takes the stance that two humans aren't worth twice as much as one. Furthermore, we look into the influence of the threshold. Having a large threshold means that piles with little pheromones remain relatively likely to be picked by a robot. The first settings are given by | |||
name = "Kant1" | |||
size=(500, 500) | |||
cz=(0,0) | |||
nRobots=100 | |||
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0), | |||
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5), | |||
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3), | |||
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)] | |||
obstacles=[((100,100),(200,200)), ((330,100),(340,200))] | |||
evaporatePile = lambda x:.90*x | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z**.5 + .2) #grows sublinear | |||
treshold = lambda x: 5 | |||
l=2 | |||
speed=6 | |||
distance1 = lambda x: 1 | |||
distance2 = lambda x: 1 | |||
goalSwitch = 0 | |||
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1) | |||
where the square root is chosen for its sub linear growth. Comparing this to the usual growth in the second settings | |||
name = "Kant2" | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) | |||
and repeating for different thresholds | |||
name = "Kant3" | |||
treshold = lambda x: 10 | |||
name = "Kant4" | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) | |||
treshold = lambda x: 10 | |||
name = "Kant5" | |||
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) | |||
treshold = lambda x: 1 | |||
The results are the following: <br/> | |||
[[file:Mean_total_size_for_Kant1-Kant2-Kant3-Kant4-Kant5.png]]<br/> | |||
[[file:Duration_of_simulations_in_Kant1-Kant2-Kant3-Kant4-Kant5.png]]<br/> | |||
Showing no significant differences. More data is needed to draw conclusions from this experiment. | |||
Back to: [[PRE2015_2_Groep1]] | == Conclusions and Recommendations == | ||
The above mainly shows two things: | |||
*taking distance into account makes your rescue operation more efficient | |||
*more data is needed to really investigate the influence of the other parameters | |||
An important recommendation for this specific approach is fixing the flow for the Returning. Change it into | |||
* Returning | |||
** If a local message is received it tries to follow up on that message. If no message is received: | |||
** The robot tries to go in a straight line towards the Clear Zone | |||
** If that's not possible try continuing in the previous direction | |||
** Whenever that's not possible choose left or right and go into that direction (deviating from the straight line towards the goal as little as possible) | |||
** Also send a local message to all near robots that are returning to the CZ to go into that direction | |||
the python code that would implement this would be very similar to the code in Foraging that does the same thing.<br/> | |||
A more thorough revamp of the behaviour of the robots, which is highly recommended, would be to construct a graph representation of the world on the go, so that short paths can be remembered, and another (possibly ant colony based) swarm algorithm could than be used to find the actual shortest paths (within that graph). | |||
<br/>Back to: [[PRE2015_2_Groep1]] | |||
Latest revision as of 04:18, 18 January 2016
Back to: PRE2015_2_Groep1
Simulation
In toplevel simulation some of the process of creating this simulation is described. However, as written at the end of that page, since path finding trough ant colony algorithms needs a graph representation of the world, we've decided to alter our approach and only use an ant colony algorithm for assigning robots to piles. For the path finding we now use a heuristic algorithm.
The entire behaviour of the robots can be described by states as follows: There are three states:
- Searching
- The robot tries to go in a straight line
- Whenever that's not possible it chooses a random direction to go in
- Whenever a pile is in sight, it is added to the blackboard (if it isn't already on it, or the point that is on it isn't in sight) and the robot goes to the pile
- Whenever a new element is added to the blackboard all searching robots will re-evaluate whether they want to keep searching or want to go foraging
- Foraging
- The robot tries to go in a straight line towards its goal
- Whenever that's not possible it tries to continue travelling in its previous direction
- Whenever that's not possible it will choose left or right at random and then take the minimum divergence from the straight line towards its goal in that direction
- Whenever the pile it is heading for is cleared it decides by chance whether it will go to another pile or go searching
- If the parameter goalSwitch is set to 2, whenever a pile is in sight, the robot goes to that pile
- Returning
- If a local message is received it tries to follow up on that message. If no message is received:
- The robot tries to go in a straight line towards the Clear Zone
- Whenever that's not possible choose left or right and go into that direction (deviating from the straight line towards the goal as little as possible)
- Also send a local message to all near robots that are returning to the CZ to go into that direction
Comment: It would have been better if in the Returning state, as a priority over the random option, the robot would first try to continue in its previous direction, since that would prevent erratic behaviour of going back and forth. This was originally meant (the returning algorithm should mostly be the algorithm for Foraging with a few adjustments for local messages) but reviewing our code, this appears to be missing. We will put a correction of this in our recommendations.
When a robot is at the clear zone (CZ), it drops whatever it is carrying and decides whether it will go searching or foraging. This choice is made by chance and the probability of it going to Foraging is given by the parameter searchChoice, which is a function of both the size of the blackboard (i.e. the number of coordinates in the blackboard) and the total number of robots. We will elaborate our choice for this parameter in the various simulations later in this article.
If a robot is send to go foraging (rescuing), it is assigned a pile from the blackboard by chance. The chance of choosing blackboard element x is given by:
[math]\displaystyle{ ((\text{the pheromones at }x)\cdot(\text{the treshold depending on the size of the blackboard}))^l \cdot (\text{a function of the distance between the robot and }x) \text{divided by the sum of that expression for all x on the blackboard} }[/math]
where the function of the distance the parameter distance2 if the robot is at the CZ, or distance1 otherwise. If the function of the distance is constantly 1, and the treshold is constant in the size of the blackboard, this coincides with the probability in Media:Liu,_Chen,_Wang_-_2013_-_A_Model_of_Rescue_Task_in_Swarm_Robots_System.pdf.
The following code makes up the simulation. Runnable versions and settings files can be found in media:Total_simulation.zip. Note that the doc-strings aren't entirely accurate. This is because we decided that it would be more useful to write the full documentation on this wiki. The easiest way of running both the simulation (with and without graphics) and the script for processing the data is to install a package containing both python 2.7.x and matplotlib and then installing pygame to that. The package we used was anaconda (see https://www.continuum.io/downloads), in which I installed pygame by typing "conda install -c https://conda.anaconda.org/krisvanneste pygame" (as described in https://anaconda.org/krisvanneste/pygame) into command prompt. If you don't need to see the graphics, you don't have to install pygame (note that I can't guaranty the safety of using the aforementioned method of installing pygame). The simulation, as shown at our presentation can be viewed at https://goo.gl/photos/xCoAm1C48F3FVqD97 (since this wiki doesn't allow files larger than 10 mb). For running the simulation trough the scripts in .zip file, just run the settings file that contains the settings you want to use (n.b. the settings file should contain quite an elaborate block for the
if __name__=="__main__"
statement for the final version of the simulation, so e.g. settings1.py will work, but settings.py is just the choice of parameters we used for the simulation during the presentation). However, the "simulation 1 final (with USE) - plaatjes.py" file is still in the old format and requires a separate "settings.py" file. It can be run by running "simulation 1 final (with USE) - plaatjes.py". This inconsistency is due to the need for running many simulations with different settings on different computers simultaneously, which made it more practical to move the actual running of things to the settings file.
"""the simulation actually used for running over and over again.
All graphics stuff has been either commented out or deleted for efficiency"""
#todo add parameters for ethical choices
import random
import math
#import multiprocessing
#import pygame
#from pygame.locals import *
#import pygame.font
#pygame.init() #this kinda sucks if we don't actually use the graphics but soit
#pygame.font.init()
extremeDebug=False
debug=False
def distance(a,b):
return sum( [(a[i]-b[i])**2 for i in range(len(a))])**.5
def distanceq(a,b):
return sum( [(a[i]-b[i])**2 for i in range(len(a))])
class AO(object):
"""Represents area of operation"""
size = None
obstacles = None
piles = None
robotsInAO = None
blackboard =None
CZ=None
l=2#the "sensitivity of the choice process"
speed=1
def __init__(self, size, cz, nRobots, piles, obstacles,
evaporatePile = lambda x:x,
dropPile = lambda x,y,z:y+1,
treshold = lambda x: 1,
l=2,
searchChoice = lambda bblen, nrob: min((10.*bblen)/(2*nrob),1),
distance1 = lambda x: 1/(x+1),
distance2 = lambda x: 1,
speed=1,
goalSwitch=0):
"""
needs as input:
-the size of the AO
-the coordinates for the CZ (just one point for now)
-the number of robots
-a list of piles
two points per pile giving two corners of the pile which is assumed to be rectangular (possibly degenerated)
a list of objects as ints indicating the number of robots needed to move the object
the number of people trapped
e.g. [ ((1,2), (3,4), [1,1,6,3,1],5), ((6,7), (8,12), [3,1,1,3,4],0)]
-a list of obstacles
two points per obstacle giving two corners of the obstacle which is assumed to be rectangular (possibly degenerated)
e.g. [((1,1),(2,2)), ((3,1),(4,3))]
-a function that determines the speed of evaporation of the pheromones for the piles (mapping floats to floats in a suitable manner)
-a function that determines the speed of evaporation of the pheromones for the paths (mapping floats to floats in a suitable manner)
-a function called by a robot to increase the pheromone concentration at a pile (three arguments: pilesize, pheromone concentration, treshold)
-a function called by a robot to increase the pheromone concentration at a path (to floats)
- goalSwitch: if 0, don't try to go to near piles if goal, but don't avoid getting into the wrong pile either
if 1, explicitly don't want to get into the wrong pile
if 2, whenever a pile - possibly other than the goal pile - is in sight, go to that pile
"""
self.l=l#the "sensitivity of the choice process"
self.speed=speed
self.size = (int(size[0]),int(size[1]))
#automatically checks for right type this way
self.CZ=(int(cz[0]),int(cz[1]))
self.__evaporatePile=evaporatePile
self.__dropPile=dropPile
self.treshold = treshold
self.searchChoice = searchChoice
#for i in range(nRobots):
#self.robotsInAO.append(Robot(self.CZ,self.__drop))#fill the list with robots
#want to fill the list of robots one at a time so they don't all live at the same time
self.numrobots=nRobots
self.researchData={}
self.goalSwitch=goalSwitch
self.distance1 = distance1
self.distance2 = distance2
self.piles=[]
pileID=0
for pile in piles:#create all the piles according to input
pileID+=1
x1=int(min(pile[0][0],pile[1][0]))
x2=int(max(pile[0][0],pile[1][0]))
y1=int(min(pile[0][1],pile[1][1]))
y2=int(max(pile[0][1],pile[1][1]))
self.piles.append(
Pile(
self,
pileID,
(x1,y1),
(x2,y2),
[int(obj) for obj in pile[2]],
pile[3]
))
self.researchData[pileID]=[{"size":sum(pile[2]),"robotsAtPile":0}]
self.obstacles = []
self.researchData["total size"]=[sum([pile.pileSize() for pile in self.piles])]
self.researchData["total victims"]=[sum([pile.pileVictims() for pile in self.piles])]
#if extremeDebug: self.obstaclePoints=[]
for obstacle in obstacles:
#all obstacles are assumed to be rectangles
x1=int(min(obstacle[0][0],obstacle[1][0]))
x2=int(max(obstacle[0][0],obstacle[1][0]))
y1=int(min(obstacle[0][1],obstacle[1][1]))
y2=int(max(obstacle[0][1],obstacle[1][1]))
self.obstacles.append((
(x1,y1),
(x2,y2),
((x2-x1)/2,(y2-y1)/2),
(max(distance(
((x2-x1)/2,(y2-y1)/2),(x1,y1)),
distance(
((x2-x1)/2,(y2-y1)/2),(x2,y2)))+self.speed)**2
))
# if extremeDebug:
# for a in range(x1, x2+1):
# for b in range(y1, y2+1):
# self.obstaclePoints.append((a,b))
self.robotsInAO = []
self.blackboard = []
self.researchData["blackboard"]=dict(bbelem) for bbelem in self.blackboard#have to copy it because otherwise the data will be synchronised
self.precircle = [(n, m) for n in range(-self.speed, self.speed+1) for m in range(-self.speed, self.speed+1)
if n*n + m*m <= self.speed*self.speed]
def update(self):
if self.numrobots>0:#release robots one at a time
self.robotsInAO.append(Robot(self,
self.CZ,
self.speed,
self.__dropPile,
self.treshold,
self.searchChoice,
self.distance1,
self.distance2))
self.numrobots-=1
bblen=len(self.blackboard)
for robot in self.robotsInAO:
robot.update()
for pile in self.piles:
if min(pile.coordinates[0][0],pile.coordinates[1][0])<=robot.coordinates[0]<=max(pile.coordinates[0][0],pile.coordinates[1][0]) and \
min(pile.coordinates[0][1],pile.coordinates[1][1])<=robot.coordinates[1]<=max(pile.coordinates[0][1],pile.coordinates[1][1]):
#the robot has arrived at the pile
pile.update(robot, self)
if len(self.blackboard)>bblen:
for robot in self.robotsInAO:
robot.setForage() #makes a portion of the searching robots go foraging
#now do evaporation:
for bbelem in self.blackboard:
bbelem["pheromones"]= self.__evaporatePile(bbelem["pheromones"])
if debug:
czlen= len([robot for robot in self.robotsInAO if robot.coordinates==self.CZ])
if czlen>0: print czlen
for pile in self.piles:
self.researchData[pile.id].append({"size":pile.pileSize(), "robotsAtPile":pile.totalRobots()})
self.researchData["blackboard"].append([dict(bbelem) for bbelem in self.blackboard])
self.researchData["total size"].append(sum([pile.pileSize() for pile in self.piles]))
self.researchData["total victims"].append(sum([pile.pileVictims() for pile in self.piles]))
return len(self.piles)#this will be the check for the main loop
def removePile(self, pile):
pile.dropRobots()
self.piles.remove(pile)
toBeRemoved=[]
for bbelem in self.blackboard:
if pile.isAt((bbelem["coordinates"],)):
toBeRemoved.append(bbelem)
print "one bb element removed"
if not toBeRemoved:
"print no bb element removed"
self.blackboard=[bbelem
for bbelem in self.blackboard
if not bbelem in toBeRemoved]
def totalRobots(self):
return len(self.robotsInAO)+sum([pile.totalRobots() for pile in self.piles])
#def allowedMove(self, coordinates1, coordinates2):
# """Decides wether moving from coordinates1 to coordinates2 is possible"""
# #a move is possible if there is no obstacle intersecting with [coordinates1, coordinates2] and also no other pile than that at coordinates2 is intersecting with [coordinates1, coordinates2]
# length = ((coordinates2[0]-coordinates1[0])**2+(coordinates2[1]-coordinates1[1])**2)**.5
# direction = (float(coordinates2[0]-coordinates1[0])/length,
# float(coordinates2[1]-coordinates1[1])/length)
# line=[(round(coordinates1[0] + .1*n*direction[0]),round(coordinates1[1]+.1*n*direction[1])) for n in range(round(10*length)+1)]
#isn't practical
def onALine(self, x, y, z):
try:
lefthand = ((z[0]-x[0])/distance(z,x), (z[1]-x[1])/distance(z,x))
righthandp = ((y[0]-x[0])/distance(y,x), (y[1]-x[1])/distance(y,x))
righthandm = (-righthandp[0], -righthandp[1])
return min(distance(lefthand, righthandp), distance(lefthand, righthandm))<.01
except ZeroDivisionError:
return True
#finetuning: due to rounding off in floatingpoint arithmetic we're forced to use a small number for comaparisson. This might need finetuning
def getMovements(self,coordinates):
#coordinates=(int(coordinatess[0]),int(coordinatess[1]))#not needed
circle=[(coordinates[0]+p[0],coordinates[1]+p[1])
for p in self.precircle
if 0<=coordinates[0]+p[0]<=self.size[0]
and 0<=coordinates[1]+p[1]<=self.size[1]] #circle around the point
freeSpace = list(circle)
#pilepoints=[]
#shaddow=[]
speed=self.speed
Distance = distance
onALine = self.onALine
#possibleObstacles = [obstacle
# for obstacle in self.obstacles
# if distanceq(obstacle[2],coordinates)<=obstacle[3]+1]
possibleObstacles = [obstacle
for obstacle in self.obstacles
if obstacle[0][0]-speed <= coordinates[0] <= obstacle[1][0]+speed\
and obstacle[0][1]-speed <= coordinates[1] <= obstacle[1][1]+speed]
#for coord in freeSpace:
#remove all points where there are obstacles
#for obstacle in possibleObstacles:
# if obstacle[0][0]<=coord[0]<=obstacle[1][0] and \
# obstacle[0][1]<=coord[1]<=obstacle[1][1]:
# #freeSpace.remove(coord)
# obstaclepoints.append(coord)
# if extremeDebug: print "trew away " + str(coord)
obstaclepoints =[coord
for coord in freeSpace
for obstacle in possibleObstacles
if obstacle[0][0]<=coord[0]<=obstacle[1][0]\
and obstacle[0][1]<=coord[1]<=obstacle[1][1]]
#if extremeDebug: print str(obstaclepoints)
freeSpace = [coord for coord in freeSpace if not coord in obstaclepoints]
if len(freeSpace)!=len(circle):
#for coord in freeSpace:
# for obst in obstaclepoints:
# if self.onALine(coordinates, obst, coord) \
# and Distance(coordinates, obst)<Distance(coordinates, coord):
# shaddow.append(coord)
shaddow=[coord
for coord in freeSpace
for obst in obstaclepoints
if onALine(coordinates, obst, coord)\
and Distance(coordinates, obst)<Distance(coordinates, coord)]
freeSpace = [coord
for coord in freeSpace
if not coord in shaddow]
#possiblePiles = [pile
# for pile in self.piles
# if distanceq(pile.centre, coordinates)<=pile.radius+1]
possiblePiles = [pile
for pile in self.piles
if pile.coordinates[0][0]-speed <= coordinates[0] <= pile.coordinates[1][0] + speed\
and pile.coordinates[0][1]-speed <= coordinates[1] <= pile.coordinates[1][1] + speed]
#for coord in freeSpace:
# for pile in possiblePiles:
# if pile.coordinates[0][0]<=coord[0]<=pile.coordinates[1][0] and \
# pile.coordinates[0][1]<=coord[1]<=pile.coordinates[1][1]:
# pilepoints.append(coord)
pilepoints=[coord
for coord in freeSpace
for pile in possiblePiles
if pile.coordinates[0][0]<=coord[0]<=pile.coordinates[1][0]\
and pile.coordinates[0][1]<=coord[1]<=pile.coordinates[1][1]]
if extremeDebug: print [pt for pt in freeSpace if pt in obstaclepoints]
return [freeSpace, pilepoints, circle] #n.b. this way a robot might go to a pile unintendedly
def getPileSizeAt(self, coordinates):
"""returns the pile size of the pile at the coordinates"""
for pile in self.piles:
if min(pile.coordinates[0][0],pile.coordinates[1][0])<=coordinates[0]<=max(pile.coordinates[0][0],pile.coordinates[1][0]) and \
min(pile.coordinates[0][1],pile.coordinates[1][1])<=coordinates[1]<=max(pile.coordinates[0][1],pile.coordinates[1][1]):
return pile.pileSize()
return None
def getVictimsAt(self,coordinates):
for pile in self.piles:
if pile.coordinates[0][0] <= coordinates[0] <= pile.coordinates[1][0] and\
pile.coordinates[0][1] <= coordinates[1] <= pile.coordinates[1][1]:
return pile.pileVictims()
def pilesAt(self, coordinateList):
return list(set([pile for pile in self.piles if pile.isAt(coordinateList)])) #set filters out duplicates
def sendLocalMessage(self, centre, radius, message, pileID):
for robot in self.robotsInAO:
if robot.distance(robot.coordinates, centre)<=radius:
robot.setLocalMessage(message, pileID)
class Pile(object):
objects=None
coordinates = None
__que = None
id=0
def __init__(self,ao,pileID,coordinate1, coordinate2, objects, humans):
#all piles are assumed to be rectangles
self.objects=[obj for obj in objects]
self.__que=[]
self.coordinates = (coordinate1, coordinate2)
self.id=pileID
self.ao=ao
self.centre = ((coordinate2[0]-coordinate1[0])/2, (coordinate2[1]-coordinate1[1])/2)
self.radius = (max(distance(self.centre, coordinate1), distance(self.centre, coordinate2))+ao.speed)**2
self.humans=humans#the number of humans trapped at the pile
def update(self, robot, ao):
self.__que.append(ao.robotsInAO.pop(ao.robotsInAO.index(robot)))
try:
if len(self.__que)>=self.objects[0]:
obj=self.objects.pop(0)#remove the object and get the number of needed robots
for i in range(obj):
rob = self.__que.pop()#remove a robot from the que
rob.carrying = True #tell that robot it is carrying an object
rob.sendToCZ(self.id)#send that robot to the clear zone
self.ao.robotsInAO.append(rob)#add that robot to the list of the AO
if len(self.objects)==0:
self.ao.removePile(self)#if the pile is empty, remove it from the list of piles
except IndexError:
self.ao.removePile(self)
def totalRobots(self):
return len(self.__que)
def pileSize(self):
return sum(self.objects)
def pileVictims(self):
return self.humans
def dropRobots(self):
for robot in self.__que:
robot.carrying = True
robot.sendToCZ(self.id)
self.ao.robotsInAO.append(robot)
self.__que=[]
def isAt(self, coordinateList):
ret=False
for coordinates in coordinateList:
if min(self.coordinates[0][0],self.coordinates[1][0])<=coordinates[0]<=max(self.coordinates[0][0],self.coordinates[1][0]) and \
min(self.coordinates[0][1],self.coordinates[1][1])<=coordinates[1]<=max(self.coordinates[0][1],self.coordinates[1][1]):
ret = True
return ret
class Robot(object):
coordinates=None
__previousCoordinates=None
direction=None
#Robots are assumed to be small enough to be well represented by a single coordinate and even so small that multiple robots can be in the same spot
__goal=None
__task=None
carrying=False
ao=None
__localMessage=None
__lastID=None
def __init__(self,ao, coordinates, speed, dropPile, treshold, searchChoice, distance1, distance2):
self.coordinates=(int(coordinates[0]),int(coordinates[1]))
self.__previousCoordinates=self.coordinates
self.__dropPile = dropPile
self.treshold = treshold
self.searchChoice=searchChoice
self.ao= ao
self.speed = speed
self.distance1=distance1
self.distance2=distance2
def sendToCZ(self, pileID):
self.__lastID = pileID
self.__goal = self.ao.CZ
self.__task="Return"
#last coordinate was at the pile, so for simplicity assume it is still there
def pickCoordinates(self, target, options):
"""
input: the floating point coordinates the robot wants to go to
output: integer coordinates in option that according to a combination of ceiling and floor correspond to target, or none if none exist
"""
rounders=[math.floor, math.ceil]
targets=[(int(fun1(target[0])),int(fun2(target[1]))) for fun1 in rounders for fun2 in rounders]
targets=[e for e in targets if e in options]
if not targets: return None
#return targets[0]
return min(targets, key=lambda x: self.distance(x,target))#take the one closest to the original target
def distance(self,a, b):
return ((a[0]-b[0])**2 + (a[1]-b[1])**2)**.5
def pickDirection(self,goal, coord):
dist = self.distance(goal,coord)
if dist >= self.speed:
return (coord[0] + self.speed*(goal[0]-coord[0])/dist, coord[1] + self.speed*(goal[1]-coord[1])/dist)
else:
return goal
def chooseRandomDirection(self, options):
return random.choice(
[point
for point in options
if self.distance(point, self.coordinates)>=self.speed-2
])
def setLocalMessage(self, coordinates, pileID):
if pileID==self.__lastID:
self.__localMessage = coordinates
def setForage(self):
if random.random()<self.searchChoice(len(self.ao.blackboard), self.ao.totalRobots()) and self.__task=="Search":
self.__task="Forage"
rnum = random.random()
denominator = sum([((pile["pheromones"]+self.treshold(len(self.ao.blackboard)))**self.ao.l)*self.distance1(distance(self.coordinates,pile["coordinates"]))
for pile in self.ao.blackboard])
treshold = 0
for pile in self.ao.blackboard:
treshold += ((pile["pheromones"] + self.treshold(len(self.ao.blackboard)))**self.ao.l)*self.distance1(distance(self.coordinates, pile["coordinates"]))
if rnum<treshold/denominator:
self.__goal = pile["coordinates"]
break
def update(self):
Distance=distance
if extremeDebug: print "new update"
if self.coordinates == self.ao.CZ:
self.carrying = False
#assign a task and if needed a pile and a path
rnum = random.random()
if rnum>self.searchChoice(len(self.ao.blackboard), self.ao.totalRobots()):
self.__task = "Search"
#print "going to search"
else:
self.__task = "Forage"
#print "going to forage"
#now, if it is assigned a forage task, pick a pile from the blackboard
if self.__task=="Forage":
#example of what a blackboard element may look like:
#{"coordinates":..., "pheromones":..., "treshold": (k in the articles)}
#function from articles
rnum = random.random()
denominator = sum([((pile["pheromones"]+self.treshold(len(self.ao.blackboard)))**self.ao.l) * self.distance2(Distance(self.coordinates,pile["coordinates"]))
for pile in self.ao.blackboard])
treshold = 0#this is a different treshold. Sorry for using the same word twice
for pile in self.ao.blackboard:
treshold += ((pile["pheromones"]+self.treshold(len(self.ao.blackboard)))**self.ao.l)*self.distance2(Distance(self.coordinates,pile["coordinates"]))
if rnum <treshold/denominator:
self.__goal=pile["coordinates"]
break
#this is the pile it gets assigned too
#at this point it is clear what the robot should do
movements=self.ao.getMovements(self.coordinates)#looks like (where I can go, where the piles are)
#if extremeDebug: print "movements is "+ str(movements)
if debug:
if len(movements[0])<=1: print "no movements possible except for staying"
if len(movements[0])<=len(movements[1])+1: print "only pile moves or staying"
if not movements[0]:
print "no movements"
if self.__task == "Forage":
if not self.ao.getPileSizeAt(self.__goal):
self.__task="Search" #the pile was removed before this robot arrived
#self.direction=None
#set random direction
newdirection = self.chooseRandomDirection(movements[0])
self.direction = (newdirection[0]-self.coordinates[0],
newdirection[1]-self.coordinates[1])
self.setForage()#chance of going to forage for another pile
#hence start searching for another pile
elif self.__goal in movements[0]:
self.__previousCoordinates=self.coordinates
self.coordinates=self.__goal
self.direction = (self.__previousCoordinates[0]-self.coordinates[0], self.__previousCoordinates[1]-self.coordinates[1]) #mirrored direction
blackboardElement=[bbelem
for bbelem in self.ao.blackboard
if bbelem["coordinates"]==self.__goal][0]
#n.b. we assume that piles don't overlap
#if not self.ao.getPileSizeAt(self.__goal):
#print "no pile at goal "+str(self.__goal)
#print "but do have blackboard element "+ str(blackboardElement)
blackboardElement["pheromones"]=self.__dropPile(
blackboardElement["pheromones"],
self.ao.getPileSizeAt(self.__goal),
self.ao.getVictimsAt(self.__goal)) #drop pheromones
###### hier gaat het fout als de robot op pad is naar een pile die niet meer bestaat
elif movements[1] and self.ao.goalSwitch==2:
#pick a pile point and just go for it
relevantBlackboard = [bbelem for bbelem in self.ao.blackboard if bbelem["coordinates"] in movements[1]]
if relevantBlackboard:
bbchoice = random.choice(relevantBlackboard)
self.__previousCoordinates = self.coordinates
self.coordinates = bbchoice["coordinates"]
self.direction = (self.__previousCoordinates[0]-self.coordinates[0], self.__previousCoordinates[1]-self.coordinates[1]) #mirrored direction
bbchoice["pheromones"] = self.__dropPile(
bbchoice["pheromones"],
self.ao.getPileSizeAt(self.coordinates),
self.ao.getVictimsAt(self.coordinates))
else:
coordchoice = random.choice(movements[1])
self.ao.blackboard.append(
{"coordinates":coordchoice,
"pheromones": self.__dropPile(
0,
self.ao.getPileSizeAt(coordchoice),
self.ao.getVictimsAt(coordchoice))})#treshold will be changed anyways
self.__previouscoordinates = self.coordinates
self.coordinates = coordchoice
self.direction = (self.__previousCoordinates[0]-self.coordinates[0], self.__previousCoordinates[1]-self.coordinates[1]) #mirrored direction
else:
if self.ao.goalSwitch == 1:
movements[0] = [movement for movement in movements[0] if not movement in movements[1]]#explicitly don't want to get into a wrong pile if self.ao.goalSwitch == 1
preferedDirection = self.pickDirection(self.__goal, self.coordinates)
preferedCoordinate = self.pickCoordinates(preferedDirection, movements[0])
if preferedCoordinate:#if it's not None
self.__previousCoordinates=self.coordinates
self.coordinates = preferedCoordinate #since we can go there and that's where we want to go
self.direction = (self.coordinates[0]-self.__previousCoordinates[0], self.coordinates[1]-self.__previousCoordinates[1])
else: #traveling in a straight line to the target is not possible :(
#try riding in the preset direction
try:
#this goes wrong if self.direction=(0,0)
preferedCoordinate = self.pickCoordinates(
self.pickDirection(
(self.coordinates[0]+self.direction[0],
self.coordinates[1]+self.direction[1]),
self.coordinates),
movements[0])
if preferedCoordinate:
self.__previousCoordinates=self.coordinates
self.coordinates = preferedCoordinate
#self.direction stays the same
#else choose a left or right at random
else:
rot = random.choice((-1,1))
preferedCoordinate = self.pickCoordinates(
self.pickDirection(
self.__goal,
self.coordinates),
movements[2]) #Where we would have wanted to go
if not preferedCoordinate:
print "no prefered coordinate found"
print self.__goal
print self.pickDirection(self.__goal,self.coordinates)
attempts=1
chosen=False
while attempts<3 and not chosen:
rotlist = [point
for point in movements[0]
if (point[0]*preferedCoordinate[1] -\
point[1]*preferedCoordinate[0])*rot>0\
and point!=self.coordinates]# points with the correct rotation direction
if len(rotlist)>0:
#we want the one closest to the prefered coordinates
#TODO prevent loop movements #meh (see other comment about it)
chosenCoordinate = min(rotlist,
key=lambda point:
Distance(
point,
preferedCoordinate))
chosen =True
else:
rot = -rot
attempts+=1
if not chosen:
#can this occur?
raise Exception #I have no inspiration right now
if not chosenCoordinate in movements[0]: print "blaaaa :S"
self.__previousCoordinates = self.coordinates
self.coordinates=chosenCoordinate
self.direction = (self.coordinates[0]-self.__previousCoordinates[0],self.coordinates[1]-self.__previousCoordinates[1])
except TypeError: #no preset direction
rot = random.choice((-1,1))
preferedCoordinate = self.pickCoordinates(
self.pickDirection(
self.__goal,
self.coordinates),
movements[2]) #Where we would have wanted to go
attempts=1
chosen=False
while attempts<3 and not chosen:
rotlist = [point
for point in movements[0]
if ((point[0]-self.coordinates[0])*(preferedCoordinate[1]-self.coordinates[1]) -\
(point[1]-self.coordinates[1])*(preferedCoordinate[0]-self.coordinates[0]))*rot>0\
and point!=self.coordinates]#points with the correct rotation direction
if len(rotlist)>0:
#we want the one closest to the prefered coordinates
#TODO prevent loop movements #meh (see other comment about it)
chosenCoordinate = min(rotlist,
key=lambda point:
Distance(point,preferedCoordinate))
chosen =True
else:
rot = -rot
attempts+=1
if not chosen:
#can this occur?
raise Exception #I have no inspiratino right now
if not chosenCoordinate in movements[0]: print "I'm going yellow"
self.__previousCoordinates = self.coordinates
self.coordinates=chosenCoordinate
self.direction = (self.coordinates[0]-self.__previousCoordinates[0],self.coordinates[1]-self.__previousCoordinates[1])
elif self.__task == "Return":
#due to the randomnes in the algorithm for foraging, we need to do some extra work to keep the group together
#the idea is as follows:
#whenever a choice needs to be made (based on randomnes), the first robot to "think" makes the choice
#this robots than puts a local message out, so that all the robots within a small radius, say self.speed, make the same decision
#to prevent miscommunication, all local messages are deleted after the execution of update()
#if a local message is recieved, attempt to obey it
#else try to go to the CZ
#if that's not possible, choose a direction and send that direction as a local message
if self.__localMessage:
direction = self.pickDirection(self.__localMessage, self.coordinates)
#take the coordinate closest to direction
if self.coordinates not in movements[1]:
preferedCoordinate = min(
[coord for coord in movements[0] if coord not in movements[1]]
,key=lambda x:Distance(x,direction)
)#it is important now to not get into another pile
else:
preferedCoordinate = min(movements[0], key=lambda x: Distance(x,direction))
#this might go verry badly #nope
self.__previousCoordinates = self.coordinates
self.coordinates = preferedCoordinate
self.direction = (self.coordinates[0]-self.__previousCoordinates[0],self.coordinates[1]-self.__previousCoordinates[1])
else:
preferedDirection = self.pickDirection(self.__goal, self.coordinates)
preferedCoordinate = self.pickCoordinates(preferedDirection, movements[0])
if preferedCoordinate and not preferedCoordinate in movements[1]:#it is important now that we don't accidentaly go into another pile
self.__previousCoordinates = self.coordinates
self.coordinates = preferedCoordinate
self.direction = (self.coordinates[0]-self.__previousCoordinates[0],self.coordinates[1]-self.__previousCoordinates[1])
else:
# a choice needs to be made
rot = random.choice((-1,1))
preferedCoordinate = self.pickCoordinates(
self.pickDirection(self.__goal,self.coordinates),
movements[2]) #Where we would have wanted to go
if not preferedCoordinate:
print "no prefered coordinate in return"
print self.pickDirection(self.__goal,self.coordinates)
print self.__goal
attempts=1
chosen=False
while attempts<3 and not chosen:
rotlist = [ point for point in movements[0]
if ((point[0]-self.coordinates[0])*(preferedCoordinate[1]-self.coordinates[1]) -\
(point[1]-self.coordinates[1])*(preferedCoordinate[0]-self.coordinates[0]))*rot>0\
and point!=self.coordinates]# points with the correct rotation direction
if len(rotlist)>0:
#we want the one closest to the prefered coordinates
#TODO prevent loop movements #meh, doesn't seem to be necessary (would only occur in very nasty situations
chosenCoordinate = min(rotlist, key=lambda point: Distance(point,preferedCoordinate))
chosen =True
else:
rot = -rot
attempts+=1
if not chosen:
#can this occur?
raise Exception #I have no inspiratino right now
self.ao.sendLocalMessage(self.coordinates, self.speed, chosenCoordinate, self.__lastID)
#finetuning: radius might need to be finetuned # meh
self.__previousCoordinates = self.coordinates
self.coordinates=chosenCoordinate
self.direction = (self.coordinates[0]-self.__previousCoordinates[0],self.coordinates[1]-self.__previousCoordinates[1])
elif self.__task == "Search":
if not self.direction or self.direction==(0,0):
newdirection = self.chooseRandomDirection(movements[0])
self.direction = (newdirection[0]-self.coordinates[0],
newdirection[1]-self.coordinates[1])
if extremeDebug: print "had no direction, so chose "+str(self.direction)
#except IndexError:
# self.direction = self.chooseRandomDirection(movements[2])
#wait... this shouldn't be possible
#try to go in self.direction
#if that isn't possible, choose a different direction
#whenever a pile is encountred, add it to the blackboard and go to the pile
if movements[1]: #there is a pile that can be reached
#we assume the robots can see the size of a pile
#we assume that the robot can see what pile what point belongs to
if extremeDebug: print "could reach piles at "+str(len(movements[1]))+" coordinates"
pilesInReach = self.ao.pilesAt(movements[1])
#we want to add only those piles that aren't already in the blackboard
newPiles = [pile
for pile in pilesInReach
if pile not in self.ao.pilesAt([p["coordinates"]
for p in self.ao.blackboard])]
#this is ugly and inefficient
if newPiles:#non empty
newcoord=[]
for pile in newPiles:
nc = random.choice([coord
for coord in movements[1]
if pile.isAt((coord,))])
self.ao.blackboard.append({
"coordinates":nc,
"pheromones":self.__dropPile(0,pile.pileSize(),pile.pileVictims())
})
newcoord.append(nc)
if not self.ao.getPileSizeAt(nc):
print "wrong bbelem added"
raise Exception
#USE
#just pick a coordinate in view for the pile and add {coordinate, pheromones} to the blackboard
#now that all new piles are added to the blackboard, let's go to one of them
chosenCoordinate = random.choice(newcoord)
self.__previousCoordinates = self.coordinates
self.coordinates=chosenCoordinate
self.direction = (self.__previousCoordinates[0]-self.coordinates[0], self.__previousCoordinates[1]-self.coordinates[1]) #mirrored direction
else: #no new piles
#see if any of the coordinates are already on the blackboard
blackboardOptions = [bbelem
for bbelem in self.ao.blackboard
if bbelem["coordinates"] in movements[1]]
if blackboardOptions:#nonempty
choice = random.choice(blackboardOptions)
choice["pheromones"] = self.__dropPile(
choice["pheromones"],
self.ao.getPileSizeAt(choice["coordinates"]),
self.ao.getVictimsAt(choice["coordinates"]))
self.__previousCoordinates = self.coordinates
self.coordinates = choice["coordinates"]
self.direction = (self.__previousCoordinates[0]-self.coordinates[0],
self.__previousCoordinates[1]-self.coordinates[1]) #mirrored direction
else:
#so no of the pile points we can reach are on the blackboard. W
#there are two main options for action:
#the first is to choose one of the piles and head for the point in the pile that is in the blackboard
#the downside is that that might be verry inefficient
#the other is to add a new point to the blackboard
#the downside to that is that the same pile will now be in the blackboard more than once
#we'll take the second approach since it kinda makes more sence in the case of large piles
#we'll do this to only one of the piles though, to prevent enormous growth of the blackboard
pileChoice = random.choice(pilesInReach)
reachable = [coord
for coord in movements[1]
if pileChoice.isAt((coord,))]
nc = random.choice(reachable)
self.ao.blackboard.append({
"coordinates":nc,
"pheromones":self.__dropPile(0,pileChoice.pileSize(),pileChoice.pileVictims())
})
if not self.ao.getPileSizeAt(nc):
print "wrong bbelem added"
raise Exception
self.__previousCoordinates = self.coordinates
self.coordinates = nc
self.direction = (self.__previousCoordinates[0]-self.coordinates[0], self.__previousCoordinates[1]-self.coordinates[1]) #mirrored direction
else:
#no piles can be reached in one step, so try continuing in a straight line. If this fails, pick a random direction that can be moved in.
preferedCoordinate = self.pickCoordinates(
self.pickDirection(
(self.coordinates[0]+self.direction[0],
self.coordinates[1]+self.direction[1]),
self.coordinates),
movements[0]
)
if extremeDebug:
print "pref coord 1 "+str(preferedCoordinate)
print "with direction "+ str(self.direction)\
+" and coordinates "+str(self.coordinates)
if preferedCoordinate:
self.__previousCoordinates = self.coordinates
self.coordinates = preferedCoordinate
self.direction = (self.coordinates[0]-self.__previousCoordinates[0],self.coordinates[1]-self.__previousCoordinates[1])
if extremeDebug: print "went to that"
else:
if extremeDebug: print "so didn't go for that"
self.__previousCoordinates = self.coordinates
self.coordinates = random.choice(
[coord
for coord in movements[0]
if Distance(self.coordinates, coord)>= self.speed-2
])#pick a random direction we can go in
self.direction = self.direction = (self.coordinates[0]-self.__previousCoordinates[0],self.coordinates[1]-self.__previousCoordinates[1])
if extremeDebug:
print "but went for "+str(self.coordinates)\
+" wo I now have direction "+ str(self.direction)
if self.coordinates not in movements[0]:
print "went yellow on search"
#for debugging:
#newmovements= self.ao.getMovements(self.coordinates)
#if extremeDebug: print "now the new movements are "+ str(newmovements)
#if not newmovements[0]:
# print "magic happned at search"
self.__localMessage = None #clear the local message
#print "new coordinates are "+ str(self.coordinates)
def runSimulation(size=(500, 500),
cz=(0,0),
nRobots=100,
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],30000),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3)],
obstacles=[((100,100),(200,200)), ((30,100),(40,200)),((300,300),(340, 320))],
evaporatePile = lambda x:.90*x,
dropPile = lambda x,y,z:x+.05*y*(z/10.+.1),
treshold = lambda x: min(1,10-x),
goalSwitch = 0,
distance1=lambda x:1,
distance2=lambda x:1,
searchChoice = lambda bblen, nrob: min((10.*bblen)/(2*nrob),1),
l=2,
speed=6,
waitingtime = 100):
done = False
#it = 0
simulation = AO(size=size, cz=cz, nRobots=nRobots, piles=piles, obstacles=obstacles,
evaporatePile=evaporatePile, dropPile=dropPile, treshold=treshold, l=l,
speed=speed, distance1=distance1, distance2=distance2, goalSwitch = goalSwitch)
while not done:
try :
if not simulation.update():
done = True
except IndexError:
return simulation
#if not graphics:
# it +=1
# print it
#pygame.time.wait(waitingtime)
#pygame.quit()
return simulation
if __name__=="__main__":
import settings
import os
def runner(num=1):
researchData=[]
for i in range(num):
simulation = runSimulation(
size = settings.size,
cz = settings.cz,
nRobots = settings.nRobots,
piles = settings.piles,
obstacles = settings.obstacles,
evaporatePile = settings.evaporatePile,
dropPile = settings.dropPile,
treshold = settings.treshold,
l = settings.l,
distance1 = settings.distance1,
distance2 = settings.distance2,
speed = settings.speed,
goalSwitch = settings.goalSwitch) #run the simulation to obtain researchData
researchData.append(simulation.researchData)# the stuff we're interested in
#output everything to the file location
try:
f=open("./results/"+settings.name+str(len(os.listdir("./results")))+".py", "w")
f.write("data = "+repr(researchData))
f.close()
return True
except IOError:
return False
#pool = multiprocessing.Pool(10)
#pool.map(runner, ["output"+str(i)+".py" for i in range(10)])
runner()
Parameters and USE
To incorporate ethical decision making in the design of our algorithms and simulation, we have 8 parameters for decision making. In this section we will give an overview of these parameters. We have also run the simulation with different values for the parameters based on underlying ethical choices. We will elaborate on these choices and review the results.
The parameters for decision making are the following:
- evaporatePile, a function that decides the speed of evaporation of pheromones. Fast evaporation equalizes priorities fast while slow evaporation will fix priorities.
- Input: pheromone level at the end of time step t
- Output: pheromone level at the beginning of time step t+1
- dropPile, Amount of pheromones dropped by a robot. Dropping large amounts of pheromones will increase the relevance of the pile more than dropping small amounts. An ethical choice to be made here is how the relevance of a pile is determined by the number of victims trapped at it, and by the difficulty of freeing them.
- Input: current pheromone level, pile size (amount of robots needed to clear the pile entirely), number of victims trapped at the pile
- Output: updated pheromone level
- threshold, a function of the blackboard size which plays the role of k in Media:Liu,_Chen,_Wang_-_2013_-_A_Model_of_Rescue_Task_in_Swarm_Robots_System.pdf. A high treshold will give piles with little pheromones a relatively larger chance of being chosen when a robot goes foraging
- Input: number of blackboard elements
- Output: threshold
- l, the sensitivity of the choice process to differences in pheromones. Large l will make piles with large of amounts of pheromones much more likely to be chosen
- This is a constant
- distance1, a function of the distance between the robot and a pile that influences the chance of the robot choosing that pile as its goal if the robot goes foraging from a position other than the CZ. This can be used to make robots prefer nearby piles over piles that are far away.
- Input: the distance between the robot and a pile
- Output: a factor in the probability of this pile being chosen
- distance2, a function of the distance between the CZ and a pile that influences the chance of a robot choosing that pile as its goal if the robot goes foraging from the CZ. This can be used to give higher priorities to piles that are nearby the CZ (and thus prioritizing easier rescue).
- Input: the distance between the CZ and a pile
- Output: a factor in the probability of this pile being chosen
- goalSwitch, a parameter deciding whether or not a robot may ignore its original goal in order to go to a pile it can immediately reach. This corresponds to the ethical dilemma of whether, if a robot is set out to save person a, it may ignore person b who can be saved by it immediately.
- 0: don't consciously change goals, but if the robot happens to get into another pile, it will start helping out there.
- 1: avoid other piles than the goal, so don't help out at piles that aren't the original goal.
- 2: if another pile is reachable in one time step, go for that pile, no matter what the original goal was.
- searchChoice, a function determining chance of going to foraging mode or going to search mode. This reflects the choice of how important finding unknown victims is compared to saving known victims
- Input: size of blackboard, number of available robots
- Output: the probability of a robot going foraging (n.b. 1-this value is the probability of a robot going searching)
As mentioned, varying these parameters based on both ethical decisions and research interests as to their influence, we've created different settings for running the simulation. We will now discuss these settings and the accompanying results. Many graphs we have created but haven't put into this wiki can be found in media:results1.zip and media:results2.zip.
Influence of dropPile and evaporatePile when ignoring presence of victims
The first experiment we will describe here is to the influence of the drop size and evaporation speed when ignoring the presence of victims. The first settings where
name = "dropNoHumans1"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 1
distance2 = lambda x: 1
goalSwitch = 0
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
We don't take distance into account and our searchChoice comes down to saying that if we have less than 10 robots per blackboard element, we want to go foraging for sure since we then can't miss the robots to searching, and otherwise the chance of going foraging should be linear in the number of blackboard elements.
These settings resulted in the following progress of the total size of the piles for 20 simulations
with which comes down to the following average progress
For the second settings we used a larger drop
name = "dropNoHumans2" dropPile = lambda x,y,z:x+.07*y
which resulted in
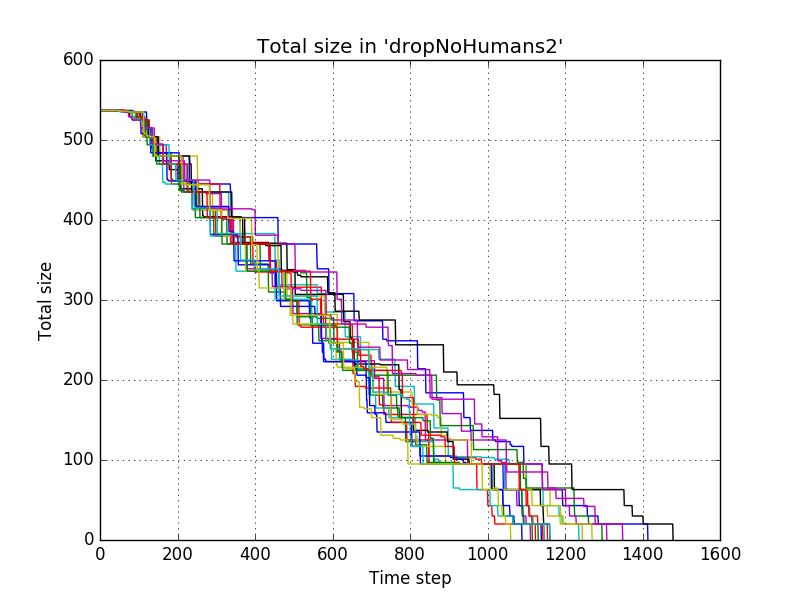
and with averaging
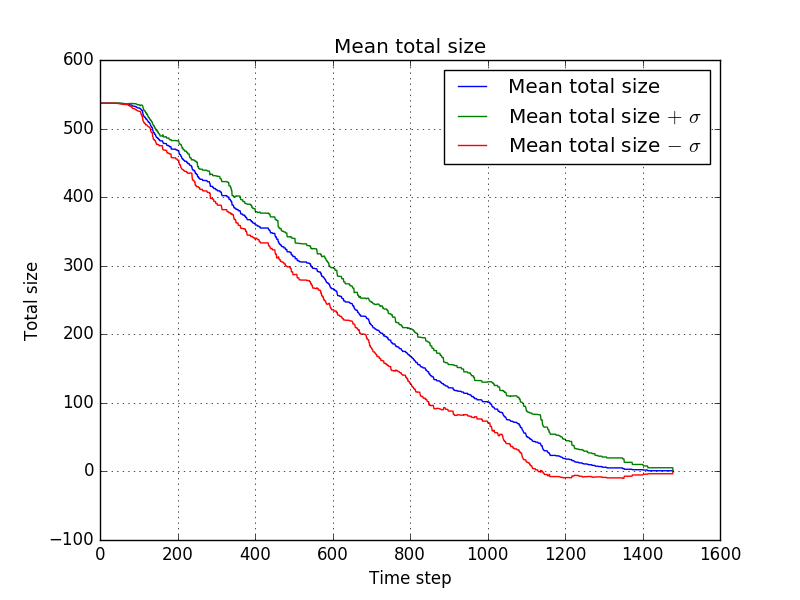
For the third a smaller drop
name = "dropNoHumans3" dropPile = lambda x,y,z:x+.03*y
which resulted in
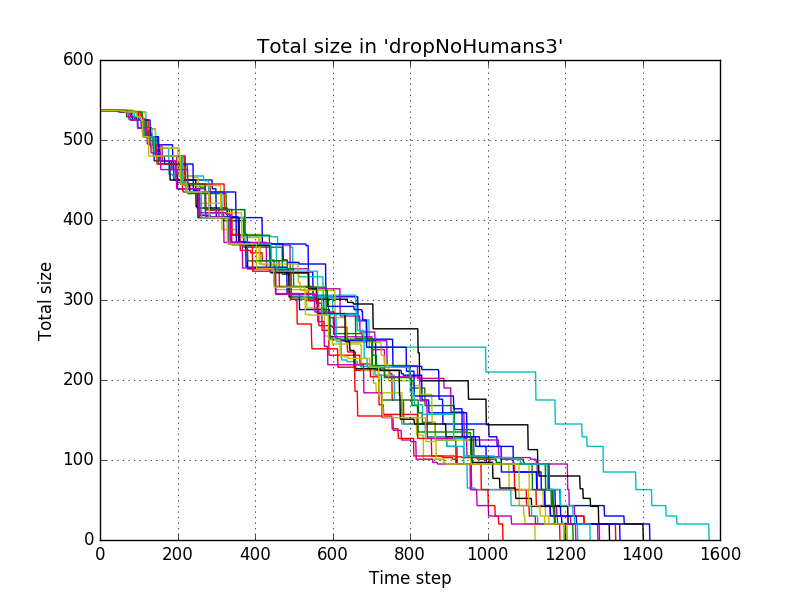
and with averaging
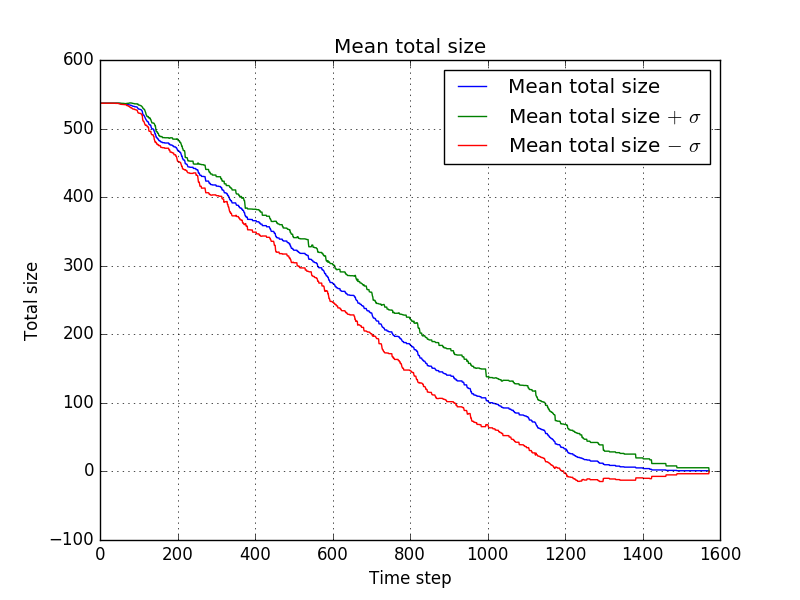
for the fourth settings, the difference with the first settings was in the evaporation speed
name = "evaporateNohumans1" evaporatePile = lambda x:.80*x
which resulted in
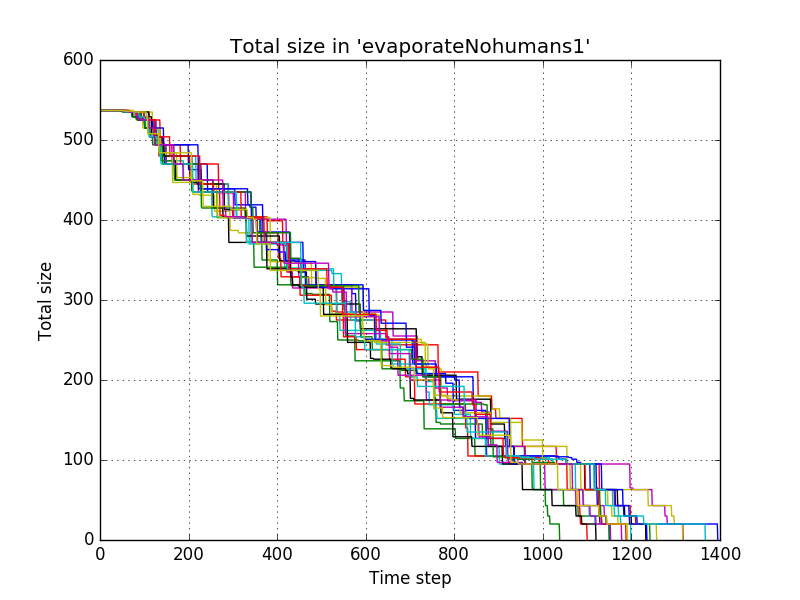
and with averaging
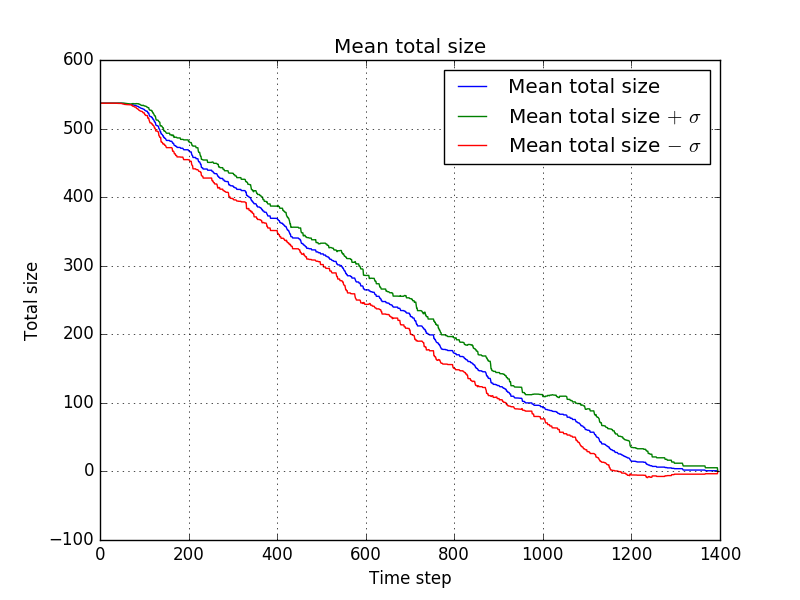
for the fifth settings, the difference with the first settings was again in the evaporation speed
name = "evaporateNohumans2" evaporatePile = lambda x:.95*x
which resulted in
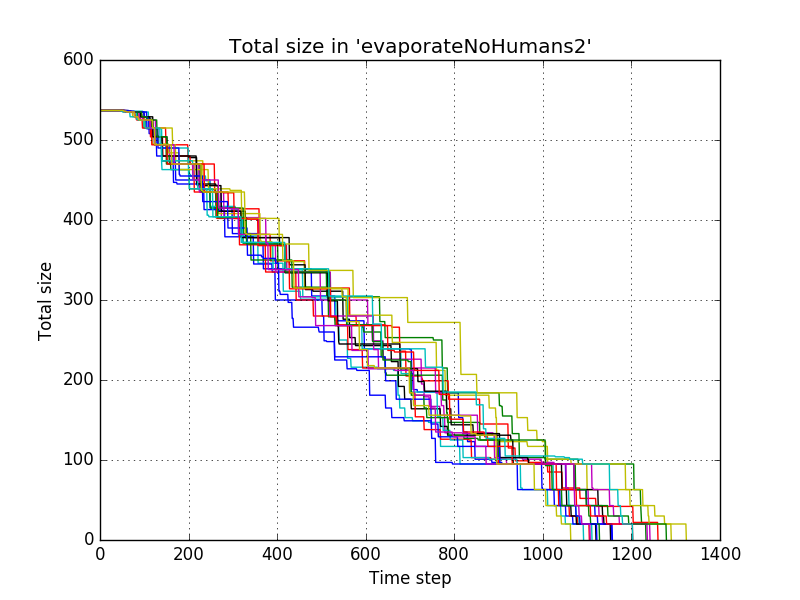
and with averaging
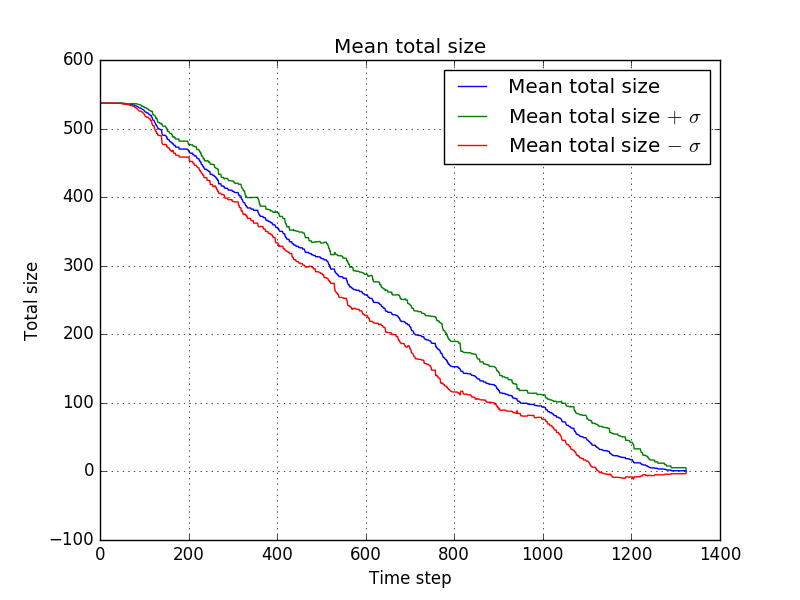
Now, to give an overview of the differences, the mean progress for the different settings is shown by
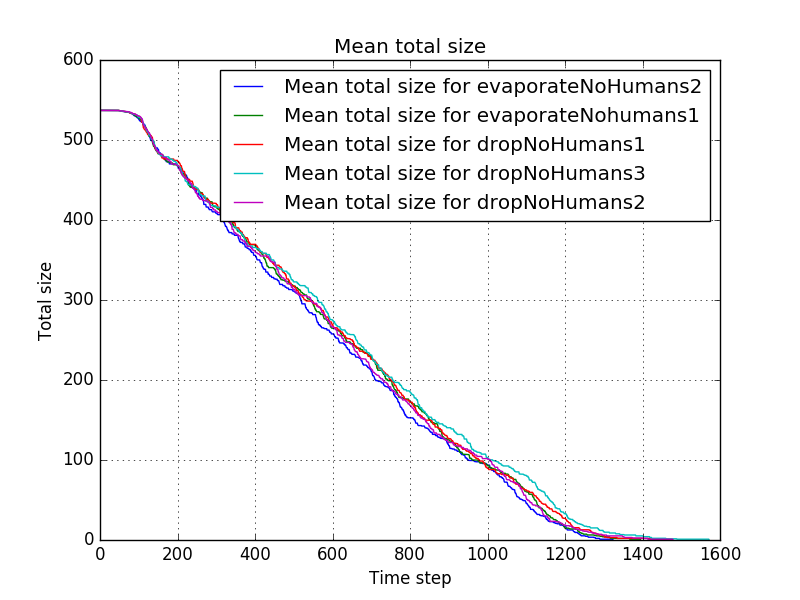
and the duration of the simulations (hence the duration before all piles are cleared) is shown by
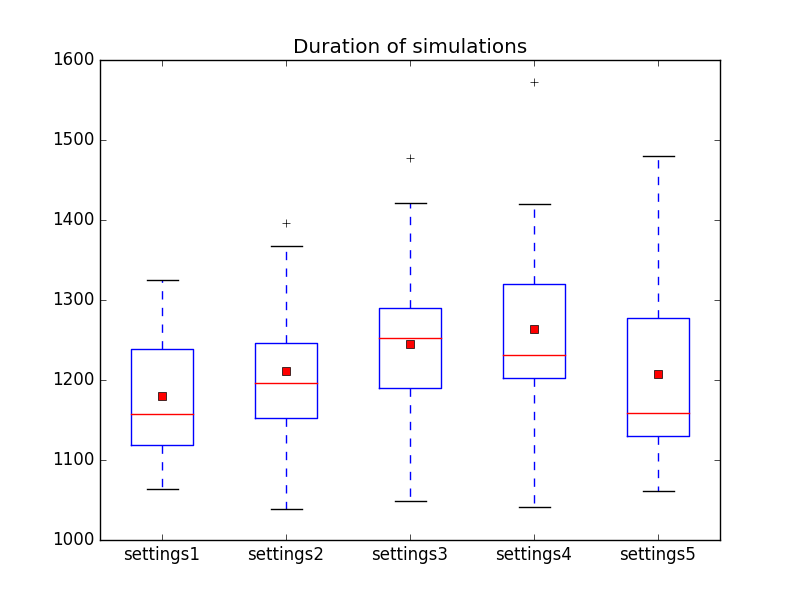
This indicates that some settings might be better than others (e.g. settings 1 might be better than settings 3) but we have to little data to draw hard conclusions. It seems that out of these possibilities, the first settings might be the best, but more simulations might be necessary to investigate this further.
Influence of dropPile and evaporatePile when taking victims into account
In the second experiment we do the same, but do take the number of victims into account, as can be seen from our choice of dropPile. For our first settings we took
name = "dropHumans1"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 1
distance2 = lambda x: 1
goalSwitch = 0
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
Now the number of victims at the pile is taken into account. We take it as [math]\displaystyle{ .2\cdot \text{number of victims} + .2 }[/math]
The [math]\displaystyle{ +.2 }[/math] is necessary to ensure that piles without victims are still cleared (efficiently). We choose this approach because it is somewhat utilitarian in the sense that every human life is worth as much, it being somewhat linear in the number of victims. We will look at sub linear growth later. For compactness we will not show all the graphs for all the settings, but only show the combined results.
For the second settings:
name = "dropHumans2" dropPile = lambda x,y,z:x+.07*y*(.2*z + .2) #normal (1) if z == 4
For the third:
name = "dropHumans3" dropPile = lambda x,y,z:x+.03*y*(.2*z + .2) #normal (1) if z == 4
For the fourth:
name = "evaporateHumans1" evaporatePile = lambda x:.80*x
For the fifth:
name = "evaporateHumans2" evaporatePile = lambda x:.95*x
All using the first settings as a base.
The mean progress is shown by
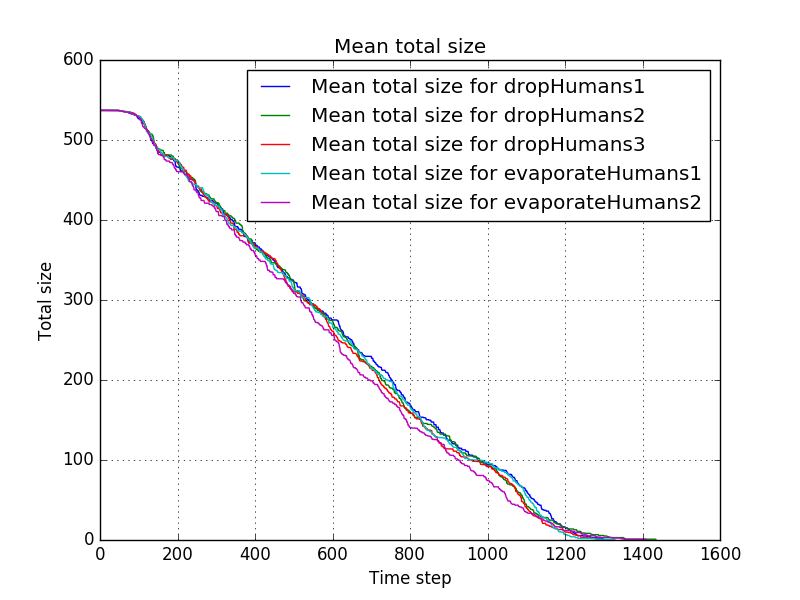
and the duration is shown by
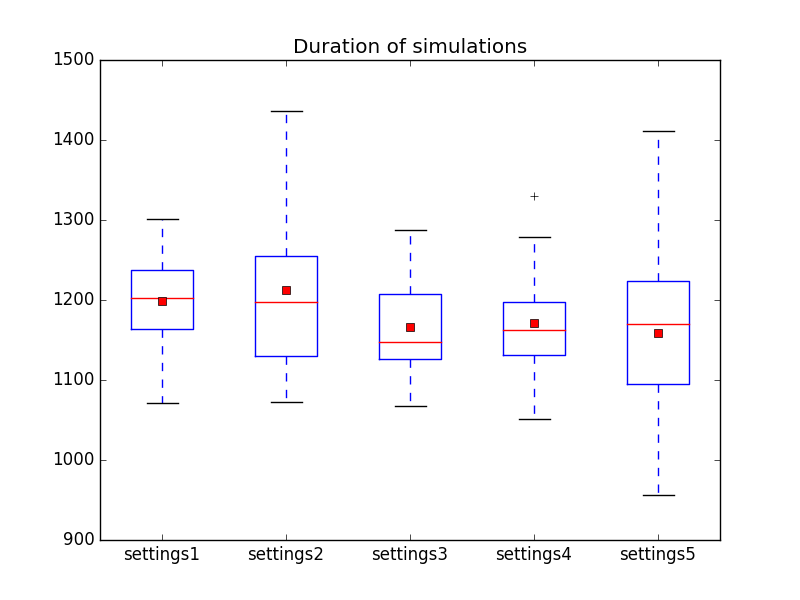
In this case the results are even closer and although settings3 seems to give somewhat better results than the other settings, this might be purely by chance. One thing that does strike the eye is that all of these settings seem to perform better than most of the settings in the previous experiment where humans wheren't taken into account. Note that we're note measuring when all humans are rescued (although that usually coincides with the duration of the simulation for this particular map), so it might be just a quirk of this particular choice of where the piles are. It would be interesting however to look more into this by using larger data sets, taking different maps into account.
Influence of distance functions
For the third experiment we will look into the influence of the distance functions. We will do this from the perspective of ethical decision making, taking stance that we shouldn't ignore humans near us that need help. We will also investigate the influence of taking the same distance functions but without taking the number of victims at a pile into account, and the influence of choosing to search more - from the perspective that known victims should be helped first. The first settings file looks as follows:
name = "ClosestFirst1"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed
distance2 = lambda x: 1
goalSwitch = 2
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
Note that we've put the goalSwitch to 2, so that if a robot comes across a pile it will always go for it. Now distance2 is still constant, so that distance doesn't play a role when starting at the CZ, but distance1 decreases for increasing distance, so that if a robot goes from searching to foraging, or switches goals during foraging due to its original goal being cleared, the robot gives more priority to piles nearby. We'll now show the rest of the settings files, which are basically explained above.
name = "ClosestFirst2"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed
distance2 = lambda x: 11.*speed/(1+x) #normal for x==10*speed
goalSwitch = 2
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
The next two will not take the number of victims at a pile into account
name = "ClosestFirst3"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed
distance2 = lambda x: 1
goalSwitch = 2
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
name = "ClosestFirst4"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed
distance2 = lambda x: 11.*speed/(1+x) #normal for x==10*speed
goalSwitch = 2
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
The next two make it less likely for a robot to go searching, so opting for rescuing known victims instead of looking for unknown victims faster
name = "ClosestFirst5"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed
distance2 = lambda x: 1
goalSwitch = 2
searchChoice = lambda bblen, nrob: min((20.*bblen)/(nrob),1)
name = "ClosestFirst6"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 2.*speed/(1+x) #normal for x==speed
distance2 = lambda x: 11.*speed/(1+x) #normal for x==10*speed
goalSwitch = 2
searchChoice = lambda bblen, nrob: min((20.*bblen)/(nrob),1)
The mean progress is shown in
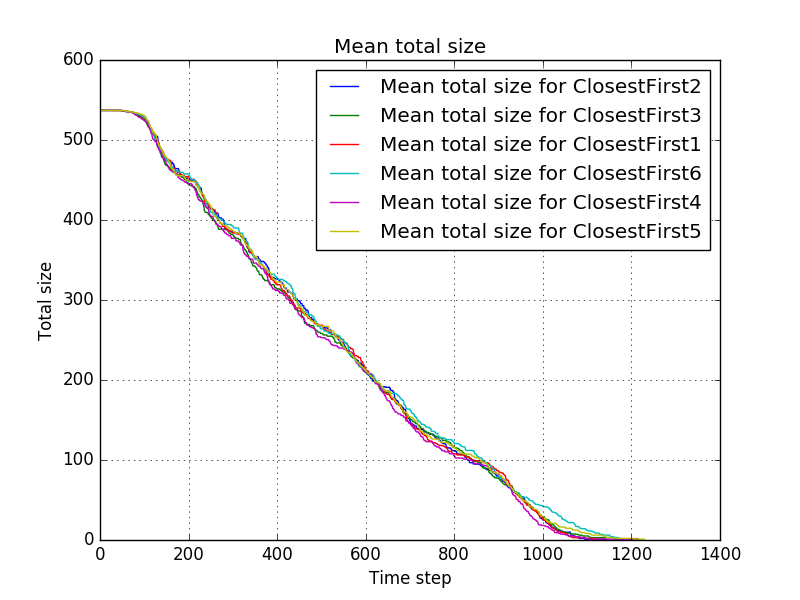
and the duration for the different settings is shown in
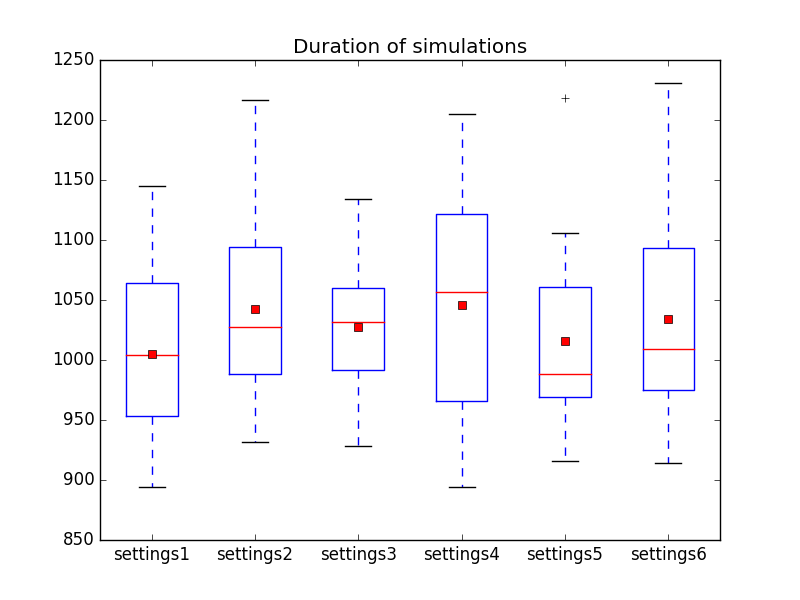
Which shows that going for the closest pile, especially when already in the field, yield much better results than in the previous two experiments. Taking distance into account when starting from the CZ seems however slightly worse than not doing so, although it might be so that this parameter needs some optimisation.
Dedication
Another stance one might take is that when you have committed to saving a certain person, you should stick to that goal, because that person is depending on you. In this experiment, this point of view is explored. The first settings are given by
name = "Dedication1"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) #normal (1) if z == 4
treshold = lambda x: max(1,5-x)
l=2
speed=6
distance1 = lambda x: 1
distance2 = lambda x: 1
goalSwitch = 1
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
where the goalSwitch is set to 1, meaning that even when a robot could go to another pile in just one step, it will keep going for its original goal. In the following settings we will experiment with the influence of the searchChoice, since for sticking to a goal to be justified, the goal must be set well informed, and also from the point of view that searching may be a task worth sticking to itself. We also again looked at the influence of taking the number of victims into account. Furthermore, to look into the reliability of an n=20 experiment, we ran another 20 simulations with the same settings as the first settings. We'll now list the divergence in settings from settings1:
name = "Dedication2" searchChoice = lambda bblen, nrob: min((20.*bblen)/(nrob),1)
making searching less likely
name = "Dedication3" searchChoice = lambda bblen, nrob: min((5.*bblen)/(nrob),1)
making searching more likely
name = "Dedication4" dropPile = lambda x,y,z:x+.05*y searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
not taking victims into account
name = "Dedication5"
The last settings are the same as the first.
The mean progress is shown by
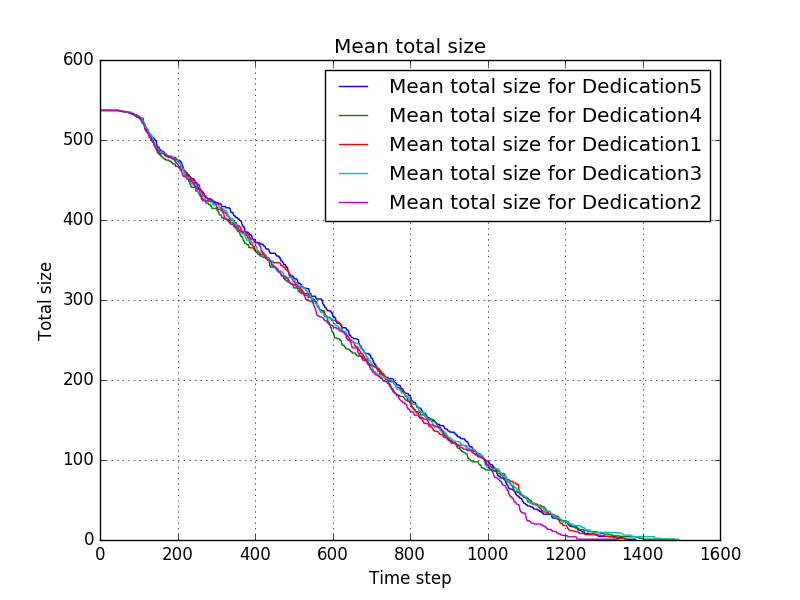
and the duration of the simulations by
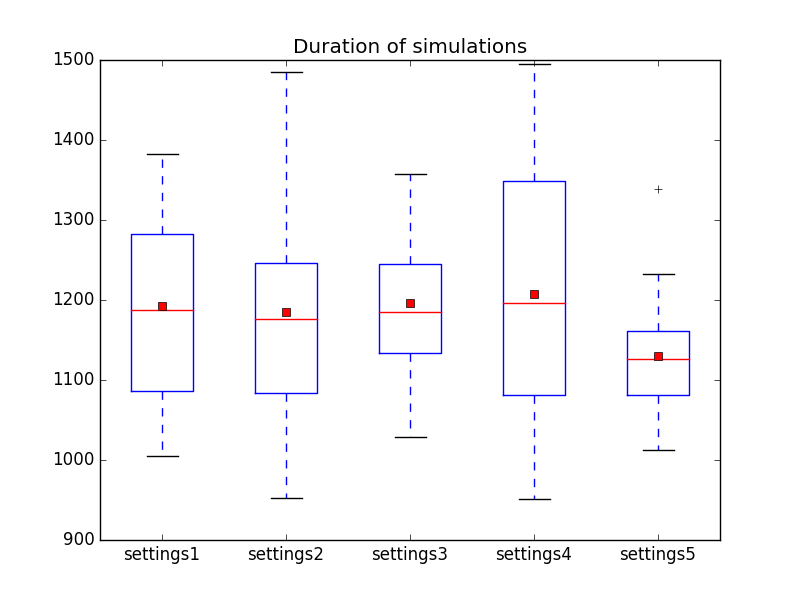
Which shows that the role of chance is still very large for such a small experiment.
Kant
In the last experiment, we look at what happens if one takes the stance that two humans aren't worth twice as much as one. Furthermore, we look into the influence of the threshold. Having a large threshold means that piles with little pheromones remain relatively likely to be picked by a robot. The first settings are given by
name = "Kant1"
size=(500, 500)
cz=(0,0)
nRobots=100
piles=[((100,200), (130,240), [1,1,6,3,1,10, 20, 11, 30],0),
((350,71), (400,120), [30,1,20,3,31,16, 12, 22],5),
((0,300),(100, 360),[21,24,33,2,32,33,34,35],3),
((390,380),(420,450),[1,1,2,4,2,30,2,20,13,10,20],1)]
obstacles=[((100,100),(200,200)), ((330,100),(340,200))]
evaporatePile = lambda x:.90*x
dropPile = lambda x,y,z:x+.05*y*(.2*z**.5 + .2) #grows sublinear
treshold = lambda x: 5
l=2
speed=6
distance1 = lambda x: 1
distance2 = lambda x: 1
goalSwitch = 0
searchChoice = lambda bblen, nrob: min((10.*bblen)/(nrob),1)
where the square root is chosen for its sub linear growth. Comparing this to the usual growth in the second settings
name = "Kant2" dropPile = lambda x,y,z:x+.05*y*(.2*z + .2)
and repeating for different thresholds
name = "Kant3" treshold = lambda x: 10
name = "Kant4" dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) treshold = lambda x: 10
name = "Kant5" dropPile = lambda x,y,z:x+.05*y*(.2*z + .2) treshold = lambda x: 1
The results are the following:
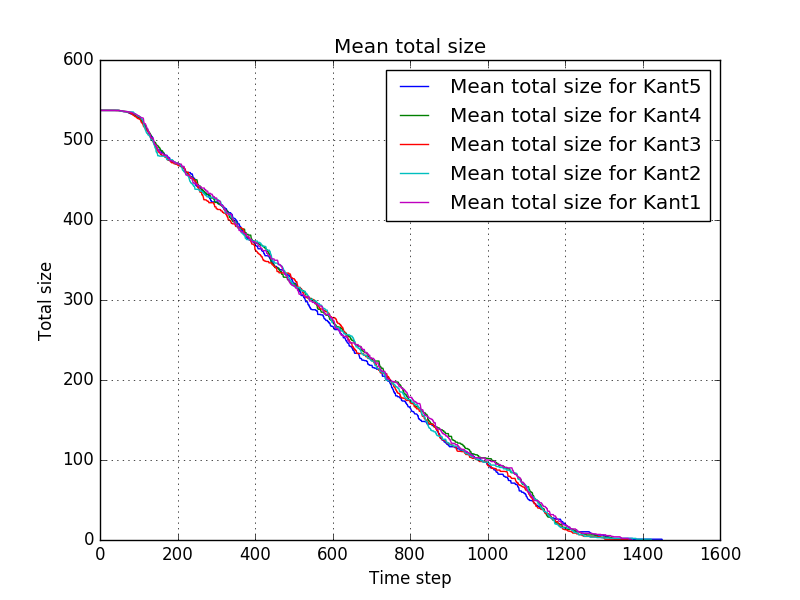
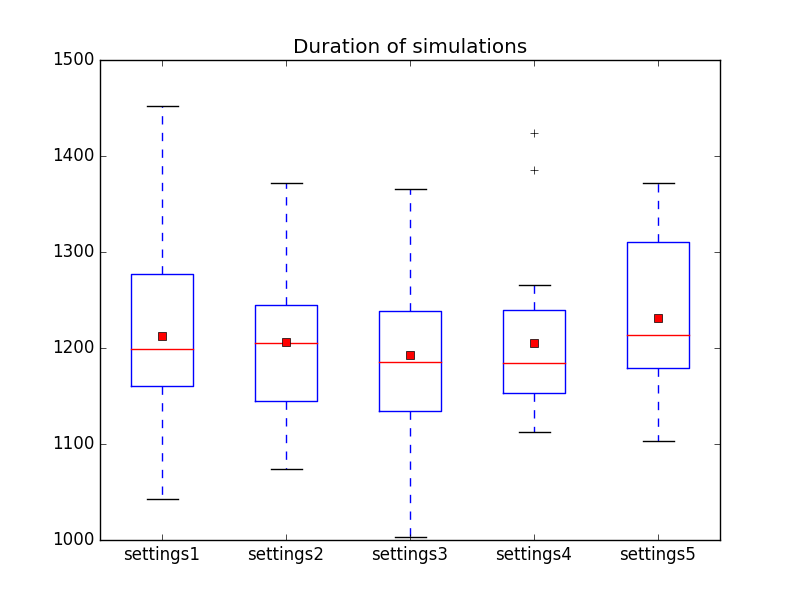
Showing no significant differences. More data is needed to draw conclusions from this experiment.
Conclusions and Recommendations
The above mainly shows two things:
- taking distance into account makes your rescue operation more efficient
- more data is needed to really investigate the influence of the other parameters
An important recommendation for this specific approach is fixing the flow for the Returning. Change it into
- Returning
- If a local message is received it tries to follow up on that message. If no message is received:
- The robot tries to go in a straight line towards the Clear Zone
- If that's not possible try continuing in the previous direction
- Whenever that's not possible choose left or right and go into that direction (deviating from the straight line towards the goal as little as possible)
- Also send a local message to all near robots that are returning to the CZ to go into that direction
the python code that would implement this would be very similar to the code in Foraging that does the same thing.
A more thorough revamp of the behaviour of the robots, which is highly recommended, would be to construct a graph representation of the world on the go, so that short paths can be remembered, and another (possibly ant colony based) swarm algorithm could than be used to find the actual shortest paths (within that graph).
Back to: PRE2015_2_Groep1